
First we consider the raw size of the password space, or in other
words, its information content assuming users are equally likely
to pick any element as their password. The raw size is an upper
bound on the information content of the distribution that users
choose in practice. We need some way to delimit the password space
in order to obtain a finite answer, or in probabilistic terms, a
way to ascribe probability zero to an infinite subset of
passwords, leaving a finite subset that we will count. We
assume that all passwords of total length (as defined in
Section 3.1) greater than some fixed
value have probability zero. We compute the size
![]() of the space of passwords of total length
less than or equal to
of the space of passwords of total length
less than or equal to ![]() on a grid of size
on a grid of size ![]() .
. ![]() is defined in terms of the number of passwords with
total length equal to L, P(L,G) by:
is defined in terms of the number of passwords with
total length equal to L, P(L,G) by:
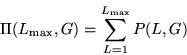
In turn, P(L,G) can be defined in terms of N(l,G), the number of strokes of length equal to l by:
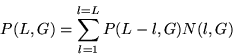
The following recurrence relation defines N(l,G). Let
n(x,y,l,G) be the number of strokes of length l ending at the
cell (x,y) in a grid of size ![]() . Then N can be
defined in terms of n by
. Then N can be
defined in terms of n by
![]()
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 5 | 10 | 14 | 19 | 24 | 29 | 33 | 38 | 43 | 48 | |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
| 53 | 58 | 63 | 67 | 72 | 77 | 82 | 87 | 91 | 96 |
The data in Table 1 shows that the raw size of
the graphical password space surpasses that of textual passwords
for reasonable password configurations. While these numbers are
encouraging, in practice not all graphical passwords are equally
likely to be chosen by users, rendering a uniform distribution
overly optimistic. For example, although the number of passwords
of length greater than or equal to 12 is already greater than the
number of textual passwords of 8 characters or less constructed
from the printable ASCII codes (![]() ), this includes
all possible combinations of twelve isolated dots.
), this includes
all possible combinations of twelve isolated dots.
In order to obtain a more realistic estimate of the information content, in the following section we suggest a model in which we characterize passwords as being ``memorable'' in terms of the programs which generate them.