
Consider an interface consisting of a rectangular grid of size ![]() . Each cell in this grid is denoted by discrete
rectangular coordinates
. Each cell in this grid is denoted by discrete
rectangular coordinates ![]() . Suppose
that the the user is given a stylus with which she can draw a
design on this grid. The drawing is then mapped to a sequence of
coordinate pairs by listing the cells through which the drawing
passes in the order in which it passes through them, with a
distinguished coordinate pair inserted in the sequence for each
``pen up'' event, i.e., whenever the user lifts the stylus from
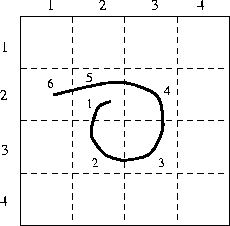
the drawing surface. For example, consider the drawing in
Figure 2. Here, the coordinate sequence
generated by this drawing is
. Suppose
that the the user is given a stylus with which she can draw a
design on this grid. The drawing is then mapped to a sequence of
coordinate pairs by listing the cells through which the drawing
passes in the order in which it passes through them, with a
distinguished coordinate pair inserted in the sequence for each
``pen up'' event, i.e., whenever the user lifts the stylus from
the drawing surface. For example, consider the drawing in
Figure 2. Here, the coordinate sequence
generated by this drawing is
(2,2), (3,2), (3,3), (2,3), (2,2), (2,1), (5,5)
where (5,5) is the distinguished ``pen up'' indicator. If there were a second stroke in this example, then its sequence would be appended to the end of the sequence above, and similarly for subsequent strokes. In this way, we divide the space of possible drawings into equivalence classes, two drawings being equivalent if they have the same encoding, or in other words if they cross the same sequence of grid cells, with the breaks between strokes occurring in the same places.
 |
First we give some terminology. We define the neighbors,
![]() , of a cell (x,y) to be the subset of the
set of cells
, of a cell (x,y) to be the subset of the
set of cells ![]() whose
elements exist in the grid. We then define a stroke to be a
sequence of cells
whose
elements exist in the grid. We then define a stroke to be a
sequence of cells ![]() , in which
, in which ![]() , and which does not contain a ``pen up'' event. A
password is then defined to be a sequence of strokes separated by
``pen up'' events. The length of a stroke is the number of
coordinate pairs it contains, while the total length of a password
is the sum of the lengths of its component strokes (excluding the
``pen up'' characters).
, and which does not contain a ``pen up'' event. A
password is then defined to be a sequence of strokes separated by
``pen up'' events. The length of a stroke is the number of
coordinate pairs it contains, while the total length of a password
is the sum of the lengths of its component strokes (excluding the
``pen up'' characters).
As with the scheme of Section 2, this scheme is most viable if the user's strokes are echoed as curves while they are drawn. Again we appeal to the maneuverability of the devices we are targeting (i.e., PDAs) to support the restriction that the user must shield the input display from onlookers.
Our requirement of repeatability constrains the parameters of this scheme. As long as the user's current drawing lies in the same equivalence class as the original drawing, she has successfully repeated a chosen password. In general, this gives the user sufficient tolerance when (involuntarily) varying the drawing, provided that the cells of the grid are not too small. Indeed, this was the purpose of separating the drawings into equivalence classes to begin with. Difficulties might arise however, when the user chooses a drawing that contains strokes that pass too close to a grid-line. In those cases, the user might vary the drawing in such a way as to change the resulting sequence of coordinates. There are at least two solutions to this problem: (1) The user is offered to view the internal representation, depicting the path of cells, when she chooses a password so that she can confirm which cells were actually touched by the drawing. (2) The system does not accept a drawing which contains strokes that are located ``too close'' to a grid line. In the implementation, described in Section 3.2, we offer both alternatives.