 |

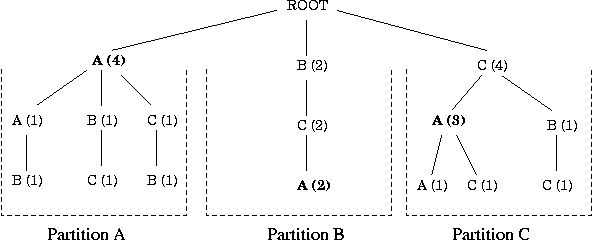
To address the space requirements of FMOCM, we developed the Partitioned Context Model. This model divides the trie into partitions, where each partition consists of a first order node and all of its descendants. The number of nodes in each partition is limited to a static number that is a parameter of the model. The effect of these changes is to reduce the model space requirements from O(nm) to O(n). Figure 3 shows the trie from Figure 2 with these static partitions.
When a new node is needed in a partition that is full, all node counts in the partition are divided by two (integer division), any nodes with a count of zero are cleared to make space for new nodes. If no space becomes available, the access is ignored. Another benefit of restricting space in this manner is that when new access patterns occur, existing node counts decay exponentially, causing the model to adapt faster to new access patterns. While PCM solves the space problem, our experiments showed that it did not predict far enough into the future to give time for the prefetch to complete, so we developed EPCM.