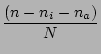|
SRUTI '05 Paper
[SRUTI '05 Technical Program]
Analyzing Cooperative Containment of Fast Scanning Worms
Jayanthkumar Kannan, Lakshminarayanan Subramanian, Ion Stoica, and
Randy H. Katz
Computer Science Division, University of
California, Berkeley
{kjk, lakme, istoica, randy}@cs.berkeley.edu
Abstract:
Fast scanning worms, that can infect nearly the entire vulnerable
population in order of minutes, are among the most serious threats to
the Internet today. In this work, we investigate the efficacy of
cooperation among Internet firewalls in containing such worms. We
first propose a model for firewall-level cooperation and then study
the containment in our model of cooperation using analysis and
simulation. Our results suggest that, with moderate overhead,
cooperation among Internet firewalls can provide 95% containment
under 10% deployment while being resilient to 100-1000 malicious
firewalls.
Scanning worms that probe IP addresses to find vulnerable hosts are
the most common worms today. Several recent worms, such as Slammer,
Witty, CodeRed, and Blaster, fall in this category. Slammer, one of
the fastest scanning worms seen so far, took less than 10 minutes to
infect 90% of the Internet's vulnerable population
[1]. Scanning worms that are more carefully designed
using techniques discussed in [2] can accomplish
infection even faster. This threat is further acerbated by the
possibility of worms that exploit unknown vulnerabilities. It is clear
that automatic mechanisms are required to defend against these worms.
Unfortunately, many existing defenses, like patching and address
blacklisting, hold out little hope in containing novel fast worms
[3].
An emerging approach that offers hope in containing such worms is a
decentralized solution in which firewalls in various access networks
exchange information amongst themselves to defend against worm
attacks. Such a scheme may be easier to deploy compared to end-host
based schemes [4,5,6], schemes
that may require support from core routers [7,8], or schemes that place the burden of analysis on a
centralized infrastructure [9,10]. Recent
work [11,12,13,14] suggests that such cooperation may contain fast
worms, but an understanding of its efficacy and limitations on
robustness is still lacking.
In this paper, we aim to fill this void by modeling cooperation in a
abstract fashion, and then studying the containment in this model. In
our model, the participants in the cooperative are Internet firewalls,
each protecting an access network. Each firewall employs local
detection to detect infection within its network. Once it detects an
infection, it notifies other firewalls of the ongoing worm
infection. We consider two forms of such notifications: implicit
and explicit signaling. Firewalls that receive these signals are
alerted to the worm attack and can then filter their incoming
traffic based on these signals. Signaling between firewalls is the
essence of cooperation, and our model of signaling captures and
extends the salient features of existing schemes for
cooperation. Moreover, this model integrates various known techniques
for local detection [15,11,16] and
filtering [17,5,4] into a framework
for cooperation.
Our analytical results based on this model are as follows. First, we
show that local detection and filtering without any signaling can
contain scanning worms under certain regimes. Second, we characterize
the dependence of the containment provided by cooperation on various
worm and cooperation parameters. Our results indicate that the
containment offered by cooperation drops linearly with the scan rate
of the worm and the average time taken by the firewall to detect
infection, and drops quadratically with the size of the vulnerable
population. Third, our analysis quantifies the trade-off between the
containment offered by cooperation and robustness to malicious
participants. Our numerical results suggest that, even against the
most virulent worm seen so far, cooperation among Internet firewalls
can offer over 95% containment under 10% deployment while being
resilient to about 100-1000 malicious firewalls.
Although we primarily study Internet-level cooperation among firewalls
to contain scanning worms, our analytical approach can be applied to
other scenarios as well: to enterprise-level or Internet-level
cooperation, to host-level or firewall-level cooperation, and to a
limited extent for analyzing sophisticated worms like hit-list based
worms. The downside of our analytical approach however is that there
are inherent limitations in any tractable model amenable to
analysis. Such a model, by necessity, cannot include all ``real-life''
details. Our model includes the main factors characterizing a worm
attack and we use simulations to incorporate the effect of other
factors in our results.
2 Modeling Cooperation
We consider the Internet to consist of N access networks that are
connected to their ISPs through an access link. Each network is
monitored by a firewall which analyzes traffic on its access link and
exchanges information with other firewalls to contain worms. We focus
on containment of fast random scanning worms in this work. Such worms
perform a local topological scan followed by a global uniform random
scan: an infected host first infects all hosts in its network and then
probes external IP addresses uniformly at random to find more
vulnerable hosts. Note that, in our model, a firewall cannot prevent
infection from spreading within its network, since it may not even see
local topological scans.
The main goal of cooperation is to maximize the containment metric
C, defined as the fraction of vulnerable networks that escape
infection during a worm attack. Other desirable features of a
cooperative containment scheme include resistance to malicious
participants, effectiveness under partial deployment, and scalability
(e.g., bandwidth overhead). We now describe our model of cooperation.
2.1 Framework for Cooperation
The main purpose of this framework is to define the design space of
cooperation schemes in a simple manner suitable for analysis. Some
points in this space correspond to existing schemes [18,12,11,13,19].
We begin by making two assumptions, which we will remove later: (a)
all firewalls operate according to our protocol (b) all firewalls in
the Internet participate in our cooperative. Firewalls participating
in the cooperative perform three functions: local detection,
propagation, and filtering.
Local Detection: A firewall uses local detection
to determine whether its own network is infected by analyzing outgoing traffic. There are two advantages in analyzing outgoing
traffic as opposed to analyzing incoming traffic. A firewall can
maintain characteristics of its outgoing traffic using per-host state,
unlike incoming traffic which can be noisy due to background Internet
traffic. Also, a decision made using incoming traffic can potentially
be influenced by external malicious hosts sending traffic to the
firewall's network.
However, analyzing outgoing traffic cannot aid a firewall in
protecting its own network, since the characteristics of
outgoing traffic change only after its network is infected. We
use the term ``detected firewall'' to denote a firewall whose local
detection scheme identifies infection within its network.
One can use existing techniques [15,11,20,5] for local detection. These techniques
identify infection by analyzing various characteristics of outgoing
traffic, e.g., number of unique destination addresses, connection
failure rate, and packet payload.
Propagation: A detected firewall proceeds to
notify other firewalls of its infection. These notifications include
filters for identifying malicious packets. On receiving these
notifications, these firewalls are said to be ``alerted'' to the
attack. There are two forms of such notifications: implicit and
explicit.
Implicit Signaling: A detected firewall sends
implicit signals by marking all suspicious outgoing
packets. Suspicious packets are identified using filters inferred by
the filtering mechanism. Marking can be done by using bits in packet
headers or by encapsulating suspicious packets within special
headers. This marking serves two purposes. First, it informs the
destination firewall that the packet is possibly malicious. The
destination firewall can simply drop such packets or it can process
them in a special manner (e.g., send it to a hardened end-host for
analysis). Thus, the decision to drop/process is delegated to the
destination. Second, the destination firewall is notified that the
source network is infected. This enables the destination firewall to
install filters before its own network gets infected: this is the
essence of cooperation.
Explicit Signaling: A detected firewall sends
explicit notifications of its infection to other participating
firewalls at some fixed rate E. We only consider schemes where
signals are sent to randomly chosen participating firewalls. This
naive method can easily be improved by, say, a publish-subscribe based
system; however the security properties of such systems are harder to
characterize.
In both types of signaling, note that a firewall can report only of
its own infection; it cannot implicate other firewalls. This
rules out setup attacks in which malicious firewalls make false
accusations. We use a challenge-response protocol to verify that the
originator of a signal is the infected firewall itself. Such a
protocol also eliminates spoofing attacks by malicious end-hosts.
Filtering: We refer to a firewall that has been
alerted by a signal as an alerted firewall. Such a firewall
installs filters and drops malicious incoming traffic matching
these filters. These filters are gathered from the signals it
receives. Filtering is also used by a detected firewall during
implicit signaling: only outgoing packets identified as malicious by
the filter are marked.
A very simple filter could be based on port numbers: any traffic on
alerted ports is dropped. More sophisticated filters can be inferred
using known techniques, such as Autograph [17] which
deduces signatures from packet payloads, and Vigilante
[5], TaintCheck[4], which infer
signatures by host-based mechanisms to track the flow of network data
in a program.
To summarize, in our scheme, every firewall is in one
of the following four states: normal, alerted, infected, and
detected. Our model can also be extended to the case when multiple
worms may be propagating. The filtering mechanism would infer filters
for each propagating worm, and firewalls can maintain state and
perform propagation on a per-worm basis.
We now discuss the security of our model against malicious firewalls
and evasive worms. First, in a cooperative framework, it is important
to distinguish between a global Internet-wide attack and an infection
localized to a small set of networks. Thus, if a small number of
firewalls report that they have been infected, even if they are being
truthful, this attack could simply be a localized one. Thus, a
fundamental necessity in the cooperative framework is that a firewall
should enter the alerted stage and install filters only if it receives
signals from T distinct firewalls. Second, it is also necessary to
defend against firewalls attempting to trigger false
positives/negatives. Since the alerted state is entered only upon
receiving T signals, our scheme can resist up to T malicious
firewalls that trigger a false alarm. This design choice is also
fundamental since it may be impossible to detect whether a
notification sent by a firewall is a false alarm (e.g., if a firewall
originates traffic as if its own network had been infected).
False negatives occur when a firewall deliberately/otherwise fails to
report of its infection. We have also devised schemes to defend
against such attacks [21], although we do not discuss
them here.
Finally, cooperation should also be resilient to sophisticated worms
that attempt to evade propagation (worms that evade local detection
and filtering are beyond our scope). A worm could use pre-generated
hit-lists [2] to ensure that most of its probes are
successful, and also alter its scanning pattern over time to thwart
propagation. In the limit, a worm could simply stop scanning after
its firewall has entered the detected stage, since beyond this point,
all its scans will be marked and cannot infect any new hosts. In this
case, implicit signaling is completely ineffective. Explicit signaling
will however continue to perform well. We consider such a worm in
Section 4.2.
Under partial deployment, the main limitation of our model is that it
is not possible to prevent undeployed networks from getting infected
eventually, since infected hosts in undeployed networks can always
infect other undeployed networks. This limitation cannot be overcome
without support from core routers. We therefore choose our metric for
the partial deployment case as the containment among the deployed firewalls. As a baseline solution, our existing scheme for
propagation works in this case as well. Only deployed firewalls
perform detection and propagation: undeployed firewalls do not engage
in local detection, propagation, or filtering. We also improved on
this scheme using a technique called rerouting discussed in
[21]; we omit details due to lack of space.
There are three salient features in our model of cooperation. First,
in our model, signals can be verified using a challenge-response
mechanism. This makes the security properties of our model much easier
to characterize as compared to existing work [14,13]. Second, our model incorporates both forms of signaling,
implicit and explicit, whereas existing work has dealt mainly with
explicit signaling. There are trade-offs associated with both
approaches; implicit signaling has lesser overhead and may be simpler
to implement, but explicit signaling is necessary to contain smart
worms. Finally, our model integrates the various techniques proposed
for local detection and filtering in a framework for
cooperation. Decoupling the various mechanisms used in cooperative
containment also aids analysis, as will be seen in the following
section.
3 Analyzing Cooperation
In this section, we analyze the containment metric C (the fraction
of vulnerable networks that escape infection) of our cooperative model
under three cases: all firewalls are deployed and operate according to
the protocol (Section 3.2,
3.3,3.4), all
firewalls are deployed but some of them may be malicious
(Section 3.5), and finally under partial
deployment (Section 3.6).
We now introduce the assumptions and the parameters used in our
analysis (parameter names are in bold type). In our worm model, an
infected host first infects all vulnerable hosts in its own network in
zero time, and then proceeds to probe external addresses. The
scanning rate of a fast worm is limited by access bandwidth, and hence
we use the scanning rate ``s'' of a single infected
network in our analysis. The probability of a successful probe ``p'' is the number of vulnerable hosts divided by the size of the IP
address space. We denote the total number of vulnerable networks as
``N''. We use the homogeneous cluster model, used for modeling
Slammer victims in [1]. This assumes that the vulnerable
hosts are uniformly distributed among all vulnerable networks.
For purposes of analysis, we assume that the time taken for an
infected firewall to detect its infection is an exponential variable
with mean ``
td''. This assumption is certainly not
true for all local detection schemes, but considerably simplifies the
analysis. Thus, our model includes several simplifications, such as
the uniform distribution of vulnerable hosts. In the following
results, the environment used for simulation exactly matches the one
used in analysis, and thus, the simulation only serves as a validation
for the analysis. We also simulated environments with non-uniform host
distributions and network delays, and obtained similar results (not
presented here for lack of space).
3.2 Effectiveness of Detection and Filtering
First, we analyze a simplified variant of our scheme without any
propagation under complete deployment. Thus, there is no sharing of
information between firewalls. In this variant, a firewall performs
only local detection and filtering (once a firewall enters the
detected stage, outgoing scans are marked and cannot infect any more
hosts). Thus, the defense against a worm attack is that an infected
host can effectively probe only until its firewall does not detect
infection. The following lemma shows that such a simplified scheme is
surprisingly effective under some conditions. We define 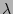 as
the expected value of the number of successful infections by an
infected network before its firewall detects infection. as
the expected value of the number of successful infections by an
infected network before its firewall detects infection. 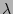 can
be written in terms of our parameters as can
be written in terms of our parameters as
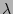 = sptd. We now
state the following lemma without proof (for all proofs, see our
technical report [21]). = sptd. We now
state the following lemma without proof (for all proofs, see our
technical report [21]).
If
(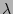 < 1), then as
N < 1), then as
N 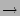 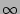 , the containment metric
C , the containment metric
C 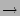 1. Further, if I0
denotes the number of infected firewalls at time t = 0, for any N,
C 1. Further, if I0
denotes the number of infected firewalls at time t = 0, for any N,
C 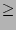 1 - 1 - 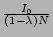 . .
Interestingly, the above lemma holds irrespective of
the scanning strategy employed by the worm. The condition 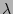 < 1
can be enforced by deploying firewalls at as fine a granularity as
necessary. This can be used to control the effective scanning rate s
and thus the parameter < 1
can be enforced by deploying firewalls at as fine a granularity as
necessary. This can be used to control the effective scanning rate s
and thus the parameter 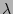 . Earlier worms like Blaster had low
scan rates leading to low values of . Earlier worms like Blaster had low
scan rates leading to low values of 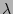 , and could have been
controlled by simple detection and filtering even if the firewalls
were deployed at the level of class B networks. Recent worms like
Slammer used much higher scan rates and require very fine grain
deployment to enforce , and could have been
controlled by simple detection and filtering even if the firewalls
were deployed at the level of class B networks. Recent worms like
Slammer used much higher scan rates and require very fine grain
deployment to enforce 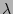 < 1. < 1.
Surprisingly, even if
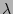 > 1, detection and filtering still
provide some containment against a random scanning worm,
although the effectiveness degrades rapidly with > 1, detection and filtering still
provide some containment against a random scanning worm,
although the effectiveness degrades rapidly with 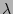 . The reason
this occurs is that as the infection proceeds, it takes longer for a
random scanning worm to find uninfected hosts, and thus the local
detection schemes have a greater chance of throttling the infection. . The reason
this occurs is that as the infection proceeds, it takes longer for a
random scanning worm to find uninfected hosts, and thus the local
detection schemes have a greater chance of throttling the infection.
If
(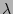 > 1), assuming I0 > 1), assuming I0 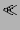 N,
C N,
C 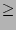 1 - 1 - 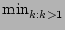 ( (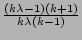 - - 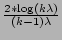 ) against a
random scanning worm (k is a variational parameter used in
minimization). ) against a
random scanning worm (k is a variational parameter used in
minimization).
Our analytical results based on the above lemma
indicate that detection and filtering provide about 40% containment
at
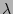 = 1.5 and about 20% at = 1.5 and about 20% at
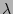 = 2.0. We show later that = 2.0. We show later that
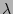 = 2.0 corresponds to the one of the most virulent worms seen
so far. = 2.0 corresponds to the one of the most virulent worms seen
so far.
3.3 Effectiveness of Implicit Signaling
In this section, we analyze the containment metric when implicit
signaling is used along with detection and filtering under complete
deployment. Denote the total number of deployed firewalls as n. We
model the infection process as follows.
At time t, denote by ni(t) the number of infected firewalls, by
nd(t) the number of detected firewalls, and by na(t) the number
of alerted firewalls (the remaining firewalls are in the ``normal''
state). Note that ni(t) represents all infected firewalls, so
ni(t) - nd(t) is the number of infected firewalls that have not yet
detected infection.
A simple differential equation model for implicit signaling is as
follows:
 (ni) (ni) |
= |
(ni - nd) x s x 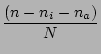 |
(1) |
 (nd) (nd) |
= |
 |
(2) |
 (na) (na) |
= |
nd x s x 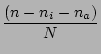 |
(3) |
The first and third equations count the number of successful scans and
alerts per unit time respectively. The second equation is based on the
assumption of an exponential distribution for detection: the
probability that an infected and undetected network identifies
infection during time dt is equal to dt/td.
We could not solve these equations exactly, so we present a
closed-form upper bound:
For
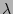 > 1 and I0 > 1 and I0  N, with implicit signaling,
C N, with implicit signaling,
C 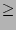 1 - 1 - 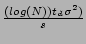 ( (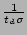 + 1) where + 1) where
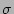 = ( = (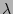 -1)/td and -1)/td and
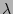 = pstd. = pstd.
By substituting for 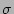 in the region in the region 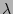 > 1, the above
lemma suggests that the containment metric decreases linearly with
td and s and drops quadratically with p. > 1, the above
lemma suggests that the containment metric decreases linearly with
td and s and drops quadratically with p.
3.4 Effectiveness of Explicit Signaling
In the case of explicit signaling at rate E along with implicit
signaling, the containment metric can be obtained by simply
substituting s = s + E in the denominator of Lemma 3
to obtain
C 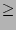 1 - 1 - 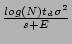 ( (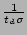 + 1).
Notice that the containment metric varies with the rate of explicit
signaling as 1/(1 + E/s). + 1).
Notice that the containment metric varies with the rate of explicit
signaling as 1/(1 + E/s).
3.5 Effectiveness under Threshold T
In this case, a firewall enters the alerted state after receiving
alerts from T distinct firewalls. Our differential equation model in
Section 3.3 can be extended to model this
case by adding (T + 1) differential equations to track the number of
firewalls that have received
0, 1,...,(T - 1), T alerts. This
approach is however cumbersome even for low values of T. However,
the lower bound on containment metric for the implicit signaling case
(Lemma 3) can be applied to obtain:
For
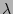 > 1 and I0 > 1 and I0 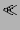 N, the containment metric C
obtained by implicit signaling is at least
1 - N, the containment metric C
obtained by implicit signaling is at least
1 - 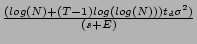 ( (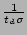 + 1) where + 1) where
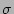 = = 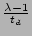 . .
The main implication of this result is that the containment drops
linearly with the threshold T. This quantifies the trade-off between
the robustness of cooperation and the containment C.
3.6 Effectiveness under Partial Deployment
The differential equation model in Section
3.3 can be suitably modified by introducing
a differential equation for the number of infected undeployed
firewalls at time t. Unfortunately, we could not obtain a
closed-form analytical bound (as in the complete deployment case). We
numerically solve our differential equation model to evaluate
cooperation under partial deployment.
We now evaluate the containment offered by cooperation against worms
of varying virulence and how this containment depends on the various
mechanisms used in cooperation. Our results are obtained by two
means: (a) numerical integration of the differential equation model
(b) discrete-time event simulation to validate the analytical method
(marked ``Sim'' in our plots). The number of initial infected networks
is set to 10 by default, and the simulation is run until all the
networks are infected/alerted.
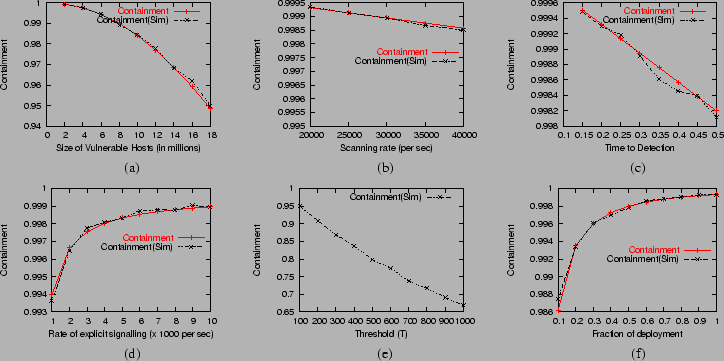
Figure:
(a) Containment Vs. Size of vulnerable
population (b) Containment Vs. Scanning Rate (c) Containment
Vs. Time to detection (d) Containment Vs. Rate of Explicit
Signaling (e) Containment Vs. Threshold T (f) Containment
Vs. Deployment
 |
In the following results, the default parameters are as follows. We
used p = 0.0005 corresponding to a vulnerable population of about 2
million, twice that of Blaster, one of the most wide-spread worms. We
set the scanning rate s as 20000 (the average scan rate of Slammer
[1], one of the fastest worms so far). Thus, these
settings correspond to one of the most virulent worms seen yet. The
number of firewalls N was set to 100000 based on the number of
observed BGP prefixes (obtained from routeviews.org). Thus, every
network has an address space of 215 and about 20 vulnerable
hosts. Under these settings, the worm takes 0.6 seconds to infect
99% of all vulnerable hosts, assuming no network congestion. We
set
td = 0.2s in our analysis and use implicit signaling for
propagation. By default, we assume all networks are deployed. Note
that
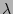 = 2 under these settings, so as per
Lemma 2, signaling is necessary for containment
under these settings. = 2 under these settings, so as per
Lemma 2, signaling is necessary for containment
under these settings.
4.2 Varying Worm Virulence
We present results corresponding to three axes of worm virulence in
order to evaluate the performance of cooperation against known worms
and worms of the future.
Number of Vulnerable Hosts: The size of the
vulnerable population is a key parameter of worm virulence, and we
plotted the containment metric against this parameter in
Figure 1(a). The number of vulnerable networks was
kept constant, and the vulnerable population size was varied between
2 and 20 million hosts (corresponding to
p = 0.0005 - 0.005). As
suggested by the analysis, there is roughly a quadratic drop in C
with p.
Scanning Rate: Figure 1(b)
plots the containment metric against the worm scanning rate, since the
propagation time of the worm is also influenced by this rate. The
containment metric exhibits a slow linear drop with scanning rate of
the worm. Since implicit signals are piggybacked on worm scans, faster
the worm scanning rate, greater the effective signaling rate as well.
Number of Initial Seeds: Our analytical bounds
assume that the set of hosts used to seed the infection is a small
subset of the vulnerable population. This assumption may not be true
if botnets (networks consisting of already infected zombie hosts) are
used to seed a worm attack, given that botnets of up to 50000 hosts
have been discovered. At one extreme, if all these hosts are in
different networks, our results indicate 48.63% containment. At the
other extreme, either all hosts within a network belong to the botnet
or none of them do. In our settings, each network has 20 vulnerable
hosts, which means that 2500 networks are under attacker control. In
this case, cooperation provides 96.88% containment.
This section presents results illustrating the impact of detection
time td, signaling parameters (explicit signaling rate E and
threshold T), and level of deployment, on containment.
Local Detection: Figure 1(c)
illustrates the sensitivity of cooperation to local detection. As
suggested by the analysis in the previous section, the dependence is
roughly linear. Though the worm propagates in about 0.6s, even with
time to detection td as high as 0.5s, cooperation performs very
well. This might appear surprising, but note that 0.5s seconds is
the mean time to detection, and with a finite probability,
detection occurs before 0.5s.
Rate of Explicit Signaling: The rate of
explicit signaling corresponds to the overhead of cooperation, and we
plotted containment metric obtained through explicit signaling for
varying rates E (100-10000) in Figure 1(d). In
obtaining this plot, only explicit signaling is used. The containment
metric improves with the ratio E although the variation is very low.
Threshold T: Since the security of the scheme
is determined by the threshold T (number of alerts required to
transition to the alerted state), in Figure 1(e), we
varied the threshold T from 100 to 1000 firewalls (0.1% to
1.0% of the total number of firewalls). Since the differential
equation model is cumbersome for threshold T  1, we show only the
results obtained through simulation. The containment drops by as much
as 30%, and clearly T is the most sensitive of all the parameters
we have considered so far. This means that in our model, cooperation
is resilient to a small fraction of malicious firewalls, but cannot
deal with large scale collusion (for example, when the worm infects
firewalls). 1, we show only the
results obtained through simulation. The containment drops by as much
as 30%, and clearly T is the most sensitive of all the parameters
we have considered so far. This means that in our model, cooperation
is resilient to a small fraction of malicious firewalls, but cannot
deal with large scale collusion (for example, when the worm infects
firewalls).
Level of Deployment:
Figure 1(f) shows the containment obtained under
various levels of deployment. Cooperation continues to perform well
even at deployment levels as low as 10%. The reason is that as soon
as a certain fraction of deployed firewalls are infected, the
propagation of alerts outpaces the worm scan rate.
5 Related Work
We classify related work into three main categories. The first
includes works that analyze traffic at an end-host or a single
observation point to detect worm attacks, e.g.,
Vigilante [5], Throttling [15],
TaintCheck [4], Threshold random walks
[16,20],
Honeypot-based architectures. Any of these proposals can serve as a
local detection scheme in our model (in a firewall or host-based
cooperative). In general, host-based mechanisms can detect a wider
class of worms, but involve a heavy deployment cost. The second
category relies on inferring and deploying filters to contain worms
e.g., Autograph [17], Dynamic
Quarantine [7]. Filter placement within the
Internet core is necessary for most of these schemes. In contrast,
existing mechanisms for inferring filters can be used as filtering
mechanisms in our model to achieve good containment without modifying
core routers.
The final category relates to proposed architectures for worm
containment involving multiple vantage points. Architectures, such as
[9], perform distributed data collection followed by
centralized analysis. Decentralized designs include Hard
Perimeters [11], Weaver et
al [12], Domino [18]. In
[11,12], data collection and
analysis are performed by firewalls, while [18] splits these
functionalities between satellites and an axis overlay. All
participants are implicitly trusted in these proposals. Our model
accomodates malicious participants by using simple verification along
with a thresholding mechanism. Nojiri et al [13]
handles malicious participants, but unlike our model, assumes the
existence of apriori trust relationships among firewalls. Anagnostakis
et al [14] proposes a signaling protocol very similar
to our explicit signaling, but their focus is more on multiple
propagating worms as against fast worms. Finally, Staniford et
al [22] proposes an analytical model for worm
containment, which however does not study cooperative containment.
6 Conclusion
In this work, we have discussed a framework for modeling cooperation
in order to conduct a preliminary analysis of its efficacy, resilience
and deployability. This framework is intended to be as general as
possible, and to capture and extend the notion of cooperation proposed
in recent work. The advantage of analyzing a general framework is that
our results can be applied to cooperation in a wide-variety of
scenarios: at the enterprise-level or Internet-level, at the
host-level or firewall-level, and also to a limited extent for
analyzing sophisticated worms like hit-list based worms. Our analysis
can be used to decide if cooperation is necessary, and if so, can help
tune local detection and signaling.
In an Internet-level cooperative of firewalls, our results indicate
that cooperation can indeed be an effective solution to containing
fast uniform scanning worms, and may also be effective against more
sophisticated worms of the future. Cooperation can be made resilient
to a small number of malicious participants (100-1000), and even
at low levels of deployment (about 10%), effective containment can
be achieved. As part of future work, we are working on hybrid
protocols that use implicit signaling in the early stages of a worm,
and switch to explicit signaling beyond a threshold.
- 1
-
N. Weaver, I. Hamadeh, G. Kesidis, and V. Paxson,
``Preliminary results using scaledown to explore worm dynamics,''
in Proc. ACM CCS WORM, Oct 2004.
- 2
-
Stuart Staniford, Vern Paxson, and Nicholas Weaver,
``How to Own the Internet in Your Spare Time,''
in Proc. USENIX Security, Aug 2002.
- 3
-
David Moore, Colleen Shannon, Geoffrey M. Voelker, and Stefan Savage,
``Internet quarantine: Requirements for containing self-propagating
code,''
in Proc. INFOCOM, Apr 2003.
- 4
-
James Newsome and Dawn Song,
``Dynamic taint analysis for Automatic Detection, Analysis, and
Signature Generation of Exploits on Commodity Software,''
in Proc. NDSS, Feb 2005.
- 5
-
Manuel Costa, Jon Crowcroft, Miguel Castro, Antony Rowstron, Colleen Shannon,
and Jeffery Brown,
``Can we contain Internet worms?,''
in Proc. HOTNETS, Nov 2004.
- 6
-
Christina Warrender, Stephanie Forrest, and Barak A. Pearlmutter,
``Detecting intrusions using system calls: Alternative data models,''
in IEEE Symposium on Security and Privacy, May 1999.
- 7
-
Cynthia Wong, Chenxi Wang, Dawn Song, Stan Bielski, and Gregory R. Ganger,
``Dynamic Quarantine of Internet Worms,''
in Proc. DSN, Jun 2004.
- 8
-
V. Berk, G. Bakos, and R. Morris,
``Designing a framework for active worm detection on global
networks,''
in IEEE Intl Workshop on Information Assurance, Mar 2003.
- 9
-
Nicholas Weaver, Vern Paxson, and Stuart Staniford,
``Wormholes and a Honeyfarm: Automatically Detecting Novel Worms,''
in DIMACS Large Scale Attacks Workshop, Sep 2003.
- 10
-
J. Wu, S. Vangala, L. Gao, , and K. Kwiat,
``An Effective Architecture and Algorithm for Detecting Worms with
Various Scan Techniques,''
in Proc. NDSS, Feb 2004.
- 11
-
Nicholas Weaver, Dan Ellis, Stuart Staniford, and Vern Paxson,
``Worms vs Perimeters: The Case for HardLANs,''
in Proc. Hot Interconnects, Aug 2004.
- 12
-
Nicholas Weaver, Stuart Staniford, and Vern Paxson,
``Very Fast Containment of Scanning Worms,''
in Proc. USENIX Security, Aug 2004.
- 13
-
D. Nojiri, J. Rowe, and K. Levitt,
``Cooperative Response Strategies for Large Scale Attack
Mitigation,''
in Proc. DISCEX, Apr 2003.
- 14
-
K. G. Anagnostakis, M. B. Greenwald, S. Ioannidis, A. D. Keromytis, and D. Li,
``A Cooperative Immunization System for an Untrusting Internet,''
in Proc. ICON, Oct 2003.
- 15
-
J. Twycross and M. M. Williamson,
``Implementing and testing a virus throttle,''
in Proc. USENIX Security, Aug 2003.
- 16
-
Jaeyeon Jung, Vern Paxson, Arthur W. Berger, and Hari Balakrishnan,
``Fast portscan detection using sequential hypothesis testing,''
in Proc. IEEE Security and Privacy, May 2004.
- 17
-
H. A. Kim and B. Karp,
``Autograph: Toward automated, distributed worm signature
detection,''
in Proc. Usenix Security, Aug 2004.
- 18
-
Vinod Yegneswaran, Paul Barford, and Somesh Jha,
``Global Intrusion Detection in the Domino Overlay System,''
in Proc. NDSS, Feb 2004.
- 19
-
C. G. Senthilkumar and K. Levitt,
``Hierarchically Controlled Co-operative Response Strategies for
Internet Scale Attacks,''
in Proc. DSN, June 2003.
- 20
-
Stuart E. Schechter, Jaeyeon Jung, and Arthur W. Berger,
``Very Fast Containment of Scanning Worms,''
in Proc. RAID, Sep 2004.
- 21
-
Jayanthkumar Kannan, Lakshminarayanan Subramanian, Ion Stoica, Scott Shenker,
and Randy Katz,
``Cooperative containment of fast scanning worms,''
Tech. Rep. CSD-04-1359, UC Berkeley, Nov 2004.
- 22
-
S. Staniford,
``Containment of scanning worms in enterprise networks,''
Journal of Computer Security, 2005 (to appear).
Analyzing Cooperative Containment of Fast Scanning Worms
This document was generated using the
LaTeX2HTML translator Version 2002-2-1 (1.70)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
|