|
CARDIS '02 Paper
[CARDIS '02 Tech Program Index]
| Pp. 125-134 of the Proceedings |  |
MICROCAST: Smart Card Based (Micro)pay-per-view for
Multicast Services
Josep Domingo-Ferrer, Antoni Martınez-Ballesté and Francesc Sebé
Universitat Rovira i Virgili
Dept. of Computer Engineering and Maths
Av. Paısos Catalans 26,
E-43007 Tarragona, Catalonia
e-mail {jdomingo,anmartin,fsebe}@etse.urv.es
With the increased availability of broadband fixed and mobile
communications, multicast content delivery can be expected
to become a very important market. Especially for wireless
multicast delivery, it is important that payment collection
be fine-grain: the customer should pay only for the content
that she actually consumes. This can be achieved by using
pay-per-view based on micropayments.
This paper proposes the first method for enabling pay-as-you-watch
services in a multicast content delivery
environment. On the customer's side,
micropayment generation is implemented in a smart card which can
be plugged into the customer's receiving device
(computer, digital video receiver, PDA, mobile phone, etc.).
Micropayment collection and verification are distributed among
multicast routers, which avoids bottlenecks inherent to
many-to-one payment transmission.
Keywords: Multicast delivery, Pay-per-view, Pay-as-you-watch,
Micropayments, Smart cards in the Internet.
Introduction
Communication technologies have been evolving in
many important aspects over the last few years.
On one hand, broadband communications such as city-wide WLANs,
ADSL, cable networks and UMTS
are becoming widespread. On the other hand, audio and
video compression codecs such
as DivX, Realmedia, etc. improve the use of the
available bandwidth. Finally, the appearance
of mobile phones with high-resolution color display and
Internet-enabled PDA's will bring
brand new multimedia services to everybody, everywhere.
There are great opportunities to create a huge
market for multimedia content delivery, featuring news broadcasting,
videoconferencing, movie channels, on-line gambling, etc.
Consequently, it seems natural
to use mobile communications and portable devices,
along with traditional desktop PC's, as new privileged outlets
for digital content delivery in pay-per-view mode.
Smart card based micropayments stand out as one of the
most promising solutions
to obtain a fine-grain fee collection service:
the customer uses her smart card to perform micropayments as content
is being received.
Most multimedia delivery services operate
in multicast mode to send content over the Internet.
By using multicast, one single data stream can reach hundreds, thousands and
even millions of target media players.
This paper describes a method for enabling pay-per-view
services in a multicast content delivery
environment. On the customer's side,
micropayment generation is implemented in a smartcard which can
be plugged into the customer's receiving device
(computer, digital video receiver, PDA, mobile phone, etc.).
Micropayment collection and verification are distributed among
multicast routers, which avoids bottlenecks inherent to
many-to-one payment transmission.
Section 2 gives some background on multicast communication;
the use of pay-per-view and micropayments in multicast is also
approached.
Section 3 describes the architecture
of MICROCAST, a system for
pay-per-view multicast content delivery.
The MICROCAST micropayment protocol suite is fully described in
Section 4.
Finally, Section 5 contains some
conclusions and suggestions for future work.
Multicast communication
Depending on the number of receivers, three types of communication
can be distinguished:
- Unicast communication: one source and one receiver.
- Broadcast communication: one source node and all remaining
nodes acting as receivers. As an example, consider
video broadcast in a LAN: the same data are streamed from the
source to the entire network by using the broadcast IP address.
- Multicast communication: one source and a group of receivers.
As an example, consider a local digital cable TV network, where a particular
piece of video content is to be distributed only to subscribers
who are paying for it (rather than to the entire neighborhood).
If a source is to communicate with 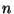 receivers, one could
naively think of
using receivers, one could
naively think of
using 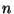 unicast communications
(which results in the
source being an output bottleneck) or one broadcast channel
(which results in the entire network being flooded). Both
solutions are wasteful in terms of bandwidth.
It should be noted that the Internet is nowadays already
full of millions of IP packets only controlled by their
time-to-live or by the TCP protocol. unicast communications
(which results in the
source being an output bottleneck) or one broadcast channel
(which results in the entire network being flooded). Both
solutions are wasteful in terms of bandwidth.
It should be noted that the Internet is nowadays already
full of millions of IP packets only controlled by their
time-to-live or by the TCP protocol.
A better option to avoid increasing
network congestion
is for receivers to join a multicast group
and have the content sent to them by using their
multicast group IP address [5,14].
A multicast group 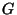 is a set of receivers that are interested
in receiving a particular kind of information. is a set of receivers that are interested
in receiving a particular kind of information.
Efficient multicast design and implementation is currently an open issue.
The multicast task is carried out by multicast routers, which
join previously established multicast groups identified
by a multicast IP address1.
These routers are capable of sending the data flow to multicast group 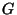 . .
The basic tasks to be performed in multicast communication are:
advertise the multicast session, manage group enrollment
by the customers who want to receive the stream and, concurrently to
group enrollment, build
the multicast routing tree. Several multicast protocols have
been proposed in the literature, such as
MOSPF[6], PIM-DM[3], PIM-SM[2].
The name ``pay-per-view'' is certainly misleading.
In current digital TV platforms,
a fixed monthly fee is paid to subscribe
to a basic package of channels and services. It is also
possible
to view some special ``pay-per-view events''
(e.g. movies, football matches) by paying in advance
the price corresponding to the event. This form of pay-per-view
means that the content is viewed after the customer
has paid. There are at least two problems with the fee collection
scheme just described. One problem
is that the customer pays for a basic offer that is usually expensive
for her. The other problem is that, in pay-per-view events, the customer
pays for the whole piece of content: if she wants to stop watching
anytime, she is losing a part of her money.
Pay-per-view as contents are being streamed from the server to
the customer (pay-as-you-watch)
seems an option that fits better the customer needs.
Successive payments can be performed every minute, for example.
If a customer switches her player off, she only has
paid for the minutes viewed so far. Of course,
these frequent payment will be small ones, so
credit card transactions or electronic payment systems like SET are
too expensive, too complicated or both [7].
The operating costs of standard electronic payment systems
are unaffordable for small amounts and can be split into communication
and computation costs, the latter being
caused by the use of complex cryptographic techniques such as digital
signatures. Micropayments are electronic payment
methods specifically designed to keep operating costs very low.
In most micropayment systems in the literature,
computational costs are dramatically reduced by replacing digital
signatures with hash functions[11].
For example, this is the case
of PayWord and Micromint[9], where
the security of coin minting rests on one-way hash functions.
The main barrier to using traditional micropayment
schemes for fee collection in multicast environments is their
lack of scalability: a large number of receiving subscribers
eventually overload the source with payment implosion.
The MICROCAST protocol achieves scalability
by distributing
the effort of micropayment collection and verification among
multicast routers. Unlike traditional micropayment schemes,
MICROCAST does not concentrate on minimizing computation for
micropayment generation and verification. By requiring micropayments
to be less frequent (say every few minutes) and
verification to be distributed, MICROCAST can still
use short-exponent discrete exponentiations and provide
the content source with a proof that every customer has paid.
More specifically, the scalability of
our system is based on the following properties not fulfilled
by conventional micropayment schemes (which are inherently unicast):
- Aggregation
- Payments collected by routers at one
level of the multicast tree can be aggregated and
forwarded to the next upper level towards the source.
Each aggregation only requires one product and one addition.
- Single-step verification
- Verifying an aggregated
payment can be done in a single step. There is no
need to verify each individual payment included in
the aggregation, which would imply non-scalability.
Payment verification requires
one short-exponent exponentiation, but this is no problem, since
verification is performed only once per micropayment period
by each tree node (regardless of the number of its child nodes).
Note 1
As it can be seen in
Section 4.4 below,
using the discrete exponentiation as a one-way function
is justified by its homomorphic properties,
which allow
payment aggregation and single-step verification and
are not shared by the (faster) one-way hash functions.
Multicast routers form a group that receives a multicast data stream.
The router will possibly send the info to a hub
that floods all its output connections, thus making the information
reach every node in the subLAN, including
nodes whose customers have not paid for the content.
Cryptography should be used to prevent cheaters from
being able to view the content by using packet sniffers.
Customers in the multicast group have
a decoding key to be able to decode the content
they receive.
Hence, legitimate customers are those who pay every multicast period 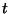 (a multicast period typically lasts a few minutes).
When a customer does not pay, she will be considered non-legitimate;
in this case,
a rekeying procedure will start which consists of
distributing a new decoding key to every remaining legitimate customer.
As a result, the removal of a group member will involve
as many unicast transmissions
as legitimate customers remain in the group.
Fortunately, rekeying reaches a maximum cost of
(a multicast period typically lasts a few minutes).
When a customer does not pay, she will be considered non-legitimate;
in this case,
a rekeying procedure will start which consists of
distributing a new decoding key to every remaining legitimate customer.
As a result, the removal of a group member will involve
as many unicast transmissions
as legitimate customers remain in the group.
Fortunately, rekeying reaches a maximum cost of 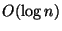 when using
tree structure controls[12,1].
Even if rekeying is an important multicast issue, the reader of
this paper only needs
to keep in mind that it is the procedure started when a customer
in a multicast group is removed due to lack of valid payment or when a new
customer joins the group. when using
tree structure controls[12,1].
Even if rekeying is an important multicast issue, the reader of
this paper only needs
to keep in mind that it is the procedure started when a customer
in a multicast group is removed due to lack of valid payment or when a new
customer joins the group.
MICROCAST architecture
As it was pointed out in Section 1, MICROCAST is a
pay-as-you-watch system for multicast content delivery.
A typical application for MICROCAST could the pay-as-you-watch video
distribution to thousands of customers. By using
her smart card plugged into her video receiver, a customer
can join a multicast group
when she is interested in watching an event. After joining
a group, the customer makes a micropayment every period 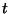 to keep watching the event.
to keep watching the event.
In a conventional micropayment system,
a bottleneck would arise at the video source
as a result of micropayment collection,
because thousands of coins arrive every
period2.
RFC 3170[8] on multicast applications
recommends that multicast protocols
should be able to use the
multicast router link to provide
bidirectional communications instead of using unicast channels
to communicate receivers with the source.
The MICROCAST architecture follows that design principle: multicast
routers handle customers and coins, which results in a dramatical
reduction of the amount of payment data sent to the content source.
The MICROCAST system
consists of a source, a set of multicast routers, the customer smart cards
and receivers, a rekeying
system and a bank (see Figure 1). Each component
is described next:
- Source. The source is the provider of the multicast content.
Typical sources can be a movie channel,
a news service, a music station, a sports service, etc.
The source sells the content to thousands, even millions, of potential
customers. As content is being delivered,
the source expects some kind of payment from customers or at least
something that certifies whether each particular customer
is currently paying.
- Multicast router. The router in the multicast tree
also acts as a micropayment subcollector. It requests micropayment
from its customers and, after a timeout, it collects and
verifies customer micropayments.
Then, the router forwards
valid payments to his parent router in the multicast tree,
in order for payment information to reach the source (or
the main micropayment collector, depending on the business model).
Figure 1:
System architecture for MICROCAST
|
- Customer device. The customer receiving device
(say a digital video receiver) is smart card enabled.
Firstly, the smart card certifies through
some easy calculations (see Section 4)
that a payment is done by
the customer. Thus, the role of the
smart card is twofold: 1) authenticate payment
origin; 2) help enforcing subscription certificate revocation
when the customer is not backed
by enough money in her bank account.
- Rekeying system. The rekeying system maintains a
structure of legitimate customers (those who pay) and
generates and distributes a new decoding key whenever
any router of the system informs that some customer has failed
to pay.
- Bank. The bank's role is to act as certification authority
for customers.
If a customer has enough funds in her account, the bank gives her
a kind of public key (see Section 4).
The MICROCAST protocol suite
The MICROCAST protocol suite consists of protocols
for bank setup, customer subscription, multicast session join,
micropayment, customer removal,
coin redemption and subscriber certificate revocation.
As can be inferred from the previous section,
the bank is a trusted party. It
has a public/private key pair which is used to
issue customer subscription certificates.
The bank setup protocol works as follows:
We next show that publication of 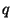 does not turn factoring does not turn factoring
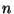 into an easy problem. After Protocol 1,
an intruder knows into an easy problem. After Protocol 1,
an intruder knows 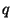 , which is a divisor of , which is a divisor of 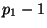 .
Equivalently, .
Equivalently, 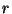 exists such that exists such that 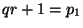 .
Note that the intruder does not know .
Note that the intruder does not know 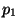 . Therefore,
the only strategy to find . Therefore,
the only strategy to find 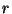 is by brute search until
an is by brute search until
an 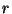 is found such that is found such that 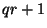 is a divisor of is a divisor of 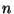 .
Now, according to Protocol 1, .
Now, according to Protocol 1,
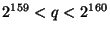 and
and
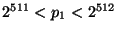 ;
therefore, the intruder only knows
that ;
therefore, the intruder only knows
that
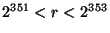 , so brute search of , so brute search of 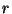 is computationally infeasible.
is computationally infeasible.
In order to be able to use the system, a customer
needs a subscription certificate. Through this certificate,
the bank certifies that the customer has a bank account
which backs the customer's payments.
Subscription certificates are only valid for a
period 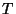 (e.g. one day) and are
generated using the protocol below. Short certificate
validity periods allow implicit revocation to be used in the way
explained in [4]. The duration of
period (e.g. one day) and are
generated using the protocol below. Short certificate
validity periods allow implicit revocation to be used in the way
explained in [4]. The duration of
period 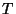 is a trade-off between the cost of
key generation and the risk of revoked keys being re-used
as described in [4]. is a trade-off between the cost of
key generation and the risk of revoked keys being re-used
as described in [4].
The security of the private keys 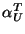 generated in Protocol 2
is based on the difficulty of computing discrete logarithms
in the subgroup of size
generated in Protocol 2
is based on the difficulty of computing discrete logarithms
in the subgroup of size 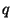 generated by generated by 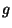 . This problem
is similar to the modulo . This problem
is similar to the modulo 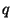 discrete logarithm problem
used in [15]. discrete logarithm problem
used in [15].
Let us assume that, at micropayment period 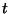 and at public key validity period
and at public key validity period 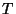 ,
a set of customers wish to join
a multicast session ,
a set of customers wish to join
a multicast session 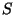 (see Section 3 for an explanation
of what a micropayment period is). To keep the discussion simple and
without loss of generality, we assume
that a session starts and ends within the same public key validity
period (see Section 3 for an explanation
of what a micropayment period is). To keep the discussion simple and
without loss of generality, we assume
that a session starts and ends within the same public key validity
period 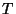 . The following joining
protocol is used: . The following joining
protocol is used:
Micropayment protocols
Every time a period 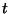 finishes, a customer must perform a
micropayment to keep receiving the content during the next period.
The micropayment collector
(i.e. the router in charge of a group
of customers) asks all customers in his
group to perform the next payment as follows: finishes, a customer must perform a
micropayment to keep receiving the content during the next period.
The micropayment collector
(i.e. the router in charge of a group
of customers) asks all customers in his
group to perform the next payment as follows:
Customers in a group react to micropayment request by generating
a coin using the protocol below:
Coins are generated by customers that correspond to the
multicast tree leaves.
In the last
step of Protocol 5, coins are sent by customers
to parent routers.
Such routers
check the validity of the received coins and aggregate
valid coins. Aggregation uses the homomorphic property of
the discrete exponentiation (namely that
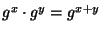 ),
which is one strong argument in favor of using the discrete
exponentiation as one-way function
(see Note 1).
The aggregated coin is then forwarded by the verifying router
to his parent router and so on
up to the tree root (micropayment collector).
Thus, depending on its level, a router can receive two kinds of coin: ),
which is one strong argument in favor of using the discrete
exponentiation as one-way function
(see Note 1).
The aggregated coin is then forwarded by the verifying router
to his parent router and so on
up to the tree root (micropayment collector).
Thus, depending on its level, a router can receive two kinds of coin:
- A single coin from a customer leaf node directly connected
to the router.
- An aggregated coin from a direct child router
(see Protocol 6 below for a description of how coins
are aggregated).
The protocol to aggregate coins by an intermediate router
is as follows:
Protocol 6 (Coin aggregation)
- Initialize the new aggregated coin as
- For each single coin received from customer
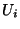 , that is, , that is,
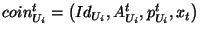 , do , do
- For each aggregated coin received from router
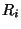 , that is, , that is,
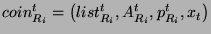 , do , do
- Send the aggregated coin
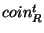 up to the parent router. up to the parent router.
The protocol to check coin validity is:
Protocol 7 (Coin validity check)
- If a single coin is received from customer
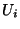 ,
the following check is performed: ,
the following check is performed:
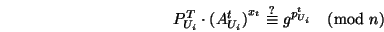 |
(1) |
Note that Check (1) is consistent with the structure
of coins constructed by Protocol 5.
- If an aggregated coin is received from a child router
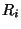 ,
the following check is performed: ,
the following check is performed:
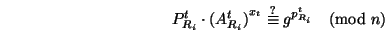 |
(2) |
Lemma 1
Assuming that the discrete logarithm problem as
sketched in Protocol 1 and the RSA
problem are difficult, coin forgery by an intruder is infeasible.
Proof:
To impersonate customer 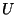 and
mint a single coin belonging to and
mint a single coin belonging to 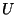 at public key validity period
at public key validity period 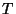 ,
an intruder knows ,
an intruder knows 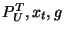 and and 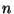 and must find and must find
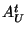 and and 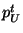 such that Equation (1)
is satisfied. There are two ways to proceed: such that Equation (1)
is satisfied. There are two ways to proceed:
- Follow Protocol 5. In that case, the intruder
must know the legitimate customer's private key
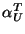 (which is protected by the difficulty of the
discrete logarithm problem over the subgroup generated by
(which is protected by the difficulty of the
discrete logarithm problem over the subgroup generated by  ). ).
- Generate a random
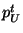 and compute and compute 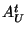 as as
Now, given 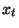 , computing , computing
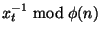 without
knowing the factorization of without
knowing the factorization of 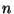 is the RSA problem. is the RSA problem.
Forging an aggregate coin that satisfies Equation 2
is analogous. 
Lemma 2
The security of a customer's private key does not decrease
as the number of coins she mints increases.
Proof:
Without loss of generality, compare the situation where one
coin has been minted with the situation where two coins have
been minted. Assume one coin has been generated during
micropayment period 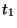 and public key validity period
and public key validity period 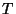 . Then the following
equation holds: . Then the following
equation holds:
where, only 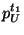 and and 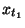 are known to possible
intruders (such quantities are part of the coin). Thus,
there is one equation and two unknowns are known to possible
intruders (such quantities are part of the coin). Thus,
there is one equation and two unknowns 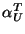 and and
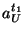 , so , so 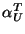 cannot be determined.
If a second coin is generated during micropayment period cannot be determined.
If a second coin is generated during micropayment period
the number of equations increases to two, but there are
now three unknowns 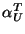 , , 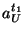 and and 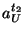 .
In general, it can be seen that generation of .
In general, it can be seen that generation of 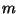 coins
results in coins
results in 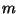 equations with equations with 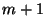 unknowns, one of which
is the customer's private key unknowns, one of which
is the customer's private key 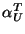 . .  . .
Customer removal from a group is caused by lack of valid payment.
There may be two situations behind the lack of valid payment:
1) a customer does not send any coin to her parent router;
2) a customer sends an invalid coin to her parent router.
Both situations are handled by the following protocol:
During a multicast session, the micropayment collector
stores the final aggregated coin for each performed
micropayment. This coin contains a list including
the identifiers of all customers that performed a payment.
When the number of collected coins is large enough,
the micropayment collector contacts the bank
in order to redeem them.
Protocol 9 (Coin redemption)
- When the aggregated coin corresponding to period
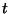 has to be redeemed, the micropayment collector
sends to the bank the session identifier has to be redeemed, the micropayment collector
sends to the bank the session identifier
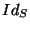 , the session start date and time , the session start date and time
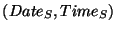 , the value , the value 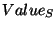 of individual coins
in that session, the micropayment period of individual coins
in that session, the micropayment period 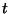 , and
the final aggregated coin , and
the final aggregated coin
- The bank does:
- If this is the first coin redemption of the current
multicast session then
check that the public key of all customers in the list
field is correctly certified and compute
 . .
- If this is not the first coin redemption of the session,
then
- If
 in in 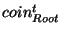 is the
same as is the
same as
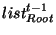 in in
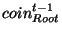 , then , then
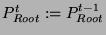 . .
- If
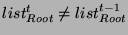 , then obtain , then obtain
 as the modulo as the modulo 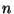 product of
product of
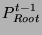 times the public keys of the new
customers times the multiplicative inverses of the
public keys of the removed customers. times the public keys of the new
customers times the multiplicative inverses of the
public keys of the removed customers.
- Compute
- Check
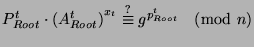
- If all checks are correct, transfer the appropriate
amounts from each customer account to the account of the
micropayment collector
(or directly to the account of the multicast content source,
depending on the business model). In order to avoid
performing microtransfers from each customer, a better strategy
is to cluster several successive micropayments
and perform a larger transfer from each customer.
It is possible for a customer to run out of funds before all
of her certificates expire. In this situation, it would be possible
for her to perform micropayments not backed by enough funds
in her bank account.
This situation is detected by the bank during coin
redemption. In this case, the bank would revoke all
her subscription certificates for future time intervals.
The implicit revocation mechanism described in [4]
is used: the bank does not supply any more encrypted private
keys to the customer's smart card for joining the session
in subsequent periods (Protocol 3).
Conclusions and future work
A micropayment protocol suite for multicast pay-per-view
content delivery has been presented. The customer is represented
by her smart card in all protocols in the suite. The proposed
scheme has been simulated and works well as long as synchronization
between customers is maintained.
The main goal of the protocol is to
to distribute micropayment collection so as eliminate the
bottleneck associated to Mto1 applications.
Future work will be directed
to scenarios where synchronization within a multicast group has
been lost. A second line of work is to speed up coin
generation by the customer smart card and coin validity check
by routers: this would require replacing the discrete exponentiation
with a faster homomorphic one-way function.
This work has been partly supported by the European
Commission under project IST-2001-32012
``Co-Orthogonal Codes'' and by the Spanish
Ministry of Science and Technology and the European FEDER
Fund under project TIC2001-0633-C03-01 ``STREAMOBILE''.
-
- 1
- G. Caronni, K. Waldvogel, D. Sun and B. Plattner,
``Efficient security for large and dynamic multicast
groups'', in IEEE 7th Workshop on Enabling Technologies: Infrastructure
for Collaborative Enterprises (WET ICE '98). Los Alamitos CA:
IEEE Computer Society, pp. 376-383, 1998.
- 2
- S. Deering, D. Estrin, D. Farinacci, V. Jacobson, C. Liu
and L. Wei,
``The PIM architecture for wide-area multicast routing'',
IEEE/ACM Transactions on Networking, vol. 4, no. 2, pp. 153-162,
Apr. 1996.
- 3
- S. Deering, D. Estrin, D. Farinacci, V. Jacobson,
A. Helmy, D. Meyer and L. Wei, ``Protocol independent multicast
version 2 dense mode specification'', IETF Internet Draft, Nov. 1998.
http://www.ietf.org
- 4
- J. Domingo-Ferrer, M. Alba and F. Sebé,
``Asynchronous large-scale certification based on
certificate verification trees'', in
Communications and Multimedia Security'2001. Norwell MA:
Kluwer Academic Publishers, pp. 185-196, 2001.
- 5
- C. K. Miller, Multicast Newtorking and Applications.
Reading MA: Addison Wesley, 1999.
- 6
- J. Moy, ``Multicast extensions to OSPF'', Internet
RFC 1584, March 1994. http://www.ietf.org
- 7
- R. Oppliger, Security Technologies for the World Wide Web.
Norwood MA: Artech House, 2000.
- 8
- B. Quinn and K. Almeroth,
``IP multicast applications: challenges and solutions'',
Internet RFC 3170, Sept. 2001. http://www.ietf.org.
- 9
- R. Rivest and A. Shamir, ``PayWord and Micromint: Two simple
micropayment schemes'', Technical Report, MIT LCS, Nov. 1995.
- 10
- R. L. Rivest, A. Shamir and L. Adleman,
``A method for obtaining digital signatures and public-key cryptosystems'',
Communications of the ACM, vol. 21, pp. 120-126, Feb. 1978.
- 11
- B. Schneier, Applied Cryptography. New York: Wiley, 1996.
- 12
- J. Snoeyink, S. Suri and G. Varghese,
``A lower bound for multicast key
distribution'', in Proceedings of IEEE INFOCOM 2001. Piscataway NJ:
IEEE Computer and Communications Society, pp. 422-431, 2001.
- 13
- D. R. Stinson, Cryptography. Theory and Practice,
Boca Raton FL: CRC Press, 1995.
- 14
- R. Wittmann and M. Zitterbart,
Multicast Communication, Protocols and Applications.
San Mateo CA: Morgan Kaufmann, 2001.
- 15
- Digital Signature Standard, FIPS PUB 186,
National Institute of Standards, Washington D. C., May 1994.
MICROCAST: Smart Card Based (Micro)pay-per-view for
Multicast Services
This document was generated using the
LaTeX2HTML translator Version 2K.1beta (1.50)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -html_version 3.2,unicode -t MICROCAST -split 0 -no_navigation index.tex
Footnotes
- ... address1
- Multicast addresses are IP numbers
in the range between 224.0.0.0 and 239.255.255.255
- ...
period2
- A coin can be a 200-bit vector, and
period
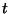 is short enough
to keep payment fine grain, i.e.
for content reception and payment to progress nearly concurrently. is short enough
to keep payment fine grain, i.e.
for content reception and payment to progress nearly concurrently.
Antoni Martinez
2002-09-19
|
