
2007 USENIX Annual Technical Conference
Pp. 199–204 of the Proceedings


Implementation and Performance Evaluation of Fuzzy File Block Matching
Bo Han
Department of Computer Science
University of Maryland
College Park, MD 20742, USA
bohan@cs.umd.edu
Pete Keleher
Department of Computer Science
University of Maryland
College Park, MD 20742, USA
keleher@cs.umd.edu
The fuzzy file block matching technique (fuzzy matching for short), was first proposed for opportunistic use of Content Addressable Storage. Fuzzy matching aims to increase the hit ratio in the content-addressable storage providers, and thus can improve the performance of underlying distributed file storage systems by potentially saving significant network bandwidth and reducing file transmission costs. Fuzzy matching employs shingling to represent the fuzzy hashing of file blocks for similarity detection, and error-correcting information to reconstruct the canonical content of a file block from some similar blocks. In this paper, we present the implementation details of fuzzy matching and a very basic evaluation of its performance. In particular, we show that fuzzy matching can recover new versions of GNU Emacs source from older versions.
Recent work in file systems has shown that the use of content-addressable storage (CAS) can enhance the performance of distributed file systems, especially in the wide area [7,11,16]. The basic idea of CAS is to describe files in terms of recipes that enumerate a set of blocks that make up the file's contents. Similar files, or different versions of the same files, may contain blocks in common. CAS-based file systems can exploit this property by requesting remote copies of only those blocks that are not already present locally, or at least nearby.
Tolia et al. [16] proposed extending this technique by using fuzzy matching to identify local blocks similar to a target block, and then using error correcting codes to correct such a local block to the target. However, Tolia did not present any experimental data on how well the idea works in practice, nor any implementation details.
The purposes of this brief paper are to (1) provide an existence proof of the idea, (2) describe our approach in enough detail to enable other researchers to extend it, and (3) make a preliminary evaluation of its performance on real data. We make no claim here of exhaustive analysis or experiments. However, our results do show that the technique has promise, and can be highly beneficial in the right circumstances. In particular, we evaluate the use of fuzzy matching to reconstruct later versions of GNU Emacs source [1] from earlier versions. We also evaluate the performance impact of varying several important parameters, such as average block size, the number of subblocks per block and error correcting code rate, etc.
The rest of this paper is organized as follows. In Section 2, we introduce the background of fuzzy matching. We next describe details of our implementation in Section 3. In Section 4 we evaluate the performance of fuzzy matching and the effect of several parameters. After summarizing related work in Section 5, we conclude and present our future directions in Section 6.
2 Fuzzy Matching
In this section, we describe fuzzy matching and subsidiary techniques in more detail. These techniques include Rabin fingerprints [14], shingling [3], and error correcting codes.
A file recipe in a standard CAS system consists of an ordered list of block signatures. The signatures are generated from the blocks' contents through a cryptographically secure hash, such as SHA-1. Without fuzzy matching, this hash value is sufficient to completely identify each block needed to reconstruct the file.
Fuzzy matching extends the description of each block into a specification that includes four pieces of information: (a) an exact hash value that matches only the correct block; (b) a fuzzy hash value that matches blocks similar to the correct block; (c) fingerprints of a block's fixed-length subblocks for identifying them in similar blocks, and (d) error-correcting information that may sometimes recover the correct block, when applied to a similar block.
Fuzzy matching works as follows: (1) The client sends the target block's recipe to its nearby CAS provider (which may be local). (2) The CAS provider first determines whether it holds a file block whose hash matches the exact hash value of the requested block; if so, it returns this block to the client. (3) If the CAS provider doesn't hold the correct block, it next uses the block's fuzzy hash value to identify any candidate blocks that approximately match the file block requested by the client. (4) The CAS provider applies the error-correcting information to each such candidate block. If the corrected block's hash matches the exact hash value of the requested block, the CAS provider returns the corrected block to the client. (5) If none of the CAS provider's candidate blocks can be corrected to match the exact hash, the CAS provider returns a negative result to the client, which then sends a request to a remote file server [16].
Fuzzy matching uses Rabin fingerprints to construct content-defined data blocks, and to compute shingles for similarity detection. Fingerprints are short tags for large objects. The property of fingerprints is that if two fingerprints are different then the corresponding objects are certainly different. The probability that two different objects have the same fingerprint is extremely small. For more information about Rabin fingerprints, please refer to [14].
Shingling was proposed by Broder et al. to determine the syntactic similarity of web pages [3]. They view each web page as a sequence of words, and a contiguous subsequence contained in the web page is called a shingle. Fingerprints of shingles are computed using sliding window to efficiently create a shingling vector for a web page. Instead of comparing entire documents, they use shingling vectors to measure the resemblance and containment of documents in a large collection of web pages. Shingling is also called super-fingerprint in REBL [8]. Fuzzy matching selects the 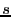 smallest fingerprints among the shingling vector to form a shingleprint, and stores it in the block recipe as the fuzzy hash value of a block. smallest fingerprints among the shingling vector to form a shingleprint, and stores it in the block recipe as the fuzzy hash value of a block.
The essence of fuzzy matching is to store enough error-correcting information to recover the original data from similar blocks. Therefore, we give a brief introduction of Error Correcting Code (ECC) in this subsection. An error correcting code is a code which constructs data signals conforming to specific rules, such that errors in the received signal can be automatically detected and corrected. There are two important subclasses of error correction: Forward Error Correction (FEC) and Backward Error Correction (BEC). In the following, we will focus on FEC which is suitable for fuzzy matching. FEC is accomplished by adding redundancy to data bits using a predetermined algorithm. The two main categories of FEC are block coding and convolutional coding.
A  block code contains sequences of block code contains sequences of 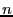 symbols. Each sequence of length symbols. Each sequence of length 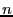 is a code word or code block, and contains is a code word or code block, and contains 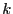 information digits. The remaining information digits. The remaining 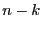 digits are called redundant digits. Here, the code rate is defined as the ratio digits are called redundant digits. Here, the code rate is defined as the ratio 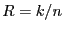 . Examples of block codes include (7, 4) and (11, 7) Hamming code which can correct single-bit errors and detect double-bit errors; (23, 12) and (11, 6) Golay code which can correct 3 and 2 errors, respectively; (255, 223) and (65535, 65503) Reed-Solomon code which can correct 16 errors and 32 erasures (errors whose locations are known in advance). Fore more detailed information about Error-Correction Coding, we refer the interested reader to [4,10]. In our implementation, we use a (255, 223) Reed-Solomon code for its higher code rate and error-correction capability. Evaluating the performance of other error correcting codes is part of our future work. . Examples of block codes include (7, 4) and (11, 7) Hamming code which can correct single-bit errors and detect double-bit errors; (23, 12) and (11, 6) Golay code which can correct 3 and 2 errors, respectively; (255, 223) and (65535, 65503) Reed-Solomon code which can correct 16 errors and 32 erasures (errors whose locations are known in advance). Fore more detailed information about Error-Correction Coding, we refer the interested reader to [4,10]. In our implementation, we use a (255, 223) Reed-Solomon code for its higher code rate and error-correction capability. Evaluating the performance of other error correcting codes is part of our future work.
3 Implementation Details
Our implementation of fuzzy matching has two main building blocks: recipe creation and file block reconstruction. In the following, we describe the details of these two parts, respectively.
The first step of constructing file recipes is to divide a file into variable-length content-defined blocks using Rabin fingerprints. Content-defined chunking (CDC) has been used in LBFS [11], Pastiche [5] and TAPER [7]. CDC sets block boundaries based on file contents, rather than on position within a file. Therefore, insertions and deletions can only affect the surrounding blocks and not the entire file. A sliding window is used to evaluate a fingerprint of the preceding 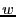 bytes at each point in the file. A point is considered to be a boundary of a data block if its 64-bit Rabin fingerprint matches a predetermined marker value. Rabin fingerprints are chosen because they are efficient to compute on a sliding window over a file. The number of bits in a Rabin fingerprint that are used to match the marker determines the expected block size. For example, if the low-order bytes at each point in the file. A point is considered to be a boundary of a data block if its 64-bit Rabin fingerprint matches a predetermined marker value. Rabin fingerprints are chosen because they are efficient to compute on a sliding window over a file. The number of bits in a Rabin fingerprint that are used to match the marker determines the expected block size. For example, if the low-order 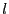 bits are used, the expected block size will be bits are used, the expected block size will be 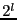 . .
After a file is divided into variable-length blocks, a shingleprint is computed for each block. Define a shingle to be a sequence of 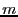 contiguous bytes in a block. There are totally contiguous bytes in a block. There are totally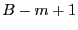 overlapping shingles in a overlapping shingles in a 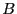 -byte block. We again use Rabin fingerprints to compute a hash of each shingle in the block. These fingerprints are then sampled to compute a shingleprint of the block. We employ -byte block. We again use Rabin fingerprints to compute a hash of each shingle in the block. These fingerprints are then sampled to compute a shingleprint of the block. We employ 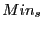 sampling [3] which selects the set of sampling [3] which selects the set of 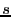 fingerprints with the smallest values to represent the approximate content of a block. Two blocks are similar if they share in common fingerprints with the smallest values to represent the approximate content of a block. Two blocks are similar if they share in common 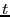 (similarity threshold) out of (similarity threshold) out of 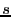 values in the shingleprint. Note that bloom filters could also be utilized for similarity detection [7]. In the future, we plan to compare these two approaches associated with fuzzy matching to understand the relative detection performance. values in the shingleprint. Note that bloom filters could also be utilized for similarity detection [7]. In the future, we plan to compare these two approaches associated with fuzzy matching to understand the relative detection performance.
The last step is to generate error-correcting information for each block. As mentioned above, we choose the (255, 223) Reed-Solomon code for its high code rate. Here, suppose a file block is equally divided into seven subblocks (because the ratio between the number of information digits and that of erasures which can be corrected is about 7). To identify these subblocks, the Rabin fingerprint of each subblock is first stored in the block recipe. Then another subblock is constructed to keep the error-correcting information. To do so, each subblock is further divided into several 31-byte pieces. The first seven pieces of each subblock are packed together to form a 217-byte data chunk. After padding with 6 null bytes, we get a 223-byte chunk and use the (255, 223) Reed-Solomon Code to compute the 32-byte error-correcting information. Finally this 32-byte data piece is put at its corresponding position in the ECC subblock. The same method is used to process other data pieces in each subblock to construct the ECC subblock for the entire data block. This procedure is also demonstrated in Figure 1.
Figure 1:
Generating ECC subblock and recovering a block from a similar block
|
Assume that a CAS provider has identified a candidate block by finding a shingleprint match of the target and candidate blocks. We use the example in Figure 1 to illustrate how the provider can then recover the target block from the candidate. Compared with the target block, the candidate block contains an deletion in the 3rd subblock. Suppose there are 1024 bytes in each subblock. The CAS provider computes the Rabin fingerprint for each contiguous 1024-byte subblock of the candidate block, and identifies those subblocks whose Rabin fingerprints match those provided by the client. In this case, the CAS provider can find out 6 unchanged subblocks: 1, 2, 4, 5, 6 and 7. These subblock correspondences between the two blocks are shown by vertical arrows in Figure 1. Thereafter, using the error-correcting subblock, the CAS provider can overcome the ``erasure'' (the missing 3rd subblock) of the modified subblock, to form the target block. As a final check, the CAS provider computes the exact hash over the entire corrected block, and compares it with the exact hash of the target block.
As mentioned above, each content-defined block is further divided into seven subblocks for generating the ECC subblocks. This approach can only correct from candidate blocks with modifications to a single subblock. Increasing the number of subblocks can potentially allow more changes to be corrected by separating their error correction information. Therefore, we also propose two other approaches, Separate Selection and Grouped Selection, to dividing each block into 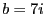 (for some small non-negative integer (for some small non-negative integer  ) subblocks. For example, when ) subblocks. For example, when 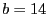 , separate selection generates a single ECC subblock for subblocks 0, 2, 4, 6, 8, 10 and 12, and another one for subblocks 1, 3, 5, 7, 9, 11 and 13. Grouped selection creates a ECC subblock for the first seven subblocks, and another one for the last seven subblocks. , separate selection generates a single ECC subblock for subblocks 0, 2, 4, 6, 8, 10 and 12, and another one for subblocks 1, 3, 5, 7, 9, 11 and 13. Grouped selection creates a ECC subblock for the first seven subblocks, and another one for the last seven subblocks.
4 Performance Evaluation
This section provides a performance evaluation of fuzzy matching using five different releases of Emacs source: emacs-21.4, emacs-21.3, emacs-21.2, emacs-21.1 and emacs-20.7. We study the effect of several parameters on the performance of fuzzy matching, investigating primarily along two dimensions: the size of file recipes (overhead) and the probability that a file in the new release can be recovered from those in the adjacent old version (effectiveness).
Fuzzy matching's performance depends on several parameters: the sliding window size 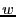 , the average block size , the average block size 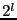 , the sliding window size for shingling , the sliding window size for shingling 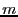 , the number of shingles in a shingleprint , the number of shingles in a shingleprint 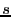 , similarity threshold , similarity threshold 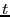 , and the number of subblocks per block , and the number of subblocks per block 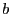 . Our default values are: . Our default values are:  , , 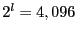 , ,  , ,  , ,  and and 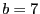 . .
The size of the sliding window can determine how effective the chunking algorithm is in defining block boundaries similarly, despite intervening edits. Table 1 shows a sampling of our results for the number of recovered files versus different window sizes. The recovered files are files that can be corrected from their similar (not exactly identical) old versions. The reason for the small numbers in the first row is that there are only 10 different files between emacs-21.3 and emacs-21.4. The results change little, showing that the chunking mechanism is relatively insensitive to the window size.
Table 1:
Number of recovered files for various sliding window sizes for CDC.
| |
Sliding Window Sizes |
| |
12B |
24B |
48B |
96B |
21.3 21.4 21.4 |
9 |
9 |
9 |
10 |
21.2 21.3 21.3 |
243 |
243 |
246 |
237 |
21.1 21.2 21.2 |
185 |
179 |
175 |
182 |
20.7 21.1 21.1 |
142 |
134 |
143 |
133 |
|
Table 2 summarizes the number of recovered files for different average block sizes. Larger blocks can increase the size of subblock which will potentially make changes occur in one subblock rather than span several subblocks. Therefore, they can improve the probability that a block can be recovered from a similar block. Moreover, larger blocks require less overhead to track the exact hash value and numerous shingleprints and fingerprints per file which is also verified by our experiment results (not shown here for space limitation). In addition, larger blocks also decrease the number of comparisons. The possible reason for the exception in the last row of Table 2 is that changing average block size may also alter the block and subblock boundaries which will sometimes reduce the file recovery probability.
Table 2:
Number of files that can be recovered from similar files for various average block sizes.
| |
Average Block Sizes |
| |
0.5K |
1K |
2K |
4K |
8K |
16K |
21.3 21.4 21.4 |
9 |
9 |
9 |
9 |
9 |
9 |
21.2 21.3 21.3 |
224 |
231 |
251 |
246 |
246 |
245 |
21.1 21.2 21.2 |
152 |
154 |
163 |
175 |
186 |
191 |
20.7 21.1 21.1 |
151 |
151 |
148 |
143 |
144 |
140 |
|
This sliding window size is, in fact, the shingle size. A shingle should be large enough to create many possible substrings, which minimizes spurious matches, and small enough to prevent small modifications from affecting many shingles. Common values in past studies have ranged from four to twenty bytes [8]. Our experimental results (omitted for space) indicate that shingling window size does not significantly affect the performance of fuzzy matching.
Shingling is used to identify candidate blocks. The similarity threshold is the number of fingerprints in a shingleprint that must match to declare two blocks similar. Table 3 reports the number of recovered files for different similarity thresholds. The last three rows illustrate that reducing similarity thresholds can slightly increase the number of recovered files. The reason is that lower thresholds lead to the identification of more candidate blocks. However, larger candidate sets lead to more computational overhead. Given that the number of recovered files is nearly identical for all but the last column, setting the threshold near, but not equal to the number of shingles in the shingleprint, seems to be a good compromise.
Table 3:
Number of recovered files for different similarity thresholds.
| |
Similarity Thresholds |
| |
0 |
2 |
4 |
6 |
8 |
10 |
21.3 21.4 21.4 |
9 |
9 |
9 |
9 |
9 |
6 |
21.2 21.3 21.3 |
248 |
247 |
246 |
246 |
246 |
205 |
21.1 21.2 21.2 |
180 |
179 |
178 |
178 |
175 |
132 |
20.7 21.1 21.1 |
147 |
147 |
147 |
147 |
143 |
100 |
|
Figure 2 and Figure 3 present the number of recovered files with differing numbers of subblocks, for grouped selection and separate selection, respectively. Using small subblocks allows the algorithms to tolerate more errors (modifications) because there is another ECC subblock for each seven subblocks in the block. One drawback is that a single error, which may have been contained in a single large subblock, can span several small subblocks. With grouped selection, neighboring subblocks are usually corrected by a single ECC subblock. Recall that ECC subblocks can only correct a single faulty subblock, so errors spanning consecutive subblocks usually result in a correction failure for grouped selection. Separate selection does a better job in this case because neighboring subblocks are always protected by different ECC subblocks. In either case, recipe size increases linearly with the number of subblocks.
Figure 2:
Number of recovered files for different number of subblocks using grouped selection
|
Figure 3:
Number of recovered files for different number of subblocks using separate selection
|
The above experiment only attempts to recover a file from older versions with the same path names. For example, file emacs-21.4/src/coding.c is compared with emacs-21.3/src/coding.c. We would like to answer the following, more general, question: given a target file 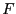 and a corpus of files and a corpus of files 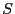 , with what probability can we find another file , with what probability can we find another file 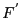 in in 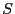 which is similar enough to which is similar enough to 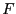 ? That is, given the error-correcting information of ? That is, given the error-correcting information of 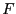 , we can reconstruct , we can reconstruct 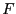 from from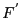 . We randomly selected 100 files from emacs-21.3 and attempted to recover each from the set of all files in emacs-21.2, excepting the file with the same path name. Using separate selection with 28 subblocks, we were only able to recover a single file in its entirety. . We randomly selected 100 files from emacs-21.3 and attempted to recover each from the set of all files in emacs-21.2, excepting the file with the same path name. Using separate selection with 28 subblocks, we were only able to recover a single file in its entirety.
The above experiment was performed at the level of complete files. We carried out a similar experiment at the block level, attempting to recover 100 random blocks from emacs-21.3 from the set of blocks contained in emacs-21.2, again excepting only blocks from the same file. We were only able to recover two such blocks.
Table. 4 shows more detailed results for separate selection with the following parameters:  , ,  , ,  , ,  and and 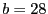 . `R #' is the number of files successfully recovered. The second column shows that the average sizes of the fuzzy file recipes are less than or equal to 18% of the full file sizes in all cases. `S %' is the size percentage of recovered files plus unchanged files, and hence is an indication of potential savings. The fourth column shows the total number of blocks in the unrecoverable files, and the fifth column shows the number of unrecoverable blocks. For example, a single unrecoverable block is preventing a 10-block file from being recovered in the emacs-21.4 distribution. . `R #' is the number of files successfully recovered. The second column shows that the average sizes of the fuzzy file recipes are less than or equal to 18% of the full file sizes in all cases. `S %' is the size percentage of recovered files plus unchanged files, and hence is an indication of potential savings. The fourth column shows the total number of blocks in the unrecoverable files, and the fifth column shows the number of unrecoverable blocks. For example, a single unrecoverable block is preventing a 10-block file from being recovered in the emacs-21.4 distribution.
Table 4:
Summary of more detailed experiment results.
| |
R # |
R |
S % |
B # |
E # |
21.3 21.4 21.4 |
9 |
18.00 |
99.81 |
10 |
1 |
21.2 21.3 21.3 |
296 |
17.92 |
58.08 |
2345 |
1678 |
21.1 21.2 21.2 |
243 |
17.98 |
62.11 |
2187 |
1525 |
20.7 21.1 21.1 |
213 |
13.85 |
7.39 |
4002 |
3523 |
|
5 Related Work
Fuzzy matching utilizes SHA-1 hash of a block's contents as the exact hash value. The use of content-hash to uniquely identify blocks (compare-by-hash) has been widely explored previously. For example, a unique hash of a block's contents is used as the block identifier for read and write operations in Venti [13]. Pastiche also employs content-hash to find redundant data across versions of files for backup [5].
Finding similar data blocks has also been extensively studied. Policroniades and Pratt evaluate three techniques for discovering identical pieces of data: whole file content hashing, fixed size blocking, and a chunking strategy [12]. Kulkarni et al. propose a scheme, called Redundancy Elimination at the Block Level (REBL), for storage reduction [8]. REBL uses super-fingerprints to reduce the data needed to identify similar blocks. TAPER [7] provides a content-based similarity detection technique which uses Bloom filters [2] to identify similar files.
In conjunction with conventional compression and caching, the Low Bandwidth File System (LBFS) [11] takes advantage of commonality between distinct files and successive versions of the same file in the context of a distributed file system. Lee et al. describe a technique, called operation-based update propagation, for efficiently transmitting updates to large files that have been modified on a weakly connected client of a distributed file system [9]. They also use error correcting codes to correct short replacements in similar blocks.
6 Conclusions
In this paper we describe the design, implementation, and performance of a fuzzy file block matching scheme. The main advantage of fuzzy file recipes is in saving network bandwidth as, for purposes of a wide-area file system, we can treat CPU cycles and disk space as effectively being free. If we accept the percentages shown in Table 4, the average file recipe size is about 18% of the size of the corresponding file. Hence, approximately one in five of recipes transmitted across the network must be ``useful'' (prevent a subsequent download of the corresponding file) in order for the system overall to reduce network bandwidth.
Our results anecdotally show that fuzzy file recipes are seldom able to find matches among random blocks. Instead, the utility of this approach would seem to lie in finding and exploiting commonality among different versions of the same files. For example, the distributer of a new version of the GNU Emacs source might pre-process files, identifying those files that can be recreated from one or more earlier versions of the source. Only those files would be included as fuzzy file recipes; the others would be distributed as either patches or complete copies. Though explicit patches would generally take less space than fuzzy file recipes, patches are only useful if the recipient has the exact version referenced by the patch. In the absence of complete information, fuzzy file recipes would be preferable.
Fuzzy file recipes would also be useful for versioning file systems [15]. Such systems are becoming more common as increasing disk capacities remove the incentive to destroy old file versions. In future work, we plan to expand ourdata set, try other error correcting codes, and experiment with more parameter combinations. Finally, we plan to integrate fuzzy matching into an existing distributed file system, such as MoteFS[6].
We thank Niraj Tolia and Kan-Leung Cheng for their valuable feedback and suggestions. We thank Henry Minsky for making the implementation of Reed-Solomon Code available and Hyang-Ah Kim for making the Rabin fingerprints code available. We also thank Benjie Chen et al. for opening the source code of their Low-Bandwidth Network File System.
- 1
- Gnu emacs, https://www.gnu.org/software/emacs/.
- 2
- BRODER, A., AND MITZENMACHER, M.
Network Applications of Bloom Filters: A Survey.
Internet Mathematics 1, 4 (2005), 485-509.
- 3
- BRODER, A. Z., GLASSMAN, S. C., MANASSE, M. S., AND ZWEIG, G.
Syntactic Clustering of the Web.
In Proceedings of the 6th International WWW Conference (April 1997).
- 4
- CLARK, G. C., AND CAIN, J. B.
Error-Correction Coding for Digital Communications.
New York: Plenum Press, June 1981.
- 5
- COX, L. P., MURRAY, C. D., AND NOBLE, B. D.
Pastiche: Making Backup Cheap and Easy.
In Proceedings of the Fifth USENIX Symposium on Operating Systems Design and Implementation (Boston, MA, December 2002), pp. 285-298.
- 6
- GABURICI, V., KELEHER, P., AND BHATTACHARJEE, B.
File System Support for Collaboration in the Wide Area.
In Proceedings of the 26th International Conference on Distributed Computing Systems (Lisboa, Portugal, July 2006).
- 7
- JAIN, N., DAHLIN, M., AND TEWARI, R.
TAPER: Tiered Approach for Eliminating Redundancy in Replica Synchronization.
In Proceedings of the 4th USENIX Conference on File and Storage Technologies (December 2005), pp. 281-294.
- 8
- KULKARNI, P., DOUGLIS, F., LAVOIE, J., AND TRACEY, J. M.
Redundancy Elimination within Large Collections of Files.
In Proceedings of the USENIX 2004 Annual Technical Conference (Boston, MA, June 2004), pp. 59-72.
- 9
- LEE, Y.-W., LEUNG, K.-S., AND SATYANARAYANAN, M.
Operation-based Update Propagation in a Mobile File System.
In Proceedings of the USENIX 1996 Annual Technical Conference (Monterey, CA, June 1996), pp. 43-56.
- 10
- MOON, T. K.
Error Correction Coding: Mathematical Methods and Algorithms.
Wiley-Interscience, June 2005.
- 11
- MUTHITACHAROEN, A., CHEN, B., AND MAZIERES, D.
A Low-Bandwidth Network File System.
In Proceedings of the 18th ACM Symposium on Operating Systems Principles (Chateau Lake Louise, Banff, Canada, October 2001), pp. 174-187.
- 12
- POLICRONIADES, C., AND PRATT, I.
Alternatives for Detecting Redundancy in Storage Systems Data.
In Proceedings of the USENIX 2004 Annual Technical Conference (Boston, MA, June 2004), pp. 73-86.
- 13
- QUINLAN, S., AND DORWARD, S.
Venti: A New Approach to Archival Storage.
In Proceedings of the First USENIX conference on File and Storage Technologies (January 2002), pp. 89-101.
- 14
- RABIN, M. O.
Fingerprinting by Random Polynomials.
Tech. Rep. TR-15-81, Center for Research in Computing Technology, Harvard University, 1981.
- 15
- SANTRY, D. S., FEELEY, M. J., HUTCHINSON, N. C., VEITCH, A. C., CARTON, R. W., AND OFIR, J.
Deciding When to Forget in the Elephant File System.
In Proceedings of the 17th ACM Symposium on Operating Systems Principles (near Charleston, SC, December 1999), pp. 110-123.
- 16
- TOLIA, N., KOZUCH, M., SATYANARAYANAN, M., KARP, B., PERRIG, A., AND BRESSOUD, T.
Opportunistic Use of Content Addressable Storage for Distributed File Systems.
In Proceedings of the USENIX 2003 Annual Technical Conference (San Antonio, TX, June 2003), pp. 127-140.
Implementation and Performance Evaluation of Fuzzy File Block Matching
This document was generated using the
LaTeX2HTML translator Version 2002-2-1 (1.71)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 -show_section_numbers -local_icons matching_final.tex
The translation was initiated by Bo Han on 2007-04-21



Bo Han
2007-04-21
|
