|
USENIX 2006 Annual Technical Conference Refereed Paper
[USENIX 2006 Annual Technical Conference Technical Program]
1 Introduction
The growth of the world-wide web to a size of billions of
pages, and the emergence of large-scale search engines that allow
real-time keyword searches over a large fraction of these pages,
has fundamentally changed the manner in which we locate and
access information. Such search engines work by downloading pages
from the web and then building a full-text index on the pages.
Thus, they are retrospective in nature, as they allow us
only to search for currently already existing pages - including
many outdated pages. In contrast, prospective search
allows a user to upload a query that will then be evaluated by
the search engine against documents encountered in the future. In
essence, the user subscribes to the results of the query. The
user can be notified of new matches in one of several ways, e.g.,
via email or an RSS reader.
A naive implementation of a prospective search engine might
simply execute all the subscription queries periodically against
any newly arrived documents. However, if the number of
subscriptions is very large, this would result either in a
significant delay in identifying new matches, if we only execute
the queries very rarely, or a significant query processing load
for the engine. Following the approach in [11], we essentially reverse the
roles of the documents and the queries. That is, we build an
inverted index on the subscriptions instead of the documents, and
then issue a number of queries into the index for each newly
arriving document. We note, however, that the two cases are not
completely symmetric. In this paper, we study techniques for
optimizing the performance of prospective search engines. A more
detailed version is available from the first author.
Applications of Prospective Search: One of the popular
implementations of prospective search is the News Alert
feature in Google News. It allows users to subscribe to a keyword
search, in which case they will be notified via email of any
newly discovered results matching all the terms. Similar services
include specialized search applications created for job or real
estate searches. Prospective search can be performed with the
help of RSS (RSS 2.0: Really Simple Syndication) feeds, which
allow web sites to syndicate their new content at a specified
URL. Thus, a prospective search engine can find the new content
on a site by periodically downloading the appropriate RSS feed.
There are a number of existing weblog and RSS search engines
based on RSS feeds, including PubSub, Bloglines, Technorati, and
Feedster.
Problem Setup: We are given 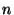 queries
queries 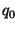 to to 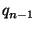 , where each query , where each query 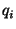 contains
contains 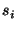 terms (keywords) terms (keywords)
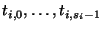 .
We define .
We define 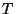 as the union of all the as the union of all the
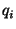 , i.e., the set of terms that
occur in at least one query. The terms in a query may be arranged
in some Boolean formula, though we will mainly focus on the AND
queries. Given these queries, we are allowed to precompute
appropriate data structures, say, an inverted index. After
preprocessing the queries, we are presented with a sequence of
documents , i.e., the set of terms that
occur in at least one query. The terms in a query may be arranged
in some Boolean formula, though we will mainly focus on the AND
queries. Given these queries, we are allowed to precompute
appropriate data structures, say, an inverted index. After
preprocessing the queries, we are presented with a sequence of
documents
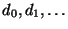 , where each
document , where each
document 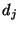 is a set of terms. We
assume that is a set of terms. We
assume that
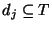 for all for all
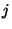 ; this can be enforced by
pruning from ; this can be enforced by
pruning from 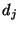 any terms that do
not occur in any query any terms that do
not occur in any query 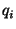 . We process
the documents one by one where for each . We process
the documents one by one where for each 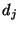 we have to determine all we have to determine all 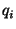 such that
such that 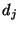 matches matches 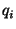 . Within our matching system, queries are assigned
integer query IDs (QID), and documents are assigned integer
document IDs (DID), and all terms in the queries and documents
are replaced by integer term IDs (TID). The output of the
matching process is a stream of (QID, DID) pairs indicating
matches. . Within our matching system, queries are assigned
integer query IDs (QID), and documents are assigned integer
document IDs (DID), and all terms in the queries and documents
are replaced by integer term IDs (TID). The output of the
matching process is a stream of (QID, DID) pairs indicating
matches.
While retrospective search engines typically store their index
on disk, we assume that for prospective search, all the index
structures fit into main memory. Tens of millions of queries can
be kept in memory on a single machine with the currently
available memory sizes. In case of more queries, our results
indicate that CPU cycles become a bottleneck before main
memory.
Discussion of Query Semantics: Most current search
engines assume AND semantics, where a query matches any document
containing all query terms, in combination with ranking. As we
show, AND queries can be executed very efficiently in an
optimized system for prospective search; moreover, several other
interesting types of queries can be efficiently reduced to AND
queries. Therefore, we focus on AND queries. Boolean queries
involve a number of terms connected by AND, OR, and NOT
operators. In our framework, they are executed by converting them
to DNF, inserting each conjunction as a separate AND query, and
then removing duplicate matches from the output stream.
In the RSS search scenario, it might be preferable to restrict
the keyword queries to certain fields. It is well understood that
inverted index structures with appropriate extensions can
efficiently process many such queries for retrospective search,
and similar extensions are also possible for prospective
search.
Contributions of this Paper:
- We describe the design of a high-performance subscription
matching processor based on an inverted index, with several
optimizations based on term frequencies and a Bloom filter
structure.
- We study preprocessing schemes that cluster subscriptions
into superqueries.
- We evaluate our schemes against a search engine trace, and
detail the performance improvements created by our
optimizations.
2 The Core Query Processor
In our query processor, TIDs are assigned from  to to 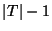 ,
and the terms in each query are ordered by TID; thus we can refer
to the first, second, etc., term in a query. Any incoming
documents have already been preprocessed by parsing out all
terms, translating them into TIDs, and discarding any duplicate
terms or terms that do not occur in any query. It will also be
convenient to assume that QIDs are assigned at random. Note that
we expect additions and deletions of subscriptions to be handled
in an amortized fashion, by periodic rebuilding of the structures
(including updating the assignments of TIDs and QIDs). ,
and the terms in each query are ordered by TID; thus we can refer
to the first, second, etc., term in a query. Any incoming
documents have already been preprocessed by parsing out all
terms, translating them into TIDs, and discarding any duplicate
terms or terms that do not occur in any query. It will also be
convenient to assume that QIDs are assigned at random. Note that
we expect additions and deletions of subscriptions to be handled
in an amortized fashion, by periodic rebuilding of the structures
(including updating the assignments of TIDs and QIDs).
The main data structure used in all our algorithms is an
inverted index, which is also used by retrospective
search engines. However, in our case we index the queries rather
than the documents, as proposed in [11]. The inverted index consists
of 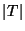 inverted lists, one
for each unique term that occurs in the queries. Each list
contains one posting for each query in which the corresponding
word occurs, where a posting consists of the QID and the position
of the term in the query (recall that terms are ordered within
each query by TID). The QID and position can usually be stored
together in a single 32-bit integer,
and thus each inverted list is a simple integer array. inverted lists, one
for each unique term that occurs in the queries. Each list
contains one posting for each query in which the corresponding
word occurs, where a posting consists of the QID and the position
of the term in the query (recall that terms are ordered within
each query by TID). The QID and position can usually be stored
together in a single 32-bit integer,
and thus each inverted list is a simple integer array.
2.1 A Primitive Matching Algorithm
We now describe the primitive matching algorithm, which (with
some variations) has been studied in a number of previous works
including [8,11,9,7]. The basic idea
is as follows. We initially build the inverted index from the
queries using standard index construction algorithms; see, e.g.,
[10]. We also reserve
space for a hash table, indexed by QIDs, of some sufficient size.
Given an incoming document consisting of a set of terms, we first
clear the hash table, and then process the terms in the document
in some sequential order. To process a term, we traverse the
corresponding inverted list in the index. For each posting of the
form (QID, position) in this list, we check if there is already
an entry in the hash table for this QID. If not, we insert such
an entry into the hash table, with an associated accumulator
(counter) set to 1. If an entry
already exists, we increase its accumulator by 1. This first phase is called the matching
phase.
In the second phase (testing phase), we iterate over
all created hash table entries. For every entry, we test if the
final value of the accumulator is equal to the number of query
terms; if so then we output the match between this query and the
document. Note that for Boolean queries other than AND, we could
reserve one bit in the accumulator for each term in the query,
and then instead of increasing a counter we set the corresponding
bit; in the testing phase we check if the accumulator matches the
query through tests applying appropriate bit masks. Also, since
QIDs are assigned at random, we can use the QID itself as our
hash function for efficiency.
2.2 Optimizations for Primitive Algorithm
Exploiting Position Information and Term Frequencies:
One problem with the primitive algorithm is that it creates an
entry in the hash table for any query that contains at least one
of the terms. This results in a larger hash table that in turn
slows down the algorithm, due to additional work that is
performed but also due to resulting cache misses during hash
lookups.
To decrease the size of the hash table, we first exploit the
fact that we are focusing on AND queries. Recall that each index
posting contains (QID, position) pairs. Thus, if we are
processing a posting with a non-zero position, then this means
that the term is not the term with the lowest TID in the query.
Suppose we process the terms in the incoming document in sorted
order, from lowest to highest TID. This means that for a posting
with non-zero position, either there already exists a hash entry
for the query, or the document does not contain any of the query
terms with lower TID, and thus the query does not match. So we
create a hash entry whenever the position in the posting is zero,
and only update existing hash entries otherwise. As we will see,
this results in significantly smaller hash table sizes. A further
reduction is achieved by simply assigning TIDs to terms in order
of frequency, that is, we assign TID 0
to the term that occurs the least frequent in the set of queries,
and TID 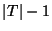 to the most
frequent term. This means that an accumulator is only created for
those queries where the incoming document contains the least
frequent term in the query. to the most
frequent term. This means that an accumulator is only created for
those queries where the incoming document contains the least
frequent term in the query.
To implement this efficiently, we split each inverted list
into two parts, a smaller list containing only postings with
positions equal to zero, and the rest of the list. We then
perform two passes over the terms in the incoming document, the
first pass generates the hash entries, and the second pass
updates the existing entries. This simplifies the critical inner
loop over the postings and also allows us to quickly determine
the optimal hash table size for each incoming document, by
summing up the lengths of the first parts of the inverted lists
involved.
Bloom Filters: As a result of the previous set of
optimizations, hash entries are only created initially, and most
of the time is spent afterwards on lookups to check for existing
entries. Moreover, most of these checks are negative, i.e., the
corresponding entry does not exist. In order to speed up these
checks, we propose to use a Bloom filter [2,3], which is a probabilistic
space-efficient method for testing set membership.
We use a Bloom filter in addition to the hash table. In the
matching phase, when hash entries are created, we also set the
corresponding bits in the Bloom filter; the overhead for this is
fairly low. In the testing phase, we first perform a lookup into
the Bloom filter to see if there might be a hash entry for the
current QID. If the answer is negative, we immediately continue
with the next posting; otherwise, we perform a lookup into the
hash table.
Use of a Bloom filter has two advantages. The Bloom filter
structure is small and thus gives better cache behavior, and the
innermost loop of our matching algorithm is also further
simplified. We experimented with different settings for the size
of the Bloom filter and the number of hash functions; our results
indicate that a single hash function (trivial Bloom filter)
performs best.
Partitioning the Queries: We note that the hash table
and Bloom filter sizes increase linearly with the number of query
subscriptions, and thus eventually grow beyond the L1 or L2 cache
sizes. This leads to our next optimization. Instead of creating a
single index, we partition the queries into a number 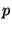 of subsets and build an index
on each subset. In other words, we partition the index into of subsets and build an index
on each subset. In other words, we partition the index into
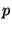 smaller indexes. An incoming
document is then processed by performing the matching
sequentially with each of the index partitions. While this does
not decrease the number of postings traversed, or the locality
for index accesses, it means that the hash table and Bloom filter
sizes that we need are decreased by a factor of smaller indexes. An incoming
document is then processed by performing the matching
sequentially with each of the index partitions. While this does
not decrease the number of postings traversed, or the locality
for index accesses, it means that the hash table and Bloom filter
sizes that we need are decreased by a factor of 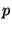 . .
2.3 Experimental Evaluation
Since we were unable to find any large publicly available
query subscription logs, we decided to use Excite search engine
query logs, collected in 1999. We note that query subscriptions
in a prospective engine would likely be different in certain ways
from standard retrospective queries; in particular, we would not
expect as many extremely broad queries. For this reason, we will
also look at how performance changes with query selectivity, by
looking at different subsets of the query logs. To be used as
incoming documents, we selected 10,000 web pages at random from a large crawl of over
120 million pages from Fall
2001.
We removed stop words and duplicate queries from the query
trace, and also converted all the terms to lower case. We also
removed queries that contained more than 32 terms; there were only 43
such queries out of a total of 1,077,958 distinct queries. Some statistics on the query
logs, documents, and resulting inverted index lookups is as
follows: There are 271,167 unique
terms in the query log, and each query contains about 3.4 terms on average. The number
of postings in the index is 3,633,970. Each incoming document contains about
144 distinct terms that also
occur in the queries. For each document, our algorithms will
visit about 200,000 postings, or about
1,400 postings per inverted list
that is traversed. Of those postings, only about 6,630 have position zero if we assign TIDs according
to term frequencies.
To experiment with numbers of queries beyond the size of the
query log, we replicated the queries several times according to a
multiplier between 1 and 14, for a maximum size of about
15 million queries. We note that
the core query processor does not exploit similarities between
different queries, and thus we believe that this scaling approach
is justified. Later, in Section 3, we will incorporate
clustering techniques into our system that exploit such
similarities; for this reason we will not use a multiplier in the
later evaluation of the clustering schemes, which limits us to
smaller input sizes.
In the experiments, we report the running times of the various
optimizations when matching different numbers of queries against
10,000 incoming documents. The
experiments are performed on a machine with a 3.0 Ghz Pentium4
processor with 16 KB L1 and 2 MB L2 cache, under a Linux
2.6.12-Gentoo-r10 environment. We used the gcc compiler
with Pentium4 optimizations. We also used the vtune
performance tools to analyze program behavior such as cache hit
ratio etc. In the charts, we separately show the times spent on
the matching and testing phases. Note that the matching phase
includes all inverted index traversals and the creation and
maintenance of the accumulators, while the testing phase merely
iterates over the created accumulators to identify matches.
Figure 2.1: Running times of the various
algorithm optimizations for different numbers of queries.
 |
In Figure 2.1,
we show the time spent by four versions of our query processor:
(i) the primitive one, (ii) with optimization for AND and
assignment of TIDs by frequency, (iii) with Bloom filter, and
(iv) with index partitioning with optimal choice of the number of
partitions. We show total running times in seconds for matching
10,000 documents against the
queries with multipliers of 1, 4, and 14. At first glance, running
times are roughly linear in the number of queries. More exactly,
they are slightly more than linear for the first three
algorithms, due to the increased sizes of the hash table and
Bloom filter structures resulting in more cache misses, while the
best algorithm (iv) remains linear by increasing the number of
partitions.
As discussed, many Excite queries may have much larger result
sizes than typical subscription queries would have. To examine
possible relationships between matching performance and query
selectivities, we partitioned our queries into quintiles
according to selectivity. To do so, we matched all queries
against a larger collection of around 144,000 documents (disjoint from the set of
10,000 we used for testing), and
counted the number of matches of each query. We then partitioned
queries into five subsets, from the
20% with the fewest number of matches to the 20% with the most. In the
Figure 2.2, we show how the
running times of the algorithms change as we go from queries with
very few results (leftmost 4 bars)
to queries with very many results (rightmost 4 bars). Not surprisingly, queries with many matches
are more costly. (Since we use a multiplier of 1, the partitioning does not seem to give any benefits
in the figure.)
Figure 2.2: Running times versus query
selectivities for the various algorithms, with multiplier 1.
 |
To illustrate the benefits of index partitioning, we performed
additional runs on a machine with 512 KB instead of
2 MB of
L2 cache. As shown in Figure 2.3, index partitioning resulted
in a gain by about a factor of 4 for
the largest query set. On the 2 MB
machine, a similar effect is expected for larger query
multipliers.
Figure 2.3: Benefit of best possible index
partitioning on a machine with smaller L2 cache.
 |
3 Optimizations using Query ClusteringIn this section, we
study clustering techniques to obtain additional performance
benefits. We note that clustering of subscriptions has been
previously studied, e.g., in [8], but in the context of
more structured queries. Our simple approach for clustering
subscriptions is as follows. In a preprocessing step, we cluster
all queries into artificial superqueries of up to a
certain size, such that every query is contained in a superquery
and shares the same least frequent term with a superquery (and
thus with all other queries in the cluster). Then we present
these superqueries to the query processor, which indexes them and
performs matching exactly as before. Thus the resulting
improvements are orthogonal to the earlier techniques. The only
changes to the core subscription processor are as follows: (i)
During matching, we set appropriate bits in the accumulators for
each update instead of counting, and (ii) in the testing phase we
need to test each query that is contained in a superquery that
has an accumulator. To do this test, we create a simple structure
for each superquery during preprocessing that contains a list of
the QIDs of the contained queries, plus for each QID a bit mask
that can be used to test the superquery accumulator for this
subquery.
We now discuss briefly how clustering impacts the cost of
matching. Consider any two queries (or superqueries) that share
the same least frequent term. Note that by combining these two
queries into one superquery, we are guaranteed to decrease the
size of the index by at least one posting. Moreover, the number
of hash entries created and accumulator updates performed during
the matching phase will never increase but may often decrease as
a result of combining the two queries. On the other hand, we need
at least one bit per term in the superquery for the accumulator,
and a very large superquery would result in higher costs for both
testing and hash table accesses. However, this effect is not easy
to capture with a formal cost model for clustering. Instead, we
will impose an upper bound  on the
size of each superquery, and try to minimize index size under
this constraint. In general, this problem is still intractable,
and we will focus on some heuristics. on the
size of each superquery, and try to minimize index size under
this constraint. In general, this problem is still intractable,
and we will focus on some heuristics.
3.1 Greedy Algorithms for Clustering
All the algorithms we present in this subsection follow the
clustering approach discussed above. They start out by initially
grouping all queries into pools based on their least frequent
terms, and then separately build superqueries within each pool.
Note that if we use index partitioning, we should make sure to
assign all queries in a pool to the same partition.
Random Selection: The simplest approach starts with the
empty superquery and then repeatedly picks an arbitrary query
from the pool and merges it into the superquery, as long as the
resulting superquery has at most b=32 terms (apart from the least frequent term). If the
result has more than b terms, then we
write out the old superquery and start a new one.
Alphabetical Ordering: We first sort all queries in the
pool in reverse alphabetical order - recall that the terms in
each query are sorted by frequency and thus we sort according to
most common, second most common, etc. terms. We then consider
queries in sorted order as we construct superqueries, rather than
in arbitrary order.
Overlap Ratio: The third greedy algorithm builds
superqueries by checking all remaining queries in the pool to
find the one with the best match, i.e., a query that has a lot of
terms in common with the current superquery.
3.2 Experimental Evaluation
We cannot use the multiplier method of Section 2.3 in the evaluation of
the proposed clustering algorithms since they exploit the
similarities among the queries in the collection. In order to
obtain at least a slightly larger collection of queries, we
combined the Excite queries with another set of queries from the
AltaVista search engine. The combined set contains 3,069,916 queries and
922,699 unique terms. The number
of postings in the resulting index is 9,239,690. We first compare the performance of the
proposed clustering algorithms in Table 3.1 when b is set to
32 terms. The
best algorithm from the previous section is shown on the last
row. Even the most naive clustering algorithm gives significant
benefits, and the algorithm based on overlap outperforms all
others.
Table 3.1: Running time of the clustering
algorithms on the combined query set (in seconds).
| |
Matching |
Testing |
Total |
| Random |
16.83 |
1.35 |
18.18 |
| Alphabetical |
14.42 |
1.34 |
15.76 |
| Overlap |
13.71 |
1.34 |
15.05 |
| Best
non-clustered |
33.28 |
6.34 |
39.62 |
In Table 3.2, we
show the number of superqueries created by each clustering
algorithm, the number of postings in the resulting inverting
index, and the number of accumulators created during the matching
process. As we see, clustering decreases the number of index
postings by about 40%, but the
number of accumulators created during the matches is reduced by a
factor of up to 20. This is
because clustering is most effective for large query pools that
have a significant number of queries with the same least common
query term that can be combined.
Table 3.2: Comparison of the clustering
algorithms and the best algorithm.
| |
(Super)
queries |
Postings |
Accumulators |
| Random |
957366 |
6089165 |
8870966 |
| Alphabetical |
948417 |
5784684 |
7670446 |
| Overlap |
939779 |
5522510 |
6543883 |
| Best |
3069916 |
9239690 |
130691462 |
Next, we investigated if there are benefits in allowing larger
superqueries with up to 64, 96, and 128 terms. We observed that there is a slight benefit in
allowing up to 64 terms, but for
96 and 128 terms any further gains are lost to additional testing
time. We also tried to improve the greedy approach based on
overlap by looking further ahead at the next 2 and
3 sets that can
be added, as opposed to a strictly one step at a time approach.
However, we did not observe any measurable gains, indicating that
maybe the overlap approach is already close to optimal. We ran
the clustering algorithms on the different selectivity ranges,
introduced in Section 2.3, which showed that
again queries with many results are more expensive to match (we
omit the figures due to space limitations). Finally, we summarize
our results by showing the throughput rates in documents per
second obtained by our various matching algorithms in Figure
3.1, on the Excite
set and the combined set of Excite and AltaVista queries. We see
that overall, throughput increases by more than a factor of
20 when all techniques are
combined.
Figure 3.1: Number of documents processed
per second for Excite and for the combined query set. (In
overlap-sq2, the superqueries can have up to 64 terms,
using two unsigned integers.)
 |
4 Related Work
Our work is most closely related to the SIFT project in
[11], which also focuses
on keyword queries and uses an inverted index structure on the
queries. In SIFT, the emphasis is on ranked queries and the
queries are represented in the vector space model using OR
semantics. Thus, users can specify term weights and a relevance
threshold (e.g., cosine measure) that are then used in
identifying matching documents. A main memory algorithm for
matching events against subscriptions is proposed in [8], where an event is an
attribute/value pair, and a subscription is a conjunction of
(attribute, comparison operator, constant) predicates. The
proposed algorithm also employs a clustering approach. The
created clusters have access predicates, where an access
predicate is defined as a conjunction of equality predicates. In
our approach, we create clusters with new artificial
superqueries. The scenario we consider is different, as the terms
in the queries as well as the content of the incoming documents
are keywords. Another body of related work is in the area of
content-based networking and publish/subscribe communication
systems [1,6]. In this model, subscribers
specify their interests by conjunctive predicates, while sources
publish their messages as a set of attribute/value pairs. The
goal is to efficiently identify and route messages to the
interested subscribers [5,4]. The forwarding algorithms
used by the routing nodes are related to our query processing
algorithm; see [7]. Previous related
work exists in the database literature about triggers and
continuous queries; in stream processing and XML filtering
systems.
5 Acknowledgments
We thank the anonymous Usenix reviewers and our shepherd John
Reumann for their comments and insights.
- 1
- R. Baldoni, M. Contenti, and A. Virgillito.
The evolution of publish/subscribe communication systems.
In Future Directions of Distributed Computing, volume
2584 of LNCS. Springer, 2003.
- 2
- B. Bloom.
Space/time trade-offs in hash coding with allowable
errors.
Communications of the ACM, 13(7):422-426, 1970.
- 3
- A. Broder and M. Mitzenmacher.
Network applications of bloom filters: A survey.
In Proc. of the 40th Annual Allerton Conf. on
Communication, Control, and Computing, pages 636-646,
2002.
- 4
- F. Cao and J. P. Singh.
Efficient event routing in content-based publish-subscribe
service networks.
In Proc. of IEEE Infocom Conf., 2004.
- 5
- A. Carzaniga, M. J. Rutherford, and A. L. Wolf.
A routing scheme for content-based networking.
In Proc. of IEEE Infocom Conf., 2004.
- 6
- A. Carzaniga and A. L. Wolf.
Content-based networking: A new communication
infrastructure.
In NSF Workshop on an Infrastructure for Mobile and
Wireless Systems, 2001.
- 7
- A. Carzaniga and A. L. Wolf.
Forwarding in a content-based network.
In Proc. of ACM Sigcomm, 2003.
- 8
- F. Fabret, H. A. Jacobsen, F. Llirbat, J. Pereira, K. A.
Ross, and D. Shasha.
Filtering algorithms and implementation for very fast publish
subscribe systems.
In Proc. of ACM Sigmod Conf., 2001.
- 9
- J. Pereira, F. Fabret, F. Llirbat, and D. Shasha.
Efficient matching for web-based publish/subscribe
systems.
In Conf. on Cooperative Information Systems,
2000.
- 10
- I. H. Witten, A. Moffat, and T. C. Bell.
Managing Gigabytes: Compressing and Indexing Documents and
Images.
Morgan Kaufmann, second edition, 1999.
- 11
- T. W. Yan and H. Garcia-Molina.
The SIFT information dissemination system.
ACM Transactions on Database Systems, 24(4):529-565,
1999.
|
