


Next: Role Classification
Up: Model
Previous: Model
Defining Similarity
We use connection behavior as a basis for host grouping, because that
information is easily available by just monitoring the network. To
group hosts, we need to define similarity in a way that captures the
extent to which pairs of hosts establish connections to the same set of
other hosts. We start by defining similarity between hosts as a function
of the number of common hosts with which they communicate. Intuitively,
hosts that share the same logical role communicate with similar sets of
hosts.
A connection is a pair consisting of a source host address and a
destination host address. The connection set of a host, C(h), is
the set,
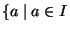 and there is a connection between h and
a}. If
and there is a connection between h and
a}. If
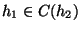 , then
, then
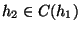 . We define the
relation neighbor(h1, h2) to be true if and only if h1 = h2
or
. We define the
relation neighbor(h1, h2) to be true if and only if h1 = h2
or
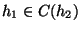 . For later use, we extend the definition of
neighbor to groups by defining neighbor(G1, G2) to be true if
and only if there exists a host
. For later use, we extend the definition of
neighbor to groups by defining neighbor(G1, G2) to be true if
and only if there exists a host 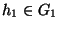 that is a
neighbor of another host
that is a
neighbor of another host 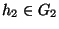 .
We can use the notion of a connection set to provide a simple definition
of similarity:
.
We can use the notion of a connection set to provide a simple definition
of similarity:
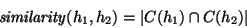 |
(1) |
That is to say that similarity(h1, h2) is equal to the number of
neighbors that h1 and h2 have in common.
We are now in a position to specify the requirements of a grouping
algorithm. Given a set of hosts, I and a similarity threshold,
Smin, it must find a partitioning, P, of I that is maximal with
respect to avg_similarity and Smin, i.e.,
- P respects avg_similarity. This constraint guarantees that
each host is within the group with which it has the strongest average
similarity.
- For all
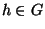 and
and 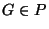 , avg_similarity(h, G)
, avg_similarity(h, G)
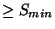 . This requirement guarantees that each host in a group is
sufficiently closely related to every other host in the group, thus
ensuring that groups are not too large.
. This requirement guarantees that each host in a group is
sufficiently closely related to every other host in the group, thus
ensuring that groups are not too large.
- There is no other partitioning P of I that meets the first
two requirements and has a larger average group size. This guarantees
that groups are not too small.
This specification is independent of the definition of
avg_similarity. For some networks, such as the one represented in
Figure 1, the above definition of
avg_similarity yields excellent results. However, for others a
slightly more complex definition works better. We present such a
definition in Section 4.2.


Next: Role Classification
Up: Model
Previous: Model
Godfrey Tan
2003-04-01
