


Next: Testing Different Feature Construction
Up: Analyzing System Logs: A
Previous: Ranking Messages by Exceptionality
Using Rank Correlation for Feature Construction
In the original feature-set of our dataset, system log 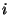 is represented as the message count vector
is represented as the message count vector 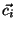 defined above. There are
defined above. There are 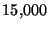 message types in our dataset, hence this results in a
message types in our dataset, hence this results in a
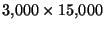 matrix. This matrix is very sparse; only about 0.6% of the entries are non-zero. The high dimensionality of the data and its sparseness make k-means clustering impractical for this representation.
Since our objective is message ranking, we propose a new feature construction scheme of the system-log dataset that measures the difference in the ranking of messages between system logs. Two known rank correlation measures can be used to achieve this: The Spearman rank correlation [12] and Kendall's tau rank correlation [12].
Let
matrix. This matrix is very sparse; only about 0.6% of the entries are non-zero. The high dimensionality of the data and its sparseness make k-means clustering impractical for this representation.
Since our objective is message ranking, we propose a new feature construction scheme of the system-log dataset that measures the difference in the ranking of messages between system logs. Two known rank correlation measures can be used to achieve this: The Spearman rank correlation [12] and Kendall's tau rank correlation [12].
Let 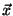 and
and 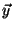 be vectors of dimension
be vectors of dimension 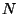 . Let
. Let 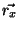 and
and 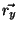 be vectors of ranks for
be vectors of ranks for 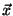 and
and 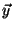 , i.e.
, i.e.
![$ r_x\!\left[i\right] = k$](img25.png) if
if
![$ x\!\left[i\right]$](img26.png) is the
is the 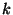 'th largest number in
'th largest number in 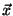 , and similarly for
, and similarly for 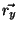 .3
The two correlation measures are defined as follows:
.3
The two correlation measures are defined as follows:
Definition 1 (Spearman Rank Correlation)
Let
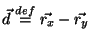
.
The Spearman rank Correlation between
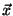
and
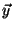
is defined by:
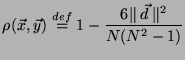 |
(1) |
Definition 2 (Kendall's Tau Rank Correlation)
Let
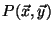
be the number of pairs
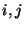
such that both
![$ r_x\!\left[i\right]>r_x\!\left[j\right]$](img32.png)
and
![$ r_y\!\left[i\right]>r_y\!\left[j\right]$](img33.png)
.
Kendall's tau rank correlation between
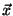
and
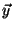
is defined by:
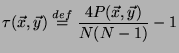 |
(2) |
We first define a new Spearman-based feature-set. In this feature-set, system log 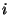 is represented by the vector
is represented by the vector
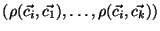 , where
, where 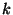 is the number of samples in our dataset. A Kendall's-tau-based feature-set can be generated in an analogous way. The resulting matrix is a sample correlation matrix, and the new feature-set has
is the number of samples in our dataset. A Kendall's-tau-based feature-set can be generated in an analogous way. The resulting matrix is a sample correlation matrix, and the new feature-set has 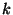 dimensions instead of the much larger
dimensions instead of the much larger 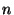 (the number of different message types in the dataset). It is generally expected that in a typical dataset,
(the number of different message types in the dataset). It is generally expected that in a typical dataset, 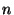 would be much larger than
would be much larger than 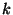 as it is in our own dataset, because of the diversity of possible messages in a computer system.
It is interesting to note that using either the Spearman-based feature-set or the Kendall's-tau-based feature set generates a kernel similarity matrix for the original dataset. This opens the possibility of using these correlation measures in kernel-based algorithms [9]. We prove that both sample correlation matrices are kernel matrices, using the fact that a kernel matrix is a Positive Semi-Definite (PSD) matrix. A matrix
as it is in our own dataset, because of the diversity of possible messages in a computer system.
It is interesting to note that using either the Spearman-based feature-set or the Kendall's-tau-based feature set generates a kernel similarity matrix for the original dataset. This opens the possibility of using these correlation measures in kernel-based algorithms [9]. We prove that both sample correlation matrices are kernel matrices, using the fact that a kernel matrix is a Positive Semi-Definite (PSD) matrix. A matrix 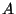 is PSD if for any non-zero vector
is PSD if for any non-zero vector 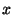 ,
,
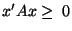 [9].
We first prove that the Pearson Sample Correlation matrix [12] is PSD, and then conclude that so are the Spearman rank correlation matrix and the Kendall's-tau sample correlation matrix.
[9].
We first prove that the Pearson Sample Correlation matrix [12] is PSD, and then conclude that so are the Spearman rank correlation matrix and the Kendall's-tau sample correlation matrix.
Definition 3 (Pearson Sample Correlation)
Let
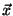
and
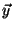
be vectors of the same dimension.
The Pearson correlation coefficient is defined by:
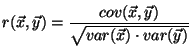 |
(3) |
where
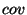
is the sample covariance function and
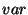
is the sample variance function.
Theorem 1
A Pearson sample correlation matrix is PSD.
Proof.
Let
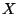
be a matrix in which each row is a sample. Let
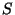
be a diagonal matrix such that entry
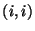
is the variance of row
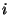
in
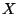
. Assume, without loss of generality, that the mean of each sample in
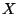
is zero. Then the Pearson correlation matrix can be written in vector form as:
For any non-zero vector
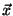
, the expression
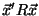
can be written as:
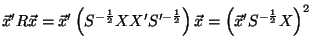 |
(4) |
The rightmost element is a square term, hence it is greater than or equal to zero. Therefore
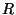
is PSD.

Theorem 2
A Spearman rank correlation matrix is PSD.
Proof.
Spearman correlation is Pearson correlation applied to ranks [
4]. Therefore, the Spearman rank correlation matrix is PSD.

Theorem 3
A Kendall's-tau correlation matrix is PSD.
Proof.
For a vector
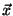
of dimension
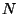
, let
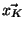
of dimension
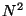
be defined by:
![$\displaystyle x_K\!\left[j+(i-1)\cdot N\right] =
\left\{
\begin{array}{ll}
...
...i\right]>r_x\!\left[j\right]
0 & \textrm{otherwise}
\end{array}
\right.$](img52.png) |
(5) |
Then
![$ P(\vec{x},\vec{y}) = \sum_{k=1}^{N^2}x_K\!\left[k\right]\cdot y_K\!\left[k\right]$](img53.png)
, and it can be easily verified that Kendall's tau correlation of
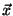
and
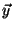
is the Pearson correlation of
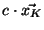
and
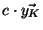
, for
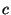
a constant that depends on
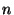
. Hence, Kendall's tau correlation matrix is also a Pearson correlation matrix, and so it is PSD.



Next: Testing Different Feature Construction
Up: Analyzing System Logs: A
Previous: Ranking Messages by Exceptionality
2007-03-12
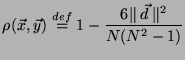

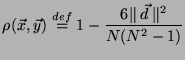
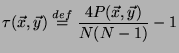
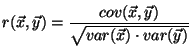
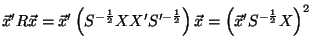
![$\displaystyle x_K\!\left[j+(i-1)\cdot N\right] =
\left\{
\begin{array}{ll}
...
...i\right]>r_x\!\left[j\right]
0 & \textrm{otherwise}
\end{array}
\right.$](img52.png)