
Figure 3: Examples of images and corresponding expressions.

One proposed hash visualization algorithm is Random Art, a technique that converts meaningless strings into abstract structured images. Random Art was developed by Andrej Bauer, and is based on an idea of genetic art by Michael Witbrock and John Mount. Originally Random Art was conceived for automatic generation of artistic images. A brief overview and demonstration of Random Art can be found at Andrej's Random Art web site [Bau98].
The basic idea is to use a binary string as a seed for a random number generator. The randomness is used to construct a random expression which describes a function generating the image--mapping each image pixel to a color value. The pixel coordinates range continuously from to , in both and dimensions. The image resolution defines the sampling rate of the continuous image. For example, to generate a image, we sample the function at locations.
Random Art is an algorithm such that given a bit-string as input, it will generate a function , which defines an image. The bit-string input is used as a seed for the pseudo-random number generator, and the function is constructed by choosing rules from a grammar depending on the value of the pseudo-random number generator. The function maps each pixel to a RGB value (r,g,b) which is a triple of intensities for the red, green and blue values, respectively. For example, the expression produces a horizontal gray grade, as shown in figure 3(a). A more complicated example is the following expression, which is shown in figure 3(b).

Figure 3: Examples of images and corresponding expressions.

Figure 4: Random Art expression tree and the corresponding image
The function can also be seen as an expression tree, which is
generated using a grammar and a depth parameter d, which
specifies the minimum depth of the expression tree that is generated. The
grammar defines the structure of the expression trees. It is a version of a
context-free grammar, in which alternatives are labeled with probabilities. In
addition, it is assumed that if the first alternative in the rule is followed
repeatedly, a terminal clause is reached. This condition is needed when the
algorithm needs to terminate the generation of a branch. For illustration,
consider the following simple grammar:
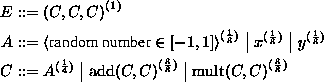
The numbers in subscripts are the probabilities with which alternatives are chosen by the algorithm. There are three rules in this simple grammar. The rule specifies that an expression is a triple of compound expression . The rule says that every compound expression is an atomic expression with probability , or either the function or applied to two compound expressions, with probabilities for each function. An atomic expression is either a constant, which is generated as a pseudorandom floating point number, or one of the coordinates or . All functions appearing in the Random Art algorithm are scaled so that they map the interval to the interval . This condition ensures that all randomly generated expression trees are valid. For example, the scaling for the add function is achieved by defining .
The grammar used in the Random Art implementation is too large to be shown in this paper. Other functions included are: sin, cos, exp, square root, division, mix. The function is a function which blends expressions and depending on the parameters and . We show an example of an expression tree of depth in figure 4, along with the corresponding image. For the other images in this paper, we used a depth of 12.