
Atul Singh![]() , Pedro Fonseca
, Pedro Fonseca![]() , Petr
Kuznetsov
, Petr
Kuznetsov![]() , Rodrigo Rodrigues
, Rodrigo Rodrigues![]() , Petros Maniatis
, Petros Maniatis![]()
![]() MPI-SWS,
MPI-SWS, ![]() Rice University,
Rice University,
![]() TU Berlin/Deutsche Telekom Laboratories,
TU Berlin/Deutsche Telekom Laboratories, ![]() Intel Research Berkeley
Intel Research Berkeley
Many distributed services are hosted at large, shared, geographically diverse data centers, and they use replication to achieve high availability despite the unreachability of an entire data center. Recent events show that non-crash faults occur in these services and may lead to long outages. While Byzantine-Fault Tolerance (BFT) could be used to withstand these faults, current BFT protocols can become unavailable if a small fraction of their replicas are unreachable. This is because existing BFT protocols favor strong safety guarantees (consistency) over liveness (availability).
This paper presents a novel BFT state machine replication protocol called Zeno that trades consistency for higher availability. In particular, Zeno replaces strong consistency (linearizability) with a weaker guarantee (eventual consistency): clients can temporarily miss each other's updates but when the network is stable the states from the individual partitions are merged by having the replicas agree on a total order for all requests. We have built a prototype of Zeno and our evaluation using micro-benchmarks shows that Zeno provides better availability than traditional BFT protocols.
Data centers are becoming a crucial computing platform for large-scale Internet services and applications in a variety of fields. These applications are often designed as a composition of multiple services. For instance, Amazon's S3 storage service and its e-commerce platform use Dynamo [15] as a storage substrate, or Google's indices are built using the MapReduce [14] parallel processing framework, which in turn can use GFS [18] for storage.
Ensuring correct and continuous operation of these services is critical, since downtime can lead to loss of revenue, bad press, and customer anger [5]. Thus, to achieve high availability, these services replicate data and computation, commonly at multiple sites, to be able to withstand events that make an entire data center unreachable [15] such as network partitions, maintenance events, and physical disasters.
When designing replication protocols, assumptions have to be made about the types of faults the protocol is designed to tolerate. The main choice lies between a crash-fault model, where it is assumed nodes fail cleanly by becoming completely inoperable, or a Byzantine-fault model, where no assumptions are made about faulty components, capturing scenarios such as bugs that cause incorrect behavior or even malicious attacks. A crash-fault model is typically assumed in most widely deployed services today, including those described above; the primary motivation for this design choice is that all machines of such commercial services run in the trusted environment of the service provider's data center [15].
Unfortunately, the crash-fault assumption is not always valid even in trusted environments, and the consequences can be disastrous. To give a few recent examples, Amazon's S3 storage service suffered a multi-hour outage, caused by corruption in the internal state of a server that spread throughout the entire system [2]; also an outage in Google's App Engine was triggered by a bug in datastore servers that caused some requests to return errors [19]; and a multi-day outage at the Netflix DVD mail-rental was caused by a faulty hardware component that triggered a database corruption event [28].
Byzantine-fault-tolerant (BFT) replication protocols are an attractive solution for dealing with such faults. Recent research advances in this area have shown that BFT protocols can perform well in terms of throughput and latency [23], they can use a small number of replicas equal to their crash-fault counterparts [37,9], and they can be used to replicate off-the-shelf, non-deterministic, or even distinct implementations of common services [29,36].
However, most proposals for BFT protocols have focused on strong
semantics such as linearizability [22], where intuitively the
replicated system appears to the clients as a single, correct, sequential
server. The price to pay for such strong semantics is that each
operation must contact a large subset (more than
![]() , or in
some cases
, or in
some cases
![]() ) of the replicas to conclude, which can cause
the system to halt if more than a small fraction (
) of the replicas to conclude, which can cause
the system to halt if more than a small fraction (
![]() or
or
![]() , respectively) of the replicas are unreachable due to
maintenance events, network partitions, or other non-Byzantine faults.
This contrasts with the philosophy of systems deployed in corporate
data centers [15,34,21], which favor
availability and performance, possibly sacrificing the semantics of
the system, so they can provide continuous service and meet tight
SLAs [15].
, respectively) of the replicas are unreachable due to
maintenance events, network partitions, or other non-Byzantine faults.
This contrasts with the philosophy of systems deployed in corporate
data centers [15,34,21], which favor
availability and performance, possibly sacrificing the semantics of
the system, so they can provide continuous service and meet tight
SLAs [15].
In this paper we propose Zeno, a new BFT replication protocol designed to meet the needs of modern services running in corporate data centers. In particular, Zeno favors service performance and availability, at the cost of providing weaker consistency guarantees than traditional BFT replication when network partitions and other infrequent events reduce the availability of individual servers.
Zeno offers eventual consistency semantics [17], which intuitively means that different clients can be unaware of the effects of each other's operations, e.g., during a network partition, but operations are never lost and will eventually appear in a linear history of the service--corresponding to that abstraction of a single, correct, sequential server--once enough connectivity is re-established.
In building Zeno we did not start from scratch, but instead adapted Zyzzyva [23], a state-of-the-art BFT replication protocol, to provide high availability. Zyzzyva employs speculation to conclude operations fast and cheaply, yielding high service throughput during favorable system conditions--while connectivity and replicas are available--so it is a good candidate to adapt for our purposes. Adaptation was challenging for several reasons, such as dealing with the conflict between the client's need for a fast and meaningful response and the requirement that each request is brought to completion, or adapting the view change protocols to also enable progress when only a small fraction of the replicas are reachable and to merge the state of individual partitions when enough connectivity is re-established.
The rest of the paper is organized as follows. Section 2 motivates the need for eventual consistency. Section 3 defines the properties guaranteed by our protocol. Section 4 describe how Zeno works and Section 5 sketches the proof of its correctness. Section 6 evaluates how our implementation of Zeno performs. Section 7 presents related work, and Section 8 concludes.
Various levels and definitions of weak consistency have been proposed by different communities [16], so we need to justify why our particular choice is adequate. We argue that eventual consistency is both necessary for the guarantees we are targetting, and sufficient from the standpoint of many applications.
Consider a scenario where a network partition occurs, that causes half of the replicas from a given replica group to be on one side of the partition and the other half on the other side. This is plausible given that replicated systems often spread their replicas over multiple data centers for increased reliability [15], and that Internet partitions do occur in practice [6]. In this case, eventual consistency is necessary to offer high availability to clients on both sides of the partition, since it is impossible to have both sides of the partitions make progress and simultaneously achieve a consistency level that provided a total order on the operations (``seen'' by all client requests) [7]. Intuitively, the closest approximation from that idealized consistency that could be offered is eventual consistency, where clients on each side of the partition agree on an ordering (that only orders their operations with respect to each other), and, when enough connectivity is re-established, the two divergent states can be merged, meaning that a total order between the operations on both sides can be established, and subsequent operations will reflect that order.
Additionally, we argue that eventual consistency is sufficient from the standpoint of the properties required by many services and applications that run in data centers. This has been clearly stated by the designers of many of these services [15,34,21,3,13]. Applications that use an eventually consistent service have to be able to work with responses that may not include some previously executed operations. To give an example of applications that use Dynamo, this means that customers may not get the most up-to-date sales ranks, or may even see some items they deleted reappear in their shoping carts, in which case the delete operation may have to be redone. However, those events are much preferrable to having a slow, or unavailable service.
Beyond data-center applications, many other examples of eventually consistent services has been deployed in common-use systems, for example, DNS. Saito and Shapiro [30] provide a more thourough survey of the theme.
We now informally specify safety and liveness properties of a generic eventually consistent BFT service. The formal definitions appear in a separate technical report due to lack of space [31].
Informally, our safety properties say that an eventually consistent system behaves
like a centralized server whose service state can be modelled as a
multi-set. Each element of the multi-set is a history (a totally ordered
subset of the invoked operations), which
captures the intuitive notion that some operations
may have executed without being aware of each other, e.g., on different
sides of a network partition, and are therefore only ordered with
respect to a subset of the requests that were executed.
We also limit the total number of divergent histories, which in the
case of Zeno cannot exceed, at any time,
![]() ,
where
,
where
![]() is the current number of failed servers,
is the current number of failed servers,
![]() is the total number of servers
and
is the total number of servers
and ![]() is the maximum number of servers that can fail.
is the maximum number of servers that can fail.
We also specify that certain operations are committed. Each history has a prefix of committed operations, and the committed prefixes are related by containment. Hence, all histories agree on the relative order of their committed operations, and the order cannot change in the future. Aside from this restriction, histories can be merged (corresponding to a partition healing) and can be forked, which corresponds to duplicating one of the sets in the multi-set.
Given this state, clients can execute two types of operations, weak and strong, as follows. Any operation begins its execution cycle by being inserted at the end of any non-empty subset of the histories. At this and any subsequent time, a weak operation may return, with the corresponding result reflecting the execution of all the operations that precede it. In this case, we say that the operation is weakly complete. For strong operations, they must wait until they are committed (as defined above) before they can return with a similar way of computing the result. We assume that each correct client is well-formed: it never issues a new request before its previous (weak or strong) request is (weakly or strongly, respectively) complete.
The merge operation takes two histories and produces a new history, containing all operations in both histories and preserving the ordering of committed operations. However, the weak operations can appear in arbitrary ordering in the merged histories, preserving the causal order of operations invoked by the same client. This implies that weak operations may commit in a different order than when they were weakly completed.
On the liveness side, our service guarantees that a request issued by a correct client is processed and a response is returned to the client, provided that the client can communicate with enough replicas in a timely manner.
More precisely, we assume a default round-trip delay ![]() and
we say that a set of servers
and
we say that a set of servers
![]() ,
is eventually synchronous
if there is a time after which every two-way message exchange
within
,
is eventually synchronous
if there is a time after which every two-way message exchange
within ![]() takes at most
takes at most ![]() time units.
We also assume that every two correct servers or clients can eventually reliably communicate.
Now our progress requirements can be put as follows:
time units.
We also assume that every two correct servers or clients can eventually reliably communicate.
Now our progress requirements can be put as follows:
In particular, (L1) and (L2) imply that if there is a
an eventually synchronous set of ![]() correct replicas,
then each (weak or strong) request issued by a correct client will eventually be committed.
correct replicas,
then each (weak or strong) request issued by a correct client will eventually be committed.
As we will explain later, ensuring (L1) in the presence of partitions may require unbounded storage. We will present a protocol addition that bounds the storage requirements at the expense of relaxing (L1).
Zeno is a BFT state machine replication
protocol. It requires ![]() replicas to tolerate
replicas to tolerate ![]() Byzantine faults, i.e., we make no assumption
about the behavior of faulty replicas. Zeno also tolerates an arbitrary
number of Byzantine clients. We assume no node can break cryptographic techniques like
collision-resistant digests, encryption, and signing.
The protocol we present in this paper uses public key digital signatures
to authenticate communication. In a separate technical report [31], we present a
modified version of the protocol that uses more efficient symmetric cryptography
based on message authentication codes (MACs).
Byzantine faults, i.e., we make no assumption
about the behavior of faulty replicas. Zeno also tolerates an arbitrary
number of Byzantine clients. We assume no node can break cryptographic techniques like
collision-resistant digests, encryption, and signing.
The protocol we present in this paper uses public key digital signatures
to authenticate communication. In a separate technical report [31], we present a
modified version of the protocol that uses more efficient symmetric cryptography
based on message authentication codes (MACs).
The protocol uses two kinds of quorums: strong quorums consisting
of any group of ![]() distinct replicas, and weak quorums of
distinct replicas, and weak quorums of
![]() distinct replicas.
distinct replicas.
The system easily generalizes to any
![]() , in which case
the size of strong quorums becomes
, in which case
the size of strong quorums becomes
![]() , and weak quorums remain the same,
independent of
, and weak quorums remain the same,
independent of ![]() .
Note that one can apply our techniques in very
large replica groups (where
.
Note that one can apply our techniques in very
large replica groups (where
![]() ) and still make progress as
long as
) and still make progress as
long as ![]() replicas are available, whereas traditional (strongly consistent)
BFT systems can be blocked unless at least
replicas are available, whereas traditional (strongly consistent)
BFT systems can be blocked unless at least
![]() replicas,
growing with
replicas,
growing with ![]() , are available.
, are available.
Like most traditional BFT state machine replication protocols, Zeno has three components: sequence number assignment (Section 4.4) to determine the total order of operations, view changes (Section 4.5) to deal with leader replica election, and checkpointing (Section 4.8) to deal with garbage collection of protocol and application state.
The execution goes through a sequence of configurations called views.
In each view, a designated leader replica (the primary) is responsible for assigning
monotonically increasing sequence numbers to clients' operations.
A replica ![]() is the primary for the view numbered
is the primary for the view numbered ![]() iff
iff
![]() .
.
At a high level, normal case execution of a request proceeds as follows. A client first sends its request to all replicas. A designated primary replica assigns a sequence number to the client request and broadcasts this proposal to the remaining replicas. Then all replicas execute the request and return a reply to the client.
Once the client gathers sufficiently many matching
replies--replies that agree on the operation result, the sequence
number, the view, and the replica history--it returns
this result to the application. For weak requests, it suffices that a
single correct replica returned the result, since that replica will
not only provide a correct weak reply by properly executing the request,
but it will also eventually commit that
request to the linear history of the service. Therefore, the client need
only collect matching replies from a weak quorum of replicas. For strong
requests, the client must wait for matching replies from a strong
quorum, that is, a group of at least ![]() distinct replicas.
This implies that Zeno can complete many weak
operations in parallel across different partitions when only weak
quorums are available, whereas it can complete strong operations only
when there are strong quorums available.
distinct replicas.
This implies that Zeno can complete many weak
operations in parallel across different partitions when only weak
quorums are available, whereas it can complete strong operations only
when there are strong quorums available.
Whenever operations do not make progress, or if replicas agree that the primary is faulty, a view change protocol tries to elect a new primary. Unlike in previous BFT protocols, view changes in Zeno can proceed with the concordancy of only a weak quorum. This can allow multiple primaries to coexist in the system (e.g., during a network partition) which is necessary to make progress with eventual consistency. However, as soon as these multiple views (with possibly divergent sets of operations) detect each other (Section 4.6), they reconcile their operations via a merge procedure (Section 4.7), restoring consistency among replicas.
In what follows, messages with a subscript of the form ![]() denote
a public-key signature by principal
denote
a public-key signature by principal ![]() . In all protocol actions, malformed or
improperly signed messages are dropped without further processing. We
interchangeably use terms ``non-faulty'' and ``correct'' to mean system
components (e.g., replicas and clients) that follow our protocol
faithfully. Table 1 collects our notation.
. In all protocol actions, malformed or
improperly signed messages are dropped without further processing. We
interchangeably use terms ``non-faulty'' and ``correct'' to mean system
components (e.g., replicas and clients) that follow our protocol
faithfully. Table 1 collects our notation.
We start by explaining the protocol state at the replicas. Then we present details about the three protocol components. We used Zyzzyva [23] as a starting point for designing Zeno. Therefore, throughout the presentation, we will explain how Zeno differs from Zyzzyva.
A prefix of the ordered
history upto sequence number ![]() is called committed when a
replica gathers a commit certificate (denoted
is called committed when a
replica gathers a commit certificate (denoted ![]() and described in detail in
Section 4.4) for
and described in detail in
Section 4.4) for
![]() ; each replica only remembers the highest CC it witnessed.
; each replica only remembers the highest CC it witnessed.
To prevent the history of requests from growing without bounds,
replicas assemble checkpoints after every
![]() sequence numbers. For every checkpoint sequence number
sequence numbers. For every checkpoint sequence number ![]() , a replica first obtains
the
, a replica first obtains
the ![]() for
for ![]() and executes all operations upto and including
and executes all operations upto and including ![]() . At
this point, a replica takes a snapshot of the application state and stores it (Section 4.8).
. At
this point, a replica takes a snapshot of the application state and stores it (Section 4.8).
Replicas remember the set of operations received from each client ![]() in
their request[c] buffer and only the last reply sent to each client in
their reply[c] buffer. The request buffer is flushed when
a checkpoint is taken.
in
their request[c] buffer and only the last reply sent to each client in
their reply[c] buffer. The request buffer is flushed when
a checkpoint is taken.
To describe how sequence number assignment works, we follow the flow of a request.
First, Zeno clients only need matching replies from a weak quorum,
whereas Zyzzyva requires at least a strong quorum; this leads to
significant increase in availability, when for example only between
![]() and
and ![]() replicas are available. It also allows for slightly lower
overhead at the client due to reduced message processing requirements, and
to a lower latency for request execution when inter-node latencies are
heterogeneous.
replicas are available. It also allows for slightly lower
overhead at the client due to reduced message processing requirements, and
to a lower latency for request execution when inter-node latencies are
heterogeneous.
Second, Zeno requires clients to use sequential timestamps instead of monotonically increasing but not necessarily sequential timestamps (which are the norm in comparable systems). This is required for garbage collection (Section 4.8). This raises the issue of how to deal with clients that reboot or otherwise lose the information about the latest sequence number. In our current implementation we are not storing this sequence number persistently before sending the request. We chose this because the guarantees we obtain are still quite strong: the requests that were already committed will remain in the system, this does not interfere with requests from other clients, and all that might happen is the client losing some of its initial requests after rebooting or oldest uncommitted requests. As future work, we will devise protocols for improving these guarantees further, or for storing sequence numbers efficiently using SSDs or NVRAM.
Third, whereas Zyzzyva offers a single-phase performance optimization, in which a request
commits in only three message steps under some conditions (when all ![]() replicas operate roughly synchronously and are all available and
non-faulty), Zeno disables that optimization. The rationale behind this
removal is based on the view change protocol (Section 4.5) so
we defer the discussion until then. A positive side-effect of this
removal is that, unlike with Zyzzyva, Zeno does not entrust potentially
faulty clients with any protocol step other than sending requests and collecting responses.
replicas operate roughly synchronously and are all available and
non-faulty), Zeno disables that optimization. The rationale behind this
removal is based on the view change protocol (Section 4.5) so
we defer the discussion until then. A positive side-effect of this
removal is that, unlike with Zyzzyva, Zeno does not entrust potentially
faulty clients with any protocol step other than sending requests and collecting responses.
Finally, clients in Zeno send the request to all replicas whereas clients in Zyzzyva send the request only to the primary replica. This change is required only in the MAC version of the protocol but we present it here to keep the protocol description consistent. At a high level, this change is required to ensure that a faulty primary cannot prevent a correct request that has weakly completed from committing--the faulty primary may manipulate a few of the MACs in an authenticator present in the request before forwarding it to others, and during commit phase, not enough correct replicas correctly verify the authenticator and drop the request. Interestingly, we find that the implementations of both PBFT and Zyzzyva protocols also require the clients to send the request directly to all replicas.
Our protocol description omits some of the pedantic details such as handling faulty clients or request retransmissions; these cases are handled similarly to Zyzzyva and do not affect the overheads or benefits of Zeno when compared to Zyzzyva.
We now turn to the election of a new primary when the current primary is
unavailable or faulty. The key point behind our view change protocol
is that it must be able to
proceed when only a weak quorum of replicas is available unlike view
change algorithms in strongly consistent BFT systems which require
availability of a strong quorum to make progress. The reason for this
is the following: strongly consistent BFT systems rely on the
quorum intersection property
to ensure that if a strong quorum ![]() decides to change view and another
strong quorum
decides to change view and another
strong quorum ![]() decides to commit a request, there is at least one
non-faulty replica in both quorums ensuring that view changes do not
``lose'' requests committed previously. This implies that the sizes of
strong quorums are at least
decides to commit a request, there is at least one
non-faulty replica in both quorums ensuring that view changes do not
``lose'' requests committed previously. This implies that the sizes of
strong quorums are at least ![]() , so that the intersection of any two
contains at least
, so that the intersection of any two
contains at least ![]() replicas, including--since no more than
replicas, including--since no more than ![]() of those
can be faulty--at least one non-faulty replica. In contrast, Zeno does
not require view change quorums to intersect;
a weak request missing from a view change will be eventually committed
when the correct replica executing it manages to reach a strong quorum
of correct replicas, whereas strong requests missing from a view change
will cause a subsequent provable divergence and application-state merge.
of those
can be faulty--at least one non-faulty replica. In contrast, Zeno does
not require view change quorums to intersect;
a weak request missing from a view change will be eventually committed
when the correct replica executing it manages to reach a strong quorum
of correct replicas, whereas strong requests missing from a view change
will cause a subsequent provable divergence and application-state merge.
In the latter case, if the replica does not receive an
![]() message
before it times out, it broadcasts
message
before it times out, it broadcasts
![]() to all replicas, but continues to participate in the current view.
If a replica receives such accusations from a weak quorum,
it stops participating in the
current view
to all replicas, but continues to participate in the current view.
If a replica receives such accusations from a weak quorum,
it stops participating in the
current view ![]() and sends a
and sends a
![]() to other replicas,
where
to other replicas,
where ![]() is the highest commit certificate, and
is the highest commit certificate, and
![]() is
is ![]() 's ordered request history since
that commit certificate, i.e., all
's ordered request history since
that commit certificate, i.e., all
![]() messages for requests with sequence
numbers higher than the one in
messages for requests with sequence
numbers higher than the one in ![]() . It then starts the view change timer.
. It then starts the view change timer.
The primary replica ![]() for view
for view ![]() starts a timer with a shorter
timeout value called the aggregation timer and waits until it collects a
set of
starts a timer with a shorter
timeout value called the aggregation timer and waits until it collects a
set of
![]() messages for view
messages for view ![]() from a strong quorum,
or until its aggregation timer expires. If the aggregation timer expires and the primary
replica has collected
from a strong quorum,
or until its aggregation timer expires. If the aggregation timer expires and the primary
replica has collected ![]() or more
such messages,
it sends a
or more
such messages,
it sends a
![]() to other replicas, where
to other replicas, where
![]() is the set of
is the set of
![]() messages it gathered (we call this a weak view change,
as opposed to one where a strong quorum of replicas participate
which is called a strong view change).
If a replica does not receive the
messages it gathered (we call this a weak view change,
as opposed to one where a strong quorum of replicas participate
which is called a strong view change).
If a replica does not receive the
![]() message
before the view change timer expires, it starts a view change into the
next view number.
message
before the view change timer expires, it starts a view change into the
next view number.
Note that waiting for messages from a strong quorum is not needed to meet our eventual consistency specification, but helps to avoid a situation where some operations are not immediately incorporated into the new view, which would later create a divergence that would need to be resolved using our merge procedure. Thus it improves the availability of our protocol.
Each replica locally calculates the initial state for the new view by executing the requests contained
in
![]() ,
thereby updating both
,
thereby updating both ![]() and the history chain digest
and the history chain digest ![]() .
The order in which these requests are executed and how the initial state for the new
view is calculated is related to how we merge divergent states from different
replicas, so we defer this explanation to Section 4.7.
Each replica then sends a
.
The order in which these requests are executed and how the initial state for the new
view is calculated is related to how we merge divergent states from different
replicas, so we defer this explanation to Section 4.7.
Each replica then sends a
![]() to all others, and
once it receives such
to all others, and
once it receives such
![]() messages matching in
messages matching in ![]() ,
, ![]() , and
, and ![]() from a weak or a strong quorum
(for weak or strong view changes, respectively) the replica becomes active in
view
from a weak or a strong quorum
(for weak or strong view changes, respectively) the replica becomes active in
view ![]() and stops processing messages for any prior views.
and stops processing messages for any prior views.
The view change protocol allows a set of ![]() correct but slow replicas to
initiate a global view change even if there is a set of
correct but slow replicas to
initiate a global view change even if there is a set of ![]() synchronized correct
replicas, which may affect our liveness guarantees (in particular, the
ability to eventually execute weak requests when there is a synchronous
set of
synchronized correct
replicas, which may affect our liveness guarantees (in particular, the
ability to eventually execute weak requests when there is a synchronous
set of ![]() correct servers).
We avoid this by prioritizing client requests over view change requests as follows.
Every replica maintains a set of client requests that it received but have not been
processed (put in an ordered request) by the primary.
Whenever a replica
correct servers).
We avoid this by prioritizing client requests over view change requests as follows.
Every replica maintains a set of client requests that it received but have not been
processed (put in an ordered request) by the primary.
Whenever a replica ![]() receives a message
from
receives a message
from ![]() related to the view change protocol
(
related to the view change protocol
(
![]() ,
,
![]() ,
,
![]() , or
, or
![]() ) for a higher view,
) for a higher view,
![]() first forwards the outstanding requests to the current primary and waits
until the corresponding ORs are received or a timer expires.
For each pending request, if a valid OR is received,
then the replica sends the corresponding response back to the client.
Then
first forwards the outstanding requests to the current primary and waits
until the corresponding ORs are received or a timer expires.
For each pending request, if a valid OR is received,
then the replica sends the corresponding response back to the client.
Then ![]() processes the original view change related messages from
processes the original view change related messages from ![]() according to
the protocol described above.
This guarantees that the system makes progress even in the presence
of continuous view changes caused by the slow replicas
in such pathological situations.
according to
the protocol described above.
This guarantees that the system makes progress even in the presence
of continuous view changes caused by the slow replicas
in such pathological situations.
The following sections describe additions to the view change protocols to incorporate functionality for detecting and merging concurrent histories, which are also exclusive to Zeno.
Concurrent histories (i.e., divergence in the service state) can be
formed for several reasons. This can occur when the view change
logic leads to the presence of two replicas that simultaneously believe
they are the primary, and there are a sufficient number of other replicas that
also share that belief and complete weak operations proposed by each primary. This
could be the case during a network partition that splits the set of replicas into
two subsets, each of them containing at least ![]() replicas.
replicas.
Another possible reason for concurrent histories is
that the base history decided during
a view change may not have the latest committed operations from prior
views. This is because a view change quorum (a weak quorum) may not
share a non-faulty replica with prior commitment quorums (strong
quorums) and remaining replicas; as a result, some committed operations
may not appear in
![]() messages and, therefore, may be missing
from the new starting state in the
messages and, therefore, may be missing
from the new starting state in the
![]() message.
message.
Finally, a misbehaving primary can also cause divergence by proposing the same sequence numbers to different operations, and forwarding the different choices to disjoint sets of replicas.
For clarity, we first describe how we detect divergence within a view and then discuss detection across views. We also defer details pertaining to garbage collection of replica state until Section 4.8.
Suppose replica ![]() is in view
is in view ![]() , has executed up to sequence number
, has executed up to sequence number
![]() , and receives a properly authenticated message
, and receives a properly authenticated message
![]() or
or
![]() from replica
from replica ![]() .
.
If ![]() , i.e.,
, i.e., ![]() has executed a request with sequence number
has executed a request with sequence number ![]() ,
then the fill-hole mechanism is
started, and
,
then the fill-hole mechanism is
started, and ![]() receives from
receives from ![]() a message
a message
![]() ,
where
,
where
![]() and
and
![]() .
.
Otherwise, if
![]() , both replicas have
executed a request with sequence number
, both replicas have
executed a request with sequence number ![]() and
therefore
and
therefore ![]() must have the
some
must have the
some
![]() message in its log, where
message in its log, where
![]() and
and
![]() .
.
If the two history digests match (the local ![]() or
or ![]() , depending on whether
, depending on whether
![]() ,
and the one received in the message), then the two histories are
consistent and no concurrency is deduced.
,
and the one received in the message), then the two histories are
consistent and no concurrency is deduced.
If instead the two history digests differ, the histories must differ as
well. If the two
![]() messages are authenticated by the same
primary, together they constitute a proof of misbehavior (POM);
through an inductive argument it can be shown that the primary must have
assigned different requests to the same sequence number
messages are authenticated by the same
primary, together they constitute a proof of misbehavior (POM);
through an inductive argument it can be shown that the primary must have
assigned different requests to the same sequence number ![]() . Such a
POM is sufficient to initiate a view change and a merge of histories (Section 4.7).
. Such a
POM is sufficient to initiate a view change and a merge of histories (Section 4.7).
The case when the two
![]() messages are authenticated by
different primaries indicates the existence of divergence, caused for
instance by a network partition, and we discuss how to handle it next.
messages are authenticated by
different primaries indicates the existence of divergence, caused for
instance by a network partition, and we discuss how to handle it next.
Now assume that replica ![]() receives a message from replica
receives a message from replica ![]() indicating that
indicating that
![]() . This could happen due to a partition, during which
different subsets changed views independently, or due to other network
and replica asynchrony. Replica
. This could happen due to a partition, during which
different subsets changed views independently, or due to other network
and replica asynchrony. Replica ![]() requests the
requests the
![]() message for
message for ![]() from
from ![]() .
(The case where
.
(The case where ![]() is similar, with the exception that
is similar, with the exception that
![]() pushes the
pushes the
![]() message to
message to ![]() instead.)
instead.)
When node ![]() receives and verifies the
receives and verifies the
![]() message, where
message, where ![]() is
the issuing primary of view
is
the issuing primary of view ![]() , it compares its local history to the
sequence of
, it compares its local history to the
sequence of
![]() messages
obtained after ordering the
messages
obtained after ordering the
![]() message present
in the
message present
in the
![]() message (according to the procedure described
in Section 4.7). Let
message (according to the procedure described
in Section 4.7). Let ![]() and
and ![]() be the lowest and highest sequence numbers of those
be the lowest and highest sequence numbers of those
![]() messages,
respectively.
messages,
respectively.
Like traditional view change protocols,
a replica ![]() does not enter
does not enter ![]() if
the
if
the
![]() message for that view did not include all of
message for that view did not include all of ![]() 's committed
requests. This is important for the safety properties providing guarantees for strong operations,
since it
excludes a situation where requests could be committed in
's committed
requests. This is important for the safety properties providing guarantees for strong operations,
since it
excludes a situation where requests could be committed in
![]() without seeing previously committed requests.
without seeing previously committed requests.
Once concurrent histories are detected, we need to merge them in a deterministic order. The solution we propose is to extend the view change protocol, since many of the functionalities required for merging are similar to those required to transfer a set of operations across views.
We extend the view change mechanism so that view changes can be
triggered by either PODs, POMs or POAs. When a replica obtains a POM, a POD, or a POA after
detecting divergence,
it multicasts a message of the form
![]() ,
,
![]() , or
, or
![]() in addition to the
in addition to the
![]() message for
message for ![]() . Note here that
. Note here that ![]() in POM and POD is one higher than the highest view number
present in the conflicting
in POM and POD is one higher than the highest view number
present in the conflicting
![]() messages, or
one higher than the view
number in the
messages, or
one higher than the view
number in the
![]() component in the case of a POA.
component in the case of a POA.
Upon receiving an authentic and valid
![]() or
or
![]() or a
or a
![]() , a replica broadcasts a
, a replica broadcasts a
![]() along with the triggering POM, POD, or POA message.
along with the triggering POM, POD, or POA message.
The view change mechanism will eventually lead to the election
of a new primary that is supposed to multicast a
![]() message.
When a node receives such a message, it needs to compute the start
state for the next view based on the information contained
in that message.
The new start state is calculated by first identifying the
highest
message.
When a node receives such a message, it needs to compute the start
state for the next view based on the information contained
in that message.
The new start state is calculated by first identifying the
highest ![]() present among all
present among all
![]() messages; this determines
the new base history digest
messages; this determines
the new base history digest ![]() for the start sequence number
for the start sequence number ![]() of
the new view.
of
the new view.
But nodes also need to determine how to order the different
![]() messages that are present in the
messages that are present in the
![]() message but not yet
committed.
Contained
message but not yet
committed.
Contained
![]() messages (potentially
including concurrent requests) are ordered using a deterministic
function of the requests that produces a total order for these
requests. Having a fixed function allows all nodes receiving the
messages (potentially
including concurrent requests) are ordered using a deterministic
function of the requests that produces a total order for these
requests. Having a fixed function allows all nodes receiving the
![]() message to easily agree on the final order for the concurrent
message to easily agree on the final order for the concurrent
![]() present in that message. Alternatively,
we could let the primary replica propose an ordering, and disseminate it
as an additional parameter of the
present in that message. Alternatively,
we could let the primary replica propose an ordering, and disseminate it
as an additional parameter of the
![]() message.
message.
Replicas receiving the
![]() message
then execute the requests in the
message
then execute the requests in the
![]() messages according to that fixed order,
updating their histories and history digests. If a replica has already executed some weak
operations in an order that differs from the new ordering, it first rolls back the
application state to the state of the last checkpoint (Section 4.8) and executes all
operations after the checkpoint, starting with committed requests and
then with the weak requests ordered by the
messages according to that fixed order,
updating their histories and history digests. If a replica has already executed some weak
operations in an order that differs from the new ordering, it first rolls back the
application state to the state of the last checkpoint (Section 4.8) and executes all
operations after the checkpoint, starting with committed requests and
then with the weak requests ordered by the
![]() message.
Finally, the replica broadcasts a
message.
Finally, the replica broadcasts a
![]() message. As mentioned, when a replica
collects matching
message. As mentioned, when a replica
collects matching
![]() messages on
messages on ![]() ,
, ![]() , and
, and ![]() it
becomes active in the new view.
it
becomes active in the new view.
Our merge procedure re-executes the concurrent operations sequentially, without running any additional or alternative application-specific conflict resolution procedure. This makes the merge algorithm slightly simpler, but requires the application upcall that executes client operations to contain enough information to identify and resolve concurrent operations. This is similar to the design choice made by Bayou [33] where special concurrency detection and merge procedure are part of each service operation, enabling servers to automatically detect and resolve conflicts.
Zeno's view changes motivate our removal of the single-phase Zyzzyva
optimization for the following reason: suppose a strong client request
![]() was executed (and committed) at sequence number
was executed (and committed) at sequence number ![]() at
at ![]() replicas. Now suppose there was a weak view change, the new primary is
faulty, and only
replicas. Now suppose there was a weak view change, the new primary is
faulty, and only ![]() replicas are available. A faulty replica
among those has the option of reporting
replicas are available. A faulty replica
among those has the option of reporting
![]() in a different order in its
in a different order in its
![]() message, which enables the primary to order
message, which enables the primary to order
![]() arbitrarily
in its
arbitrarily
in its
![]() message; this is possible because only a
single--potentially faulty--replica need report any request during a
Zeno view change. This means that linearizability is violated for this
strong, committed request
message; this is possible because only a
single--potentially faulty--replica need report any request during a
Zeno view change. This means that linearizability is violated for this
strong, committed request
![]() . Although it may
be possible to design a more involved view change to preserve such
orderings, we chose to keep things simple instead. As our results show,
in many settings where eventual consistency is sufficient for weak
operations, our availability under partitions tramps any benefits from
increased throughput
due to the Zyzzyva's optimized single-phase request commitment.
. Although it may
be possible to design a more involved view change to preserve such
orderings, we chose to keep things simple instead. As our results show,
in many settings where eventual consistency is sufficient for weak
operations, our availability under partitions tramps any benefits from
increased throughput
due to the Zyzzyva's optimized single-phase request commitment.
The protocol we have presented so far has two important shortcomings: the protocol state grows unboundedly, and weak requests are never committed unless they are followed by a strong request.
To address these issues, Zeno periodically takes checkpoints, garbage collecting its logs of requests and forcing weak requests to be committed.
When a replica receives an
![]() message from the primary for sequence number
message from the primary for sequence number ![]() , it
checks if
, it
checks if
![]() .
If so, it broadcasts the
.
If so, it broadcasts the
![]() message corresponding to
message corresponding to ![]() to other replicas.
Once a replica receives
to other replicas.
Once a replica receives ![]()
![]() messages matching in
messages matching in ![]() ,
, ![]() , and
, and ![]() ,
it creates the commit certificate for sequence number
,
it creates the commit certificate for sequence number ![]() .
It then sends a
.
It then sends a
![]() to all other replicas. The
to all other replicas. The
![]() is a snapshot of the application state after executing requests
upto and including
is a snapshot of the application state after executing requests
upto and including ![]() .
When it receives
.
When it receives ![]() matching
matching
![]() messages, it considers the
checkpoint stable, stores this proof, and discards all ordered requests with sequence number
lower than
messages, it considers the
checkpoint stable, stores this proof, and discards all ordered requests with sequence number
lower than ![]() along with their corresponding client requests.
along with their corresponding client requests.
Also, in case the checkpoint procedure is not run within the interval of
![]() time units,
and a replica has some not yet committed ordered requests, the replica also initiates
the commit step of the checkpoint procedure.
This is done to make sure that pending ordered requests are committed when the service is rarely
used by other clients and the sequence numbers grow very slowly.
time units,
and a replica has some not yet committed ordered requests, the replica also initiates
the commit step of the checkpoint procedure.
This is done to make sure that pending ordered requests are committed when the service is rarely
used by other clients and the sequence numbers grow very slowly.
Our checkpoint procedure described so far poses a challenge to the protocol for detecting concurrent histories. Once old requests have been garbage-collected, there is no way to verify, in the case of a slow replica (or a malicious replica pretending to be slow) that presents an old request, if that request has been committed at that sequence number or if there is divergence.
To address this,
clients send
sequential timestamps to
uniquely identify each one of their own operations, and we added a list of per-client timestamps
to the checkpoint messages, representing the maximum operation each client has executed
up to the checkpoint.
This is in contrast with previous BFT replication protocols, including Zyzzyva, where clients
identified operations using timestamps obtained by reading their local clocks.
Concretely, a replica sends
![]() ,
where
,
where
![]() is a
vector of
is a
vector of
![]() tuples, where
tuples, where ![]() is the timestamp of the last committed operation
from
is the timestamp of the last committed operation
from ![]() .
.
This allows us to detect concurrent requests, even if some of the replicas have garbage-collected
that request. Suppose a replica ![]() receives an
receives an
![]() with sequence number
with sequence number ![]() that corresponds to client
that corresponds to client ![]() 's request
with timestamp
's request
with timestamp ![]() . Replica
. Replica ![]() first obtains the timestamp of the last executed operation of
first obtains the timestamp of the last executed operation of ![]() in the highest checkpoint
in the highest checkpoint ![]() =
=
![]() [
[![]() ]. If
]. If
![]() , then there is no divergence since
the client request with timestamp
, then there is no divergence since
the client request with timestamp ![]() has already been committed. But if
has already been committed. But if ![]() , then we need
to check if some other request was assigned
, then we need
to check if some other request was assigned ![]() , providing a proof of divergence. If
, providing a proof of divergence. If ![]() ,
then the
,
then the
![]() and the
and the
![]() form a POD
since some other request was assigned
form a POD
since some other request was assigned ![]() . Else, we can perform regular conflict
detection procedure to identify concurrency (see Section 4.6).
. Else, we can perform regular conflict
detection procedure to identify concurrency (see Section 4.6).
Note that our checkpoints become stable only when there are at least ![]() replicas that are able to agree. In the presence of partitions or other
unreachability situations where only weak quorums can talk to each other,
it may not be possible to gather a checkpoint, which implies that Zeno must
either allow the state concerning tentative operations to grow
without bounds, or weaken its liveness guarantees. In our current
protocol we chose the latter, and so
replicas stop participating once they reach a maximum number of tentative operations they can execute,
which could be determined based on their available storage resources (memory as well as the disk space).
Garbage collecting weak operations and the resulting impact on conflict detection is left as a future work.
replicas that are able to agree. In the presence of partitions or other
unreachability situations where only weak quorums can talk to each other,
it may not be possible to gather a checkpoint, which implies that Zeno must
either allow the state concerning tentative operations to grow
without bounds, or weaken its liveness guarantees. In our current
protocol we chose the latter, and so
replicas stop participating once they reach a maximum number of tentative operations they can execute,
which could be determined based on their available storage resources (memory as well as the disk space).
Garbage collecting weak operations and the resulting impact on conflict detection is left as a future work.
In this section, we sketch the proof that Zeno satisfies the safety properties specified in Section 3. A proof sketch for liveness properties is presented in a separate technical report [31].
In Zeno , a (weak or strong) response is based on identical histories
of at least ![]() replicas, and, thus, at least one of these histories belongs to a correct replica.
Hence, in the case that our garbage collection scheme is not initiated,
we can reformulate the safety requirements as follows:
(S1) the local history maintained by a correct replica consists of a prefix of committed requests extended with a sequence of speculative requests,
where no request appears twice,
(S2) a request associated with a correct client
replicas, and, thus, at least one of these histories belongs to a correct replica.
Hence, in the case that our garbage collection scheme is not initiated,
we can reformulate the safety requirements as follows:
(S1) the local history maintained by a correct replica consists of a prefix of committed requests extended with a sequence of speculative requests,
where no request appears twice,
(S2) a request associated with a correct client ![]() appears,
in a history at a correct replica only if
appears,
in a history at a correct replica only if ![]() has previously issued the request,
and (S3) the committed prefixes of histories at every two correct replicas are
related by containment, and (S4) at any time, the number of conflicting
histories maintained at correct replica does not exceed
has previously issued the request,
and (S3) the committed prefixes of histories at every two correct replicas are
related by containment, and (S4) at any time, the number of conflicting
histories maintained at correct replica does not exceed
![]() ,
where
,
where ![]() is the number of currently failed replicas and
is the number of currently failed replicas and ![]() is the total number of replicas required
to tolerate a maximum of
is the total number of replicas required
to tolerate a maximum of ![]() faulty replicas.
Here we say that two histories are conflicting if none of them is a prefix of the other.
faulty replicas.
Here we say that two histories are conflicting if none of them is a prefix of the other.
Properties (S1) and (S2) are implied by the state maintenance mechanism of our protocol and the fact that only properly signed requests are put in a history by a correct replica. The special case when a prefix of a history is hidden behind a checkpoint is discussed later.
A committed prefix of a history maintained at a correct replica can only be modified by a commitment of a new request or a merge operation. The sub-protocol of Zeno responsible for committing requests are analogous to the two-phase conservative commitment in Zyzzyva [23], and, similarly, guarantees that all committed requests are totally ordered. When two histories are merged at a correct replica, the resulting history adopts the longest committed prefix of the two histories. Thus, inductively, the committed prefixes of all histories maintained at correct replicas are related by containment (S3).
Now suppose that at a given time, the number of conflicting
histories maintained at correct replica is more than
![]() .
Our weak quorum mechanism guarantees that each history maintained at a correct process
is supported by at least
.
Our weak quorum mechanism guarantees that each history maintained at a correct process
is supported by at least ![]() distinct processes
(through sending
distinct processes
(through sending
![]() and
and
![]() messages).
A correct process cannot concurrently acknowledge two conflicting histories.
But when
messages).
A correct process cannot concurrently acknowledge two conflicting histories.
But when ![]() replicas are faulty, there can be at most
replicas are faulty, there can be at most
![]() sets of
sets of ![]() replicas that are disjoint in the set of correct ones.
Thus, at least one correct replica acknowledged two conflicting histories --
a contradiction establishes (S4).
replicas that are disjoint in the set of correct ones.
Thus, at least one correct replica acknowledged two conflicting histories --
a contradiction establishes (S4).
Checkpointing.
Note that our garbage collection scheme may affect property (S1):
the sequence of tentative operations maintained at a correct replica may
potentially include a committed but already garbage-collected operation.
This, however, cannot happen: each round of garbage collection produces a
checkpoint that contains the latest committed service state and the
logical timestamp of the latest committed operation of every client.
Since no correct replica agrees to commit a request from a client unless
its previous requests are already committed,
the checkpoint implies the set of timestamps of
all committed requests of each client.
If a replica receives an ordered request of a client ![]() corresponding to a sequence number preceding the checkpoint state,
and the timestamp of this request is no later than the last committed
request of
corresponding to a sequence number preceding the checkpoint state,
and the timestamp of this request is no later than the last committed
request of ![]() , then the replica simply ignores the request,
concluding that the request is already committed.
Hence, no request can appear in a local history twice.
, then the replica simply ignores the request,
concluding that the request is already committed.
Hence, no request can appear in a local history twice.
We have implemented a prototype of Zeno as an extension to the publicly available Zyzzyva source code [24].
Our evaluation tries to answer the following questions: (1) Does Zeno incur more overhead than existing protocols in the normal case?
(2) Does Zeno provide higher availability compared to existing protocols
when there are more than ![]() unreachable nodes?
(3) What is the cost of merges?
unreachable nodes?
(3) What is the cost of merges?
We generate a workload with a varying fraction of strong and weak operations.
If each client issued both strong and weak operations, then most
clients would block soon after network partitions started.
Instead, we simulate two kind of
clients: (i) weak clients only issue weak requests and
(ii) strong clients always pose strong requests. This allows us to vary the ratio of weak
operations (denoted by ![]() ) in the total workload with a limited number of clients in the system
and long network partitions.
We use a micro-benchmark that executes a no-op when the execute
upcall for the client operation is invoked.
) in the total workload with a limited number of clients in the system
and long network partitions.
We use a micro-benchmark that executes a no-op when the execute
upcall for the client operation is invoked.
We have also built a simple application on top of Zeno, emulating a shopping cart service with operations to add, remove, and checkout items based on a key-value data store. We also implement a simple conflict detection and merge procedure. Due to lack of space, the design and evaluation of this service is presented in the technical report [31].
|
Our results presented in Table 2 show that Zeno and Zyzzyva's throughput are similar, with Zyzzyva achieving slightly (3-6%) higher throughput than Zeno's throughput for weak operations. The results also show that, with batching, Zeno's throughput for strong operations is also close to Zyzzyva's peak throughput: Zyzzyva has 7% higher throughput when the single phase optimization is employed. However, when a single replica is faulty or slow, Zyzzyva cannot achieve the single phase throughput and Zeno's throughput for strong operations is identical to Zyzzyva's performance with a faulty replica.
 |
In this experiment, all clients reside in the first LAN. We initiate a partition at 90 seconds which continues for a minute. Since there are no clients in the second LAN, there are no requests processed in it and hence there is no concurrency, which avoids the cost of merging. Replicas with id 0 (primary for view initial view 0) and 1 reside in the first LAN while replicas with ids 2 and 3 reside in the second LAN. We also present the results of Zyzzyva to compare the performance in both normal cases as well as under the given failure.
Second, weak operations continue to be processed and completed during the partition and this is
because Zeno requires (for ![]() ) only 2 non-faulty replicas to complete the operation. The fraction of
total requests completed increases as
) only 2 non-faulty replicas to complete the operation. The fraction of
total requests completed increases as ![]() increases, essentially improving the availability of such operations despite
network partitions.
increases, essentially improving the availability of such operations despite
network partitions.
Third, when replicas in the other LAN are reachable again, they need to obtain the missing requests from the first
LAN. Since the number of weak operations performed in the first LAN increases as ![]() increases, the time
to update the lagging replicas in the other partition also goes up; this
puts a temporary strain on the network, evidenced by the dip in the
throughput of weak operations when the partition heals. However, this dip is
brief compared to the duration of the partition. We explore the impact
of the duration of partitions next.
increases, the time
to update the lagging replicas in the other partition also goes up; this
puts a temporary strain on the network, evidenced by the dip in the
throughput of weak operations when the partition heals. However, this dip is
brief compared to the duration of the partition. We explore the impact
of the duration of partitions next.
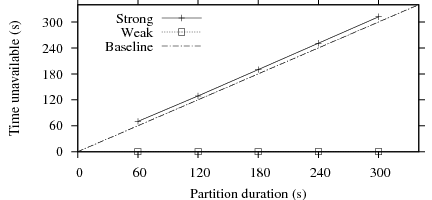 |
Figure 2 presents the results. We observe that weak operations are always available in this experiment since all weak operations were completed in the first LAN and the replicas in the first LAN are up-to-date with each other to process the next weak operation. Strong operations are unavailable for the entire duration of the partition due to unavailability of the replicas in the second LAN and the additional unavailability is introduced by Zeno due to the operation transfer mechanism. However, the additional delay is within 4% of the partition duration (12 seconds for a 5 minute partition). Our current prototype is not yet optimized and we believe that the delay could be further reduced.
 |
In this experiment, we keep half the clients on each side of a partition. This ensures that both partitions observe a steady load of weak operations that will cause Zeno to first perform a weak view change and later merge the concurrent weak operations completed in each partition. Hence, this microbenchmark additionally evaluates the cost of weak view changes and the merge procedure. As before, the primary for the initial view resides in the first LAN. We measure the overall throughput of weak and strong operations completed in both partitions. Again, we compare our results to Zyzzyva.
When ![]() , Zeno does not give additional benefits since there are no weak operations to be completed. Also,
as soon as the partition starts, strong operations are blocked and
resume after the partition heals. As above, Zyzzyva
provides greater throughput thanks to its single-phase execution of client requests,
but it is as powerless to make progress during
partitions as Zeno in the face of strong operations only.
, Zeno does not give additional benefits since there are no weak operations to be completed. Also,
as soon as the partition starts, strong operations are blocked and
resume after the partition heals. As above, Zyzzyva
provides greater throughput thanks to its single-phase execution of client requests,
but it is as powerless to make progress during
partitions as Zeno in the face of strong operations only.
When
![]() , we have only one client sending weak
operations in one LAN. Since there are no conflicts, this graph matches
that of Figure 1.
, we have only one client sending weak
operations in one LAN. Since there are no conflicts, this graph matches
that of Figure 1.
When
![]() , we have at least two weak clients, at least one in
each LAN. When a partition starts, we observe that the throughput of
weak operations first drops; this happens because weak clients in the
second partition cannot complete operations as they are partitioned from
the current primary. Once they perform the necessary view changes in the
second LAN, they resume processing weak operations; this is observed by
an increase in the overall throughput of weak operations completed since
both partitions can now complete weak operations in parallel - in fact,
faster than before the partition due to decreased cryptographic
and message overheads and reduced round trip delay of clients in the second partition
from the primary in their partition. The duration of the weak operation
unavailability in the non-primary partition is proportional to the
number of view changes required. In our experiment, since replicas with
ids 2 and 3 reside in the second LAN, two view changes were required (to make
replica 2 the new primary).
, we have at least two weak clients, at least one in
each LAN. When a partition starts, we observe that the throughput of
weak operations first drops; this happens because weak clients in the
second partition cannot complete operations as they are partitioned from
the current primary. Once they perform the necessary view changes in the
second LAN, they resume processing weak operations; this is observed by
an increase in the overall throughput of weak operations completed since
both partitions can now complete weak operations in parallel - in fact,
faster than before the partition due to decreased cryptographic
and message overheads and reduced round trip delay of clients in the second partition
from the primary in their partition. The duration of the weak operation
unavailability in the non-primary partition is proportional to the
number of view changes required. In our experiment, since replicas with
ids 2 and 3 reside in the second LAN, two view changes were required (to make
replica 2 the new primary).
When the partition heals, replicas in the first view detect the
existence of concurrency and
construct a POD, since replicas in the second LAN are in a higher view
(with ![]() ). At this point, they request a
). At this point, they request a
![]() from the primary of
view 2, move to view 2, and then propagate their locally executed weak
operations to the primary of view 2. Next, replicas in the first LAN
need to fetch the weak operations that completed in the second LAN and
needs to complete them before the strong operations can make
progress. This results in additional delay before the strong operations
can complete, as observed in the figure.
from the primary of
view 2, move to view 2, and then propagate their locally executed weak
operations to the primary of view 2. Next, replicas in the first LAN
need to fetch the weak operations that completed in the second LAN and
needs to complete them before the strong operations can make
progress. This results in additional delay before the strong operations
can complete, as observed in the figure.
Next, we simulate partitions of varying duration as before, for
![]() .
Again, we measure the unavailability of both strong and weak operations using the earlier definition:
unavailability is the duration for which the throughput in either partition was less than 10% of average throughput before the
failure. With a longer partition duration, the cost of the
merge procedure increases since the weak operations from both partitions have to be transferred prior to
completing the new client operations.
.
Again, we measure the unavailability of both strong and weak operations using the earlier definition:
unavailability is the duration for which the throughput in either partition was less than 10% of average throughput before the
failure. With a longer partition duration, the cost of the
merge procedure increases since the weak operations from both partitions have to be transferred prior to
completing the new client operations.
 |
Figure 4 presents the results. We observe that weak operations experience some unavailability in this scenario, whose duration increases with the length of the partition. The unavailability for weak operations is within 9% of the total time of the partition.
The unavailability of strong operations is at least the duration of the network partition plus the merge cost (similar to that for weak operations). The additional unavailability due to the merge operation is within 14% of the total time of the partition.
 |
We simulate a partition duration of 60 seconds and calculate the number of clients blocked and the length of
time they were blocked during the partition.
Figure 6 presents the cumulative distribution function of clients on the ![]() -axis and the
maximum duration a client was blocked on the
-axis and the
maximum duration a client was blocked on the ![]() -axis. This metric allows us to see how clients
were affected by the partition. With Zyzzyva, all clients
will be blocked for the entire duration of the partition. However, with Zeno, a large fraction of clients do not
observe any wait time and this is because they exit from the system after doing a few weak operations.
For example, more than 70% of clients do not observe any wait time as long as
the probability of performing a strong operation is less than 15%.
In summary, this result shows that Zeno significantly improves the user experience and masks the failure events from being
exposed to the user as long as the workload contains few strong operations.
-axis. This metric allows us to see how clients
were affected by the partition. With Zyzzyva, all clients
will be blocked for the entire duration of the partition. However, with Zeno, a large fraction of clients do not
observe any wait time and this is because they exit from the system after doing a few weak operations.
For example, more than 70% of clients do not observe any wait time as long as
the probability of performing a strong operation is less than 15%.
In summary, this result shows that Zeno significantly improves the user experience and masks the failure events from being
exposed to the user as long as the workload contains few strong operations.
The trade-off between consistency, availability and tolerance to network partitions in computing services has become folklore long ago [7].
Most replicated systems are designed to be ``strongly'' consistent, i.e., provide clients with consistency guarantees that approximate the semantics of a single, correct server, such as single-copy serializability [20] or linearizability [22].
Weaker consistency criteria, which allow for better availability and performance at the expense of letting replicas temporarily diverge and users see inconsistent data, were later proposed in the context of replicated services tolerating crash faults [33,17,38,30]. We improve on this body of work by considering the more challenging Byzantine-failure model, where, for instance, it may not suffice to apply an update at a single replica, since that replica may be malicious and fail to propagate it.
There are many examples of Byzantine-fault tolerant state machine replication protocols, but the vast majority of them were designed to provide linearizable semantics [8,4,11,23]. Similarly, Byzantine-quorum protocols provide other forms of strong consistency, such as safe, regular, or atomic register semantics [27]. We differ from this work by analyzing a new point in the consistency-availability tradeoff, where we favor high availability and performance over strong consistency.
There are very few examples of Byzantine-fault tolerant systems that provide weak consistency.
SUNDR [25] and BFT2F [26] provide similar forms of weak consistency (fork and fork*, respectively) in a client-server system that tolerates Byzantine servers. While SUNDR is designed for an unreplicated service and is meant to minimize the trust placed on that server, BFT2F is a replicated service that tolerates a subset of Byzantine-faulty servers. A system with fork consistency might conceal users' actions from each other, but if it does, users get divided into groups and the members of one group can no longer see any of another group's file system operations.
These two systems propose quite different consistency guarantees from
the guarantees provided by Zeno, because the weaker semantics in SUNDR
and BFT2F have very different purposes than our own.
Whereas we are trying to achieve high availability and good
performance with up to ![]() Byzantine faults, the goal in SUNDR and
BFT2F is to provide the best possible semantics in the presence of a
large fraction of malicious servers. In the case of SUNDR, this means
the single server can be malicious, and in the case of BFT2F this means
tolerating arbitrary failures of up to
Byzantine faults, the goal in SUNDR and
BFT2F is to provide the best possible semantics in the presence of a
large fraction of malicious servers. In the case of SUNDR, this means
the single server can be malicious, and in the case of BFT2F this means
tolerating arbitrary failures of up to
![]() of the
servers. Thus they associate client signatures with updates such that,
when such failures occur, all the malicious servers can do is conceal
client updates from other clients. This makes the approach of these systems
orthogonal and complementary to our own.
of the
servers. Thus they associate client signatures with updates such that,
when such failures occur, all the malicious servers can do is conceal
client updates from other clients. This makes the approach of these systems
orthogonal and complementary to our own.
Another example of a system that provides weak consistency in the presence of some Byzantine failures can be found in [32]. However, the system aims at achieving extreme availability but provides almost no guarantees and relies on a trusted node for auditing.
To our knowledge, this paper is the first to consider eventually-consistent Byzantine-fault tolerant generic replicated services.
In this paper we presented Zeno, a BFT protocol that privileges availability and performance, at the expense of providing weaker semantics than traditional BFT protocols. Yet Zeno provides eventual consistency, which is adequate for many of today's replicated services, e.g., that serve as back-ends for e-commerce websites. Our evaluation of an implementation of Zeno shows it provides better availability than existing BFT protocols, and that overheads are low, even during partitions and merges.
Zeno is only a first step towards liberating highly available but Byzantine-fault tolerant systems from the expensive burden of linearizability. Our eventual consistency may still be too strong for many real applications. For example, the shopping cart application does not necessarily care in what order cart insertions occur, now or eventually; this is probably the case for all operations that are associative and commutative, as well as operations whose effects on system state can easily be reconciled using snapshots (as opposed to merging or totally ordering request histories). Defining required consistency per operation type and allowing the replication protocol to relax its overheads for the more ``best-effort'' kinds of requests could provide significant further benefits in designing high-performance systems that tolerate Byzantine faults.
We would like to thank our shepherd, Miguel Castro, the anonymous reviewers, and the members of the MPI-SWS for valuable feedback.
This document was generated using the LaTeX2HTML translator Version 2002-2-1 (1.71)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 -show_section_numbers -local_icons -no_navigation singh_html