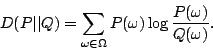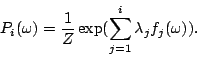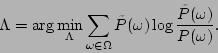|
IMC '05 Paper
[IMC '05 Technical Program]


Detecting Anomalies in Network Traffic Using Maximum Entropy
Estimation
Yu Gu, Andrew McCallum, Don Towsley
Department of Computer Science
University of Massachusetts
We develop a behavior-based anomaly detection method that detects network
anomalies by comparing the current network traffic against a baseline
distribution. The Maximum Entropy technique provides a flexible and fast
approach to estimate the baseline distribution, which also gives the network
administrator a multi-dimensional view of the network traffic. By computing a
measure related to the relative entropy of the network traffic under observation
with respect to the baseline distribution, we are able to distinguish anomalies
that change the traffic either abruptly or slowly. In addition, our method
provides information revealing the type of the anomaly detected. It requires
a constant memory and a computation time proportional to the traffic rate.
Malicious abuses of the Internet are commonly seen in today's Internet traffic.
Anomalies such as worms, port scans, denial of service attacks, etc. can be
found at any time in the network traffic. These anomalies waste network
resources, cause performance degradation of network devices and end hosts, and
lead to security issues concerning all Internet users. Thus, accurately
detecting such anomalies has become an important problem for the network
community to solve.
In this paper, we develop a network anomaly detection technique based on maximum
entropy and relative entropy techniques. Our approach exploits the idea of
behavior-based anomaly detection. We first divide packets into classes along
multiple dimensions. A maximum entropy baseline distribution of the
packet classes in the benign traffic is determined by learning a density model
from a set of pre-labeled training data. The empirical distribution of the
packet classes under observation is then compared to this baseline distribution
using relative entropy as the metric. If the two distributions differ, we show
that the packet classes primarily responsible for the difference contain packets
related to an anomaly.
The maximum entropy approach described in this work exhibits many advantages.
First, it provides the administrators a multi-dimensional view of the network
traffic by classifying packets according to a set of attributes carried by a
packet. Second, it detects anomalies that cause abrupt changes in the network
traffic, as well as those that increase traffic slowly. A large deviation from
the baseline distribution can only be caused by packets that make up an unusual
portion of the traffic. If an anomaly occurs, no matter how slowly it increases
its traffic, it can be detected once the relative entropy increases to a certain
level. Third, it provides information about the type of the anomaly detected.
Our method requires only a constant amount of memory and consists solely of
counting the packets in the traffic, without requiring any per flow information.
Our approach divides into two phases. Phase one is to learn the baseline
distribution and phase two is to detect anomalies in the observed traffic. In
the first phase, we first divide packets into multi-dimensional packet classes
according to the packets' protocol information and destination port numbers.
These packet classes serve as the domain of the probability space. Then, the
baseline distribution of the packet classes is determined by learning a density
model from the training data using Maximum Entropy estimation. The training data
is a pre-labeled data set with the anomalies labeled by a human and in which
packets labeled as anomalous are removed. During the second phase, an observed
network traffic trace is given as the input. The relative entropy of the packet
classes in the observed traffic trace with respect to the baseline distribution
is computed. The packet classes that contribute significantly to the relative
entropy are then recorded. If certain packet classes continue to contribute
significantly to the relative entropy, anomaly warnings are generated and the
corresponding packet classes are reported. This corresponding packet class
information reveals the protocols and the destination port numbers related to
the anomalies.
We test the approach over a set of real traffic traces. One of
them is used as the training set and the others are used as the
test data sets. The experimental results show that our approach
identifies anomalies in the traffic with low false negatives and low false
positives.
The rest of the paper is organized as follows. In Section 2, we
review related work. Section 3 describes how we classify
the packets in the traffic. In Section 4, we introduce the Maximum
Entropy estimation technique. In Section 5, we describe how to
detect anomalies in the network traffic based on the baseline distribution.
Section 6 gives experimental results and Section
7 discusses the implementation of the algorithm and related
practical issues. The last section summarizes the whole paper.
2 Related work
A variety of tools have been developed for the purpose of network anomaly
detection. Some detect anomalies by matching the traffic pattern or the packets
using a set of predefined rules that describe characteristics of the anomalies.
Examples of this include many of the rules or policies used in
Snort [12] and Bro [10]. The cost of applying these approaches is
proportional to the size of the rule set as well as the complexity of the
individual rules, which affects the scalability of these approaches. Furthermore
they are not sensitive to anomalies that have not been previously defined. Our
work is a behavior based approach and requires little computation.
A number of existing approaches are variations on the change detection method.
In [2], Brutlag uses the Holt Winter forecasting model
to capture the history of the network traffic variations and to predict the
future traffic rate in the form of a confidence band. When the variance of the
network traffic continues to fall outside of the confidence band, an alarm is
raised. In [1], Barford et al. use wavelet analysis
to remove from the traffic the predictable ambient part and then study the
variations in the network traffic rate. Network anomalies are detected by
applying a threshold to a deviation score computed from the analysis.
In [14], Thottan and Ji take management information base (MIB)
data collected from routers as time series data and use an auto-regressive
process to model the process. Network anomalies are detected by inspecting
abrupt changes in the statistics of the data. In [15], Wang
et al. take the difference in the number of SYNs and FINs (RSTs)
collected within one sampling period as time series data and use a
non-parametric Cumulative Sum (CUSUM) method to detect SYN flooding by
detecting the change point of the time series. While these methods can detect
anomalies that cause unpredicted changes in the network traffic, they may be
deceived by attacks that increase their traffic slowly. Our work can detect
anomalies regardless of how slowly the traffic is increased and report on the
type of the anomaly detected.
There is also research using approaches based on information theory.
In [7], Lee and Xiang study several information theoretic measures
for intrusion detection. Their study uses entropy and conditional entropy to
help data partitioning and setting parameters for existing intrusion detection
models. Our work detects network traffic anomalies that cause unusual changes in
the network traffic rate or content. In [13], Staniford
et al. use information theoretic measures to help detect stealthy port
scans. Their feature models are based on maintaining probability tables of
feature instances and multi-dimensional tables of conditional probabilities. Our
work applies a systematic framework, Maximum Entropy estimation, to estimate the
baseline distribution, and our approach is not limited to locating port scans.
Maximum Entropy estimation is a general technique that has been widely used
in the fields of machine learning, information retrieval, computer vision, and
econometrics, etc. In [11], Pietra et al. present a
systematic way to induce features from random fields using Maximum Entropy
technique. In [9], McCallum builds,
on [11], an efficient approach to induce features of
Conditional Random Fields (CRFs). CRFs are undirected graphical models used to
calculate the conditional probability of values on designated output nodes
given values assigned to other designated input nodes. And
in [8], Malouf gives a detailed comparison of several
Maximum Entropy parameter estimation algorithms. In our work, we use the L-BFGS
algorithm implemented by Malouf to estimate the parameters in the Maximum
Entropy model.
3 Packet classification
In this section, we describe how we divide packets in the network
traffic into a set of packet classes. Our work focuses on
anomalies concerning TCP and UDP packets. In order to study the
distribution of these packets, we divide them into a set of
two-dimensional classes according to the protocol information and
the destination port number in the packet header. This set of
packet classes is the common domain of the probability spaces in
this work.
In the first dimension, packets are divided into four classes according to the
protocol related information. First, packets are divided into the classes of
TCP and UDP packets. Two other classes are further split from the TCP packet
class according to whether or not the packets are SYN and RST packets.
In the second dimension, packets are divided into 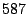 classes according to
their destination port numbers. Port numbers often determine the services
related to the packet exchange. According to the Internet Assigned Numbers
Authority [6], port numbers are divided into three categories:
Well Known Ports ( classes according to
their destination port numbers. Port numbers often determine the services
related to the packet exchange. According to the Internet Assigned Numbers
Authority [6], port numbers are divided into three categories:
Well Known Ports (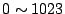 ), Registered Ports ( ), Registered Ports (
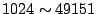 ), and Dynamic and/or Private Ports ( ), and Dynamic and/or Private Ports (
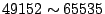 ). In our
work, packets with a destination port in the first category are divided into
classes of ). In our
work, packets with a destination port in the first category are divided into
classes of 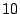 port numbers each. Since packets with port number port numbers each. Since packets with port number 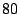 comprise
the majority of the network traffic, they are separated into a single class.
This produces comprise
the majority of the network traffic, they are separated into a single class.
This produces 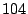 packet classes. Packets with destination port in the second
category are divided into packet classes. Packets with destination port in the second
category are divided into 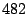 additional classes, with each class covering additional classes, with each class covering
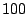 port numbers with the exception of the class that covers the last port numbers with the exception of the class that covers the last 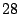 port numbers from
port numbers from 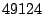 to to 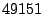 . Packets with destination port numbers
larger than . Packets with destination port numbers
larger than 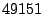 are grouped into a single class. Thus, in this dimension,
packets are divided into a total of are grouped into a single class. Thus, in this dimension,
packets are divided into a total of 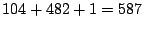 classes. classes.
Altogether, the set of two-dimensional classes consists of
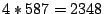 packet classes. These packet classes comprises the
probability space in this paper. We estimate the
distribution of different packets in the benign traffic according
to this classification, and use it as the baseline distribution to
detect network traffic anomalies. packet classes. These packet classes comprises the
probability space in this paper. We estimate the
distribution of different packets in the benign traffic according
to this classification, and use it as the baseline distribution to
detect network traffic anomalies.
4 Maximum Entropy estimation of the packet classes distribution
Maximum Entropy estimation is a framework for obtaining a
parametric probability distribution model from the training data
and a set of constraints on the model. Maximum Entropy estimation
produces a model with the most 'uniform' distribution among all
the distributions satisfying the given constraints. A mathematical
metric of the uniformity of a distribution 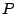 is its
entropy: is its
entropy:
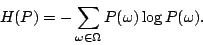 |
(1) |
Let 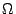 be the set of packet classes defined in the previous
section. Given a sequence of packets be the set of packet classes defined in the previous
section. Given a sequence of packets
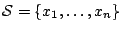 as the training data, the empirical
distribution as the training data, the empirical
distribution 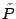 over over 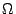 in this training data is in this training data is
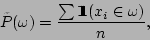 |
(2) |
where
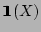 is an indicator function that takes value is an indicator function that takes value 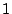 if
if 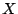 is true and is true and 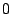 otherwise. otherwise.
Suppose we are given a set of feature functions
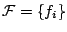 , and let , and let 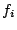 be an indicator function be an indicator function
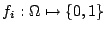 . By using Maximum Entropy estimation, we are
looking for a density model . By using Maximum Entropy estimation, we are
looking for a density model 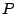 that satisfies that satisfies
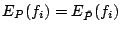 for all for all
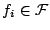 and has
maximum entropy. In [11], it has been proved
that under such constraints, the Maximum Entropy estimate is
guaranteed to be (a) unique, and (b) the same as the maximum
likelihood estimate using the generalized Gibbs distribution,
having the following log-linear form and has
maximum entropy. In [11], it has been proved
that under such constraints, the Maximum Entropy estimate is
guaranteed to be (a) unique, and (b) the same as the maximum
likelihood estimate using the generalized Gibbs distribution,
having the following log-linear form
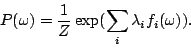 |
(3) |
For each feature 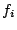 , a parameter , a parameter
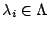 determines its weight in the model,
determines its weight in the model, 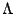 is the set of
parameters for the feature functions. is the set of
parameters for the feature functions. 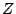 is a normalization
constant that ensures that the sum of the probabilities over is a normalization
constant that ensures that the sum of the probabilities over
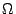 is is 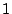 .
The difference between two given distributions .
The difference between two given distributions 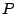 and and 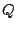 is commonly
determined using the relative entropy or Kullback-Leibler
(K-L) divergence: is commonly
determined using the relative entropy or Kullback-Leibler
(K-L) divergence:
Maximizing the likelihood of the distribution in
the form of (3) with respect to 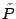 is
equivalent to minimizing the K-L divergence of is
equivalent to minimizing the K-L divergence of 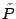 with
respect to with
respect to 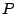
as
For the sake of efficiency, feature functions are often selected
to express the most important characteristics of the training data
in the learned log-linear model, and in return, the log-linear
model expresses the empirical distribution with the fewest feature
functions and parameters.
The Maximum Entropy estimation procedure consists of two parts:
feature selection and parameter estimation. The feature selection
part selects the most important features of the log-linear model,
and the parameter estimation part assigns a proper weight to each
of the feature functions. These two parts are performed
iteratively to reach the final model. In the following, we
describe each part in turn. More details can be found
in [11].
4.1 Feature selection
The feature selection step is a greedy algorithm which chooses the best feature
function that minimizes the difference between the model distribution and the
empirical distribution from a set of candidate feature functions.
Let 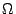 be the set of all packet classes, be the set of all packet classes, 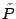 the
empirical distribution of the training data over the
empirical distribution of the training data over 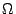 , and , and
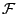 a set of candidate feature functions. The initial
model distribution over a set of candidate feature functions. The initial
model distribution over 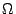 is is
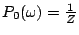 , ,
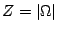 , which is a uniform distribution over , which is a uniform distribution over 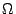 . .
Now let 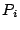 be a model with be a model with 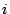 feature functions selected feature functions selected
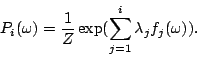 |
(4) |
and we want to select the 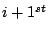 feature function. Let feature function. Let 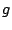 be a feature
function in be a feature
function in
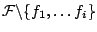 to be selected into the
model and to be selected into the
model and 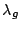 be its weight, then let be its weight, then let
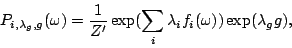 |
(5) |
and let
where 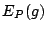 is the expected value of is the expected value of 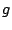 with respect to the distribution of with respect to the distribution of
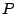 . .
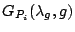 is a concave function with respect to is a concave function with respect to 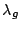 ,
and ,
and
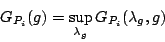 |
(6) |
is the maximum decrease of the K-L divergence that can be attained by adding
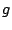 into the model. The feature function into the model. The feature function 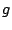 with the largest gain with the largest gain 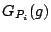 is selected as the
is selected as the 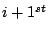 feature function to the model. feature function to the model.
In [11], it is also shown that for indicator
candidate feature functions, there are closed form formulas
related to the maxima of
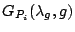 , which makes it
computationally easier. For more details on feature selection,
please refer to [11] and [4]. , which makes it
computationally easier. For more details on feature selection,
please refer to [11] and [4].
4.2 Parameter estimation
After a new feature function is added to the log-linear model, the weights of
all feature functions are updated. Given a set of training data and a set of
selected feature functions 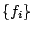 , the set of parameters is then estimated.
Maximum Entropy estimation locates a set of parameters , the set of parameters is then estimated.
Maximum Entropy estimation locates a set of parameters
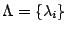 in (3) for
in (3) for 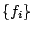 that minimizes the K-L divergence of that minimizes the K-L divergence of
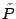 with respect to with respect to 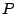 : :
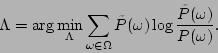 |
(7) |
There are a number of numerical methods that can be exploited. In our work, we
use the L-BFGS Maximum Entropy estimation algorithm "tao_lmvm" implemented by
Malouf in [8].
4.3 Model construction
Figure 1 shows the model construction algorithm. The model
is built by iterating the above two steps until some stopping criterion is met.
This stopping criterion can be either that the K-L divergence of 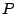 with
respect to with
respect to 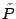 is less than some threshold value, or that the gain of
adding a new feature function is too small to improve the model. is less than some threshold value, or that the gain of
adding a new feature function is too small to improve the model.
The feature functions are selected from a set of candidate feature functions.
Since the domain 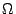 in our work consists of packet classes different in
the protocols and the destination port numbers, our candidate feature function
set comprises of three sets of indicator functions. The first set of indicator
functions checks the packet's protocol information, the second set of indicator
functions classify the packet's destination port number, and the third set
checks both the packet's protocol information and the destination port number. in our work consists of packet classes different in
the protocols and the destination port numbers, our candidate feature function
set comprises of three sets of indicator functions. The first set of indicator
functions checks the packet's protocol information, the second set of indicator
functions classify the packet's destination port number, and the third set
checks both the packet's protocol information and the destination port number.
Figure 1:
Model construction algorithm
 |
The training data used are pre-labeled by humans and the packets related to the
labeled anomalies are not used in computing the empirical distribution
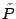 . In this way, we treat the packet classes distribution defined by
the log-linear model in (3) from Maximum Entropy estimation
as the baseline distribution, and are now able to compute the relative entropy
of any given network traffic. . In this way, we treat the packet classes distribution defined by
the log-linear model in (3) from Maximum Entropy estimation
as the baseline distribution, and are now able to compute the relative entropy
of any given network traffic.
5 Detecting network traffic anomalies
The relative entropy shows the difference between the distribution of the
packet classes in the current network traffic and the baseline distribution. If
this difference is too large, it indicates that a portion of some packet
classes that rarely appear in the training data increases significantly, or
that appear regularly decreases significantly. In other words, this serves as
an indication of the presence of an anomaly in the network traffic. Our current
work only considers the anomalies where anomaly traffic increases.
We divide time into slots of fixed length 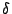 . Suppose the traffic in
a time slot contains the packet sequences . Suppose the traffic in
a time slot contains the packet sequences
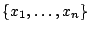 , the empirical
distribution , the empirical
distribution 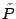 of the packet classes in this time slot is of the packet classes in this time slot is
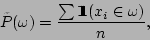 |
(8) |
For each packet class, we define
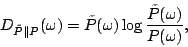 |
(9) |
where 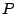 is the baseline distribution obtained from Maximum Entropy
estimation. This produces a quantitative value that describes the distortion of
the distribution for each packet class is the baseline distribution obtained from Maximum Entropy
estimation. This produces a quantitative value that describes the distortion of
the distribution for each packet class 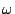 from that of the baseline
distribution, and this is used as an indication of anomalies. from that of the baseline
distribution, and this is used as an indication of anomalies.
We then use a 'sliding window' detection approach. In each time slot, we record
packet classes that have their divergences larger than a threshold 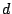 . If for a
certain packet class . If for a
certain packet class 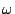 , ,
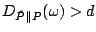 for more than for more than 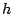 times in a window of
times in a window of 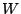 time slots, an alarm is raised together with the packet
class information time slots, an alarm is raised together with the packet
class information 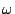 , which reveals the corresponding protocol and port
number. , which reveals the corresponding protocol and port
number.
6 Experimental results
In this section, we present initial experimental results. The data are collected
at the UMASS Internet gateway router using DAG cards made by
Endace [3]. They consist of seven hours' traffic trace collected from
9:30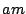 to 10:30 to 10:30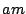 in the morning for a week from July 16th to July 22nd,
2004. All of these data are labeled by human inspection. In particular, we
select a set of high volume flows, a set of nodes with high incoming or outgoing
traffic, and a set of port numbers that have high volume of traffic. We then
examine each of them to see whether there are anomalies. For more details of the
trace collected, please refer to [4]. in the morning for a week from July 16th to July 22nd,
2004. All of these data are labeled by human inspection. In particular, we
select a set of high volume flows, a set of nodes with high incoming or outgoing
traffic, and a set of port numbers that have high volume of traffic. We then
examine each of them to see whether there are anomalies. For more details of the
trace collected, please refer to [4].
We use the data taken on July 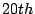 as the training data set. The Maximum
Entropy estimation algorithm is used to generate the baseline distribution of
the packet classes from the training data. We set the stopping criterion for the
construction algorithm to be whether the K-L difference of as the training data set. The Maximum
Entropy estimation algorithm is used to generate the baseline distribution of
the packet classes from the training data. We set the stopping criterion for the
construction algorithm to be whether the K-L difference of 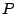 with respect to with respect to
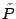 is less than is less than 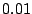 . By this criterion, the algorithm ended with a
set of . By this criterion, the algorithm ended with a
set of 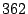 feature functions. feature functions.
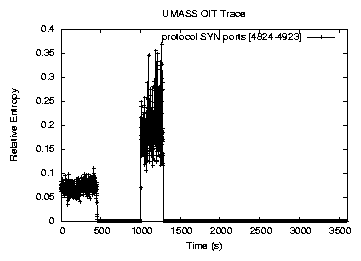
Figure 2:
Relative entropy for packets of type SYN and destination port number
from 4824 to 4923
|
As an example, we first show two cases of port scans that manifest themselves
by increasing the
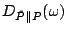 value. The parameters used are set
as value. The parameters used are set
as 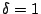 second, second, 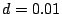 , , 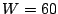 and and 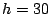 . On July 19th, 2004, from
9:30 . On July 19th, 2004, from
9:30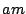 , when we began our data collection, to 9:37 , when we began our data collection, to 9:37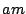 , a host outside of the
UMASS campus network performed a port scan at port , a host outside of the
UMASS campus network performed a port scan at port 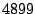 by sending many SYN
packets to different hosts in the UMASS campus network. Then from 9:46 by sending many SYN
packets to different hosts in the UMASS campus network. Then from 9:46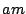 to
9:51 to
9:51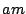 , another host outside of the UMASS campus network performed another
port scan at the same port. During these two time periods, the relative entropy
of the packet class that represents SYN packets targeting at ports from , another host outside of the UMASS campus network performed another
port scan at the same port. During these two time periods, the relative entropy
of the packet class that represents SYN packets targeting at ports from 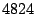 to
to 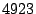 increased considerably, as shown in Figure 2. These two
port scans were successfully detected by our relative entropy detection
algorithm. increased considerably, as shown in Figure 2. These two
port scans were successfully detected by our relative entropy detection
algorithm.
We test the performance of the algorithm by running it over the remaining six
human labeled data sets. The detection algorithm provides results at every time
slot 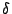 . If an anomaly is detected by the algorithm and there is a
corresponding anomaly detected by human labeling, it is a positive. All
anomalies detected by the algorithm corresponding to the same anomaly labeled by
human are treated as a single positive. If there is no human labeled anomaly
corresponding to the anomaly reported by the algorithm, it is called a
false positive. Consecutive false positives are treated as a single false
positive. Anomalies labeled by human but missed by the algorithm are called
false negatives. In each case, the algorithm detects most of the
anomalies located by human labeling. However, the algorithm also reports many
'false positives'. These 'false positives' are either 'flash crowds'
phenomenons, high rate traffic that communicates with port numbers rarely seen
in the training data, or traffic that we cannot tell what they are given the
limited packet header information. For more details, please refer
to [4]. . If an anomaly is detected by the algorithm and there is a
corresponding anomaly detected by human labeling, it is a positive. All
anomalies detected by the algorithm corresponding to the same anomaly labeled by
human are treated as a single positive. If there is no human labeled anomaly
corresponding to the anomaly reported by the algorithm, it is called a
false positive. Consecutive false positives are treated as a single false
positive. Anomalies labeled by human but missed by the algorithm are called
false negatives. In each case, the algorithm detects most of the
anomalies located by human labeling. However, the algorithm also reports many
'false positives'. These 'false positives' are either 'flash crowds'
phenomenons, high rate traffic that communicates with port numbers rarely seen
in the training data, or traffic that we cannot tell what they are given the
limited packet header information. For more details, please refer
to [4].
Table 1:
Algorithm performance
|
Date |
Humanly labeled |
Positive |
False negative |
False positive |
Precision |
Recall |
F1 |
|
July 16 |
10 |
10 |
0 |
1 |
0.91 |
1 |
0.95 |
|
July 17 |
11 |
10 |
1 |
0 |
1 |
0.91 |
0.95 |
|
July 18 |
14 |
14 |
0 |
0 |
1 |
1 |
1 |
|
July 19 |
16 |
14 |
2 |
0 |
1 |
0.88 |
0.93 |
|
July 21 |
15 |
15 |
0 |
0 |
1 |
1 |
1 |
|
July 22 |
9 |
8 |
1 |
0 |
1 |
0.89 |
0.94 |
|
In spite of the ambiguous situation concerning all the anomalies
generated by the algorithm, we found that the experimental results
regarding SYN packets give good results. Table
1 summarizes the algorithm performance in the
experiments described above. The table also summarizes the
performance of the algorithm in terms of precision, recall and F1.
Let 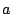 be the number of positives, be the number of positives, 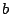 the number of false
positives, and the number of false
positives, and 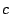 the number of false negatives, precision is
defined as the number of false negatives, precision is
defined as 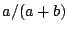 , recall is defined as , recall is defined as 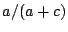 and F1 is
defined as and F1 is
defined as 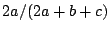 . The table shows that the Maximum Entropy
method detects most of the anomalies detected by human labeling
with few false negatives and few false positives. . The table shows that the Maximum Entropy
method detects most of the anomalies detected by human labeling
with few false negatives and few false positives.
7 Implementation and practical issues
We are currently implementing the detection algorithm using an Intel IXP 1200
packet processing engine for routers [5], which has six
processing engines, one control processor, and works at 200-MHz clock rate. The
empirical distribution of the packet classes in the network traffic is read from
the processing engine and compared to the baseline distribution every second.
The baseline distribution is estimated offline. In practice, when the traffic is
expected to experience certain changes, i.e. due to diurnal effects or planned
network reconfiguration, the baseline distribution should be updated or
retrained. How to do this is a topic of future research.
8 Conclusion
In this paper, we introduce our approach to detect anomalies in the network
traffic using Maximum Entropy estimation and relative entropy. The packet
distribution of the benign traffic is estimated using the Maximum Entropy
framework and used as a baseline to detect the anomalies. The method is able
to detect anomalies by inspecting only the current traffic instead of a change
point detection approach. The experimental results show that it effectively
detects anomalies in the network traffic including different kinds of SYN
attacks and port scans. This anomaly detection method identifies the type of
the anomaly detected and comes with low false positives. The method requires a
constant memory and a computation time proportional to the traffic rate. Many
interesting aspects of this approach still remain to be explored, and
comparison with other methods such as Holt-Winter, when possible, will be
useful.
We wish to thank Professor Paul Barford for useful comments and suggestions.
Feedback from anonymous reviewers also helped to improve the work. This research
is supported by NSF and DARPA under grants CNS-0085848 and F30602-00-2-0554. The
data collection equipment was puchased under NSF grant EIA-0080119.
- 1
-
BARFORD, P., KLINE, J., PLONKA, D., AND RON, A.
A signal analysis of network traffic anomalies.
In Proceedings of ACM SIGCOMM Internet Measurement Workshop
(2002).
- 2
-
BRUTLAG, J. D.
Aberrant behavior detection in time series for network service
monitoring.
In Proceeding of the 14th Systems Administration Conference
(2000), pp. 139-146.
- 3
-
ENDACE.
https://www.endace.com.
- 4
-
GU, Y., MCCALLUM, A., AND TOWSLEY, D.
Detecting anomalies in network traffic using maximum entropy.
Tech. rep., Department of Computer Science, UMASS, Amherst, 2005.
- 5
-
INTEL CORP.
Intel ixp 1200 network processor, 2000.
- 6
-
INTERNET ASSIGNED NUMBERS AUTHORITY.
https://www.iana.org/assignments/port-numbers.
- 7
-
LEE, W., AND XIANG, D.
Information-theoretic measures for anomaly detection.
In Proceedings of the IEEE Symposium on Security and Privacy
(2001), IEEE Computer Society, p. 130.
- 8
-
MALOUF, R.
A comparison of algorithms for maximum entropy parameter estimation.
In Proceedings of the 6th Conference on Natural Language
Learning (2002).
- 9
-
MCCALLUM, A.
Efficiently inducing features of conditional random fields.
In Nineteenth Conference on Uncertainty in Artificial
Intelligence (UAI03) (2003).
- 10
-
PAXSON, V.
Bro: A system for detecting network intruders in real-time.
- 11
-
PIETRA, S. D., PIETRA, V. D., AND LAFFERTY, J.
Inducing features of random fields.
IEEE Transactions on Pattern Analysis and Machine Intelligence
19, 4 (1997), 380-393.
- 12
-
SNORT: THE OPEN SOURCE NETWORK INTRUSION DETECTION SYSTEM".
https://www.snort.org/.
- 13
-
STANIFORD, S., HOAGLAND, J., AND MCALERNEY, J. M.
Practical automated detection of stealthy portscans.
In Proceedings of the IDS Workshop of the 7th Computer and
Communications Security Conference (2000).
- 14
-
THOTTAN, M., AND JI, C.
Anomaly detection in ip networks.
IEEE Trans. Signal Processing 51 (2003).
- 15
-
WANG, H., ZHANG, D., AND SHIN, K. G.
Detecting syn flooding attacks.
In Proceedings of IEEE INFOCOM (2002).
Detecting Anomalies in Network Traffic Using Maximum Entropy
Estimation
This document was generated using the
LaTeX2HTML translator Version 2002-2-1 (1.71)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 -show_section_numbers -local_icons re.tex
The translation was initiated by Yu Gu on 2005-08-10



Yu Gu
2005-08-10
|
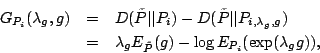
![]() . If for a
certain packet class
. If for a
certain packet class ![]() ,
,
![]() for more than
for more than ![]() times in a window of
times in a window of ![]() time slots, an alarm is raised together with the packet
class information
time slots, an alarm is raised together with the packet
class information ![]() , which reveals the corresponding protocol and port
number.
, which reveals the corresponding protocol and port
number.
![]() to 10:30
to 10:30![]() in the morning for a week from July 16th to July 22nd,
2004. All of these data are labeled by human inspection. In particular, we
select a set of high volume flows, a set of nodes with high incoming or outgoing
traffic, and a set of port numbers that have high volume of traffic. We then
examine each of them to see whether there are anomalies. For more details of the
trace collected, please refer to [4].
in the morning for a week from July 16th to July 22nd,
2004. All of these data are labeled by human inspection. In particular, we
select a set of high volume flows, a set of nodes with high incoming or outgoing
traffic, and a set of port numbers that have high volume of traffic. We then
examine each of them to see whether there are anomalies. For more details of the
trace collected, please refer to [4].
![]() as the training data set. The Maximum
Entropy estimation algorithm is used to generate the baseline distribution of
the packet classes from the training data. We set the stopping criterion for the
construction algorithm to be whether the K-L difference of
as the training data set. The Maximum
Entropy estimation algorithm is used to generate the baseline distribution of
the packet classes from the training data. We set the stopping criterion for the
construction algorithm to be whether the K-L difference of ![]() with respect to
with respect to
![]() is less than
is less than ![]() . By this criterion, the algorithm ended with a
set of
. By this criterion, the algorithm ended with a
set of ![]() feature functions.
feature functions.
![]() value. The parameters used are set
as
value. The parameters used are set
as ![]() second,
second, ![]() ,
, ![]() and
and ![]() . On July 19th, 2004, from
9:30
. On July 19th, 2004, from
9:30![]() , when we began our data collection, to 9:37
, when we began our data collection, to 9:37![]() , a host outside of the
UMASS campus network performed a port scan at port
, a host outside of the
UMASS campus network performed a port scan at port ![]() by sending many SYN
packets to different hosts in the UMASS campus network. Then from 9:46
by sending many SYN
packets to different hosts in the UMASS campus network. Then from 9:46![]() to
9:51
to
9:51![]() , another host outside of the UMASS campus network performed another
port scan at the same port. During these two time periods, the relative entropy
of the packet class that represents SYN packets targeting at ports from
, another host outside of the UMASS campus network performed another
port scan at the same port. During these two time periods, the relative entropy
of the packet class that represents SYN packets targeting at ports from ![]() to
to ![]() increased considerably, as shown in Figure 2. These two
port scans were successfully detected by our relative entropy detection
algorithm.
increased considerably, as shown in Figure 2. These two
port scans were successfully detected by our relative entropy detection
algorithm.
![]() . If an anomaly is detected by the algorithm and there is a
corresponding anomaly detected by human labeling, it is a positive. All
anomalies detected by the algorithm corresponding to the same anomaly labeled by
human are treated as a single positive. If there is no human labeled anomaly
corresponding to the anomaly reported by the algorithm, it is called a
false positive. Consecutive false positives are treated as a single false
positive. Anomalies labeled by human but missed by the algorithm are called
false negatives. In each case, the algorithm detects most of the
anomalies located by human labeling. However, the algorithm also reports many
'false positives'. These 'false positives' are either 'flash crowds'
phenomenons, high rate traffic that communicates with port numbers rarely seen
in the training data, or traffic that we cannot tell what they are given the
limited packet header information. For more details, please refer
to [4].
. If an anomaly is detected by the algorithm and there is a
corresponding anomaly detected by human labeling, it is a positive. All
anomalies detected by the algorithm corresponding to the same anomaly labeled by
human are treated as a single positive. If there is no human labeled anomaly
corresponding to the anomaly reported by the algorithm, it is called a
false positive. Consecutive false positives are treated as a single false
positive. Anomalies labeled by human but missed by the algorithm are called
false negatives. In each case, the algorithm detects most of the
anomalies located by human labeling. However, the algorithm also reports many
'false positives'. These 'false positives' are either 'flash crowds'
phenomenons, high rate traffic that communicates with port numbers rarely seen
in the training data, or traffic that we cannot tell what they are given the
limited packet header information. For more details, please refer
to [4].
![]() be the number of positives,
be the number of positives, ![]() the number of false
positives, and
the number of false
positives, and ![]() the number of false negatives, precision is
defined as
the number of false negatives, precision is
defined as ![]() , recall is defined as
, recall is defined as ![]() and F1 is
defined as
and F1 is
defined as ![]() . The table shows that the Maximum Entropy
method detects most of the anomalies detected by human labeling
with few false negatives and few false positives.
. The table shows that the Maximum Entropy
method detects most of the anomalies detected by human labeling
with few false negatives and few false positives.