
Opportunistic Computing: A New Paradigm for Scalable Realism on Many-Cores
Romain Cledat, Tushar Kumar, Jaswanth Sreeram, Santosh Pande
Georgia Institute of Technology, Atlanta, GA
romain@gatech.edu, tushark@ece.gatech.edu, jaswanth@cc.gatech.edu, santosh@cc.gatech.edu
Abstract:
With the advent of multi-cores and many-cores, traditional techniques that
seek only to improve FLOPS of performance or the degree of parallelism
have hit a roadblock with regards
to providing even greater performance.
In order to surmount this roadblock, techniques should more
directly address the underlying design objectives of an application.
Specific implementations and algorithmic choices in applications are
intended to achieve the underlying realism objectives in the
programmer's mind. We identify two specific aspects of this realism that
traditional programming and parallelization approaches do not
capture and exploit to utilize the growing number of cores.
The first aspect is that the goal of minimizing program
execution time can be satisfactorily met if the program execution
time is low with sufficiently high probability.
We exploit the fact that randomized algorithms
are available for many commonly used kernels, and that the use of parallelism can
achieve very low expected execution times with high probability for
these algorithms.
This can provide speedups
to parts of the application that were hitherto deemed sequential
and ignored for extracting performance via multi-cores.
The second aspect of realism that we exploit is that important
classes of emerging applications, like gaming and
interactive visualization, have user-interactivity and responsiveness
requirements that are as important as raw performance.
Their design goal is to maximize the functionality expressed, while maintaining
a high and smooth frame-rate.
Therefore, the primary objective for these applications
is not to run a fixed computation as fast as possible, but rather to scale the
application semantics up or down depending on the resources available.
Our framework intends to capture the responsiveness requirements of these applications as
they pertain to expressed realism and automatically scale the application
semantics expressed on every architecture, including very resource-rich many-cores.
Traditionally, to evaluate ``performance'' in an application, FLOPS are a very common
measure.
However, the underlying design criteria is realism rather
than FLOPS.
The notion of realism in an application differs depending on the application and is best
illustrated with examples.
In a simulation application,
it can be how closely the simulation matches the physical phenomenon being simulated.
In a live video encoding application, it can be how well the transmitted compressed video
reflects the original source.
In the era of single cores, measuring FLOPS was an adequate substitute to
measuring realism but this is not true for multi-cores. Today, to improve
realism, an application must make effective use of an ever growing number of cores.
When designing an application, the programmer's driving goal is
to maximize realism under constraints. For example, in a simulation
of a continuous physical phenomenon, realism can be increased with a finer grain
simulation timestep but this must be balanced with the amount of time
available for the simulation. However, while the amount of realism is usually
traded-off with total execution time, for
some applications where interactivity with users is a key component, it must also
be balanced with the need to be responsive. Video games, for example, try to maximize the
level of immersion while maintaining a good frame-rate.
Thus, the design of an application comes down to
maximizing the amount of realism you can pack given execution time constraints
and responsiveness constraints.
Traditionally, to increase the realism in applications,
programmers have relied on i) task and data parallelization techniques, and
ii) an increase in clock frequency with each new generation of processors.
Programming in a concurrency friendly way is an important goal
[6] through which significant improvements
in application realism have been gained. However, the task and data parallelism techniques
focus on breaking down an application into parts. In many applications,
such as game engines [3], this process of decomposition
quickly hits a wall. It is hard to statically decompose the application
or dynamically detect available parallelism [2,1]
to a sufficient
degree to take advantage of the growing number of processor cores.
Further, the sequential parts of an application do not benefit from the current growth
in the number of cores available in a processor. The speedup achievable on the sequential
parts of the application is limited by the relative stagnation in processor clock frequencies.
Amdahl's law dictates that the overall application speedup achievable through traditional
parallelization is limited by the amount of serial code present. For example, if 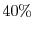 of
an application is serial code, the maximum parallel speedup is limited to
of
an application is serial code, the maximum parallel speedup is limited to 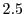 regardless of the number of cores
used. Therefore, with the stagnation of processor clock frequencies, the extent of serial
code present is fast becoming the principal bottleneck towards utilizing
multi-cores for greater realism in many applications.
regardless of the number of cores
used. Therefore, with the stagnation of processor clock frequencies, the extent of serial
code present is fast becoming the principal bottleneck towards utilizing
multi-cores for greater realism in many applications.
This paper relies on two currently unexploited application attributes to
obtain greater realism on multi-cores in the presence of serial code. First, we exploit
the fact that there are a plethora of randomized algorithms for many sequential
kernels commonly found in applications. Concurrently invoking multiple independent instances
of a randomized kernel considerably enhances the probability that at least one instance will
complete with execution time much lower than the average case execution time, thereby
speeding up the sequential kernel with high probability.
Additionally, there are numerous sequential algorithms already in use in current applications
that utilize randomness in their computation. While such algorithms are not formally considered
randomized algorithms, their probabilistic execution time characteristics are often sufficient
to achieve a speedup on multi-cores in a manner similar to formal randomized algorithms.
We specifically study genetic algorithms as examples of algorithms with suitable random
characteristics.
The second application attribute we exploit is that of scalable semantics inherent
in many applications, specially immersive application like gaming, multimedia and
interactive visualization. Due to the very nature of such applications, the
execution time complexity of their algorithms is significantly
affected by the values of a few key parameters. Parameters such as the granularity of
the simulation time-step and the types of interactions between game-world objects considered,
confer scalable semantics to the physics and Artificial Intelligence (AI) components of a game.
The programmer's design goal is to have game components execute at the highest level of
sophistication possible while also keeping the game responsive to the user by maintaining
a sufficiently high frame-rate. Such scalable semantics allow
the execution time of sequential algorithms to be dynamically adjusted when they become
bottlenecks towards achieving a high frame-rate.
Further, scalable semantics also allow selection between algorithmic models of
different levels of sophistication based on the
expected number of core resources needed by each alternative. Therefore, scalable semantics not only
alleviate sequential bottlenecks but also enable the effective utilization
of multi-core resources.
We have motivated that traditional techniques, while being
able to improve realism through increased FLOPS, will not be able
to take full advantage of the growing number of cores. Our proposed
framework effectively utilizes additional cores towards
achieving greater realism once the traditional techniques saturate
in the number of cores they can utilize.
We make the following specific contributions:
- We recognize that randomized algorithms exist for
many common compute intensive sequential kernels. Certain domain-specific
sequential algorithms that make use of randomness, such as genetic
algorithms, also benefit from our technique. We
demonstrate a runtime framework that utilizes extra cores
to dramatically improve the expected execution time of the
sequential code and hence of the overall application. We
note that for applications containing randomized algorithm
kernels, an application-agnostic runtime framework
is needed to extract the statistical characteristics of the
component kernels with sufficient accuracy. This allows correct
prediction of resources required to achieve a
sufficient application-wide speedup with high probability.
- We recognize that in a new compute-intensive class of
emerging interactive applications, responsiveness is as important
a design goal as realism. The overarching design
goal of such applications is to maximize the realism exhibited
on any given hardware platform, subject to responsiveness
constraints. Our framework allows the programmer to
intuitively express the limitations that responsiveness imposes
on realism. At runtime our framework scales the application
semantics to achieve the maximal realism possible on every
hardware platform, whether severely resource-constrained
or very resource-rich.
- We motivate that a unification of the randomized algorithms
framework and the application semantics scaling framework
serves to significantly increase the number of cores that
can be effectively utilized to allow important emerging
applications to express maximal realism. We call this
unified framework the Opportunistic Computing Paradigm.
It is important to note that the techniques we present are not a replacement
for traditional techniques for task and data parallelism. Our techniques are intended to effectively use
cores that are left idle after traditional techniques have been applied.
In Section 2 we present the framework that uses extra cores
to minimize the expected execution time of sequential randomized kernels.
Section 3 describes the framework that
utilizes extra cores to scale application semantics subject to
responsiveness constraints. Section 4 presents
the unified Opportunistic Computing framework. Section 5
concludes with future work.
2 Sequential randomized algorithms on multi-cores
For a fixed input, certain types of sequential algorithms complete
in a varying amount of time due to algorithmic non-determinism. Randomized
algorithms are a very simple example of such algorithms where the
completion time is distributed according to a known (or derivable)
probability density function (PDF). However, other types of algorithms, which
are not considered randomized algorithms, also make use of randomness.
Genetic algorithms are a good example.
For these algorithms, the PDF of their execution time, even for a fixed input,
may not be well known or well studied.
Finally, one can also view a collection of heuristics performing the same computation
as a randomized algorithm with the choice of heuristic as the random choice thus allowing
our framework to be extended to some algorithms that make use of heuristics.
For all the algorithms described above, the presence of randomness in the algorithms
leads to variation in execution time and the important measure becomes the
expected time of completion. In the simple case of randomized algorithms,
the expected completion time is the same for all inputs with the same characteristics
(such as size, etc.) and can usually be derived mathematically [4].
However, other algorithms have
more complex and less analytically evident behavior. However, for a given input,
these algorithms will still have a PDF of execution time, which can be experimentally
constructed by sampling, from which an expected completion time can be estimated.
We present an approach that seeks to utilize untapped processor cores to improve the
expected execution time to completion.
Figure 1:
Example structure of a program with a kernel  that
exhibits variations in execution time
that
exhibits variations in execution time
|
Consider Figure 1. Box  represents a sequential algorithm
identified by the programmer that has a well defined and stable PDF for execution time. The goal is
to minimize the overall execution time of the program
represents a sequential algorithm
identified by the programmer that has a well defined and stable PDF for execution time. The goal is
to minimize the overall execution time of the program 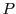 .
. 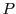 has a fixed input
but
has a fixed input
but  is invoked repeatedly within
is invoked repeatedly within 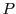 with multiple inputs
with multiple inputs 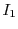 ...
...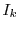 .
Our approach consists of replacing the invocation of
.
Our approach consists of replacing the invocation of  on input
on input 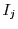 by
by 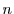 instances of
instances of  running in parallel,
running in parallel,
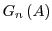 , where each
instance will operate on
, where each
instance will operate on 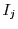 but make independent random choices.
but make independent random choices.
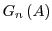 terminates when the
first
terminates when the
first 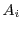 terminates.
The goal of our system is to pick the best
terminates.
The goal of our system is to pick the best 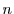 (number of instances to run in parallel)
to achieve the maximal speedup. We must thus be able to calculate the expected
speedup of running
(number of instances to run in parallel)
to achieve the maximal speedup. We must thus be able to calculate the expected
speedup of running 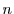 instances versus just one instance.
instances versus just one instance.
Speedup for a fixed input
Let us for now consider a fixed input 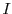 to
to  . We call
. We call 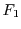 the
cumulative distribution function (CDF) of
the
cumulative distribution function (CDF) of  on input
on input 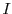 . Similarly we call
. Similarly we call 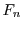 the CDF
obtained by running
the CDF
obtained by running 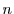 instances of
instances of  in parallel and taking the best (smallest)
execution time.
It is easy to show that
in parallel and taking the best (smallest)
execution time.
It is easy to show that
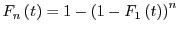 . This is because the probability
for each independent randomization of
. This is because the probability
for each independent randomization of  to not complete within time
to not complete within time
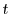 is
is
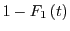 .
Therefore, supposing knowledge, either theoretical or experimental, of
.
Therefore, supposing knowledge, either theoretical or experimental, of 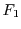 will allow
us to compute the expected
speedup
will allow
us to compute the expected
speedup
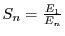 where
where 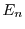 is the expected time for
is the expected time for 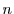 parallel
instances deduced from the CDF and
parallel
instances deduced from the CDF and  is the expected sequential execution time.
is the expected sequential execution time.
Theoretical speedups
Figure 2:
Speedups obtainable through our technique
|
In Figure 2, we show the expected theoretical speedup for
different distributions 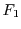 . The results show that whenever the spread
. The results show that whenever the spread
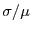 is high, our technique produces higher speedup.
This is consistent with the intuition that when the spread is large, running multiple
independent instances of
is high, our technique produces higher speedup.
This is consistent with the intuition that when the spread is large, running multiple
independent instances of  leads to a high probability that at least one instance will
complete with a low execution time, leading to a scrunching of the spread.
A very narrow Gaussian distribution for example produces almost no speedup
while one with a large spread
produces significant speedup. Note that our technique can also produce super-linear
speedups in cases with a large
leads to a high probability that at least one instance will
complete with a low execution time, leading to a scrunching of the spread.
A very narrow Gaussian distribution for example produces almost no speedup
while one with a large spread
produces significant speedup. Note that our technique can also produce super-linear
speedups in cases with a large
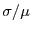 spread.
spread.
Predicting speedup
We have shown that it is possible to calculate the expected speedup for a given input
provided knowledge of the underlying completion time distribution. However, in our application,
 will be repeatedly invoked with different inputs (and not on the same fixed input).
We must thus be able to predict the statistics of the execution behavior of
will be repeatedly invoked with different inputs (and not on the same fixed input).
We must thus be able to predict the statistics of the execution behavior of  on input
on input 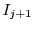 given
the observed execution behavior of
given
the observed execution behavior of  on inputs
on inputs 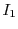 through
through 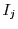 . This implies
that a certain stability of the underlying distribution must exist.
This limits the scope of our technique to kernels where the underlying execution time
distribution changes sufficiently slowly over subsequent inputs
. This implies
that a certain stability of the underlying distribution must exist.
This limits the scope of our technique to kernels where the underlying execution time
distribution changes sufficiently slowly over subsequent inputs 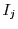 so that the
previously estimated PDF is still applicable.
so that the
previously estimated PDF is still applicable.
Distribution estimation
The calculation of expected speedups relies on the knowledge of the distribution.
In most cases, prior knowledge of the distribution is not available and it will need to be learned.
For a variety of distributions, Figure 4 shows how closely
the learned expected speedup matches the theoretical expected speedup.
Figure 3:
Evolution of GALib's distribution
|
Figure 4:
Convergence of the estimated execution time for a variety of distributions shown
with error-bars over multiple runs
|
We see that very few runs of  are required to converge on a correct value.
Note that we need to learn the
are required to converge on a correct value.
Note that we need to learn the 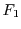 distribution but in practice, we will observe
samples from
distribution but in practice, we will observe
samples from 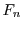 . Given the reversibility of the formula linking
. Given the reversibility of the formula linking 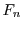 and
and 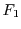 ,
we can always correct
,
we can always correct 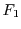 based on observations of
based on observations of 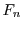 .
.
The Travelling Salesman problem with GALib
GALib [7] is a library that implements genetic algorithms.
Although the time variation in a step of the algorithm is not heavily dependent on the random choices
used in that step, they do affect how much improvement in ``population fitness'' (score)
is achieved in the step. Therefore, we can run multiple instances of each step where each instance
makes independent random choices and instead of picking the fastest instance, we pick
the instance that achieves the best population fitness.
This indirectly leads to a speedup for the application by reducing the
number of steps needed to converge
to an acceptable result.
Figure 3 shows the evolution of the score PDF for different windows of genetic algorithm steps
in the simulation. Each window consists of 15 consecutive steps.
We see a clear evolution in the PDFs and they evolve
sufficiently slowly for our techniques to apply.
There are two main challenges to running multiple instances of a sequential algorithm
in parallel:
Sand-boxing shared state
Semantically, the only issue with replacing  by
by
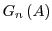 is making sure
that each
is making sure
that each 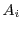 runs in a sand-boxed environment. In other words, each time an
runs in a sand-boxed environment. In other words, each time an 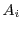 accesses
state outside its scope, it must go through our API which will ensure that each
accesses
state outside its scope, it must go through our API which will ensure that each 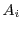 has
a unique copy of the data. Only the
has
a unique copy of the data. Only the 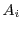 that is finally chosen will have its state merged
back into the main application's state. While this approach resembles STM [5],
it is much more lightweight as there is no need for any conflict detection.
that is finally chosen will have its state merged
back into the main application's state. While this approach resembles STM [5],
it is much more lightweight as there is no need for any conflict detection.
Minimizing overall application time
The goal of our system is to minimize overall application execution time. We have shown how to
minimize the execution time of just one algorithm  .
Suppose now that
.
Suppose now that  and
and 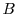 are two randomized algorithms
that run in parallel in the original application.
If the execution of
are two randomized algorithms
that run in parallel in the original application.
If the execution of  and
and 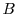 does not overlap (i.e., they do not have portions that
run in parallel), we can simply apply the first case to both
does not overlap (i.e., they do not have portions that
run in parallel), we can simply apply the first case to both  and
and 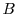 independently.
However, if they do overlap and access shared state, they may interact with each other in unpredictable ways which must be
faithfully represented when replacing
independently.
However, if they do overlap and access shared state, they may interact with each other in unpredictable ways which must be
faithfully represented when replacing  with
with
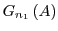 and
and 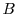 with
with
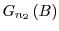 .
We can deal with this case by considering a new abstract algorithm
.
We can deal with this case by considering a new abstract algorithm
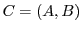 . Each instance
of
. Each instance
of  is thus associated with a single instance of
is thus associated with a single instance of 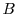 to form an instance of
to form an instance of 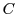 .
If
.
If  and
and 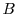 are kernels, the time span of
are kernels, the time span of 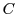 will be limited and we can
use the previous case to calculate
will be limited and we can
use the previous case to calculate 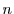 for
for
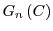 and we have
and we have
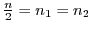 . Note that
in this case, the sand-boxing of
. Note that
in this case, the sand-boxing of  will sand-box both
will sand-box both 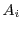 and
and 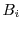 together.
together.
The scheme described above is generalizable to any number of concurrent kernels.
The runtime can dynamically form tuples of algorithms that overlap, in order to maintain
correct program semantics.
The speedup we have demonstrated for a single randomized algorithm can thus
translate into a speedup for the overall application whether the application has one or more
randomized algorithm in it.
3 Scaling semantics: Achieving realism with responsiveness
A smooth and continuous user-experience is paramount for emerging compute-intensive
applications like gaming and interactive visualization. The immersive world simulated
by these applications needs to be updated at a sufficiently high frame-rate to provide
a realistic experience to the user and to react in real-time to arbitrary user input. The
need for predictable and continuous responsiveness of the application conflicts with the
desire to pack as much realism as possible on a given hardware platform.
Programmers are willing to adjust the sophistication of the immersive world, seeking to
use models of greater sophistication when more resources are available, and using simpler
models on resource-limited architectures so as to avoid violating the responsiveness
constraints. For large complex applications like gaming, programmers eschew the use of
formal real-time constructs and languages as these require the decomposition of the application
into tasks, dependencies and deadlines. Instead, they implement their application as a monolithic
application using conventional C/C++ flows for their significant productivity advantages.
The responsiveness behavior then becomes an emergent quality of the application rather than a
quality enforced by design. The desired responsiveness on a given set of platforms is typically
achieved in a trial-and-error manner by extensive manual tweaking of the complexity of
algorithms and models used.
The Soft Real-time (SRT) part of our framework is designed to achieve the following goals:
- Scaling of Algorithmic Sophistication
- Automatically pick models and algorithms that
express the maximal realism on the current hardware platform while not violating the
responsiveness constraints.
- Scaling to unused cores
- Use idle or under-utilized cores to evaluate multiple
models or algorithm alternatives simultaneously to maximize the likelihood of picking the
most sophisticated alternative possible under responsiveness constraints.
We had to overcome the following challenges in order to achieve the above mentioned goals
in an application and domain agnostic manner. We use a gaming application shown in
Figure 5 to illustrate how each of these challenges is overcome in our framework.
Figure 5:
SRT with the Torque game engine
|
Demarcation
A conventionally written C/C++ application lacks inherent constructs using
which the application's responsiveness requirements can be inferred. However, it is simple for the
programmer to use SRT API calls to demarcate the regions of the application over which responsiveness
constraints apply. Such demarcations are applied over the existing module structure of the
application, thereby eliminating the need for restructuring the application code. The demarcations,
called frames are detected at runtime, allowing the construction of the
average frame structure of the application. In Figure 5, a programmer
knowledgeable about the application knows that the run_frame() function renders the
next time-step of the game world including evaluating all relevant game world interactions.
Therefore, the entry and exit of this function is demarcated as a frame through the SRT API,
and a desired responsiveness constraint on the frame-rate is expressed. Further, programmers
implementing the AI, Physics and Rendering modules understand that their individual modules
have the potential to dramatically impact the game frame, and they demarcate their functionality
as well so that the SRT system can track it. The Physics frame also has a responsiveness
constraint specified to use less than 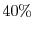 of the game-frame's execution-time with high probability.
of the game-frame's execution-time with high probability.
Scalable algorithm alternatives
In order to scale the
realism expressed by the application, the SRT system needs to be provided with
alternative algorithms that differ in their contribution to realism and the corresponding execution
complexity. This is achieved via SRT API calls where the programmer specifies multiple alternative
C/C++ functions within each abstract model API construct. A programmer typically knows the
viable algorithmic alternatives for a piece of functionality in their module and can easily
identify them via the SRT API. For example, as shown in Figure 5 the AI
programmer would know alternative parameter settings
or algorithms that can significantly vary the sophistication of the AI at the cost of running time.
In this framework, the programmer is no longer responsible for
determining or guaranteeing the impact of each algorithm alternative on the satisfaction of overall
responsiveness constraints, as this impact is discovered at runtime by SRT on the current hardware.
Making Correct Choices
The SRT system needs to choose algorithm alternatives
in each model so that the choices allow the overall responsiveness constraints to be met and
the chosen alternatives should exhibit maximal realism on the current platform. This problem
is intractable in general. However, we make this problem tractable by relying on the following:
- 1) Average Frame Structure
- Applications with responsiveness constraints have a fairly
consistent repetitive structure and this is readily captured using the dynamic demarcations of
frames. In very few iterations within the application (
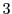 -
-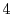 iterations within a few milliseconds),
the average frame structure (as illustrated in Figure 5) is reliably constructed and can be used to start
studying the impact of
model choices in one part of the structure on other parts of the structure.
iterations within a few milliseconds),
the average frame structure (as illustrated in Figure 5) is reliably constructed and can be used to start
studying the impact of
model choices in one part of the structure on other parts of the structure.
- 2) Reinforcement Learning
- is a proven technique that
continually trains which actions in any given state achieve the best rewards.
We use Reinforcement Learning to track the association between models and objectives, i.e., detect
which models affect which objectives, to what extent and track gradual changes in the associations.
In a system where multiple models are potentially being executed within a single high-level frame,
Reinforcement Learning is capable of detecting the complex associations between a large number of
models and objectives.
- 3) Feedback Control
- In applications such as fast-action
gaming and video encoders, the nature of the game scene or raw video sequence often changes
significantly within
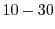 game/video-frames. Consequently, the execution time complexity previously
learned for individual model choices would no longer be valid. Reinforcement Learning would take too long to
re-learn the new mapping between model choices and expected execution times. Therefore, a Feedback Controller
that incrementally adjusts the next model choice applied based on the outcome of the previous selection is
both fast and robust in response. The SRT runtime is a fast, low space-and-time overhead implementation of
Reinforcement Learning and Feedback Control.
game/video-frames. Consequently, the execution time complexity previously
learned for individual model choices would no longer be valid. Reinforcement Learning would take too long to
re-learn the new mapping between model choices and expected execution times. Therefore, a Feedback Controller
that incrementally adjusts the next model choice applied based on the outcome of the previous selection is
both fast and robust in response. The SRT runtime is a fast, low space-and-time overhead implementation of
Reinforcement Learning and Feedback Control.
- 4) Probabilistic Satisfaction
- Large compute-intensive immersive applications are
non safety-critical. Safety-critical applications like flight control software (avionics)
are implemented using specialized hard real-time techniques and do not attempt to maximally
utilize platform resources for realism. Hence the responsiveness constraints for
large complex compute-intensive applications are probabilistic in nature as illustrated in
Figure 5. The more manageable burden on the SRT system is to meet the most
important constraints at the cost of less important ones, to meet timing constraints as closely
as possible if not exactly, and to predict impact of choices with a sufficiently high but not
100% probability. Use of RL on the Average Frame Structure suffices to achieve these more
relaxed goals.
Figure 6:
Comparing frame-times in Torque game engine with and without SRT
|
We applied the SRT system to a commercial game engine called Torque as described in Figure 5.
As shown in Figure 6, the SRT system enables the average game frame-rate to lie within
the desired window of 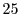 -
- frames-per-second for
frames-per-second for 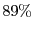 of the frames, compared to just
of the frames, compared to just  for the
unmodified Torque game. At the same time SRT more effectively utilizes the compute resources to spend
for the
unmodified Torque game. At the same time SRT more effectively utilizes the compute resources to spend 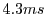 on
AI per frame on average instead of
on
AI per frame on average instead of 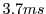 in the case of Torque without SRT. Both instances executed on a game
scenario where AI was a large part of the frame time, and the time needed by AI varied greatly over the
course of the game.
in the case of Torque without SRT. Both instances executed on a game
scenario where AI was a large part of the frame time, and the time needed by AI varied greatly over the
course of the game.
4 Unified opportunistic framework
While certain applications could benefit from using just one of the two proposed
frameworks, other emerging compute-intensive applications may need to use both
in order to achieve sufficient improvements in realism. The ability to use
both frameworks also increases the likelihood that more parts of the application
will be able to take advantage of multi-cores. Games are prime examples of
applications that need both approaches: scalable semantics in AI and physics components
for scaling the user experience subject to the resource limitations of the underlying platform,
and randomized sequential algorithms such as path-finding and AI whose speedup will enhance
realism on every platform.
Since both approaches need to consume from the same set of available cores, the goal
of best overall application realism intertwines the optimization and resource-utilization
methodology of the two approaches. Here we identify the principal considerations that would
allow a unified framework of the two approaches to maximize overall application
realism. The realism objectives in the application can be specified by the programmer
at multiple levels of hierarchy. Wherever a scalable or randomized sequential component
of the application does not have an explicit realism objective specified for it, a realism
objective would need to be inferred for it from higher level realism objectives. The objectives,
whether specified or inferred, dictate a specific execution time to be achieved
by the component (achieving minimal execution time is treated as a special case).
We allow components to contain sub-components of either type.
With this setup, we can propagate realism
objectives as needed. If a component has concurrently executing sub-components, the
specified execution time objective applies separately to all concurrent sub-components.
In the special case of the minimize-execution-time objective, the sub-component that
is expected to be the bottleneck should inherit the minimize-execution-time objective,
but other sub-components should infer a specified-execution-time
objective based on the expected execution-time of the bottleneck sub-component.
When
a component contains a sequence of sub-components executing in series, the specified
execution-time objective must be divided up into execution-time constraints for the
sub-components in a manner that allows components to contribute the maximal
realism given the amount of resources available to share.
For the special
case of minimize-execution-time objective applied to the component, the serial
sub-components would all minimize their execution-time, with any scalable semantics
sub-components achieving this by picking their least sophisticated model choices.
5 Conclusion
In this paper, we have motivated that the underlying design goal
for compute-intensive applications is maximum realism. Current
parallelization techniques limit themselves to deterministically
improving performance FLOPS, with the sequential components limiting
the number of cores that can be utilized.
We exploit two characteristics that occur in many compute-intensive
applications: algorithmic randomness and scalability of semantics, that
allow us to gain application speedup and realism above and beyond what
current parallel programming techniques allow on processors with a
growing number of cores. Our techniques work in conjunction with existing parallel
programming techniques and have the potential to deliver significantly
greater utilization of multiple cores towards achieving high realism.
Future work
We have already separately prototyped the two frameworks. We will continue
to further develop them and, at a later stage, combine them into a unified
framework that best utilizes multi-core resources for realism.
-
- 1
-
K. Knobe.
Intel concurrent collections.
https://software.intel.com/en-us/articles/intel-concurrent-collections-for-cc, 2009.
- 2
-
M. Kulkarni, K. Pingali, B. Walter, G. Ramanarayanan, K. Bala, and L. P. Chew.
Optimistic parallelism requires abstractions.
In PLDI '07, pages 211-222, 2007.
- 3
-
V. Mönkkönen.
Multithreaded game engine architectures.
www.gamasutra.com/features/20060906/monkkonen_01.shtml, 2006.
- 4
-
R. Motwani and P. Raghavan.
Randomized Algorithms.
Cambridge University Press, 1995.
- 5
-
N. Shavit and D. Touitou.
Software transactional memory.
In PODC '95: Proceedings of the fourteenth annual ACM symposium
on Principles of distributed computing, pages 204-213, New York, NY, USA,
1995. ACM Press.
- 6
-
H. Sutter.
The free lunch is over.
https://www.gotw.ca/publications/concurrency-ddj.htm, 2005.
- 7
-
M. Wall.
Galib.
https://lancet.mit.edu/ga/, 2009.

![\includegraphics[scale=0.75]{dataAndPlots/learning_crop}](img25.png)