Simulation Results

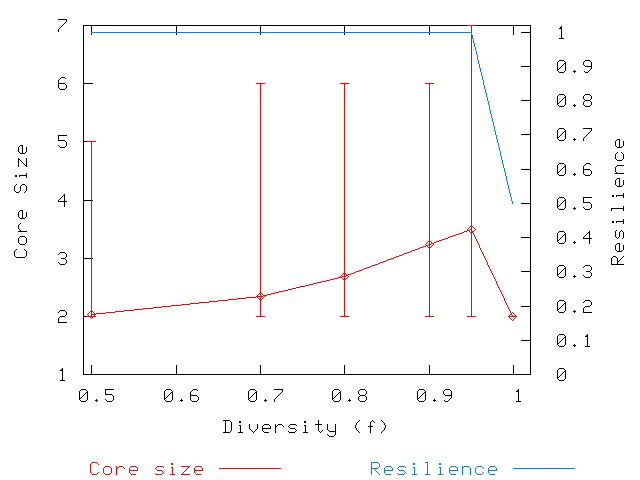
Figures 1, 2, and 3 show the results of our simulations. We simulate a system of 1,000 hosts and present results for two scenarios: 8 attributes with 2 values each (8/2) and 8 attributes with 4 values each (8/4). The choice of 8 attributes is based upon an examination of the most targeted categories of software from public vulnerability databases, such as [7,11]. From these databases, we observed 8 significant software categories and chose this value as a reasonable parameter for our simulations.

Figure 1: Core sizes as a function of diversity for 8 attributes, 2 values each.

$f$

We chose two different numbers of values per attribute to 1) explore a worst case and 2) show how core size and storage load benefit as a result of more fine-grained attribute configurations. The choice of 2 values per attribute corresponds to the coarsest division of hosts possible (e.g., Windows vs. Linux), and represents the worst case in terms of core size and storage load. We note that no vulnerabilities exploited by Internet pathogens have been so extreme, and that pathogens tend to exploit vulnerabilities at finer attribute granularities (e.g., Code Red and its variants exploited a vulnerability in Microsoft IIS running on Windows NT). The choice of 4 values per attribute represents a more fine-grained attribute configurations, and we use it to demonstrate how such configurations significantly improve core sizes and reduce storage load.

Figure 2: Core sizes as a function of diversity for 8 attributes, 4 values each.

$f$

We only show the results for one sample generated for each value of $f$, as we did not see significant variation across samples. Figures 1 and 2 show the core size averaged over cores for all of the hosts for different values of the diversity parameter $f$. We also include a measure of resilience that shows whether our algorithm was able to cover all attributes or not. A point in the resilience curve is hence the number of covered attributes, averaged over all hosts, divided by the total number of attributes. Note that resilience 1.0 means that all attributes are covered.

To show the variability in core size, we include error bars in the graphs showing the maximum and the minimum core sizes for values of $f$. The variability in core size is noticeably high in the 8/2 scenario, whereas it is lower in the 8/4 scenario. Because there are more configurations available in the 8/4 setting, it is likely that a host $p$ finds a host $q$ which has different values for every attribute even when the diversity is highly skewed.

Regarding the average core size, in the 8/2 scenario, it remains around 2 for values of $f$ under 0.7, and goes up to average sizes around 3 for higher values of $f$. In either case, storage overhead is low, although it is overall higher than the average core size for the 8/4 scenario. The result of adding more attribute values to each attribute is therefore a reduction in storage overhead. In this scenario, the average core size remains around 2 for most of the values of $f$. It only increases for $f=0.999$.

It is important to note that there is a drop in resilience for $f=0.999$ in both scenarios. Observe that, for such a value of $f$, there are 999 hosts sharing some subset $A'$ of attributes with a fixed value for each attribute and a single host $p$ not sharing this subset. As a consequence, host $p$ has to be in the core of a host $q$ sharing $A'$. Host $p$, however, may not cover all the attributes of $q$. This being the case, there are possibly other hosts that cover the remaining attributes of $q$ that $p$ does not cover. If there are no such hosts, then there is no core for $q$ which covers all attributes. The resilience for this host is therefore lower.

An important question that remains to be addressed is how much backup data a host will need to store. We address this question with the help of Figure 3. In this figure, the $y$-axis plots storage load. Thus, if $y=10$, for example, there is a host $p$ that must be in $10$ cores given the core compositions that we computed, and every other host must be in $10$ or fewer cores. As expected, storage load increases as $f$ approaches 1, and reaches 1,000 for $f=0.999$ in both scenarios. This is due to our previous observation that, for this value of $f$, there is a single host which has to be in the core of every other host. We conclude that the storage overhead for such a highly skewed diversity is small, but the total load incurred in a small percentage of the hosts can be very high.

Figure 3: Storage load as a function of diversity for the 8/2 and the 8/4 scenarios.

$f$

Although we have presented results only for 1,000 hosts, we have also looked into other scenarios with a larger number of hosts. For 10,000 hosts and the same attribute scenarios, there is no reduction in resilience, and the average core size remains in the same order of magnitude. As we add more hosts to the system, we increase the probability of a host having some particular configuration, thus creating more possibilities for cores. The trend for storage load is the same as before: the more skewed the distribution of attribute configurations, the higher the storage load. For highly skewed distributions and large number of hosts, storage load can be extremely high. One important observation, however, is that as the population of hosts in the system increases, the number of different attribute configurations and the number of hosts with some particular configuration are likely to increase. Thus, for some scenario and fixed value of $f$, storage load does not increase linearly with the number of hosts. In our diversity model, it actually remains in the same order of magnitude.

Suppose now that we want to determine a bound on $f$ for a real system given our preliminary results. According to [8], over $93\%$ of the hosts that access a popular web site run some version of Internet Explorer. This is the most skewed distribution of software they report (the second most skewed distribution is the percent of hosts running some version of Windows, which is $90\%$). There are vulnerabilities that attack all versions of Internet Explorer [11], and so $f$ for such a collection of hosts can be no larger than $0.93$. Note that as one adds attributes that are less skewed, they will contribute to the diversity of the system and reduce $f$.

In the lists provided by [8], there are 14 web browsers and 11 operating systems. For an idea of how a scenario like this would behave, consider a system of 1,000 hosts with 2 attributes and 14 values per attribute. For a value of $f=0.93$ we have an average core size of $2$, a maximum core size of $2$, and storage load of $24$. We did not see significant changes in these values when changing the number of values per attribute from 14 to 11.

A storage load of 24 means that there is some host that has to store backup data from 24 other hosts, or $4\%$ of its storage to each host. We observe that this value is high because our heuristic optimizes for storage overhead. In an environment with such a skewed diversity, a good heuristic will have to take into account not only storage overhead, but the storage load of available hosts as well.