FAST '05 Paper
[FAST '05 Technical Program]


Matrix Methods for Lost Data Reconstruction in Erasure Codes
Abstract:
Erasures codes, particularly those protecting against multiple
failures in RAID disk arrays, provide a code-specific means for
reconstruction of lost (erased) data. In the RAID application this is
modeled as loss of strips so that reconstruction algorithms are
usually optimized to reconstruct entire strips; that is, they apply
only to highly correlated sector failures, i.e., sequential sectors on
a lost disk. In this paper we address two more general problems: (1)
recovery of lost data due to scattered or uncorrelated erasures and
(2) recovery of partial (but sequential) data from a single lost disk
(in the presence of any number of failures). The latter case may
arise in the context of host IO to a partial strip on a lost disk.
The methodology we propose for both problems is completely general and
can be applied to any erasure code, but is most suitable for XOR-based
codes.
For the scattered erasures, typically due to hard errors on the disk
(or combinations of hard errors and disk loss), our methodology
provides for one of two outcomes for the data on each lost
sector. Either the lost data is declared unrecoverable (in the
information-theoretic sense) or it is declared recoverable and
a formula is provided for the reconstruction that depends only on
readable sectors. In short, the methodology is both complete and
constructive.
1 Introduction
XOR-based erasures codes for disk arrays model lost data most coarsely
as loss of entire disks but more precisely as loss of entire symbols
of the code. In practice, a symbol typically maps to a ``strip'',
that is, multiple sequential sectors with one bit of the symbol
corresponding to one or (typically) more sectors and with each
different symbol residing on a different disk (this is not always the
case, but it is a common practice). The collection of related strips
is called a ``stripe''. To deal with disk failures, each erasure code
comes complete with a specific reconstruction algorithm that is highly
dependent on the code construction. For example, the
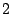 -fault-tolerant X-code [10] is constructed
geometrically, with parity values computed along diagonal paths
through the data sectors. When two disks fail, the reconstruction
follows these diagonal paths, starting at some initial point; that is,
the reconstruction is both geometrically and recursively defined.
The BCP [1] code is less geometrically designed, but
still has a recursive reconstruction algorithm. More examples are
mentioned in Section 2. -fault-tolerant X-code [10] is constructed
geometrically, with parity values computed along diagonal paths
through the data sectors. When two disks fail, the reconstruction
follows these diagonal paths, starting at some initial point; that is,
the reconstruction is both geometrically and recursively defined.
The BCP [1] code is less geometrically designed, but
still has a recursive reconstruction algorithm. More examples are
mentioned in Section 2.
Erasures then are seen as correlated sector failures: all sectors in a
strip are ``lost'' when the disk fails. However, increasing disk
capacity together with a fairly stable bit-error rate implies that
there is a significant probability of multiple uncorrelated or
scattered sector errors within a given stripe, particularly in
conjunction with one or more disk failures. For example, two disk
losses plus a sector loss may occur often enough that even a two-disk
fault tolerant code may not provide sufficient reliability. If all
correlated and uncorrelated erasures occur within at most 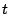 disks
where disks
where 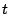 is the (disk) fault tolerance of the code, then one method
is to simulate loss of all affected disks and rebuild according to the
code-specific reconstruction algorithm. However, this has two
drawbacks. First, it is clear that this can be highly inefficient
since it requires either reconstruction of ``known'' or readable data
or it requires checking at each step of the process to see if a
reconstruction is required. More importantly, however, this approach
does not solve the more general problem when more than is the (disk) fault tolerance of the code, then one method
is to simulate loss of all affected disks and rebuild according to the
code-specific reconstruction algorithm. However, this has two
drawbacks. First, it is clear that this can be highly inefficient
since it requires either reconstruction of ``known'' or readable data
or it requires checking at each step of the process to see if a
reconstruction is required. More importantly, however, this approach
does not solve the more general problem when more than 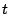 disks have been affected with sector losses. In such a case, it is
quite possible that some or all of the lost sectors can be
reconstructed, though this is not obvious a priori from the
erasure correcting power of the code. For example, the 2-fault
tolerant EVENODD code only claims to recover from two lost disks, so
any additional sector loss typically means all lost data is declared
unrecoverable. In fact, on average, anywhere from 40-60% of the lost
sectors may be recovered in this situation.
disks have been affected with sector losses. In such a case, it is
quite possible that some or all of the lost sectors can be
reconstructed, though this is not obvious a priori from the
erasure correcting power of the code. For example, the 2-fault
tolerant EVENODD code only claims to recover from two lost disks, so
any additional sector loss typically means all lost data is declared
unrecoverable. In fact, on average, anywhere from 40-60% of the lost
sectors may be recovered in this situation.
In addition, while each erasure code provides a means to reconstruct
entire strips (e.g., during a rebuild operation), to our knowledge,
the literature does not contain any methods that explicitly address
the problem of reconstructing a partial strip of lost data; such a
need may arise in a host read operation to a failed disk during an
incomplete rebuild operation. Of course, the strip reconstruction
method could be applied in this case, but it is likely that such
reconstruction will recover additional unnecessary lost sectors; that
is, do more work than is required to service the host read, thereby
adversely affecting performance. (This extra work may be worth the
performance penalty in that the additional recovered sectors can be
cached or added to the rebuild log, but that may not always be a
desirable option.)
In this paper, we address both these problems. Our methodology is
universal in that it can be applied to any erasure code of any fault
tolerance. It applies to any failure scenario from full disk to
scattered sectors to combinations of the two. It is based solely on
the generator matrix for the erasure code. Consequently, a general
erasure code reconstruction module could implement this methodology
and use the generator matrix as one of its inputs. To emphasize
the point, we address the problem of arbitrary sector (bit) erasures
for any code designed with a strip (symbol) erasure failure
model.
For the first problem of scattered (correlated and/or
uncorrelated) sector loss, our methodology provides a mathematical
guarantee: for each lost sector, either that sector's data is declared
as (information-theoretically) unrecoverable (that is, a ``data loss
event'') or the sector's data is declared recoverable and a
reconstruction formula is generated. The reconstruction formula is a
linear equation (XOR equation in case of XOR-based codes) involving
known or readable data and parity sectors. In this respect, our
methodology is both complete, constructive and universally applicable.
It provides the best guarantee to meet the following requirement:
User Contract: For any erasure scenario, the storage
system shall recover any and all lost data sectors that the erasure
code is information-theoretically capable of recovering.
It should be noted that for  -fault tolerant codes (e.g., RAID1,
RAID4 or RAID5), the solution to both these problems is quite simple
and obvious. Similarly, for Reed-Solomon codes [9]
where the symbol is mapped to bytes or words (not sets of sectors),
the standard Reed-Solomon procedure addresses both problems directly
as well. The more interesting cases then are non-Reed-Solomon multiple
fault-tolerant codes. Such codes are typically XOR-based as those have
the most practical application. Careful and complex analysis of a
specific code may produce a solution to this problem (and to our
second problem). However, our solutions are universal. It is also
clear that our methods can be extended to more general codes (e.g.,
some of the non-XOR codes in [3]). Furthermore, this
methodology can be applied not just for RAID controllers but any
application of these types of erasure codes such as dRAID (distributed
Redundant Arrangement of Independent Devices) node-based systems. -fault tolerant codes (e.g., RAID1,
RAID4 or RAID5), the solution to both these problems is quite simple
and obvious. Similarly, for Reed-Solomon codes [9]
where the symbol is mapped to bytes or words (not sets of sectors),
the standard Reed-Solomon procedure addresses both problems directly
as well. The more interesting cases then are non-Reed-Solomon multiple
fault-tolerant codes. Such codes are typically XOR-based as those have
the most practical application. Careful and complex analysis of a
specific code may produce a solution to this problem (and to our
second problem). However, our solutions are universal. It is also
clear that our methods can be extended to more general codes (e.g.,
some of the non-XOR codes in [3]). Furthermore, this
methodology can be applied not just for RAID controllers but any
application of these types of erasure codes such as dRAID (distributed
Redundant Arrangement of Independent Devices) node-based systems.
For the second problem of partial strip reconstruction, we propose a
hybrid solution: combine the inherent recursive method of the erasure
code for full rebuild with the methodology for recovering scattered
sectors. We also propose an alternative that is in many cases
equivalent to the code-specific method, better in some cases and
universally applicable to any erasure code.
Our methodology is based on principles of matrix theory and
pseudo-inverses. Many codes (see [8,9])
use full inverses to prove both that their codes have the declared
fault tolerance and to provide reconstruction formulas. However, they
apply it only to recover full code symbols, under maximal failures
(where unique inverses exist) and not to the more general
bit-within-a-symbol (a.k.a, sector within a strip) level that
we address in this work.
The paper is organized as follows. We close the introduction with
some definitions. The next section contains a few remarks on related
work. Section 3 contains a brief review of the
concepts from linear algebra that we need, particularly the notion of
pseudo-inverse. In Section 4 we present a
brief description of the generator matrix and parity check matrix for
an erasure code. Section 5 explains how we
simulate scattered sector loss and how we determine reconstructability
in addressing our first problem. Section 6 contains
algorithms for constructing pseudo-inverse matrices. We develop our
methods in a detailed example in Section 7.
Section 8 outlines the hybrid method for partial strip
reconstruction (our second problem) and includes experimental results.
We conclude with a brief summary.
1.1 Vocabulary
- sector:
- the smallest unit of IO to/from a disk (typically
512 bytes at the disk drive, but perhaps 4KB from the filesystem or
application layer).
- element:
- a fundamental unit of data or parity; this is the
building block of the erasure code. In coding theory, this is the data
that is assigned to a bit within a symbol. We assume for simplicity
that each element corresponds to a single sector; the more general
case can be derived from this case.
- stripe:
- a complete (connected) set of data and parity
elements that are dependently related by parity computation relations.
In coding theory, this is a code word; we use ``code instance''
synonymously.
- strip:
- a unit of storage consisting of all contiguous elements
(data, parity or both) from the same disk and stripe. In coding
theory, this is associated with a code symbol. It is sometimes called
a stripe unit. The set of strips in a code instance form a stripe.
Typically, the strips are all of the same size (contain the same
number of elements).
- array
- A collection of disks on which one or more instances of a
RAID erasure code is implemented.
2 Related Work
The two main results of this paper are (a) the application of
pseudo-inverses of matrices to the problem of reconstruction of
uncorrelated lost sectors and (b) a hybrid reconstruction that
combines code-specific recursive reconstruction methods with this
matrix method to efficiently reconstruct partial strips. To our
knowledge neither of these problems has been specifically addressed in
the literature. As remarked before, the theory of matrix inverses is
used in the proof that some codes meet their declared strip (i.e.,
symbol) fault tolerance. For example, the Reed-Solomon
code [8,9] proves fault tolerance by
solving a system of linear equations. In this case, the matrix
inverse method is used to solve for complete symbols (full strips in
our terminology) under maximum failures. In contrast, our method
addresses individual bits in symbols (i.e., elements) for any
distribution of erased bits (within or beyond symbol fault
tolerance). The binary BR [3] codes have a recursive
solution to two full strip losses; the authors provide a closed form
solution to the recursion. For the EVENODD code [2],
the authors give a recursion and point out that it could be solved
explicitly. An explicit solution to the recursion is equivalent to
our matrix solution in the special case of full strip losses (again,
our method has no such correlation requirements). The
BCP [1], ZZS [11],
X-code [10], and RDP [4] codes all have
recursive reconstruction algorithms. The latter two (as well as the
EVENODD code) are ``geometric'' and easy to visualize; the former are
more ``combinatorial'' and less intuitive. In either case, these
codes with recursive reconstruction algorithms are well-suited to our
hybrid methodology. In addition, a variant of our hybrid method
applies to any erasure codes suitable for disk arrays, with or without
a recursive reconstruction algorithm.
3 Binary Linear Algebra - A Review
In this section we recall and elaborate on some basic notions from
the theory of linear algebra over a binary field (which is assumed for
all operations from now on without further comment - the theory
extends easily to non-binary fields as well). A set of binary vectors
is linearly independent if no subset sums modulo 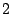 to the zero
vector. Let to the zero
vector. Let  be a rectangular matrix of size be a rectangular matrix of size 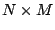 with with
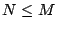 . The ``row rank'' of . The ``row rank'' of  is the maximum number of linearly
independent row vectors. The matrix is the maximum number of linearly
independent row vectors. The matrix  has ``full row rank'' if the
row rank equals has ``full row rank'' if the
row rank equals 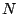 (the number of rows). A ``null space'' for (the number of rows). A ``null space'' for  is
the set of all vectors that are orthogonal (have zero
dot-product) with every row vector of is
the set of all vectors that are orthogonal (have zero
dot-product) with every row vector of  . This is a vector
space closed under vector addition modulo . This is a vector
space closed under vector addition modulo 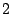 . A ``null space basis''
is a maximal set of linearly independent vectors from the null space.
If the null space basis has . A ``null space basis''
is a maximal set of linearly independent vectors from the null space.
If the null space basis has 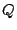 vectors, then the entire null space
has vectors, then the entire null space
has 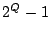 total non-zero vectors. total non-zero vectors.
We will write the null space vectors as column vectors, to make matrix
multiplication simpler to write down, though this is not the standard
convention.
Let  be a basis for the null space of be a basis for the null space of  . More precisely, . More precisely,  is
a matrix whose columns form a basis for the null space. If is
a matrix whose columns form a basis for the null space. If  has
full row rank, then has
full row rank, then  has dimensions has dimensions  where where 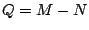 . .
Suppose  is full row rank. A ``right pseudo-inverse'' is a matrix is full row rank. A ``right pseudo-inverse'' is a matrix
 (of size (of size 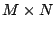 ) so that ) so that
where 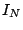 is the is the 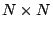 identity matrix. If identity matrix. If 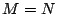 , then , then  is
the unique inverse. A right pseudo-inverse
must exist if is
the unique inverse. A right pseudo-inverse
must exist if  has full rank and is never unique if has full rank and is never unique if 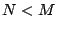 . .
More generally, let  have row rank have row rank 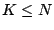 , then a ``partial right
pseudo-inverse'' (or partial pseudo-inverse) is a matrix , then a ``partial right
pseudo-inverse'' (or partial pseudo-inverse) is a matrix  so that so that
where 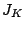 is an is an 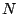 -dimensional square matrix with -dimensional square matrix with 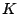 ones on the
diagonal, ones on the
diagonal, 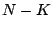 zeros on the diagonal and zeros elsewhere. Note that zeros on the diagonal and zeros elsewhere. Note that
 is a partial pseudo-inverse if the product is a partial pseudo-inverse if the product 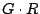 has a
maximal number of ones over all possible choices for has a
maximal number of ones over all possible choices for  . If . If  is
full row rank then is
full row rank then 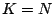 , , 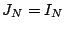 and and  is a (complete)
pseudo-inverse. The matrix is a (complete)
pseudo-inverse. The matrix 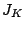 is unique; that is, the positions of
zero and non-zero diagonal elements are determined from is unique; that is, the positions of
zero and non-zero diagonal elements are determined from  and are
independent of the choice of and are
independent of the choice of  . .
Let  be a be a  basis for the null space basis for basis for the null space basis for  (perhaps padded with all-zero columns), and
(perhaps padded with all-zero columns), and  some specific
partial pseudo-inverse for some specific
partial pseudo-inverse for  . As . As 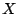 varies over all binary varies over all binary
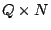 matrices, we have matrices, we have
 |
(1) |
so 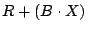 runs over all partial pseudo-inverses (the proof of
this is a simple calculation). What runs over all partial pseudo-inverses (the proof of
this is a simple calculation). What 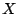 does in (1)
is add a null space vector to each of the columns of does in (1)
is add a null space vector to each of the columns of  . For our
purposes, an optimal . For our
purposes, an optimal  would have minimum weight (fewer ones) in
each column (that is, be the most sparse). In Section 6 we
discuss algorithms for computing pseudo-inverses and in
Section 6.2 we discuss algorithms for finding an
optimal pseudo-inverse. would have minimum weight (fewer ones) in
each column (that is, be the most sparse). In Section 6 we
discuss algorithms for computing pseudo-inverses and in
Section 6.2 we discuss algorithms for finding an
optimal pseudo-inverse.
For each column of 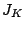 with a zero on the diagonal, the
corresponding column of with a zero on the diagonal, the
corresponding column of  can be replaced with the all-zero column
without affecting the partial pseudo-inverse property and in fact such
an action clearly improves the weight of can be replaced with the all-zero column
without affecting the partial pseudo-inverse property and in fact such
an action clearly improves the weight of  . Consequently, we add
this property to the definition of a partial pseudo-inverse. . Consequently, we add
this property to the definition of a partial pseudo-inverse.
Strictly speaking, the term ``pseudo-inverse'' applies only to real or
complex matrices and implies uniqueness (optimality in a metric
sense). We overload the term here with a slightly different meaning
- we allow for non-uniqueness and do not require optimality (most
sparse).
In the next section we apply these notions to the problem of
reconstruction of scattered sectors in a stripe.
4 Generator and Parity Check Matrices
In this section we recall the erasure code notions of ``generator
matrix'' and ``parity check matrix''. These are the basic
structures upon which we develop our methodology. For a basic
reference, see [7].
The generator matrix  of an erasure code converts the input
``word'' (incoming data) into a ``code word'' (data and parity). The
parity check matrix verifies that the ``code word'' contains
consistent data and parity (parity scrub). In the context of erasure
codes for disk arrays, the generator matrix actually provides much
more. of an erasure code converts the input
``word'' (incoming data) into a ``code word'' (data and parity). The
parity check matrix verifies that the ``code word'' contains
consistent data and parity (parity scrub). In the context of erasure
codes for disk arrays, the generator matrix actually provides much
more.
The generator matrix is given a column block structure: each block
corresponds to a strip and each column within a block corresponds to
an element within the strip. If the column contains only a single 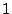 ,
then the element contains user data. We call such a column an
``identity column'' because it is a column of an identity matrix. If
the column contains multiple ,
then the element contains user data. We call such a column an
``identity column'' because it is a column of an identity matrix. If
the column contains multiple 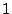 s, then it corresponds to an element
which is the XOR sum of some set of user data elements; that is, the
element is a parity element. In other words, the generator matrix
specifies the data and parity layout on the strips, the logical
ordering of the strips within the stripe,
and the equations used to compute parity values. For
example, the generator matrix for the EVENODD(3,5) code with prime s, then it corresponds to an element
which is the XOR sum of some set of user data elements; that is, the
element is a parity element. In other words, the generator matrix
specifies the data and parity layout on the strips, the logical
ordering of the strips within the stripe,
and the equations used to compute parity values. For
example, the generator matrix for the EVENODD(3,5) code with prime
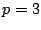 on on 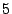 disks is disks is
(more details on this example are given in
Section 7).
Though it is not a requirement, the generator matrix for disk arrays
typically has an identity column for each user data element (so that
this data is always copied to the element's sectors verbatim in some
strip and can then be read with minimal IO costs). In coding theory,
a generator matrix of this form is called ``systematic''.
Let 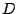 be a row vector of input user data values, then the row vector be a row vector of input user data values, then the row vector
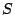 , given by the expression , given by the expression
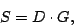 |
(2) |
represents the data and parity elements that are stored in the stripe
on the disks. The vector 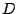 is indexed by the logical addresses of
the user data values (say, as viewed by the host). The vector is indexed by the logical addresses of
the user data values (say, as viewed by the host). The vector 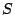 represents the physical addresses of the data and parity elements,
both the disk (actually, strip, identified by the block of the
generator matrix) and the sector addresses on the disk (element or
offset within the strip, identified by the column within the block).
represents the physical addresses of the data and parity elements,
both the disk (actually, strip, identified by the block of the
generator matrix) and the sector addresses on the disk (element or
offset within the strip, identified by the column within the block).
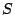 is also block-structured with blocks matching those of is also block-structured with blocks matching those of  . (See
our example in Section 7.) . (See
our example in Section 7.)
If there are 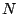 data elements input into the code and data elements input into the code and 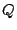 parity
elements computed by the code, then the generator matrix has
dimensions parity
elements computed by the code, then the generator matrix has
dimensions 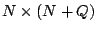 . (Note that . (Note that 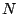 is the total number of
data elements within a stripe, not the number of strips;
similarly, is the total number of
data elements within a stripe, not the number of strips;
similarly, 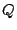 is the number of parity elements in the stripe, not the
number of parity strips.) is the number of parity elements in the stripe, not the
number of parity strips.)
The ``parity check matrix'' 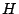 has dimensions has dimensions 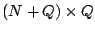 and can
be derived directly from the generator matrix (and vice-versa).
Communication channels use the parity check matrix to detect errors.
Each column corresponds to a parity element. After the data and
parity is read off the channel, the parity is XORed with the data as
indicated by its corresponding column to produce a ``syndrome''. If a
syndrome is not zero, an error has occurred (either in the received
parity symbol or in one of the dependent data symbols). For erasure
codes in disk arrays, this is a parity consistency check (or parity
scrub). In other words, with and can
be derived directly from the generator matrix (and vice-versa).
Communication channels use the parity check matrix to detect errors.
Each column corresponds to a parity element. After the data and
parity is read off the channel, the parity is XORed with the data as
indicated by its corresponding column to produce a ``syndrome''. If a
syndrome is not zero, an error has occurred (either in the received
parity symbol or in one of the dependent data symbols). For erasure
codes in disk arrays, this is a parity consistency check (or parity
scrub). In other words, with 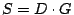 as above, the test as above, the test
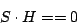 |
(3) |
is a parity consistency check.
The parity check matrix is row blocked exactly corresponding to the
column blocks of  (or (or 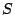 ) and it can be arranged to contain an
embedded identity matrix (corresponding to the parity elements) -
this is easy if ) and it can be arranged to contain an
embedded identity matrix (corresponding to the parity elements) -
this is easy if  is systematic. The parity check matrix for the
example generator matrix is systematic. The parity check matrix for the
example generator matrix  above is above is
In short, the generator matrix is used to compute the data and parity
(and its layout) for storage on the disks. The parity check matrix
can be used when all the data and parity are read off the disk (e.g.,
during parity scrub) to look for errors.
If a code can tolerate 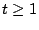 lost disks or strips, then lost disks or strips, then  must
have the property that if any must
have the property that if any 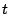 blocks of blocks of  are removed (or
zeroed), then the resulting matrix must have full row rank. The
parity check matrix is full column rank (because of the embedded
identity matrix). are removed (or
zeroed), then the resulting matrix must have full row rank. The
parity check matrix is full column rank (because of the embedded
identity matrix).
Also, (3) implies that
should hold for every data vector 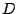 . This means that . This means that 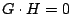 identically, so that each vector in
identically, so that each vector in 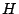 is in the null space of is in the null space of  .
A simple dimensionality argument shows that in fact .
A simple dimensionality argument shows that in fact 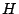 is a basis of
the null space of is a basis of
the null space of  . .
In addition, it should be clear that if  is systematic, then there
exists an is systematic, then there
exists an 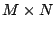 matrix matrix 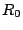 containing an embedded identity
matrix of size containing an embedded identity
matrix of size 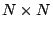 so that so that 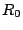 is a pseudo-inverse for is a pseudo-inverse for  . .
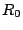 just picks off the embedded systematic portion of just picks off the embedded systematic portion of  . If . If  is not systematic, a pseudo-inverse
is not systematic, a pseudo-inverse 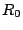 can still be constructed,
but it will not be so simple (see Section 6.3). can still be constructed,
but it will not be so simple (see Section 6.3).
5 Simulating Scattered Sector Loss and Reconstruction
In this section, we develop our theory for solving the first of our
two problems: how to deal with uncorrelated sector loss. An example
is given in Section 7
We indicated above that a 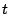 -fault-tolerant code -fault-tolerant code  must have the
property that zeroing any must have the
property that zeroing any 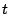 blocks of blocks of  should leave should leave  full rank so that a complete pseudo-inverse for
full rank so that a complete pseudo-inverse for  must exist. This
suggests that we can simulate correlated and/or uncorrelated
sector loss by zeroing or removing the associated individual
columns from must exist. This
suggests that we can simulate correlated and/or uncorrelated
sector loss by zeroing or removing the associated individual
columns from  . It should be clear that certain combinations of
uncorrelated sector losses will result in some or all data loss events
(some or all lost sectors having unrecoverable data); other
combinations may involve no data loss events. Our methodology will
determine, in a straightforward manner, exactly what sectors become
data loss events and for those that do not, will provide a
reconstruction formula for the data from these sectors. . It should be clear that certain combinations of
uncorrelated sector losses will result in some or all data loss events
(some or all lost sectors having unrecoverable data); other
combinations may involve no data loss events. Our methodology will
determine, in a straightforward manner, exactly what sectors become
data loss events and for those that do not, will provide a
reconstruction formula for the data from these sectors.
Suppose we detect a set 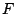 of failed sectors in a stripe
(correlated, perhaps because of disk failure, or uncorrelated, because
of medium errors, or a combination of these). Completely ignoring the
block structure of of failed sectors in a stripe
(correlated, perhaps because of disk failure, or uncorrelated, because
of medium errors, or a combination of these). Completely ignoring the
block structure of  , let , let 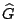 be a version of a generator matrix be a version of a generator matrix
 , with zeroed columns corresponding to the sectors in , with zeroed columns corresponding to the sectors in 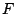 .
Suppose we can find a matrix .
Suppose we can find a matrix  of size of size 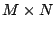 so that so that
 is a partial pseudo-inverse of is a partial pseudo-inverse of 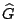 , and , and
 has zeros in all rows that correspond to the lost columns of has zeros in all rows that correspond to the lost columns of
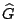 . .
We associate the columns of  to the user data values in to the user data values in 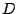 . In
Section 6 we discuss algorithms for constructing . In
Section 6 we discuss algorithms for constructing  . The
following theorem contains our main theoretical result: . The
following theorem contains our main theoretical result:
Theorem 1
Let  , , 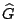 , and , and  be as above. Any theoretically recoverable
user data value corresponds to a non-zero column of be as above. Any theoretically recoverable
user data value corresponds to a non-zero column of  and the
non-zero bit positions indicate the data and parity elements whose XOR
sum equals the data value. As a special case, a directly readable
data value corresponds to an identity column in and the
non-zero bit positions indicate the data and parity elements whose XOR
sum equals the data value. As a special case, a directly readable
data value corresponds to an identity column in  . A data loss
event (unrecoverable data value) corresponds to an all-zero column of . A data loss
event (unrecoverable data value) corresponds to an all-zero column of
 . .
Proof.
Let 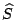 be the vector be the vector 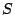 as in (2) but with zeros in
the positions corresponding to the lost elements (the zeroed columns
of as in (2) but with zeros in
the positions corresponding to the lost elements (the zeroed columns
of  ). Then it is clear that ). Then it is clear that
Consequently, we have
where 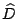 is the vector is the vector 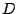 with zeros in all locations
corresponding to zero's on the diagonal of with zeros in all locations
corresponding to zero's on the diagonal of 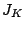 which also
corresponds to the all-zero columns of which also
corresponds to the all-zero columns of  . .
The fact that 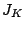 is uniquely determined by is uniquely determined by 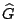 means that any
zero diagonal entry of means that any
zero diagonal entry of 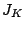 induces a zero in induces a zero in 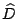 ; this
corresponds to a data loss event. Any non-zero diagonal entry of ; this
corresponds to a data loss event. Any non-zero diagonal entry of
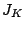 induces a non-zero (not identically zero) data value in induces a non-zero (not identically zero) data value in 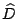 .
But the non-zero diagonal entries of .
But the non-zero diagonal entries of 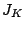 corresponds to non-zero
columns of corresponds to non-zero
columns of  and the zero diagonal entries correspond to all-zero
columns of and the zero diagonal entries correspond to all-zero
columns of  . This proves part of the first and last statements. . This proves part of the first and last statements.
Now consider a non-zero column of  . Each non-zero bit in such a
column selects into an XOR formula a data or parity element from . Each non-zero bit in such a
column selects into an XOR formula a data or parity element from
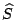 . Because . Because  has zeros in row positions corresponding to
zeroed positions in has zeros in row positions corresponding to
zeroed positions in 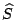 , such a formula does not depend on any
lost data or parity element. The XOR formula then indicates that a
specific XOR sum of known data and parity elements equals the data
value associated to that column. That is, such a column provides a
formula for the reconstruction. This proves the rest of the first
statement in the theorem. The second claim of the theorem is clear. , such a formula does not depend on any
lost data or parity element. The XOR formula then indicates that a
specific XOR sum of known data and parity elements equals the data
value associated to that column. That is, such a column provides a
formula for the reconstruction. This proves the rest of the first
statement in the theorem. The second claim of the theorem is clear.

We emphasize that this theorem makes no assumptions about the location
of the failed sectors, whether they are correlated, uncorrelated or
some of both. Consequently, the theorem can be applied to the case of
full disk/strip losses (highly correlated) or even to the case where
there is a lost sector on every strip (highly uncorrelated).
It also does not depend on any special structure (for example
geometric layout) of the erasure code. All the information we need is
embedded within the generator matrix.
Recall that  is not necessarily unique and that given a basis for
the null space of is not necessarily unique and that given a basis for
the null space of 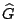 , it is easy to construct, as
in (1), other pseudo-inverses that satisfy the same
properties as , it is easy to construct, as
in (1), other pseudo-inverses that satisfy the same
properties as  in the theorem. In the next section, we discuss
methods for constructing pseudo-inverses and bases for null spaces.
We use the null space bases for improving the sparseness of the
pseudo-inverse. in the theorem. In the next section, we discuss
methods for constructing pseudo-inverses and bases for null spaces.
We use the null space bases for improving the sparseness of the
pseudo-inverse.
6 Pseudo-inverse Constructions
There are many possible algorithms for computing pseudo-inverses and
null space bases. Fundamentally, they are equivalent though the data
structures and approaches differ somewhat.
From now on, we use the label  to indicate a matrix whose columns
form a null space basis for some zeroed matrix to indicate a matrix whose columns
form a null space basis for some zeroed matrix 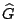 , perhaps with
all-zero column vectors as padding. Furthermore, because we are
concerned only with uncorrelated sector loss, we ignore the block
structure of , perhaps with
all-zero column vectors as padding. Furthermore, because we are
concerned only with uncorrelated sector loss, we ignore the block
structure of  . As a result, we can assume without loss of
generality that the generator matrix . As a result, we can assume without loss of
generality that the generator matrix  has its systematic identity
submatrix in the first has its systematic identity
submatrix in the first 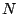 columns, with the parity columns in the
right most columns, with the parity columns in the
right most 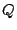 columns - we call this ``left systematic''. (If not,
a permutation of the columns of columns - we call this ``left systematic''. (If not,
a permutation of the columns of  and corresponding column positions
in and corresponding column positions
in 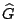 , , 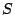 , and , and 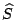 and row positions of and row positions of  , , 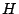 and and  will reduce us to this case.)
will reduce us to this case.)
The input to our algorithms is the original generator matrix  (and/or its parity check matrix
(and/or its parity check matrix 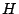 ) and a list ) and a list 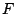 of data or parity
elements which are declared lost (unreadable) in the stripe. of data or parity
elements which are declared lost (unreadable) in the stripe.
The output of our algorithms will be two matrices  and and  : :  is
a pseudo-inverse of is
a pseudo-inverse of 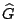 (obtained from (obtained from  by zeroing the columns
of by zeroing the columns
of  corresponding to the elements in corresponding to the elements in 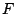 ) and ) and  is a basis for
the null space of is a basis for
the null space of 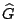 . .
Our algorithms use ``column operations'' and/or ``row operations'' to
manipulate matrices. Columns operations are equivalent to right
multiplication by simple matrices (for rows, the operations are on the
left). We consider three simplified column (or row)
operations:
- Swap: exchange two columns (or rows)
- Sum and Replace: add column
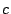 to column to column 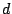 (modulo
2) and replace column (modulo
2) and replace column 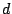 with the sum (similarly for rows). with the sum (similarly for rows).
- Zero: zero all the entries in a column (or row).
The first two are invertible (reversible), the Zero operation is not.
Our preferred algorithm, called the ``Column-Incremental''
construction, can be viewed as a dynamic or on-line algorithm. It
progressively updates data structures as new lost sectors are detected
(simulated by a incremental processing of the elements in 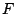 ). In
Section 6.3, we outline some additional
constructions including static or off-line algorithms. ). In
Section 6.3, we outline some additional
constructions including static or off-line algorithms.
6.1 Column-Incremental Construction
The algorithm presented here is an incremental algorithm. It starts
with a pseudo-inverse and null space basis for the matrix  (in the
``good'' state) and incrementally removes (simulates) a lost data or
parity element, while maintaining the pseudo-inverse and null space
basis properties at each step. The algorithm is space efficient and
for most well-designed codes, has relatively few operations. It
requires space in (in the
``good'' state) and incrementally removes (simulates) a lost data or
parity element, while maintaining the pseudo-inverse and null space
basis properties at each step. The algorithm is space efficient and
for most well-designed codes, has relatively few operations. It
requires space in  only for the lost data elements (there is no
need to provide recovery formulas for parity elements as these can be
easily derived from the original formulas in the generator matrix -
alternatively, parity columns may be added to only for the lost data elements (there is no
need to provide recovery formulas for parity elements as these can be
easily derived from the original formulas in the generator matrix -
alternatively, parity columns may be added to  and so provide
additional formulas for a parity computation that reflect the lost
data elements). For clarity of exposition, our description is not
optimally space efficient; we leave that to the expert implementor. and so provide
additional formulas for a parity computation that reflect the lost
data elements). For clarity of exposition, our description is not
optimally space efficient; we leave that to the expert implementor.
The process is reversible so long as the pseudo-inverse has full rank;
that is, at any step, it is possible to model reconstruction of data
values for lost elements (in any order) and compute a new
pseudo-inverse and null space basis equivalent to one in which the
recovered elements were never lost. This is described in
Section 6.4
In this algorithm, column operations are performed on a workspace
matrix. The lost data or parity elements index a row of  and and  . .
Algorithm: Column-Incremental Construction
- Construct a square workspace matrix
 of size of size 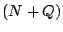 . In
the first . In
the first 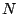 columns and rows, place an identity matrix. In the last columns and rows, place an identity matrix. In the last
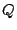 columns, place the parity check matrix columns, place the parity check matrix 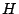 . Let . Let  represent the
first represent the
first 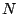 columns and columns and  represent the last represent the last 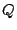 columns of columns of  , so , so
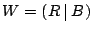 , where initially, , where initially, 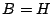 and
and
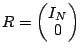 . .
- For each lost element in the list
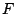 , let , let  indicate
the row corresponding to the lost element; perform the following
operation: indicate
the row corresponding to the lost element; perform the following
operation:
- Find any column
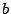 in in  that has
a one in row that has
a one in row  . If none exists, Zero any column in . If none exists, Zero any column in  that has
a one in row that has
a one in row  and continue to the next lost element. (Note
that zeroing these columns zeros the entire row and continue to the next lost element. (Note
that zeroing these columns zeros the entire row  in in  .) .)
- Sum and Replace
column
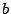 into every column into every column 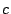 of of  (both (both  and and  portions)
that has a one in row portions)
that has a one in row  . .
- Zero column
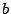 in in  ; equivalently,
add column ; equivalently,
add column 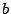 to itself. Continue to the next lost element, until
the list to itself. Continue to the next lost element, until
the list 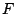 has been processed. has been processed.
-
(Optional) Use the columns of
 to improve the weight of non-trivial
columns of to improve the weight of non-trivial
columns of  (corresponding to lost data elements processed so far).
See equation (1) and Section 6.2. (corresponding to lost data elements processed so far).
See equation (1) and Section 6.2.
- Output
 (the first (the first 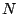 columns of columns of  ) and the non-zero
columns of ) and the non-zero
columns of  (from the last (from the last 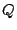 columns of columns of  ). ).
A proof that this algorithm satisfies the required properties can be
found in the appendix of the full technical report [5]. We
make the following observations.
- In practice, the workspace matrices are not very large.
For example, the EVENODD code on 8 strips (with prime
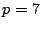 ) and
16 strips (with ) and
16 strips (with 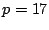 ) consumes only 288B and 8KB, respectively. In
addition, the operations are XOR or simple pointer operations, so
implementation can be very efficient. On the other hand, the
invocation of this algorithm happens in an error code-path, so
performance is less important than meeting the User Contract
set forth in Section 1. ) consumes only 288B and 8KB, respectively. In
addition, the operations are XOR or simple pointer operations, so
implementation can be very efficient. On the other hand, the
invocation of this algorithm happens in an error code-path, so
performance is less important than meeting the User Contract
set forth in Section 1.
- The runtime complexity of the algorithm (excluding the
optimizing step 3) can be bounded by
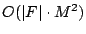 bit operations since at each of the bit operations since at each of the 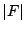 steps, at most steps, at most 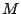 ones can appear in row
ones can appear in row  and each such one induces and each such one induces 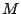 bit
operations (one column operation). This is clearly an excessive upper
bound as generally the matrices will be very sparse and only very few
(typically bit
operations (one column operation). This is clearly an excessive upper
bound as generally the matrices will be very sparse and only very few
(typically 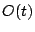 or or 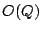 ) ones will be in each row. ) ones will be in each row.
- The optimizing step 3 on
 can be done
either as given in a penultimate or post-processing step or during the
loop after step 2c. Preferably, it is done
post-processing as this step can be quite expensive (see
Section 6.2). It can also be skipped; it is used
to possibly minimize the XOR/IO costs but is not necessary to meet the
requirements of the User Contract. can be done
either as given in a penultimate or post-processing step or during the
loop after step 2c. Preferably, it is done
post-processing as this step can be quite expensive (see
Section 6.2). It can also be skipped; it is used
to possibly minimize the XOR/IO costs but is not necessary to meet the
requirements of the User Contract.
- At step 2a, there may (most likely
will) be multiple choices for the column. There is no known theory
that provides a criterion so that the resulting
 is optimal or near
optimal. One heuristic (the greedy-choice) is to use the column in is optimal or near
optimal. One heuristic (the greedy-choice) is to use the column in
 of minimal weight, but that has not always precluded a
post-processing step 3 in our experiments.
However, this approach does introduce the optimal formula for the
current lost element (though this may change at later rounds of the loop). of minimal weight, but that has not always precluded a
post-processing step 3 in our experiments.
However, this approach does introduce the optimal formula for the
current lost element (though this may change at later rounds of the loop).
An alternative heuristic is the following: in the algorithm, a column
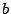 of of  is chosen with a one in position is chosen with a one in position  among all such columns
of among all such columns
of  . This selected column is added to each of the others in . This selected column is added to each of the others in  .
This suggests that a heuristic for .
This suggests that a heuristic for 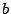 is to pick the one that
minimizes the total weight of the resulting columns. In is to pick the one that
minimizes the total weight of the resulting columns. In
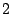 -fault-tolerant codes, there are typically at most two such columns
to choose from, so this approach is equivalent to the one of minimal
weight above; this is not true for higher fault-tolerant codes. -fault-tolerant codes, there are typically at most two such columns
to choose from, so this approach is equivalent to the one of minimal
weight above; this is not true for higher fault-tolerant codes.
- For only data elements (and systematic codes), it is always the
case that column
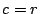 has a has a 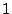 in position in position  (and no other (and no other 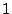 s
elsewhere) so is always acted on in the key step. In fact, the result
for this column is that we replace this column by the parity column s
elsewhere) so is always acted on in the key step. In fact, the result
for this column is that we replace this column by the parity column
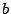 and then toggle the bit off in position and then toggle the bit off in position  . .
- We claim that after each lost element in the list is processed,
the matrix
 is a (partial or complete) pseudo-inverse for a zeroed
generator matrix is a (partial or complete) pseudo-inverse for a zeroed
generator matrix 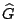 that has exactly the columns zeroed
corresponding to the set of elements processed so far. This is clear
in the first step because no elements have been processed, that has exactly the columns zeroed
corresponding to the set of elements processed so far. This is clear
in the first step because no elements have been processed,
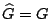 , the generator matrix, , the generator matrix,  is essentially an identity
matrix which extracts the identity portion of is essentially an identity
matrix which extracts the identity portion of  and and 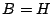 is the
parity check matrix, a.k.a. the null space basis for is the
parity check matrix, a.k.a. the null space basis for  . The
fact that this holds true at every other step will become clear from
the proof (see the appendix in the full technical
report [5]). . The
fact that this holds true at every other step will become clear from
the proof (see the appendix in the full technical
report [5]).
- We never actually write down the intermediate (or final) matrix
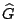 . This is all handled implicitly, and so no space is
used for this purpose. . This is all handled implicitly, and so no space is
used for this purpose.
- Because we perform only column operations on
 , it is easy to
see that what we are doing is performing, in parallel, the operations
needed to determine a reconstruction formula for all lost data
elements. That means that one could perform this process on
individual columns as needed (e.g., to recover a single element
on-demand). This would be fairly expensive globally because one
repeats the same search and process algorithm on , it is easy to
see that what we are doing is performing, in parallel, the operations
needed to determine a reconstruction formula for all lost data
elements. That means that one could perform this process on
individual columns as needed (e.g., to recover a single element
on-demand). This would be fairly expensive globally because one
repeats the same search and process algorithm on 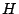 each time, but
may be marginally quicker if only one column is really needed. each time, but
may be marginally quicker if only one column is really needed.
- For the same reason, given the list of lost elements
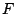 , one
can operate only on these columns in , one
can operate only on these columns in  and ignore all other columns.
In our construction, we use all columns because in principle, we do
not know what column is coming next (the algorithm does not care), so
we operate on all of and ignore all other columns.
In our construction, we use all columns because in principle, we do
not know what column is coming next (the algorithm does not care), so
we operate on all of  at once. at once.
- The algorithm can be used in an on-line fashion to maintain
recovery formulas for lost data elements as they are detected in the
stripe. As each new loss is detected, the matrices
 and and  get
updated. If a lost element's value is reconstructed, the algorithm of
Section 6.4 may be applied to again update
these matrices to incorporate this new information. Alternatively,
the algorithm can be applied as an off-line algorithm and applied
after detection of all lost elements in the stripe. get
updated. If a lost element's value is reconstructed, the algorithm of
Section 6.4 may be applied to again update
these matrices to incorporate this new information. Alternatively,
the algorithm can be applied as an off-line algorithm and applied
after detection of all lost elements in the stripe.
This algorithm was a key ingredient to the results
of [6] where it was applied to measure performance
costs for a large variety of very different  -fault-tolerant codes. -fault-tolerant codes.
6.2 Improving a Pseudo-inverse
In this section we outline some approaches to implementing the
optimizing step 3 in the Column-Incremental
construction algorithm given above. As noted earlier,
this step is not required to meet the User Contract stated in
Section 1.
The following algorithm provides a systematic (though potentially very
expensive) approach to finding an optimal  . .
Algorithm: Improve 
-
Compute all the null space vectors (by taking all possible
sums of subsets of the basis vectors).
- For each non-identity (and non-zero) column of
 , do the following: , do the following:
- For each null space vector (from step 1), do the following:
- Add the null space vector to the column of
 to
generate a new formula. to
generate a new formula.
- If the formula generated has lower weight, then
replace it in
 . .
- End
Of course, this is only practical if the null space has small enough
basis set. If the null space basis has very few vectors, then this
algorithm provides an exhaustive search solution to finding an optimal
 . In general, one can use any subset of the full null space to
find better, but perhaps not optimal, pseudo-inverses (in
Step 1 above, compute only some subset of the null
space). One simple choice, is to use only the basis vectors
themselves, or perhaps the basis vectors and all pairwise sums. It is
an open mathematical question if there are better algorithms for
finding the optimal . In general, one can use any subset of the full null space to
find better, but perhaps not optimal, pseudo-inverses (in
Step 1 above, compute only some subset of the null
space). One simple choice, is to use only the basis vectors
themselves, or perhaps the basis vectors and all pairwise sums. It is
an open mathematical question if there are better algorithms for
finding the optimal  than that given here. However, for the
extensive experiments we ran for [6], the difference
between optimal and near optimal was quite minimal. than that given here. However, for the
extensive experiments we ran for [6], the difference
between optimal and near optimal was quite minimal.
6.3 Alternative Constructions
There are alternative constructions that can be applied to computing
pseudo-inverses. Among them is a Row-Incremental variation that is
analogous to the Column-Incremental method described above but uses
row operations instead of column operations. Most of the steps are
the same as for the Column-Incremental construction. At
step 2b, for each one in positions 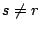 in
the selected column in
the selected column 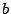 of of  , Sum and Replace row , Sum and Replace row  into row into row 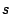 of
of  ; mirror this operation in ; mirror this operation in  . At step 2c zero
row . At step 2c zero
row  in in  and and  and proceed to the next lost element. This
algorithm has all the same properties as the column variation
(including reversibility), but is typically more expensive, requiring
more row operations. and proceed to the next lost element. This
algorithm has all the same properties as the column variation
(including reversibility), but is typically more expensive, requiring
more row operations.
Alternatively, there are both column and row versions that parallel
the classical algorithm for computing an inverse. Namely, start with
two matrices, the original generator matrix and an 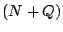 -identity
matrix. Zero the columns of the generator matrix and the identity
matrix corresponding to each lost data and parity element. Perform
column (or row) operations on the modified generator matrix to convert
it to column (or row) reduced echelon form. Parallel each of these
operations on the identity matrix; the resulting matrix contains both
the pseudo-inverse and null space basis. These variations are static,
off-line constructions as they utilize the complete set of lost
elements in the very first step. As before, the column version has
marginally less computation. -identity
matrix. Zero the columns of the generator matrix and the identity
matrix corresponding to each lost data and parity element. Perform
column (or row) operations on the modified generator matrix to convert
it to column (or row) reduced echelon form. Parallel each of these
operations on the identity matrix; the resulting matrix contains both
the pseudo-inverse and null space basis. These variations are static,
off-line constructions as they utilize the complete set of lost
elements in the very first step. As before, the column version has
marginally less computation.
We do not give proofs for any of these constructions as they vary
only slightly from the proof of the Column-Incremental construction
found in the appendix of the full technical report [5].
The static algorithms can also
be used to construct an initial pseudo-inverse matrix for the full
generator matrix in the case when  is not systematic. is not systematic.
6.4 Reversing The Column Incremental Construction
As mentioned, the incremental process can be used to start with a
fully on-line stripe and, step by step, as medium errors are detected
in the stripe, maintain a set of reconstruction formulas (or a
declaration of non-reconstructability) for every data element in the
stripe. As new medium errors are detected, the matrices are updated
and new formulas are generated.
It might be useful to reverse the process. Suppose the array has had
some set of medium errors, but no data loss events and suppose a data
element is reconstructed by its formula in  . If this reconstructed
data is replaced in the stripe, it would be helpful to update the
formulas to reflect this. There are two reasons for this. First, we
know we can replace the formula in . If this reconstructed
data is replaced in the stripe, it would be helpful to update the
formulas to reflect this. There are two reasons for this. First, we
know we can replace the formula in  by an identity column (we no
longer need the old formula). But second, it may be the case that
other lost elements can be reconstructed by better formulas that
contain this newly reconstructed element; we should update by an identity column (we no
longer need the old formula). But second, it may be the case that
other lost elements can be reconstructed by better formulas that
contain this newly reconstructed element; we should update  to
reflect this fact. to
reflect this fact.
One approach would be to use any algorithm to recompute from scratch
the formulas for the revised set of sector losses. However, the
incremental algorithm suggests that we might be able to reverse the
process; that is, to update  and and  directly to reflect the fact
that the data element has been reconstructed (e.g., its column in directly to reflect the fact
that the data element has been reconstructed (e.g., its column in  is replaced by an identity column).
is replaced by an identity column).
To fully reverse the incremental construction of the previous section,
it must be the case that no information (in the information-theoretic
sense) is lost through each step. Mathematically, this happens
whenever we perform a non-invertible matrix operation, i.e.,
that corresponds to multiplication by a non-invertible matrix. This
occurs essentially in only one place in the construction: whenever we
can find no vector in the null space basis with a one in the desired
row. This corresponds exactly to the case where we have data loss
events.
Consequently, we have the following result: so long as we never
encounter the data loss branch, then (in principle), the sequence of
steps can be reversed. However, the algorithm we give below works
even after data loss events, so long as the restored element has a
reconstruction formula in  , i.e., it is not itself a data
loss event . Note that it makes little sense to consider restoring
into the matrix an element corresponding to a data loss event (the
theorem says that this is theoretically impossible). , i.e., it is not itself a data
loss event . Note that it makes little sense to consider restoring
into the matrix an element corresponding to a data loss event (the
theorem says that this is theoretically impossible).
The algorithm below performs this incremental restoration step in the
case of a (recoverable) data element. Section 6.4.1
discusses the parity element case.
The input to this algorithm is a workspace matrix
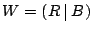 (possibly) generated by the incremental algorithm and
having the property that (possibly) generated by the incremental algorithm and
having the property that
where 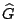 is the generator matrix with zeroed columns for each
data or parity element in the set is the generator matrix with zeroed columns for each
data or parity element in the set 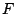 of assumed lost elements (prior
to a reconstruction). The other input is a data element index, that
is, a row number of assumed lost elements (prior
to a reconstruction). The other input is a data element index, that
is, a row number  of of  . The output of the algorithm is a
revised matrix . The output of the algorithm is a
revised matrix  so that the above formula holds with so that the above formula holds with 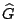 having
column having
column  replaced by the appropriate identity column. The
new matrix replaced by the appropriate identity column. The
new matrix  will have an identity column in position will have an identity column in position  . (As
before, the algorithm does not track the changes to . (As
before, the algorithm does not track the changes to 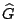 directly,
only implicitly.) Note that this process does not depend on which
element is being restored from among the set of elements removed
during the incremental phase (that is, it need not be the last element
removed). We assume that directly,
only implicitly.) Note that this process does not depend on which
element is being restored from among the set of elements removed
during the incremental phase (that is, it need not be the last element
removed). We assume that  contains enough all-zero columns so that
it has contains enough all-zero columns so that
it has 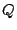 columns in total. columns in total.
If the restored element is not from the set 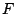 , then this algorithm
has no work to do, so we assume that the lost element is from , then this algorithm
has no work to do, so we assume that the lost element is from 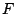 . .
Algorithm: Reverse Incremental Construction
- (Optional) For each column
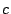 in the inverse portion of in the inverse portion of  (first (first
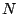 columns) that has a one in every row that column columns) that has a one in every row that column  has (that
is, if the AND of the columns has (that
is, if the AND of the columns 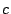 and and  equals column equals column  ), do the
following: ), do the
following:
- Sum and Replace column
 into column into column 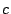 ; that is, for each
position of column ; that is, for each
position of column  that has a one, set the corresponding value
in column that has a one, set the corresponding value
in column 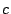 to zero. to zero.
- Set position
 in column in column 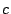 to the value to the value 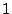 . .
- Find any all-zero column
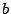 in the null space portion of in the null space portion of  (in the last
(in the last 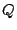 columns). columns).
- Set position
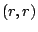 and and 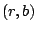 in in  to the value to the value 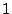 . .
- Swap columns
 and and 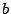 of of  . .
- (Optional) Use the null space basis vectors in
 of of  to
reduce the weight of any column in the inverse portion to
reduce the weight of any column in the inverse portion  of of  . .
- Return the updated
 . .
This algorithm works because it takes the reconstruction formula for
the data element and unfolds it back into the null space basis, then
replaces the formula with an identity column.
The first optional step replaces any occurrence of the formula for
data element  in the original in the original  by that element itself. In
particular, it explicitly restores into other columns a
dependence on the restored data element. In the process, it improves
the weight of these formulas. by that element itself. In
particular, it explicitly restores into other columns a
dependence on the restored data element. In the process, it improves
the weight of these formulas.
This algorithm does not necessarily completely reverse the incremental
algorithm in that it does not necessarily produce identical matrices
going backward as were seen going forward. However, the difference
will always be something in the null space.
A proof of this construction is given in
the appendix of the full technical report [5].
6.4.1 Restoring parity elements
To add a parity element back in to the matrices, we need to have the
original parity column from the generator matrix  (for the data
columns, we know a priori that this column is an identity
column so we do not need to keep track of this externally). Suppose
that this parity is indexed by column (for the data
columns, we know a priori that this column is an identity
column so we do not need to keep track of this externally). Suppose
that this parity is indexed by column 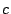 in in  . .
Take this parity column and for each 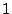 in the column, sum together
(modulo 2) the corresponding columns of in the column, sum together
(modulo 2) the corresponding columns of  in in  and place the
result in an all-zero column of and place the
result in an all-zero column of  in in  . (This is exactly what we
did for a data column since there was only one such column!) Replace
the zero in position . (This is exactly what we
did for a data column since there was only one such column!) Replace
the zero in position 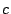 of this new column by of this new column by 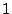 . Replace column . Replace column
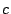 of of 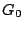 by this parity column (restore it). (Again, this is
exactly what we did for a restored data column, except we also had to
set the by this parity column (restore it). (Again, this is
exactly what we did for a restored data column, except we also had to
set the 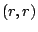 position in the inverse portion of position in the inverse portion of  to to 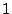 - in
the case of a parity column, no such position exists in the inverse
portion so this step is skipped.) - in
the case of a parity column, no such position exists in the inverse
portion so this step is skipped.)
A proof is given in the appendix of the full technical
report [5].
7 An Example: EVENODD Code
Consider the EVENODD(3,5) code [2] with prime 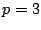 , ,
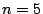 total disks, total disks, 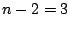 data disks and two parity disks. The data
and parity layout in the strips and stripe for one instance is given
in the following diagram: data disks and two parity disks. The data
and parity layout in the strips and stripe for one instance is given
in the following diagram:
The columns labeled 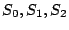 are the data strips in the stripe
(one per disk); the columns labeled are the data strips in the stripe
(one per disk); the columns labeled 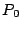 and and  are the horizontal
and diagonal parity strips, respectively. We order the data elements
first by strip and then, within the strip, down the columns (this is
the same view as the ordering of host logical blocks within the
stripe). In this example, are the horizontal
and diagonal parity strips, respectively. We order the data elements
first by strip and then, within the strip, down the columns (this is
the same view as the ordering of host logical blocks within the
stripe). In this example, 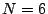 and and 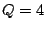 . .
The generator matrix  defined for this code is: defined for this code is:
This is column blocked to indicate the strip boundaries.
The matrix indicates that the parity 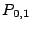 is the XOR sum of
the data elements indexed by the 0th, 3th, 4th and 5th rows of is the XOR sum of
the data elements indexed by the 0th, 3th, 4th and 5th rows of  , i.e., , i.e.,
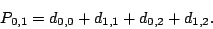 |
(4) |
The parity check matrix 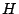 is: is:
The parity check matrix is row blocked exactly to correspond to the
column blocks of  and it contains in the lower portion an embedded
identity matrix. It is easy to see that and it contains in the lower portion an embedded
identity matrix. It is easy to see that 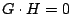 ; that is, ; that is, 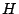 is
in the null space of is
in the null space of  (and forms a basis as well). Each column of
the parity check matrix corresponds to a parity value in the array
(the identity rows and the block structure provide this association). (and forms a basis as well). Each column of
the parity check matrix corresponds to a parity value in the array
(the identity rows and the block structure provide this association).
For example, column 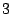 of the parity check matrix says of the parity check matrix says
If this equation is not satisfied for the actual data and parity read
from the disks (or detected on a channel), then an error has occurred
somewhere.
More generally, we interpret these matrices in the following way. As
labeled above, we consider the user data values as a row vector
(ordered as already indicated):
The product 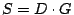 equals equals
indicates the data layout in strips (via the block structure) as well
as the formulas for computing the parity. We saw an example of this
in equation (4).
The parity check matrix implies that
regardless of the actual values of the data elements.
Any binary linear combination of the columns of  will also be
orthogonal to all the vectors in will also be
orthogonal to all the vectors in  . E.g., take the binary sum (XOR)
of columns . E.g., take the binary sum (XOR)
of columns 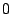 and and 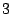 in in 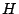 : :
It is easy to see that this has the desired orthogonality property.
We can replace any column in 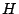 by any such combination and still
have a ``parity check matrix''. Typically, the by any such combination and still
have a ``parity check matrix''. Typically, the
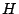 constructed directly from the parity equations is the most sparse. constructed directly from the parity equations is the most sparse.
7.1 The Example - Scattered Sector Loss
Suppose we loose strip  and only data element and only data element 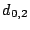 of of  in the EVENODD(3,5) code above. We then have a ``zeroed'' matrix
in the EVENODD(3,5) code above. We then have a ``zeroed'' matrix
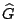 in the form: in the form:
where the  over the column indicates the column has been
removed by zeroing. over the column indicates the column has been
removed by zeroing.
Using the data vector 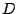 , we see that we have a revised set of
relationships: , we see that we have a revised set of
relationships:
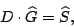 |
(5) |
where
When we view the vector 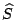 as ``known'' data and parity
elements (in fact, the labeled components represent the sectors that
are still readable in the stripe), this equation represents a system
of linear equations for the ``unknown'' vector as ``known'' data and parity
elements (in fact, the labeled components represent the sectors that
are still readable in the stripe), this equation represents a system
of linear equations for the ``unknown'' vector 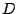 in terms of the
known vector in terms of the
known vector 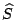 . .
The following two matrices  and and 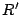 are easily seen to be
pseudo-inverses for are easily seen to be
pseudo-inverses for 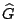 : :
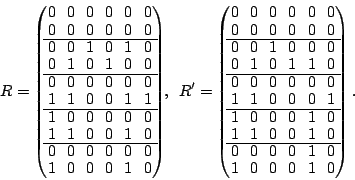 |
(6) |
We show how these matrices are obtained in
Section 7.2.
The columns of  (or (or 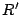 ) correspond to the data elements as
ordered in the vector ) correspond to the data elements as
ordered in the vector 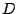 . Each non-zero row corresponds to a
position in the vector . Each non-zero row corresponds to a
position in the vector 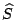 of known elements. Each all-zero row
matches a lost element in of known elements. Each all-zero row
matches a lost element in 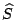 . Each column represents an XOR
formula for reconstructing the data element to which it corresponds.
For example, to reconstruct . Each column represents an XOR
formula for reconstructing the data element to which it corresponds.
For example, to reconstruct 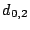 , we look at column , we look at column 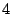 of of  .
It indicates the following formula: .
It indicates the following formula:
and by looking at column 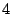 of of 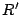 we get the formula: we get the formula:
It is easy to see from the original code that both of these formulas
are correct (and that they do not depend on any lost sectors!).
Because the code is MDS and can tolerate two disk/strip failures, it
is easy to see from dimension counting that 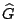 has only one
non-zero vector in its null space. This vector turns out to be has only one
non-zero vector in its null space. This vector turns out to be
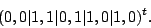 |
(7) |
This is also the sum of columns  of of  and and 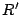 (indicating that (indicating that
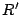 is derived from is derived from  by adding a vector from the null space). by adding a vector from the null space).
The weight of each of the formulas for reconstructing data via  is
at least as good as those in is
at least as good as those in 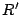 , consequently, , consequently,  is a better
solution than is a better
solution than 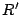 for our purposes. In fact, with only one vector in
the null space, it is clear that for our purposes. In fact, with only one vector in
the null space, it is clear that  is optimal. is optimal.
7.2 The Example - Constructing 
We start with the EVENODD(3,5) code as before and assume as above that
data elements 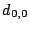 , , 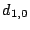 , and , and 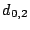 are lost from strips are lost from strips
 and and  . These elements correspond to columns . These elements correspond to columns 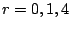 of of
 (and also to this set of rows in our workspace). (and also to this set of rows in our workspace).
The initial workspace is
For row 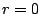 , we find some column in , we find some column in  that has a one in this row.
There are two choices, that has a one in this row.
There are two choices, 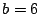 or or 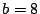 . We choose . We choose 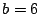 because its
weight is less. We add this to columns because its
weight is less. We add this to columns 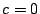 and and 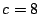 (where there
is a one in row (where there
is a one in row  ), then zero column ), then zero column 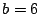 . The result is . The result is
For 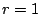 , select column , select column 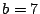 (again, this has the minimum weight),
then add this to columns (again, this has the minimum weight),
then add this to columns  , then zero column , then zero column 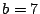 . This gives: . This gives:
Similarly, for  (using (using 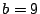 ), the result is ), the result is
Note that the left portion of this workspace equals  in (6). Furthermore, our null space basis
in (6). Furthermore, our null space basis  contains
only the vector in (7); adding this vector to
column contains
only the vector in (7); adding this vector to
column 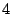 of of  produces produces 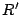 from (6). As from (6). As  contains
the optimal reconstruction formulas, no post-process step is required
in this example. contains
the optimal reconstruction formulas, no post-process step is required
in this example.
It can be checked that at each stage the claimed properties of
pseudo-inverse and null space of the intermediate results all hold.
It should be noted that this is not against the final 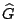 but the intermediate
but the intermediate 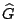 which we never write down). which we never write down).
7.3 The Example - Additional Sector Loss
Now suppose in addition that element 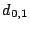 of strip of strip  is also
lost. This corresponds to a situation where sectors are lost from all
three data strips of the stripe. Nominally, the EVENODD(3,5) code can
only protect against losses on is also
lost. This corresponds to a situation where sectors are lost from all
three data strips of the stripe. Nominally, the EVENODD(3,5) code can
only protect against losses on  strips; we have three partial
strips, a case not covered in the literature. strips; we have three partial
strips, a case not covered in the literature.
The element 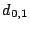 corresponds to corresponds to 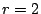 . We select column . We select column 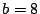 ,
perform the operations in the algorithm and the result is ,
perform the operations in the algorithm and the result is
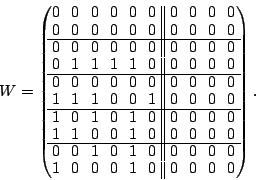 |
(8) |
At this point, we have no more null space basis vectors ( is all
zero). Any further sector loss implies a ``data loss event'' (see
below). is all
zero). Any further sector loss implies a ``data loss event'' (see
below).
Observe that any column corresponding to a data element that is
not lost has remained unchanged as an identity column.
In addition, even though we have lost sectors in three strips, all
sectors are still recoverable.
If we further assume that data element 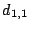 (corresponding to row
(corresponding to row 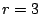 ) is also lost, we can continue the
algorithm. In this case, there is no null space basis vector with a
one in this row. So, the algorithm says to zero all columns in ) is also lost, we can continue the
algorithm. In this case, there is no null space basis vector with a
one in this row. So, the algorithm says to zero all columns in  with a one in this row (that is, columns
with a one in this row (that is, columns  ). This produces
the matrix ). This produces
the matrix
This indicates that data elements corresponding to columns  are ``data loss events''. However, column
are ``data loss events''. However, column  corresponding to data
element corresponding to data
element 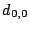 is still recoverable (as is is still recoverable (as is 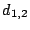 which was
never lost). which was
never lost).
7.4 The Example - Reversing The Construction
We start with the result of our incremental construction example in
equation (8) where we have lost sectors 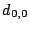 , ,
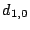 , , 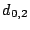 and and 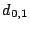 corresponding to columns corresponding to columns
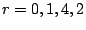 of of  . Suppose we have reconstructed data element . Suppose we have reconstructed data element
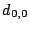 of column of column 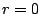 (which is not the last element we
simulated as lost). The reverse incremental algorithm above has the
following steps. (We include the optional steps for completeness.) (which is not the last element we
simulated as lost). The reverse incremental algorithm above has the
following steps. (We include the optional steps for completeness.)
First, we examine each of the first six columns to see if column 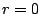 is contained in it. Column
is contained in it. Column 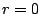 has one's in positions has one's in positions 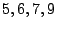 .
No other column has ones in all these positions, so we continue to
the next step. .
No other column has ones in all these positions, so we continue to
the next step.
Next we select the all-zero column 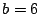 and set position and set position  in this
column and in column in this
column and in column 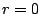 to the value to the value  , then we swap these two
columns: , then we swap these two
columns:
Next we look for null space basis elements (there's only one to choose
from) that might improve the inverse portion. For example,
column 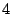 has weight has weight 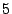 . If we combine (XOR) columns . If we combine (XOR) columns 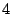 and
and 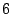 , we get a new matrix , we get a new matrix
where the new column 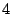 now has weight now has weight 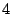 . This step improved the
weight of this column, as we wanted. . This step improved the
weight of this column, as we wanted.
Note that our final result does have an identity column in position
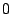 so we have restored this data element. so we have restored this data element.
8 Efficient Reconstruction of Partial Strips
In this section we introduce the hybrid reconstruction method. It
applies the reconstruction methodology based on the matrix method in
another way to address the problem of partial strip reconstruction.
Suppose the array's erasure code can tolerate two strip failures.
Most such erasure codes have a recursive algorithm defined for
reconstructing the two lost strips. This can be quite efficient for
rebuild of both lost strips in their entirety. The steps are
generally quite simple and explicitly assume use of intermediate
reconstructed elements. However, such a method will be very
code-dependent; that is, the recursion will depend on the specific
code layout and parity formulas. On the other hand, the matrix
methodology above is completely generic. If applied without the
Reverse Incremental construction, no intermediate results are used;
consequently, the amount of XOR computation could be quite large
compared to a recursive method. But the Reverse Incremental
construction would directly take advantage of intermediate results and
improve overall XOR computation costs. In fact, if applied
appropriately (as a special case of our algorithm below), the matrix
method (including the Reverse Incremental construction) would reduce
to the recursive method in most cases (and be very similar in all
others).
Now consider a host request to read a single block from one of the two
lost strips (prior to completion of any background process to
reconstruct the stripe). If the element is very deep into the
recursion, a number of intermediate reconstructions (of lost elements)
must take place; these intermediate results are not needed for the
immediate host request and, though they can be cached, are potentially
extraneous work for the task at hand. The matrix method above,
however, gives a (near) optimal formula for direct reconstruction of
any single element without
reconstruction of any additional elements.
We see that for single element reconstruction, the generic direct
method of the matrix methodology is generally more efficient than the
recursive method provided with a specific code. Conversely, for
reconstruction of all lost elements the generally preferred method is
the recursive method (either explicitly using the code's specific
theory or implicitly using the matrix method together with the Reverse
Incremental construction).
We now consider the problem of reconstructing a partial strip, say, to
satisfy a host read for multiple consecutive blocks that span multiple
elements in a strip. We assume that multiple strips are lost (though
that is not a requirement at all). The above discussion suggests that
neither the direct nor the recursive methods may be optimal to address
this problem efficiently. We propose the following algorithm. The
input to the algorithm is the set of lost sectors  , the parity
check matrix (or the generator matrix) and a subset , the parity
check matrix (or the generator matrix) and a subset 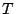 of of 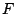 containing sectors to reconstruct (we assume that no element in
containing sectors to reconstruct (we assume that no element in 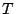 is
a data loss event). The output is the data values for the elements in is
a data loss event). The output is the data values for the elements in
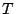 . That is, . That is, 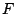 is the complete set of lost sectors and is the complete set of lost sectors and 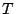 is that
partial set we need to reconstruct. is that
partial set we need to reconstruct.
Algorithm: Code-specific Hybrid Reconstruction
- Compute the pseudo-inverse
 and a (padded) null space basis
for and a (padded) null space basis
for  for the lost sectors for the lost sectors 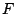 (say, using the Column Incremental
construction). (say, using the Column Incremental
construction).
- Do the following until all of
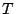 has been reconstructed: has been reconstructed:
- Find an unreconstructed element
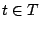 whose reconstruction vector in
whose reconstruction vector in  has minimal weight; reconstruct
the value for has minimal weight; reconstruct
the value for 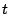 . .
- Examine the recursion to see if any
other element
 can be reconstructed by some fixed number of
iterations of the recursion when starting that recursion at can be reconstructed by some fixed number of
iterations of the recursion when starting that recursion at 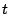 .
(e.g., for .
(e.g., for 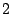 -fault-tolerant codes, this typically means at most
two steps). -fault-tolerant codes, this typically means at most
two steps).
- If such a
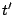 exists, reconstruct exists, reconstruct 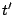 following the recursion; set
following the recursion; set
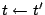 and return to
step 2b. and return to
step 2b.
- If no such
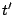 exists, do: exists, do:
- (Optional) Update
 and and  using
the Reverse Incremental construction for all values
reconstructed so far. using
the Reverse Incremental construction for all values
reconstructed so far.
- Return to step 2a.
- Return the reconstructed values for the sectors in
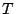 . .
Essentially, this algorithm uses the direct method to jump into the
recursion at the first point the recursion intersects the set 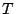 (thereby avoiding reconstruction of unneeded values). The optional
step 2(d)i ensures that we have factored into the direct
reconstruction formulas all values reconstructed to this point,
thereby allowing these elements to be used in later reconstruction
formulas (lowering XOR computational costs).
(thereby avoiding reconstruction of unneeded values). The optional
step 2(d)i ensures that we have factored into the direct
reconstruction formulas all values reconstructed to this point,
thereby allowing these elements to be used in later reconstruction
formulas (lowering XOR computational costs).
During step 2c, we can avoid physical reconstruction
of intermediate steps in the recursion that are not in set 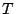 (that is, not immediately required for the host) by logically
collapsing the recursion equations. That is, we combine the steps of
the recursions to get from
(that is, not immediately required for the host) by logically
collapsing the recursion equations. That is, we combine the steps of
the recursions to get from 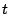 to to 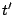 . This has two advantages.
First, it avoids a computation and temporary memory store of any
unneeded intermediate result. Second, the combination can eliminate
the need for some data or parity values that appear multiply (an even
number of times) in the set of recursive formulas. This avoids a
possible disk read to access this data as well as the memory bandwidth
costs to send this data into and out of the XOR engine multiple times. . This has two advantages.
First, it avoids a computation and temporary memory store of any
unneeded intermediate result. Second, the combination can eliminate
the need for some data or parity values that appear multiply (an even
number of times) in the set of recursive formulas. This avoids a
possible disk read to access this data as well as the memory bandwidth
costs to send this data into and out of the XOR engine multiple times.
Step 2b looks for efficient ways to utilize the
recursion. If none exist, we reapply the direct method (updated,
perhaps) to jump back into the recursion at some other point in 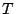 of
minimal direct costs. of
minimal direct costs.
Together, these steps enable efficient reconstruction of only those
elements that are needed (those in 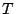 ) and no others. There are two
special cases: (a) if ) and no others. There are two
special cases: (a) if 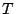 is a singleton, then this method will apply
the direct method in the first step then exit; (b) if is a singleton, then this method will apply
the direct method in the first step then exit; (b) if 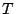 is the union
of all the elements on all lost strips, then the algorithm will
default to the application of the recursion alone. We see then that
this algorithm interpolates between these two extremes to find
efficient reconstruction of partial strips. (Note that is the union
of all the elements on all lost strips, then the algorithm will
default to the application of the recursion alone. We see then that
this algorithm interpolates between these two extremes to find
efficient reconstruction of partial strips. (Note that 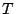 need not
be a partial strip, but that is the most likely application.) need not
be a partial strip, but that is the most likely application.)
More generically, we can apply the following algorithm as a means to
efficiently solve the same problem, without reference to the specific
recursion of the code (assuming it has one).
Algorithm: Generic Hybrid Reconstruction
- Compute the pseudo-inverse
 and a (padded) null space basis
matrix and a (padded) null space basis
matrix  for the lost sectors for the lost sectors 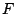 (say, using the Column Incremental
Construction). (say, using the Column Incremental
Construction).
- Do the following until all of
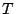 has been reconstructed: has been reconstructed:
- Find an unreconstructed element
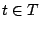 whose reconstruction
vector in whose reconstruction
vector in  has minimal weight and reconstruct it. has minimal weight and reconstruct it.
- Update
 and and  using the
Reverse Incremental construction with input using the
Reverse Incremental construction with input 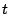 . .
- Return to step 2a.
- Return the reconstructed values for the sectors in
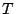 . .
It is not hard to see that in the presense of a straight forward
recursion, the code-specific and generic hybrid methods will produce
similar results (perhaps in different order of reconstruction, but
with the same or similar costs). The application of the recursion in
step 2c in the code-specific algorithm implicitly
applies the Reverse Incremental algorithm.
Figure 1 shows the advantages of this hybrid method
for the EVENODD code [2]. The chart shows the
XOR costs (total number of XOR input and output variables) for disk
array sizes from 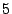 to to 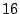 . These numbers are the average over all
1/2-strip-sized (element-aligned) host read requests to lost strips
and averaged over all possible . These numbers are the average over all
1/2-strip-sized (element-aligned) host read requests to lost strips
and averaged over all possible 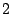 strip failures. They are
normalized to the Direct XOR costs. The figure shows that the direct
cost is generally (except for very small arrays) more expensive than
application of the recursive method (as one would expect for long
reads), but it also shows that the Hybrid method is significantly more
efficient than both. strip failures. They are
normalized to the Direct XOR costs. The figure shows that the direct
cost is generally (except for very small arrays) more expensive than
application of the recursive method (as one would expect for long
reads), but it also shows that the Hybrid method is significantly more
efficient than both.
Figure 1:
Comparision of Direct, Recursive and Hybrid reconstruction
methods for 1/2 lost strip reconstruction, EVENODD code.
|
We developed a language to model uncorrelated and/or correlated loss
of sectors (or elements) in arbitrary array codes. We provided a
direct methodology and constructive algorithms to implement a
universal and complete solution to the recoverability and
non-recoverability of these lost sectors. This method and algorithm
meets the User Contract that says that what is theoretically
recoverable shall be recovered. Our solution can be applied
statically or incrementally. We demonstrated the power of the direct
method by showing how it can recover data in lost sectors when these
sectors touch more strips in the stripe than the fault tolerance of
the erasure code. The direct method can be joined with any
code-specific recursive algorithm to address the problem of efficient
reconstruction of partial strip data. Alternatively, the incremental
method can be reversed when some data is recovered to provide a
completely generic method to address this same partial strip recovery
problem. Finally, we provided numerical results that demonstrate
significant performance gains for this hybrid of direct and recursive
methods.
10 Acknowledgements
The authors thank Tapas Kanungo and John Fairhurst for their
contributions to this work and the reviewers for helpful suggestions
to improve the exposition.
- 1
-
S. Baylor, P. Corbett, and C. Park.
Efficient method for providing fault tolerance against double device
failures in multiple device systems, January 1999.
U. S. Patent 5,862,158.
- 2
-
M. Blaum, J. Brady, J. Bruck, and J. Menon.
EVENODD: an efficient scheme for tolerating double disk failures in
RAID architectures.
IEEE Transactions on Computers, 44:192-202, 1995.
- 3
-
M. Blaum and R. M. Roth.
On lowest density MDS codes.
IEEE Transactions on Information Theory, 45:46-59, 1999.
- 4
-
P. Corbett, B. English, A. Goel, T. Grcanac, S. Kleiman, J. Leong, and
S. Sankar.
Row-diagonal parity for double disk failure.
In Proceedings of the Third USENIX Conference on File and
Storage Technologies, pages 1-14, 2004.
- 5
-
V. Deenadhayalan, J. L. Hafner, KK Rao, and J. A. Tomlin.
Matrix methods for lost data reconstruction in erasure codes.
Technical Report RJ 10354, IBM Research, San Jose, CA, 2005.
- 6
-
J. L. Hafner, V. Deenadhayalan, T. Kanungo, and KK Rao.
Performance metrics for erasure codes in storage systems.
Technical Report RJ 10321, IBM Research, San Jose, CA, 2004.
- 7
-
F. J. MacWilliams and N. J. A. Sloane.
The Theory of Error-Correcting Codes.
Northolland, Amsterdam, The Netherlands, 1977.
- 8
-
J. Plank.
A tutorial on Reed-Solomon coding for fault-tolerance in
RAID-like systems.
Software: Practice and Experience, 27:995-1012, 1997.
- 9
-
I. S. Reed and G. Solomon.
Polynomial codes over certain finite fields.
Journal of the Society for Industrial and Applied Mathematics,
8:300-304, 1960.
- 10
-
L. Xu and J. Bruck.
X-code: MDS array codes with optimal encoding.
IEEE Transactions on Information Theory, IT-45:272-276, 1999.
- 11
-
G. V. Zaitsev, V. A. Zinovev, and N. V. Semakov.
Minimum-check-density codes for correcting bytes of errors.
Problems in Information Transmission, 19:29-37, 1983.
Matrix Methods for Lost Data Reconstruction in Erasure Codes
This document was generated using the
LaTeX2HTML translator Version 2002-2-1 (1.71)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 -show_section_numbers -local_icons matrix_hybrid_fast05
The translation was initiated by on 2005-10-07
Footnotes
- ... Tomlin
![[*]](footnote.png)
- This work was done while Dr. Tomlin was at the IBM Almaden Research Center



2005-10-07
|


![[*]](footnote.png)

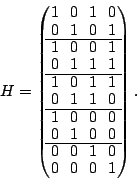
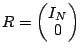 .
.

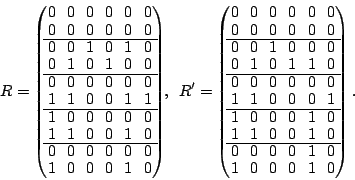
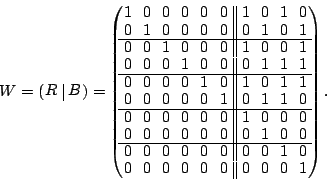



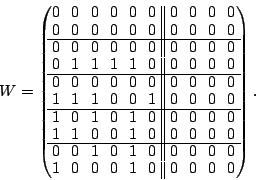

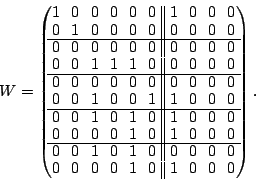

![\includegraphics[width=\graphicwidth,bb=57 401 504 717]{figs/hybrid_ks_rj}](img147.png)