
Blaine Nelson
Marco Barreno
Fuching Jack Chi
Anthony D. Joseph
Benjamin I. P. Rubinstein
Udam Saini
Charles Sutton
J. D. Tygar
Kai Xia
University of California, Berkeley
Using statistical machine learning for making security decisions introduces new vulnerabilities in large scale systems. This paper shows how an adversary can exploit statistical machine learning, as used in the SpamBayes spam filter, to render it useless--even if the adversary's access is limited to only 1% of the training messages. We further demonstrate a new class of focused attacks that successfully prevent victims from receiving specific email messages. Finally, we introduce two new types of defenses against these attacks.
This paper demonstrates how attackers can exploit machine learning to subvert spam filters. Our attack strategies exhibit two key differences from previous work: traditional attacks modify spam emails to evade a spam filter, whereas our attacks interfere with the training process of the learning algorithm and modify the filter itself; and rather than focus only on placing spam emails in the victim's inbox, we subvert the spam filter to remove legitimate emails from the inbox. In this paper, we explore the implications of the contamination assumption: the adversary can control some of the user's training data.
An attacker may have one of two goals: expose the victim to an advertisement or prevent the victim from seeing a legitimate message. Potential revenue gain for a spammer drives the first goal, while the second goal is motivated, for example, by an organization competing for a contract that wants to prevent competing bids from reaching their intended recipient.
An attacker may have detailed knowledge of a specific email the victim is likely to receive in the future, or the attacker may know particular words or general information about the victim's word distribution. In many cases, the attacker may know nothing beyond which language the emails are likely to use.
When an attacker wants the victim to see spam emails, a broad dictionary attack can render the spam filter unusable, causing the victim to disable the filter (Section 3.2). With more information about the email distribution, the attacker can select a smaller dictionary of high-value features that are still effective. When an attacker wants to prevent a victim from seeing particular emails and has some information about those emails, the attacker can target them with a focused attack (Section 3.3).
We demonstrate the potency of these attacks and then present two defenses. The Reject On Negative Impact (RONI) defense tests the impact of each email on training and doesn't train on messages that have a large negative impact. The dynamic threshold defense dynamically sets the spam filter's classification thresholds based on the data rather than using SpamBayes' static choice of thresholds. We show that both defenses are effective in preventing some attacks from succeeding.
We focus on the learning algorithm underlying several spam filters, including SpamBayes (spambayes.sourceforge.net), BogoFilter (bogofilter.sourceforge.net), and the machine learning component of SpamAssassin (spamassassin.apache.org).1We target SpamBayes because it uses a pure machine learning method, it is familiar to the academic community [14], and it is popular with over 700,000 downloads. Although we specifically attack SpamBayes, the widespread use of its statistical learning algorithm suggests that other filters may also be vulnerable to similar attacks. However, some filters, such as SpamAssassin, use the learner only as one component of a broader filtering strategy.
Our experimental results confirm that this class of attacks presents a serious concern for statistical spam filters. A dictionary attack can make a spam filter unusable when controlling just 1% of the messages in the training set, and a well-informed focused attack can remove the target email from the victim's inbox 90% of the time. Of our two defenses, one significantly mitigates the effect of the dictionary attack and the other provides insight into the strengths and limitations of threshold-based defenses.
SpamBayes produces a classifier from labeled examples to label future emails. The labels are spam (bad, unsolicited email), ham (good, legitimate email), and unsure (SpamBayes isn't confident one way or the other). The classifier learns from a labeled training set of ham and spam emails.
Email clients use these labels in different ways--some clients filter email labeled as spam and unsure into ``Spam-High'' and ``Spam-Low'' folders, respectively, while other clients only filter email labeled as spam into a separate folder. Since the typical user reads most or all email in their inbox and rarely (if ever) looks at the spam/spam-high folder, the unsure labels can be problematic. If unsure messages are filtered into a separate folder, users may periodically read the messages in that folder to avoid missing important email. If instead unsure messages are not filtered, then the user faces those messages when checking the email in their inbox. Too much unsure email is almost as troublesome as too many false positives (ham labeled as spam) or false negatives (spam labeled as ham). In the extreme, if everything is labeled unsure then the user obtains no time savings at all from the filter.
In our scenarios, an organization uses SpamBayes to filter multiple users' incoming email2and trains on everyone's received email. SpamBayes may also be used as a personal email filter, in which case the presented attacks and defenses are likely to be equally effective.
To keep up with changing trends in the statistical characteristics of both legitimate and spam email, we assume that the organization retrains SpamBayes periodically (e.g., weekly). Our attacks are not limited to any particular retraining process; they only require that the attacker can introduce attack data into the training set somehow (the contamination assumption).
We assume that the attacker can send emails that the victim will use for training--the contamination assumption--but incorporate two significant restrictions: attackers may specify arbitrary email bodies but not headers, and attack emails are always trained as spam and not ham. We examine the implications of the contamination assumption in the remainder of this paper.
How can an attacker contaminate the training set? Consider the following alternatives. If the victim periodically retrains on all email, any email the attacker sends will be used for training. If the victim manually labels a training set, the attack emails will be included as spam because they genuinely are spam. Even if the victim retrains only on mistakes made by the filter, the attacker may be able to design emails that both perform our attacks and are also misclassified by the victim's current filter. We do not address the possibility that a user might inspect training data to remove attack emails; our attacks could be adjusted to evade detection strategies such as email size or word distributions, but we avoid pursuing this arms race here.
Our focus on spam-labeled attack emails should be viewed as a restriction and not a necessary condition for the success of the attacks--using ham-labeled attack emails could enable more powerful attacks that place spam in a user's inbox.
SpamBayes classifies using token scores based on a simple model of spam status proposed by Robinson [14,17], based on ideas by Graham [7] together with Fisher's method for combining independent significance tests [6].
SpamBayes tokenizes the header and body of each email before constructing token
spam scores. Robinson's method assumes that the presence or
absence of tokens in an email affect its spam status independently. For
each token ![]() , the raw token spam score
, the raw token spam score
Robinson smooths
![]() through a convex combination with
a prior belief
through a convex combination with
a prior belief ![]() , weighting the quantities by
, weighting the quantities by ![]() (the number of training
emails with
(the number of training
emails with ![]() ) and
) and ![]() (chosen for strength of prior), respectively:
(chosen for strength of prior), respectively:
For a new message ![]() , Robinson uses Fisher's method to combine the
spam scores of the most significant tokens3 into a message score
, Robinson uses Fisher's method to combine the
spam scores of the most significant tokens3 into a message score
The inclusion of an unsure category spam and ham prevents us from purely using misclassification rates (false positives and false negatives) for evaluation. We must also consider spam-as-unsure and ham-as-unsure emails. Because of the considerations in Section 2.1, unsure misclassifications of ham emails are nearly as bad for the user as false positives.
In a previous paper, we categorize attacks against machine learning systems along three axes [1]. For concreteness, we will describe the taxonomy in the context of spam filtering, but it applies readily to other security applications. The axes of the taxonomy are:

The first axis of the taxonomy describes the capability of the attacker: whether (a) the attacker has the ability to influence the training data that is used to construct the classifier (a Causative attack) or (b) the attacker does not influence the learned classifier, but can send new emails to the classifier, and observe its decisions on these carefully crafted emails (an Exploratory attack).
The second axis indicates the type of security violation caused: (a) to create false negatives, in which spam messages slip through the filter (an Integrity violation); or (b) to create false positives, in which ham messages are incorrectly filtered (an Availability violation).
The third axis refers to how specific the attacker's intention is: whether (a) the attack is Targeted to degrade the classifier's performance on one particular type of email or (b) the attack aims to cause the classifier to fail in an Indiscriminate fashion on a broad class of email.
Our focus is on Causative Availability attacks, which manipulate the filter's training data to increase false positives. We consider both Indiscriminate and Targeted attacks. In Indiscriminate attacks, enough false positives force the victim to disable the spam filter, or at least frequently search through spam/unsure folders to find legitimate messages that were filtered away. In either case, the victim is forced to view more spam. In Targeted attacks, the attacker does not disable the filter but surreptitiously prevents the victim from receiving certain types of email. For example, a company may wish to prevent its competitors from receiving email about a bidding process in which they are all competing.
Our first attack is an Indiscriminate attack. The idea is to send attack emails that contain many words likely to occur in legitimate email. When the victim trains SpamBayes with these attack emails marked as spam, the words in the attack emails will have higher spam score. Future legitimate email is more likely to be marked as spam if it contains words from the attack email.
When the attacker lacks knowledge about the victim's email, one simple attack is to include an entire dictionary of the English language. This technique is the basic dictionary attack. We use the GNU aspell English dictionary version 6.0-0, containing 98,568 words.
A further refinement uses a word source with distribution closer to the victim's email distribution. For example, a large pool of Usenet newsgroup postings may have colloquialisms, misspellings, and other ``words'' not found in a dictionary; furthermore, using the most frequent words in such a corpus may allow the attacker to send smaller emails without losing much effectiveness.
Our second attack--the focused attack--assumes knowledge of a specific legitimate email or type of email the attacker wants blocked by the victim's spam filter. This is a Causative Targeted Availability attack. In the focused attack, the attacker sends attack emails to the victim containing words likely to occur in the target email. When SpamBayes trains on this attack email, the spam scores of the targeted tokens increase, so the target message is more likely to be filtered as spam. For example, consider a malicious contractor wishing to prevent the victim from receiving messages with competing bids. The attacker sends spam emails to the victim with words such as the names of competing companies, their products, and their employees. The bid messages may even follow a common template, making the attack easier to craft.
The attacker may have different levels of knowledge about the target email. In the extreme case, the attacker might know the exact content of the target email and use all of its words. More realistically, the attacker only guesses a fraction of the email's content. In either case, the attack email may include additional words as well.
The focused attack is more concise than the dictionary attack because the attacker has detailed knowledge of the target and need not affect other messages.
The dictionary and focused attacks can be seen as two instances of a
common attack in which the attacker has different amounts of
knowledge about the victim's email.
Without loss of generality, suppose the attacker generates only a
single attack message
![]() . The victim adds it to the training set, trains, and classifies a
new message
. The victim adds it to the training set, trains, and classifies a
new message
![]() .
Both
.
Both
![]() and
and
![]() are indicator vectors,
where the
are indicator vectors,
where the
![]() component is true if word
component is true if word ![]() appears in the email.
The attacker also has some (perhaps limited)
knowledge of the next email the victim will receive. This
knowledge can be represented as a distribution
appears in the email.
The attacker also has some (perhaps limited)
knowledge of the next email the victim will receive. This
knowledge can be represented as a distribution
![]() --the
vector of
probabilities that each word appears in the next message.
--the
vector of
probabilities that each word appears in the next message.
The goal of the attacker is to choose an attack email
![]() that maximizes the expected spam score
that maximizes the expected spam score
![]() (Equation 3 with the attack message
(Equation 3 with the attack message
![]() in the spam training set) of the next legitimate email
in the spam training set) of the next legitimate email
![]() drawn from distribution
drawn from distribution
![]() ; that is,
; that is,
![]() In order to describe the optimal attacks under this criterion, we make two
observations. First, the spam scores of distinct words do
not interact; that is, adding a word
In order to describe the optimal attacks under this criterion, we make two
observations. First, the spam scores of distinct words do
not interact; that is, adding a word ![]() to the attack does not change the
score
to the attack does not change the
score ![]() of some different word
of some different word ![]() . Second, it can be shown that
. Second, it can be shown that
![]() is monotonically non-decreasing in each
is monotonically non-decreasing in each ![]() .
Therefore the best way to increase
.
Therefore the best way to increase
![]() is to include additional
words in the attack message.
is to include additional
words in the attack message.
Now let us consider specific choices for the next email's distribution
![]() .
First, if the attacker has little knowledge about the words
in target emails, we model this by setting
.
First, if the attacker has little knowledge about the words
in target emails, we model this by setting
![]() to be uniform
over all vectors
to be uniform
over all vectors
![]() representing emails.
We can optimize the expected spam score by
including all possible words in the attack email.
This optimal attack is infeasible in practice but
can be simulated:
one approximation includes all words in the victim's primary language,
such as an English dictionary. This yields the dictionary
attack.
representing emails.
We can optimize the expected spam score by
including all possible words in the attack email.
This optimal attack is infeasible in practice but
can be simulated:
one approximation includes all words in the victim's primary language,
such as an English dictionary. This yields the dictionary
attack.
Second, if the attacker has specific knowledge of a target email,
we can represent this by setting ![]() to 1 if and only if
the
to 1 if and only if
the
![]() word is in the target email.
The optimal attack still maximizes the expected spam score,
but a more compact attack that is also optimal
is to include all of the words in the target email.
This is the focused attack.
word is in the target email.
The optimal attack still maximizes the expected spam score,
but a more compact attack that is also optimal
is to include all of the words in the target email.
This is the focused attack.
The attacker's
knowledge usually falls between these extremes. For example,
the attacker may use information about the distribution of words
in English text to make the attack more efficient, such as
characteristic
vocabulary or jargon typical of the victim. Either of
these results in a distribution
![]() over words in the victim's email.
From this it should be possible to derive an optimal constrained
attack, but we leave this to future work.
over words in the victim's email.
From this it should be possible to derive an optimal constrained
attack, but we leave this to future work.
In our experiments we use the Text Retrieval Conference (TREC) 2005 spam corpus [4], which is based on the Enron email corpus [11] and contains 92,189 emails (52,790 spam and 39,399 ham). This corpus has several strengths: it comes from a real-world source, it has a large number of emails, and its creators took care that the added spam does not have obvious artifacts to differentiate it. We also use a corpus constructed from a subset of Usenet English postings to generate words for our attacks [18].
We restrict the attacker to have limited control over the headers of attack emails. We implement this assumption either by using the entire header from a randomly selected spam email from TREC (focused attack) or by using an empty header (all other attacks).
We measure the effect of each
attack by comparing classification performance of the control and
compromised filters using ![]() -fold cross-validation
(or
-fold cross-validation
(or ![]() repetitions with new random dataset samples in the case
of the focused attack).
In cross-validation, we partition the dataset into
repetitions with new random dataset samples in the case
of the focused attack).
In cross-validation, we partition the dataset into ![]() subsets and
perform
subsets and
perform ![]() train-test epochs. During the
train-test epochs. During the
![]() epoch,
the
epoch,
the
![]() subset is set aside as a test set and the remaining
subset is set aside as a test set and the remaining ![]() subsets are used for training. Each email
from our original dataset serves independently as both training and
test data.
subsets are used for training. Each email
from our original dataset serves independently as both training and
test data.
In the following sections, we show the effect of our attacks on test sets of held-out messages. Because our attacks are designed to cause ham to be misclassified, we only show their effect on ham messages; their effect on spam is marginal. Our graphs do not include error bars since we observed that the variation on our tests was small. See Table 1 for our experimental parameters.
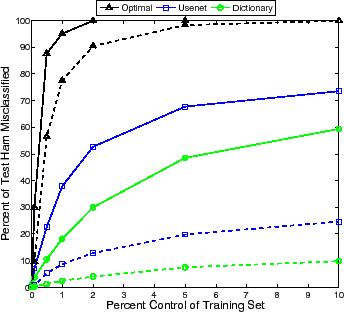
We examined dictionary attacks as a function of the percent of attack messages in the training set (see Figure 1). It shows the misclassification rates of three dictionary attack variants averaging over ten-fold cross-validation. The optimal attack quickly causes the filter to label all ham emails as spam. The Usenet dictionary attack (90,000 top ranked words from the Usenet corpus) causes significantly more ham emails to be misclassified than the Aspell dictionary attack, since it contains common misspellings and slang terms that are not present in the Aspell dictionary (the overlap between the Aspell and Usenet dictionaries is around 61,000 words). These variations of the attack require relatively few attack emails to significantly degrade the SpamBayes accuracy. By 101 attack emails (1% of 10,000), the accuracy falls significantly for each attack variation; at this point most users will gain no advantage from continued use of the filter.
To be fair, although the attack emails make up a small percentage of the number of messages in a poisoned inbox, they make up a large percentage of the number of tokens. For example, at 204 attack emails (2% of the messages), the Usenet attack includes approximately 6.4 times as many tokens as the original dataset and the Aspell attack includes 7 times. An attack with fewer tokens likely would be harder to detect; however, the number of messages is a more visible feature. It is of significant interest that so few attack messages can degrade a widely-deployed filtering algorithm to such a degree.
|
|
|
We run each repetition of the focused attack as follows. First we randomly select a ham email from the TREC corpus to serve as the target of the attack. We use a clean, non-malicious 5,000-message inbox with 50% spam. We repeat the entire attack procedure independently for 20 randomly-selected target emails.
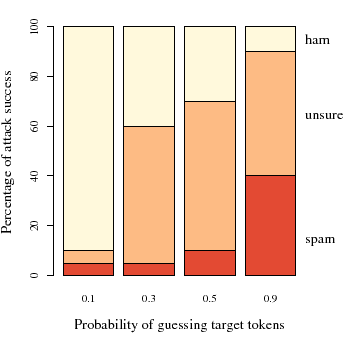
In Figure 2, we examine the effectiveness of the
attack when the attacker has increasing knowledge of the target
email by simulating the process of the attacker guessing tokens from
the target email. For this figure, there are 300 attack emails--16%
of the original number of training emails. We assume that the
attacker correctly guesses each word in the target with probability
![]() in
in
![]() --the
--the ![]() -axis of
Figure 2. The
-axis of
Figure 2. The ![]() -axis shows the proportion of the 20
targets classified as ham, unsure and spam. As
expected, the attack is increasingly effective as
-axis shows the proportion of the 20
targets classified as ham, unsure and spam. As
expected, the attack is increasingly effective as ![]() increases.
If the attacker guesses only 30% of the tokens in the
target, classification changes on 60% of the target emails.
increases.
If the attacker guesses only 30% of the tokens in the
target, classification changes on 60% of the target emails.
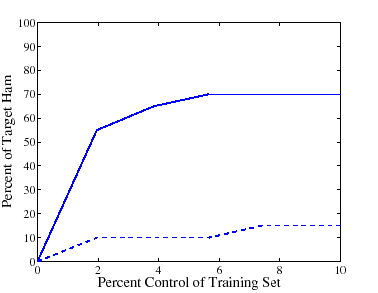
In Figure 3, we examine the attack's
effect on misclassifications of the targeted emails as the number of
attack messages increases.
In this
figure, we fix the probability of guessing each target token at 0.5.
The ![]() -axis is the number
of messages in the attack and the
-axis is the number
of messages in the attack and the ![]() -axis is the percent of messages misclassified.
With 100 attack emails, out of a initial mailbox size of 5,000, the
target email is misclassified 32% of the time.
-axis is the percent of messages misclassified.
With 100 attack emails, out of a initial mailbox size of 5,000, the
target email is misclassified 32% of the time.
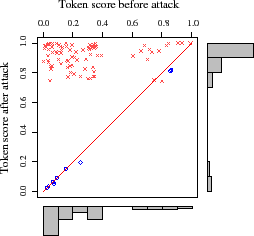
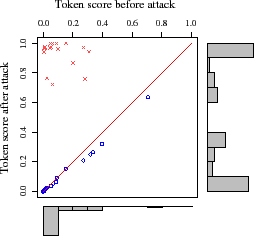
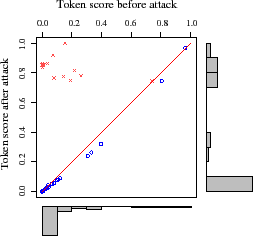
We find more insight by examining the attack's
effect on three representative emails (see Figure 4).
Each of the panels in the figure represents a single target email from
each of three attack results: ham misclassified as spam
(Left), ham misclassified as unsure (Middle), and
ham correctly classified as ham (Right).
Each point in the graph represents the before/after score of a token;
any point above the line ![]() increased due to the attack and any
point below is a decrease.
From these graphs it is clear that tokens included in the attack typically
increase significantly while those not included decrease slightly. Since
the increase in score is more significant for included tokens than the
decrease in score for excluded tokens, the attack has substantial impact
even when the attacker has a low probability of guessing tokens as seen in
Figure 2. Further, the before/after histograms in
Figure 4 provide a direct indicator of the attack's success.
increased due to the attack and any
point below is a decrease.
From these graphs it is clear that tokens included in the attack typically
increase significantly while those not included decrease slightly. Since
the increase in score is more significant for included tokens than the
decrease in score for excluded tokens, the attack has substantial impact
even when the attacker has a low probability of guessing tokens as seen in
Figure 2. Further, the before/after histograms in
Figure 4 provide a direct indicator of the attack's success.
|
Our Causative attacks work because training on attack emails causes the filter to learn incorrectly and misclassify emails. Each attack email contributes towards the degradation of the filter's performance; if we can measure each email's impact, then we can remove deleterious messages from the training set.
In the Reject On Negative Impact (RONI) defense, we measure the incremental effect of each
query email ![]() by testing the performance difference with and
without that email. We independently sample a 20-message training set
by testing the performance difference with and
without that email. We independently sample a 20-message training set ![]() and
a 50-message validation set
and
a 50-message validation set ![]() five times from the initial pool of emails
given to SpamBayes for training. We
train on both
five times from the initial pool of emails
given to SpamBayes for training. We
train on both ![]() and
and
![]() and measure the impact of each
query email as the average change in incorrect classifications
on
and measure the impact of each
query email as the average change in incorrect classifications
on ![]() over the five trials. We eliminate
over the five trials. We eliminate ![]() from training
if the impact is significantly negative. We
test with 120 random non-attack spam messages and 15 repetitions each
of seven variants of the dictionary attacks in
Section 3.2.
from training
if the impact is significantly negative. We
test with 120 random non-attack spam messages and 15 repetitions each
of seven variants of the dictionary attacks in
Section 3.2.
Preliminary experiments show that the RONI defense is extremely successful against dictionary attacks, identifying 100% of the attack emails without flagging any non-attack emails. Each dictionary attack message causes at least an average decrease of 6.8 ham-as-ham messages. In sharp contrast, non-attack spam messages cause at most an average decrease of 4.4 ham-as-ham messages. This clear region of separability means a simple threshold on this statistic is effective at separating dictionary attack emails from non-attack spam.
We plan to extend our initial experiments for the RONI defense with larger test sets along with a larger variation in the number of attack emails. Our initial small experiment, however, gives us confidence that this defense would work given a larger test set due to the large impact a small number of attack emails have on performance.
However, the RONI defense fails to differentiate focused attack emails from non-attack emails. The explanation is simple: the dictionary attack broadly affects emails, including training emails, while the focused attack is targeted at a future email, so its effects may not be evident on the training set alone.
Distribution-based attacks increase the spam score of ham email but
they also tend to increase the spam score of spam. Thus
with new
![]() thresholds, it may still be possible to
accurately distinguish between these kinds of messages after an attack.
Based on this hypothesis, we
propose and test a dynamic threshold defense, which dynamically
adjusts
thresholds, it may still be possible to
accurately distinguish between these kinds of messages after an attack.
Based on this hypothesis, we
propose and test a dynamic threshold defense, which dynamically
adjusts
![]() . With an adaptive
threshold scheme, attacks that shift all scores
will not be effective since rankings are invariant to such shifts.
. With an adaptive
threshold scheme, attacks that shift all scores
will not be effective since rankings are invariant to such shifts.
To determine dynamic values of ![]() and
and ![]() , we split
the full training set in half. We use one half to train a SpamBayes
filter
, we split
the full training set in half. We use one half to train a SpamBayes
filter ![]() and the other half as a validation set
and the other half as a validation set ![]() . Using
. Using
![]() , we obtain a score for each email in
, we obtain a score for each email in ![]() . From this information,
we can pick threshold values that more accurately separate
ham and spam emails. We define a utility function for choosing
threshold
. From this information,
we can pick threshold values that more accurately separate
ham and spam emails. We define a utility function for choosing
threshold ![]() ,
,
![]() ,
where
,
where
![]() is the number of spam emails with scores less than
is the number of spam emails with scores less than ![]() and
and
![]() is the number of ham emails with scores greater than
is the number of ham emails with scores greater than ![]() .
We select
.
We select ![]() so that
so that
![]() is 0.05 or 0.10, and we select
is 0.05 or 0.10, and we select
![]() so that
so that
![]() is 0.95 or 0.90, respectively.
is 0.95 or 0.90, respectively.
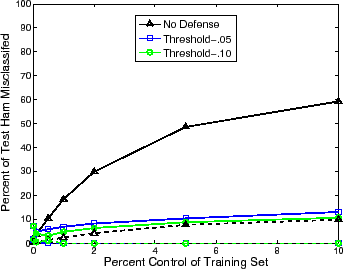
This defense shows some promise against the dictionary attacks in a preliminary experiment. As shown in Figure 5, the misclassification of ham emails is significantly reduced compared to SpamBayes alone. At all stages of the attack, ham emails are never classified as spam and only a moderate amount of them are labeled as unsure. However, while ham messages are often classified properly, the dynamic threshold causes almost all spam messages to be classified as unsure even when the attack is only 1% of the inbox. This shows that the dynamic threshold defense failed to adequately separate ham and spam given the number of spam also classified as unsure; we are exploring this defense under other choices of the thresholds.
|
Many authors have examined adversarial learning from a more
theoretical perspective. For example, within the Probably
Approximately Correct framework, Kearns and Li bound the
classification error an adversary that has control over a fraction
![]() of the training set can cause [9]. Dalvi
et al. apply game theory to the classification
problem [5]. They model interactions between
the classifier and attacker as a game and find the optimal
counter-strategy for the classifier against an optimal opponent.
of the training set can cause [9]. Dalvi
et al. apply game theory to the classification
problem [5]. They model interactions between
the classifier and attacker as a game and find the optimal
counter-strategy for the classifier against an optimal opponent.
In this paper we focus on Causative attacks. Most existing attacks against content-based spam filters are Exploratory attacks that do not influence training but engineer spam messages so they pass through the filter. For example, Lowd and Meek explore reverse-engineering a spam classifier to find high-value messages that the filter does not block [12,13], Karlberger et al. study the effect of replacing strong spam words with synonyms [8], and Wittel and Wu study the effect of adding common words to spam to get it through a spam filter [19].
Several others have recently developed Causative attacks against machine learning systems. Chung and Mok [2,3] present a Causative Availability attack against the Autograph worm signature generation system [10], which infers blocking rules based on patterns observed in traffic from suspicious nodes. The main idea is that the attack node first sends traffic that causes Autograph to mark it suspicious, then sends traffic similar to legitimate traffic, resulting in rules that cause denial of service.
Newsome, Karp, and Song [16] present attacks against Polygraph [15], a polymorphic virus detector that uses machine learning. They primarily focus on conjunction learners, presenting Causative Integrity attacks that exploit certain weaknesses not present in other learning algorithms (such as that used by SpamBayes). They also suggest a correlated outlier attack, which attacks a naive-Bayes-like learner by adding spurious features to positive training instances, causing the filter to block benign traffic with those features (a Causative Availability attack). They speculate briefly about applying such an attack to spam filters; however, several of their assumptions about the learner are not appropriate in the case of SpamBayes, such as that the learner uses only features indicative of the positive class. Furthermore, although they present insightful analysis, they do not evaluate the correlated outlier attack against a real system. Our attacks use similar ideas, but we develop and test them on a real system. We also explore the value of information to an attacker, and we present and test defenses against the attacks.
In this paper, we show that an adversary can effectively disable the SpamBayes spam filter with relatively little system state information and relatively limited control over training data. Our Usenet dictionary attack causes misclassification of 36% of ham messages with only 1% control over the training messages, rendering SpamBayes unusable. Our focused attack changes the classification of the target message 60% of the time with knowledge of only 30% of the target's tokens.
We also explore two successful defenses. The RONI defense filters out dictionary attack messages with complete success. The dynamic threshold defense also mitigates the effect of the dictionary attacks. Focused attacks are especially difficult to defend against because of the attacker's extra knowledge; developing effective defenses is an important open problem. In future work, we intend to continue refining our defenses.
Our attacks and defenses should also apply to other spam filtering systems based on similar learning algorithms, such as BogoFilter and the Bayesian component of SpamAssassin although their effect may vary. Similar techniques may also be effective against other learning systems, such as worm or intrusion detection.
We would like to thank Satish Rao, Carla Brodley, and our anonymous reviewers for their useful comments and suggestions on this research.
This work was supported in part by the Team for Research in Ubiquitous Secure Technology (TRUST), which receives support from the National Science Foundation (NSF award #CCF-0424422), the Air Force Office of Scientific Research (AFOSR #FA9550-06-1-0244), Cisco, British Telecom, ESCHER, Hewlett-Packard, IBM, iCAST, Intel, Microsoft, ORNL, Pirelli, Qualcomm, Sun, Symantec, Telecom Italia, and United Technologies; in part by California state Microelectronics Innovation and Computer Research Opportunities grants (MICRO ID#06-148 and #07-012) and Siemens; and in part by the cyber-DEfense Technology Experimental Research laboratory (DETERlab), which receives support from the Department of Homeland Security Homeland Security Advanced Research Projects Agency (HSARPA award #022412) and AFOSR (#FA9550-07-1-0501). The opinions expressed in this paper are solely those of the authors and do not necessarily reflect the opinions of any funding agency, the State of California, or the U.S. government.
This document was generated using the LaTeX2HTML translator Version 2002-2-1 (1.71)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 -show_section_numbers -local_icons -no_navigation leet08.tex
The translation was initiated by Blaine Nelson on 2008-04-08