Next: Related Work Up: The Case Study Previous: Model the asset-flow in

After encoding the relevant information of asset-flows, we specify security properties using LTL/CTL formulae. We use LTL (Linear Temporal Logic) to reason on the computational path scenarios of an asset (e.g., what can happen as asset travels along different locations) and CTL (Computational Tree Logic) to reason about the existence of specific states (e.g., is there any particular state in which an asset can be altered in an undesired way).
In the example we have shown (in the extended model), for instance, it is possible to implement at least three different attacks. The first one consists in replacing the software which is sent to the polling stations. By reading the key (or name it also password) with which the electionSW is encrypted and substituting a modified version of the software in the MemorySupport it is possible, for a malicious actor, to deliver a modified copy of the software to the polling station. The second one consists in replacing the PIN. A malicious actor with access to the PIN code may substitute the PIN which is loaded in the envelope and thus, have a wrong PIN delivered to the polling station (eventually causing a denial of service -- namely the voting functions cannot be activated by the polling officers). The third attack consists in deleting (or destroying) the envelope during transportation, possibly causing another denial of service.
Below we show two examples of properties that allows us to highlight such attacks.
i) Delivery of election software. In this example, we want
to check that: "It is never the case that poll officers receive an
altered version of the election software that can be run on the machines".
In other words, we want to verify that the procedures guarantee the integrity
of the software.
The property is specified in CTL as:
AG ! (sw.content = garbageSW && sw.location = pollStation && PollOfficersActive )
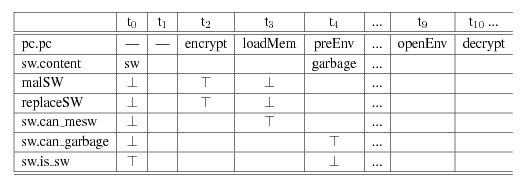
When checking the above property on the extended model with NuSMV, the property proves to be false -- namely, it is possible for an attacker to have delivered the wrong software to the polling stations . The generated counter-example is shown in Figure 7. The key point here is that, by having access to the password to encrypt the software and by being able to substitute the software before it is put in the envelope, a modified or useless version of the software can be delivered to the polling station (See 7 for the NuSMV counterexample in which the malSW and replaceSW variables set to true highlight the execution of threat actions).
The counter-example thus highlights a possible attack and the resources that are needed to carry the attack out. Based on this information, analysts can try and suggest possible counter-measures. In the example we have shown, the attacks can be performed by having access to two assets (password and election software), when the assets are under the responsibility of the Electoral Office. The information provided by the counter-example, thus, allows analysts to focus on what assets need to be protected or on where additional controls are more effective to detect the attack.
 |
ii) Denial of Service. In this case, we are interested in
checking whether a denial of service attack could happen in a polling station.
As an example, consider the following property: "It is never the case
that poll officers get the wrong PIN code". (Notice that the PINs are used
by poll officers to activate the voting machines and voting functions.) This
property is expressed in CTL formula as:
AG ! (PIN.can_garbage && PIN.location = pollStation)
We give the above property on the extended model to check that the property
holds. However, the tool generates the counter-example depicted
in Figure 8.
The attack is similar to the previous: during the preparation of the envelopes with software and PINs, a PIN is replaced with a wrong one, as shown by figure 8. Once again, the information can be used by analysts to devise counter-measures.
The examples, although trivial, show how -- by reasoning on
the extended model -- it is possible to explicitly represent the
attacks that can be carried out, determine what assets are needed by
the attackers and when, and who can carry the attacks.
Similarly to what happens in model checking, we do not provide any
quantitative information about the likelihood of the attacks. However,
even in this simple case, we believe that the output of the attacks can
provide experts the information and the requirements to enhance the
current procedures, to eliminate certain attacks or, at least, to make
them more difficult to implement.
komminist 2008-06-30