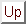|
|
Figure 4: Region intervals corresponding to the relational operators.
|



The key ingredient to an implementation of text constraints is choice of representation: how shall region sets be represented? One alternative is a bitvector, with one bit for each possible region in lexicographic order. With a bitvector representation, every region set requires O(n2) space, where n is the length of the document. Considering that the region sets generated by matchers and parsers typically have only O(n) elements, the bitvector representation wastes space. Another alternative represents a region set as a list of explicit pairs [b,e], which is more appropriate for sparse sets. Unfortunately the region sets generated by relational operators are not sparse. To choose a pathological example, after [0,0] matches every region in the document. In general, for any region relation op and region set S, the set matching op S may have O(n2) elements.
Other systems have dealt with this problem by restricting region sets to nested sets [19] or overlapped sets [5], sacrificing expressiveness for linear storage and processing. Instead of restricting region sets, we compress dense region sets with a representation called region intervals. A region interval is a quadruple [b,c;d,e], representing the set of all regions [x,y] such that b <= x <= c and d <= y <= e. Essentially, a region interval is a set of regions whose starts and ends are given by intervals, rather than points. A region interval is depicted by extending the region notation for regions (|--|), replacing the vertical lines denoting the region's endpoints with boxes denoting intervals.
A few facts about region intervals follow immediately from the definition:
Region intervals are particularly useful for representing the result of applying a region relation operator. Given any region X and a region relation op, the set of regions which are related to X by op can be represented by exactly one region interval, as shown in Figure 4.

|
|
Figure 4: Region intervals corresponding to the relational operators.
|
This result extends to region intervals as well: applying a region relation operator to a region interval yields exactly one region interval. For example, the result of before [b,c;d,e] is the set of all regions which lie before some region in [b,c;d,e]. Assuming the region interval is nonempty, every region ending at or before c qualifies, so the result of this operator can be described by the region interval [0,c;0,c]. We can represent an arbitrary region set by a union of region intervals, which is simply a collection of tuples. The size of this collection may still be O(n2) in the worst case (consider, for example, the set of all regions [b,e] of even length, which must be represented by O(n2) singleton region intervals), but most collections are O(n) in practice.
To summarize, the union-of-region-intervals representation enables a straightforward implementation of the text constraints language: