|
| |||||||||||||||||||||||||||||||||||||||||||||||||||

| ||||||||||||||||||||||||||||||||||||||||||||||||||||
|
USENIX '04 Paper
[USENIX '04 Technical Program]
Handling Churn in a DHTSean Rhea, Dennis Geels, Timothy Roscoe,
and John Kubiatowicz Abstract:This paper addresses the problem of churn--the continuous process of node arrival and departure--in distributed hash tables (DHTs). We argue that DHTs should perform lookups quickly and consistently under churn rates at least as high as those observed in deployed P2P systems such as Kazaa. We then show through experiments on an emulated network that current DHT implementations cannot handle such churn rates. Next, we identify and explore three factors affecting DHT performance under churn: reactive versus periodic failure recovery, message timeout calculation, and proximity neighbor selection. We work in the context of a mature DHT implementation called Bamboo, using the ModelNet network emulator, which models in-network queuing, cross-traffic, and packet loss. These factors are typically missing in earlier simulation-based DHT studies, and we show that careful attention to them in Bamboo's design allows it to function effectively at churn rates at or higher than that observed in P2P file-sharing applications, while using lower maintenance bandwidth than other DHT implementations.
|
 |
In this section we present a brief review of DHT routing, using Pastry [24] as an example. The geometry and routing algorithm of Bamboo are identical to Pastry; the difference (and the main contribution of this paper) lies in how Bamboo maintains the geometry as nodes join and leave the network and the network conditions vary.
DHTs are structured graphs, and we use the term geometry to mean the pattern of neighbor links in the overlay network, independent of the routing algorithms or state management algorithms used [12].
Each node in Pastry is assigned a numeric identifier in
![]() , derived either from the SHA-1
hash of the IP address and port on which the node receives packets
or from the SHA-1 hash of a public key. As such, they are
well-distributed throughout the identifier space.
, derived either from the SHA-1
hash of the IP address and port on which the node receives packets
or from the SHA-1 hash of a public key. As such, they are
well-distributed throughout the identifier space.
In Pastry, a node maintains two sets of neighbors, the leaf
set and the routing table (see Figure 1). A node's leaf set is the set
of ![]() nodes immediately preceding and following
it in the circular identifier space. We denote this set by
nodes immediately preceding and following
it in the circular identifier space. We denote this set by
![]() , and we use the notation
, and we use the notation ![]() with
with ![]() to denote the members of
to denote the members of
![]() , where
, where ![]() is the
node itself.
is the
node itself.
In contrast, the routing table is a set of nodes whose
identifiers share successively longer prefixes with the source
node's identifier. Treating each identifier as a sequence of digits
of base ![]() and denoting the routing table
entry at row
and denoting the routing table
entry at row ![]() and column
and column ![]() by
by ![]() , a node chooses its
neighbors such that the entry at
, a node chooses its
neighbors such that the entry at ![]() is a
node whose identifier matches its own in exactly
is a
node whose identifier matches its own in exactly ![]() digits and whose
digits and whose ![]() th digit is
th digit is
![]() . In the experiments in this paper,
Bamboo uses binary digits (
. In the experiments in this paper,
Bamboo uses binary digits (![]() ), though it
can be configured to use any base.
), though it
can be configured to use any base.
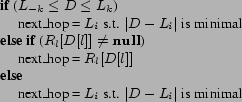
|
The basic operation of a DHT is to consistently map identifiers
onto nodes from any point in the system, a function we call
routing or lookup. Pastry achieves consistent lookups
by directing each identifier to the node with the numerically
closest identifier. Algorithmically, routing proceeds as shown in
Figure 2. To
route a message with key ![]() , a node first checks whether
, a node first checks whether
![]() lies within its leaf set, and if so, forwards
it to the numerically closest member of that set (modulo
lies within its leaf set, and if so, forwards
it to the numerically closest member of that set (modulo
![]() ). If that member is the local
node, routing terminates. If
). If that member is the local
node, routing terminates. If ![]() does not
fall within the leaf set, the node computes the length
does not
fall within the leaf set, the node computes the length
![]() of the longest matching prefix between
of the longest matching prefix between
![]() and its own identifier. Let
and its own identifier. Let ![]() denote the
denote the ![]() th digit of
th digit of
![]() . If
. If ![]() is
not empty, the message is forwarded on to that node. If
neither of these conditions is true, the message is forwarded
to the member of the node's leaf set numerically closest to
is
not empty, the message is forwarded on to that node. If
neither of these conditions is true, the message is forwarded
to the member of the node's leaf set numerically closest to
![]() . Once the destination node is reached,
it sends a message back to the originating node with its
identifier and network address, and the lookup is
complete.
. Once the destination node is reached,
it sends a message back to the originating node with its
identifier and network address, and the lookup is
complete.
We note that a node can often choose between many different
neighbors for a given entry in its routing table. For example, a
node whose identifier begins with a ![]() needs a
neighbor whose identifier begins with a
needs a
neighbor whose identifier begins with a ![]() , but such
nodes make up roughly half of the total network. In such
situations, a node can choose between the possible candidates
based on some metric. Proximity neighbor selection is
the term used to indicate that nodes in a DHT use network
latency as the metric by which to choose between neighbor
candidates.
, but such
nodes make up roughly half of the total network. In such
situations, a node can choose between the possible candidates
based on some metric. Proximity neighbor selection is
the term used to indicate that nodes in a DHT use network
latency as the metric by which to choose between neighbor
candidates.
 |
 |
Using this design, Pastry and Bamboo perform lookups in
![]() hops [24], while the leaf set allows forward
progress (in exchange for potentially longer paths) in the case
that the routing table is incomplete. Moreover, the leaf set adds a
great deal of static resilience to the geometry; Gummadi et
al. [12] show that with a
leaf set of 16 nodes, even after a random 30% of the links are
broken there are still connected paths between all node pairs in a
network of 65,536 nodes. This resilience is important in handling
failures in general and churn in particular, and was the reason we
chose the Pastry geometry for use in Bamboo. We could also have
used a pure ring geometry as in Chord, extending it to account for
proximity in neighbor selection as described in [12].
hops [24], while the leaf set allows forward
progress (in exchange for potentially longer paths) in the case
that the routing table is incomplete. Moreover, the leaf set adds a
great deal of static resilience to the geometry; Gummadi et
al. [12] show that with a
leaf set of 16 nodes, even after a random 30% of the links are
broken there are still connected paths between all node pairs in a
network of 65,536 nodes. This resilience is important in handling
failures in general and churn in particular, and was the reason we
chose the Pastry geometry for use in Bamboo. We could also have
used a pure ring geometry as in Chord, extending it to account for
proximity in neighbor selection as described in [12].
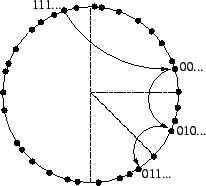
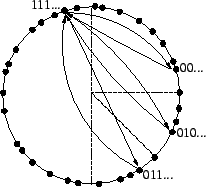
The manner in which we have described routing so far is commonly called recursive routing (Figure 3). In contrast, lookups may also be performed iteratively. As shown in Figure 4, an iterative lookup involves the same nodes as a recursive one, but the entire process is controlled by the source of the lookup. Rather than asking a neighbor to forward the lookup through the network on its behalf, the source asks that neighbor for the network address of the next hop. The source then asks the newly-discovered node the same question, repeating the process until no further progress can be made, at which point the lookup is complete.
|
There have been very few large-scale DHT-based application deployments to date, and so it is hard to derive good requirements on churn-resilience. However, P2P file-sharing networks provide a useful starting point. These systems provide a simple indexing service for locating files on those peer nodes currently connected to the network, a function which can be naturally mapped onto a DHT-based mechanism. For example, the Overnet file-sharing system uses the Kademlia DHT to store such an index. While some DHT applications (such as file storage as in CFS [10]) might require greater client availability, others may show similar churn rates to file-sharing networks (such as end-system multicast or a rendezvous service for instant messaging). As such, we believe that DHTs should at least handle churn rates observed in today's file-sharing networks. To that end, in this section we survey existing studies of churn in deployed file-sharing networks, describe the way we model such churn in our emulated network, and quantify the performance of mature DHT implementations under such churn.
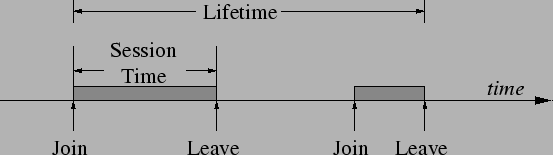
Studies of existing file-sharing systems mainly use two metrics of churn (see Figure 5). A node's session time is the elapsed time between it joining the network and subsequently leaving it. In contrast, a node's lifetime is the time between it entering the network for the first time and leaving the network permanently. The sum of a node's session times divided by its lifetime is often called its availability. One representative study [5] observed median session times on the order of tens of minutes, median lifetimes on the order of days, and median availability of around 30%.
With respect to the lookup functionality of a DHT, we argue that session time is the most important metric. Even temporary loss of a routing neighbor weakens the correctness and performance guarantees of a DHT, and unavailable neighbors reduce a node's effective connectivity, forcing it to choose suboptimal routes and increasing the destructive potential of future failures. Since nodes are often unavailable for long periods, remembering neighbors that have failed is of little value in performing lookups. While remembering neighbors is useful for applications like storage [6], it is of little value for lookup operations.
Elsewhere [23] we have surveyed published studies of deployed file-sharing networks. Table 1 shows a summary of observed session times. At first sight, some of these values are surprising, and may be due to methodological problems with the study in question or malfunctioning of the system under observation. However, it is easy to image a user joining the network, downloading a single file (or failing to find it), and leaving, making session times of a few minutes at least plausible. To be conservative, then, we would like a DHT to be robust for median session times from as much as an hour to as little as a minute.
Our platform for measuring DHT performance under churn is a cluster of 40 IBM xSeries PCs, each with Dual 1GHz Pentium III processors and 1.5GB RAM, connected by Gigabit Ethernet, and running either Debian GNU/Linux or FreeBSD. We use ModelNet [28] to impose wide-area delay and bandwidth restrictions, and the Inet topology generator [3] to create a 10,000-node wide-area AS-level network with 500 client nodes connected to 250 distinct stubs by 1 Mbps links. To increase the scale of the experiments without overburdening the capacity of ModelNet by running more client nodes, each client node runs two DHT instances, for a total of 1,000 DHT nodes.
Our control software uses a set of wrappers which communicate locally with each DHT instance to send requests and record responses. Running 1000 DHT instances on this cluster (12.5 nodes/CPU) produces CPU loads below one, except during the highest churn rates. Ideally, we would measure larger networks, but 1000-node systems already demonstrate problems that will surely affect larger ones.
In an experiment, we first bring up a network of 1000 nodes, one
every 1.5 seconds, each with a randomly assigned gateway node to
distribute the load of bootstrapping newcomers. We then churn nodes
until the system performance levels out; this phase normally lasts
20-30 minutes but can take an hour or more. Node deaths are timed
by a Poisson process and are therefore uncorrelated and bursty. A
new node is started each time one is killed, maintaining the total
network size at 1000. This model of churn is similar to that
described by Liben-Nowell et all [17]. In a Poisson process, an event rate
![]() corresponds to a median inter-event
period of
corresponds to a median inter-event
period of ![]() . For each event we
select a node to die uniformly at random, so each node's
session time is expected to span
. For each event we
select a node to die uniformly at random, so each node's
session time is expected to span ![]() events,
where
events,
where ![]() is the network size. Therefore a
churn rate of
is the network size. Therefore a
churn rate of ![]() corresponds to a
median node session time of
corresponds to a
median node session time of
Each live node continually performs lookups for identifiers chosen uniformly at random, timed by a Poisson process with rate 0.1/second, for an aggregate system load of 100 lookups/second. Each lookup is simultaneously performed by ten nodes, and we report both whether it completes and whether it is consistent with the others for the same key. If there is a majority among the ten results for a given key, all nodes in the majority are said to see a consistent result, and all others are considered inconsistent. If there is no majority, all nodes are said to see inconsistent results. This metric of consistency is more strict than that required by some DHT applications. However, both MIT's Chord and our Bamboo implementation show at least 99.9% consistency under 47-minute median session times [23], so it does not seem unreasonable.
There are two ways in which lookups fail in our tests. First, we do not perform end-to-end retries, so a lookup may fail to complete if a node in the middle of the lookup path leaves the network before forwarding the lookup request to the next node. We observed this behavior primarily in FreePastry as described below. Second, a lookup may return inconsistent results. Such failures occur either because a node is not aware of the correct node to forward the lookup to, or because it erroneously believes the correct node has left the network (because of congestion or poorly chosen timeouts). All DHT implementations we have tested show some inconsistencies under churn, but carefully chosen timeouts and judicious bandwidth usage can minimize them.
In this section we report the results of testing two mature DHT implementations under churn. Our intent here is not to place a definitive bound on the performance of either implementation. Rather, it is to motivate our work by demonstrating that handling churn in DHTs is both an important and a non-trivial problem. While we have discussed these experiments extensively with the authors of both systems, it is still possible that alternative configurations could have improved their performance. Moreover, both systems have seen subsequent development, and newer versions may show improved resilience under churn.
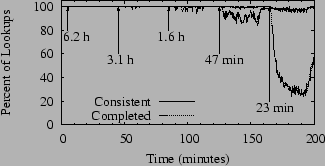 |
It is clear from Figure 6 that while successful lookups are mostly consistent, FreePastry fails to complete a majority of lookup requests under heavy churn. A likely explanation for this failure is that nodes wait so long on lookup requests to time out that they frequently leave the network with several requests still in their queues. This behavior is probably exacerbated by FreePastry's use of Java RMI over TCP as its message transport, and the way that FreePastry nodes handle the loss of their neighbors. We present evidence to support these ideas in Section 4.1.
We make a final comment on this graph. FreePastry generally recovers well between churn periods, once again correctly completing all lookups. The difficulty with real systems is that there is no such quiet period; the network is in a continual state of churn.
 |
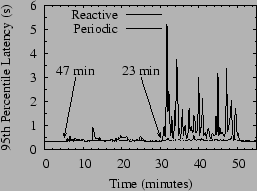
In contrast to FreePastry, almost all lookups in a Chord network complete and return consistent results. Chord's shortcoming under churn is in lookup latency, as shown in Figure 7, which shows the result of running Chord under the same workload as shown in Figure 6, but where we have averaged the lookup latency over each churn period. Shown for comparison are two lines representing Bamboo's performance in the same test, with and without proximity neighbor selection (PNS). Under all churn rates, Bamboo is using slightly under 750 bytes per second per node, while Chord is using slightly under 2,400.
We discuss in detail the differences that enable Bamboo to outperform Chord in Sections 4.2 and 4.3, but some of the difference in latency between Bamboo and Chord is due to their routing styles. Bamboo performs lookups recursively, whereas Chord routes iteratively. Chord could easily be changed to route recursively; in fact, newer versions of Chord support both recursive routing and PNS. Note, however, that Chord's latency grows more quickly under increasing churn than does Bamboo's. In Section 4.2, we will show evidence to support our belief that this growth is due to Chord's method of choosing timeouts for lookup messages and is independent of the lookup style employed.
To summarize this section, we note that we have observed several effects of churn on existing DHT implementations. A DHT may fail to complete lookup requests altogether, or it may complete them but return inconsistent results for the same lookup launched from different source nodes. On the other hand, a DHT may continue to return consistent results as churn rates increase, but it may suffer from a dramatic increase in lookup latency in the process.
Having briefly described the way in which DHTs perform lookups, and having given evidence indicating that their ability to do so is hindered under churn, we now turn to the heart of this paper: a study of the factors contributing to this difficulty, and a comparison of solutions that can be used to overcome them. In turn, we discuss reactive versus periodic recovery from neighbor failure, the calculation of good timeout values for lookup messages, and techniques to achieve proximity in neighbor selection. The remainder of this paper focuses only on the Bamboo DHT, in which we have implemented each alternative design choice studied here. Working entirely within a single implementation allows us to minimize the differences between experiments comparing one design choice to another.
 |
Early implementations of Bamboo suffered performance degradation under churn similar to that of FreePastry. MIT Chord's performance, however, does not degrade in the same way. A significant difference in its behavior is a design choice about how to handle detected node failures. We will call the two alternative approaches reactive and periodic recovery.
Reactive recovery runs the risk of creating a positive feedback cycle as follows. Consider a node whose access link to the network is sufficiently congested that timeouts cause it to believe that one of its neighbors has failed. If the node is recovering reactively, recovery operations begin, and the node will add even more packets to its already congested network link. This added congestion will increase the likelihood that the node will mistakenly conclude that other neighbors have failed. If this process continues, the node will eventually cause congestion collapse on its access link.
Observations of these cycles in early Bamboo (and examination of the Chord code) originally led us to propose periodic recovery for handling churn. By decoupling the rate of recovery from the discovery of failures, periodic recovery prevents the feedback cycle described above. Moreover, by lengthening the recovery period with the observation of message timeouts, we can introduce a negative feedback cycle, further improving resilience.
Another way to mitigate the instability associated with reactive recovery is to be more conservative when detecting node failure. We have found one effective approach to be to conclude failure only after 15 consecutive message timeouts to a neighbor. Since timeouts are backed off multiplicatively to a maximum of five seconds, it is unlikely that a node will conclude failure due to congestion. One drawback with this technique, however, is that neighbors that have actually failed remain in a node's routing table for some time. Lookups that would route through these neighbors are thus delayed, resulting in long lookup latencies. To remedy this problem, a node stops routing through a neighbor after seeing five consecutive message timeouts to that neighbor. We have found these changes make reactive recovery feasible for small leaf sets and moderate churn.
Experiments show little difference in correctness between
periodic and reactive recovery. To see why, consider a node
![]() that joins a network, and let
that joins a network, and let ![]() be the node in the existing network whose identifier
most closely matches that of
be the node in the existing network whose identifier
most closely matches that of ![]() . As in
Pastry,
. As in
Pastry, ![]() retrieves its initial leaf set by
contacting
retrieves its initial leaf set by
contacting ![]() , and
, and ![]() adds
adds
![]() to its leaf set immediately after
confirming its IP address and port (with a probe message).
Until
to its leaf set immediately after
confirming its IP address and port (with a probe message).
Until ![]() 's arrival propagates through the
network, another node
's arrival propagates through the
network, another node ![]() may still route
messages that should go to
may still route
messages that should go to ![]() to
to ![]() instead, but
instead, but ![]() will just forward these
messages on to
will just forward these
messages on to ![]() . Likewise, should
. Likewise, should
![]() fail,
fail, ![]() will still be in
will still be in
![]() 's leaf set, so once routing messages to
's leaf set, so once routing messages to
![]() time out,
time out, ![]() and other
nearby nodes will generally all agree that
and other
nearby nodes will generally all agree that ![]() is the next best choice.
is the next best choice.
While both periodic and reactive recovery achieve roughly identical correctness, there is a large difference in the bandwidth consumed under different churn rates and leaf set sizes. (A commonly accepted rule of thumb is that to provide sufficient resilience to massive node failure, the size of a node's leaf set should be logarithmic in the system size.) Under low churn, reactive recovery is very efficient, as messages are only sent in response to actual changes, whereas periodic recovery is wasteful. As churn increases, however, reactive recovery becomes more expensive, and this behavior is exacerbated by increasing leaf set size. Not only does a node see more failures when its leaf set is larger, but the set of other nodes it must notify about the resulting changes in its own leaf set is larger. In contrast, periodic recovery aggregates all changes in each period into a single message.
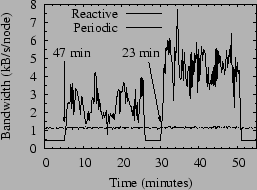
Figure 8 shows this contrast in Bamboo using leaf sets of 24 nodes, the default leaf set size in FreePastry. In this figure, we ran Bamboo using both configurations for two 20-minute churn periods of 47 and 23 minute median session times separated by five minutes with no churn.
We note that during the periods of the test where there is no churn, reactive recovery uses less than half of the bandwidth of periodic recovery. On the other hand, under churn its bandwidth use jumps dramatically. As discussed above, Bamboo does not suffer from positive feedback cycles on account of this increased bandwidth usage. Nevertheless, the extra messages sent by reactive recovery compete with lookup messages for the available bandwidth, and as churn increases we see a corresponding increase in lookup latency. Although not shown in the figure, the number of hops per lookup is virtually identical between the two schemes, implying that the growth in bandwidth is most likely due to contention for the available bandwidth.
Since our goal is to handle median session times down to a few minutes with low lookup latency, we do not explore reactive recovery further in this work. The remainder of the Bamboo results we present are all obtained using periodic recovery.
In this section, we discuss the role that timeout calculation on lookup messages plays in handling churn.
To understand the relative importance of timeouts in a DHT as opposed to a more traditional networked system, consider a traditional client-server system such as the networked file system (NFS). In NFS, the server does not often fail, and when it does there are generally few options for recovery and no alternative servers to fail over to. If a response to an NFS request is not received in the expected time, the client will usually try again with an exponentially increasing timeout value.
In a peer-to-peer system under churn, in contrast, requests will be frequently sent to a node that has left the system, possibly forever. At the same time, a DHT with routing flexibility (static resilience) has many alternate paths available to complete a lookup. Simply backing off the request period is thus a poor response to a request timeout; it is often better to retry the request through a different neighbor.
A node should ensure that the timeout for a request was judiciously selected before routing to an alternate neighbor. If it is too short, the node to which the original was sent may be yet to receive it, may be still processing it, or the response may be queued in the network. If so, injecting additional requests may result in the use of additional bandwidth without any beneficial result--for example, in the case that the local node's access link is congested. Conversely, if the timeout is too long, the requesting node may waste time waiting for a response from a node that has left the network. If the request rate is fixed at too low a value, these long waits cause unbounded queue growth on the request node that might be avoided with shorter timeouts.
For these reasons, nodes should accurately choose timeouts such that a late response is indicative of node failure, rather than network congestion or processor load.
We discuss and study three alternative timeout calculation strategies. In the first, we fix all timeouts at a conservative value of five seconds as a control experiment. In the second, we calculate TCP-style timeouts using direct measurement of past response times. Finally, we explore using indirect measurements from a virtual coordinate algorithm to calculate timeouts.
Virtual coordinates provide one approach to computing timeouts without previously measuring the response time to every node in the system. In this scheme, a distributed machine learning algorithm is employed to assign to each node coordinates in a virtual metric space such that the distance between two nodes in the space is proportional to their latency in the underlying network.
Bamboo includes an implementation of the Vivaldi coordinate
system employed by Chord [11]. Vivaldi keeps an
exponentially-weighted average of the error of past round-trip
times calculated with the coordinates, and computes the RTO
as
TCP-style timeouts assume a recursive routing algorithm, and a virtual coordinate system is necessary only when routing iteratively. While we would ideally compare the two approaches by measuring each in its intended environment, this would prevent us from isolating the effect of timeouts from the differences caused by routing styles.
Instead, we study both schemes under recursive routing. If timeouts calculated with virtual coordinates provide performance comparable to those calculated in the TCP-style under recursive routing, we can expect the virtual coordinate scheme to not be prohibitively expensive under iterative routing. While other issues may remain with iterative routing under churn (e.g. congestion control--see Section 6), this result would be a useful one.
|
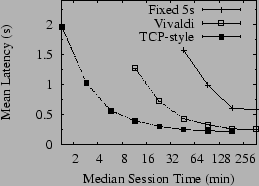
Figure 9 shows a direct comparison of the three timeout calculation methods under increasing levels of churn. In all cases in this experiment, the Bamboo configurations differed only in choice of timeout calculation method. Proximity neighbor selection was used, but the latency measurements for PNS used separate direct probing and not the virtual coordinates.
Even under light levels of churn, fixing all timeouts at five seconds causes lookup timeouts to pull the mean latency up to more than twice that of the other configurations, confirming our intuition about the importance of good timeout values in DHT routing under churn. Moreover, by comparing Figure 9 to Figure 7, we note that under high churn timeout calculation has a greater effect on lookup latency than the use of PNS.
Virtual coordinate-based timeouts achieve very similar mean latency to TCP-style timeouts at low churn. Furthermore, they perform within a factor of two of TCP-style measurements until the median churn rate drops to 23 minutes. Past this point, their performance quickly diverges, but virtual coordinates continue to provide mean lookup latencies under two seconds down to twelve-minute median session times.
Finally, we note the similarity in shape of Figure 9 to Figure 7, where we compared the performance of Chord to Bamboo, suggesting that the growth in lookup latency under Chord at high churn rates is due to timeout calculation based on virtual coordinates.
Perhaps one of the most studied aspects of DHT design has been
proximity neighbor selection (PNS), the process of choosing among
the potential neighbors for any given routing table entry according
to their network latency to the choosing node. This research is
well motivated. The stretch of a lookup operation is defined
as the latency of the lookup divided by the round-trip time between
the lookup source and the node discovered by the lookup in the
underlying IP network. Dabek et al. present an argument and
experimental data that suggest that PNS allows a DHT of
![]() nodes to achieve median stretch of only
1.5, independent of the size of the network and despite using
nodes to achieve median stretch of only
1.5, independent of the size of the network and despite using
![]() hops [11]. Others have proved that PNS
can be used to provide constant stretch in locating replicas
under a restricted network model [21]. This is the first study of
which we are aware, however, to compare methods of achieving
PNS under churn. We first take a moment to discuss the common
philosophy and techniques shared by each of the algorithms we
study.
hops [11]. Others have proved that PNS
can be used to provide constant stretch in locating replicas
under a restricted network model [21]. This is the first study of
which we are aware, however, to compare methods of achieving
PNS under churn. We first take a moment to discuss the common
philosophy and techniques shared by each of the algorithms we
study.
One of the earliest insights in DHT design was the separation of
correctness and performance in the distinction between neighbors in
the leaf set and neighbors in the routing table [24,27]. So long as the leaf sets in the
system are correct, lookups will always return correct results,
although they may take ![]() hops to do so. Leaf set
maintenance is thus given priority over routing table maintenance
by most DHTs. In the same manner, we note that so long as each
entry in the routing table has some appropriate neighbor
(i.e. one with the correct identifier prefix), lookups will
always complete in
hops to do so. Leaf set
maintenance is thus given priority over routing table maintenance
by most DHTs. In the same manner, we note that so long as each
entry in the routing table has some appropriate neighbor
(i.e. one with the correct identifier prefix), lookups will
always complete in ![]() hops, even though
they make take longer than if the neighbors had been chosen for
proximity. We say such lookups are efficient, even though
they may not have low stretch. By this argument, we reason that it
is desirable to fill a routing table entry quickly, even with a
less than optimal neighbor; finding a nearby neighbor is a lower
priority.
hops, even though
they make take longer than if the neighbors had been chosen for
proximity. We say such lookups are efficient, even though
they may not have low stretch. By this argument, we reason that it
is desirable to fill a routing table entry quickly, even with a
less than optimal neighbor; finding a nearby neighbor is a lower
priority.
There is a further argument to treating proximity as a lower priority in the presence of churn. Since we expect our set of neighbors to change over time as part of the churn process, it makes little sense to work too hard to find the absolute closest neighbor at any given time; we might expend considerable bandwidth to find them only to see them leave the network shortly afterward. As such, our general approach is to run each of the algorithms described below periodically. In the case where churn is high, this technique allows us to retune the routing table as the network changes. When churn is low, rerunning the algorithms makes up for latency measurement errors caused by transient network conditions in previous runs.
Our general approach to finding nearby neighbors thus takes the following form. First, we use one of the algorithms below to find nodes that may be near to the local node. Next, we measure the latency to those nodes. If we have no existing neighbor in the routing table entry that the measured node would fill, or if it is closer than the existing routing table entry, we replace that entry, otherwise we leave the routing table unchanged. Although the bandwidth cost of multiple measurements is high, the storage cost to remember past measurements is low. As a compromise, we perform only a single latency measurement to each discovered node during any particular run of an algorithm, but we keep an exponentially weighted average of past measurements for each node, and we use this average value in deciding the relative closeness of nodes. This average occupies only eight bytes of memory for each measured node, so we expect this approach to scale comfortably to very large systems.
The techniques for proximity neighbor selection that we study here are global sampling, sampling of our neighbors' neighbors, and sampling of the nodes that have our neighbors as their neighbors. We describe each of these techniques in turn.
There are some cases, however, where global sampling will take unreasonably long to find the closest possible neighbor. For example, consider two nodes separated from the core Internet by the same, high latency access link, as shown in Figure 11. The relatively high latency seen by these two nodes to all other nodes in the network makes them attractive neighbors for each other; if they have different first digits in a network with logarithm base two, they can drastically reduce the cost of the first hop of many routes by learning about each other. However, the time for these nodes to find each other using global sampling is proportional to the size of the total network, and so they may not find each other before their sessions end. It is this drawback of global sampling that leads us to consider other techniques.
 |
The motivation for sampling neighbors' neighbors is illustrated in Figure 10; it relies on the expectation that proximity in the network is roughly transitive. If a node discovers one nearby node, then that node's neighbors are probably also nearby. In this way, we expect that a node can ``walk'' through the graph of neighbor links to the set of nodes most near it.
 |
To see one possible shortcoming of sampling our neighbors' neighbors, consider again Figure 11. While the two isolated nodes would like to discover each other, it is unlikely that any other nodes in the network would prefer them as neighbors; their isolation makes them unattractive for routing lookups that originate elsewhere, except in the rare case that they are the result of those lookups. As such, since neighbor links in DHTs are rarely symmetric, it is unlikely that there is a path through the graph of neighbor links that will lead one isolated node to the other, despite their relative proximity.
Normally, a DHT node would not record the set of nodes that use it as a neighbor. Actively managing such a list, in fact, requires additional probing bandwidth. Currently, the Bamboo implementation does actively manage this set, but it could be easily approximated at each node by keeping track of the set of nodes which have sent it liveness probes in the last minute or so. We plan to implement this optimization in our future work.
|
To remedy this final problem, we can perform the sampling of
nodes in a manner similar to that used by the Tapestry nearest
neighbor algorithm (and the Pastry optimized join algorithm).
Pseudo-code for this technique is shown in Figure 12. Starting with the highest
level ![]() in its routing table, a node
contacts the neighbors at that level and retrieves their
neighbors (or inverse neighbors). The latency to each newly
discovered nodes is measured, and all but the
in its routing table, a node
contacts the neighbors at that level and retrieves their
neighbors (or inverse neighbors). The latency to each newly
discovered nodes is measured, and all but the ![]() closest are discarded. The node then decrements
closest are discarded. The node then decrements
![]() and retrieves the level-
and retrieves the level-![]() neighbors from each non-discarded node. This process is
repeated until
neighbors from each non-discarded node. This process is
repeated until ![]() . Along the way,
each discovered neighbor is considered as a candidate for use
in the routing table. To keep the cost of this algorithm low,
we limit it to having at most three outstanding messages
(neighbor requests or latency probes) at any time.
. Along the way,
each discovered neighbor is considered as a candidate for use
in the routing table. To keep the cost of this algorithm low,
we limit it to having at most three outstanding messages
(neighbor requests or latency probes) at any time.
Note that although this process starts by sampling from the routing table, the set of nodes on which it recurses is not constrained by the prefix-matching structure of that table. As such, it does not suffer from the small rendezvous set problem discussed above. In fact, under certain network assumptions, it has been proved that this process finds a node's nearest neighbor in the underlying network.
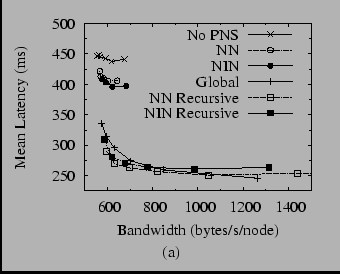
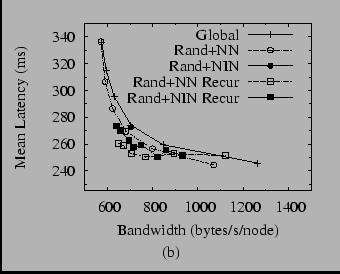
In order to compare the techniques described above, it is important to consider not only effective they are at finding nearby neighbors, but also at what bandwidth cost they do so. For example, global sampling at a high enough rate relative to the churn rate would achieve perfect proximity, but at the cost of a very large number of lookups and latency probes. To make this comparison, then, we ran each algorithm (and some combinations of them) at various periods, then plotted the mean lookup latency under churn versus bandwidth used. The results for median session times of 47 minutes are shown in Figure 13, which is split into two graphs for clarity.
Figure 13(a) shows several interesting results. First, we note that only a little bit of global sampling is necessary to produce a drastic improvement in latency versus the configuration that is not using PNS. With virtually no increase in bandwidth, global sampling drops the mean latency from 450 ms to 340 ms.
Next, much to our surprise, we find that simple sampling of our neighbor's neighbors or inverse neighbors is not terribly effective. As we argued above, this result may be in part due to the constraints of the routing table, but we did not expect the effect to be so dramatic. On the other hand, the recursive versions of both algorithms are at least as effective as global sampling, but not much more so. This result agrees with the contention of Gummadi et al. that only a small amount of global sampling is necessary to achieve near-optimal PNS.
Figure 13(b) shows several combinations of the various algorithms. Global sampling plus sampling of neighbors' neighbors--the combination used in our earlier work [23]--does well, offering a small decrease in latency without much additional bandwidth. However, the other combinations offer similar results. At this point, it seems prudent to say that the most effective technique is to combine global sampling with any other technique. While there may be other differences between the techniques not revealed by this analysis, we see no clear reason to prefer one over another as yet.
As we noted at the start of this paper, while DHTs have been the subject of much research in the last 4 years or so, there have been few studies of the resilience of real implementations at scale, perhaps because of the difficulty of deploying, instrumenting, and creating workloads for such deployments. However, there has been a substantial amount of theoretical and simulation-based work.
Gummadi et al. [12] present a comprehensive analysis of the static resilience of the various DHT geometries. As we have argued earlier in this work, static resilience is an important first step in a DHT's ability to handle failures in general and churn in particular.
Liben-Nowell et al. [17] present a theoretical analysis of structured peer-to-peer overlays from the point of view of churn as a continuous process. They prove a lower bound on the maintenance traffic needed to keep such networks consistent under churn, and show that Chord's algorithms are within a logarithmic factor of this bound. This paper, in contrast, has focused more on the systems issues that arise in handling churn in a DHT. For example, we have observed what they call ``false suspicions of failure'', the appearance that a functioning node has failed, and shown how reactive failure recovery can exacerbate such conditions.
Mahajan et al. [19] present a simulation-based analysis of Pastry in which they study the probability that a DHT node will forward a lookup message to a failed node as a function of the rate of maintenance traffic. They also present an algorithm for automatically tuning the maintenance rate for a given failure rate. Since this algorithm increases the rate of maintenance traffic in response to losses, we are concerned that it may cause positive feedback cycles like those we have observed in reactive recovery. Moreover, we believe their failure model is pessimistic, as they do not consider hop-by-hop retransmissions of lookup messages. By acknowledging lookup messages on each hop, a DHT can route around failed nodes in the middle of a lookup path, and in this work we have shown that good timeout values can be computed to minimize the cost of such retransmissions.
Castro et al. [7] presented a number of optimizations they have performed in MSPastry, the Microsoft Research implementation of Pastry, using simulations. Also, Li et al. [16] performed a detailed simulation-based analysis of several different DHTs under churn, varying their parameters to explore the latency-bandwidth tradeoffs presented. It was their work that inspired our analysis of different PNS techniques.
As opposed to the emulated network used in this study, simulations do not usually consider such network issues as queuing, packet loss, etc. By not doing so, they either simulate far larger networks than we have studied here as in [7,19], or they are able to explore a far larger space of possible DHT configurations as in [16]. On the other hand, they do not reveal subtle issues in DHT design, such as the tradeoffs between reactive and periodic recovery. Also, they do not reveal the interactions of lookup traffic and maintenance traffic in competing for network bandwidth. We are interested in whether a useful middle ground exists between these approaches.
Finally, a number of useful features for handling churn have been proposed, but are not implemented by Bamboo. For example, Kademlia [20] maintains several neighbors for each routing table entry, ordered by the length of time they have been neighbors. Newer nodes replace existing neighbors only after failure of the latter. This design decision is aimed at mitigating the effects of the high ``infant mortality'' observed in peer-to-peer networks.
Another approach to handling churn is to introduce a hierarchy into the system, through stable ``superpeers'' [2,29]. While an explicit hierarchy is a viable strategy for handling load in some cases, this work has shown that a fully decentralized, non-hierarchical DHT can in fact handle high rates of churn at the routing layer.
As discussed in the introduction, there are several other limitations of this study that we think provide for important future work. At an algorithmic level, we would like to study the effects of alternate routing table neighbors as in Kademlia and Tapestry. We would also like to continue our study of iterative versus recursive routing. As discussed by others [11], congestion control for iterative lookups is a challenging problem. We have implemented Chord's STP congestion control algorithm and are currently investigating its behavior under churn, but we do not yet have definitive results about its performance.
At a methodological level, we would like to broaden our study to include better models of network topology and churn. We have so far used only a single network topology in our work, and so our results should be not be taken as the last word on PNS. In particular, the distribution of internode latencies in our ModelNet topology is more Gaussian than the distribution of latencies measured on the Internet. Unfortunately for our purposes, these measured latency distributions do not include topology information, and thus cannot be used to simulate the kind of network cross traffic that we have found important in this study. The existence of better topologies would be most welcome.
In addition to more realistic network models, we would also like to include more realistic models of churn in our future work. One idea that was suggested to us by an anonymous reviewer was to scale traces of session times collected from deployed networks to produce a range of churn rates with a more realistic distribution. We would like to explore this approach. Nevertheless, we believe that the effects of the factors we have studied are dramatic enough that they will remain important even as our models improve.
Finally, in this work we have only shown the resistance of the Bamboo routing layer to churn, an important first step verifying that DHTs are ready to become the dominant building block for peer-to-peer systems, but a limited one. Clearly other issues remain. Security and possibly anonymity are two such issues, but we are unclear about how they relate to churn. We are currently studying the resilience to churn of the algorithms used by the DHT storage layer. We hope that the existence of a routing layer that is robust under churn will provide a useful substrate on which these remaining issues may be studied.
In this work we have summarized the rates of churn observed in deployed peer-to-peer systems and shown that existing DHTs exhibit less than desirable performance at the higher end of these churn rates. We have presented Bamboo and explored various design tradeoffs and their effects on its ability to handle churn.
The design tradeoffs we studied in this work fall into three broad categories: reactive versus periodic recovery from neighbor failure, the calculation of timeouts on lookup messages, and proximity neighbor selection. We have presented the danger of positive feedback cycles in reactive recovery and discussed two ways to break such cycles. First, we can make the DHT much more cautious about declaring neighbors failed, in order to limit the possibility that we will be tricked into recovering a non-faulty node by network congestion. Second, we presented the technique of periodic recovery. Finally, we demonstrated that reactive recovery is less efficient than periodic recovery under reasonable churn rates when leaf sets are large, as they would be in a large system.
With respect to timeout calculation, we have shown that TCP-style timeout calculation performs best, but argued that it is only appropriate for lookups performed recursively. It has long been known that recursive routing provides lower latency lookups than iterative, but this result presents a further argument for recursive routing where the lowest latency is important. However, we have also shown that while they are not as effective as TCP-style timeouts, timeouts based on virtual coordinates are quite reasonable under moderate rates of churn. This result indicates that at least with respect to timeouts, iterative routing should not be infeasible under moderate churn.
Concerning proximity neighbor selection, we have shown that global sampling can provide a 24% reduction in latency for virtually no increase in bandwidth used. By using an additional 40% more bandwidth, a 42% decrease in latency can be achieved. Other techniques are also effective, especially our adaptations of the Pastry and Tapestry nearest-neighbor algorithms, but not much more so than simple global sampling. Merely sampling our neighbors' neighbors or inverse neighbors is not very effective in comparison. Some combination of global sampling an any of the other techniques seems to provide the best performance at the least cost.
We would like to thank a number of people for their help with this work. Our shepherd, Atul Adya, and the anonymous reviewers all provided valuable comments and guidance. Frank Dabek helped us tune our Vivaldi implementation, and he and Emil Sit helped us get Chord up and running. Likewise, Peter Druschel provided valuable debugging insight for FreePastry. David Becker helped us with ModelNet. Sylvia Ratnasamy, Scott Shenker, and Ion Stoica provided valuable guidance at several stages of this paper's development.
This document was generated using the LaTeX2HTML translator Version 2002 (1.62)
Copyright © 1993, 1994, 1995, 1996, Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999, Ross Moore, Mathematics
Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 -no_navigation
usenix-cr.tex
The translation was initiated by Sean Rhea on 2004-05-04
|
This paper was originally published in the
Proceedings of the 2004 USENIX Annual Technical Conference,
June 27-July 2, 2004, Boston, MA, USA Last changed: 10 June 2004 aw |
|