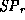A binary consists of the assembled native code together with an encoding of the proof of its safety predicate. To validate the binary, the code consumer first extracts the native code and then computes its safety predicate using the VC rules. Then, it checks that the safety proof is a valid proof of the safety predicate.
This method ensures safety even if the native code or the proof in the binary is tampered with. If the code is modified, then in all likelihood its safety predicate changes, so the given proof will not correspond to it. If the proof is modified, then either it will be invalid, or else not correspond to the safety predicate. If the code is modified in such a way that the safety predicate is unchanged (for example, instruction scheduling and register allocation might do this in typical circumstances), or if both the code and the proof are modified so that we still have a valid proof of the new safety predicate, the validation succeeds and we continue to retain a guarantee of safety.
To automate the validation process, we must first choose a concrete representation language for predicates and their proofs. From the many available choices, we have selected the Edinburgh Logical Framework [7] (also called LF) as the representation framework for predicates and proofs. LF is an extension of the simply typed lambda calculus and was designed as a meta language for high-level specification of languages in logic and computer science. The most attractive property of LF is that it has a powerful yet simple typechecking algorithm, which we use to check the validity of proofs.
We represent the predicates and the proofs in LF in such a way that the
validity of a proof is implied by the well typedness of the proof
representation. Thus, proof validation amounts to typechecking. Also, LF
allows us to represent in an elegant way a few key issues in logical proof
correctness, such as the manipulation of logical parameters and assumptions. It
is well beyond the scope of this paper to discuss in detail LF and the
typechecking algorithm, however it is worth mentioning that typechecking is
decidable and is described by a few simple rules. Indeed, typechecking is so
simple that any programmers who do not trust the publicly available
implementation can implement it easily themselves. Our implementation has about
five pages of C code, even though it incorporates a few optimizations to the
basic algorithm. With this implementation, it takes 1.4 milliseconds to
validate the proof of the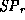 
predicate.
For flexibility and to allow easy exchange of proofs between system components, we have designed a binary encoding of LF representations. Thus, a typical binary contains a section with the native code ready to be mapped into memory and executed, followed by a symbol table used to reconstruct the LF representation at the code consumer site, and the binary encoding of the LF representation of the safety proof. The latter component is the safety proof. ex-pcc shows the sizes of these sections for the binary corresponding to the resource access example.
Figure: The layout of the binary for the resource access example. The
offsets are in bytes.
Currently, binaries for standard packet filters, including the native code, safety proof, and relocation section, are about 400 to 1200 bytes in size, with the proof about 3 times larger than the code. The size of the relocation section increases linearly with the number of distinct proof rules used in the proof. In the case of packet filter safety proofs, the relocation section is a third of the binary but we expect this ratio be much smaller for larger proofs. There is a considerable amount of design latitude in the encodings of the proofs, and we have barely scratched the surface on what can be done to reduce the size of the binaries as well as the time required for validation. But already, with relatively little effort, we have achieved acceptably small binaries and low validation times.