|
BSDCon 2002 Paper
[BSDCon '02 Tech Program Index]
| Pp. 47–54 of the Proceedings |  |
An implementation of the Yarrow PRNG for FreeBSD
Mark R. V. Murray
FreeBSD Services, Ltd
Amersham, Buckinghamshire, UK
markm@freebsd-services.com
Abstract
Computers are by their definition predictable. The problem of obtaining
good-quality random numbers is well known.
There is a great need for entropy in the running kernel, as well as in
user-space. The kernel needs to randomise TCP sequences, seed keys for
IPSec, randomise PIDs, and so on. Starvation of these random numbers
is a critical problem. Users need random keys, random filenames,
nondeterministic games, random numbers for Monte-Carlo simulation and
so on.
Kelsey, Schneier and Ferguson proposed an improved algorithm for providing
statistically random numbers, at the same time cryptographically protecting
their sequence and state. This is the Yarrow algorithm.
This work presents an implementation of this algorithm as the entropy
device (/dev/random) in FreeBSD's kernel.
1 Introduction
In an earlier work[Mur00], the author introduced the new
entropy device to FreeBSD-CURRENT as a work-in progress. In that work,
attack methodologies were briefly discussed, and the difference between
the older entropy device and this device were discussed.
Yarrow[KSF99] was briefly explained.
It is important to remember that this device is not designed to
produce pure1 random numbers.
Computers do not produce enough natural randomness for that approach
to be useful in entropy-consuming environments.
Instead, this device is a free-running pseudo-random number generator (PRNG),
one in which great effort has been made to cryptographically protect the state
of the generator. Further, the internal state is constantly perturbed with
``harvested'' entropy to thwart attackers.
The algorithm is divided into four parts (see Figure 1):

#1 Simplified Yarrow Structure
- Entropy Accumulator and Pools
These are used to ``harvest'' entropy from the running kernel. The
API provided by the author is intended to be simple to use anywhere
in the kernel.
- Reseed
Reseeding is entirely internal to Yarrow. The author has attempted to
stay as close as possible to the published algorithm.
- Reseed Control
Reseeds happen in response to harvested entropy, and to reads from
the entropy device. There are statistical requirements to these reseeds
that are unimplemented.
- Output Generator
The generator is similar to ``classic'' PRNG's, excepting:
- It uses a large, cryptographically secure hash instead of a simple
feedback formula.
- It is perturbed on a regular basis by harvested entropy.
2 Design Issues
An API for ``harvesting'' entropy was needed, so that
kernel programmers could easily provide such randomness their
subsystem could produce. The requirements were that the API should
be extensible, fast, simple and able to operate in interrupt context.
Where practical, entropy sources needed the ability to be disabled
at the whim of the system administrator.
256-Bit storage pools were desired, as this was deemed to hold a
reasonable amount of entropy without being overly expensive. It
should be remembered that Yarrow uses two accumulation ``pools''
(fast and slow), so this meant that up to
512 bits of environmental entropy could be held.
This decision meant that a 256-bit hashing algorithm and a 256-bit
block cipher were needed. The need for a 256-bit hash ruled out using
MD2, MD4, MD5 or SHA-1 unless a lengthening algorithm was also used. There
were a few choices for 256-bit block ciphers, however availability (or
potential availability) in the FreeBSD kernel was a limiting factor.
As a suitable ``natural'' hash did not exist, a hash had to
be constructed using block ciphers.
Likely candidates were initially Blowfish and DES (reluctantly,
as a block-lengthening process would be needed). Other
AES candidates were considered, but as a finalist had not
been selected they were not initially used.
The output generator needed to be fast, and also needed good key-setup
speed, as the key is changed often. In order to preserve the strength
of Yarrow, its block size was deemed to be the same size as the hash
buffer. This made the choice of the encryption cipher simple, as the hash
cipher could be used.
Further research[Sch96a] indicated that lengthening
algorithms were most probably unwise.
2.1 Entropy Harvesting
As entropy could be found in any part of the kernel, both bottom-half
and top-half, the entropy harvesting needed to be cheap, non-invasive
and non-blocking.
A fixed-size circular buffer is used to accumulate entropy for later
processing. If the buffer becomes full, further attempts to add entropy
are ignored. The buffer is never locked when written to; this does not
matter, as data corruption would be beneficial.
Entropy is added to the buffer by a subsystem calling the
random_harvest(9) function. This is declared in
sys/random.h as follows:
enum esource { \
RANDOM_WRITE, RANDOM_KEYBOARD, \
RANDOM_MOUSE, RANDOM_NET, \
RANDOM_INTERRUPT, ENTROPYSOURCE \
};
void random_harvest(void *data, \
u_int count, u_int bits, \
u_int frac, enum esource source);
Entropy is accumulated in up to HARVESTSIZE2
byte chunks.
The arguments are:
- data
- a pointer to the stochastic data
- count
- the number of bytes of data
- bits
- an estimate of the random bits
- frac
- as above, except fractional ([ frac/1024] bits)
- source
- the source of the entropy
The stochastic events added to the buffer are stored in a structure:
struct harvest {
u_int64_t somecounter;
u_char entropy[HARVESTSIZE];
u_int size, bits, frac;
enum esource source;
};
The structure holds all of the information provided by
random_harvest plus a timestamp.
The timestamp is taken from the CPU's fast counter register
(like the Intel Pentium(tm) processor's TSC register).
CPUs that do not have this register (like the Intel i386)
use nanotime(9) instead. This has an
unfortunate time penalty.
It is not important that this timestamp is an accurate
reflection of real-world time, nor is it important that
multiple CPUs in an SMP environment would have different
values. It is important that the counter/timestamp
increase quickly and linearly with time.
A count of accumulated entropy is kept, and this is used to
reseed the output generator on occasion. The
fractional entropy count supplied in the frac parameter
is used in very low entropy situations. For example, a particular
device can be said to produce 1 bit of randomness every 20 events.
Kernel programmers wishing to supply entropy from their code
should extend the enum esource list, leaving the
constant at the end of the list. Then, the
randomness should be gathered and supplied as efficiently as
possible.
In sys/random.h:
enum esource {
RANDOM_WRITE,
RANDOM_KEYBOARD,
RANDOM_MOUSE,
RANDOM_NET,
RANDOM_INTERRUPT,
RANDOM_MYSTUFF, /* New */
ENTROPYSOURCE };
In the code to be harvested:
:
#include <sys/types>
:
#include <sys/random>
int
somefunc(...)
{
:
struct {
u_int32_t junk;
u_int32_t garbage;
u_char rubbish[8];
} randomstuff;
:
randomstuff.junk = somelocaljunk;
randomstuff.garbage = otherjunk;
strncpy(randomstuff.rubbish, dirt, 8);
:
/* harvest the entropy in
* randomstuff. Be really
* conservative and estimate the
* the random bit count as only 4.
*/
random_harvest(randomstuff,
sizeof(randomstuff), 4, 0,
RANDOM_MYSTUFF);
:
If control over the new harvesting is required, then a sysctl
may be added to src/sys/dev/random/randomdev.[ch]:
SYSCTL_PROC(_kern_random_sys_harvest,
OID_AUTO, interrupt,
CTLTYPE_INT|CTLFLAG_RW,
&harvest.mystuff, 0,
random_check_boolean, "I",
"Harvest mystuff entropy");
The call to random_harvest should then be made conditional
on harvest.mystuff:
:
if (random.mystuff)
random_harvest(randomstuff,
sizeof(randomstuff), 4, 0,
RANDOM_MYSTUFF);
:
Writing to the entropy device from the user's perspective (ie,
writing to /dev/random) is similar to writing to
/dev/null; it has no discernible effect. In actual fact,
the data written is ``harvested'' using the harvesting calls, with the
proviso that the entropy is estimated to be nothing. This has
the effect of not causing reseeds, but perturbing the internal
state anyway. If the user is the superuser, then closing the device
after a write will cause an explicit reseed.
A kernel thread ``kthread'' constantly runs, polling
the circular buffer, and if data is present, it accumulates each
event alternately into the two accumulation hashes (or ``entropy pools'').
2.2 Accumulation Pools
An initial version of the 256-bit accumulation hash was constructed
using a Davies-Meyer[Sch96b] hash with Blowfish[Sch96c]
as the block cipher.
The hash works by repeatedly encrypting an initial (zero) state while
cycling the hash data through the key. At each iteration, the previous
value of the hash is exclusive-or-ed into the newly encrypted value.
This can be represented as:
Hi = EMi(Hi-1) XOR Hi-1
where Hn is the nth iteration of the hash result,
Mj is the jth fragment of the data to be hashed and
Ek(m) is the result of encrypting m with block cipher E()
and key k.
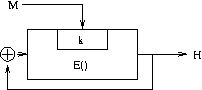
Davies-Meyer hash from block cipher.
While this worked, it was unbearably slow as Blowfish has an extremely
expensive key schedule. Slowness was experienced as very bad kernel
latency, and a kernel thread running with unacceptably high CPU usage.
The (by this time) newly released AES (``Rijndael'')[NIS]
algorithm was then tried, and a crude benchmark produced extremely
promising results. (Here, Blowfish was replaced with Rijndael.)
The benchmark is a timed 16MB read from each device:
$ dd if=${DEVICE} of=/dev/null \
count=16 bs=1048576
For comparison, /dev/zero was also read.
The time is the time in seconds for the 16MB read, and the rate is
measured in KB/s.
| $device | Time (s) | Rate (kB/s) |
| Blowfish | 137.7 | 122 |
| AES | 6.5 | 2595 |
| Zero | 0.2 | 81861 |
After consulting literature
[SKW+][WSB][FKL+],
it was suspected that AES was the ideal algorithm, but further investigation
was considered prudent, particularly as the benchmark measured output
performance, not hashing performance.
The hash routines were broken out of the kernel, and various speeds were
measured using alternative block ciphers. A Null algorithm and 160-bit
SHA-1 were included for comparison.
The ``Null'' cipher simply duplicates the input data, ignoring the key:
Nk(m) = m
This reduced the Davies-Meyer algorithm to the XOR and data-movement
parts only.
Each result represents the time taken to hash 2MB of pseudo-random
data.
| Algorithm | Time (s) | Rate (kB/s) |
| AES | 3.1 | 461.6 |
| Blowfish | 40.2 | 35.2 |
| DES | 2.9 | 491.7 |
| SHA-1 | 2.0 | 693.3 |
| Null | 1.8 | 786.7 |
It can be seen that AES with 256-bit keys and 256-bit blocks is
approximately as fast as DES with 56-bit keys and 64-bit blocks.
160-bit SHA-1 is about 50% faster than the AES hash, but the AES
hash has an approximately 50% larger capacity for storing bits.
The ``Null'' algorithm confirms that encryption overhead is
acceptably low in comparison with other code overhead.
2.3 Output Generator
The output generator is a counter that is repeatedly encrypted,
producing the output:
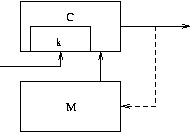
The Output Generator
Oi = Ek(Ct)
Ct+1 = Ct+1
where Ct is the (256-bit) counter3 at time t, Oi
is the ith output, and Ek(Ct) is the result of
encrypting counter Ct using cipher E() and key k.
The dashed line represents the data path during a gate event. The
key ``k'' is inserted during a reseed. This is the point
at which environmental noise (``harvested'' entropy) is used.
To compromise the output generator, a key compromise
of the cipher is necessary. This is computationally difficult;
nevertheless, to thwart this, the counter is regularly replaced
with data from the output stream:
Ct+1 = Ct+1
Ct+1 = Ek(C)
The data thus used is not used as part of the output.
This is called a gate event, and it happens at a time
configurable by the system administrator via sysctl(9). It
defaults to happening every 10 blocks. If a user process reads less
than a 256-bit block, the remainder is cached for future reads.
To show that the output was statistically acceptable, some tests
were done.
A simple histogram of 8M single-byte values was plotted:
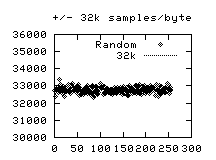
Spectrum of 8M 8-bit values
A straight line was fitted to this data, and was found to substantiate
the fact that the slope was » 0 and the mean value was » 32k.
The spread of values around 32k was plotted, and the distribution found
to be reassuringly normal:
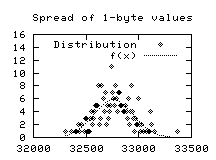
Distribution of values around expected norm of 32k
This corresponded to a mean (m) of 32759.5 and a s of
187.2
Further tests were done using a more sophisticated random number ``torture
chamber'' called Diehard[Mar]. Its use produced voluminous output
which indicated, on careful perusal, that the generator's output was
statistically acceptable.
It must be noted that the output generator does not block.
This is intentional.
2.4 Reseed Control
This is the trickiest part of the algorithm to write. The Yarrow
specification mandates three separate estimates of incoming entropy
``harvest-units'':
- A programmer-supplied estimate. This has been
very conservatively set. This is given as a constant
to each entropy-harvesting call.
- A system-wide ``density''. This is set at [ 1/2], meaning
no sample of N bits can supply more than [ N/2] bits of
entropy.
- A statistically determined, per-source continuous estimate.
This is unimplemented, as the mechanism for doing the statistical
estimation has been deemed too expensive for the kernel.
The algorithm states that the lowest of these three is taken
as the entropy supplied for the individual unit. The author has endeavoured
to ensure that the programmer-supplied estimate will always be low enough.
3 Impact on the Running System
The running device has great potential to be very invasive to the running
kernel, as early experiments with slow ciphers showed. In the current
code, however, the system is proving to be no such hindrance.
l2.85in
last pid: 19524; load averages: 0.25, 0.22, 0.18 up 3+09:01:43 21:52:53
92 processes: 3 running, 74 sleeping, 15 waiting
CPU states: 4.3% user, 0.0% nice, 2.3% system, 0.4% interrupt, 93.0% idle
Mem: 27M Active, 5536K Inact, 18M Wired, 4348K Cache, 14M Buf, 4856K Free
Swap: 68M Total, 34M Used, 33M Free, 50% Inuse
PID USERNAME PRI NICE SIZE RES STATE TIME WCPU CPU COMMAND
10 root -16 0 0K 12K RUN 59.9H 86.47% 86.47% idle
18128 root 96 0 16636K 5932K select 15:37 1.61% 1.61% XFree86
18169 mark 96 0 15884K 3216K select 4:53 1.61% 1.61% kdeinit
18217 mark 96 0 17116K 4540K select 1:47 0.39% 0.39% kdeinit
18227 mark 96 0 10872K 5916K select 1:59 0.29% 0.29% xemacs-21.1
19524 mark 96 0 2096K 1144K RUN 0:00 0.75% 0.20% top
22 root -64 -183 0K 12K WAIT 40:57 0.10% 0.10% irq14: ata0
12 root -48 -167 0K 12K RUN 20:06 0.10% 0.10% swi6: tty:sio
18205 mark 96 0 17836K 5928K select 1:38 0.10% 0.10% kdeinit
18203 mark 96 0 21428K 4080K select 1:07 0.10% 0.10% kdeinit
6 root 20 0 0K 12K syncer 4:02 0.00% 0.00% syncer
14 root 76 0 0K 12K sleep 3:19 0.00% 0.00% random
18183 mark 60 -36 5244K 2044K select 3:09 0.00% 0.00% artsd
15 root -28 -147 0K 12K WAIT 2:58 0.00% 0.00% swi5: task qu
18810 mark 96 0 9728K 3076K select 1:30 0.00% 0.00% acroread
18208 mark 96 0 16372K 3964K select 1:21 0.00% 0.00% kdeinit
#1Snapshot of a running system
This snapshot of a running FreeBSD workstation shows that the
random process (the kthread that runs the
reseed process) has approximately the same impact on the system
as the syncer process, ie negligible.
The use of random numbers by security-conscious engineers has been taken
into account over and above the concerns of the professional cryptographic
community. Speed was deemed to be more important than the production of
number-theoretic-quality random numbers (eg: suited to generating
one-time-pads). It is believed that FreeBSD is used by many more
system-administrators than professional cryptographers.
The author is, however, appreciative of the concerns of those who
would want a more austere presentation of random numbers from the
operating system. Those members of the community are considered to
be a specialist minority, though.
4 Future plans
There are two main expansion areas in the FreeBSD entropy device.
- More entropy harvesting. Any ``cheap'' entropy that may be
found in the kernel may be used in the future. The
user community is encouraged to submit likely sources.
The author has provisional code to harvest entropy from
Intel chipsets fitted with hardware random number generators.
- Provision of a ``distilled'' device for those who wish to
be assured of an ``entropy-in = entropy-out''
conservation-of-entropy device. This needs to be
conservative enough to not provide a denial-of-service
attack by its very existence.
5 Thanks
Thanks are due to Sue Bourne and Brian Somers for proofreading
and helpful comments.
Thanks are also due to FreeBSD Services, Ltd for giving me the time to produce
this work.
My fondest thanks are also given to my father. Thanks, Dad. I'll miss you.
References
- [FKL+]
-
Niels Ferguson, John Kelsey, Stefan Lucks, Bruce Schneier, Mike Stay, David
Wagner, and Doug Whiting.
Improved cryptanalysis of rijndael.
http://www.counterpane.com.
- [KSF99]
-
John Kelsey, Bruce Schneier, and Niels Ferguson.
Yarrow-160: Notes on the design and analysis of the yarrow
cryptographic pseudorandom number generator.
Sixth Annual Workshop on Selected Areas in Cryptography, August 1999.
- [Mar]
-
George Marsaglia.
Diehard.
http://www/stat.fsu.edu/[ \tilde]geo/diehard.html.
- [Mur00]
-
Mark R. V. Murray.
Effective entropy from the freebsd kernel.
In BSDCon, pages 92-98, 2000.
- [NIS]
-
NIST.
The aes algorithm (rijndael) information.
http://csrc.nist.gov/encryption/aes/rijndael/.
- [Sch96a]
-
Bruce Schneier.
Applied Cryptography, pages 430-431.
Wiley, second edition, 1996.
- [Sch96b]
-
Bruce Schneier.
Applied Cryptography, pages 446-455.
Wiley, second edition, 1996.
- [Sch96c]
-
Bruce Schneier.
Applied Cryptography, pages 336-339.
Wiley, second edition, 1996.
- [SKW+]
-
Bruce Schneier, John Kelsey, Doug Whiting, David Wagner, and Chris Hall.
Performance comparison of the aes submissions.
http://www.counterpane.com.
- [WSB]
-
Doug Whiting, Bruce Schneier, and Steve Bellovin.
Aes key agility issues in high-speed ipsec implementations.
http://www.counterpane.com.
Footnotes:
1In the number-theoretic sense; the numbers remain
statistically random and include environmental noise
2Currently 16
3Internal to the
FreeBSD kernel, the 256-bit value is represented as a structure
containing four 64-bit unsigned integers. Only 64 bits are incremented.
The author does not believe this is a problem.
| 

