| Page 1 |
A Dollar from
15 Cents:
Cross-Platform
Management for Internet Services
Christopher
Stewart
†
Terence Kelly
∗
Alex Zhang
∗
Kai Shen
†
†
University of
Rochester
∗
Hewlett-Packard
Laboratories
Abstract
As
Internet services become ubiquitous, the selection
and
management of diverse server platforms now af-
fects the
bottom line of almost every firm in every in-
dustry.
Ideally, such cross-platform management would
yield high
performance at low cost, but in practice, the
performance
consequences of such decisions are often
hard to
predict. In this paper, we present an approach
to guide
cross-platform management for real-world In-
ternet
services. Our approach is driven by a novel per-
formance
model that predicts application-level perfor-
mance
across changes in platform parameters, such as
processor
cache sizes, processor speeds, etc., and can be
calibrated
with data commonly available in today’s pro-
duction
environments. Our model is structured as a com-
position
of several empirically observed, parsimonious
sub-models.
These sub-models have few free parameters
and can be
calibrated with lightweight passive observa-
tions on a
current production platform. We demonstrate
the
usefulness of our cross-platform model in two man-
agement
problems. First, our model provides accurate
performance
predictions when selecting the next gener-
ation of
processors to enter a server farm. Second, our
model can
guide platform-aware load balancing across
heterogeneous
server farms.
1
Introduction
In recent
years, Internet services have become an in-
dispensable
component of customer-facing websites and
enterprise
applications. Their increased popularity has
prompted a
surge in the size and heterogeneity of the
server
clusters that support them. Nowadays, the man-
agement of
heterogeneous server platforms affects the
bottom line
of almost every firm in every industry. For
example,
purchasing the right server makes and models
can improve
application-level performance while reduc-
ing
cluster-wide power consumption. Such management
decisions
often span many server platforms that, in prac-
tice, cannot
be tested exhaustively. Consequently, cross-
platform
management for Internet services has histori-
cally been
ad-hoc and unprincipled.
Recent
research [9,14,31,37,40,41,44]has shown that
performance
models can aid the management of Internet
services by
predicting the performance consequences of
contemplated
actions. However, past models for Inter-
net services
have not considered platform configurations
such as
processor cache sizes, the number of processors,
and processor
speed. The effects of such parameters
are
fundamentally hard to predict, even when data can
be collected
by any means. The effects are even harder
to predict in
real-world production environments, where
data
collection is restricted to passive measurements of
the running
system.
This paper
presents a cross-platform performance
model for
Internet services, and demonstrates its use
in making
management decisions. Our model predicts
application-level
response times and throughput from a
composition
of several sub-models, each of which de-
scribes a
measure of the processor’s performance(hence-
forth, a
processor metric) as a function of a system pa-
rameter. For
example, one of our sub-models relates
cache misses
(a processor metric) to cache size (a system
parameter).
The functional forms of our sub-models are
determined
from empirical observations across several
Internet
services and are justified by reasoning about the
underlying
design of Internet services. Our knowledge-
lean
sub-models are called trait models because, like hu-
man
personality traits, they stem from empirical obser-
vations of
system behaviors and they characterize only
one aspect of
a complex system. Figure 1 illustrates the
design of our
cross-platform model.
The
applicability of our model in real-world produc-
tion
environments was an important design considera-
tion. We
embrace the philosophy of George Box, “All
models are
wrong, but some [hopefully ours] are use-
ful.” [10]
To reach a broad user base, our model targets
third-party
consultants. Consultants are often expected
to propose
good management decisions without touch-
ing their
clients’ production applications. Such inconve-
nient but
realistic restrictions forbid source code instru-
mentation
and controlled benchmarking. In many ways
the
challenge in such data-impoverished environments
fits the
words of the old adage, “trying to make a dol-
lar from 15
cents.” Typically, consultants must make do
with data
available from standard monitoring utilities and
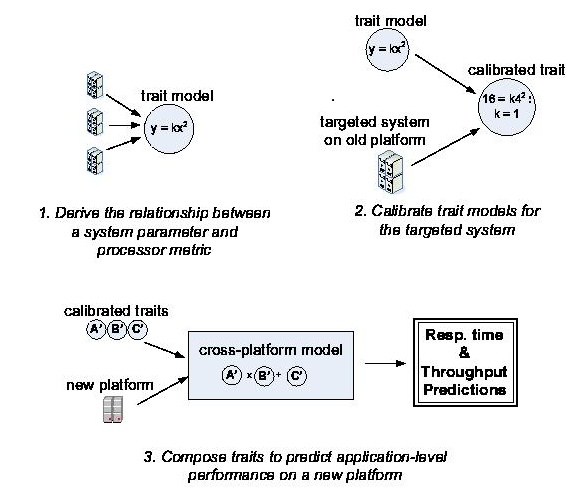
Figure 1:
The design
of our cross-platform performance
model. The
variable x represents a system parameter, e.g.,
number of
processors or L1 cache size. The variable y rep-
resents a
processor metric (i.e., a measure of processor per-
formance),
such as instruction count or L1 cache misses.
Application-level
performance refers to response time and
throughput,
collectively.
application-level
logs. The simplicity of our sub-models
allows us to
calibrate our model using only such readily
available
data.
We
demonstrate the usefulness of our model in the
selection of
high-performance, low-power server plat-
forms.
Specifically, we used our model (and proces-
sor power
specifications) to identify platforms with high
performance-per-watt
ratios. Our model outperforms al-
ternative
techniques that are commonly used to guide
platform
selection in practice today. We also show that
model-driven
load balancing for heterogeneous clusters
can improve
response times. Under this policy, request
types are
routed to the hardware platform that our model
predicts is
best suited to their resource requirements.
The
contributions of this paper are:
1. We
observe and justify trait models across several
Internet
services.
2. We
integrate our trait models into a cross-platform
model of
application-level performance.
3. We
demonstrate the usefulness of our cross-
platform
model for platform selection and load bal-
ancing in a
heterogeneous server farm.
The
remainder of this paper is organized as follows.
Section 2
overviews the software architecture, process-
ing
patterns, and deployment environment of the realistic
Internet
services that we target. Section 3 presents sev-
eral trait
models. Section 4 shows how we compose trait
models into
an established framework to achieve an ac-
curate
cross-platform performance prediction and com-
pares our
approach with several alternatives. Section 5
shows how
trait-based performance models can guide the
selection of
server platforms and guide load balancing in
a
heterogeneous server cluster. Section 6 reviews related
work and
Section 7 concludes.
2
Background
Internet
services are often designed according to a
three-tier
software architecture. A response to an end-
user request
may traverse software on all three tiers. The
first tier
translates end-user markup languages into and
out of
business data structures. The second tier (a.k.a. the
business-logic
tier) performs computation on business
data
structures. Our work focuses on this tier, so we will
provide a
detailed example of its operation below. The
third tier
provides read/write storage for abstract business
objects.
Requests traverse tiers via synchronous com-
munication
over local area networks (rather than shared
memory) and
a single request may revisit tiers many
times [26].
Previous studies provide more information
on
multi-tier software architectures [29,44].
Business-logic
computations are often the bottleneck
for Internet
services. As an example, consider the busi-
ness logic
of an auction site: computing the list of cur-
rently
winning bids can require complex considerations
of bidder
histories, seller preferences, and shipping dis-
tances
between bidders and sellers. Such workloads
are
processor intensive, and their effect on application-
level
performance depends on the underlying platform’s
configuration
in terms of cache size, on-chip cores, hy-
perthreading,
etc. Therefore, our model, which spans
a wide range
of platform configurations, naturally tar-
gets the
business-logic tier. Admittedly, application-level
performance
for Internet services can also be affected
by disk and
network workloads at other tiers. Previous
works
[14,41] have addressed some of these issues, and
we believe
our model can be integrated with such works.
Internet
services keep response times low to satisfy
end-users.
However as requests arrive concurrently, re-
sponse times
increase due to queuing delays. In produc-
tion
environments, resources are adequately provisioned
to limit the
impact of queuing. Previous analyses of sev-
eral real
enterprise applications [40] showed max CPU
utilizations
below 60% and average utilizations below
25%. Similar
observations were made in [8]. Services
are
qualitatively different when resources are adequately
provisioned
compared to overload conditions. For exam-
ple,
contention for shared resources is more pronounced
under
overload conditions [29].
Aggregate
counts
Time
Type
Type
Instr. count
L1
L2
stamp
1
2
...
(x10
4
)
miss
miss
2:00pm
18
42
...
280322
31026
2072
2:01pm
33
36
...
311641
33375
2700
Table 1:
Example of
data available as input to our model.
Oprofile [2]
collects instruction counts and cache misses.
Apache logs
[1] supply frequencies of request types.
2.1
Nonstationarity
End-user
requests can typically be grouped into a
small number
of types. For example, an auction site
may support
request types such as bid for item, sell item,
and browse
items. Requests of the same type often fol-
low similar
code paths for processing, and as a result,
requests of
the same type are likely to place similar de-
mands on the
processor. A request mix describes the pro-
portion of
end-user requests of each type.
Request mix
nonstationarity describes a common phe-
nomenon in
real Internet services: the relative frequen-
cies of
request types fluctuate over long and short inter-
vals [40].
Over a long period, an Internet service will
see a wide
and highly variable range of request mixes.
On the
downside, nonstationarity requires performance
models to
generalize to previously unseen transaction
mixes. On
the upside, nonstationarity ensures that ob-
servations
over a long period will include more unique
request
mixes than request types. This diversity over-
constrains
linear models that consider the effects of each
request type
on a corresponding output metric (e.g., in-
struction
count), which enables parameter estimation us-
ing
regression techniques like Ordinary Least Squares.
2.2 Data
Availability
In
production environments, system managers must
cope with
the practical (and often political) issues of trust
and risk
during data collection. For example, third-party
consultants—a
major constituent of our work—are typ-
ically seen
as semi-trusted decision makers, so they are
not allowed
to perform controlled experiments that could
pose
availability or security risks to business-critical pro-
duction
systems. Similarly, managers of shared host-
ing centers
are bound by business agreements that pre-
vent them
from accessing or modifying a service’s source
code. Even
trusted developers of the service often re-
linquish
their ability to perform invasive operations that
could cause
data corruption.
Our model
uses data commonly available in most
production
environments, even in consulting scenarios.
Specifically,
we restrict our model inputs to logs of re-
quest
arrivals and CPU performance counters. Table 1
provides an
example of our model’s inputs. Our model
also uses
information available from standard platform
specification
sheets such as the number of processors and
on-chip
cache sizes [6].
3 Trait
Models
Trait models
characterize the relationship between a
system
parameter and a processor metric. Like personal-
ity traits,
they reflect one aspect of system behavior (e.g.,
sensitivity
to small cache sizes or reaction to changes in
request
mix). The intentional simplicity of trait models
has two
benefits for our cross-platform model. First, we
can extract
parsimonious yet general functional forms
from
empirical observations of the parameter and out-
put metric.
Second, we can automatically calibrate trait
models with
data commonly available in production en-
vironments.
Our trait
models take the simplest functional form that
yields low
prediction error on the targeted system param-
eter and
processor metric. We employ two sanity checks
to ensure
that our traits reflect authentic relationships—
not just
peculiarities in one particular application. First,
we
empirically validate our trait models across several
applications.
Second, we justify the functional form of
our trait
models by reasoning about the underlying struc-
ture of
Internet services.
In this
section, we observe two traits in the busi-
ness logic
of Internet services. First, we observe that a
power law
characterizes the miss rate for on-chip pro-
cessor
caches. Specifically, data-cache misses plotted
against
cache size on a log-log scale are well fit by a
linear
model. We justify such a heavy-tail relationship
by reasoning
about the memory access patterns of back-
ground
system activities. Compared to alternative func-
tional
forms, a power law relationship achieves excellent
prediction
accuracy with few free model parameters.
Second, we
observe that a linear request-mix model
describes
instruction count and aggregate cache misses.
This trait
captures the intuition that request type and vol-
ume are the
primary determinants of runtime code paths.
Our
experiments demonstrate the resiliency of request
mix models
under a variety of processor configurations.
Specifically,
request-mix models remain accurate under
SMP,
multi-core, and hyperthreading processors.
3.1 Error
Metric
The
normalized residual error is the metric that we use
to evaluate
trait models. We also use it in the validation
of our full
cross-platform model. Let Y andY represent
observed and
predicted values of the targeted output met-
ric,
respectively. The residual error, E = Y − Y tends
toward zero
for good models. The normalized residual
error,
|E|
Y
, accounts
for differences in the magnitude of Y.
0
20
40
60
80
100
120
140
1
I
n
s
t
r
.
E
x
e
c
u
t
e
d
(
x
1
0
7
)
0
100
200
300
400
500
600
700
A
r
r
i
v
a
l
r
a
t
e
Instructions
Most popular
type
Request
arrival rate
2nd most
popular type
2 hours
4
6
8
10
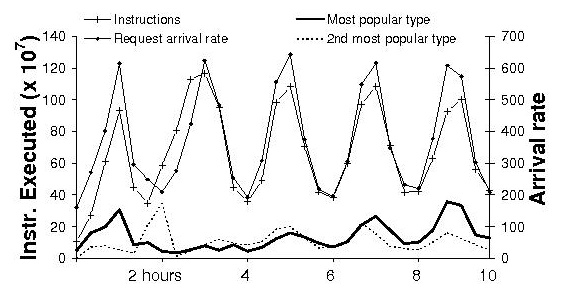
Figure 2:
Nonstationarity
during a RUBiS experiment. Re-
quest
arrivals fluctuate in a sinusoidal fashion, which corre-
spondingly
affects the aggregate instructions executed. The ra-
tio of the
most popular request type to the second most popular
type (i.e.,
freq
most
freq
2nd
) ranges
from 0.13 to 12.5. Throughout this
paper, a
request mix captures per-type frequencies over a 30
second
interval.
3.2
Testbed Applications
We study the
business logic of three benchmark In-
ternet
Services. RUBiS is a J2EE application that cap-
tures the
core functionalities of an online auction site [3].
The site
supports 22 request types including browsing
for items,
placing bids, and viewing a user’s bid history.
The software
architecture follows a three-tier model con-
taining a
front-end web server, a back-end database, and
Java
business-logic components. The StockOnline stock
trading
application [4] supports six request types. End
users can
buy and sell stocks, view prices, view hold-
ings, update
account information, and create new ac-
counts.
StockOnline also follows a three-tier software
architecture
with Java business-logic components. TPC-
W simulates
the activities of a transactional e-commerce
bookstore.
It supports 13 request types including search-
ing for
books, customer registration, and administrative
price
updates. Applications run on the JBoss 4.0.2 appli-
cation
server. The database back-end is MySQL 4.0. All
applications
run on the Linux 2.6.18 kernel.
The workload
generators bundled with RUBiS, Stock-
Online, and
TPC-W produce synthetic end-user requests
according to
fixed long-term probabilities for each re-
quest type.
Our previous work showed that the resulting
request
mixes are qualitatively unlike the nonstationary
workloads
found in real production environments [40].
In this
work, we used a nonstationary sequence of in-
tegers to
produce a nonstationary request trace for each
benchmark
application. We replayed the trace in an
open-arrival
fashion in which the aggregate arrival rate
fluctuated.
Figure 2 depicts fluctuations in the aggregate
arrival rate
and in the relative frequencies of transaction
types during
a RUBiS experiment. Our nonstationary se-
quence of
integers is publicly available [5] and can be
used to
produce nonstationary mixes for any application
with
well-defined request types.
M
i
s
s
e
s
/
1
0
0
0
0
I
n
s
t
.
2
0
2
2
2
4
2
6
2
10
2
8
Cache
Size (KB)
16
16384
256
RUBiS
StockOnline
TPC-W
16
16384
256
16
16384
256
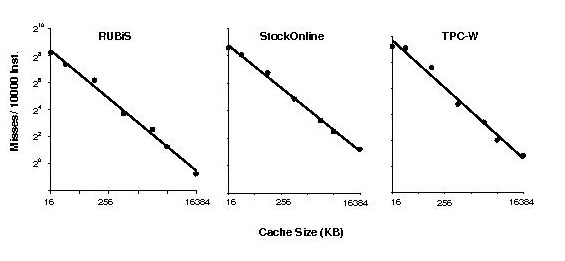
Figure 3:
Cache misses
(per 10k instructions) plotted against
cache size
on a log-log plot. Measurements were taken from
real Intel
servers using the Oprofile monitoring tool [2]. The
same
nonstationary workload was issued for each test. Cache
lines were
64 bytes.
3.3 Trait
Model of Cache Size on Cache Misses
Figure 3
plots data-cache miss rates relative to cache
size on a
log-log scale. Using least squares regres-
sion, we
calibrated linear models of the form ln(Y) =
Bln(X)
+ A. We observe low residual errors for each
application
in our testbed. Specifically, the largest nor-
malized
residual error observed for RUBiS, StockOnline,
and TPCW is
0.08, 0.03, and 0.09 respectively. The cali-
brated B
parameters for RUBiS, StockOnline, and TPCW
are -0.83,
-0.77, and -0.89 respectively. Log-log linear
models with
slopes between (-2, 0) are known as power
law
distributions [19,33,43]
We justify
our power-law trait model by making ob-
servations
on its rate of change, shown in Equation 1.
dY
dX
= Be
A
X
B−1
(1)
For small
values of X, the rate of change is steep, but
as X tends
toward infinity the rate of change decreases
and slowly (i.e.,
with a heavy tail) approaches zero.
The
heavy-tail aspect of a power law means the rate of
change
decreases more slowly than can be described us-
ing an
exponential model. In terms of cache misses,
this means a
power-law cache model predicts significant
miss rate
reductions when small caches are made larger,
but almost
no reductions when large caches are made
larger. The
business logic tier for Internet services ex-
hibits such
behavior by design. Specifically, per-request
misses due
to lack of capacity are significantly reduced
by larger L1
caches. However, garbage collection and
other
infrequent-yet-intensive operations will likely in-
cur misses
even under large cache sizes.
A power law
relationship requires the calibration of
only two
free parameters (i.e., A, and B), which makes it
practical
for real-world production environments. How-
ever, there
are many other functional forms that have
only two
free parameters; how does our trait model
compare to
alternatives? Table 2 compares logarithmic,
Log
Exp.
Power
Log
law
-normal
lowest
0.011
0.105
0.005
0.001
RUBiS
median
0.094
0.141
0.028
0.027
highest
0.168
0.254
0.080
0.072
lowest
0.013
0.010
0.010
0.012
Stock
median
0.075
0.099
0.023
0.024
highest
0.026
0.142
0.034
0.042
lowest
0.046
0.044
0.011
0.007
TPCW
median
0.109
0.084
0.059
0.060
highest
0.312
0.146
0.099
0.101
Table 2:
Normalized
residual error of cache models that have
fewer than
three free parameters. The lowest, median, and
highest
normalized residuals are reported from observations on
seven
different cache sizes.
exponential,
and power law functional forms. Power
law models
have lower median normalized residual er-
ror than
logarithmic and exponential models for each
application
in our testbed. Also, we compare against
a
generalized (quadratic) log-normal model, ln(Y) =
B
2
ln(X)
2
+B
1
ln(X)+A.
This model allows for an addi-
tional free
parameter (B
2
) in
calibration, and is expected
to provide a
better fit, though it cannot be calibrated from
observations
on one machine. Our results show that the
additional
parameter does not substantially reduce resid-
ual error.
For instance, the median residual error for the
power law
distribution is approximately equal to that of
the
generalized log-normal distribution. We note that
other
complex combinations of these models may pro-
vide better
fits, such as Weibull or power law with expo-
nential
cut-off. However, such models are hard to cali-
brate with
the limited data available in production envi-
ronments.
3.4 Trait
Models of Request Mix on Instruc-
tions and
Cache Misses
Figure 4
plots a linear combination of request type fre-
quencies
against the instruction count, L1 misses, and L2
misses for
RUBiS. Our parsimonious linear combination
has only one
model parameter for each request type, as
shown below.
C
k
=
∑
types j
α
jk
N
j
(2)
Where C
k
represents
one of the targeted processor met-
rics and N
j
represents
the frequency of requests of type
j.
The model parameter
α
jk
transforms
request-type
frequencies
into demand for processor resources. Intu-
itively,
α
jk
represents
the typical demand for processor
resource k
of type j. We refer to this as a request-mix
model, and
we observe excellent prediction accuracy.
The 90th
percentile normalized error for instructions, L1
misses, and
L2 misses were 0.09, 0.10, 0.06 respectively.
100
10000
1000000
100
10000
1000000
Actual
P
r
e
d
ic
t
io
n
y = 1.15x
y = .85x
Instructions
L1 misses
L2 misses
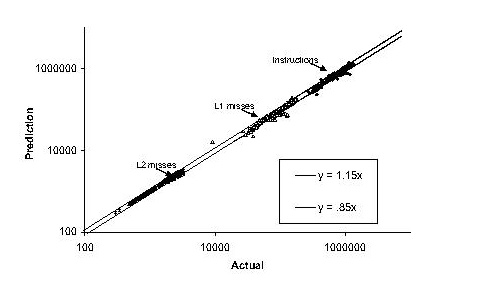
Figure 4:
RUBiS
instruction count and aggregate cache misses
(L1 and L2)
plotted against a linear request mix model’s predic-
tions.
Measurements were taken from a single processor Intel
Pentium D
server. Lines indicate 15% error from the actual
value.
Collected with OProfile [2] at sampling rate of 24000.
Request-mix
models are justifiable, because business-
logic
requests of the same type typically follow similar
code paths.
The number of instructions required by a
request will
likely depend on its code path. Similarly,
cold-start
compulsory misses for each request will de-
pend on code
path, as will capacity misses due to a re-
quest’s
working set size. However, cache misses due to
sharing
between requests are not captured in a request-
mix model.
Such misses are not present in the single
processor
tests in Figure 4.
Table 3
evaluates request-mix models under platform
configurations
that allow for shared misses. The first
three
columns report low normalized error when re-
sources are
adequately provisioned (below 0.13 for all
applications),
as they would be in production environ-
ments.
However under maximum throughput conditions,
accuracy
suffers. Specifically, we increased the volume
of the
tested request mixes by a factor of 3. Approx-
imately 50%
of the test request mixes achieved 100%
processor
utilization. Normalized error increased for the
L1 miss
metric to 0.22–0.34. These results are consis-
tent with
past work [29] that attributed shared misses in
Internet
services to contention for software resources. In
the
realistic, adequately provisioned environments that
we target,
such contention is rare. We conclude that
request-mix
models are most appropriate in realistic en-
vironments
when resources are not saturated.
Request-mix
models can be calibrated with times-
tamped
observations of the targeted processor metric and
logs of
request arrivals, both of which are commonly
available in
practice. Past work [40] demonstrated that
unrealistic
stationary workloads are not sufficient for cal-
ibration.
Request-mix models can require many observa-
tions before
converging to good parameters. For the real
and
benchmark applications that we have seen, request
mix models
based on ten hours of log files are typically
sufficient.
2-way SMP
Dual-core
Hyperthreading
Max tput
(L1 miss)
(L2 miss)
(L1 miss)
(L1 miss)
RUBiS
0.044
0.030
0.045
0.349
Stock
0.060
0.077
0.096
0.276
TPCW
0.035
0.084
0.121
0.223
Table 3:
Median
normalized residual error of a request-mix
model under
different environments. Evaluation spans 583 re-
quest mixes
from a nonstationary trace. The target architectural
metric is
shown in parenthesis. All tests were performed on
Pentium D
processors. Hyperthreading was enabled in the sys-
tem BIOS.
2-way SMP and dual-cores were enabled/disabled
by the
operating system scheduler. The “max tput” test was
performed on
a configuration with 2 processors and 4 cores en-
abled with
hyperthreading on.
4
Cross-Platform Performance Predictions
Section 3
described trait models, which are parsimo-
nious
characterizations of only one aspect of a complex
system. In
this section, we will show that trait mod-
els can be
composed to predict application-level perfor-
mance for
the whole system. Our novel composition is
formed from
expert knowledge about the structure of In-
ternet
services. In particular, we note that instruction and
memory-access
latencies are key components of the pro-
cessing time
of individual requests, and that Internet ser-
vices fit
many of the assumptions of a queuing system.
Our model
predicts application-level performance across
workload
changes and several platform parameters in-
cluding:
processor speed, number of processors (e.g., on-
chip cores),
cache size, cache latencies, and instruction
latencies.
Further, our model can be calibrated from the
logs
described in Table 1. Source code access, instru-
mentation,
and controlled experiments are not required.
We attribute
the low prediction error of our model to ac-
curate trait
models (described in Section 3) and a princi-
pled
composition based on the structure of Internet ser-
vices.
The
remainder of this section describes the composi-
tion of our
cross-platform model, then presents the test
platforms
that we use to validate our model. Finally, we
present
results by comparing against alternative model-
ing
techniques. In Section 5, we complete the challenge
of turning
15-cent production data into a dollar by using
our model to
guide management decisions like platform
selection
and load balancing.
4.1
Composition of Traits
The amount
of time spent processing an end-user re-
quest,
called service time, depends on the instructions
and memory
accesses necessary to complete the request.
Average CPU
service time can be expressed as
s =
I ×(CPI+(H
1
C
1
+H
2
C
2
+M
2
C
mem
)))
CPU
speed×number of requests
where I is
the aggregate number of instructions required
by a request
mix, CPI is the average number of cycles per
instruction
(not including memory access delays), H
k
is
the
percentage of hits in the L
k
cache per
instruction, M
k
is the
percentage of misses in the L
k
cache per
instruc-
tion, and C
k
is the
typical cost in cycles of accesses to the
L
k
cache [22]. CPI,
CPUspeed, and C
k
are
typically re-
leased in
processor spec sheets [6]. Recent work [16] that
more
accurately approximates CPI and C
k
could trans-
parently
improve the prediction accuracy of our model.
This model
is the basis for our cross-platform perfor-
mance
prediction. Subsequent subsections will extend
this base to
handle changes in application-level workload
and cache
size parameters, and to predict the application-
level
performance.
4.1.1
Request Mix Adjustments
In Section
3, we observed that both instruction counts
and cache
misses, at both L1 and L2, are well modeled
as a linear
combination of request type frequencies:
I =
∑
types j
α
I j
N
j
and
#M
k
=
∑
types j
α
M
k
j
N
j
where I is
the number of instructions for a given volume
and mix of
requests, N
j
is the
volume of requests of type
j,
and #M
k
is the
number of misses at cache level k. The
intuition
behind these models is straightforward:
α
I j
, for
example,
represents the typical number of instructions
required to
serve a request of type j. We apply ordinary
least
squares regression to a 10-hour trace of nonstation-
ary request
mixes to calibrate values for the
α
parame-
ter. After
calibration, the acquired
α
parameters
can be
used to
predict performance under future request mixes.
Specifically,
we can predict both instruction count and
aggregate
cache misses for an unseen workload repre-
sented by a
new vector N of request type frequencies.
4.1.2
Cache Size Adjustments
Given L1 and
L2 cache miss rates observed on the cur-
rent
hardware platform, we predict miss rates for the
cache sizes
on a new hardware platform using the power-
law cache
model: M
k
= e
A
S
B
k
where S
k
is the size
of the
level-k cache.
We calibrate
the power law under the most strenuous
test
possible: using cache-miss observations from only
an L1 and L2
cache. This is the constraint under which
many
consultants must work: they can measure an ap-
plication
running in production on only a single hard-
ware
platform. Theoretically, the stable calibration of
power law
models desires observations of cache misses
on 5 cache
sizes [19]. Calibration from only two obser-
vations
skews the model’s predictions for smaller cache
sizes [33].
However in terms of service time prediction,
the penalty
of such inaccuracies—L1 latency—is low.
4.1.3
Additional Service Time Adjustments
Most modern
processors support manual and/or dynamic
frequency
adjustments. Administrators can manually
throttle CPU
frequencies to change the operation of the
processor
under idle and busy periods. Such manual poli-
cies
override theCPUspeed parameter in processor spec.
sheets.
However, power-saving approaches in which the
frequency is
automatically adjusted only during idle pe-
riods are
not considered in our model. Such dynamic
techniques
should not affect performanceduring the busy
times in
which the system is processing end-user re-
quests.
We consider
multi-processors as one large virtual pro-
cessor.
Specifically, the CPUspeed parameter is the sum
of cycles
per second across all available processors. We
do not
distinguish between the physical implementations
of logical
processors seen by the OS (e.g., SMT, multi-
core, or
SMP). We note however that our model accuracy
could be
improved by distinguishing between cores and
hyperthreads.
4.1.4
Predicting Response Times
Service time
is not the only component of a request’s
total
response time; often the request must wait for re-
sources to
become available. This aspect of response
time, called
queuing delay, increases non-linearly as the
demand for
resources increases. Queuing models [27]
attempt to
characterize queuing delay and response time
as a
function of service time, request arrival rate, and
the
availability of system resources. Our past work pre-
sented a
queuing model that achieves accurate response
time
prediction on real Internet services [40]. That par-
ticular
model has two key advantages: 1) it considers the
weighted
impact of request mix on service times and 2) it
can be
easily calibrated in the production environments
that we
target. It is a model of aggregate response time y
for a given
request mix and is shown below:
y =
n
∑
j=1
s
j
N
j
+
∑
r
( 1
λ
·
U
2
r
1−U
r
)·
n
∑
j=1
N
j
where
λ
and U
r
respectively
denote the aggregate count
of requests
in the given mix (i.e., arrival rate) and the av-
erage
utilization of resource r, respectively. Utilization is
the product
of average service time and arrival rate. The
first term
reflects the contribution of service times to ag-
gregate
response time, and the second considers queuing
delays. For
average response time, divide y by
λ
. The
parameter s
j
captures
average service time for type j and
can be
estimated via regression procedures using obser-
vations of
request response times and resource utiliza-
tions [40].
Note that y reflects aggregate response time
for the
whole system; s
j
includes
delays caused by other
resources—
not just processing time at the business-logic
tier. Our
service time predictions target the portion of s
j
attributed
to processing at the business-logic tier only.
4.2
Evaluation Setup
We
empirically evaluate our service and response time
predictions
for RUBiS, StockOnline, and TPC-W. First,
we compare
against alternative methods commonly used
in practice.
Such comparisons suggest that our model
is
immediately applicable for use in real world prob-
lems. Then
we compare against a model recently pro-
posed in the
research literature [25]. This comparison
suggests
that our principled modeling methodology pro-
vides some
benefits over state-of-the-art models.
4.2.1
Test Platforms
We
experiment with 4 server machines that allow for a
total of 11
different platform configurations. The various
servers are
listed below:
PIII Dual-processor
PIII Coppermine with 1100 MHz
clock rate,
32 KB L1 cache, and 128 KB L2 cache.
PRES Dual-processor
P4 Prescott with 2.2 GHz clock
rate, 16 KB
L1 cache, and 512 KB L2 cache.
PD4 Four-processor
dual-core Pentium D with 3.4 GHz
clock rate,
32 KB L1 cache, 4 MB L2 cache, and
16 MB L3
cache.
XEON Dual-processor
dual-core Pentium D Xeon that
supports
hyperthreading. The processor runs at
2.8 GHz and
has a 32 KB L1 cache and 2 MB L2
cache.
We used a
combination of BIOS features and OS
scheduling
mechanisms to selectively enable/disable hy-
perthreading,
multiple cores, and multiple processors on
the XEON
machine, for a total of eight configurations.
We describe
configurations of the XEON using nota-
tion of the
form “#H/#C/#P.” For example, 1H/2C/1P
means
hyperthreading disabled, multiple cores enabled,
and multiple
processors disabled. Except where other-
wise noted,
we calibrate our models using log files from
half of a
10-hour trace on the PIII machine. Our log files
contain
aggregate response times, request mix informa-
tion,
instruction count, aggregate L1 cache misses, and
aggregate L2
cache misses. The trace contains over 500
mixes
cumulatively. Request mixes from the remain-
ing half of
the trace were used to evaluate the normal-
ized
residual error
|predicted−actual|
actual
on the
remaining ten
platforms/configurations.
Most mixes in the second half
of the trace
constitute extrapolation from the calibration
data set;
specifically, mixes in the second half lie outside
the convex
hull defined by the first half.
4.2.2
Alternative Models Used In Practice
Because
complex models are hard to calibrate in data-
constrained
production environments, the decision sup-
port tools
used in practice have historically preferred
simplicity
to accuracy. Commonly used tools involve
simple
reasoning about the linear consequences of plat-
form
parameters on CPU utilization and service times.
Processor
Cycle Adjustments Processor upgrades
usually mean
more clock cycles per second. Although
the rate of
increase in clock speeds of individual proces-
sor cores
has recently slowed, the number of cores per
system is
increasing. Highly-concurrent multi-threaded
software
such as business-logic servers processing large
numbers of
simultaneous requests can exploit the in-
creasing
number of available cycles, so the net effect is
a
transparent performance improvement. A common ap-
proach to
predicting the performance impact of a hard-
ware upgrade
is simply to assume that CPU service times
will
decrease in proportion to the increase in clock speed.
For service
time prediction, this implies
st
new
= st
orig
×
cycles
orig
cycles
new
(3)
However,
this approach does not account for differences
in cache
sizes on the old and new CPUs. Section 3 has
shown that
changes to the cache size have non-linear ef-
fects on the
number of cache misses for business-logic
servers,
which in turn affects CPU service times and
CPU
utilization. Furthermore, cache miss latencies dif-
fer across
hardware platforms, and these differences too
may affect
CPU service times.
Benchmark-Based
Adjustments A more sophisti-
cated
approach used widely in practice is to predict per-
formance
using ratios of standard application benchmark
scores.
Specifically, these approaches measure the ser-
vice times
and maximum throughput for a target applica-
tion on both
the new and original platform. This applica-
tion’s
performance is expected to be representative of a
larger class
of applications. This model is shown below:
st
new
= st
orig
×
TPC score
orig
TPC score
new
(4)
This
approach improves on the processor cycle adjust-
ments by
considering the effect of caching and other
architectural
factors. However, modern business-logic
servers can
vary significantly from standard benchmark
applications.
Indeed, standard benchmarks differ sub-
stantially from
one another in terms of CPI and miss fre-
quencies
[39]!
Workload
Adjustments
Workload
fluctuations are
ubiquitous
in Internet services, and we frequently wish
to predict
the effects of workload changes on system re-
sources. One
typical approach is to model CPU utiliza-
tion as a
linear function of request volume.
utilization
new
= utilization
orig
×
request rate
new
request rate
orig
(5)
The problem
with this approach is that while it accounts
for changes
in the aggregate volume of requests, it ig-
nores
changes in the mix of request types. We call such
a model a
scalar performance model because it treats
workload as
a scalar request rate rather than a vector of
type-specific
rates. Nonstationarity clearly poses a seri-
ous problem
for scalar models. For example, if request
volume
doubles the model will predict twice as much
CPU
utilization. However if the increase in volume was
due entirely
to a lightweight request type, actual utiliza-
tion may
increase only slightly.
4.3
Results
4.3.1
Accuracy of Service Time Predictions
We first
consider the problem of predicting average per-
request CPU
service times of an application on a new
hardware
platform given observations of the application
running on
our PIII platform. We compare our method
with three
alternatives: 1) the näıve cycle-based adjust-
ment of
Equation 3 with linear workload adjustments of
Equation 5,
2) a variant in which we first predict service
time as a
function of request mix using a linear weighted
model and
then apply the cycle-based adjustment, and
3) the
benchmark-based method of Equation 4 with re-
quest mix
workload adjustments.
Table 4
shows the prediction error for RUBiS. Our
method has
less error than the benchmark-based method
for all
target platforms. In all cases except one, our
method has
lower error than its three competitors. Most
often, our
model has less than one third the error of
competing
approaches. The results for StockOnline and
TPC-W are
similar. Table 5 shows that our predictions
are always
the most accurate for the StockOnline appli-
cation. Our
results for TPC-W (Table 6) show consis-
tently low
error for our model (always below 0.17).
Target
Cycle pred
Bench-
Our
Processor
scalar
req-mix
mark
Method
PRES
0.48
0.35
0.30
0.06
PD4
0.24
0.17
0.32
0.07
XEON 1H/1C/1P
0.63
0.49
0.27
0.10
XEON 1H/1C/2P
0.43
0.28
0.24
0.08
XEON 1H/2C/1P
0.39
0.30
0.26
0.02
XEON 1H/2C/2P
0.36
0.27
0.57
0.03
XEON 2H/1C/1P
0.42
0.28
0.24
0.02
XEON 2H/1C/2P
0.12
0.05
0.29
0.24
XEON 2H/2C/1P
0.35
0.22
0.32
0.02
XEON 2H/2C/2P
0.18
0.13
0.38
0.09
Table 4:
Median
normalized residual error of service time pre-
dictions
for RUBiS. Models are calibrated on our PIII platform
from half
of a 10-hour nonstationary trace. The numbers pre-
sented are
the median error when the models are used to predict
the second
half of the nonstationary trace on the targeted plat-
forms. The
median across platforms for our method is 0.07.
Target
Cycle pred
Bench-
Our
Processor
scalar
req-mix
mark
Method
PRES
0.35
0.23
0.56
0.18
PD4
0.38
0.28
0.42
0.12
XEON
1H/1C/1P
0.55
0.41
0.21
0.10
XEON
1H/1C/2P
0.48
0.38
0.34
0.12
XEON
1H/2C/1P
0.44
0.39
0.35
0.09
XEON
1H/2C/2P
0.36
0.26
0.71
0.12
XEON
2H/1C/1P
0.48
0.38
0.34
0.17
XEON
2H/1C/2P
0.22
0.16
0.52
0.14
XEON
2H/2C/1P
0.45
0.37
0.47
0.15
XEON
2H/2C/2P
0.36
0.29
0.39
0.02
Table 5:
Median
normalized residual error of service time pre-
dictions
for StockOnline. The median across platforms for our
method is
0.12.
Target
Cycle pred
Bench-
Our
Processor
scalar
req-mix
mark
Method
PRES
0.48
0.35
–
0.11
PD4
0.28
0.24
–
0.09
XEON
1H/1C/1P
0.38
0.32
–
0.13
XEON
1H/1C/2P
0.23
0.16
–
0.13
XEON
1H/2C/1P
0.22
0.16
–
0.12
XEON
1H/2C/2P
0.27
0.22
–
0.17
XEON
2H/1C/1P
0.28
0.23
–
0.06
XEON
2H/1C/2P
0.24
0.20
–
0.11
XEON
2H/2C/1P
0.20
0.15
–
0.16
XEON
2H/2C/2P
0.18
0.21
–
0.14
Table 6:
Median
normalized residual error of service time pre-
dictions
for TPC-W. Note, the benchmark method is not appli-
cable for
TPC-W, since observations on the new platform are
required
for calibration. The median across platforms for our
method is
0.13.
0%
25%
50%
75%
100%
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
0.45
Normalized
Residual Error
C
D
F
PIII to XEON
PIII to PRES
PRES to XEON
XEON to PIII
(a) RUBiS
0%
25%
50%
75%
100%
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
0.45
0.5
0.55
C
D
F
PI I to XEON
PI I to PRES
PRES to XEON
XEON to PI I
(b)
StockOnline
0%
25%
50%
75%
100%
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
0.45
0.5
0.55
0.6
0.65
C
D
F
PI I to XEON
PI I to PRES
PRES to XEON
XEON to PI I
(c) TPCW
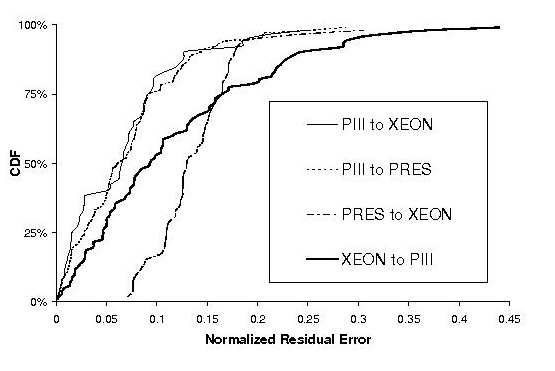
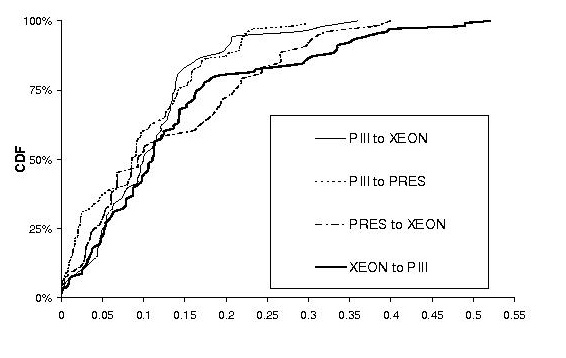
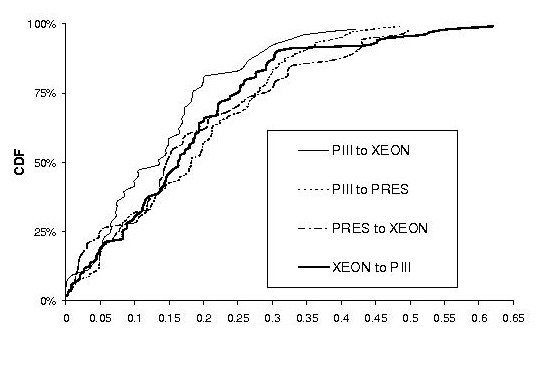
Figure 5:
Cumulative
distributions of normalized residual er-
ror for
response time predictions across nonstationary request
mixes. Mean
response times on the PIII, P4, and XEON were
256, 106,
and 93 ms respectively. XEON shortens XEON
2H/2T/2P
according to our naming conventions.
4.3.2
Accuracy of Response Time Predictions
Figure 5
shows the prediction accuracy of our queuing
model. For
predictions from PIII to XEON, our model
converts
median service time error of 0.09, 0.02, and
0.14 into
response time predictions with median error of
0.06, 0.09,
and 0.13, for RUBiS, TPC-W, and StockOn-
line
respectively. Even though response time is a more
complex
metric, our prediction error remains low.
Figure 5
also demonstrates the robustness of our
method. The
85th percentile of our prediction error for
RUBiS is
always below 0.21 no matter which platforms
we use for
calibration and validation. For StockOnline
and TPC-W,
the 85th percentile prediction error is below
0.29 and
0.30, respectively.
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
RUBiS Stock
TPC-W
RUBiS Stock
TPC-W
N
o
r
m
a
l
i
ze
d
E
r
r
o
r
Artificial
Neural Network
Our
Cross-Platform Model
New
workload only
New platform
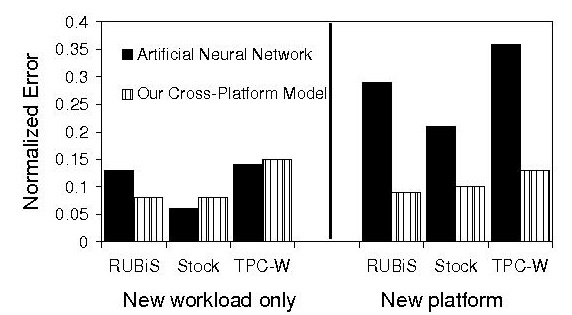
Figure 6:
Comparison
of an artificial neural network to our
cross-platform
model. The median normalized error for pre-
dictions of
average response time are reported. We trained the
ANN on
several subsets of the training data. The reported val-
ues are
from the training subset that yielded the lowest predic-
tion error
for each application.
4.3.3
Comparison to Neural Net Model
Ipek et
al. used an artificial neural network to pre-
dict
performance across changes in platform parame-
ters [25].
Artificial neural networks can be automatically
calibrated
without knowledge of the form of the func-
tional
relationship between input parameters and output
variables.
Also, they operate with categorical and con-
tinuous
data. However, the limited amount of available
data for
cross-platform management for real-world In-
ternet
services presents a challenge for neural networks.
Neural
networks require many observations of the input
parameters
and output variables in order to learn the un-
derlying
structure of the system. In contrast, our compo-
sition of
trait models is based on our knowledge of the
underlying
structure of Internet services.
We
implemented an artificial neural network (ANN) as
described
in [25]. We used 16 hidden states, a learning
rate
0.0001, a momentum value of 0.5, and we initial-
ized the
weights uniformly. The output variable for the
ANN was the
average response time. The training set for
the ANN
consisted of observations on the PIII and PRES
platforms.
The validation set consisted of observations
under new
transaction mixes on the PRES and XEON
platforms.
Figure 6
shows the median prediction error of the
ANN
compared to our model on the validation set. Our
model has
comparable accuracy, within 0.02, under sit-
uations in
which the ANN predicts only the effects of
workload
changes. However, the ANN has up to 3X the
error of
our model when predicting response time on the
unseen XEON
platform. Observations on two platforms
are not
enough for the ANN to learn the relationship be-
tween
platform parameters and response time. These re-
sults
suggest that our methodology, a composition of trait
models, may
be better suited for cross-platform manage-
ment in
data-constrained production environments.
5
Enhanced System Management
In this
section, we use our model to improve cross-
platform
management decisions for Internet services. In
general,
such management decisions can have significant
consequences
on the bottom line for service providers,
which
completes our metaphor of creating a dollar from
15 cents.
We explore two specific management problems
often
encountered in real-word production environments.
• Platform
Selection When building or augmenting a
server
cluster, service providers wish to select plat-
forms that
will maximize performance relative to a
cost. We
look at the problem of choosing the hard-
ware
platform that yields maximum response-time-
bounded
throughput per watt. This problem is chal-
lenging
because architectural features and config-
uration
options that enhance performance also in-
crease
power consumption. Of course, the problem
could also
be solved by testing the application of
interest on
each target processor configuration, but
such
exhaustive testing is typically too expensive
and time
consuming in real-world scenarios.
• Platform-Aware
Load Balancing for Heterogeneous
Servers Service
providers wish to extract maxi-
mum
performance from their server infrastructure.
We show
that näıvely distributing arriving requests
across all
machines in a server cluster may yield
sub-optimal
performance for certain request types.
Specifically,
certain types of requests execute most
efficiently
only under certain platform configura-
tions in
the server cluster. Our cross-platform per-
formance
predictions can identify the best platform
for each
request type.
5.1
Platform Selection
Our metric
for platform selection is throughput per
watt. We
leverage our performancemodel of application-
level
response time to predict the maximum request ar-
rival rate
that does not violate a bound on aggregate
response
time. Given an expected request mix, we it-
eratively
query our model with increased aggregate ar-
rival
rates. The response-time-bounded throughput is the
maximum
arrival rate that does not exceed the response
time bound.
The other half of our metric for platform
selection
is power consumption, which we acquire from
processor
spec sheets [6]. Admittedly, processor specs
are not the
most accurate source for power consump-
tion data
[17,21], but they will suffice for the purpose of
demonstrating
our model’s ability to guide management
decisions.
For this
test, we compare our model against the other
cross-platform
prediction methods commonly used in
practice.
The competing models are not fundamentally
0%
20%
40%
60%
80%
100%
Best
Top 2
Top 3
P
e
r
c
e
n
t
a
g
e
o
f
W
r
o
n
g
D
e
c
i
s
i
o
n
s
Cycle-based
Benchmark-based
Our
extensions
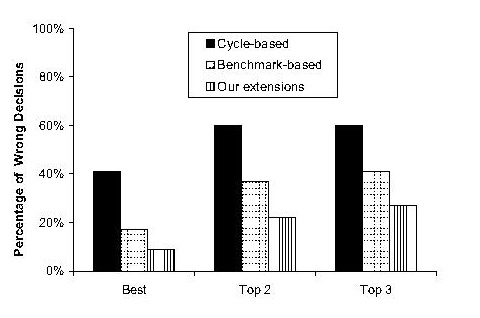
Figure 7:
Probability
of incorrect decisions for model-driven
platform
selection.
intended to
model response time, so we apply our queue-
ing model
to each. Specifically, the difference in results
in this
section come from the different methods of ser-
vice time
prediction presented in Section 4. We cali-
brate
performancemodels on the PIII platform, and show
results for
the RUBiS auction service. Table 7 com-
pares the
measured throughput per watt to the predic-
tions of
each method. The absolute value of the dif-
ference
between the actual ranking and the predicted
ranking (i.e.,
|pred − act|), is never greater than 1 with
our method.
Comparatively, the cycle-based and bench-
mark
approach have mis-rankings of 5 and 3 respec-
tively. In
practice, mis-rankings could cause service
providers
to purchase an inefficient platform. One way
to measure
the cost of such mis-predictions is to mea-
sure the
net loss in throughput per watt between the mis-
predicted
platform and the properly ranked platform, i.e.,
tpw
predicted
rank k
tpw
actual
rank k
× 100%. The
maximum loss is only 5%
for our
method, but is 45% and 12% for the cycle-based
and
benchmark methods, respectively.
Often in
practice, platform selections are made from a
few
properly priced platforms. We divided our platform
into
subsets of five, and then predicted the best platform
in the
subset. We report how often each performance
prediction
method does NOT correctly identify the best,
the top
two, and the top three platforms. Figure 7 shows
that our
method selects the best processor configuration
for 230 of
252 (91%) combinations. More importantly,
alternative
methods are 2X and 4X more likely to make
costly
wrong decisions. For the problems of correctly
identifying
the top two and top three platforms, our ap-
proach
yields the correct decision for all but 25% of plat-
form
subsets whereas our competitors are wrong more
than 41%
and 60% of the time.
Processor
Rankings
actual
our
cycle-
bench-
method
based
mark
PD4
1
1
1
1
XEON
2H/2C/2P
2
2
6
2
XEON
2H/2C/1P
3
4
3
5
XEON
2H/1C/1P
4
3
4
3
XEON
2H/1C/2P
5
5
5
6
XEON
1H/1C/1P
6
7
7
7
PRES
7
6
2
4
XEON
1H/2C/1P
8
8
8
8
XEON
1H/1C/2P
9
9
9
9
XEON
1H/2C/2P
10
10
10
10
Table 7:
Platform
rankings of the response-time-bounded
throughput
per watt on RUBiS. Response time bound was
150ms.
Power consumption data was taken from [6]. Actual
response-time-bounded
throughput was measured as a base-
line.
5.2
Platform-Aware Load Balancing
In this
section, we first observe that the best proces-
sor for
one request type may not be the best processor
for
another. Second, we show that the techniques de-
scribed in
Section 4 enable black-box ranking of pro-
cessors for
each request type. Our techniques comple-
ment
advanced type-based load distribution techniques,
like
locality-aware request distribution, in heterogeneous
clusters
and do not require intrusive instrumentation or
benchmarking.
A mapping of request type to machine
can be made
with the limited data available to consul-
tants.
Table 8
shows the expected and actual response time
for four
request types that contribute significantly to the
overall
response time of RUBiS. These types were cho-
sen because
they are representative of different demands
for
processor resources in RUBiS. The first type rep-
resents
requests for static content. Since XEON and
PRES have
similar clock rates there is not much dif-
ference
between their processing power on this request
type. Search
Items by Region has a large working set
and
benefits from fewer L2 cache misses on XEON. View
Item has
a small working set size that seems to fit mostly
within the
larger L1 cache of XEON. Lookup user infor-
mation,
however, has unique cache behavior. Its working
set is
medium-sized consisting of user information, user
bid
histories, and user items currently for sale. This re-
quest type
seems to benefit more from the lower-latency
512KB cache
of PRES, than it does from the larger 32KB
L1 cache of
Xeon.
Table 8
also shows our ability to predict the best ma-
chine on a
per-request-type basis. We achieve this by us-
Response
Time Per-type (ms)
PRES
Dual-core
Xeon
actual
predict
actual
predict
Browse.html
53
49
48
47
Search
Items by Reg.
423
411
314
354
View Item
102
110
89
92
Lookup User
Info
80
75
132
109
Table 8:
Expected
response time of each request-type when is-
sued in
isolation. Predictions are based on log file observations
from PIII.
The dual-core Xeon is a single processor. Request
mix
consisted of only requests of the tested type at a rate of ten
requests
per second.
ing the
techniques described in Section 4. In particular,
we
calibrate the parameters of our business-logic traits
using only
lightweight passive observations of a system
serving a
realistic nonstationary workload. Then, we pre-
dict
performance under a workload mix that consists of
only one
type of request. This is done for each machine
and request
type in the system.
6
Related Work
Our
contributions in this paper span model-driven sys-
tem
management, workload characterization, and perfor-
mance
modeling. The general literature on these topics
is vast;
this section briefly reviews certain related works.
6.1
Model-Driven Management
Networked
services are now too complex for ad-hoc,
human-centric
management. Performance predictions,
the
by-product of performance models, offer a conve-
nient
abstraction for principled, human-free manage-
ment. Our
previous work [41] presented a whole-system
performance
model capable of guiding the placement
and
replication of interacting software components (e.g.,
web server,
business-logic components, and database)
across a
cluster. Shivam et al. [34,37] model scientific
applications
on a networked utility. Their model can be
used to
guide the placement of compute and I/O-bound
tasks and
the order in which workflows execute. Doyle
et al. provide
a detailed model of file system caching
for
standard web servers that is used to achieve resource
management
objectives such as high service quality and
performance
isolation [14]. Magpie [9] models the con-
trol flow
of requests through distributed server systems,
automatically
clustering requests with similar behavior
and
detecting anomalous requests. Aguilera et al. [7]
perform
bottleneck analysis under conditions typical of
real-world
Internet services. Thereska and Ganger [42]
investigate
real-world causes for inaccuracies in storage
system
models and study their effect on management
policies.
Finally, our most recent work proposed a model
of
application-level performance that could predict the
effects of
combining two or more applications onto the
same
machine (i.e., consolidation).
The
contribution of this work is a practical method
for
performanceprediction across platform and workload
parameters
that can be used to guide cross-platform de-
cisions for
real-world Internet services.
6.2
Workload Characterization
Internet
services have certain innate resource demands
that span
hardware platforms, underlying systems soft-
ware, and
even the end-user input supplied to them. Pre-
vious work
[32,36] advocated separating the characteri-
zation of
application-specific demands from the charac-
terization
of underlying systems and high-level inputs.
Our trait
models continue in this tradition by providing
parsimonious
and easy-to-calibratedescriptions of an ap-
plication’s
demand for hardware resources. We believe
trait
models exist and can be derived for other types of
applications,
such as databases and file systems.
Characterizations
of application resource demand that
have
functional forms similar to our trait models have
been
observed in past research. Saavedra & Smith
model the
execution time of scientific
FORTRAN
pro-
grams as a
weighted linear combination of “abstract op-
erations”
such as arithmetic and trigonometric opera-
tions [35].
Our request-mix models characterize much
higher
level business-logic operations in a very different
class of
applications. Another difference is that Saave-
dra &
Smith calibrate their models using direct measure-
ments
obtained through invasive application instrumen-
tation
whereas we analyze lightweight passive observa-
tions to
calibrate our models.
Chow
considers the optimal design of memory hierar-
chies under
the assumption of a power-law relationship
between
cache size and miss rates [13]. Smith presents
very
limited empirical evidence, based on a single in-
ternal
Amdahl benchmark, that appears to be roughly
consistent
with Chow’s assumption [38]. Thiebaut and
Hartstein et
al. explore a special case of Chow’s assump-
tion from a
theoretical standpoint [20, 43]. This prior
work is
primarily concerned with the design of cache
hierarchies
and typically employs traces of memory ac-
cesses. We
compose a power-law model with request-
mix models
and queuing models to predict the impact
on response
times of both workload changes and archi-
tectural
changes. Furthermore we employ only passive
observations
of a running application to estimate power-
law
parameters.
The growing
commercial importance of Java-based
middleware
and applications has attracted considerable
attention
in the architecture community. Recent stud-
ies
investigate interactions between Java benchmarks and
architectural
features including branch prediction, hy-
perthreading,
and the CPU cache hierarchy [11,24,29].
One
important difference between these investigations
and our
work is that they focus on throughput whereas
we
emphasize application-level response times. Also,
our work
incorporates expert knowledge about Internet
services
via a novel composition of trait models. We
demonstrated,
in Section 4.3.3, that our composition im-
proves
cross-platform performance prediction when only
limited
production data is available.
6.3
Cross-Platform Performance Models
Chihaia
& Gross report that simple analytic mem-
ory models
accurately predict the execution times of sci-
entific
codes across hardware architectures [12]. We
predict
response times in business-logic servers across
platforms,
and we too find that succinct models suf-
fice for
our purposes. More sophisticated approaches
typically
fall into one of two categories: Knowledge-
free
machine learning techniques [23, 25, 30] and de-
tailed
models based on deep knowledge of processor de-
sign
[16,28,32].
Detailed
knowledge-intensive models typically re-
quire more
extensive calibration data than is available
to
consultants in the practical scenarios that motivate
our work, e.g.,
data available only through simulated
program
execution. Knowledge-free machine learning
methods, on
the other hand, typically offer only limited
insight
into application performance: The structure and
parameters
of automatically-induced models are often
difficult
to explain in terms that are meaningful to a hu-
man
performance analyst or useful in an IT management
automation
problem such as the type-aware load distri-
bution
problem of section 5.2. Furthermore the accu-
racy of
knowledge-free data-mining approaches to cross-
platform
performanceprediction has been a controversial
subject:
See, e.g., Ein-Dor & Feldmesser for sweeping
claims of
accuracy and generality [15] and Fullerton for
a failure
to reproduce these results [18].
Our
contribution is a principled composition of con-
cise and
justifiable models that are easy to calibrate in
practice,
accurate, and applicable to online management
as well as
offline platform selection.
7
Conclusion
This paper
describes a model-driven approach for
cross-platform
management of real-world Internet ser-
vices. We
have shown that by composing trait models—
parsimonious,
easy-to-calibrate characterizations of one
aspect of a
complex system—we can achieve accurate
cross-platform
performance predictions. Our trait mod-
els
themselves are typically accurate to within 10% and
our
application-level performance predictions are typi-
cally
accurate to within 15%. Our approach relies only
on
lightweight passive observations of running produc-
tion
systems for model calibration; source code access,
invasive
instrumentation, and controlled benchmarking
are not
required. Applied to the problem of selecting
a platform
that offers maximal throughput per watt, our
approach
correctly identifies the best platform 91% of
the time
whereas alternative approaches choose a sub-
optimal
platform 2x–4x more frequently. Finally, we
have shown
that our model can improve load balancing in
a
heterogeneous server cluster by assigning request types
to the most
suitable platforms.
8
Acknowledgments
More people
assisted in this work than we can ac-
knowledge
in this section. Keir Fraser, our shepherd,
helped us
polish the camera-ready version. The anony-
mous
reviewers gave rigorous, insightful, and encourag-
ing
feedback, which improved the camera-ready version.
Reviews
from our friends Kim Keeton, Xiaoyun Zhu,
Zhikui
Wang, Eric Anderson, Ricardo Bianchini, Nidhi
Aggarwal,
and Timothy Wood helped us nail down the
contributions.
Jaap Suermondt helped formalize an eval-
uation
methodology for the decision problems in Sec-
tion 5.
Eric Wu (HP) and Jim Roche (Univ. of Rochester)
maintained
the clusters used in our experiments. Part of
this work
was supported by the National Science Foun-
dation
grants CNS-0615045 and CCF-0621472.
References
[1] Apache
software foundation. https://www.apache.
org.
[2]
Oprofile: A sytem profiler for linux.
https://
[3] Rice
university bidding system.
[4]
Stock-online.
stockonline.
models.html.
[6] x86
technical information. https://www.sandpile.
org.
[7] M.
Aguilera, J. Mogul, J. Wiener, P. Reynolds, and
A.
Muthitacharoen.
Performance
debugging for dis-
tributed
systems of black boxes. In SOSP, 2003.
[8] A.
Andrzejak, M. Arlitt, and J. A. Rolia. Bounding the
resource
savings of utility computing models. Technical
report, HP
Labs, Dec. 2002.
[9] P.
Barham, A. Donnelly, R. Isaacs, and R. Mortier. Using
magpie for
request extraction and workload modeling. In
OSDI,
Dec. 2004.
[10] G. Box
and N. Draper. Empirical model-building and re-
sponse
surfaces. Wiley, 1987.
[11] H.
Cain, R. Rajwar, M. Marden, and M. Liphasti. An ar-
chitectural
evaluation of java tpc-w. In HPCA, Dec. 2001.
[12] I.
Chihaia and T. Gross. Effectiveness of simple mem-
ory models
for performance prediction. In ISPASS, Mar.
2004.
[13] C.
Chow. On optimization of storage hiearchy. In IBM J.
Res. Dev.,
May 1974.
[14] R.
Doyle, J. Chase, O. Asad, W. Jin, and A. Vahdat.
Model-based
resource provisioning in a web service util-
ity. In USENIX
Symp. on Internet Tech. & Sys., Mar. 2003.
[15] P.
Ein-Dor and J. Feldmesser. Attributes of the perfor-
mance of
central processing units: A relative performance
prediction
model. CACM, 30(4):308–317, Apr. 1987.
[16] S.
Eyerman, L. Eeckhout, T. Karkhanis, and J. Smith. A
performance
counter architecture for computing accurate
CPI
components. In ASPLOS, Oct. 2006.
[17] X.
Fan, W. Weber, and L. Barroso. Power provisioning
for a
warehouse-sized computer. In ISCA, June 2007.
[18] G. D.
Fullerton. An evaluation of the gains achieved by
using
high-sped memory in support of the system pro-
cessing
unit. CACM, 32(9):1121–1129, 1989.
[19] M.
Goldstein, S. Morris, and G. Yen. Problems with fit-
ting to the
power-law distribution. In The European Phys-
ical
Journal B - Condensed Matter and Complex Systems,
June 2004.
[20] A.
Hartstein, V. Srinivasan, T. Puzak, and P. Emma.
Cache miss
behavior: is it sqrt(2)? In Conference on
Computing
Frontiers, May 2006.
[21] T.
Heath, A. Centeno, P. George, L. Ramos, Y. Jaluria,
and R.
Bianchini. Mercury and freon: Temerature emu-
lation and
management for server systems. In ASPLOS,
Oct. 2006.
[22] J.
Hennessey and D. Patterson. Computer architecture:
A
quantitative approach, fourth edition. In The Morgan
Kaufmann
Series, 2007.
[23] K.
Hoste, A. Phansalkar, L. Eeckhout, A. Georges,
L. John,
and K. Bosschere. Performance prediction based
on inherent
program similarity. In Int’l Conf. on Parallel
Architectures
& Compilation Techniques, Sept. 2006.
[24] W.
Huang, J. Liu, Z. Zhang, and M. Chang. Performance
characterization
of Java applications on SMT processors.
In ISPASS,
Mar. 2005.
[25] E.
Ipek, S. McKee, B. Supinski, M. Schultz, and R. Caru-
ana.
Efficiently exploring archtectural design spaces via
predictive
modeling. In ASPLOS, Oct. 2006.
[26] R.
Isaacs and P. Barham. Performance analysis in loosely-
coupled
distributed systems. In Cabernet Radicals Work-
shop,
Feb. 2002.
[27] R.
Jain. The art of computer systems performance analy-
sis. In Wiley,
1991.
[28] T.
Karkhanis and J. Smith. A first-order superscalar pro-
cessor
model. In ISCA, June 2004.
[29] M.
Karlsson, K. Moore, E. Hagersten, and D. Wood.
Memory
system behavior of java-based middleware. In
HPCA,
Feb. 2003.
[30] B. Lee
and D. Brooks. Accurate and efficient regression
modeling
for microarchitectural performance and power
prediction.
In ASPLOS, Oct. 2006.
[31] X. Li,
Z. Li, P. Zhou, Y. Zhou, S. Adve, and S. Ku-
mar.
Performance-directed energy management for main
memory and
disks. In ASPLOS, Oct. 2004.
[32] G.
Marin and J. Mellor-Crummey. Cross-architecture per-
formance
predictions for scientific applications using pa-
rameterized
models. In SIGMETRICS, June 2004.
[33] M.
Newman. Power laws pareto distributions and zipf’s
law. In Contemporary
Physics, 2005.
[34] S. B.
P. Shivam and J. Chase. Active and accelerated
learning of
cost models for optimizing scientific applica-
tions. In VLDB,
Sept. 2006.
[35] R. H.
Saavedra and A. J. Smith. Analysis of bench-
mark
characteristics and benchmark performance predic-
tion. ACM
Trans. Comp. Sys., 14(4):344–384, Nov. 1996.
[36] M.
Seltzer, D. Krinsky, K. Smith, and X. Zhang. The case
for
application-specific benchmarking. June 1999.
[37] P.
Shivam, A. Iamnitchi, A. Yumerefendi, and J. Chase.
Model-driven
placement of compute tasks in a networked
utility. In
ACM International Conference on Autonomic
Computing,
June 2005.
[38] A.
Smith. Cache memories. In ACM Computing Surveys.
[39] R.
Stets, L. Barroso, and K. Gharachorloo.
A de-
tailed
comparison of two transaction processing work-
loads. In IEEE
Workshop on Workload Characterization,
Nov. 2002.
[40] C.
Stewart, T. Kelly, and A. Zhang. Exploiting nonsta-
tionarity
for performance prediction. In EuroSys, Mar.
2007.
[41] C.
Stewart and K. Shen. Performance modeling and sys-
tem
management for multi-component online services. In
NSDI,
May 2005.
[42] E.
Thereska and G. Ganger. Ironmodel: Robust perfor-
mance
models in the wild. In SIGMETRICS, June 2008.
[43] D.
Thiebaut. On the fractal dimension of computer pro-
grams. In IEEE
Trans. Comput., July 1989.
[44] B.
Urgoankar, G. Pacifici, P. Shenoy, M. Spreitzer, and
A. Tantawi.
An analytical model for multi-tier inter-
net
services and its applications. In SIGMETRICS, June
2005.
