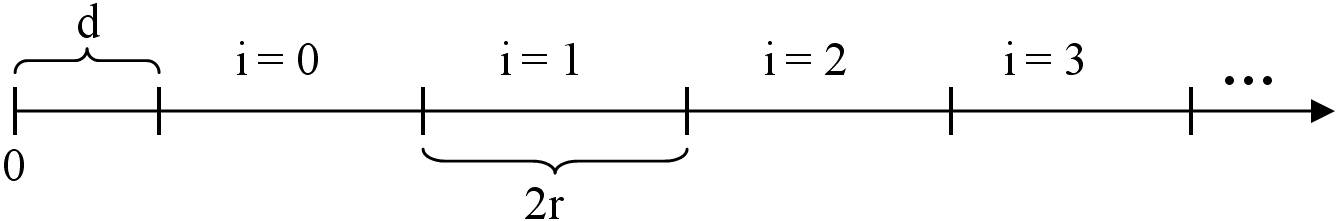Centered Discretization with Application
to Graphical Passwords (full paper)
Sonia Chiasson
Carleton University
Ottawa, Canada
|
Jayakumar Srinivasan
Toronto, Canada
|
Robert Biddle
Carleton University
Ottawa, Canada
|
P. C. van Oorschot
Carleton University
Ottawa, Canada
|
chiasson@scs.carleton.ca, jay.srini@usask.ca, robert_biddle@carleton.ca, paulv@scs.carleton.ca |
|
Abstract
Discretization is used in click-based graphical passwords so that approximately correct entries can be accepted by the system. We show that the existing discretization scheme of Birget et al.(2006) allows for false accepts and false rejects because the tolerance region is not guaranteed to be centered on the original click-point, causing usability and security concerns. Using empirical data from a large user study, we show that this is a significant issue in practice. We then introduce Centered Discretization, a simpler discretization method that eliminates false accepts and false rejects. It also allows for smaller tolerance regions without impacting the usability of the system.
1 Introduction
Graphical passwords have received considerable attention lately as potential alternatives to text-based passwords. One such category are click-based graphical passwords [3, 16, 17, 5, 6, 7] where a password is composed of a series of clicks on one or more pixel-based images. To log in, users re-enter their click-points in the correct order. Click-points that fall within some acceptable tolerance of the original points should be accepted by the system since it is unrealistic to expect users to accurately target individual pixels.
Robust Discretization was proposed by Birget et al. [2] in conjunction with PassPoints [16, 17] as a means of performing discretization of click-points so that approximately correct entries are accepted. As we explain in this paper, it allows for false accepts and false rejects when re-entering passwords because the tolerance region is not guaranteed to be centered on the original click-point. By analyzing data from a large-scale user study, we provide empirical evidence that this likely causes significant problems in practice.
We present Centered Discretization, an alternative scheme that eliminates false accepts and false rejects as defined herein, providing system behaviour consistent with users’ likely mental model of the system. It also allows for a larger theoretical full password space because the tolerance squares can be smaller while still providing the same guaranteed minimum tolerance as Robust Discretization. We compare the usability and security of Centered Discretization and Robust Discretization using data collected from a previous user study of PassPoints. For example on one of the images tested, with a guaranteed tolerance of 9 pixels around a click-point, up to 79% of passwords were found in one guessing attack against Robust Discretization compared to 26% for Centered Discretization.
The paper is organized as follows. Section 2 reviews click-based graphical passwords, describes Robust Discretization, and identifies some important limitations. Centered Discretization is introduced in Section 3. The usability of the two schemes is compared in Section 4 while Section 5 examines how they fare against different security threats. The paper concludes with discussion of the results and final remarks.
2 Background and Related Work
Many graphical password schemes have been proposed in recent years. Surveys of several graphical passwords schemes, circa 2005, are provided by Monrose and Reiter [10] and Suo et al. [14]. As they are most relevant to this current work, we focus on the category of click-based graphical passwords. Click-based graphical passwords were introduced by Blonder [3] who described a system where an image contains a set of predefined clickable regions and a password is a sequence of clicks on these regions. The password space is limited by the number of predefined regions within the image.
More recent systems such as PassPoints [16, 17], Cued Click-Points [6], Persuasive Cued Click-Points [7] and the Two-Level Texto-Graphical Authentication system [13] allow users to choose any pixel within an image as a click-point. Such systems must allow for some level of inaccuracy when re-entering passwords because it is unrealistic to expect users to always identify and target the exact same pixel. As with regular text passwords, rather than store graphical password coordinates “in the clear” they are ideally cryptographically hashed to provide an additional layer of security in case the password file is compromised. However, an approximately correct entry must result in the same hash value as the original password so that the system can recognize it as correct. A simple solution is to overlay a static grid (potentially invisible to users) onto the image and associate each pixel with the grid-square that contains it. The hashed password consists of the identifiers of the grid-squares rather than the original pixels. During re-entry, if a click-point falls within the same grid-square as the original point, then the entry is accepted since its hashed value matches the original. However, using a static grid leads to the “edge problem”: if an original click-point is very close to a grid line, then during re-entry a click-point may be within tolerance but fall in an adjacent grid-square, and thus be rejected by the system because the hash values of the two points do not match. More sophisticated discretization methods are required, as discussed later in this paper.
2.1 Security Threats
Shoulder-surfing, where an attacker may be able to observe a user’s password, is a concern for click-based graphical passwords. The discretization scheme has little impact on the success of a shoulder-surfing attack except that smaller grid-squares dictates that an attacker gaining information through shoulder-surfing must make more accurate observations to be successful.
Dictionary attacks on click-based graphical passwords may be successful when users select click-points falling within hotspots (i.e., areas on an image that are more likely to be selected across users) [8, 15], as part of their password. Knowledge of such hotspots can be used to prune and prioritize an attack dictionary. Thorpe and van Oorschot [15] show that dictionary attacks can crack a significant number of passwords with a relatively small dictionary for PassPoints, using a dictionary based on either sample passwords collected from actual users or likely hotspots as determined through automated image processing techniques. Dirik et al. [8] also had some success using automated image processing to guess PassPoints passwords.
Hotspots are tied to the background images used, the nature of the password selection task (such as having to select 5 points on one image), and the degree of user choice during password selection, but not to the underlying discretization mechanism used. More recent click-based graphical password systems [6, 7] have been designed to significantly increase the effort required by attackers to conduct hotspot analysis and to reduce likelihood that users select click-points that fall within hotspots.
2.2 Robust Discretization
To address the edge problem discussed in Section 2, Birget et al. [2] proposed “Robust Discretization”. This approach involves using three offset grids to guarantee that every point in the image is a “safe” distance away from the edges of at least one grid. It was shown that three grids were necessary and sufficient to guarantee that for any given point in a 2-dimensional space, the system: (1) “guarantees the acceptance of approximately correct passwords”, i.e., if a login click-point is within distance r from the original click-point then the input is accepted; and, (2) “guarantees the rejection of significantly wrong passwords”: if a login click-point is at a distance greater than rmax (see Section 2.2.1) from the original click-point for some specified tolerance, the input is guaranteed to be interpreted as different from the original click-point.
Parameter r represents the minimum tolerance level desired. To achieve the stated objectives, the three grids are diagonally offset from each other by a distance of 2r and each grid-square is of size 6rx6r. When an original click-point is selected, a grid is chosen such that the click-point falls at least distance r from the grid’s edges. We say that the user-entered click-point is r-safe in this particular grid.
When creating a password, a Robust Discretization system selects one of the three grids for each click-point. More specifically, for each point, the system stores the grid identifier in the clear, and determines which grid-square contains the click-point. The coordinates of this grid-square are cryptographically hashed and the hash is stored along with the grid identifier. For each click-point in future login attempts, the system overlays the pre-selected grid onto the image and finds the coordinates of the grid-square containing the click-point. The resulting password is hashed to see if it matches the stored hash value.
2.2.1 False accepts and false rejects
While Robust Discretization guarantees at least an r-safe tolerance around each point, it does not guarantee that this tolerance is exactly r-safe. For example, with grid-squares of size 6rx6r, a reasonable interpretation by users might assume that a 3r tolerance buffer exists around the original click-point. We define an evenly distributed buffer as the centered-tolerance. However, in Robust Discretization, an original click-point is only guaranteed to be at least distance r from edges of the grid-square. So in the worst case, a click-point is of distance r from one edge, but is consequently a distance of 5r=rmax from the opposite edge. Figure 1 shows this discrepancy between centered-tolerance and a Robust Discretization grid-square in the worst case. This means that users clicking r+1 pixels away in one direction could have their login attempt rejected, but could click as far as 5r pixels in the opposite direction and be successful, which may confuse users. Furthermore, to have a usable implementation, r needs to be sufficiently large to allow a reasonable minimum tolerance around an original click-point. This means that the grid-squares will be correspondingly large (at 6rx6r), reducing the password search space for attackers.
In light of these circumstances, we introduce the terms false rejects and false accepts in the context of PassPoints implemented using Robust Discretization (see Figure 1). False rejects occur when a user clicks within the centered-tolerance area of a point but the click is rejected because it falls outside of the Robust Discretization grid-square (as little as r+1 away from the original point). False accepts describe the opposite scenario, where a click falls outside of the centered-tolerance area but is accepted because it is still contained within the correct Robust Discretization grid-square (as far as 5r pixels from the original point). In the best case, the Robust Discretization square and the centered-tolerance square are perfectly overlaid and the click-point is centered in the grid-square, but in practice the squares are usually offset.
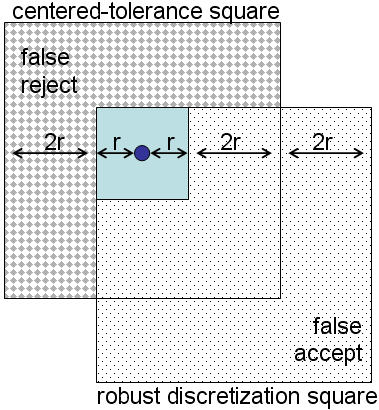
| Figure 1: The small circle is the original click-point. The centered-tolerance square is the evenly distributed tolerance likely expected by a user. The dotted square is the grid-square used by Robust Discretization in the worst-case. The non-overlapping region of the centered-tolerance square is the area where false rejects would occur in Robust Discretization, while the non-overlapping region of the Robust Discretization square indicates false accepts in Robust Discretization. |
2.2.2 Size of grid-squares
To be usable, the grid-squares must be sufficiently large to tolerate reasonable inaccuracies in targeting the original click-points. For example with Robust Discretization, to guarantee at least a 6-pixel tolerance around the original click-point, grid-squares must be 36x36 pixels (6rx6r). This will avoid rejects for login click-points that fall within 6 pixels of original click-point, but it will increase the potential for false accepts as a large area outside of the 13x13 pixel1 centered-tolerance square will also be accepted. Furthermore, requiring such large grid-squares significantly reduces the password search space for attackers. For example, a 640x480 pixel image contains only 252 36x36 grid-squares per grid, giving a theoretical full password space of only 39.9 bits for a 5-click password, as opposed to 54.3 bits if centered-tolerance and 13x13 grid-squares (r=6) were used. In comparison, the theoretical full password space for a randomly generated 8-character text password is 52.5 bits for a standard 95-letter alphabet.
In essence, a usable implementation of Robust Discretization reduces security by significantly reducing the password space. This contradicts one of the major goals of a graphical password scheme [9], i.e., to achieve a larger password space (assuming large images are used).
3 Centered Discretization
Motivated by these observations, we propose Centered Discretization, which offers usability and security improvements. It offers centered-tolerance, which increases security because the size of grid squares can be reduced (to 2rx2r instead of 6rx6r), thereby increasing the password search space without negatively impacting usability since the same minimum tolerance r is guaranteed. It further increases usability by behaving in accordance with users’ likely mental models and eliminating false rejects and false accepts. We first introduce Centered Discretization in 1-dimension and then show how it can be expanded to 2-D for click-based graphical passwords or to higher dimensions.
3.1 1-D Centered Discretization
Consider a 1-dimensional line, L, with a continuous set of data points. A particular point on this line is represented by a real number x. Our initial objective is to discretize this line into equal segments where x falls in the center of the segment containing it. This ensures an even tolerance on both sides of x. A tolerance r is selected based on system or user preferences. Each segment is of length 2r as shown in Figure 2. To ensure that x is centered in its segment, segment 0 may need to be offset from the origin. This offset is represented by parameter d.
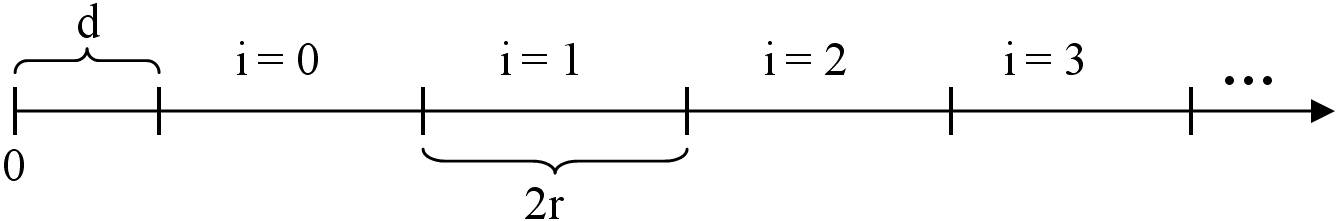
| Figure 2: The continuous line L is divided into segments of length 2r. |
First assume that a 1-D password consists of a single click-point x. To store this password, we must discretize the point by calculating its offset d (where 0 ≤ d < 2r) and its corresponding segment identifier i (where i ≥ −1, with i=−1 occurring if x is within r of the origin). Offset d is stored in the clear, while i is stored in protected form as its hash value h(i, d). The offset d is included in the hash to uniquely identify the segment. The system must also be aware of tolerance r that specifies the acceptable inaccuracy during password re-entry. The segment identifier i is computed by i = ⌊(x − r) / 2r⌋, identifying the segment containing x. The offset d = (x − r) mod2r determines the distance between the origin and the left boundary of segment 0.
To verify if a re-entered click-point x′ is acceptable, the system computes i′ = ⌊(x′ − d) / 2r⌋. This calculates which segment contains x′ using the same offset as the original point. Note that x′ is not necessarily centered within its segment; we are simply calculating which segment contains x′ based on x’s pre-determined segments. If x′ is within tolerance r of x, then i′ = i and hence h(i′, d) equals the stored value of h(i, d) and system accepts the entry. If x′ is outside of the accepted tolerance r, it falls in a different segment and i′ ≠ i, thus h(i′, d) ≠ h(i, d) and the system rejects it.
For example, assume x = 13 and r = 5.5. We compute i = ⌊(x − r) / 2r⌋ = ⌊(13−5.5) / 11⌋ = 0 and d = (x − r) mod2r = (13 − 5.5) mod11 = 7.5. Offset d = 7.5 is stored in the clear along with protected h(i, d) = h(0,7.5). If a user enters x′ = 10 during login, the system calculates i′ = ⌊(x′ − d) / 2r⌋ = ⌊(10− 7.5) / 11⌋ = 0. It then compares h(i′, d) and h(i, d) and the click-point is accepted since they match. In practice, if a password consists of more than one click-point, all segment indices and their offsets are concatenated and hashed together as one. This stops attackers from matching individual points, and thus carrying out an efficient divide-and-conquer attack.
3.2 Applicability to 2-D spaces
Centered Discretization can also be applied to click-based graphical passwords on a 2-D image. This is achieved by taking a point (x,y) in 2-D and discretizing each coordinate value individually along its corresponding axis. The segments along the x-axis can be combined with those of the y-axis to form a grid.
For example, if we use a tolerance value of r = 9.5 pixels,2 then 2r = 19 pixels. Thus the grid-squares will be 19x19 pixels. If we treat the click-point as coordinates on two 1-D lines, then the grid identifier will be composed of the offset for each dimension (dx, dy). Here, there are 192 = 361 possible grids.
For a 5 click-point graphical password, each of the 5 click-points (x1, y1), …, (x5, y5) will have an associated grid-square index (composed for the two 1-D segment indices) (ix, iy) and grid identifier (composed of the two 1-D offsets) (dx, dy). Grid identifiers (d1x, …, d5x, d5y) are stored in the clear, while the encrypted portion consists of:
h(d1x, d1y, i1x, i1y,…,d5x, d5y, i5x, i5y).
To prevent a pre-calculated dictionary attack, a user identifier could be added to the hash (and also stored in clear-text), essentially serving as a salt. To address any concerns that offline attacks might be mounted to match hashed password values, the cost of such an attack could be increased by using iterated hashing, e.g., using h1000 effectively adds 10 bits of security (1000 ≈ 210).
Centered Discretization may be expanded to n-dimensional objects for n ≥ 3 by computing results for each dimension separately and then combining them to form an n-dimensional grid. While this paper discusses the applicability to 2-D images, other proposed graphical password schemes are based on 3-D spaces [1]. Such schemes currently allow users to select predefined objects in a room as possible click-points, limiting the password space to the number of predefined clickable objects. Moving to a scheme that allows discretization of an entire 3-D space could significantly enlarge the password space, depending on system parameters.
4 Usability Analysis
To understand the severity of false rejects and false accepts in practice, we implemented both Robust Discretization and Centered Discretization to analyze a large data set containing coordinates of passwords and login attempts for these passwords on a PassPoints system. This data was collected during a field study with 191 participants [5]. The system implemented a centered-tolerance scheme without hashing to allow the collection of information about the actual click-points. In total, 481 passwords were created and 3339 login attempts were recorded. Two different 451x331-pixel images were used; approximately half of the participants saw the Cars image (Figure 3) and the others used the Pool image (Figure 4).

| Figure 3: The Cars image [4]. |

| Figure 4: The Pool image [11]. |
For this current analysis, we used reconstructions to determine whether the actual login attempts in the collected data set would have been accepted if the system implemented each of the two discretization schemes discussed herein with various sizes of tolerance grid-squares. Our Centered Discretization scheme was fairly straightforward to implement since it involves centered-tolerance; if a login click-point was within centered-tolerance for some tolerance r of the original click-point, it was accepted, otherwise it was rejected.
Robust Discretization proved more challenging. Implementation decisions such as which grid to select when a click-point is r-safe in more than one grid and how to deal with rounding when moving from real numbers to pixels were not addressed in the earlier literature [2]. To avoid misrepresenting the scheme, we sought clarification from the original authors, and learned [12] that Robust Discretization was not implemented in their prototype system. Since they were not concerned with protecting password confidentiality in their usability studies [16, 17], their prototype stored all details in the clear and used essentially a centered-tolerance algorithm to determine whether a login attempt was successful. It is therefore an open question as to how false rejects and false accepts as defined herein would have affected usability and user success rates in earlier publications [16, 17], had Robust Discretization actually been used.
We attempted to implement an optimal Robust Discretization algorithm that minimized the occurrence of false accepts and false rejects. In cases where more than one grid was r-safe, we calculated the distance from the click-point to the grid edges and selected the grid where the point was closest to the center of the grid-square. We used real numbers for our computations and comparisons to minimize rounding errors.
4.1 False accepts and false rejects
With Centered Discretization, the rate of false accepts and false rejects is zero by definition since centered-tolerance implies that the system will only accept click-points that are within r from the original point. With Robust Discretization, false positives occur when a click-point is accepted by the system but falls outside of the centered-tolerance grid square of the original point. Conversely, false negatives occur when a click-point falls within the centered-tolerance grid square of the original point but is rejected by the system.

| Figure 5: When the grid-square sizes are kept constant, r (the minimum guaranteed tolerance) is larger for Centered Discretization. |
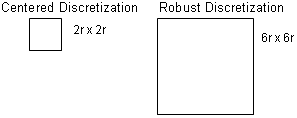
| Figure 6: When r is kept constant, the grid-squares for Centered Discretization are smaller, so the password search space is larger. |
There are two approaches to measuring false negatives and false positives. The first is to assume that the Centered Discretization square is the same size as the Robust Discretization square (see Figure 5), but the Robust Discretization square may not be centered on the click-point. Table 1 shows the percentage of passwords that would have been falsely accepted and falsely rejected with Robust Discretization, with tolerance squares of the same size as Centered Discretization. For example, using the dataset as described in Section 4 with a tolerance square of 13x13 pixels, 21.1% of passwords are falsely rejected during login using Robust Discretization, but would have been accepted by Centered Discretization using a 13x13 grid. This indicates serious usability issues if a click-based graphical password scheme was implemented using Robust Discretization, since more than a fifth of passwords were falsely rejected.3
The second approach is to keep parameter r constant rather than the size of tolerance squares (see Figure 6). This means that the minimum guaranteed tolerance around a click-point is kept constant between Centered Discretization and Robust Discretization, but it also means that the Robust Discretization squares are much larger than the Centered Discretization squares. For this comparison, there can be no false rejects in Robust Discretization because everything within r is guaranteed to be accepted. However, the larger squares required by Robust Discretization lead to false accepts. For example, with r=6, 14.1% of passwords are falsely accepted as correct in our dataset.
| Table 1: False accept and reject rates for Robust Discretization when grid-square for both schemes are of equal size. |
| Grid | Robust Disc. | False | False |
| Size | (r in pixels) | Accept | Reject |
| 9x9 | 1.50 | 3.5% | 21.8% |
| 13x13 | 2.17 | 1.7% | 21.1% |
| 19x19 | 3.17 | 0.5% | 10.0% |
| Table 2: False accept and reject rates for Robust Discretization when r is the same as for Centered Discretization. |
| r | Robust Discr. | False | False |
| (in pixels) | Grid Size | Accept | Reject |
| 4 | 24x24 | 32.1% | 0% |
| 6 | 36x36 | 14.1% | 0% |
| 9 | 54x54 | 4.3% | 0% |
The number of false accepts and false rejects seen with Robust Discretization raise usability concerns since the system will appear to perform erratically: accepting some clicks as correct when they were far from the original click-point and rejecting other clicks that should have been accepted from the users’ perspective. The discrepancy between user expectations and system behaviour may lead users to feel frustrated and mistrust of the system. Furthermore, if a Robust Discretization system is implemented with reasonable-size grid-squares such as those recommended in the literature [16, 17, 5, 6], then the value of r becomes unreasonably small (in the range of 1-2 pixels), meaning that it is increasingly likely that click-points very near the original point are rejected. These problems have not been identified earlier because as mentioned in Section 4, none of the original user studies [16, 17] were conducted on systems that implemented Robust Discretization.
5 Preliminary Security Analysis
Although the usability advantages are clear, to be acceptable Centered Discretization should provide at least comparable security as Robust Discretization. We examine how click-based graphical passwords implemented using both schemes withstand various attacks and how the theoretical full password space is affected.
The password space depends on both the size of an image and the size of the tolerance grid-squares, with larger images and smaller tolerances leading to a larger theoretical full password space. Table 3 shows how these two variables affect the theoretical full password space. While the table is organized by grid size, it is also possible to see the smaller password space for Robust Discretization when r is equal in both schemes, due to Robust Discretization’s larger grid squares. For example, on a 640x480 image the full theoretical password space is 59.6 bits for r = 4 using Centered Discretization but only 45.4 bits for Robust Discretization.
| Table 3: Bitsize of full theoretical password space for 5-click passwords. |
| Image Size | Grid Size | Centered Discr. | Robust Discr. | # of Squares | Pswd Space for |
| (pixels) | | r (pixels) | r (pixels) | per Grid | 5-Clicks (bits) |
| 451x331 | 9x9 | 4 | 1.50 | 1887 | 54.4 |
| | 13x13 | 6 | 2.17 | 910 | 49.1 |
| | 19x19 | 9 | 3.17 | 432 | 43.8 |
| | 24x24 | 11.5 | 4 | 266 | 40.3 |
| | 36x36 | 17.5 | 6 | 130 | 35.1 |
|
| 54x54 | 26.5 | 9 | 63 | 29.9 |
| 640x480 | 9x9 | 4 | 1.50 | 3888 | 59.6 |
| | 13x13 | 6 | 2.17 | 1850 | 54.3 |
| | 19x19 | 9 | 3.17 | 884 | 48.9 |
| | 24x24 | 11.5 | 4 | 540 | 45.4 |
| | 36x36 | 17.5 | 6 | 252 | 39.9 |
|
| 54x54 | 26.5 | 9 | 108 | 33.8 |
5.1 Human-seeded dictionary attacks
We attempted to crack PassPoints passwords from our field study (described in Section 4) using passwords collected from an earlier lab study [5]. We used the click-points collected in the lab study and generated a dictionary containing all possible 5-click-point permutations as entries. Thirty lab passwords were used for each image, giving dictionaries with 30C5≈ 236 entries for the Cars and Pool images separately. Our dictionaries represented the simplest attack dictionary that could be built with 30 collected passwords per image. This is similar to the approach of Thorpe et al. [15].
Offline dictionary attack with known grid identifiers. The first scenario assumes that attackers have access to the clear-text grid identifiers and hash values stored by the system. In a targeted attack against a specific user, this reduces the password search space since each guess can be mapped directly to the user’s stored grid identifiers to compute the hash rather than having to iterate through all possible grid combinations. For example, if an attacker knows that user A’s grid-identifier for the first click-point is (dx, dy)=(10,10), all guesses for that click-point can be discretized using this grid. This may occur in an offline attack if attackers gain access to the server-side files containing the grid identifiers and hashed passwords.
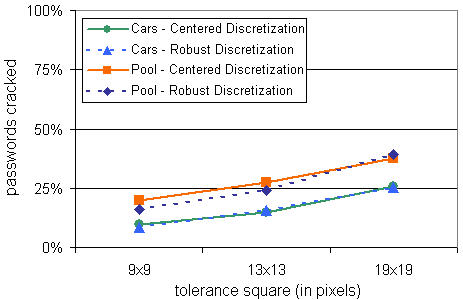
| Figure 7: Offline dictionary attack with known grid identifiers for Robust and Centered Discretization with a 36-bit dictionary and equal grid-square sizes assumed. |

| Figure 8: Offline dictionary attack with known grid identifiers for Robust and Centered Discretization with a 36-bit dictionary and equal r-values assumed. |
Using our dictionary of 5-click-point passwords, we searched for matches to passwords collected in the field study (which collected 162 passwords for the Cars image and 187 for Pool). For a successful match, all click-points in a dictionary entry had to be within the grid-squares of the user’s click-points. The grid-squares were computed using either Robust Discretization or Centered Discretization and we calculated how many matches were made under each scheme.
We initially kept the size of the grid-squares constant (as shown in Figure 5) for both schemes. As expected, they performed similarly under this condition (see Figure 7) since having grid-squares of similar size means that roughly the same number of guesses would be accepted as correct.
Conversely, if we keep r constant across both schemes as in Figure 6 (to ensure similar usability in terms of the guaranteed size of the tolerance around a click-point), then Centered Discretization is significantly more secure in the face of this particular attack strategy since its grid-squares are much smaller (with comparable usability). Many guesses that are successful within Robust Discretization’s larger grid-square are rejected by Centered Discretization. For example, Figure 8 shows that with r=6, 14.8% of Cars passwords are cracked with Centered Discretization, as compared to 45.1% for Robust Discretization. With r=9, Robust Discretization reaches up to 79% of passwords cracked. For this flavor of dictionary attack where the grid identifier is known, Centered Discretization can be more secure than Robust Discretization because smaller grid squares can be used without negatively affecting usability.
As mentioned earlier, this type of attack may be slowed or stopped by including a user identifier as a salt for the hashed values, forcing attackers to re-compute all of the hash values for every user. This can be made even more computationally expensive by using iterated hashing so that each password guess requires more computational effort.
We assume that if attackers gain access to the password file, they will have access to both the hash values and the clear-text grid identifiers. However, in the unusual case where only the hashed passwords are known, the size of attack dictionaries to have the same attack efficacy would have to increase significantly. For each dictionary entry, attackers would need to compute a hash for each possible grid identifier combination. This would require significantly more work for Centered Discretization since the number of grids is proportional to the size of the grid-squares (13x13 grid-squares implies 132=169 grid identifiers). Conversely, Robust Discretization has only 3 possible grids.
Online dictionary attack. Alternatively, attackers without access to the password file may attempt an online attack. While attackers may not explicitly know the grid identifiers, these are not necessary since the system will automatically use the correct grids when interpreting the login attempt. The attacker need not worry about pre-determining hash values. The attacker enters each guessed password through the regular login user interface to see if the system accepts it. The system may limit the number of incorrect login attempts for individual accounts, slowing or stopping the attack. As with the offline attacks, smaller grid-squares mean that guessed click-points must be much closer to the real password click-points in order to be accepted so the password search space is increased.
5.2 Information Revealed
Robust Discretization requires 2 bits of information to store one of its three grid identifiers, whereas Centered Discretization as proposed herein needs log2(2r * 2r) bits (e.g., for r = 8, this equals 8 bits). As the grid identifiers are (by design) stored in the clear for both schemes, they may be accessible to an attacker. This may have security implications, however to our knowledge, this does not lead to weaker security for the attacks discussed so far.
When attackers know the grid-identifier and the image, visual information may be leaked. Attackers may overlay the grid onto the image to see which parts of the image fall near the center of the grid-squares and thus may be able to predict which squares have a more likely click-point (either by using knowledge of hotspots or by personally evaluating the image). They may allow prioritization of entries in the attack dictionary to test more likely entries first. With Centered Discretization, a single pixel at the center of each grid-square is identified, while for Robust Discretization, a central region is revealed. Knowing the center pixel does not appear to provide much advantage for attackers over knowing the center region since guessed click-points are correct as long as they are within the correct grid-square and the items targeted by users as click-points are usually much larger than a single pixel. However we have not yet pursued this attack strategy sufficiently to have full confidence and it is possible that combining this information with knowledge of hotspots may lead to new attacks on Centered Discretization.
6 Discussion and Conclusion
Click-based graphical passwords have been proposed as a more usable and more secure alternative to text passwords. Usability testing of such systems [16, 17, 5, 6, 7] so far has been conducted using a centered-tolerance discretization approach and Robust Discretization may well make them less usable. Our results suggest that this would be the case, but since our analysis was conducted post hoc, it is unknown whether users of a Robust Discretization system would resort to some kind of compensatory behaviour. This still indicates usability issues however, since users would be responsible for coping with the system’s behaviour.
We present the first analysis of how the usability and security of click-based graphical passwords are affected by the type of discretization implemented. We identified weaknesses in Robust Discretization that lead to false rejects and false accepts, which we expect makes the system appear unreliable from the users’ point of view. To compensate, Robust Discretization must use larger tolerance squares, which reduces the password space considerably, making it more susceptible to attack. Centered Discretization guarantees centered-tolerance, increases the password space since smaller grid squares can be used, and makes graphical passwords more usable in real systems by making system behaviour more predictable since the tolerance square is centered on the original click-point (avoiding false accepts and false rejects). We provide evidence of the usability and security of both schemes by analyzing data collected from a large user study of PassPoints. It remains open to further study whether Centered Discretization opens the door to new types of password attacks.
References
-
[1]
-
Alsulaiman, F.A. and Saddik, A.E. A Novel 3D Graphical Password Schema. IEEE International Conference on Virtual Environments, Human-Computer Interfaces and Measurement Systems. July 2006.
- [2]
-
Birget, J.C., Hong, D., and Memon, N. Graphical Passwords Based on Robust Discretization. IEEE Transactions on Information Forensics and Security, vol. 1, no. 3, September 2006.
- [3]
-
Blonder, G.E. Graphical Passwords. United States Patent 5559961, 1996.
- [4]
-
Britton, Ian. https://www.freefoto.com Accessed Feb. 2007.
- [5]
-
Chiasson, S. Biddle, R., and van Oorschot, P.C. A Second Look at the Usability of Click-Based Graphical Passwords. Symp. on Usable Privacy and Security (SOUPS) 2007.
- [6]
-
Chiasson, S., van Oorschot, P.C., Biddle, R. Graphical Password Authentication Using Cued Click-points. ESORICS 2007.
- [7]
-
Chiasson, S., A. Forget, R. Biddle, P.C. van Oorschot. Influencing Users Towards Better Passwords: Persuasive Cued Click-Points. Technical Report TR-07-16, School of Computer Science, Carleton University, Ottawa ON, 2007. (in submission).
- [8]
-
Dirik, A.E., Memon, N., and Birget, J.C. Modeling user choice in the PassPoints graphical password scheme. Symp. on Usable Privacy and Security (SOUPS) 2007.
- [9]
-
Jermyn, I., Mayer, A., Monrose, F., Reiter, M.K., and Rubin, A.D.
The Design and Analysis of Graphical Passwords. Proceedings of the 8th USENIX Security Symposium, 1999.
- [10]
-
Monrose, F. and Reiter, M.K. Graphical Passwords. Chapter 9 in Security and Usability: Designing Secure Systems that People Can Use. L.F Cranor and S. Garfinkel (eds). O’Reilly, 2005.
- [11]
-
PD Photo. https://pdphoto.org Accessed Feb. 2007.
- [12]
-
Personal communication, A. Brodskiy. September 3, 2006.
- [13]
-
Sharma, M. and Bansal, T. Two-Level Texto-Graphical Authentication. Unpublished manuscript. Last accessed July 2007. https://www-static.cc.gatech.edu/grads/m/manus/projects.html
- [14]
-
Suo, X., Zhu, Y., and Owen, G.S. Graphical Passwords: A Survey. ACSAC 2005.
- [15]
-
Thorpe, J. and van Oorschot, P.C. Human-Seeded Attacks and Exploiting Hot-Spots in Graphical Passwords. USENIX Security Symp. 2007.
- [16]
-
Wiedenbeck, S., Birget, J.C., Brodskiy, A., and Memon, N. Authentication Using Graphical Passwords: Effects of Tolerance and Image Choice. Symp. on Usable Privacy and Security (SOUPS) 2005.
- [17]
-
Wiedenbeck, S., Waters, J., Birget, J.C., Brodskiy, A., and Memon, N. PassPoints: Design and longitudinal evaluation of a graphical password system. Int. Journal of Human-Computer Studies 63, pp. 102-127, 2005.
This document was translated from LATEX by
HEVEA.