
| Robert Beverly
MIT CSAIL rbeverly@mit.edu |
Mike Afergan
Akamai/MIT afergan@alum.mit.edu |
Self-reorganization offers the promise of improved performance, scalability and resilience in Peer-to-Peer (P2P) overlays. In practice however, the benefit of reorganization is often lower than the cost incurred in probing and adapting the overlay. We employ machine learning feature selection in a novel manner: to reduce communication cost thereby providing the basis of an efficient neighbor selection scheme for P2P overlays. In addition, our method enables nodes to locate and attach to peers that are likely to answer future queries with no a priori knowledge of the queries.
We evaluate our neighbor classifier against live data from the Gnutella unstructured P2P network. We find Support Vector Machines with forward fitting predict suitable neighbors for future queries with over 90% accuracy while requiring minimal (<2% of the features) knowledge of the peer's files or type. By providing a means to effectively and efficiently select neighbors in a self-reorganizing overlay, this work serves as a step forward in bringing such architectures to real-world fruition.
Simple unstructured Peer-to-Peer (P2P) networks are both popular and widely deployed [8,10]. Nodes issue queries that propagate through the overlay and receive answers from peers able to satisfy the query. Because unstructured networks allow nodes to interconnect organically with minimal constraints, they are well-suited to self-reorganization. For example, prior research investigates reorganization for improved query recall, efficiency and speed, as well as increased system scalability and resilience [1,2,3,11,13].
In practice however, the benefit of reorganization is often lower than the cost in a classic exploration versus exploitation paradox. A critical question prior research does not address is how nodes within a self-reorganizing P2P system can determine the suitability of another node, and hence whether or not to connect, in real-time. Nodes must classify potential peers as good or poor attachment points both effectively (with high success) and efficiently (with few queries).
Given an omniscient oracle able to determine a node's future queries and the fraction of those queries matched by other nodes, neighbor selection is readily realizable. Naturally, nodes do not have access to such an oracle. This work seeks to understand how to emulate, in a distributed fashion with minimum communication cost, the functionality of an online oracle as a component of a self-reorganizing network. In particular, nodes within a self-reorganizing network face two primary challenges: minimizing load induced on other network participants and locating neighbors that are likely to answer future queries.
We abstract these challenges into a distributed, uncoordinated, per-node machine learning classification task. Based on minimal queries, nodes predict whether or not to connect to a peer. A key insight of this work is that minimizing the induced load on other nodes maps to a feature selection problem. We wish to build an effective classification model by finding a small set of highly discriminatory queries.
Our analysis uses live Gnutella data to understand the efficacy and parameterization of machine learning techniques for neighbor selection. We determine the accuracy, precision and recall performance of Support Vector Machines (SVMs) [14] and empirically find a training size with high prediction performance. We then experiment with forward fitting and mutual information feature selection algorithms as a means of finding queries with high discrimination power. The major contributions of our research are:
Consequently, we hope this paper serves as a step forward for research in the space of self-reorganizing overlays by providing a scalable means of neighbor selection.
Unstructured overlays can adapt, grow organically and reorganize dynamically. Earlier work [9] recognized that, if locality exists, preferentially connecting peers with similar interests together in unstructured P2P networks can minimize query flooding. The work of Sripanidkulchai, et. al [11] relies on the presence of interest-based locality to create ``shortcuts.'' Each peer builds a shortcut list of nodes that answered previous queries. To find content, a peer first queries the nodes on its shortcut list and, only if unsuccessful, floods the query. These systems present promising reorganization methods within unstructured P2P networks, but do not address the neighbor selection task.
In the domain of structured overlays, Tang, et. al propose pSearch [13] as a means to semantically organize nodes. Within their semantically organized network, search proceeds using traditional information retrieval methods that return results based on document similarity, not just keywords. Several pieces of work [4,6] examine neighbor selection within structured overlays, particularly the impact of routing geometry and the ability to choose neighbors in different structured overlays for resilience and proximity.
In many respects, our problem is most akin to text categorization and we draw upon the rich literature of prior work espousing machine learning theory. One of the earlier works in application of SVMs to text categorization is from Joachims [7]. Yang and Liu examine several text categorization methods against standard new corpora, including SVMs and Naïve Bayes [15]. Our results similarly find SVMs outperforming Naïve Bayes for our application; we omit Naïve Bayes results in this paper. Finally, as in Yang's comparative study [16], forward fitting also outperforms mutual information feature selection on our dataset.
Finding peer nodes in unstructured P2P networks is accomplished in a variety of ways. For instance in Gnutella-like overlays, bootstrap nodes maintain pointers into the network while every node advertises the addresses of its neighbors. However, it is not obvious how a node can, in real-time, determine whether or not to connect to another node. Exploring other nodes incurs cost and presents a paradox: the only way to learn about another node is to issue queries, but issuing queries makes a node less desirable and the system less scalable.
A key insight of our research is that efficient neighbor selection maps to machine learning feature selection. We ask: ``for a node i, does there exist an efficient method, i.e. a small set of key features, by which i can optimize its choice of neighbors?'' While feature selection is traditionally used in machine learning problems to reduce the computational complexity of performing classification, we use it in a novel way. Specifically, we use feature selection to minimize the number of queries, which equates to network traffic and induced query load.
In this section, we concretely describe the neighbor selection problem in the context of self-reorganizing P2P systems. We start by giving details of our dataset. We then formulate the problem and data as a machine learning task.
We experiment on real, live Gnutella datasets from two independent
sources: our own measurement of 1,500 nodes![]() and a public, published repository of approximately 4,500 nodes from
Goh, et al. [5]. Both datasets include timestamped
queries and files offered across all nodes. The collection
methodology is similar for both datasets. A capture program
establishes itself as a Gnutella UltraPeer and promiscuously gathers
queries and file lists from all leaf node connections.
and a public, published repository of approximately 4,500 nodes from
Goh, et al. [5]. Both datasets include timestamped
queries and files offered across all nodes. The collection
methodology is similar for both datasets. A capture program
establishes itself as a Gnutella UltraPeer and promiscuously gathers
queries and file lists from all leaf node connections.
While our datasets focus on Gnutella, we believe that they are sufficiently representative of general P2P usage (in particular, the Gnutella network is estimated to contain approximately 3.5M users [10]). Detailed inspection of the datasets reveals a wide range of searches and content including music, videos, programs, images, etc of all sizes and type. While other popular P2P file sharing networks exist, it is reasonable to believe that most general-purpose networks will see comparable usage patterns. Many additional motivations for using Gnutella as a reference P2P network, including size, scope and growth, are given in [12].
We tokenize queries and file names in data by eliminating: i)
non-alphanumerics; ii) stop-words: ``it, she, of, mpeg, mp3,'' etc.;
and iii) single character tokens. The resulting tokens are produced
by separating on white-space. We assume tokenization in the remainder
of this work. Let ![]() be the set of all nodes and
be the set of all nodes and ![]() . Let
. Let
![]() and
and
![]() represent the tokenized queries and file store
of node
represent the tokenized queries and file store
of node ![]() respectively. We represent the set of all unique tokens
across the queries and files as
respectively. We represent the set of all unique tokens
across the queries and files as
![]() and
and
![]() .
.
Encouragingly, our experiments yield similar results using either dataset, lending additional credence to our methodology. Due to space constraints however, the results presented in this paper are limited to the Goh dataset.
To qualitatively compare peers, we introduce the notion of a utility
function. Given
![]() and
and
![]() for every node
for every node ![]() , we can
evaluate whether a potential neighbor has positive utility, i.e. nodes are individual, selfish utility maximizers. Utility may be a
function of many variables including induced query load, query success
rate, etc. However, we are primarily interested not in the specific
mechanics of a utility-based self-reorganizing network, but rather the
neighbor selection task. Therefore, in this work, we define
, we can
evaluate whether a potential neighbor has positive utility, i.e. nodes are individual, selfish utility maximizers. Utility may be a
function of many variables including induced query load, query success
rate, etc. However, we are primarily interested not in the specific
mechanics of a utility-based self-reorganizing network, but rather the
neighbor selection task. Therefore, in this work, we define ![]() ,
node
,
node ![]() 's utility in connecting to node
's utility in connecting to node ![]() , simply as the number of
successful queries from
, simply as the number of
successful queries from ![]() matched by
matched by ![]() . A single query from
. A single query from ![]() matches a single file held by
matches a single file held by ![]() if and only if all of the query
tokens are present in that file
if and only if all of the query
tokens are present in that file![]() .
.
We represent the dataset with the two matrices in Figure 1, an adjacency and word token matrix:
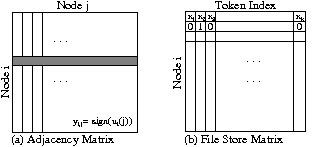
|
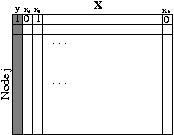
From the adjacency and file store matrices we create a per-node
matrix,
![]() , as shown in Figure 2.
Note that we compute the adjacency and file store token matrices
explicitly only in order to evaluate the performance of our neighbor
selection algorithm; our scheme does not require complete
knowledge of all files and queries in the network. Rather, we employ
the omniscient oracle only to evaluate the performance of our neighbor
prediction algorithm.
, as shown in Figure 2.
Note that we compute the adjacency and file store token matrices
explicitly only in order to evaluate the performance of our neighbor
selection algorithm; our scheme does not require complete
knowledge of all files and queries in the network. Rather, we employ
the omniscient oracle only to evaluate the performance of our neighbor
prediction algorithm.
|
Given the hypothetical off-line (oracle) representation of a node's state as depicted in Figure 2, we now turn to the problem of classification. Note that the problem we face is slightly non-standard - we have a separate classification problem for each node. That is, the features that are optimal can, and likely will, be different from node to node. In addition, the optimal features need not match the node's queries. For instance, while a node may issue queries for ``lord of the rings,'' the single best selective feature might be ``elves.'' This example provides some basic intuition of how our system finds peers that are capable of answering future queries. By connecting to peers using ``elves'' as a selection criterion, a future query for ``the two towers'' is likely to succeed given interest-based locality.
Figure 3 shows how the conjoined matrices as shown in
Figure 2 are split and used as input to machine learning
algorithms. Some number of nodes, significantly fewer than the total
number of nodes ![]() , are selected at random to serve as training
samples. The learner is given the word token features present for
each training node (
, are selected at random to serve as training
samples. The learner is given the word token features present for
each training node (
![]() a row subset of
a row subset of
![]() ) along with
the corresponding classification labels (
) along with
the corresponding classification labels (
![]() ). For our neighbor
selection task, the label is a binary decision variable,
). For our neighbor
selection task, the label is a binary decision variable,
![]() where
where ![]() indicates a good connection and
indicates a good connection and ![]() a
poor connection. We consider the size and complexion of the training
data in the next Section. Using the training data, the learner
develops a model that uses a small number of features
a
poor connection. We consider the size and complexion of the training
data in the next Section. Using the training data, the learner
develops a model that uses a small number of features
![]() in order to predict future connection decisions. We
evaluate the efficacy of this model against the test data, i.e. whether the model correctly predicts the unknown
in order to predict future connection decisions. We
evaluate the efficacy of this model against the test data, i.e. whether the model correctly predicts the unknown ![]() connection labels
in the test set. Thus, in the testing phase, the input to the
classifier is the small number features (
connection labels
in the test set. Thus, in the testing phase, the input to the
classifier is the small number features (
![]() )
where
)
where ![]() , without either the labels (
, without either the labels (![]() ) or the full word
tokens (
) or the full word
tokens (
![]() ).
).
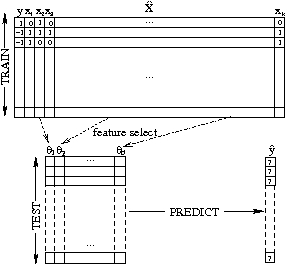
|
Notice that the features we train and test on do not include any
queries ![]() from our dataset. Only the
from our dataset. Only the ![]() labels depend on the
queries. Thus, successful connection predictions imply the ability to
predict queries yet to be asked.
labels depend on the
queries. Thus, successful connection predictions imply the ability to
predict queries yet to be asked.![]()
We find that some nodes in the dataset have queries that are matched
by very few other nodes. Therefore, a prediction model that
deterministically predicts not to connect will yield a high accuracy
- and thus a misleading result. Consider a node whose query is
matched by only 1 of 500 other nodes. A classifier that always
predicts not to connect gives an accuracy of
![]() . To
better assess our neighbor selection scheme without bias or skewing
the results, we randomly select 50 nodes that have at least 20%
positive labels, i.e. a non-trivial number of suitable potential
peers. In this way, we choose to evaluate the nodes that are
most difficult to accurately perform predictions with and
thereby stress our approach.
. To
better assess our neighbor selection scheme without bias or skewing
the results, we randomly select 50 nodes that have at least 20%
positive labels, i.e. a non-trivial number of suitable potential
peers. In this way, we choose to evaluate the nodes that are
most difficult to accurately perform predictions with and
thereby stress our approach.
These nodes include ![]() unique file store tokens. We provide
both average and variance measures across these nodes from our
dataset. Thus, we wish to show that our scheme is viable for the vast
majority of all nodes.
unique file store tokens. We provide
both average and variance measures across these nodes from our
dataset. Thus, we wish to show that our scheme is viable for the vast
majority of all nodes.
We note that incorrect predictions in our scheme are not fatal. In the overlays we consider, a node that attaches to a peer who in fact provides no utility can simply disconnect that peer. Therefore, while the statistical methods we employ provide only probabilistic measures of accuracy, they are well-suited to the neighbor selection task.
Our evaluation methodology simulates the following algorithm on nodes
from our dataset and measures prediction accuracy. For a node ![]() in the system that wishes to optimize its connection topology:
in the system that wishes to optimize its connection topology:
|
We obtain the best neighbor selection prediction results using SVMs. SVM classifiers [14] find an optimal separating hyperplane that maximizes the margin between two classes of data points. The hyperplane separator is orthogonal to the shortest line between the convex hulls of the two classes. Because this separator is defined only on the basis of the closest points on the convex hull, SVMs generalize well to unseen data. Additional data points do not affect the final solution unless they redefine the margin. While the separator may be linear in some higher-dimensional feature space, it need not be linear in the input space. Determining the separating hyperplane for the data in some high dimensional space is performed via constrained optimization.
SVMs are a natural selection for neighbor selection since the problem is separable, we may need to consider high-dimensional data, and the underlying distribution of the data points and independence are not fully understood. We use the MySVM package for our experiments [7].
To reduce possible dependence on the choice of training set, all results we present are the average of five independent experiments. We randomly permute the order of the dataset so that, after splitting, the training and test samples are different between experiments. In this way, we ensure generality, a critical measure of learning effectiveness. We evaluate model performance on the basis of classification accuracy, precision and recall.
Accuracy is simply the ratio of correctly classified test samples to total samples. Precision measures the number of positive predictions that were truly positive. Finally, recall gives a metric of how many positive samples were predicted positive. All three measures are important in assessing performance; for instance, a model may have high accuracy, but poor recall as mentioned in the previous section when nodes have few suitable peers in the entire system.
An important first consideration is the sensitivity of the model to the number of training points (step 1 in §3.4). In Figure 4 we plot the test accuracy, precision and recall versus the number of training points.
Test error decreases significantly in the range [10,70]. Test error is minimized around 150 points, after which a small amount of over-fitting is present. Beyond 100 training points, accuracy, precision and recall all remain fairly stable. Because we are interested in obtaining the best combination of the three performance metrics while minimizing the number of training points, we select 100 training points for the remainder of our experiments.
In order to find a small number of highly discriminative features
(step 5 in §3.4), we turn to feature selection
methods [16]. Recall that we use feature
selection in a novel manner, not to reduce the computation complexity
of classification, but rather to minimize communication cost for
neighbor selection in the network. The first feature selection method
we consider is mutual information (MI). Mutual information attempts
to use combinations of feature probabilities to assess how much
information each feature, i.e. word token, contains about the
classification. MI evaluates the mutual information score
![]() for each feature
for each feature
![]() and sequentially
picks the highest scoring features independently of the classifier.
The MI score is in the range
and sequentially
picks the highest scoring features independently of the classifier.
The MI score is in the range ![]() and will be zero if the feature
is completely independent of the label or one if they are
deterministically related.
and will be zero if the feature
is completely independent of the label or one if they are
deterministically related.
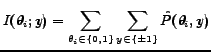 log log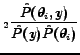 |
(1) |
| (2) |
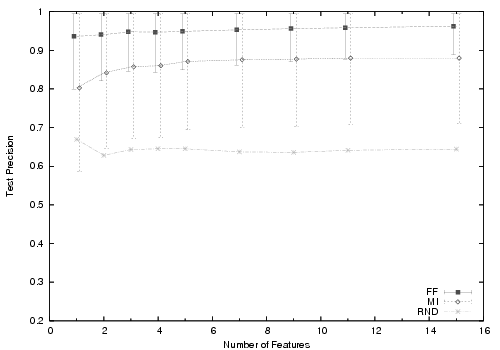
Figure 5 summarizes the most meaningful results from our feature selection and SVM experiments (step 6 in §3.4). The experiment is run five times for each configuration and the average numbers are presented in the graph along with the standard deviation error range. We include random feature selection as a baseline measure. The primary observations from these graphs are:
Here we examine the larger conclusions that can be drawn from our findings:
While our input space is of high dimension, it can be effectively summarized with very few parameters. The summarization aspect of our problem inspired us to consider an SVM approach. Forward fitting reveals that a small number of features effectively correlates to accurate predictions. Our findings are in stark contrast to the standard motivation for SVMs in text classification problems where the inputs are independent and the primary motivation for SVMs is to reduce the computational complexity.
SVMs allow us to accurately model the problem with little or no underlying understanding of the inputs. While we have a general understanding of the data, we face the challenge that we do not totally understand the relationship between the features and moreover the nature of these relationships vary from node to node. Nodes in a real system face this same challenge. Therefore SVMs, which make no underlying assumptions regarding the data, are particularly well-suited for our problem.
For our problem, forward fitting outperforms mutual information. The literature is mixed on the relative merit of mutual information and forward fitting. In our problem, we were interested in seeing if, as enough features were added via MI, the combination of features could outperform FF, where features are selected in a greedy fashion. Empirically this was not the case.
One reason FF performs well is the high degree of correlation between features in the dataset. For example, if a user has songs by ``Britney Spears'' both ``Britney'' and ``Spears'' may be descriptive features. However, simple MI will not take into account that once it adds ``Britney'', adding ``Spears'' will not improve prediction performance. In future work, we plan to investigate the ability to remove correlated features found via MI by computing feature-to-feature MI. Conversely, forward fitting will likely only add one of these terms, moving on to a more descriptive second term. The danger of forward fitting of course is over-fitting but we do not observe over-fitting in practice.
For our problem, SVMs do not suffer significantly from over-fitting. As witnessed by varying the number of training points, SVMs are robust against over-fitting. While some over-fitting is present in our empirical results with forward fitting, in the context of our particular problem it has little impact. In particular, we are attempting to minimize the number of features with as little impact on prediction performance as possible. Therefore, the fact that too many features leads to worse classification performance is not as problematic as it may be for other problems.
Our neighbor selection algorithm is computationally practical. Nodes can use the SVM prediction we describe in a completely decentralized fashion. While forward fitting gives the highest accuracy, it requires training many SVMs. Nodes with limited computational power can use MI to achieve comparable accuracy. In future work, we may consider FF over multiple features at once. While this method of forward fitting may be more expensive computationally, it could run as a background process on a user's desktop (say overnight) and thus not be prohibitively expensive in practice.
Our neighbor selection algorithm is practical in real networks.
While we simulate and model the operation of nodes using machine
learning algorithms to predict suitable neighbors, our scheme is
viable in practice. P2P systems, and Gnutella in particular, utilize
a system of caches which store IP addresses of nodes in the overlay
thereby allowing new clients to locate potential peers. Our
experiments show that randomly selecting
![]() peers on which
to train suffices to build an effective classifier. Because we
randomly permute the set of training nodes in each experiment, the
density of ``good neighbors'' in 100 peers is sufficiently high for
accurate future predictions.
peers on which
to train suffices to build an effective classifier. Because we
randomly permute the set of training nodes in each experiment, the
density of ``good neighbors'' in 100 peers is sufficiently high for
accurate future predictions.
Efficient neighbor selection is a general problem. While we focus only on P2P overlays, minimizing the communication overhead via feature selection methods such as those in our algorithm may generalize to tasks in other networks or applications.
In this work, we examined efficient neighbor selection in self-reorganizing P2P networks. While self-reorganizing overlays offer the potential for improved performance, scalability and resilience, their practicality has thus far been limited by a node's ability to efficiently determine neighbor suitability. We address this problem by formulating neighbor selection into a machine learning classification problem. Using a large dataset collected from the live Gnutella network, we examined the efficacy of Support Vector Machine classifiers to predict good peers. A key insight of our work was that nodes can use feature selection methods in conjunction with these classifiers into order to reduce the communication cost inherent in neighbor selection. Using forward fitting feature selection, we successfully predicted suitable neighbor nodes with over 90% accuracy using only 2% of features.
By addressing the efficiency of neighbor selection in the formation of self-reorganizing networks, we hope our work serves as a step forward in bringing self-reorganizing architectures to real-world fruition.