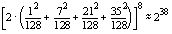|
USENIX Technical Program - Paper - Smartcard 99
[Technical Program]
Investigations of Power Analysis Attacks on Smartcards
Thomas S. Messerges
Motorola Labs, Motorola
tomas@ccrl.mot.com
Ezzy A. Dabbish
Motorola Labs, Motorola
dabbish@ccrl.mot.com
Robert H. Sloan
Dept. of EE and Computer Science, University of Illinois at Chicago
sloan@eecs.uic.edu
Abstract
This paper presents actual results from monitoring
smartcard power signals and introduces techniques that help maximize such
side-channel information. Adversaries will obviously choose attacks that
maximize side-channel information, so it is very important that the strongest
attacks be considered when designing defensive strategies. In this paper,
power analysis techniques used to attack DES are reviewed and analyzed.
The noise characteristics of the power signals are examined and an approach
to model the signal to noise ratio is proposed. Test results from monitoring
power signals are provided. Next, approaches to maximize the information
content of the power signals are developed and tested. These results provide
guidance for designing smartcard solutions that are secure against power
analysis attacks.
Introduction
Cryptographers have traditionally analyzed cipher systems
by modeling cryptographic algorithms as ideal mathematical objects. Conventional
techniques such as differential [1] and
linear
[2]
cryptanalysis are very useful
for exploring weaknesses in algorithms represented as mathematical objects.
These techniques, however, cannot address weaknesses in cryptographic algorithms
that are due to a particular implementation in hardware. The realities
of a physical implementation can be extremely difficult to control and
often result in the leakage of side-channel information. Techniques developed
in [3] show how surprisingly little side-channel
information is required to break some common ciphers. Attacks have been
proposed that use such information as timing measurements [ 4
, 5
],
power consumption [6], electromagnetic
emissions [7] and faulty hardware [ 8
, 9
].
Eliminating side-channel information or preventing it from being used to
attack a secure system is an active area of research.
A growing number of researchers are beginning to address this issue
of implementation. Systems that rely on smartcards to provide security
are of particular concern. In such systems, smartcards are often viewed
as tamper-resistant devices that are secure against all but the most determined
and well-financed attackers. However, this reliance on the tamper resistance
of smartcards needs to be carefully scrutinized [10]
.
This becomes even more important in light of the recent attacks using side-channel
information. It is often the case that important data stored on smartcards,
such as a cryptographic key or an authentication certificate, needs to
be kept secret to prevent counterfeiting of cards or the breaking of a
system's security. Examples of smartcard systems that rely on the secrecy
of the data resident on smartcards can be found in [11]
.
Such systems are potentially vulnerable because every time the smartcard
system performs a computation using the secret data, side-channel information
may be leaked.
Of all the previously mentioned sources of side-channel information,
power measurements are perhaps the most difficult to control. Ultimately
all calculations performed by a smartcard operate on logical ones or zeros.
Current technological constraints result in different power consumptions
when manipulating a logical one compared to manipulating a logical zero.
An attacker of a smartcard can monitor such power differences and obtain
useful side-channel information. Differential Power Analysis (DPA) [6]
is a statistical approach to monitoring such power signals from a smartcard.
Kocher et al.
[6]
claim one can monitor
the actions of a single transistor within a smartcard using DPA. In [6]
,
the authors outline a specific DPA attack against smartcards running the
DES [12]
algorithm.
The purpose of this paper is to present actual results from monitoring
smartcard power signals and to introduce techniques that help maximize
such side-channel information. Whereas [3]
showed
how little side-channel information is required by an attacker, this paper
takes the alternate approach and provides a first step towards showing
how such information can be maximized. Adversaries will obviously choose
attacks that maximize side-channel information, so it is very important
that the strongest attacks be considered when designing defensive strategies.
In this paper, power analysis techniques for attacking DES are reviewed
and analyzed. The noise characteristics of the power signals are examined
and an approach to model the signal to noise ratio is proposed. Test results
from monitoring power signals are provided. Next, approaches to maximize
the information content of the power signals are developed and tested.
These results provide guidance for designing smartcard solutions that are
secure against power analysis attacks.
Smartcard Power Dissipation
The circuit shown in Figure 1 gives
a simple lumped component model that is useful for understanding power
dissipation measurements. Power dissipated by the smartcard can be monitored
at the ground pin of the smartcard by using a small resistor (R 1)
in series between the V SS pin on the card and the true ground.
Current moving through R 1 creates a time varying voltage that
can be sampled by a digital oscilloscope. The current flows out of the
smartcard through a bond wire that acts as an inductor L bond.
The values of the inductor, L bond, and the capacitors will determine
the shape of the power signal that is observed at V scope. In
a CMOS circuit, most power is dissipated when the circuit is clocked. This
is known as dynamic power dissipation
[13]
.
As V gate changes from 0 to 5 volts, the transistors Q 1
and Q 2 are both conducting for a brief period causing current
to flow from V dd to ground. Also during this time, the capacitor
C load will be discharged (or charged) causing more (or less)
current to flow through the V SS pin.
Information useful to a cryptanalyst is leaked because the amount of
current being drawn when the circuit is clocked is directly related to
the change of state of Cload or the resulting current drawn
by the other gates attached to Cload. On a microprocessor, each
clock pulse causes many bit transitions to occur simultaneously. In a typical
smartcard microprocessor, a large portion of the power dissipation occurs
in the gates attached to internal buses. Our experiments showed that activity
on the data and address bus is a dominant cause of power consumption changes.
These changes can be observed at Vscope.
Two types of information leakage from the data bus that have been observed
are Hamming weight leakage and transition count leakage. Hamming weight
information leaks when the dominant source of current is caused by the
discharging of C load. A situation where Hamming weight information
leaks is when a precharged bus design is used. In this case, the number
of zeros driven onto the precharged bus directly determines the amount
of current that is being discharged. Transition count information leaks
when the dominant source of current is due to the switching of the gates
that are driven by the data bus. When the data bus changes state, many
of the gates driven by the bus will briefly conduct current. Thus, the
more bits that change state, the more power that is dissipated.

Experimental results that show transition count leakage from a typical
8-bit, microprocessor-based smartcard are given in Figure
2 . In this figure, an 8-bit data byte from memory is transferred into
a register. Initially, the bus contains the memory address, but after a
clock pulse, the data from memory is put onto the bus. The magnitude of
the voltage pulse is directly proportional to the number of bits that changed.
Waveforms for different values of memory data are plotted on top of each
other to effectively show this relationship. The difference in voltage
between i transitions and i+1 transitions is about 6.5 mV.
We observed similar plots for smartcards that leak Hamming weight information.
The type of information that a particular smartcard leaks depends on the
circuit design of the microprocessor and the type of operation being performed
by the card. For instance, accessing EEPROM may yield different information
than accessing RAM. Knowing which type of information is leaked will enable
an adversary to optimize an attack strategy.
Simple Power Analysis (SPA)
An SPA attack, as described in [6],
involves directly observing a system's power consumption. Different attacks
are possible depending on the capabilities of the attacker. In some situations
the attacker may be allowed to run only a single encryption or decryption
operation. Other attackers may have unlimited access to the card. The most
powerful attackers not only have unlimited access, but also have detailed
knowledge of the software and hardware running in the card. If an attacker
can determine where certain instructions are being executed, it can be
relatively simple to extract useful information. For example, during the
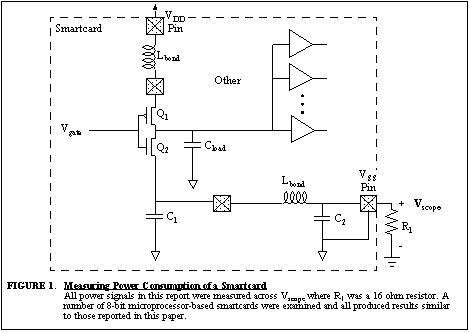
PC1 permutation in DES, we could determine the Hamming weight of each key
byte by measuring the pulse height at the cycle of the instruction that
accesses this data. In an 8-bit microprocessor, knowing the Hamming weight
of all eight DES key bytes reduces the brute-force search space from 256
to
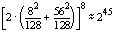 or or 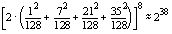
keys depending on whether or not the parity bits are used. This was
just an example; with algorithms using more key bits than DES or with triple-DES,
knowing Hamming weight information alone does not help much with this type
of brute-force attack.
A more powerful attack can result if the attacker can see
Hamming weight information about the key bytes and also information about
shifted versions of the key bytes. In DES, such information can be leaked
when shifting the C and D registers. In fact, given the weight of each
byte for eight of the C and D shifts there is enough information to solve
for the value of every key bit using the equation
 (1) (1)
where  is a 56x1
vector of Hamming weights, wi; 
is a 56x1 binary vector of the key bits, kj; and
A
is a 56x56 binary matrix such that
Aij is 1 if and only
if weight wi includes key bit kj. Even
algorithms with more than 56 key bits, such as triple-DES would be vulnerable
to this attack.
If transition count information rather than Hamming weight information
is available, an SPA attack can still be mounted, but it may be more difficult.
The attacker would need to know the contents of the data bus before or
after the data being sought is accessed. Many times this data is easy to
determine because it is a fixed address or an instruction opcode. Attackers
with access to the code can easily get this data and set up equations similar
to Equation (1) . Other less knowledgeable
attackers may need to resort to trial and error to determine the correct
equations. Due to the limited number of possibilities such an approach
is reasonable.
Our experiments confirmed that poor implementations of DES will almost
always be vulnerable to SPA attacks. Shifting the key bytes or the use
of conditional branches to test bit values can be especially vulnerable.
Also, if the code or portions of the code run in variable time, power analysis
could be used to enable a timing attack
[4]
.
Fortunately, implementors of cryptographic algorithms have known about
these issues for a number of years. Kocher et al. [6]
reported
that it is not particularly difficult to build SPA-resistant devices. However,
the attackers keep getting smarter so further research and vigilance will
always be necessary.
Differential Power Analysis (DPA)
A DPA attack, described in [6]
and
reviewed here, is more powerful than an SPA attack because the attacker
does not need to know as many details about how the algorithm was implemented.
The technique also gains strength by using statistical analysis to help
recover side-channel information. The objective of the DPA attacks described
in this paper is to determine the secret key used by a smartcard running
the DES algorithm. These techniques can also be generalized to attack other
similar cryptographic algorithms.
A DPA attack begins by running the encryption algorithm for N
random values of plain-text input. For each of the N plain-text
inputs, PTIi, a discrete time power signal, Sij,
is collected and the corresponding cipher-text output, CTOi,
may also be collected. The power signal Sij is a sampled
version of the power consumed during the portion of the algorithm that
is being attacked. The i index corresponds to the PTIi that
produced the signal and the j index corresponds to the time of the
sample. The Sij are split into two sets using a partitioning
function, D( . , . , . ):
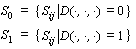 (2)
(2)
The next step is to compute the average power signal for each set:
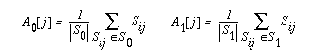 (3) (3)
where |S0| + |S1| = N. By
subtracting the two averages a discrete time DPA bias signal, T[j],
is obtained:
 (4) (4)
Selecting an appropriate D function will result in a DPA bias
signal that an attacker can use to verify guesses of the secret key. An
example of such a D function is as follows:
 (5) (5)
where
C1 = the 1 bit of CTOi that is XOR'ed
with bit #1 of S-box #1
C6 = the 6 bits of CTOi that are XOR'ed
with subkey K16
K16 = 6 bits of the 16th round subkey feeding into S-box
#1
SBOX1(x) = a function returning bit #1 resulting from looking up x in
S-box #1
The D function of Equation
(5)
is chosen because at some point during a DES implementation, the
software needs to compute the value of this bit. When this occurs or anytime
data containing this bit is manipulated, there will be a slight difference
in the amount of power dissipated depending on whether this bit is a zero
or a one. If this difference is  , and the instructions
manipulating the D bit occurs at times j*, the following
expected difference in power equation results: , and the instructions
manipulating the D bit occurs at times j*, the following
expected difference in power equation results:
 (6) (6)
When j is not equal to j*, the smartcard
is manipulating bits other than the D bit, and the power dissipation
is independent of the D bit:
 (7) (7)
As the number N of PTI inputs is increased, Equation
(4) , converges to the expectation equation:
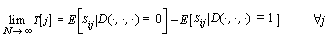 (8) (8)
Thus, a review of Equation
(6) , (7) and (8)
shows
that if enough PTI samples are used, T[ j] will show power
biases of  at times j*, and will converge
to zero all other times. Due to small statistical biases in the S-box outputs,
the assumption of independence in Equation (7)
is
not completely true. In reality, T[ j] will not always converge
to zero; however the largest biases will occur at times j*.
One input to the D function was K 16, six bits of
the subkey. The attacker does not know these bits, but can use brute force
and try all 2 6 possible values. For each guess, the attacker
constructs a new partition for the power signatures and gets a new bias
signal, T[ j]. If the proper D function was chosen,
the bias signal will show spikes whenever the D bit was manipulated.
If the
D function was not chosen correctly (i.e., the wrong subkey
bits were guessed), then the resulting T[ j] will not show any biases.
Using this approach, an attacker can determine the six subkey inputs to
S-box #1 at round 16 of DES. Repeating this approach for the seven other
DES S-boxes allows the attacker to learn the entire round 16 subkey (48
bits). The remaining 8 bits can be found by brute force or by successively
applying this approach backwards to previous rounds. Figure
3 compares the bias signal for a correctly chosen key to that of an
incorrectly chosen key. The signal for the incorrect key shows a few small
biases, but the correct key has biases that are twice as large, so it is
easily recognized. We created the signals in Figure
3 using
N = 1300.

Noise in Power Analysis Attacks
There is a rich history of methods to reduce noise in electrical circuits.
Many good textbooks have been written on this topic (e.g., [14]
).
Techniques for noise reduction are particularly important when trying to
measure side-channel emanations because the magnitude of these signals
can be extremely small. The DPA attack uses averaging to reduce noise,
but it is important to investigate other strategies that may lead to further
reductions in the amount of noise. Experts quoted in [15]
report
that one way to prevent a power analysis attack is to mask the side-channel
information with random calculations that increase the measurement noise.
A good understanding of the achievable noise levels using typical electronic
measuring techniques is needed to evaluate the effectiveness of such a
solution.
Noise Characteristics
There are four types of noise present when performing power analysis
of smartcards: external, intrinsic, quantization and algorithmic. External
noise is generated by an external source and coupled into the smartcard.
Intrinsic noise is due to the random movement of charge carriers within
conductors. Quantization noise is due to the quantizer in the A/D that
is used to sample the power signals. Algorithmic noise is due to the randomness
of the data bytes being processed by the smartcard. Intrinsic and quantization
noise are small when compared to present day side-channel signals, but
will likely play a larger role as future designs minimize side-channel
signals. External noise can be reduced through careful use of measuring
equipment, good circuit design practices and filtering. Algorithmic noise
can be reduced if an attack strategy can use unbiased random data that
can be averaged out.
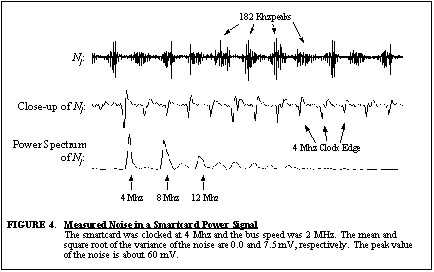
Figure 4 illustrates a sample of the
noise measured in a power analysis experiment. The top waveform, Nj,
was determined using the following equation:

where the value of E[ Sj] was estimated
by averaging the power traces obtained when encrypting the same input data
5,000 times and Sj is one of the traces. Clearly any
deviation of Nj from zero should be considered noise.
The noise shown in Figure 4 has a slow beat
frequency around 182 Khz that could be due to external coupling from test
equipment or more likely due to the superposition of the digital oscilloscope's
sampling frequency and the smartcard's clock frequency. The power spectrum
of the noise also reveals significant spikes at the smartcard's clock frequency
and its harmonics. A close-up of the noise reveals that a significant amount
of the noise energy is concentrated at the edges of the smartcard's 4 Mhz
clock edges. Figure 4 does not contain
algorithmic noise since the data being encrypted was kept constant. The
effect of algorithmic noise would be to cause spikes to appear in the portion
of the signal where the data is being processed. These spikes could be
used by an attacker to mark locations in the power trace that are data
dependent. Algorithm noise can be modeled as shot noise using a generalized
Poisson random process [16]
:

In this case, ci is a random variable (r.v.)
corresponding to the Hamming weight of the data being processed, ji
is a Poisson r.v. that models the seemingly random locations of the data
dependencies and F would be the shape of the bias signal. If random
data is used, then ci would have a binomial distribution.
An accurate model of the various noise components would be very useful
for simulating the effectiveness of DPA attacks and solutions.
Filtering the Noise
Filtering strategies can be used to reduce the noise shown in Figure
4 , but care needs to be taken so that the components necessary to
create a power bias signal are not affected. The algorithmic noise can
be reduced by averaging using unbiased random data. Filtering will not
work on algorithmic noise because any filter would also reduce the desired
bias signal. If the noise in Figure 4 is
assumed to be white noise, then the optimal filter that maximizes the signal-to-noise
ratio (SNR) is the matched filter. We designed and tested such a filter
for the bias signal shown in Figure 3 .
The original voltage SNR was 17.3. After using the matched filter, the
SNR was increased to 23.2. This gives some indication of how much an attacker
with a perfect matched filter can improve the SNR.
The Effect of Averaging
A DPA attack is successful because averaging reduces noise energy,
thus revealing any concentrations of signal energy that occur at constant
positions in time. To see the effect of averaging on the noise refer back
to Equation (3) . Let the average variance
of Sij be  and assume Sij
is independent of Skj when 
. If the N signals were equally split between sets S 0
and S 1, then the variance of A 0 and A 1
is  . Therefore, when A 0 and A 1
are combined the resulting DPA bias signal has a variance of 
.
The averaging effect on the signal was shown in Equation
(6) produce a bias spike of size  . The D
function, proposed in Equation (5) , has
the effect of fixing one bit of the data being processed. If a data word
is m bits wide, then the remaining unfixed bits in the word have
an average Hamming weight of ( m-1)/2 with a variance (i.e., algorithmic
noise) of ( m-1)/4. Averaging over N samples has a similar
effect on this signal variance as it did on the noise variance. Assuming
independence of the different sources of noise yields the following signal
and noise parameters:
 (9) (9)
In the variance of the noise, the term 
is the percentage of T[ j] that is dependent on the data being
encrypted, thus the percentage of algorithmic noise. The success of a DPA
attack depends on distinguishing the signal from noise, so the final voltage
SNR is:
 (10) (10)
Equation (10) can be checked with previously
measured experimental results. Setting  =7.5
mV (from Figure 4 ), 
= 6.5 mV (from
Figure 2 ), m = 8,
N
= 1000, and  yields SNR = 7.5. Experimental
results using these parameters showed a SNR between 7 and 10, thus confirming
that Equation (10)
is a valid approximation.
Maximizing DPA Bias Signal
One way to increase the SNR in Equation
(10) is to increase  . The value of 
is dependent on the number of bits output by the D function. In
Equation
(5)
, D outputs only one bit, but in general the D function
could output d bits. In this general case  = dl,
where l is a constant equal to the voltage difference seen between
two data words with Hamming weight i and i+1. Figure
2 showed that these differences can be considered approximately equal,
for all i.
When performing the differential power analysis there would be three
sets used for partitioning:

The other DPA equations would all remain the same and the power signals
in set S2 would not be used. The following signal and noise
equations would result:
 (11) (11)
4-bit DPA Attack on DES
In DES, a 4-bit D function based on the four bits output from
an S-box can be used to partition the sets S 0 and S 1.
Equation
(5) can be modified to output four bits:
 (12) (12)
where SBOX14(x) returns all four bits resulting from looking
up x in SBOX #1. Similar D functions would be used for the other
S-boxes to enable all the key bits to be eventually determined.
The question arises as to whether
Equation
(12) will result in partitions that are unbiased enough so that the
incorrect choices of K 16 will result in random power signals
that average to zero. A simulation was written to see what type of biases
could be expected. The results for 4-bit DPA and 1-bit DPA using random
PTI inputs and a typical key are graphed in
Figure
5 . The graph shows that the expected Hamming weight biases of the
S-box #1 lookup for each of the 64 possible key guesses. The correct key
guess clearly shows the most bias; however in the case of 4-bit DPA there
is a case where an incorrect key guess has the same magnitude bias as the
correct key. In this case, if the attacker did not know the sign of the
expected bias, a very small brute-force search might be needed.

Multiple Bit DPA
In general, other multiple bit D functions can
be defined. In software implementations, the S-box lookups are performed
using a load instruction from a table storing all the S-box data. To compress
the table size, the four bit S-box data is frequently stored in pairs of
two or more, depending on the word size of the processor. If the attacker
knows how the S-box data is packed into this table, it would be possible
to maximize the bit biases even further. For example, power signals with
S-box lookups that yield many zeros can be separated from signals with
S-box lookups containing many ones. Again, the number of bits that can
be biased will proportionally increase the SNR.
Another way to mount an attack would be to partition
S0 and S1 based on the addresses used for the S-box
lookups rather than the data. The attacker forms two partitions, one that
maximizes the number of address bus transitions and one that minimizes
the number of address bus transitions. Power signatures from both partitions
are averaged and then subtracted. If the address bus is larger than the
data bus, even larger biases could be achieved.
When mounting a d-bit DPA attack the attacker may need to use
more power signals. After all, an average of 1-2 1-d of
the power signals are placed in partition S 2 and are unused.
This suggests that an attacker cannot increase d too much without
requiring an excessive number of power signals. An attacker running 1-bit
DPA using N signals would need Nd =
2 d-1N/ d2 power signals
to maintain the same SNR when running d-bit DPA. Table
1 shows that for small values of d actually fewer power signals
are necessary and with 8-bit DPA only twice as many signals are needed.
The main advantage of d-bit DPA is that the resulting signal levels
are magnified d times.
Experiments were run on a smartcard to confirm the effectiveness
of 4-bit, 8-bit and address-bit DPA. The resulting signal levels are shown
in Table2. In these experiments, the 8-bit
DPA attack was only able to create an average bias of 6.0 bits because
the S-box data was never all zeros or all ones. The address-bit DPA had
similar problems so only an average bias of 6.5 bits was achieved. As can
be seen the signal levels for these multiple bit DPA attacks are much stronger.
It is clear that countermeasures to DPA attacks need to consider all these
more powerful attacks.
Table1:
|
d
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|
N
|
N
|
0.5N
|
0.44N
|
0.5N
|
0.64N
|
0.88N
|
1.3N
|
2N
|
Table 2:
|
Attack type:
|
1-bit DPA
|
4-bit DPA
|
8-bit DPA
|
Address DPA
|
|
Signal Level:
|
9.3 mV
|
38.5mV
|
79.5mV
|
74.4mV
|
Hiding the DPA Bias Spike
One suggested solution to prevent DPA attacks is to add
random calculations that increase the noise level enough to make the DPA
bias spikes undetectable. The results presented in this paper give some
indication of how much noise needs to be added. The main goal is to add
enough random noise to stop an attack, but to add minimal overhead. A rough
approximation of the noise necessary can be found by looking at the probability
density function (p.d.f.) of the DPA bias signal plotted in Figure
6 . The DPA spike obviously stands out from the noise because it is
very improbable that it was generated by noise. Ideally, the p.d.f. of
the bias signal would stretch out to cover the DPA spike or the DPA spike
would be reduced so that it is closer to the noise. One suggested design
criterion is that the DPA bias spike have equal amounts of noise distributed
above and below it. This means the median of the noise signal would be
at the level of the DPA bias spike. If the noise were Guassian, the median
would be when the SNR=0.67. One could then use Equation
(11)
to determine what amount of noise is necessary to prevent the
desired level of attack. Of course a different strategy would need to be
used if the noise p.d.f. was not normal or the noise around the DPA spike
was non-stationary. The fact that the DPA bias spikes and most of the noise
energy occurs near the clock edges can also be considered. Less noise may
be necessary because the DPA spikes occur in these areas of high noise
energy. 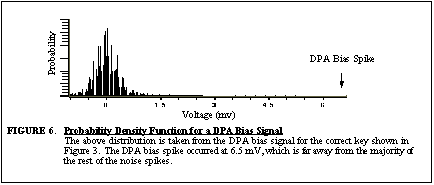
Future Work
Future research in this area will investigate power analysis
attacks on hardware encryption devices and public-key cryptosystems. Preliminary
work suggests that such systems will also be vulnerable, but specific attacks
have not yet been evaluated. The analysis of more symmetric-key algorithms
is also an important topic that will be investigated. Ways to design and
implement new algorithms that are not vulnerable to these attacks will
be researched. The solutions to prevent these types of side-channel attacks
need to be carefully scrutinized. Comprehensive analysis techniques, testing
procedures and more advanced modeling methods will be developed.
Conclusions
Attacks that monitor side-channel information and in particular power
analysis attacks have recently been getting much attention by experts in
the smartcard industry. The results presented in this paper confirm that
power analysis attacks can be quite powerful and need to be addressed.
Ways an attacker might maximize the side-channel signals have been investigated
and were found to be very effective. Solutions to prevent DPA attacks need
to consider these advanced attacks in order to provide the maximum amount
of security. Understanding the noise characteristics of the power signals
is also very important. The experimental and theoretical results presented
in this paper hopefully will be helpful for modeling the problem and designing
the solutions.
Much of the concern in industry is how to safeguard existing products.
These products are mostly software implementations similar to the ones
examined in this paper. The new attacks and analysis results presented
in this paper are applicable to these designs and to future designs and
hardware implementations. When creating a new hardware encryption circuit
or algorithm implementation, a designer needs to ask the question: "What
is the strongest potential power analysis attack that can be mounted by
an attacker?" With the answer to this in mind, a designer can successfully
protect against power analysis attacks.
References
[1] E. Biham and A. Shamir, "Differential
Cryptanalysis of DES-like Crytptosystems," Journal of Cryptography, Vol.
4, No. 1, 1991, pp. 3-72.
[2] M. Matsui, "Linear Cryptanalysis
Method for DES Cipher," in Proceedings of Advances in Cryptology-Eurocrypt
`93, Springer-Verlag, 1994, pp. 386-397.
[3] J. Kelsey, B. Schneier, D.
Wagner, and C. Hall, "Side Channel Cryptanalysis of Product Ciphers," in
Proceedings of ESORICS '98, Springer-Verlag, September 1998, pp. 97-110.
[4] P. Kocher, "Timing Attacks on Implementations
of Diffie-Hellman, RSA, DSS, and Other Systems," in Proceedings of Advances
in Cryptology-CRYPTO `96, Springer-Verlag, 1996, pp. 104-113.
[5] J. F. Dhem, F. Koeune, P.
A. Leroux, P. Mestré, J. J. Quisquater and J. L. Willems, "A Practical
Implementation of the Timing Attack," in Proceedings of CARDIS 1998, September
1998.
[7] W. van Eck, "Electromagnetic
Radiation from Video Display Units: An Eavesdropping Risk," Computers and
Security, v. 4, 1985, pp. 269-286.
[8] D. Boneh and R. A. Demillo
and R. J. Lipton, "On the Importance of Checking Cryptographic Protocols
for Faults," in Proceedings of Advances in Cryptology-Eurocrypt `97, Springer-Verlag,
1997, pp. 37-51.
[9] E. Biham and A. Shamir, "Differential
Fault Analysis of Secret Key Cryptosystems," in Proceedings of Advances
in Cryptology-CRYPTO `97, Springer-Verlag, 1997, pp. 513-525.
[10] R. Anderson and M. Kuhn,
"Tamper Resistance-A Cautionary Note," The Second USENIX Workshop on Electronic
Commerce Proceedings, 1996, pp. 1-11. [11] Cardtech/Securtech `98 -
Conference Proceedings, Volume II: Applications, 1998.
[12] ANSI X.392, "American National
Standard for Data Encryption Algorithm (DEA)," American Standards Institute,
1981.
[13] N. Weste and K. Eshraghian,
Principles of CMOS VLSI Design, Addison-Wesley Publishing Company, 1993.
[14] E. R. Davies, Electronics
Noise and Signal Recovery, San Diego, CA: Academic Press Inc., 1993.
[16] A. Papoulis, Probability,
Random Variables, and Stochastic Processes, New York: McGraw-Hill, Inc.
1991.
| 


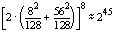 or
or