 |
 |
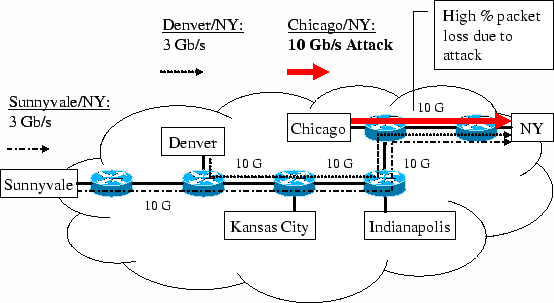
| (a)Attack along Chicago/NY | (b)Shielded Sunnyvale/NY and Denver/NY traffic from collateral damage |
Jerry Chou,
Bill Lin
University of California San Diego
Subhabrata Sen,
Oliver Spatscheck
AT&T Labs-Research
 |
 |
| (a)Attack along Chicago/NY | (b)Shielded Sunnyvale/NY and Denver/NY traffic from collateral damage |
 |

| 
| 
| (a) 1st iteration | (b) 2nd iteration |
(a) 1st iteration | (b) 2nd iteration | Figure 3:Network. |
Figure 4:Mean-PSP water-filling illustrated. |
Figure 5:CDF-PSP water-filling illustrated. |
| ||||
|
|
|
|
|
|
| Impacted | Impacted | Mean packet loss rate | |
| OD Pairs(%) | Demand(%) | of impacted OD pairs(%) | |
| US | 41.37 | 37.79 | 49.15 |
| [39.64, 42.72] | [35.16, 39.37] | [47.62, 50.43] | |
| EU | 43.18 | 45.33 | 68.11 |
| [38.48, 47.81] | [38.90, 52.05] | [65.51, 70.46] |
 |
| Figure 9:The crossfire OD pair total packet loss rate ratio over No-PSP across 24 hours.(48 attack time intervals, 30 minutes apart). |
|

| 
| 
|  |
| (a) US | (b) Europe | (a) US | (b) Europe |
| Figure 10:The mean OD packet loss rate ratio over No-PSP across 24 hours.(48 attack time intervals, 30 minutes apart). | Figure 11:The ratio of number of crossfire OD-pairs with packet loss over No-PSP across 24 hours.(48 attack time intervals, 30 minutes apart). | ||
|
|
|
|

| 
| 
|  |
| (a) US | (b) Europe | (a) US | (b) Europe |
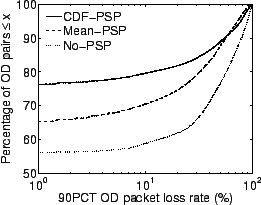
| Figure 12:CDF of the loss frequency for all crossfire OD pairs. | Figure 13:CDF of the 90 percentile packet loss rate for all crossfire OD pairs. | ||

| 
| 
|  |
| (a) US | (b) Europe | (a) US | (b) Europe |
| Figure 14:The correlation scatter plot for all crossfire OD-pairs between its 90 percentile OD packet loss rate under No-PSP/CDF-PSP and its historical traffic demand. | Figure 15:The correlation scatter plot for all crossfire OD-pairs between its 90 percentile OD packet loss rate under No-PSP/CDF-PSP and its historical activity factor. | ||

| 
| 
|  |
| (a) US | (b) Europe | (a) US | (b) Europe |
| Figure 16:CCDF of percentage of time that the loss rate for a crossfire OD pair under No-PSP and Mean-PSP exceeds that under CDF-PSP | Figure 17:The time-averaged mean crossfire OD-pair packet loss rate as the attack volume scaling factor increases from 0 to 3. | ||