The Practical Subtleties of Biometric Key Generation

Lucas Ballard Department of Computer Science The Johns Hopkins University

Seny Kamara Department of Computer Science The Johns Hopkins University

Michael K. Reiter Department of Computer Science University of North Carolina at Chapel Hill

Abstract

The inability of humans to generate and remember strong secrets makes it difficult for people to manage cryptographic keys. To address this problem, numerous proposals have been suggested to enable a human to repeatably generate a cryptographic key from her biometrics, where the strength of the key rests on the assumption that the measured biometrics have high entropy across the population. In this paper we show that, despite the fact that several researchers have examined the security of BKGs, the common techniques used to argue the security of practical systems are lacking. To address this issue we reexamine two well known, yet sometimes misunderstood, security requirements. We also present another that we believe has not received adequate attention in the literature, but is essential for practical biometric key generators. To demonstrate that each requirement has significant importance, we analyze three published schemes, and point out deficiencies in each. For example, in one case we show that failing to meet a requirement results in a construction where an attacker has a 22% chance of finding ostensibly 43-bit keys on her first guess. In another we show how an attacker who compromises a user's cryptographic key can then infer that user's biometric, thus revealing any other key generated using that biometric. We hope that by examining the pitfalls that occur continuously in the literature, we enable researchers and practitioners to more accurately analyze proposed constructions.

1 Introduction

While cryptographic applications vary widely in terms of assumptions, constructions, and goals, all require cryptographic keys. In cases where a computer should not be trusted to protect cryptographic keys--as in laptop file encryption, where keeping the key on the laptop obviates the utility of the file encryption--the key must be input by its human operator. It is well known, however, that humans have difficulty choosing and remembering strong secrets (e.g., [2,14]). As a result, researchers have devoted significant effort to finding input that has sufficient unpredictability to be used in cryptographic applications, but that remains easy for humans to regenerate reliably. One of the more promising suggestions in this direction are biometrics--characteristics of human physiology or behavior. Biometrics are attractive as a means for key generation as they are easily reproducible by the legitimate user, yet potentially difficult for an adversary to guess.

There have been numerous proposals for generating cryptographic keys from biometrics (e.g., [33,34,28]). At a high level, these Biometric Cryptographic Key Generators, or BKGs, follow a similar design: during an enrollment phase, biometric samples from a user are collected; statistical functions, or features, are applied to the samples; and some representation of the output of these features is stored in a data structure called a biometric template. Later, the same user can present another sample, which is processed with the stored template to reproduce a key. A different user, however, should be unable to produce that key. Since the template itself is generally stored where the key is used (e.g., in a laptop file encryption application, on the laptop), a template must not leak any information about the key that it is used to reconstruct. That is, the threat model admits the capture of the template by the adversary; otherwise the template could be the cryptographic key itself, and biometrics would not be needed to reconstruct the key at all.

Generally, one measures the strength of a cryptographic key by its entropy, which quantifies the amount of uncertainty in the key from an adversary's point of view. If one regards a key generator as drawing an element uniformly at random from a large set, then the entropy of the keys can be easily computed as the base-two logarithm of the size of the set. Computing the entropy of keys output by a concrete instantiation of a key generator, however, is non-trivial because "choosing uniformly at random" is difficult to achieve in practice. This is in part due to the fact that the key generator's source of randomness may be based on information that is leaked by external sources. For instance, an oft-cited flaw in Kerberos version 4 allowed adversaries to guess ostensibly 56-bit DES session keys in only $2^{20}$ guesses [13]. The problem stemmed from the fact that the seeding information input to the key generator was related to information that could be easily inferred by an adversary. In other words, this auxiliary information greatly reduced the entropy of the key space.

In the case of biometric key generators, where the randomness used to generate the keys comes from a user's biometric and is a function of the particular features used by the system, the aforementioned problems are compounded by several factors. For instance, in the case of certain biometric modalities, it is known that population statistics can be strong indicators of a specific user's biometric [10,36,3]. In other words, depending on the type of biometric and the set of features used by the BKG, access to population statistics can greatly reduce the entropy of a user's biometric, and consequently, reduce the entropy of her key. Moreover, templates could also leak information about the key. To complicate matters, in the context of biometric key generation, in addition to evaluating the strength of the key, one must also consider the privacy implications associated with using biometrics. Indeed, the protection of a user's biometric information is crucial, not only to preserve privacy, but also to enable that user to reuse the biometric key generator to manage a new key. We argue that this concern for privacy mandates not only that the template protect the biometric, but also that the keys output by a BKG not leak information about the biometric. Otherwise, the compromise of a key might render the user's biometric unusable for key generation thereafter.

The goal of this work is to distill the seemingly intertwined and complex security requirements of biometric key generators into a small set of requirements that facilitate practical security analyses by designers.

Specifically, the contributions of this paper are:

• The specification of three practical requirements that allow designers to ensure that a BKG ensures the privacy of a user's biometric and generates keys that are suitable for cryptographic applications.

• The analyses of three published BKGs. These are contributions in their own right, but more importantly serve as concrete evidence of the importance of the requirements.

• The description of Guessing Distance, a new heuristic measure that, given empirical data, can quickly estimate the security afforded by a BKG.

• Discussion of common pitfalls and subleties in current standards for empirical evaluation.

Throughout this paper we focus on the importance of considering adversaries who have access to public information, such as templates, when performing security evaluations. We hope that our observations will promote critical analyses of BKGs and temper the spread of flawed (or incorrectly evaluated) proposals.

2 Related Work

To our knowledge, Soutar and Tomko [34] were the first to propose biometric key generation. Davida et al. [9] proposed an approach that uses iris codes, which are believed to have the highest entropy of all commonly-used biometrics. However, iris code collection can be considered somewhat invasive and the use of majority-decoding for error correction--a central ingredient of the Davida et al. approach--has been argued to have limited use in practice [16].

Monrose et al. proposed the first practical system that exploits behavioral (versus physiological) biometrics for key generation [29]. Their technique uses keystroke latencies to increase the entropy of standard passwords. Their construction yields a key at least as secure as the password alone, and an empirical analysis showed that in some instances their approach increases the workload of an attacker by a multiplicative factor of $2^{15}$ . Later, a similar approach was used to generate cryptographic keys from voice [28,27]. Many constructions followed those of Monrose et al., using biometrics such as face [15], fingerprints [33,39], handwriting [40,17] and iris codes [16,45]. Unfortunately, many are susceptible to attacks. Hill-climbing attacks have been leveraged against fingerprint, face, and handwriting-based biometric systems [1,37,43] by exploiting information leaked during the reconstruction of the key from the biometric template.

There has also been an emergence of generative attacks against biometrics [5,23], which use auxiliary information such as population statistics along with limited information about a target user's biometric. The attacks we present in this paper are different from generative attacks because we assume that adversaries only have access to templates and auxiliary information. Our attacks, therefore, capture much more limited, and arguably more realistic, adversaries. Despite such limited information, we show how an attacker can recover a target user's key with high likelihood.

There has also been recent theoretical work to formalize particular aspects of biometric key generators. The idea of fuzzy cryptography was first introduced by Juels and Wattenberg [21], who describe a commitment scheme that supports noise-tolerant decommitments. In Section 7 we provide a concrete analysis of a published construction that highlights the pitfalls of using fuzzy commitments as biometric key generators. Further work included a fuzzy vault [20], which was later analyzed as an instance of a secure-sketch that can be used to build fuzzy extractors [11,6,12,22]. Fuzzy extractors treat biometric features as non-uniformly distributed, error-prone sources and apply error-correction algorithms and randomness extractors [18,30] to generate random strings.

Fuzzy cryptography has made important contributions by specifying formal security definitions with which BKGs can be analyzed. Nevertheless, there remains a gap between theoretical soundness and practical systems. For instance, while fuzzy extractors can be effectively used as a component in a larger biometric key generation system, they do not capture all the practical requirements of a BKG. In particular, it is unclear whether known constructions can correct the kinds of errors typically generated by humans, especially in the case of behavioral biometrics. Moreover, fuzzy extractors require biometric inputs with high min-entropy but do not address how to select features that achieve this requisite level of entropy. Since this is an inherently empirical question, much of our work is concerned with how to experimentally evaluate the entropy available in a biometric.

Lastly, Jain et al. enumerate possible attacks against biometric templates and discuss several practical approaches that increase template security [19]. Similarly, Mansfield and Wayman discuss a set of best practices that may be used to measure the security and usability of biometric systems [24]. While these works describe specific attacks and defenses against systems, they do not address biometric key generators and the unique requirements they demand.

3 Biometric Key Generators

Before we can argue about how to accurately assess biometric key generators (BKGs), we first define the algorithms and components associated with a BKG. These definitions are general enough to encompass most proposed BKGs.

BKGs are generally composed of two algorithms, an enrollment algorithm ( $\ensuremath{\mathsf{Enroll}}$ ) and a key-generation algorithm ( $\ensuremath{\mathsf{KeyGen}}$ ):

• $\ensuremath{\mathsf{Enroll}}(\ensuremath{{\beta}}_1, \dots, \ensuremath{{\beta}}_\ell)$ : The enroll algorithm is a probabilistic algorithm that accepts as input a number of biometric samples ( $\ensuremath{{\beta}}_1, \dots, \ensuremath{{\beta}}_\ell$ ), and outputs a template ( $\ensuremath{\mathcal{T}}$ ) and a cryptographic key ( $\ensuremath{\mathcal{K}}$ ). In the event that $\ensuremath{{\beta}}_1, \dots, \ensuremath{{\beta}}_\ell$ do not meet some predetermined criteria, the enroll algorithm might output the failure symbol $\bot$ .

• $\ensuremath{\mathsf{KeyGen}}(\ensuremath{{\beta}}, \ensuremath{\mathcal{T}})$ : The key generation algorithm accepts as input one biometric sample ( $\ensuremath{{\beta}}$ ), and a template ( $\ensuremath{\mathcal{T}}$ ). The algorithm outputs either a cryptographic key ( $\ensuremath{\mathcal{K}}$ ), or the failure symbol $\bot$ if $\ensuremath{{\beta}}$ cannot be used to create a key.

The enrollment algorithm estimates the variation inherent to a particular user's biometric reading and computes information needed to error-correct a new sample that is sufficiently close to the enrollment samples. $\ensuremath{\mathsf{Enroll}}$ encodes this information into a template and outputs the template and the associated key. The key-generation algorithm uses the template output by the enrollment algorithm and a new biometric sample to output a key. If the provided sample is sufficiently similar to those provided during enrollment, then $\ensuremath{\mathsf{KeyGen}}$ and $\ensuremath{\mathsf{Enroll}}$ output the same keys.

Generally speaking, there are four classes of information associated with a BKG.

• The Biometric (${\beta}$ ): A biometric is a measurement of a person's behavior or physiology. A BKG extracts $\ensuremath{{\beta}}$ as algorithmically interpretable representations (e.g., a set of signals). The BKG typically applies statistical functions, or features ( $\phi_1, \dots, \phi_n$ ), to the representations, and uses the output to either derive [17,41] or lock [33,16,38] a cryptographic key.

• A Template ( $\mathcal{T}$ ): A template is any piece of information that is stored on the system for the purpose of re-generating the cryptographic key. Templates are generally created during an enrollment process and stored so that a user can easily recreate her key. For all practical purposes, templates must be considered publicly available. Note that this assumption implies that more standard biometric templates, which are typically employed for authentication purposes and are simply the encoding of a biometric [42], cannot be used securely in this setting.

• The Key ( $\mathcal{K}$ ): A cryptographic key that is derived from (or locked by) one or more biometric samples during an enrollment phase. The key may later be regenerated using another biometric sample that is "close" to the original samples and the template that was also output during enrollment.

• Auxiliary Information ( $\mathcal{A}$ ): Auxiliary information encompasses any public information not intended to be used for key-derivation purposes but that is still readily available to an adversary. Auxiliary information is specified with respect to one user and includes any biometric, template, or key other than those associated with the user in question. It could also include any other information about the environment that might leak information about the biometric, or results of using the key.

For the remainder of the paper if a component of a BKG is associated with a specific user, then we subscript the information with the user's unique identifier. So, for example, $\ensuremath{{\beta}}_u$ , is $u$ 's biometric and $\ensuremath{\mathcal{A}}_{\bar{u}}$ is auxiliary information derived from all users $u' \ne u$ .

3.1 Evaluation Recommendations

At a high level, the evaluation of a BKG requires designers to show that two properties hold: correctness and security. Intuitively, a scheme that achieves correctness is one that is usable for a high percentage of the population. That is, the biometric of choice can be reliably extracted to within some threshold of tolerance, and when combined with the template the correct key is output with high probability. As correctness is well understood, and is always presented when discussing the feasibility of a proposed BKG, we do not address it further.

In the context of biometric key generation, security is not as easily defined as correctness. Loosely speaking, a secure BKG outputs a key that "looks random" to any adversary that cannot guess the biometric. In addition, the templates and keys derived by the BKG should not leak any information about the biometric that was used to create them. We enumerate a set of three security requirements for biometric key generators, and examine the components that should be analyzed mathematically (i.e., the template and key) and empirically (i.e., the biometric and auxiliary information). While the necessity of the first two requirements has been understood to some degree, we will highlight and analyze how previous evaluations of these requirements are lacking. Additionally, we discuss a requirement that is often overlooked in the practical literature, but one which we believe is necessary for a secure and practical BKG.

We consider a BKG secure if it meets the following three requirements for each enrollable user in a population:

• Key Randomness ( $\ensuremath{\mathsf{REQ\mbox{-}KR}}$ ): The keys output by a BKG appear random to any adversary who has access to auxiliary information and the template used to derive the key. For instance, we might require that the key be statistically or computationally indistinguishable from random.

• Weak Biometric Privacy ( $\ensuremath{\mathsf{REQ\mbox{-}WBP}}$ ): An adversary learns no useful information about a biometric given auxiliary information and the template used to derive the key. For instance, no computationally bounded adversary should be able to compute any function of the biometric.

• Strong Biometric Privacy ( $\ensuremath{\mathsf{REQ\mbox{-}SBP}}$ ): An adversary learns no useful information about a biometric given auxiliary information, the template used to derive the key, and the key itself. For instance, no computationally bounded adversary should be able to compute any function of the biometric.

The necessity of $\ensuremath{\mathsf{REQ\mbox{-}KR}}$ and $\ensuremath{\mathsf{REQ\mbox{-}WBP}}$ is well known, and indeed many proposals make some sort of effort to argue security along these lines (see, e.g., [29,11]). However, many different approaches are used to make these arguments. Some take a cryptographically formal approach, whereas others provide an empirical evaluation aimed at demonstrating that the biometrics and the generated keys have high entropy. Unfortunately, the level of rigor can vary between works, and differences in the ways $\ensuremath{\mathsf{REQ\mbox{-}KR}}$ and $\ensuremath{\mathsf{REQ\mbox{-}WBP}}$ are typically argued make it difficult to compare approaches. Also, it is not always clear that the empirical assumptions required by the cryptographic algorithms of the BKG can be met in practice.

Even more problematic is that many approaches for demonstrating biometric security merely provide some sort of measure of entropy of a biometric (or key) based on variation across a population. For example, one common approach is to compute biometric features for each user in a population, and compute the entropy over the output of these features. However, such analyses are generally lacking on two counts. For one, if the correlation between features is not accounted for, the reported entropy of the scheme being evaluated could be much higher than what an adversary must overcome in practice. Second, such techniques fail to compute entropy as a function of the biometric templates, which we argue should be assumed to be publicly available. Consequently, such calculations would declare a BKG "secure" even if, say, the template leaked information about the derived key. For example, suppose that a BKG uses only one feature and simply quantizes the feature space, outputting as a key the region of the feature space that contains the majority of the measurements of a specific user's feature. The quantization is likely to vary between users, and so the partitioning information would need to be stored in each user's template. Possession of the template thus reduces the set of possible keys, as it defines how the feature space is partitioned.

As far as we know, the notion of Strong Biometric Privacy ( $\ensuremath{\mathsf{REQ\mbox{-}SBP}}$ ) has only been considered recently, and only in a theoretical setting [12]. Even the original definitions of fuzzy extractors [11, Definition 3] do not explicitly address this requirement. Unfortunately, $\ensuremath{\mathsf{REQ\mbox{-}SBP}}$ has also largely been ignored by the designers of practical systems. Perhaps this oversight is due to lack of perceived practical motivation--it is not immediately clear that a key could be used to reveal a user's biometric. Indeed, to our knowledge, there have been few, if any, concrete attacks that have used keys and templates to infer a user's biometric. We observe, however, that it is precisely practical situations that motivate such a requirement; keys output by a BKG could be revealed for any number of reasons in real systems (e.g., side-channel attacks against encryption keys, or the verification of a MAC). If a key can be used to derive the biometric that was used to generate the key, then key recovery poses a severe privacy concern. Moreover, key compromise would then preclude a user from using this biometric in a BKG ever again, as the adversary would be able to recreate any key the user makes thereafter. Therefore, in Section 7 we provide specific practical motivation for this requirement by describing an attack against a well-accepted BKG. The attack combines the key and a template to infer a user's biometric.

In what follows, we provide practical motivation for the importance of each of our three requirements by analyzing three published BKGs. It is not our goal to fault specific constructions, but instead to critique evaluation techniques that have become standard practice in the field. We chose to analyze these specific BKGs because each was argued to be secure using "standard" techniques. However, we show that since these techniques do not address important requirements, each of these constructions exhibit significant weaknesses despite security arguments to the contrary.

4 Biometrics and "Entropy"

Before continuing further, we note that analyzing the security of a biometric key generator is a challenging task. A comprehensive approach to biometric security should consider sources of auxiliary information, as well as the impact of human forgers. Though it may seem impractical to consider the latter as a potential threat to a standard key generator, skilled humans can be used to generate initial forgeries that an algorithmic approach can then leverage to undermine the security of the BKG.

To this point, research has accepted this "adversarial multiplicity" without examining the consequences in great detail. Many works (e.g., [33,29,17,15,40,16]) report both False Accept Rates (i.e., how often a human can forge a biometric) and an estimate of key entropy (i.e., the supposed difficulty an algorithm must overcome in order to guess a key) without specifically identifying the intended adversary. In this work, we focus on algorithmic adversaries given their importance in offline guessing attacks, and because we have already addressed the importance of considering human-aided forgeries [4,5]. While our previous work did not address biometric key generators specifically, those lessons apply equally to this case.

The security of biometric key generators in the face of algorithmic adversaries has been argued in several different ways, and each approach has advantages and disadvantages. Theoretical approaches (e.g., [11,6]) begin by assuming that the biometrics have high adversarial min-entropy (i.e., conditioned on all the auxiliary information available to an adversary, the entropy of the biometric is still high) and then proceed to distill this entropy into a key that is statistically close to uniform. However, in practice, it is not always clear how to estimate the uncertainty of a biometric. In more practical settings, guessing entropy [25] has been used to measure the strength of keys (e.g., [29,27,10]), as it is easily computed from empirical data. Unfortunately, as we demonstrate shortly, guessing entropy is a summary statistic and can thus yield misleading results when computed over skewed distributions. Yet another common approach (e.g., [31,7,16,41,17]), which has lead to somewhat misleading views on security, is to argue key strength by computing the Shannon entropy of the key distribution over a population. More precisely, if we consider a BKG that assigns the key $\ensuremath{\mathcal{K}}_u$ to a user $u$ in a population $P$ , then it is considered "secure" if the entropy of the distribution $\P(\ensuremath{\mathcal{K}}) = \vert\{u \in P: \ensuremath{\mathcal{K}}_u = \ensuremath{\mathcal{K}}\}\vert / \vert P\vert$ is high. We note, however, that the entropy of the previous distribution measures only key uniqueness and says nothing about how difficult it is for an adversary to guess the key. In fact, it is not difficult to design BKGs that output keys with maximum entropy in the previous sense, but whose keys are easy for an adversary to guess; setting $\ensuremath{\mathcal{K}}_u = u$ is a trivial example.

To address these issues, we present a new measure that is easy to compute empirically and that estimates the difficulty an adversary will have in guessing the output of a distribution given some related auxiliary distribution. It can be used to empirically estimate the entropy of a biometric for any adversary that assumes the biometric is distributed similarly to the auxiliary distribution. Our proposition, Guessing Distance, involves determining the number of guesses that an adversary must make to identify a biometric or key, and how the number of guesses are reduced in light of various forms of auxiliary information.

4.1 Guessing Distance

We assume that a specific user $u$ induces a distribution $\ensuremath{\mathcal{U}}$ over a finite, $n$ -element set $\Omega$ . We also assume that an adversary has access to population statistics that also induce a distribution, $P$ , over $\Omega$ . $P$ could be computed from the distributions of other users $u' \ne u$ . We seek to quantify how useful $P$ is at predicting $\ensuremath{\mathcal{U}}$ . The specification of $\Omega$ varies depending on the BKG being analyzed; $\Omega$ could be a set of biometrics, a set of possible feature outputs, or a set of keys. It is up to system designers to use the specification of $\Omega$ that would most likely be used by an adversary. For instance, if the output of features are easier to guess than a biometric, then $\Omega$ should be defined as the set of possible feature outputs. Although at this point we keep the definition of $P$ and $\ensuremath{\mathcal{U}}$ abstract, it is important when assessing the security of a construction to take as much auxiliary information as possible into account when estimating $P$ . We return in Section 5 with an example of such an analysis.

We desire a measure that estimates the number of guesses that an adversary will make to find the high-probability elements of $\ensuremath{\mathcal{U}}$ , when guessing by enumerating $\Omega$ starting with the most likely elements as prescribed by $P$ . That is, our measure need not precisely capture the distance between $\ensuremath{\mathcal{U}}$ and $P$ (as might, say, $L_1$ -distance or Relative Entropy), but rather must capture simply $P$ 's ability to predict the most likely elements as described by $\ensuremath{\mathcal{U}}$  ¹. Given a user's distribution $\ensuremath{\mathcal{U}}$ , and two (potentially different) population distributions $\P_1$ and $\P_2$ , we would like the distance between $\ensuremath{\mathcal{U}}$ and $\P_1$ and $\ensuremath{\mathcal{U}}$ and $\P_2$ to be the same if and only if $\P_1$ and $\P_2$ prescribe the same guessing strategy for a random variable distributed according to $\ensuremath{\mathcal{U}}$ . For example, consider the distributions $\ensuremath{\mathcal{U}}$ , $\P_1$ and $\P_2$ , and the element $\omega \in \Omega$ such that $\P_1(\omega) = .9$ , $\P_2(\omega) = .8$ , and $\ensuremath{\mathcal{U}}(\omega) = 1$ . Here, an adversary with access to $\P_1$ would require the same number of guesses to find $\omega$ as an adversary with access to $\P_2$ (one). Thus, we would like the distance between $\ensuremath{\mathcal{U}}$ and $\P_1$ and between $\ensuremath{\mathcal{U}}$ and $\P_2$ to be the same.

Guessing Distance.

Let $\omega^* = \mathop{\mathrm{argmax}}_{\omega \in \Omega} \ensuremath{\mathcal{U}}(\omega)$ . Let $L_\P = (\omega_1, \dots, \omega_n)$ be the elements of $\Omega$ ordered such that $\P(\omega_i) \ge \P(\omega_{i+1})$ for all $i \in [1,n-1]$ . Define $t^-$ and $t^+$ to be the smallest index and largest index $i$ such that $\vert \P(\omega_{i}) - \P(\omega^*) \vert \le \delta$ . The Guessing Distance between $\ensuremath{\mathcal{U}}$ and $P$ with tolerance $\delta$ is defined as:

$$\ensuremath{\mathsf{GD}}_{\delta}(\ensuremath{\mathcal{U}},\P) = \log \frac{t^- + t^+}{2}$$

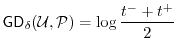
Guessing Distance measures the number of guesses that an adversary who assumes that $\ensuremath{\mathcal{U}}\approx \P$ makes before guessing the most likely element as prescribed by $\ensuremath{\mathcal{U}}$ (that is, $\omega^*$ )². We take the average over $t^-$ and $t^+$ as it may be the case that several elements may have similar probability masses under $P$ . In such a situation, the ordering of $L_\P$ may be ambiguous, so we report an average measure across all equivalent orderings. As $\ensuremath{\mathcal{U}}$ and $P$ will typically be empirical estimates, we use a tolerance $\delta$ to offset small measurement errors when grouping elements of similar probability masses. The subscript $\delta$ is ignored if $\delta = 0$ .

Discussion.

Intuitively, one can see that this definition makes sense by considering the following three cases: (1) $P$ is a good indicator of $\ensuremath{\mathcal{U}}$ (i.e., $\omega^* = \omega_1$ ); (2) $P$ is uniform; and (3) $P$ is a poor indicator of $\ensuremath{\mathcal{U}}$ (i.e., $\omega^* = \omega_n$ ). In case (1) the adversary clearly benefits from using $P$ to guess $\omega^*$ , and this relation is captured as $\ensuremath{\mathsf{GD}}(\ensuremath{\mathcal{U}},\P) = \log 1 = 0$ . In case (2), the adversary learns no information about $\ensuremath{\mathcal{U}}$ from $P$ and thus would be expected to search half of $\Omega$ before guessing the correct value; indeed $\ensuremath{\mathsf{GD}}(\ensuremath{\mathcal{U}},\P) = \log \frac{1 + n}{2}$ . Finally, in case (3), a search algorithm based on $P$ would need to enumerate all of $\Omega$ before finding $\omega^*$ , and this is reflected by $\ensuremath{\mathsf{GD}}(\ensuremath{\mathcal{U}},\P) = \log\frac{n + n}{2} = \log \vert\Omega\vert$ .

An important characteristic of $\ensuremath {\mathsf {GD}}$ is that it compares two probability distributions. This allows for a more fine-tuned evaluation as one can compute $\ensuremath {\mathsf {GD}}$ for each user in the population. To see the overall strength of a proposed approach, one might report a CDF of the $\ensuremath {\mathsf {GD}}$ 's for each user, or report the minimum over all $\ensuremath {\mathsf {GD}}$ 's in the population.

Guessing Distance is superficially similar to Guessing Entropy [25], which is commonly used to compute the expected number of guesses it takes to find an average element in a set assuming an optimal guessing strategy (i.e., first guessing the element with the highest likelihood, followed by guessing the element with the second highest likelihood, etc.) Indeed, one might view Guessing Distance as an extension of Guessing Entropy (see Appendix A); however, we prefer Guessing Distance as a measure of security as it provides more information about non-uniform distributions over a key space. For such distributions, Guessing Entropy is increased by the elements that have a low probability, and thus might not provide as conservative an estimate of security as desired. Guessing Distance, on the other hand, can be computed for each user, which brings to light the insecurity afforded by a non-uniform distribution. We provide a concrete example of such a case in Appendix A.

5 The Impact of Public Information on Key Randomness

We now show why templates play a crucial role in the computation of key entropy ( $\ensuremath{\mathsf{REQ\mbox{-}KR}}$ from Section 3). Our analysis brings to light two points: first that templates, and in particular, error-correction information, can indeed leak a substantial amount of information about a key, and thus must be considered when computing key entropy. Second, we show how standard approaches to computing key entropy, even if they were to take templates into account, must be conducted with care to avoid common pitfalls. Through our analysis we demonstrate the flexibility and utility of Guessing Distance. While we focus here on a specific proposal by Vielhauer and Steinmetz [40,41], we argue that our results are generally applicable to a host of similar proposals (see, e.g., [44,7,35,17]) that use per-user feature-space quantization for error correction. This complicates the calculation of entropy and brings to light common pitfalls.

Figure 1: CDF of the guesses required by an adversary to find a key. We compare the Standard metric to two estimates of $\ensuremath {\mathsf {GD}}$ , one that uses the target user's template (GD-U), and one that uses each individual user's template (GD-P).

The construction works as follows. Given 50 features $\phi_1, \dots, \phi_{50}$  [40] that map biometric samples to the set of non-negative integers, and $\ell$ enrollment samples $\ensuremath{{\beta}}_1, \dots, \ensuremath{{\beta}}_\ell$ , let $\Delta_i$ be the difference between the minimum and maximum value of $\phi_i(\ensuremath{{\beta}}_1), \dots, \phi_i(\ensuremath{{\beta}}_\ell)$ , expanded by a small tolerance. The scheme partitions the output range of $\phi_i$ into $\Delta_i$ -length segments. The key is derived by letting $L_i$ be the smallest integer in the segment that contains the user's samples, computing $\Gamma_i = L_i \bmod \Delta_i$ , and setting the $i^{\rm th}$ key element $c_i = \left\lfloor \frac{\phi_i(\ensuremath{{\beta}}_1) - \Gamma_i}{ \Delta_i}\right\rfloor$ . The key is $\ensuremath{\mathcal{K}}= c_1 \vert\vert\dots\vert\vert c_{50}$ , and the template $\ensuremath{\mathcal{T}}$ is composed of $\{(\Delta_1, \Gamma_1), \dots, (\Delta_{50}, \Gamma_{50})\}$ . To later extract $\ensuremath{\mathcal{K}}$ given a biometric sample $\ensuremath{{\beta}}'$ , and a template $\ensuremath{\mathcal{T}}$ , set $c'_i = \left\lfloor \frac{\phi_i(\ensuremath{{\beta}}') - \Gamma_i}{ \Delta_i}\right\rfloor$ and output $\ensuremath{\mathcal{K}}' = c'_1 \vert\vert\dots\vert\vert c'_{50}$ . We refer the reader to [41] for details on correctness.

As is the case in many other proposals, Vielhauer et al. perform an analysis that addresses requirement $\ensuremath{\mathsf{REQ\mbox{-}KR}}$ by arguing that given that the template leaks only error correcting information (i.e., the partitioning of the feature space) it does not indicate the values $c_i$ . To support this argument, they conduct an empirical evaluation to measure the Shannon entropy of each $c_i$ . For each user $u$ they derive $\ensuremath{\mathcal{K}}_u$ from $\ensuremath{\mathcal{T}}_u$ and $\ensuremath{{\beta}}_u$ , then compute the entropy of each element $c_i$ across all users. This analysis is a standard estimate of entropy. To see why this is inaccurate, consider two different users $a$ and $b$ such that $a$ outputs consistent values on feature $\phi$ and $b$ does not. Then the partitioning over $\phi$ 's range differs for each user. Thus, even if the mean value of $\phi$ is the same when measured over both $a$ 's and $b$ 's samples, this mean will be mapped to different partitions in the feature space, and thus, a different key. This implies that computing entropy over the $c_i$ overestimates security because the mapping induced by the templates artificially amplifies the entropy of the biometrics. A more realistic estimate of the utility afforded an adversary by auxiliary information can be achieved by fixing a user's template, and using that template to error-correct every other user's samples to generate a list of keys, then measuring how close those keys are to the target user's key. By conditioning the estimate on the target users template we are able to eliminate the artificial inflation of entropy and provide a better estimate of the security afforded by the construction.

Analysis.

We implemented the construction and tested the technique using all of the passphrases in the data set we collected in [3], which consists of over 9,000 writing samples from 47 users. Each user wrote the same five passphrases 10-20 times. In our analysis we follow the standard approach to isolate the entropy associated with the biometric: we compute various entropy measures using each user's rendering of the same passphrase [29,5,36] (this approach is justified as user selected passphrases are assumed to have low entropy). Tolerance values were set such that the approach achieved a False Reject Rate (FRR) of $0.1\%$ (as reported in [40]) and all outliers and samples from users who failed to enroll [24] were removed.

Figure 1 shows three different measures of key uncertainty. The first measure, denoted Standard, is the common measure of interpersonal variation as reported in the literature (e.g., [17,7]) using the data from our experiments. Namely, if the key element $c_i$ has entropy $H_i$ across the entire population, then the entropy of the key space is computed as $H = \sum_{i=1}^{50} H_i$ . We also show two estimates of guessing distance, the first ( $\ensuremath{\mathsf{GD}}(\ensuremath{\mathcal{U}},\P)$ , plotted as GD-P) does not take a target user's template into account and $P$ is just the distribution over all other users's keys in the population (the techniques we use to compute these estimates are described in Appendix B). The second ( $\ensuremath{\mathsf{GD}}(\ensuremath{\mathcal{U}},\P[\ensuremath{\mathcal{T}}_u])$ , plotted as GD-U) takes the user's template into account, computing $\P[\ensuremath{\mathcal{T}}_u]$ by taking the biometrics from all other users in the population, and generating keys using $\ensuremath{\mathcal{T}}_u$ , then computing the distribution over these keys.

Figure 1 shows the CDF of the number of guesses that one would expect an adversary to make to find each user's key. There are several important points to take away from these results. The first is the common pitfalls associated with computing key entropy. The difference between $\ensuremath{\mathsf{GD}}(\ensuremath{\mathcal{U}},\P)$ and the standard measurement indicates that the standard measurement of entropy ($43$ bits in this case) is clearly misleading--under this view one would expect an adversary to make $2^{42}$ guesses on average before finding a key. However, from $\ensuremath{\mathsf{GD}}(\ensuremath{\mathcal{U}},\P)$ it is clear that an adversary can do substantially better than this. The difference in estimates is due to the fact that $\ensuremath {\mathsf {GD}}$ takes into account conditional information between features whereas a more standard measure does not.

The second point is the impact of a user's template on computing $\ensuremath {\mathsf {GD}}$ . We can see by examining $\ensuremath{\mathsf{GD}}(\ensuremath{\mathcal{U}},\P)$ that if we take the usual approach of just computing entropy over the keys, and ignore each user's template, we would assume only a small probability of guessing a key in fewer than $2^{21}$ attempts. On the other hand, since the templates reduce the possible key space for each user, the estimate $\ensuremath{\mathsf{GD}}(\ensuremath{\mathcal{U}},\P[\ensuremath{\mathcal{T}}_u])$ provides a more realistic measurement. In fact, an adversary with access to population statistics has a $50\%$ chance of guessing a user's key in fewer than $2^{22}$ attempts, and $15.5\%$ chance guessing a key in a single attempt!

These results also shed light on another pitfall worth mentioning--namely, that of reporting an average case estimate of key strength. If we take the target user's template into account in the current construction, $15.5\%$ of the keys can be guessed in one attempt despite the estimated Guessing Entropy being approximately $2^{22}$ . In summary, this analysis highlights the importance of conditioning entropy estimates on publicly available templates, and how several common entropy measures can result in misleading estimates of security.

6 The Impact of Public Information on Weak Biometric Privacy

Recall that a scheme that achieves Weak Biometric Privacy uses templates that do not leak information about the biometrics input during enrollment. A standard approach to arguing that a scheme achieves $\ensuremath{\mathsf{REQ\mbox{-}WBP}}$ is to show (1) auxiliary information leaks little useful information about the biometrics, and (2) templates do not leak information about a biometric. This can be problematic as the two steps are generally performed in isolation. In our description of $\ensuremath{\mathsf{REQ\mbox{-}WBP}}$ , however, we argue that step (2) should actually show that an adversary with access to both templates and auxiliary information should learn no information about the biometric. The key difference here is that auxiliary information is used in both steps (1) and (2). This is essential as it is not difficult to create templates that are secure when considered in isolation, but are insecure once we consider knowledge derived from other users (e.g., population-wide statistics). In what follows we shed light on this important consideration by examining the scheme of Hao and Wah [17]. While our analysis focuses on their construction, it is pertinent to any BKG that stores partial information about the biometric in the template [43,26].

For completeness, we briefly review the construction. The BKG generates DSA signing keys from $n$ dynamic features associated with handwriting (e.g., pen tip velocity or writing time). The range of each feature is quantized based on a user's natural variation over the feature. Each partition of a feature's range is assigned a unique integer; let $p_i$ be the integer that corresponds to the partition containing the output of feature $\phi_i$ when applied to the user's biometric. The signing key is computed as $\ensuremath{\mathcal{K}}= {\rm SHA1}(p_1\vert\vert\dots\vert\vert p_n)$ . The template stores information that describes the partitions for each feature, as well as the $(x,y)$ coordinates that define the pen strokes of the enrollment samples, and the verification key corresponding to $\ensuremath{\mathcal{K}}$ . The $(x,y)$ coordinates of the enrollment samples are used as input to the Dynamic Time Warping [32] algorithm during subsequent key generation; if the provided sample diverges too greatly from the original samples, it is immediately rejected and key generation aborted.

Figure 2: Search results against the BKG proposed by Hao et al. [17]. Our search algorithm has a 22% chance of finding a user's key on the first guess.

Hao et al. performed a typical analysis of $\ensuremath{\mathsf{REQ\mbox{-}WBP}}$  [17]. First, they compute the entropy of the features over the entire population of users to show that auxiliary information leaks little information that could be used to discern the biometric. Second, the template is argued to be secure by making the following three observations. First, since the template only specifies the partitioning of the range of each feature, the template only leaks the variation in each feature, not the output. Second, for a computationally bound adversary, a DSA verification key leaks no information about the DSA signing key. Third, since the BKG employs only dynamic features, the static $(x,y)$ coordinates leak no relevant information. Note that in this analysis the template is analyzed without considering auxiliary information. Unfortunately, while by themselves the auxiliary information and the templates seem to be of little use to an adversary, when taken together, the biometric can be easily recovered.

Analysis.

To demonstrate this, we apply the techniques of [3] to generate guesses of the user's biometric samples. In [3] we describe a set of statistical measures that can be computed using population statistics, and map these spatial measures ³ to the most likely pen speed. In that work we assume limited knowledge of the target user's biometric, and compose static samples from the user to create a partial forgery, then infer timing information to make a complete forgery. In the current approach, we need not assume access to the target user's biometric because the $(x,y)$ coordinates of the enrollment samples are stored in the template. Thus, we apply our approach from [3], to make a guess at the user's biometric. Then, we use an intelligent search algorithm that enumerates other biometrics that are "close" to the first guess. The algorithm focuses the bulk of its work searching for the outputs of the features that exhibit high variance across the population, and reduces the search space by exploiting conditioning between features.

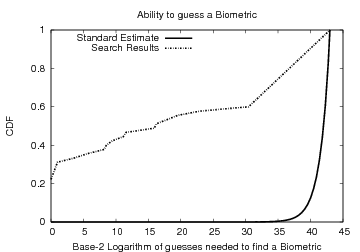
To empirically evaluate our attack, we used the same data set as in Section 5. Our implementation of the BKG had a FRR of 29.2% and a False Accept Rate (FAR) of $1.7\%$ , which is inline with the FRR/FAR of 28%/1.2% reported in [17]. Moreover, if we follow the computation of inter-personal variation as described in [17], then we would incorrectly conclude that the scheme creates keys with over 40 bits of entropy with our data set, which is the same estimate provided in [17]. However, this is not the case (see Figure 2). In particular, the fact that the template leaks information about the biometric enables an attack that successfully recreates the key $22\%$ of the time on the first try; approximately $50\%$ of the keys are correctly identified after making fewer than $2^{15}$ guesses. In summary, the significance of this analysis does not lie in the effectiveness of the described attack, but more so in the fact that the original analysis failed to take auxiliary information into consideration when evaluating the security of the template.

7 The Impact of Key Compromise on Strong Biometric Privacy

Lastly, we highlight the importance of quantifying the privacy of a user's biometric against adversaries who have access to the cryptographic key (i.e., $\ensuremath{\mathsf{REQ\mbox{-}SBP}}$ from Section 3). We examine a BKG proposed by Hao et al. [16].⁴ The construction generates a random key and then "locks" it with a user's iris code. The construction uses a cryptographic hash function $h : \ensuremath{\{0,1\}}^* \rightarrow \ensuremath{\{0,1\}}^s$ and a "concatenated" error correction code consisting of an encoding algorithm $C: \ensuremath{\{0,1\}}^{140} \rightarrow \ensuremath{\{0,1\}}^{2048}$ , and the corresponding decoding algorithm $D: \ensuremath{\{0,1\}}^{2048} \rightarrow \ensuremath{\{0,1\}}^{140}$ . This error correction code is the composition of a Reed-Solomon and Hadamard code [16, Section 3]. Iris codes are elements in $\ensuremath{\{0,1\}}^{2048}$  [8].

The BKG works as follows: given a user's iris code $\ensuremath{{\beta}}$ , select a random string $\ensuremath{\mathcal{K}}\in \ensuremath{\{0,1\}}^{140}$ , and derive the template $\ensuremath{\mathcal{T}}= \langle h(\ensuremath{\mathcal{K}}), \ensuremath{{\beta}}\oplus C(\ensuremath{\mathcal{K}}) \rangle$ , and output $\ensuremath{\mathcal{T}}$ and $\ensuremath{\mathcal{K}}$ . To later derive the key given an iris code $\ensuremath{{\beta}}'$ and the template $\ensuremath{\mathcal{T}}= \langle t_1, t_2 \rangle$ , compute $\ensuremath{\mathcal{K}}' = D(t_2 \oplus \ensuremath{{\beta}}')$ . If $h(\ensuremath{\mathcal{K}}') = t_1$ , then output $\ensuremath{\mathcal{K}}'$ , otherwise, fail. If $\ensuremath{{\beta}}$ and $\ensuremath{{\beta}}'$ are "close" to one another, then $t_2 \oplus \ensuremath{{\beta}}'$ is "close" to $C(\ensuremath{\mathcal{K}})$ , perhaps differing in only a few bits. The error correcting code handles these errors, yielding $\ensuremath{\mathcal{K}}' = \ensuremath{\mathcal{K}}$ .

Hao et al. provide a security analysis arguing requirement $\ensuremath{\mathsf{REQ\mbox{-}KR}}$ using both cryptographic reasoning and a standard estimate of entropy of the input biometric. That is, they provide empirical evidence that auxiliary information cannot be used to guess a target user's biometric, and a cryptographic argument that, assuming the former, the template and auxiliary information cannot be used to guess a key. They conservatively estimate the entropy of $\ensuremath{\mathcal{K}}$ to be 44 bits. Moreover, the authors note that if the key is ever compromised, the system can be used to "lock" a new key, since $\ensuremath{\mathcal{K}}$ is selected at random and is not a function of the biometric.

Unfortunately, given the current construction, compromise of $\ensuremath{\mathcal{K}}$ , in addition to the public information $\ensuremath{\mathcal{T}}= \langle t_1, t_2 \rangle$ , allows one to completely reconstruct $\ensuremath{{\beta}}= C(\ensuremath{\mathcal{K}}) \oplus t_2$ . Thus, even if a user were to create a new template and key pair, an adversary could use the old template and key to derive the biometric, and then use the biometric to unlock the new key. The significance of this is worth restating: because this BKG fails to meet $\ensuremath{\mathsf{REQ\mbox{-}SBP}}$ , the privacy of a user's biometric is completely undermined once any key for that user is ever compromised.

8 Conclusion

In this paper, we examine a series of requirements, pitfalls, and subtleties that are commonly overlooked in the evaluation of biometric key generators. Our goal is to encourage rigorous empirical evaluations that consider the impact of publicly available data to show that a BKG (I.) ensures the privacy of a user's biometric, and (II.) outputs keys that are suitable for cryptographic applications. Our exposition brings to the forefront practical ways of thinking about existing requirements that help elucidate subtle nuances that are commonly overlooked in regards to biometric security. As we demonstrate, failure to consider these requirements may result in estimates that overstate the security of proposed schemes.

To underscore the practical significance of each of these requirements, we present analyses of three published systems. While we point out weaknesses in specific constructions, it is not our goal to fault the those specific works. Instead, we aim to bring to light flaws in the standard approaches that were followed in each setting. In one case we exploit auxiliary information to show that an attacker can guess $15\%$ of the keys on her first attempt. In another case, we highlight the importance of ensuring biometric privacy by exploiting the information leaked by templates to yield a $22\%$ chance of guessing a user's key in one attempt. Lastly, we show that subtleties in BKG design can lead to flaws that allow an adversary to derive a user's biometric given a compromised key and template, thereby completely undermining the security of the scheme.

We hope that our work encourages designers and evaluators to analyze BKGs with a degree of skepticism, and to question claims of security that overlook the requirements presented herein. To facilitate this type of approach, we not only ensure that our requirements can be applied to real systems, but also introduce Guessing Distance--a heuristic measure that estimates the uncertainty of the outputs of a BKG given access to population statistics.

Acknowledgements

We would like to thank Fabian Monrose for invaluable contributions to this work. We would also like to thank Dan Lopresti for providing helpful feedback on earlier versions of this paper. This research was funded in part by NSF Grant CNS-0430338.

Bibliography

1

ADLER, A.
Images can be Regenerated from Quantized Biometric Match Score Data.
In Proceedings of the Canadian Conference on Electrical and Computer Engineering (Niagara Falls, Canada, May 2004), pp. 469-472.

2

ALVARE, A.
How crackers crack passwords or what passwords to avoid.
In Proceedings of the Second USENIX Security Workshop (August 1990), pp. 103-112.

3

BALLARD, L., LOPRESTI, D., AND MONROSE, F.
Evaluating the security of handwriting biometrics.
In The $10^{th}$ International Workshop on the Foundations of Handwriting Recognition (October 2006), pp. 461-466.

4

BALLARD, L., LOPRESTI, D., AND MONROSE, F.
Forgery quality and its implications for behavioral biometric security.
IEEE Transactions on Systems, Man, and Cybernetics, Part B (Special Edition) 37, 5 (October 2007), 1107-1118.

5

BALLARD, L., MONROSE, F., AND LOPRESTI, D.
Biometric authentication revisited: Understanding the impact of wolves in sheep's clothing.
In Proceedings of the 15$^{\rm th}$ Annual Usenix Security Symposium (Vancouver, BC, Canada, August 2006), pp. 29-41.

6

BOYEN, X.
Reusable cryptographic fuzzy extractors.
In ACM Conference on Computer and Communications Security--CCS 2004 (2004), New-York: ACM Press, pp. 82-91.

7

CHANG, Y.-J., ZHANG, W., AND CHEN, T.
Biometrics-Based Cryptographic Key Generation.
In Proceedings of IEEE International Conference on Multimedia and Expo (ICME) (2004), vol. 3, pp. 2203-2206.

8

DAUGMAN, J.
The importance of being random: Statistical principles of iris recognition.
Pattern Recognition 36 (2003), 279-291.

9

DAVIDA, G. I., FRANKEL, Y., AND MATT, B. J.
On enabling secure applications through off-line biometric identification.
In Proceedings of the 1998 IEEE Symposium on Security and Privacy (May 1998), pp. 148-157.

10

DAVIS, D., MONROSE, F., AND REITER, M. K.
On user choice in graphical password schemes.
In Proceedings of the $13^{\rm th}$ USENIX Security Symposium (August 2004), pp. 151-164.

11

DODIS, Y., REYZIN, L., AND SMITH, A.
Fuzzy extractors: How to generate strong keys from biometrics and other noisy data.
In Advances in Cryptology - EUROCRYPT 2004 (2005), vol. 3027 of Lecture Notes in Computer Science, Springer-Verlag, pp. 523-540.
Full version appears as Y. Dodis, R. Ostrovsky, L. Reyzin, and A. Smith. Fuzzy Extractors: How to Generate Strong Keys from Biometrics and Other Noisy Data, IACR ePrint Cryptography Archive 2003/235.

12

DODIS, Y., AND SMITH, A.
Correcting errors without leaking partial information.
In Proc. $37$ th ACM Symp. on Theory of Computing (2005), ACM, pp. 654-663.

13

DOLE, B., LODIN, S., AND SPAFFORD, E.
Misplaced trust: Kerberos 4 session keys.
In Proceedings of the 1997 Symposium on Network and Distributed System Security (Washington, DC, USA, 1997), IEEE Computer Society, p. 60.

14

FELDMEIER, D., AND KARN, P.
UNIX password security - ten years later.
In Advances in Cryptology - CRYPTO '89 Proceedings (Berlin, Germany, 1990), vol. 435 of Lecture Notes in Computer Science, Springer-Verlag, pp. 44-63.

15

GOH, A., AND NGO, D. C. L.
Computation of cryptographic keys from face biometrics.
In Proceedings of Communications and Multimedia Security (2003), pp. 1-13.

16

HAO, F., ANDERSON, R., AND DAUGMAN, J.
Combining cryptography with biometrics effectively.
IEEE Transactions on Computers (2006).

17

HAO, F., AND WAH, C.
Private key generation from on-line handwritten signatures.
Information Management and Computer Security 10, 4 (2002), 159-164.

18

HASTAD, J., IMPAGLIAZZO, R., LEVIN, L., AND LUBY, M.
A pseudorandom generator from any one-way function.
SIAM Journal on Computing 28 (1998).

19

JAIN, A. K., ROSS, A., AND ULUDAG, U.
Biometric Template Security: Challenges and Solutions.
In Proceedings of European Signal Processing Conference (EUSIPCO) (September 2005).

20

JUELS, A., AND SUDAN, M.
A fuzzy vault scheme.
In IEEE International Symposium on Information Theory (2002).

21

JUELS, A., AND WATTENBERG, M.
A fuzzy commitment scheme.
In Proceedings of the $6^{\rm th}$ ACM Conference on Computer and Communication Security (November 1999), pp. 28-36.

22

LI, Q., SUTCU, Y., AND MEMON, N.
Secure sketch for biometric templates.
In In Proceedings of Advances in Cryptology - ASIACRYPT 2006, 12th International Conference on the Theory and Application of Cryptology and Information Security (2006), pp. 99-113.

23

LOPRESTI, D. P., AND RAIM, J. D.
The effectiveness of generative attacks on an online handwriting biometric.
In Proceedings of the International Conference on Audio- and Video-based Biometric Person Authentication. Hilton Rye Town, NY, USA, 2005, pp. 1090-1099.

24

MANSFIELD, A. J., AND WAYMAN, J. L.
Best practices in testing and reporting performance of biometric devices, August 2002.

25

MASSEY, J. L.
Guessing and entropy.
In Proceedings of the 1994 IEEE International Symposium on Information Theory (1994), p. 204.

26

MOHANTY, P., SARKAR, S., AND KASTURI, R.
A non-iterative approach to reconstruct face templates from match scores.
In 18th International Conference on Pattern Recognition (ICPR 2006) (August 2006), pp. 598-601.

27

MONROSE, F., REITER, M., LI, Q., LOPRESTI, D., AND SHIH, C.
Towards speech-generated cryptographic keys on resource-constrained devices.
In Proceedings of the Eleventh USENIX Security Symposium (2002), pp. 283-296.

28

MONROSE, F., REITER, M. K., LI, Q., AND WETZEL, S.
Cryptographic key generation from voice (extended abstract).
In Proceeedings of the 2001 IEEE Symposium on Security and Privacy (May 2001), pp. 12-25.

29

MONROSE, F., REITER, M. K., AND WETZEL, S.
Password hardening based on keystroke dynamics.
International Journal of Information Security 1, 2 (February 2002), 69-83.

30

NISAN, N., AND ZUCKERMAN, D.
Randomness is linear in space.
Journal of Computer and Systems Science 52, 1 (1996), 43-52.

31

RATHA, N. K., CONNELL, J. H., AND BOLLE, R. M.
Enhancing security and privacy in biometrics-based authentication systems.
IBM Syst. J. 40, 3 (2001), 614-634.

32

SANKOFF, D., AND KRUSKAL, J.
Time Warps, String Edits and Macromolecules: The Theory and Practice of Sequence Comparison, second ed.
Addison-Wesley Publishing, Reading, MA, 1999.

33

SOUTAR, C., ROBERGE, D., STOIANOV, A., GILROY, R., AND KUMAR, B. V.
Biometric encryption$^{\rm tm}$ using image processing.
In Optical Security and Counterfeit Deterrence Techniques II (1998), vol. 3314, IS&T/SPIE, pp. 178-188.

34

SOUTAR, C., AND TOMKO, G. J.
Secure private key generation using a fingerprint.
In Cardtech/Securetech Conference Proceedings (May 1996), pp. 245-252.

35

SUTCU, Y., SENCAR, H. T., AND MEMON, N.
A Secure Biometric Authentication Scheme based on Robust Hashing.
In Proceedings of the 7th Workshop on Multimedia and Security (New York, NY, USA, 2005), pp. 111-116.

36

THORPE, J., AND VAN OORSCHOT, P.
Human-Seeded Attacks and Exploiting Hot-Spots in Graphical Passwords.
In Proceedings of the 16$^{\rm th}$ Annual Usenix Security Symposium (Boston, MA, August 2007).

37

ULUDAG, U., AND JAIN, A.
Attacks on biometric systems: A case study in fingerprints.
In Proceedings of SPIE-EI 2004, Security, Steganography and Watermarking of Multimedia Contents VI, vol. 5306, pp. 622-633.

38

ULUDAG, U., AND JAIN, A.
Securing fingerprint template: Fuzzy vault with helper data.
In Proceedings of the IEEE Workshop on Privacy Research In Vision (PRIV) (New York, NY, June 2006).

39

ULUDAG, U., PANKANTI, S., PRABHAKAR, S., AND JAIN, A. K.
Biometric cryptosystems: Issues and challenges.
Proceedings of the IEEE: Special Issue on Multimedia Security of Digital Rights Management 92, 6 (2004), 948-960.

40

VIELHAUER, C., AND STEINMETZ, R.
Handwriting: Feature correlation analysis for biometric hashes.
EURASIP Journal on Applied Signal Processing 4 (2004), 542-558.

41

VIELHAUER, C., STEINMETZ, R., AND MAYERHOFER, A.
Biometric hash based on statistical features of online signatures.
In Proceedings of the Sixteenth International Conference on Pattern Recognition (2002), vol. 1, pp. 123-126.

42

WAYMAN, J.
Fundamentals of biometric authentication technologies.
International Journal of Image & Graphics 1, 1 (January 2001), 93-114.

43

YAMAZAKI, Y., NAKASHIMA, A., TASAKA, K., AND KOMATSU, N.
A study on vulnerability in on-line writer verification system.
In Proceedings of the Eighth International Conference on Document Analysis and Recognition (Seoul, South Korea, August-September 2005), pp. 640-644.

44

ZHANG, W., CHANG, Y.-J., AND CHEN, T.
Optimal thresholding for key generation based on biometrics.
In Proceedings of the International Conference on Image Processing (ICIP04) (2004), vol. 5, pp. 3451-3454.

45

ZHENG, G., LI, W., AND ZHAN, C.
Cryptographic key generation from biometric data using lattice mapping.
In ICPR '06: Proceedings of the 18th International Conference on Pattern Recognition (Washington, DC, USA, 2006), IEEE Computer Society, pp. 513-516.

A. Guessing Distance and Guessing Entropy

Guessing Entropy [25] is commonly used for measuring the expected number of guesses it takes to find an average element in a set assuming an optimal guessing strategy (i.e., first guessing the element with the highest likelihood, followed by guessing the element with the second highest likelihood, etc.). Given a distribution $P$ over $\Omega$ and the convention that $\P(\omega_i) \ge \P(\omega_{i+1})$ , Guessing Entropy is computed as $G(\P) = \sum_{i=1}^n i\P(\omega_i)$ .

Guessing Entropy is commonly used to determine how many guesses an adversary will take to guess a key. At first, Guessing Entropy and Guessing Distance appear to be quite similar. However, there is one important difference: Guessing Entropy is a summary statistic and Guessing Distance is not. While Guessing Entropy provides an intuitive and accurate estimate over distributions that are close to uniform, the fact that there is one measure of strength for all users in the population may result in somewhat misleading results when Guessing Entropy is computed over skewed distributions.

To see why this is the case, consider the following distribution: let $P$ be defined over $\Omega = \{\omega_1, \dots, \omega_n\}$ as $\P(\omega_1) = \frac{1}{2}$ , and $\P(\omega_i) = \frac{1}{2(n-1)}$ for $i \in [2,n]$ . That is, one element (or key) is output by 50% of the users and the remaining elements are output with equal likelihood. The Guessing Entropy of $P$ is:

$$G(\P) = \sum_{i=1}^n i \P(\omega_i)$$

$$= \P(\omega_1) + \sum_{i=2}^n i \P(\omega_i)$$

$$= \frac{1}{2} + \frac{1}{2(n-1)} \sum_{i=2}^n i$$

$$= \frac{1}{2} + \frac{1}{2(n-1)} \left(\frac{n(n+1)}{2} - 1\right)$$

$$\approx \frac{n}{4}$$

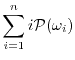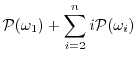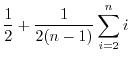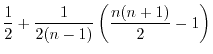Thus, although the expected number of guesses to correctly select $\omega$ is approximately $\frac{n}{4}$ , over half of the population's keys are correctly guessed on the first attempt following the optimal strategy. To contrast this, consider an analysis of Guessing Distance with threshold $\delta = \frac{1}{N}$ . (Assume for exposition that distributions are estimated from a population of $N = 2(n-1)$ users.) To do so, evaluate each user in the population independently. Given a population of users, first remove a user to compute $\ensuremath{\mathcal{U}}$ and use the remaining users to compute $P$ . Repeat this process for the entire population.

In the case of our pathological distribution, we may consider only two users without loss of generality: a user with distribution $\ensuremath{\mathcal{U}}_1$ who outputs key $\omega_1$ , and user with distribution $\ensuremath{\mathcal{U}}_2$ who outputs key $\omega_2$ . In the first case, we have $\ensuremath{\mathsf{GD}}_\delta(\ensuremath{\mathcal{U}}_1,\P) = \log 1 = 0$ , because the majority of the mass according to $P$ is assigned to $\omega_1$ , which is the most likely element according to $\ensuremath{\mathcal{U}}_1$ . For $\ensuremath{\mathcal{U}}_2$ , we have $t^- = 2$ and $t^+ = n$ , and thus $\ensuremath{\mathsf{GD}}_\delta(\ensuremath{\mathcal{U}}_2,\P) = \log \frac{n+2}{2}$ . Taking the minimum value (or even reporting a CDF) shows that for a large proportion of the population (all users with distribution $\ensuremath{\mathcal{U}}_1$ ), this distribution offers no security--a fact that is immediately lost if we only consider a summary statistic. However, it is comforting to note, that if we compute the average of $2^\ensuremath{\mathsf{GD}}$ over all users, we obtain estimates that are identical to that of guessing entropy for sets that are sufficiently large:

$$\frac{1}{N} \sum_{(\ensuremath{\mathcal{U}},\P)} 2^{\ensuremath{\mathsf{GD}}_\delta(\ensuremath{\mathcal{U}},\P)} = \frac{1}{N}\left( \frac{N}{2} 2^{\log 1} + \frac{N}{2} 2^{\log \frac{n+2}{2}}\right)$$

$$= \frac{1}{2} + \frac{1}{2}\left(\frac{n + 2}{2}\right)$$

$$\approx \frac{n}{4}$$

B. Estimating $\ensuremath {\mathsf {GD}}$

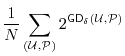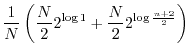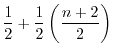As noted in Section 5, it is difficult to obtain a meaningful estimate of probability distributions over large sets, e.g., $\ensuremath{\mathbb{N}}^{50}$ . In order to quantify the security defined by a system, it is necessary to find techniques to derive meaningful estimates. This Appendix discusses how we estimate $\ensuremath {\mathsf {GD}}$ . The estimate also implicitely defines an algorithm that can be used to guess keys.

For convenience we use $\phi$ to denote both a biometric feature and the random variable that is defined using population statistics over $\phi$ (taken over the set $\Omega_\phi$ ). If a distribution is not subscripted, it is understood to be taken over the key space $\Omega = \Omega_{\phi_1} \times \dots \times \Omega_{\phi_n}$ . Our estimate uses of several tools from information theory:

Entropy.

The entropy of a random variable $X$ defined over the set $\Omega$ is

$$H(X) = -\sum_{\omega \in \Omega} {\Pr\left[{X = \omega}\right]} \log {\Pr\left[{X = \omega}\right]}$$

Mutual Information.

The amount of information shared between two random variables $X$ and $Y$ defined over the domains $\Omega_X$ and $\Omega_Y$ is measured as

$$I(X,Y) = \sum_{x \in \Omega_x}\sum_{y \in \Omega_y} {\Pr\left[{X ... ...[{X = x \wedge Y = y}\right]}}{{\Pr\left[{X=x}\right]}{\Pr\left[{Y=y}\right]}}$$

We use the notation $I(X;Y,Z)$ to denote the mutual information between the random variable $X$ and the random variable defined by the joint distribution between the random variables $Y$ and $Z$ .

The Estimate.

Let $\ensuremath{\mathsf{GD}}_\delta(\ensuremath{\mathcal{U}}_{\phi_i}, \P_{\phi_i}\vert u_{i-1}, \dots, u_1)$ be the guessing distance between the user's and population's distribution over $\phi_i$ conditioned on the even that $\phi_{i-1}\!=\!u_{i-1},\ \dots,\ \phi_{1}\!=\!u_{1}$ . In particular, let $L_{\P_{\phi_i}} = (\omega_1, \dots, \omega_n)$ be the elements of $\Omega_{\phi_i}$ ordered such that

$$\P_{\phi_i}(\omega_j\vert\phi_{i-1}\!=\!u_{i-1},\ \dots,\ \phi_{1... ...P_{\phi_i}(\omega_{j+1}\vert\phi_{i-1}\!=\!u_{i-1},\ \dots,\ \phi_{1} = u_{1})$$

As before, let $\omega^* = \mathop{\mathrm{argmax}}_{\omega \in \Omega_{\phi_i}} \ensuremath{\mathcal{U}}_{\phi_i}(\omega)$ , and $t^-$ and $t^+$ be the smallest and largest indexes $j$ such that

$$\vert \P_{\phi_i}(\omega_{j}\vert\phi_{i-1}\!=\!u_{i-1},\ \dots,\... ...ega^*\vert\phi_{i-1}\!=\!u_{i-1},\ \dots,\ \phi_{1}\!=\!u_{1})\vert \le \delta$$

Then, $\ensuremath{\mathsf{GD}}_\delta(\ensuremath{\mathcal{U}}_{\phi_i}, \P_{\phi_i}~\vert~u_{i-1}, \dots, u_1) = \log(t^- + t^+) - 1$ . In other words, if an adversary assumes that a target user is distributed according to the population and fixes the values of certain features, this is the number of guesses she will need to make to guess another feature. Unfortunately, this quantity is also infeasible to compute in light of data constraints so we endeavor to find an easily computable estimate. To this end, define the weight ($d_i$ ) of an element in $\omega \in \Omega_{\phi_i}$ as:

$$d_i(\omega~\vert~u_{i-1}, \dots, u_{1}) = \sum_{h=1}^{i-1} \sum_{... ...phi_i;\phi_h,\phi_j)~\P_{\phi_i}(\omega~\vert~\phi_h = u_h \wedge \phi_j = u_j)$$

The weights of elements that are more likely to occur given the values of other features will be larger than the weights that are less likely to occur. Intuitively, each of the values ($u$ ) has an influence on $d_i(\omega)$ and those values that correspond to features that have a higher correlation with $\phi_i$ have more influence. We also note that we only use two levels of conditional probabilities, which are relatively easy to compute, instead of conditioning over the entire space. Now, we use the weights to estimate the probability distributions as:

$$\hat{\P}_{\phi_i}(\omega_j~\vert~u_{i-1}, \dots, u_{1}) = d_i(\om... ...1}) / \sum_{\omega \in \Omega_{\phi_i}} d_i(\omega~\vert~u_{i-1}, \dots, u_{1})$$

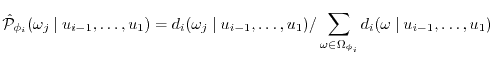Note that while this technique may not provide a perfect estimate of each probability, our goal is to discover the relative magnitude of the probabilities because they will be used to estimate Guessing Distance. We believe that this approach achieves this goal.

We are almost ready to provide an estimate of $\ensuremath {\mathsf {GD}}$ . First, we specify an ordering for the features. The ordering will be according to an ordering measure ($M(\phi)$ ) such that features with a larger measure have a low entropy (and are therefore easier to guess) and have a high correlation with other features. An adversary could then use this ordering to reduce the number of guesses in a search by first guessing features with a higher measure. Define the feature-ordering measure for $\phi_i$ as:

$$M(\phi_i) = \sum_{i \ne j} \left(1 + \frac{H(\phi_j)}{H(\phi_i)}\right) ^ { 1 + I(\phi_i,\phi_j) }$$

Finally, we reindex the features such that $M(\phi_i) \ge M(\phi_{i+1})$ for all $i \in [1,50]$ , and estimate the guessing distance for a specific user with $\phi_i = x_i$ as:

$$\ensuremath{\widehat{\mathsf{GD}}}(\ensuremath{\mathcal{U}},\P) =... ..._comment_mark>197 \prod_{j=i+1}^{50}\vert \Omega_{\phi_j} \vert \right) \right)$$

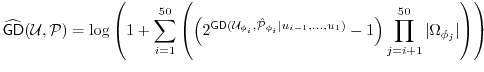This estimate helps in modeling an adversary that performs a brute-force search over all of the features by starting with the features that are easiest to guess and using those features to reduce the uncertainty about features that are more difficult to guess. For each feature, the adversary will need to make $2^{\ensuremath{\mathsf{GD}}(\ensuremath{\mathcal{U}}_{\phi_i},\hat{\P}_{\phi_i}\vert u_{i-1}, \dots, u_1)}$ guesses to find the correct value. Since each incorrect guess ( $2^{\ensuremath{\mathsf{GD}}(\ensuremath{\mathcal{U}}_{\phi_i},\hat{\P}_{\phi_i}\vert u_{i-1}, \dots, u_1)} - 1$ of them) will cause a fruitless enumeration of the rest of the features, we multiply the number of incorrect guesses by the sizes of the ranges of the remaining features. Finally, we take the log to represent the number of guesses as bits.

Section 5 uses this estimation technique to measure $\ensuremath {\mathsf {GD}}$ of a user versus the population ( $\ensuremath{\widehat{\mathsf{GD}}}(\ensuremath{\mathcal{U}},\P)$ ), and for a user versus the population conditioned on the user's template ( $\ensuremath{\widehat{\mathsf{GD}}}(\ensuremath{\mathcal{U}},\P[\ensuremath{\mathcal{T}}_u])$ ). The only way in which the estimation technique differs between the two settings is the definition of $\P_{\phi_i}$ . In the case of $\ensuremath{\widehat{\mathsf{GD}}}(\ensuremath{\mathcal{U}},\P)$ , $\P_{\phi_i}$ is computed by measuring the $i^{\rm th}$ key element for every other user in the population. In the case of $\ensuremath{\widehat{\mathsf{GD}}}(\ensuremath{\mathcal{U}},\P[\ensuremath{\mathcal{T}}_u])$ , $\P_{\phi_i}$ is computed using all of the other user's samples in conjuction with the target user's template to derive a set of keys and taking the distribution over the $i$ th element of the keys.

Footnotes

¹

Typically, $\ensuremath{\mathcal{U}}$ is computed over error-corrected values, and so the most likely element will also be the only element that has any probability mass.

²

We note that Guessing Distance is not a distance metric as it does not necessarily satisfy symmetry or the triangle inequality.

³

These measures can be reproduced given the ($x,y$ ) coordinates of handwriting.

⁴

This BKG is technically an instance of the fuzzy commitment proposed by Juels and Wattenberg [21], which was later shown to be an instance of a secure sketch [11].