
16th USENIX Security Symposium
Pp. 275–290 of the Proceedings
Binary Obfuscation Using Signals
Igor V. Popov, Saumya K. Debray, Gregory R. Andrews
Department of Computer Science, The University of Arizona,
Tucson, AZ 85721, USA
Email: {ipopov, debray, greg}@cs.arizona.edu
Abstract
Reverse engineering of software is the process of recovering
higher-level structure and meaning from a lower-level program representation.
It can be used for legitimate purposes-e.g., to recover
source code that has been lost-but it is often used for
nefarious purposes, e.g., to search for security vulnerabilities in
binaries or to steal intellectual property.
This paper addresses the problem of making it hard to
reverse engineering binary programs
by making it difficult to disassemble machine code statically.
Binaries are obfuscated by changing many control
transfers into signals (traps)
and inserting dummy control transfers and "junk" instructions after
the signals.
The resulting code is still a correct program, but even the best current
disassemblers are unable to disassemble 40%-60% of the
instructions in the program.
Furthermore, the disassemblers have a mistaken understanding of
over half of the control flow edges.
However, the obfuscated program necessarily executes
more slowly than the original.
Experimental results quantify the degree of obfuscation,
stealth of the code, and effects on execution time and code size.
1. Introduction
Software is often distributed in binary form, without source code.
Many groups have developed technology that enables one to reverse
engineer binary programs and thereby reconstruct the actions and
structure of the program.
This is accomplished by disassembling machine code into assembly code
and then possibly decompiling the assembly code into higher level
representations [5,6,13].
While reverse-engineering technology has many legitimate uses (in particular,
an important application of binary-level reverse engineering is to
analyse malware in order to understand its behavior
[4,17,16,18,25,27,33]), it can also
be used to discover vulnerabilities,
make unauthorized modifications, or steal
intellectual property.
Since the first step in reverse engineering a binary is disassembly, many
approaches to binary obfuscation focus on disrupting this step. This is
typically done by identifying assumptions made by disassemblers, then
transforming the program systematically so as to violate these assumptions without
altering program functionality. Two fundamental assumptions made by
disassemblers are that (1) the address where each instruction begins can be
determined; and (2) control transfer instructions can be identified and
their targets determined. The first assumption is used to identify the
actual instructions to disassemble; most modern disassemblers use
the second assumption to determine which memory regions get disassembled (see
Section 2). In this context, this paper makes the
following contributions:
- It shows how the second of these assumptions can be violated, such that
actual control transfers in the program cannot be identified by a static
disassembler. This is done by replacing control transfer instructions-jumps,
calls, and returns-by "ordinary" instructions whose execution raises
traps at runtime; these traps are then fielded by signal handling code that
carries out the appropriate control transfer. The effect is to replace control
transfer instructions either with apparently innocuous arithmetic or memory
operations or with what appear to be illegal instructions that suggest an
erroneous disassembly.
-
It shows how the code resulting from this first transformation can be further
obfuscated to additionally violate the first assumption stated
above. This is done using a secondary transformation that inserts
(unreachable) code, containing fake control transfers, after these
trap-raising instructions, in order to make it hard to find the beginning of
the true next instructions.
In earlier work, we showed how disassembly could be disrupted by violating
the first assumption [20]; this paper extends that work by
showing a different way to obfuscate binaries by replacing control
transfer instructions with apparently-innocuous non-control-transfer
instructions. It is also very
different from our earlier work on intrusion detection [21],
which proposed a way to hinder certain kinds of mimicry attacks by
obfuscating system call instructions. That work sought simply to disguise
the instruction (`int $0x80' in Intel x86 processors) used by
applications to trap into the OS kernel; more importantly, it required
kernel modifications in order to to work. By contrast, the work described
in this paper applies to arbitrary control transfers in programs and
requires no kernel modifications. Taken together, these two differences
lead to significant differences between the two approaches in terms of
goals, techniques, and effects.
It is important to note that code obfuscation is merely a technique: just
as it can be used to protect software against attackers, so too it can be
used to hide malicious content.
The work presented here can therefore be seen from two
perspectives: as a "defense model" of a new approach for protecting
intellectual property, or as an "attack model" of a new approach for hiding
malicious content. In either case, it goes well beyond current approaches
to hiding the content of executable code.
In particular, the obfuscations
cause the best existing disassemblers to miss 40%-60%
of the instructions in test programs and to make mistakes on
over half of the control flow edges.
The remainder of the paper is organized as follows.
Section 2 provides background information on
static disassembly algorithms.
Section 3 describes the new techniques for thwarting disassembly
and explains how they are implemented.
Section 4 describes how we evaluate the efficacy of our
approach.
Section 5 gives experimental results for programs
in the SPECint-2000 benchmark suite.
Section 6 describes related work,
and Section 7 contains concluding remarks.
2. Disassembly Algorithms
This section summarizes the operation of disassemblers in order
to provide the context needed to understand how our obfuscation techniques
work.
Broadly speaking, there are two approaches to disassembly:
static and dynamic, the difference between them being that the
former examines the program without execution, while
the latter monitors the program's execution (e.g., through a debugger)
as part of the disassembly process.
Static disassembly processes the entire input program all at once, while dynamic
disassembly only disassembles those
instructions that were executed for the particular input that was used.
Moreover, with static disassembly it is easier to apply offline program
analyses to reason about semantic aspects of the program under
consideration. Finally, programs being disassembled statically are not able to
defend themselves against reverse engineering using anti-debugging
techniques (see, for example, [2,3]).
For these reasons, static disassembly is a popular choice
for low level reverse engineering.
This paper focuses on static disassembly: its goal is to render static
disassembly of programs sufficiently difficult and expensive as to force
attackers to resort to dynamic approaches (which, in principle, can then be
defended against).
There are two generally used techniques for
static disassembly: linear sweep and recursive traversal
[26].
The linear sweep algorithm begins disassembly at the input program's
first executable location, and simply sweeps through the entire text section
disassembling each instruction as it is encountered.
This method is used by programs such as the GNU utility objdump
[24] as well as a number of link-time optimization tools
[8,23,29].
The main weakness of linear sweep is that it is prone to
disassembly errors resulting from the misinterpretation of data,
such as jump tables, embedded in the instruction stream.
The recursive traversal algorithm uses the control
flow instructions of the program being disassembled in order to determine what
to disassemble. It starts with the program's entry point, and
disassembles the first basic block.
When the algorithm encounters a control flow instruction, it
determines the possible successors of
that instruction-i.e., addresses where execution could continue-and
proceeds with disassembly at those addresses.
Variations on this basic approach to disassembly
are used by a number of binary translation and
optimization systems [6,28,30].
The main virtue of recursive traversal is that by following the control flow
of a program, it is able to "go around" and thus avoid
disassembly of data embedded in the text section. Its main weakness is
that it depends on being able to determine the possible successors of each
such instruction, which is difficult for indirect jumps
and calls.
The algorithm also depends on being able to find all
the instructions that affect control flow.
A recently proposed generalization of recursive traversal is that of
exhaustive disassembly [14,15], which is the most
sophisticated disassembly algorithm we are aware of. This approach
aims to work around certain kinds of binary obfuscations by considering all
possible disassemblies of each function. It examines the control
transfer instructions in these alternative disassemblies to identify basic
block boundaries, then uses a variety of heuristic and statistical reasoning
to rule out alternatives that are unlikely or impossible. Like the
recursive traversal algorithm it generalizes, the exhaustive algorithm thus
also relies fundamentally on identifying and analyzing the behavior of
control transfer instructions.
3. Signal-Based Obfuscation
3.1. Overview
In order to confuse a disassembler, we have to disrupt its notion
of where the instructions are, what they are doing,
and what the control flow is.
The choices we have for altering the program are
(1) changing instructions to others that produce the same result, and
(2) adding instructions that do not have visible effects.
Simple, local changes will obviously not confuse a disassembler or
a human.
More global and drastic changes are required.
 Figure 1: A Simple Example of our Approach to Obfuscation
The essential intuition of our approach can be illustrated via a simple
example, given in Figure 1. The original code fragment
on the left-hand side of the figure contains an unconditional
jump to a location
; the jump is preceded by Code-before
and followed by Code-after. This code is obfuscated
by replacing the jump by code that attempts to access an illegal memory
location
and thereby generates a trap, which raises a signal. This
is fielded by a handler
that uses the address of the instruction that caused the trap to determine
the target address
of the original jump instruction and to
cause control to branch to
.
In addition, Bogus Code is inserted after the trap point;
this code appears to be reachable, but in fact it is not. Judicious choice
of bogus code can throw off the disassembly even further.
This example illustrates a number of
key aspects of our approach that increases the difficulty of statically
deobfuscating programs:
Figure 1: A Simple Example of our Approach to Obfuscation
The essential intuition of our approach can be illustrated via a simple
example, given in Figure 1. The original code fragment
on the left-hand side of the figure contains an unconditional
jump to a location
; the jump is preceded by Code-before
and followed by Code-after. This code is obfuscated
by replacing the jump by code that attempts to access an illegal memory
location
and thereby generates a trap, which raises a signal. This
is fielded by a handler
that uses the address of the instruction that caused the trap to determine
the target address
of the original jump instruction and to
cause control to branch to
.
In addition, Bogus Code is inserted after the trap point;
this code appears to be reachable, but in fact it is not. Judicious choice
of bogus code can throw off the disassembly even further.
This example illustrates a number of
key aspects of our approach that increases the difficulty of statically
deobfuscating programs:
-
A variety of different instructions and addresses can be used to raise a
signal at runtime. The example uses a load from an illegal address, but
we could have used many other alternatives, e.g.,
a store to a write-protected location, or a load from a
read-protected location. Indeed, on an architecture such as the Intel x86,
any instruction that can take a memory operand, including all the familiar
arithmetic instructions, can be used for this purpose.
Moreover, the address
used
to generate the trap can be a legal address, albeit one that does not (at
runtime) permit a particular kind of memory access. We can
further hamper static reverse engineering by using something like an
mprotect() system call to (possibly temporarily) change the protection
of the address
being used to generate the trap at runtime, so that it
is not statically obvious that attempting a
particular kind of memory access at address
will raise a trap.
-
The address
used to generate the trap need not be a determinate
value. For example, suppose that, as in typical 32-bit Linux systems, the
top 1 GB of the virtual address space
(i.e., addresses 0xC0000000 to 0xFFFFFFFF) is reserved for
the kernel, and is inaccessible to user processes. Then, any value of
in that address range
will serve to generate the desired trap. Such values can be computed by
starting with an arbitrary value and then
using bit manipulations to obtain a value in the appropriate range, as shown
below (one can imagine many variations on this theme), where
and
are arbitrary legal memory locations:
:= contents of
:= contents of
:=
- 0xC0 /*
's low byte
*/
:=
/*
*/
:=
-
The actual runtime contents of memory locations
and
are unimportant
here: the value computed into
-which may be different on
different executions of this code-will nevertheless always point into
protected kernel address space, causing memory accesses through
to generate a trap.
Such indeterminacy can further complicate the task of reverse engineering
the obfuscated code. Note that such indeterminate address computations can
also be applied to generate an arbitrary address within a page (or pages)
protected using mprotect() as discussed above.
-
A variety of different traps can be used. For example, in addition to the
memory access traps mentioned above, we can use arithmetic exceptions, e.g.,
divide-by-zero. In fact, the "instruction" generating a trap need not be
a legal instruction at all-i.e., we can use a byte pattern that does not
correspond to any legal instruction to effect a control transfer via
an illegal instruction trap. Such illegal byte sequences-which in general
are indistinguishable from data legitimately embedded in the instruction
stream-can be very effective in confusing disassemblers.
-
The location following the trap-generating instruction is
unreachable, but this is not evident from standard control flow
analyses. We can exploit this by inserting additional "bogus"
code after the trap-generating instruction to further confuse disassembly.
Section 3.2 discusses this in more detail.
We could conceivably obfuscate every jump, call, or return
in the source code.
However, this would cause the program to execute much more slowly
because of signal-processing overhead. We allow the user to
specify a hot-code threshold, and we only obfuscate
control transfers that are not in hot parts of the original program
(see Section 5 for details).
Even so, we are able to obfuscate about a third of the instructions
in hot code blocks.
Before obfuscating a program, we first instrument the program to
gather edge profiles, and then we run the instrumented version on
a training input.
The obfuscation process itself has several steps.
First, using the profile data and hot-cold threshold,
determine which control transfers should be obfuscated
and modify each such instruction as shown in Figure 1.
Second, insert bogus code at unreachable code locations such as after
trap-generating instructions.
Third, intersperse signal handling and restore (return from signal) code with
the original program code.
Fourth, compute the new memory layout, construct a table of mappings from
trap instructions to target addresses,
and patch the restore code to use this table via a perfect hash function.
Finally, assemble a new, obfuscated binary.
3.2. Program Obfuscations
Within our obfuscator, the original program is represented as
an interprocedural control-flow graph (ICFG).
The nodes are basic blocks of machine instructions; the edges
represent the control flow in the program.
Obfuscating Control Transfers
After some initialization actions, our obfuscator makes
one pass through the original program to flip
conditional branches-i.e., reverse the sense of the
branch condition and insert an explicit unconditional jump after it to maintain
the program's semantics. This transformation has
the effect of increasing the set of candidate locations where our
obfuscation can be applied.
Our obfuscator
then makes a second pass through the program to find and modify all
control transfer instructions that are to be obfuscated.
To obfuscate a control transfer instruction, we insert Setup code
that prepares for raising a signal and then Trap code that
causes a signal.
The Setup code
(1) allocates space on the stack for
use by the signal handler to store the address of the trap instruction,
and (2) sets a flag that indicate to the signal handler that the coming
signal is from obfuscated code, not the original program itself.
To set a flag, we use a pre-allocated array (initialized to zero),
and the Setup code moves a random non-zero value into a randomly chosen
element of the array.
Jump, return, and call instructions are obfuscated in nearly identical
ways; the only essential difference is the amount of stack space that we
need to allocate in order to effect the intended control transfer.
The Trap code generates a trap, which in turn raises a signal.
In order not to interfere with signal handlers that might be installed
in the original program,
we only raise signals for which the default action is to dump core
and terminate the program.
In particular we use illegal instruction (SIGILL), floating point exception
(SIGFPE), and segmentation violation (SIGSEGV).
To determine which kind of trap to raise-and to avoid the need
to save and later restore program registers-we first do liveness
analysis to determine which registers are live at the trap point
and which are available for us to use.
If no register is available, we randomly generate an illegal instruction
from among several possible choices.
Otherwise, we generate code to load a zero into a free register
,
then either dereference
(to cause a segmentation fault), or
divide by
(to cause a floating point exception).
Since indirect loads are far more frequent than divides in real programs,
most of the time we choose the former.
If we simply moved a zero into a register
each time that we wanted to trigger a floating point exception
or segmentation fault, there would be dozens of such instructions
that would be a signature for our obfuscation.
To avoid this, we generate a sequence of instructions
by using multiple, randomly chosen rewriting
rules that perform value-preserving transformations on
the registers that are free at each obfuscation point.
Appendix A describes how we randomize the computation of values.
Inserting Bogus Code
After obfuscating a control transfer instruction, we next insert bogus
code-a conditional branch and some junk bytes-to further
confuse disassemblers. This is shown in Figure 2.
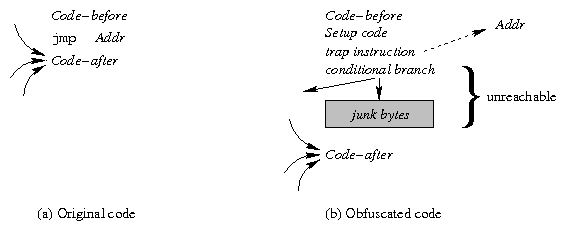 Figure 2: Bogus code insertion
Since the trap instruction has the effect of an unconditional control
transfer, the conditional branch immediately following the trap is
"bogus code" that will not be reachable in the obfuscated program, and hence
it will not be executed.
The purpose of adding this instruction is to confuse the control flow
analysis of the program by misleading the disassembler
into identifying a spurious edge in the control flow graph; the
control flow edge so introduced can also lead to further disassembly errors
at the target of this control transfer.
A secondary benefit of such bogus
conditional branches is that they help improve the stealthiness of the
obfuscation, since otherwise the disassembly would produce what appeared to
be long sequences of straight-line code without any branches, which would
not resemble code commonly encountered in practice.
We randomly select an unconditional branch-based on how frequently
the different kinds occur in normal programs-and use a random
PC-relative displacement.
The junk bytes are a proper prefix of a legal instruction.
The goal is to cause a disassembler to consume the first few bytes of
Code-after when it completes the instruction that starts with
the junk bytes.
This will ideally cause it to continue to misidentify the true instruction
boundaries for at least a while.
We determine the prefix length
that maximizes the disassembly error for
subsequent instructions (
depends only on the instructions in
Code-after), and insert the first
bytes of an instruction chosen
randomly from a number of different alternatives.
Figure 2: Bogus code insertion
Since the trap instruction has the effect of an unconditional control
transfer, the conditional branch immediately following the trap is
"bogus code" that will not be reachable in the obfuscated program, and hence
it will not be executed.
The purpose of adding this instruction is to confuse the control flow
analysis of the program by misleading the disassembler
into identifying a spurious edge in the control flow graph; the
control flow edge so introduced can also lead to further disassembly errors
at the target of this control transfer.
A secondary benefit of such bogus
conditional branches is that they help improve the stealthiness of the
obfuscation, since otherwise the disassembly would produce what appeared to
be long sequences of straight-line code without any branches, which would
not resemble code commonly encountered in practice.
We randomly select an unconditional branch-based on how frequently
the different kinds occur in normal programs-and use a random
PC-relative displacement.
The junk bytes are a proper prefix of a legal instruction.
The goal is to cause a disassembler to consume the first few bytes of
Code-after when it completes the instruction that starts with
the junk bytes.
This will ideally cause it to continue to misidentify the true instruction
boundaries for at least a while.
We determine the prefix length
that maximizes the disassembly error for
subsequent instructions (
depends only on the instructions in
Code-after), and insert the first
bytes of an instruction chosen
randomly from a number of different alternatives.
Building the Mapping Table
After obfuscating control flow and inserting bogus code,
our obfuscator computes a memory layout for the obfuscated program and
determines final memory addresses.
Among these are the addresses of all the trap instructions that
have been inserted.
The obfuscator then goes through the control flow graph and gathers
the information it needs to build a table that maps trap locations to
original targets.
Suppose that
control transfer instructions have been obfuscated.
Then there are
rows in the mapping table, one for each trap point.
Each row contains a flag that indicates the type of transfer that was
replaced, and zero, one, or two target addresses,
depending on the value of the flag.
To make it hard to reverse engineer the contents and use of this table,
we use two techniques.
First, we generate a perfect hash function that maps the
trap
addresses to distinct integers from 0 to
[12], and
we use this function to get indices into the mapping table;
this machine code is quite inscrutable and hence hard
to reverse engineer.
Second, to make it hard to discover the target addresses in the mapping table,
in place of each target
address
we store a value
that is the XOR
of
and the corresponding trap address
.
3.3. Signal Handling
When an instruction raises a signal, the processor stores its address
on the stack, then traps into the kernel.
Figure 3(a) shows the components
and control transfers that normally occur when a program raises a
signal at address
and has installed a signal handler
that returns back to the program at the same address.
(If no handler has been installed, the kernel takes the
default action for the signal.)
Figure 3(b) shows the components and control
transfers that occur in our implementation.
The essential differences are that we return
control to a different target address
,
and we do so by causing the kernel to transfer control to our restore
code rather than back to the trap address.
We allow obfuscated programs to install their own signal
handlers, as described below.
 Figure 3: Signal Handling: Normal and Obfuscated Cases
Figure 3: Signal Handling: Normal and Obfuscated Cases
Handler and Restore Code Actions
We trigger the path shown in Figure 3(b)
when a signal is raised from a trap location that we
inserted in the binary.
However, other instructions in the original program might raise the
illegal instruction, floating point exception, or segmentation fault
signals.
To tell the difference, we use a global array
that is initialized to zero.
In the Setup code before each of the traps we insert in the program,
we set a random element of this array to a non-zero value.
In our signal handler, we loop through this array to see if any
value is nonzero (and we then reset it to zero).
In the normal case where our signal handler is processing one
of the traps we inserted in the program,
it overwrites the kernel restore function's return address
with the address of our restoration code.
That code (1) invokes the perfect hash function on the trap
address
(which was put in the stack space allocated by
our signal handler), (2) looks up the original target address,
(3) resets the stack frame as appropriate for the type of control transfer
and (4) transfers control (via a return instruction)
to the original target address.
To make it harder for an attacker to find and reverse engineer the signal
handler, we disperse our handler and restore code over the program,
i.e., we split the code into multiple basic blocks
and interleave these in with the original program code.
We also make multiple slightly different copies of each code block
so that we are not always using the same locations each time we handle
a signal.
As will be shown in Section 5, we are able to obfuscate
many hot instructions as a side effect of obfuscating cold code.
These include some of the code we introduce to handle signals.
Interaction With Other Signals
We allow the original program to install signal handlers
and dynamically to change signal handling semantics.
By analyzing the binary, we determine whether it installs signal
handlers: this is done by checking to see whether there are any calls to
system library routines (e.g., signal()) that install signal
handlers. We transform the code to intercept these calls at runtime
and record, in a table, the signals that are being handled and the
address of the corresponding signal handler.
When our signal handler determines that a signal did not get
raised by one of our obfuscations (by examining the array of flags),
it consults this table.
If the user installed a handler, we call that handler then return
to the original program.
Otherwise, we take the default action for that kind of signal.
Although in general we are able to handle interactions between
signal handling in our code and the original program,
we discovered one instance of a race condition.
In particular, one of the SPECint-95 benchmark programs, m88ksim,
installs a handler for SIGINT, the interrupt signal.
If we obfuscate that program, run the code, and interrupt the program
while it happens to be in our handler,
the program will cause a segmentation fault and crash.
To solve this type of problem, our signal handler needs to delay
the processing of other signals that might be raised.
(On Unix this can be done by having the signal handler call the
sigprocmask function, or by using sigaction when we
(re)install the handler.)
Once our trap processing code gets
back to the restore code block of the obfuscated program, it can safely be
interrupted because it is through manipulating kernel addresses.
However, our current implementation does not yet block other signals.
An even worse problem would occur in a multithreaded program, because
multiple traps could occur and have to be handled at the same time.
Signal handling is not thread safe in general in Unix systems,
so our obfuscation method cannot be used in an arbitrary
multithreaded program.
However, this is a limitation of Unix, not our method.
3.4. Attack Scenarios
Recall that our goal is to make static disassembly difficult enough to force
any adversary to resort to dynamic techniques. Here we discuss why we
believe our scheme is able to attain this goal.
We assume that our approach is known to the adversary. As discussed in
Section 3.2, the specifics of the obfuscation as applied to a
particular program-the setup code, the kind of trap used for any
particular control transfer, the code sequence used to generate traps, as
well as the bogus control transfers inserted after the trap
instruction-are chosen randomly. This makes it difficult for an adversary
to identify the location of trap instructions and bogus control transfers
simply by inspecting the obfuscated code.
Since locating the obfuscation code by simple inspection is not feasible,
the only other possibility to consider, for statically identifying the
obfuscation instructions, is static analysis. This is difficult for two
reasons. The first is the sheer number of candidates: for example, in
principle any memory operation can raise an exception and is therefore
potentially a candidate for analysis. Secondly, the problem of statically
determining the values of the operands of such candidate instructions is
difficult, both theoretically [22] and in practice, especially
because, as discussed in Section 3.1, such operands need not
be fixed constant values. Furthermore, if a byte sequence is encountered
in the disassembly that does not encode a legal instruction (and therefore
cannot be subjected to static analysis), it can be either a part of the
obfuscation (i.e., is "executed" and causes a trap), or it can be data
embedded in the instruction stream: determining which of these is the case
is in general an undecidable problem.
4. Evaluation
We measure the efficacy of obfuscation in two ways: by the extent of
incorrect disassembly of the input, and by the extent of errors in control
flow analysis of the disassembled input. These quantities are related, in
the sense that an incorrect disassembly of a control transfer instruction
will result in a corresponding error in the control flow graph obtained for
the program. However, it is possible, in principle, to have a perfect
disassembly and yet have errors in control flow analysis because
control transfer instructions have been disguised as innocuous arithmetic
instructions or bogus control transfers have been inserted.
4.1. Evaluating Disassembly Errors
We measure the extent of disassembly errors using a measure we call the
confusion factor for the instructions, basic blocks, and functions.
Intuitively, the confusion factor measures the fraction of program units
(instructions, basic blocks, or functions) in the obfuscated code that were
incorrectly identified by a disassembler. More formally, let
be
the set of all actual instruction addresses, i.e., those that would
be encountered when the program is executed, and let
be the set of
all perceived instruction addresses, i.e., those addresses produced
by a static disassembly. Then
is the set of addresses that
are not correctly identified as instruction addresses by the disassembler.
We define the confusion factor
to be the fraction of instruction
addresses that the disassembler fails to identify correctly:
.
Confusion factors for functions and basic blocks are calculated analogously:
a basic block or function is counted as being "incorrectly
disassembled" if any of the instructions in it is incorrectly disassembled.
The reason for computing confusion factors for basic blocks and functions
as well as for instructions is to determine whether the errors in disassembling
instructions are clustered in a small region of the code, or whether they
are distributed over significant portions of the program.
4.2. Evaluating Control Flow Errors
Two kinds of errors can occur when comparing the control flow structure of the
disassembled program
with that of the original
program
. First,
may contain some edge that does not
appear in
, i.e., the disassembler may mistakenly find a
control flow edge where the original program did not have one.
Second,
may not contain some
edge that appears in
, i.e., the disassembler may fail to find
an edge that was present in the original program. We term the first kind of
error overestimation errors (written
) and the
second kind underestimation errors
(written
), and express them relative to
the number of edges in the original program. Let
be the
set of control flow edges in the original program and
the set of control flow edges identified by the disassembler, then:
Even if we assume a perfect "attack disassembler" that does not incur any
disassembly errors, its output will nevertheless contain control flow
errors arising from two sources. First, it will fail to identify control
transfers that have been transformed to trap-raising instructions. Second,
it will erroneously identify bogus control transfers introduced by the
obfuscator. We can use this to
bound the control flow errors even for a perfect disassembly. Suppose that
control flow edges are lost from a program due to
control transfer instructions being converted to traps, and
bogus control flow edges are added by the obfuscator. Then, a
lower bound on underestimation errors,
,
is obtained when the only control transfers that
the attack disassembler fails to find are those that were lost due to
conversion to trap instructions:
.
An upper bound on overestimation errors,
,
is obtained when every bogus conditional branch inserted by the obfuscator
is reported by the disassembler:
.
5. Experimental Results
We evaluated the efficacy of our techniques using eleven programs from the
SPECint-2000 benchmark suite.
Our experiments were run on an otherwise unloaded 2.4 GHz Pentium IV
system with 1 GB of main memory running RedHat Linux (Fedora Core 3). The
programs were compiled with gcc version 3.4.4 at optimization level
-O3. The programs were profiled using the SPEC training inputs
and these profiles were used to identify any hot spots during our
transformations. The final performance of the transformed programs was
then evaluated using the SPEC reference inputs. Each execution time
reported was derived by running seven trials, removing the highest and lowest
times from the sampling, and averaging the remaining five.
We experimented with three different "attack disassemblers" to evaluate
our techniques: GNU objdump [24]; IDA Pro [11], a
commercially available disassembly tool that is generally regarded to be
among the best disassemblers available;
and an
exhaustive disassembler by
Kruegel et al. that was engineered to handle
obfuscated binaries [15]. Objdump uses a straightforward
linear sweep algorithm, while IDA Pro uses recursive traversal.
The exhaustive disassembler of Kruegel et al. takes into
account the possibility that the input binary may be obfuscated by not
making any assumptions about instruction boundaries. Instead, it considers
alternative disassemblies starting at every byte in the code region of the
program, then examines these alternatives using a variety of statistical and
heuristic analyses to discard those that are unlikely or impossible.
Kruegel et al. report that this approach yields significantly better
disassemblies on obfuscated inputs than other existing disassemblers
[15]; to our knowledge, the exhaustive disassembler is the most
sophisticated disassembler currently available.
In order to maintain a reasonable balance between the extent of obfuscation
and the concomitant runtime overhead, we obfuscated only the "cold code" in
the program-where a basic block is considered "cold" if, according to the
execution profiles used, it is not executed.
We evaluated a number of different combinations of obfuscations. The data
presented below correspond to the combination that gave the highest
confusion factors without excessive performance overhead:
flip branches to increase the number of unconditional jumps in the code
(see Section 3.2);
convert all unconditional control transfers (jumps, calls, and function
returns) in cold code to traps; insert bogus code after traps; and insert
junk bytes after jmp, ret, and halt instructions.
Disassembly Error
The extent of disassembly error, as measured by confusion
factors (Section 4.1) is shown in Figure
4(a).
The results differ depending on the attack disassembler, but the
results for each disassembler are remarkably consistent across the
benchmark programs.
Because we have focused primarily on
disguising control transfer instructions by transforming them into
signal-raising instructions, it does not come as a surprise that
the straightforward linear sweep algorithm used by the objdump
disassembler has the least confusion at 43% of the instructions on average.
However, these are spread across 68% of the basic blocks and 90% of the
functions. The other disassemblers are confused to a much greater
extent-55% for the exhaustive disassembler
and 57% for IDA Pro, on average-but these are more somewhat more clustered
as they cover only about 60% of the basic blocks and slightly
fewer functions (89% and 85%, respectively).
Overall, the instruction confusion factors show that a significant
portion of each binary is disassembled incorrectly; the basic block and
function confusion factors show that the errors in disassembly are
distributed over most of the program. Taken together, these data show that
our techniques are effective even against state-of-the-art disassembly tools.
We have also measured the relative confusion factors for hot and cold
instructions, i.e., those in hot versus cold basic blocks.
For objdump, the confusion factors are nearly identical
at 42% of the hot instructions and 44% of the cold
instructions (again on average).
The exhaustive disassembler was confused by fewer of the
hot instructions (35%) but more of the cold instructions (59%).
IDA Pro did the best on hot instructions at 28% confusion, on average,
but worst on cold instructions at 62% confusion.
It is not surprising that Kruegel and IDA Pro did better with hot code,
because we did not obfuscate it except to insert
junk after hot unconditional jumps, and junk by itself should not confuse
an exhaustive or recursive descent disassembler.
Then again, these disassemblers still failed to disassemble
about a third of the hot code.
As an aside, we had thought that interleaving hot and cold basic blocks
would cause more of the obfuscations in cold code to cause disassembly
errors to "spill over" into succeeding hot code and increase the confusion
there. This turns out to be the case for objdump, which
is especially confused by junk byte insertion. However, IDA Pro and
the exhaustive disassembler are still able to find most hot code
blocks. In fact, such interleaving introduces additional unconditional
jumps in the code, e.g., from one hot block to the next one, jumping around
the intervening cold code. The exhaustive disassembler and IDA Pro
are able to find these jumps and use them to improve disassembly,
resulting in less confusion when hot and cold code are interleaved.
Morever, programs run more slowly when hot and cold blocks are interleaved
due to poorer cache utilization.
| Program
| Objdump
| Exhaustive
| IDA Pro |
| Instrs
| Blocks
| Func
| Instrs
| Blocks
| Funcs
| Instrs
| Blocks
| Funcs
| |
| bzip2
| 44.19 | 69.62 | 89.59 | 55.57 | 60.29 | 89.33 | 59.88 | 62.94 | 85.99 |
| crafty
| 41.09 | 68.70 | 90.26 | 55.94 | 61.04 | 87.92 | 54.22 | 59.26 | 84.71 |
| gap
| 42.98 | 66.78 | 90.19 | 52.64 | 56.13 | 87.04 | 55.70 | 57.92 | 83.77 |
| gcc
| 46.32 | 68.67 | 89.26 | 55.89 | 58.24 | 87.58 | 54.67 | 55.49 | 82.28 |
| gzip
| 44.26 | 69.56 | 90.25 | 53.61 | 58.91 | 87.13 | 61.65 | 63.45 | 85.18 |
| mcf
| 44.85 | 69.91 | 89.20 | 57.32 | 60.53 | 87.80 | 58.68 | 61.27 | 84.85 |
| parser
| 44.28 | 68.83 | 91.70 | 55.19 | 59.40 | 88.87 | 57.85 | 61.27 | 85.06 |
| perlbmk
| 45.34 | 69.08 | 89.80 | 55.62 | 58.82 | 90.09 | 55.16 | 56.14 | 85.89 |
| twolf
| 41.90 | 68.32 | 89.03 | 56.29 | 61.63 | 88.80 | 57.77 | 61.74 | 84.77 |
| vortex
| 39.80 | 69.40 | 93.28 | 58.05 | 65.77 | 93.10 | 55.96 | 64.04 | 90.98 |
| vpr
| 42.31 | 68.19 | 86.67 | 54.20 | 59.91 | 87.49 | 59.01 | 63.27 | 82.16 | |
| Geom. mean:
| 43.35 | 68.82 | 89.92 | 55.46 | 60.02 | 88.63 | 57.28 | 60.55 | 85.03 |
(a) Disassembly Errors (Confusion Factor, %)
| Program
|
|
|
|
|
| Objdump
| Exhaustive
| IDA Pro |
| | | |
|
|
|
|
|
|
|
| |
| bzip2
| 47933
| 13933
| 42236
| 88.11
| 29.07
| 72.60
| 64.82
| 28.31
| 61.40
| 40.44
| 65.66
|
| crafty
| 59507
| 17243
| 50868
| 85.48
| 28.98
| 72.26
| 62.17
| 25.28
| 60.71
| 43.12
| 62.20
|
| gap
| 98793
| 26603
| 82374
| 83.38
| 26.93
| 69.94
| 60.90
| 25.35
| 57.20
| 41.49
| 60.84
|
| gcc
| 237491
| 67818
| 193570
| 81.51
| 28.56
| 67.18
| 63.98
| 25.41
| 58.36
| 41.93
| 59.32
|
| gzip
| 48467
| 13931
| 42722
| 88.15
| 28.74
| 72.56
| 64.56
| 29.64
| 59.64
| 38.34
| 66.09
|
| mcf
| 43376
| 12329
| 38220
| 88.11
| 28.42
| 72.57
| 65.32
| 26.13
| 61.46
| 42.79
| 63.74
|
| parser
| 59823
| 16688
| 50858
| 85.01
| 27.90
| 70.65
| 63.94
| 27.77
| 59.78
| 40.87
| 63.46
|
| perlbmk
| 116711
| 33748
| 100298
| 85.94
| 28.92
| 70.67
| 64.75
| 26.99
| 59.31
| 43.27
| 59.66
|
| twolf
| 62210
| 18061
| 52916
| 85.06
| 29.03
| 71.90
| 62.27
| 28.55
| 61.48
| 40.85
| 63.94
|
| vortex
| 97242
| 32507
| 81734
| 84.05
| 33.43
| 72.37
| 63.29
| 30.28
| 65.25
| 41.62
| 66.18
|
| vpr
| 55187
| 15811
| 47414
| 85.92
| 28.65
| 71.76
| 61.92
| 27.92
| 59.76
| 38.60
| 65.56
| |
| Geom. mean:
| 85.50 | 28.93 | 71.30 | 63.43 | 27.37 | 60.36 | 41.18 | 63.28 |
(b) Control Flow Errors (%)
| Key: |
: | edges in original program
| |
: | upper bound on overestimation
errors |
|
: | control flow edges lost due to trap conversion
| |
: | lower bound on underestimation
errors |
|
: | bogus control flow edges added
| | |
Figure 4: Efficacy of obfuscation
Control Flow Obfuscation
Figure 4(b) shows the effect of our transformations in
obfuscating the control flow graph of the program. The second column gives,
for each program, the actual number of control flow edges in the
original program.
These are counted as follows: each conditional branch gives rise to two
control flow edges; each unconditional branch (direct or indirect) gives
rise to a single edge; and each function call gives two control flow
edges-one corresponding to a "call edge" to the callee's entry point,
the other to a "return edge" from the callee back to the caller.
Column 3 gives the number of control flow edges
removed due to the conversion of control flow instructions to traps, while
column 4 gives the number of bogus control flow edges added by the
obfuscator.
Columns 5 and 6 give, respectively, an upper bound on the overestimation
error and a lower bound on the underestimation error. The
remaining columns give, for each attack disassembler, the extent to which it
incurs errors in constructing the control flow graph of the program,
as discussed in Section 4.2.
It can be seen from Figure 4(b) that none of the three
attack disassemblers tested fares very well at constructing the control flow
graph of the program. Objdump fails to find over 63% of the
control flow edges in the original program; at the same time, it reports
over 71% spurious edges (relative to the number of original edges in the
program) that are not actually present in the program. The exhaustive
disassembler fails to find over 60% of the edges in the original program,
and reports over 27% spurious edges. IDA Pro fails to find over 63%
of the control flow edges in the original program and reports
over 41% spurious edges.
Again the results for each disassembler are very consistent across
the benchmark programs.
Also significant are the error bounds reported in columns 5 and 6 of
Figure 4(b). These numbers indicate that,
even if we suppose perfect disassembly, the result would incur up to 85.5%
overestimation error and at least 28.93% underestimation error.
| Execution time (secs) |
| Program | Original | Obfuscated | Slowdown |
|
|
|
| |
| bzip2
| 283.011
| 377.620
| 1.334
|
| crafty
| 140.741
| 1222.992
| 1.584
|
| gap
| 146.367
| 152.673
| 1.043
|
| gcc
| 151.624
| 247.552
| 1.633
|
| gzip
| 210.036
| 209.502
| 0.997
|
| mcf
| 425.971
| 427.132
| 1.003
|
| parser
| 301.079
| 302.040
| 1.003
|
| perlbmk
| 220.851
| 461.828
| 2.091
|
| twolf
| 569.163
| 586.259
| 1.030
|
| vortex
| 235.649
| 240.648
| 1.021
|
| vpr
| 319.475
| 328.563
| 1.028
| |
| Geom. mean | 1.210 |
Figure 5: Effect of Obfuscation on Execution Speed
Execution Speed
Figure 5 shows the effect of obfuscation on execution
speed. For some programs-such as gap, gzip,
mcf, parser, twolf, vortex, and vpr-the
execution characteristics on profiling input(s) closely match those
on the reference input, so there is essentially no slowdown.
(In fact, gzip ran faster after obfuscation;
we believe this is due to a combination of cache effects
and experimental errors resulting from clock granularity.)
For other programs-such as crafty, gcc and perlbmk-the
profiling inputs are not as good predictors of the runtime
characteristics of the program on the reference inputs, and this results in
significant slowdowns: a factor of 1.6 for crafty and gcc
and 2.1 for perlbmk.
The mean slowdown seen for all eleven benchmarks is 21%.
We also measured the effect on execution speed of obfuscating a portion
of the hot code blocks.
Let
specify the fraction of the total number of instructions
executed at runtime that should be accounted for by hot basic blocks.
(The execution times in Figure 5 are for
,
i.e., all basic blocks with an execution count greater than 0 are
consider hot.)
If we run our obfuscator with
-which means that,
in addition to cold basic blocks, we obfuscate the hot basic blocks
that account for just
a tenth of a percent of the dynamic execution count-then
the mean slowdown for the eleven benchmarks increases to 2.38.
For smaller values of
, the situation is far worse:
at
the mean slowdown is 6.79, and at
the mean slowdown climbs to 43.39.
The confusion factor increases somewhat when
is decreased,
but even at
the increase in confusion is less than 10%
relative to the confusion at
.
| Text section (KB)
| Initialized Data section (KB)
| Combined: Text+Data (KB) |
| Program
| Original | Obfusc. | Change
| Original | Obfusc. | Change
| Original | Obfusc. | Change |
| (
)
| (
)
| (
)
| (
)
| (
)
| (
)
| (
)
| (
)
| (
)
| |
| bzip2
| 343.6 | 694.2 | 2.02
| 6.4 | 145.4 | 22.64
| 350.0 | 840.0 | 2.40
|
| crafty
| 474.5 | 903.1 | 1.90
| 19.7 | 192.4 | 9.78
| 494.2 | 1,095.5 | 2.22
|
| gap
| 690.9 | 1,351.6 | 1.96
| 6.8 | 273.1 | 39.95
| 697.8 | 1,624.7 | 2.33
|
| gcc
| 1,494.4 | 3,051.8 | 2.04
| 21.9 | 675.5 | 30.88
| 1,516.3 | 3,727.3 | 2.46
|
| gzip
| 344.9 | 699.8 | 2.03
| 5.8 | 145.0 | 24.94
| 350.7 | 844.8 | 2.41
|
| mcf
| 301.6 | 618.8 | 2.05
| 3.3 | 128.2 | 39.03
| 304.9 | 747.0 | 2.45
|
| parser
| 402.6 | 833.1 | 2.07
| 5.7 | 180.0 | 31.32
| 408.3 | 1,013.f | 2.48
|
| perlbmk
| 808.6 | 1,612.2 | 1.99
| 32.8 | 359.0 | 10.95
| 841.4 | 1,971.3 | 2.34
|
| twolf
| 472.f | 930.9 | 1.97
| 3.3 | 192.2 | 58.46
| 475.7 | 1,123.2 | 2.36
|
| vortex
| 725.3 | 1,513.5 | 2.09
| 19.8 | 340.7 | 17.23
| 745.1 | 1,854.2 | 2.49
|
| vpr
| 407.1 | 800.7 | 1.97
| 3.4 | 165.5 | 48.45
| 410.5 | 966.2 | 2.35
| |
| Geom. mean
|
| 2.01
|
| 26.46
|
| 2.39
|
Figure 6: Effect of Obfuscation on Text and Data Section Sizes
Program Size
Figure 6 shows the impact of obfuscation
on the size of the text and initialized data sections.
It can be seen that the size of the text section increases by factors
ranging from 1.90 (crafty) to almost 2.1
(vortex), with a mean increase of a factor of 2.01.
The relative growth in the size of the initialized data section is
considerably larger, ranging from a factor of about 10 (crafty) to
a factor of over 58 (twolf), with a mean growth of a factor of
26.46. The growth in the size of the initialized data is due to the addition
of the mapping tables used to compute the type of each
branch as well as its target address. However, this large relative
growth in the data section size is due mainly to the fact that
the initial size of
this section is not very large. When we consider the total increase in
memory requirements due to our technique, obtained as the sum of the text
and initialized data sections, we see that it ranges from a factor of 2.22
(crafty) to about 2.5 (parser and vortex), with a
mean growth of a factor of about 2.4.
The increase in the size of the text section arises from three sources.
The first of these is the code required to set up and raise the trap
for each obfuscated control transfer instruction. The second is the junk
bytes and bogus conditional branch inserted after a trap instruction.
Finally, there is the signal handler and restore code.
In our current implementation,
the first two of these sources-the setup code for a trap
and bogus code inserted after a trap-introduces on average
an additional 30 bytes of memory for each
obfuscated control transfer instruction. This
accounts for over 95% of the total increase in the text section size.
Each obfuscated control transfer also adds three memory words (12 bytes) to
the initialized data section, accounting for the increase in the size of
this section.
Stealth
The stealth of an obfuscation refers to the difficulty of
distinguishing code introduced by an obfuscator from the original program
code. We estimate the stealth of our obfuscations by comparing the
distributions of
opcodes and
opcode pairs from adjacent
instructions.
The points of comparison are the original program, the obfuscated
program (for which we know the actual instructions), and the
instructions observed by the different attack disassemblers we tested.
The idea is to see whether the obfuscation process introduces any atypical
instruction sequence signatures that could be used to identify the
obfuscation code statically.
Figure 7 shows the distribution of individual opcodes.
Because of the large number of opcodes in the x86 architecture,
we have grouped the commonly used opcodes into 27 sets-moves,
conditional jumps, and so on-and also added sets for illegal
instructions and all other instructions.
The 29 different sets of opcodes are given along the x-axis
("jc" denotes conditional jumps), while the y-axis
shows the percentage of
instructions in any program accounted for by that opcode. The y-axis uses a
logarithmic scale to in order to magnify the data ranges for small
percentage values. Each data point was obtained by computing the opcode
distribution for each of the SPECint-2000 benchmarks in our test suite:
the original binary, the distribution in the obfuscated program
obtained from the obfuscator, and the distributions for the
disassemblies produced by each of the attack disassemblers.
We then used these data to compute
the arithmetic mean, minimum, and maximum values of instruction percentages
for that opcode across all of our test programs. For each opcode, the dark
line in Figure 7 shows the mean instruction percentage for
each opcode, together with the range of its values. This line is then
followed immediately to the right by a set of lighter lines that show the
values for the obfuscated programs as well as those in the disassemblies
obtained from the attack disassemblers.
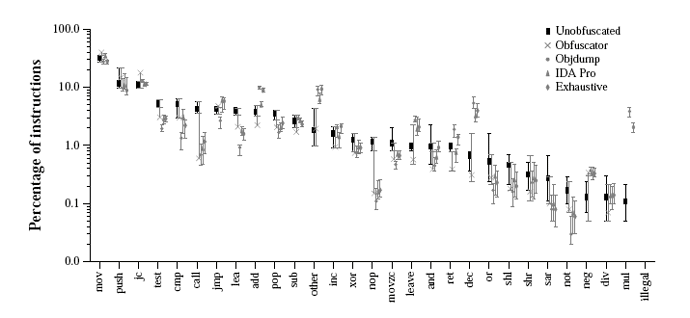 Figure 7: Obfucation Stealth I: Distribution of Individual Opcodes
Figure 7: Obfucation Stealth I: Distribution of Individual Opcodes
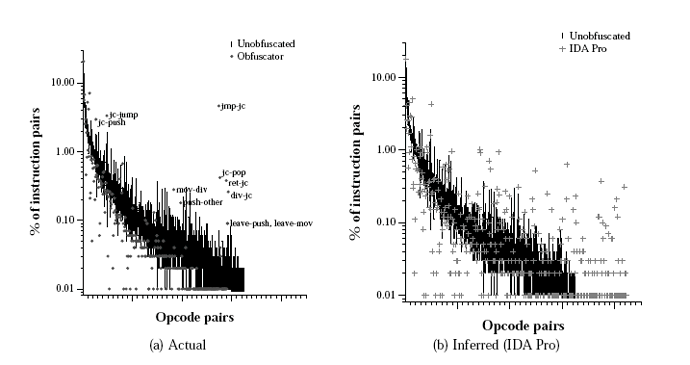 Figure 8: Obfucation Stealth II: Distribution of Opcode Pairs
Figure 7 illustrates that, in most cases,
the mean value of each opcode's range in the obfuscated code
is within the range of values in the unobfuscated benchmark code.
Calls, returns, and jumps are somewhat less frequent for the obvious reason
that we obfuscated many of those instructions. Conditional
jumps are somewhat more frequent because we added these to bogus code.
On balance, however, there are no obvious outliers that an attacker
could use to use as a signature for where obfuscations occur.
Figure 8 shows the distribution of pairs of adjacent
opcodes, not including pairs involving illegal opcodes.
Due to space constraints, we show the data for just one attack
disassembler, IDA Pro; the data are generally similar
for the other attack disassemblers.
Figure 8(a) shows the actual distribution of opcode pairs in
the obfuscated code, while Figure 8(b) shows the
distribution for the disassembly obtained from IDA Pro.
To reduce visual clutter in these
figures, we plot the ranges of values for each opcode pair in the
unobfuscated code (the dark band running down the graph), but only the mean
values for the obfuscated code.
There are two broad conclusions to be drawn from Figure 8.
First, as can be seen
from Figure 8(a), the actual
distribution of adjacent opcode pairs in the obfuscated code is, by and
large, reasonably close to that of the original code; however, there are a
few opcode pairs, very often involving conditional jumps, that occur with
disproportionate frequency. The selection of obfuscation code to eliminate
such atypical situations is an area of future work. The second
conclusion is that,
as indicated by Figure 8(b), the opcode-pairs in the
obfuscated code are significantly more random than in the unobfuscated
code, partly because of disassembly errors caused by "junk bytes"
inserted by our obfuscator. The outliers in this figure might serve as
starting points for an attacker, but there are dozens of such points, they
correspond to thousands of actual opcode pairs in the program, and
there is no obvious pattern.
In summary, the individual opcodes and pairs of adjacent opcodes have
approximately similar distributions in both unobfuscated and
obfuscated programs. Thus, our obfuscation method
is on balance quite stealthy.
Figure 8: Obfucation Stealth II: Distribution of Opcode Pairs
Figure 7 illustrates that, in most cases,
the mean value of each opcode's range in the obfuscated code
is within the range of values in the unobfuscated benchmark code.
Calls, returns, and jumps are somewhat less frequent for the obvious reason
that we obfuscated many of those instructions. Conditional
jumps are somewhat more frequent because we added these to bogus code.
On balance, however, there are no obvious outliers that an attacker
could use to use as a signature for where obfuscations occur.
Figure 8 shows the distribution of pairs of adjacent
opcodes, not including pairs involving illegal opcodes.
Due to space constraints, we show the data for just one attack
disassembler, IDA Pro; the data are generally similar
for the other attack disassemblers.
Figure 8(a) shows the actual distribution of opcode pairs in
the obfuscated code, while Figure 8(b) shows the
distribution for the disassembly obtained from IDA Pro.
To reduce visual clutter in these
figures, we plot the ranges of values for each opcode pair in the
unobfuscated code (the dark band running down the graph), but only the mean
values for the obfuscated code.
There are two broad conclusions to be drawn from Figure 8.
First, as can be seen
from Figure 8(a), the actual
distribution of adjacent opcode pairs in the obfuscated code is, by and
large, reasonably close to that of the original code; however, there are a
few opcode pairs, very often involving conditional jumps, that occur with
disproportionate frequency. The selection of obfuscation code to eliminate
such atypical situations is an area of future work. The second
conclusion is that,
as indicated by Figure 8(b), the opcode-pairs in the
obfuscated code are significantly more random than in the unobfuscated
code, partly because of disassembly errors caused by "junk bytes"
inserted by our obfuscator. The outliers in this figure might serve as
starting points for an attacker, but there are dozens of such points, they
correspond to thousands of actual opcode pairs in the program, and
there is no obvious pattern.
In summary, the individual opcodes and pairs of adjacent opcodes have
approximately similar distributions in both unobfuscated and
obfuscated programs. Thus, our obfuscation method
is on balance quite stealthy.
6. Related Work
The earliest work on the topic of binary obfuscation that we are aware of
is by Cohen, who proposes overlapping adjacent instructions to fool a
disassembler
[7].
We are not aware of any actual
implementations of this proposal, and our own experiments with this idea
proved to be disappointing. More recently, we described an approach to make
binaries harder to disassemble using a combination of two techniques: the
judicious insertion of ``junk bytes'' to throw off disassembly; and the use
of a device called ``branch functions'' to make it harder to identify
branch targets
[20].
These techniques proved effective
at thwarting most disassemblers, including the commercial IDA Pro system.
Conceptually, this paper can be seen as extending this work by disguising
control transfer instructions and inserting misleading control transfers.
More recently, we described a way to use signals to disguise the instruction
used to make system calls (`int $0x80' in
Intel x86 processors), with the goal of preventing injected malware code
from finding and executing system calls; this work required kernel
modifications. By contrast, the work described in this paper is applicable
to arbitrary control transfers in programs and does not require any changes to
the kernel. These two differences lead to significant
differences between the two approaches in terms of goals, techniques, and effects.
There has been some recent work by Kapoor [14] and
Kruegel et al.
[15]
focusing on
disassembly techniques aimed specifically at
obfuscated binaries. They work around the possibility of ``junk bytes''
inserted in the instruction stream by producing an for each function, i.e., where a recursive disassembly is
produced starting at every byte in the code for that function. This results
in a set of alternative disassemblies, not all of which are viable. The
disassembler then uses a variety of heuristic and statistical reasoning to
rule out alternatives that are unlikely or impossible. To our knowledge,
these exhaustive disassemblers are the most sophisticated disassemblers
currently available. One of the "attack disassemblers" used for our
experiments is an implementation of Kruegel et al.'s exhaustive
disassembler.
There is a considerable body of work on code obfuscation that focuses
on making it harder for an attacker to decompile a program and extract high
level semantic information from it
[9,10,31,32]. Typically,
these authors rely on the use of computationally difficult static analysis
problems-e.g., involving complex Boolean expressions, pointers, or indirect
control flow-to make it harder to construct a precise control flow
graph for a program.
Our work is orthogonal to these proposals, and
complementary to them. We aim to make a program harder to disassemble
correctly, and to thereby sow uncertainty in an attacker's mind about
which portions of a disassembled program have been correctly disassembled
and which parts may contain disassembly errors. If the program has already
been obfuscated using any of these higher-level obfuscation techniques, our
techniques add an additional layer of protection that makes it even harder
to decipher the actual structure of the program.
Even greater security may be obtained by maintaining the software in
encrypted form and decrypting it as needed during execution, as suggested
by Aucsmith [1]; or by using specialized hardware, as discussed
by Lie et al. [19]. Such
approaches have the disadvantages of high performance overhead (in the case
of runtime decryption in the absence of specialized hardware support) or a
loss of flexibility because the software can no longer be run on stock
hardware.
7. Conclusions
This paper has described a new approach to obfuscating
executable binary programs and evaluated its effectiveness on programs
in the SPECint-2000 benchmark suite.
Our goals are to make it hard for disassemblers (and humans) to find the
real instructions in a binary and to give them a mistaken
notion of the actual control flow in the program.
To accomplish these goals, we replace many control transfer instructions
by traps that cause signals, inject signal handling code that actually
effects the original transfers of control, and insert bogus code that
further confuses disassemblers. We also use randomization to vary
the code we insert so it does not stand out.
These obfuscations confuse even the best disassemblers.
On average, the GNU objdump program [24]
misunderstands over 43% of the
original instructions, over-reports the
control flow edges by 71%, and misses 63% of the
original control flow edges.
The IDA Pro system [11], which is considered the best commercial
disassembler, fails to disassemble 57% of the original
instructions, over-reports control flow edges by 41%, and under-reports
control flow edges by 85%.
A recent disassembler [15]
that has been designed to deal with obfuscated
programs fails to disassemble over 55% of the instructions,
over-reports control flow edges by 27%, and under-reports
control flow edges by over 60%.
These results indicate that we successfully make it hard to disassemble
programs, even when we only obfuscate code that is in cold code blocks.
If we obfuscate more of the code, we can confuse disassemblers even more.
However, our obfuscation method slows down program execution, so there is
a tradeoff between the degree of obfuscation and execution time.
When we obfuscate only cold code blocks, the average slow-down is 21%,
and this result is skewed by three benchmarks for which the training input is
not a very good predictor for execution on the reference input.
On many programs, the slowdown is negligible.
An interesting possibility-which we have not explored but could
easily add to our obfuscator-would be selectively to obfuscate some of the
hot code, e.g., that which the creator of the code especially
wants to conceal.
Acknowledgements
We are grateful to Christopher Kruegel for the use of the code for his
exhaustive disassembler for our experiments.
References
- [1]
-
D. Aucsmith.
Tamper-resistant software: An implementation.
In Information Hiding: First International Workshop:
Proceedings, volume 1174 of Lecture Notes in Computer Science, pages
317-333. Springer-Verlag, 1996.
- [2]
-
Black Fenix.
Black fenix's anti-debugging tricks.
https://in.fortunecity.com/
skyscraper/browser/12/sicedete.html.
- [3]
-
S. Cesare.
Linux anti-debugging techniques (fooling the debugger), January 1999.
VX Heavens. https://vx.netlux.org/lib/vsc04.html.
- [4]
-
M. Christodorescu, S. Jha, S. A. Seshia, D. Song, and R. E. Bryant.
Semantics-aware malware detection.
In Proc. 2005 IEEE Symposium on Security and Privacy (Oakland
2005), pages 32-46, May 2005.
- [5]
-
C. Cifuentes.
Reverse Compilation Techniques.
PhD thesis, Queensland University of Technology, Australia, July
1994.
- [6]
-
C. Cifuentes and K. J. Gough.
Decompilation of binary programs.
Software-Practice and Experience, 25(7):811-829, July
1995.
- [7]
-
F.~B. Cohen.
Operating system protection through program evolution, 1992.
https://all.net/books/IP/evolve.html.
-
- [8]
-
R. S. Cohn, D. W. Goodwin, and P. G. Lowney.
Optimizing Alpha executables on Windows NT with Spike.
Digital Technical Journal, 9(4):3-20, 1997.
- [9]
-
C. Collberg and C. Thomborson.
Watermarking, tamper-proofing, and obfuscation - tools for software
protection.
IEEE Transactions on Software Engineering, 28(8), August
2002.
- [10]
-
C. Collberg, C. Thomborson, and D. Low.
Breaking abstractions and unstructuring data structures.
In Proc. 1998 IEEE International Conference on Computer
Languages, pages 28-38.
- [11]
-
DataRescue sa/nv, Liége, Belgium.
IDA Pro.
https://www.datarescue.com/idabase/.
- [12]
-
M. L. Fredman, J. Komlós, and E. Szemerédi.
Storing a sparse table with
worst case access time.
Journal of the ACM, 31(3):538-544, July 1984.
- [13]
-
C. R. Hollander.
Decompilation of object programs.
PhD thesis, Stanford University, 1973.
- [14]
-
A. Kapoor.
An approach towards disassembly of malicious binaries.
Master's thesis, University of Louisiana at Lafayette, 2004.
- [15]
-
C. Kruegel, W. Robertson, F. Valeur, and G. Vigna.
Static disassembly of obfuscated binaries.
In Proc. 13th USENIX Security Symposium, August 2004.
- [16]
-
C. Kruegel, E. Kirda, D. Mutz, W. Robertson, and G. Vigna.
Polymorphic worm detection using structural information of
executables.
In Recent Advances in Intrusion Detection, volume 3858 of
Lecture Notes in Computer Science, pages 207-226. Springer, 2005.
- [17]
-
E. U. Kumar, A. Kapoor, and A. Lakhotia.
DOC - answering the hidden `call' of a virus.
Virus Bulletin, April 2005.
- [18]
-
A. Lakhotia, E. U. Kumar, and M. Venable.
A method for detecting obfuscated calls in malicious binaries.
IEEE Transactions on Software Engineering, 31(11):955-968,
2005.
- [19]
-
D. Lie, C. Thekkath, M. Mitchell, P. Lincoln, D. Boneh, J. Mitchell, and
M. Horowitz.
Architectural support for copy and tamper resistant software.
In Proc. 9th. International Conference on Architectural Support
for Programming Languages and Operating Systems (ASPLOS-IX), pages
168-177, November 2000.
- [20]
-
C. Linn and S.K. Debray.
Obfuscation of executable code to improve resistance to static
disassembly.
In Proc. 10th. ACM Conference on Computer and Communications
Security (CCS 2003), pages 290-299, October 2003.
- [21]
-
C. M. Linn, M. Rajagopalan, S. Baker, C. Collberg, S. K. Debray, and J. H.
Hartman.
Protecting against unexpected system calls.
In Proc. Usenix Security '05, pages 239-254, August 2005.
- [22]
-
R. Muth and S. K. Debray.
On the complexity of flow-sensitive dataflow analyses.
In Proc. 27th ACM Symposium on Principles of Programming
Languages (POPL-00), pages 67-80, January 2000.
- [23]
-
R. Muth, S. K. Debray, S. Watterson, and K. De Bosschere.
alto : A link-time optimizer for the Compaq Alpha.
Software-Practice and Experience, 31:67-101, January 2001.
- [24]
-
Objdump.
GNU Manuals Online.
GNU Project-Free Software Foundation.
www.gnu.org/manual/binutils-2.10.1/
html_chapter/binutils_4.html.
- [25]
-
M. Prasad and T. Chiueh.
A binary rewriting defense against stack based buffer overflow
attacks.
In Proc. USENIX Technical Conference, June 2003.
- [26]
-
B. Schwarz, S. K. Debray, and G. R. Andrews.
Disassembly of executable code revisited.
In Proc. IEEE 2002 Working Conference on Reverse Engineering
(WCRE), pages 45-54, October 2002.
- [27]
-
P. K. Singh, M. Mohammed, and A. Lakhotia.
Using static analysis and verification for analyzing virus and worm
programs.
In Proc. 2nd. European Conference on Information Warfare, June
2003.
- [28]
-
R. L. Sites, A. Chernoff, M. B. Kirk, M. P. Marks, and S. G. Robinson.
Binary translation.
Communications of the ACM, 36(2):69-81, February 1993.
- [29]
-
A. Srivastava and D. W. Wall.
A practical system for intermodule code optimization at link-time.
Journal of Programming Languages, 1(1):1-18, March 1993.
- [30]
-
H. Theiling.
Extracting safe and precise control flow from binaries.
In Proc. 7th Conference on Real-Time Computing Systems and
Applications, December 2000.
- [31]
-
C. Wang, J. Davidson, J. Hill, and J. Knight.
Protection of software-based survivability mechanisms.
In Proc. International Conference of Dependable Systems and
Networks, July 2001.
- [32]
-
C. Wang, J. Hill, J. Knight, and J. Davidson.
Software tamper resistance: Obstructing static analysis of programs.
Technical Report CS-2000-12, Dept. of Computer Science, University of
Virginia, 12 2000.
- [33]
-
Z. Xu, B. P. Miller, and T. Reps.
Safety checking of machine code.
In Proc. ACM SIGPLAN '00 Conference on Programming Language
Design and Implementation, pages 70-82, June 18-21, 2000.
Appendix - Randomizing the Computation of Values
The essential idea is to carry out multiple, random, value-preserving
rewritings of the syntax tree for an expression. We start with a simple
expression, e.g., an integer constant or a variable, and repeatedly rewrite
it, using value-preserving transformation rules, to produce an equivalent
expression (i.e., one that will always evaluate to the same value).
Figure 9 gives
a non-exhaustive list of example rewrite rules.
In the rules, we
use `
' and `
' to denote variables, i.e., the values of registers or memory
locations; `
,' `
', and `
' to denote integer constants; and
to denote something that is either a variable or a constant.
Note that equivalences that hold for integers may not hold at the machine
level, e.g.,
need not evaluate to
. Thus, in general
we cannot use associative and distributive laws for rewriting.
| Zero:
| 0 |
|
| |
| 0 |
|
^
| |
| 0 |
|
&
| |
| 0 |
|
?
:
|
; arbitrary
|
| |
| Nonzero
:
|
|
| ~
| |
|
|
|
{rotl, rotr}
|
, and any
|
| | | | (rotr = rotate right;
rotl = rotate left) |
|
|
|
<<
|
,
where
is the position of the |
| | | | least significant `1' bit in
, and
is the
machine |
| | | | word size in bits. |
|
|
|
^
|
|
| |
| Arbitrary
:
|
|
|
+
| |
|
|
|
*
| |
|
|
|
?
:
|
is any value |
|
|
|
?
:
|
is any value;
|
Figure 9: A (non-exhaustive) list of rewriting rules (Operators are as in the
C language)
The expression being rewritten is maintained as a syntax tree. Initially,
the tree consists of a single node, namely, the variable or constant being
rewritten. Each node of the tree has an associated label indicating what
kind of value is being computed (zero, nonzero, arbitrary, etc.). The
rewriting proceeds as follows. We first choose a positive random value as
the number of rewriting steps. Each rewriting step consists of the following:
- Randomly choose a leaf node
of the tree.
- Randomly choose a rewrite rule
from
the set of rules corresponding to the label of the chosen leaf node.
- Modify the syntax tree by adding the appropriate instance of
(i.e., with all occurrences of
replaced by
) as child nodes of
and update the set of leaf nodes appropriately.
The rewritten expression may contain "free variables," i.e., variables that
are not initialized to any value. The value of the overall expression does
not depend on the actual value taken on by such a free variable, so any
value will do. In our implementation, we simply use the contents of any
arbitrary register or legal memory location for such variables.
Once the rewritten expression has been generated, we generate code for it
via a straightforward post-order traversal of the final syntax tree.
Footnotes:
This work was supported in
part by NSF Grants EIA-0080123, CCR-0113633, and CNS-0410918.
This technique only works on variable-instruction-length architectures
such as the IA-32.
Moreover, disassemblers tend to resynchronize relatively quickly, so
that on average they are confused for only three or four instructions
before again finding the true instruction boundaries.
We
also considered taking into account the set
of addresses that are
erroneously identified as instruction addresses by the disassembler, but
we rejected this approach because it "double counts" the effects of
disassembly errors.
We did not use
the eon programs from this benchmark suite
because we were not able to build it.
We used IDA Pro
version 4.3 for the results reported here.
File translated from
TEX
by
TTM,
version 3.72.
On 18 Apr 2007, 13:47.
|
