|
| |||||||||||||||||||||||||||||||||||||||||||||||||||

| ||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Security '05 Paper
[Security '05 Technical Program]
On the Effectiveness of Distributed Worm Monitoring
Johns Hopkins University {moheeb,fabian,terzis}@cs.jhu.edu
Abstract:Distributed monitoring of unused portions of the IP address space holds the promise of providing early and accurate detection of high-profile security events, especially Internet worms. While this observation has been accepted for some time now, a systematic analysis of the requirements for building an effective distributed monitoring infrastructure is still missing. In this paper, we attempt to quantify the benefits of distributed monitoring and evaluate the practicality of this approach. To do so we developed a new worm propagation model that relaxes earlier assumptions regarding the uniformity of the underlying vulnerable population. This model allows us to evaluate how the size of the monitored address space, as well the number and locations of monitors, impact worm detection time. We empirically evaluate the effect of these parameters using traffic traces from over 1.5 billion suspicious connection attempts observed by more than 1600 intrusion detection systems dispersed across the Internet. Our results show that distributed monitors with half the allocated space of a centralized monitor can detect non-uniform scanning worms in half the time. Moreover, a distributed monitor of the same size as a centralized monitor can detect the worm four times faster. Furthermore, we show that even partial knowledge of the vulnerable population density can be used to improve monitor placement. Exploiting information about the location of the vulnerable population leads, in some cases, to detection time that is seven times as fast compared to random monitor deployment.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||
Since our traffic logs are obtained from IDS reports, it is safe to assume that they represent unwanted traffic. This traffic originates either from compromised hosts or active scanners.1 We further filter the data by considering only sources attempting connections to ports 80, 135, and 445. We chose these ports because they are targeted by many well-known worms (e.g. CodeRed, Nimda, and MS Blaster). We assume that all connection attempts to these ports originate from previously compromised hosts attempting to transfer the infection to other hosts by scanning the address space. Therefore, we assume that the collected set of source IP addresses attempting connections to one of the above specified ports, is the set of hosts that were originally vulnerable to (and subsequently infected by) a worm instance. There is a caveat, however, with identifying hosts based solely on their IP addresses: because DHCP is heavily used, hosts may be assigned different addresses over time. Indeed, Moore et. al. [15] argue that IP addresses are not an accurate measure of the spread of a worm on time-scales longer than 24 hours. Unfortunately, without a better notion at hand, we proceed to use IP addresses to identify hosts, but keep this observation in mind.
We group the IP addresses in each of the three sets according to two granularities: (i) in /16 prefixes, and (ii) in /8 prefixes. We chose these two groupings because they are important from the perspective of worm spreading behavior. Specifically, it is known that many examples of popular worms (e.g. [6,8,12]) use localized target selection algorithms targeting hosts with different scanning probabilities applied on the /16 and /8 prefix boundaries.
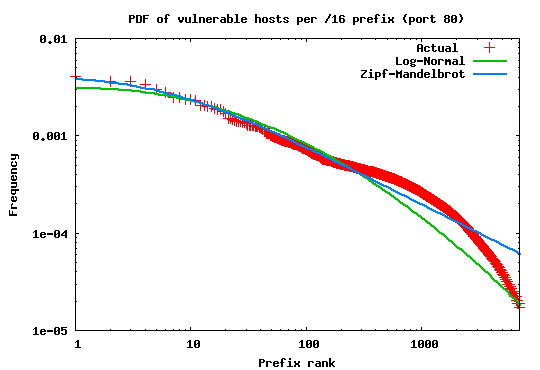
The rank plots in Figures 1 and 2 show the percentage of malicious sources in each /16 and /8 prefix over the total number of sources. It is clear that in both cases the population distribution is far from being uniform. This result can be interpreted intuitively by the fact that the utilization of the address space is not uniform--some portions of the space are unallocated, large prefixes are owned by corporations with small number of hosts, while others (belonging to edge ISPs, for example) may contain a large number of less protected client machines.
In fact, the relatively straight lines in these log-log plots indicate
that the distributions of vulnerable hosts among prefixes follow a
power law. To better explore this conjecture, we fit the curve
representing sources attempting connections to port 80 to well known
power-law probability distributions. Figure 3 shows the
result of this fitting. As the graph shows the source distribution
best fits a Log-normal with parameters (![]() ) and (
) and (![]() )
2.
)
2.
 |
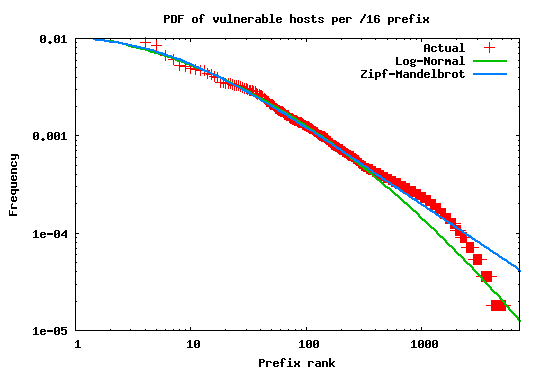
To further validate this observation we performed a similar evaluation
on a traffic log of the Witty worm [18] obtained from CAIDA
[3]. We applied the same aggregation methodology described
above on the set of unique sources of scans detected by CAIDA's /8
network telescope. These sources are, without any doubt, infected
hosts attempting to spread the worm infection to other potential
victims. Figure 4 shows that the heavy tailed tendency
in the infected population distribution is even more pronounced.
Again, the trend appears to closely fit a Log-normal distribution with
parameters (![]() ) and (
) and (![]() ).
).
 |
These results provide clear evidence that the vulnerable population distribution is far from being uniformly distributed. In the next sections we develop an extended worm model that incorporates this observation and then use this model to evaluate various aspects of distributed monitoring. Our subsequent analyzes are based on the DShield data set as it is not tied to any particular event and it is therefore more general.
First, we derive an extended model based off the AAWP model given in [4]. Our extended model allows us to account for the non-uniformity in the distribution of the vulnerable population, and later we show how this extension significantly impacts the predictions made by previous models specifically for the case of non-uniform scanning worms.
For a non-uniform scanning worm with a Nimda-like scanning behavior,
to compute the expected number of infected hosts at time tick ![]() ,
we first compute the expected number of incoming scans into each /16
prefix at time tick
,
we first compute the expected number of incoming scans into each /16
prefix at time tick ![]() and use the result to predict the number of
infected hosts in each /16 subnet at time step
and use the result to predict the number of
infected hosts in each /16 subnet at time step ![]() . Let
. Let ![]() denote the total number of incoming scans into the
denote the total number of incoming scans into the ![]() /16 prefix
at time tick
/16 prefix
at time tick ![]() . Then
. Then ![]() is the sum of the scans originating
from infected hosts within the same /16 prefix (each scanning with
rate
is the sum of the scans originating
from infected hosts within the same /16 prefix (each scanning with
rate ![]() , where
, where ![]() is the probability that the worm
scans hosts within the same /16 prefix as the infected host), scans
from infected hosts within the encompassing /8 subnet (each scanning
with a rate
is the probability that the worm
scans hosts within the same /16 prefix as the infected host), scans
from infected hosts within the encompassing /8 subnet (each scanning
with a rate ![]() , where,
, where, ![]() is the probability that the
worm scans hosts within the same /8 prefix as the infected host), and
scans originating from infected hosts from anywhere in the address
space (each scanning with rate
is the probability that the
worm scans hosts within the same /8 prefix as the infected host), and
scans originating from infected hosts from anywhere in the address
space (each scanning with rate ![]() , where,
, where, ![]() is the
probability the worm scans a host selected at random from the whole IP
space). Therefore,
is the
probability the worm scans a host selected at random from the whole IP
space). Therefore, ![]() can be expressed as follows:
can be expressed as follows:
where ![]() denotes the average scanning rate of the worm,
denotes the average scanning rate of the worm,
![]() the number of infected hosts in the
the number of infected hosts in the ![]() /16 aggregate at
time tick
/16 aggregate at
time tick ![]() ,
, ![]() the number of infected hosts in all
/16 subnets within the same /8 prefix.
Then, using a similar derivation as in Equation (2), the
expected number of infected hosts per /16 subnet at time tick
the number of infected hosts in all
/16 subnets within the same /8 prefix.
Then, using a similar derivation as in Equation (2), the
expected number of infected hosts per /16 subnet at time tick ![]() can
be expressed as:
can
be expressed as:
The expected total number of infected hosts by the worm at time tick
![]() is simply the sum of the infected hosts in all possible
is simply the sum of the infected hosts in all possible
![]() /16 prefixes:
/16 prefixes:
 |
REMARK: We note that our decision to study a worm with a Nimda-like target selection algorithm is for illustrative purposes only. The analysis presented here can be generalized to other classes of worms that apply different scanning strategies on prefix boundaries other than the /16 and /8 boundaries. However, preferentially scanning at the /16 and /8 prefix boundaries is considered a successful strategy and a widely used practice by most non-uniform scanning worms [6,8,12]; therefore a Nimda-like worm behavior serves our purpose well.
To validate the extended model we compare it to the original AAWP model, using the same set of assumptions and simulation parameters as those used in [4]. For completeness, we restate these parameters in Table 3. We compare our model for both a uniform and non-uniform scanning worm. Clearly, if our model is correct we should arrive at an identical propagation evolution as that in [4]. Figure 5 depicts the infection propagation in both scenarios. Our results are identical to those found in [4], and (we believe) lead to an incorrect conclusion--that a uniform scanning worm propagates faster than its non-uniform counterpart.
|
| |||||||||||||||||||||||||||||||||||
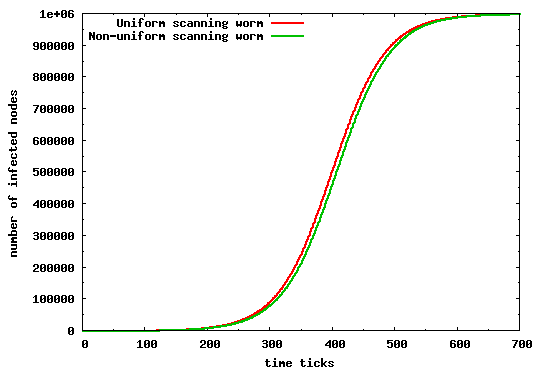
To see why this is not the case, we demonstrate the impact of the vulnerable population distribution on the results predicted by the model. We do so by using the set of sources attempting suspicious connections to port 80 extracted from the DShield data set. Again, we apply the same simulation parameters from Table 3, but with 632,472 sources (i.e., the number of sources in the DShield data) attempting connections to port 80. We use this data set to drive our simulation model under two different scenarios. In the first scenario we ignore the actual locality of hosts and assume that they are evenly distributed over the IP space, while in the latter we use the actual distribution of sources per /16 prefix extracted from the DShield data set.
The difference in propagation speed between these two cases is dramatic; the leftmost line in Figure 6 depicts the infection evolution of the worm with an underlying population distribution inferred from DShield traces, while the rightmost line shows the evolution of the infection based on the uniform population distribution assumption. The AAWP model would predict that the non-uniform scanning worm would be able to infect the whole population after 1000 time ticks from the breakout. However, under the more realistic distribution derived from the actual data set, we see that a non-uniform worm would infect the whole vulnerable population in less than 200 time ticks -- 5 times faster than the previous case. Clearly, the significant discrepancy between the two predictions underscores the fact that the underlying locality distribution of the vulnerable population is an important factor that can not be overlooked especially when modeling non-uniform scanning worms.
Finally, we revisit the claim that a uniform scanning worm propagates faster than its non-uniform counterpart. We do so by comparing the propagation behavior of a uniform scanning worm to a non-uniform scanning worm but with vulnerable population distribution derived from the DShield traces. As Figure 7 illustrates, a non-uniform scanning worm can spread significantly faster than a uniform scanning worm with the same average scanning rate and same vulnerable population size. The results are enough to warrant restatement: that a simply designed non-uniform scanning worm would reach saturation much faster than one with uniform scanning characteristics. Intuitively, worm instances within heavily populated subnets, quickly infect all vulnerable hosts within these subnets by applying a biased target selection algorithm towards these hosts; recall that a Nimda worm instance sends 75% of its scans to hosts within the same /16 prefix and same /8 prefix. This behavior exploits the power law distribution shown in Figure 1, where the majority of hosts are in a relatively low number of heavily populated prefixes. Therefore, even a single infected host within such prefixes is enough to spread the infection to a large number of vulnerable hosts in a very short time. This explains the sharp initial increase in the number of infections for the non-uniform scanning worm.
These above observations support Staniford et. al.'s earlier conjecture that a non-uniform scanning worm would spread faster than its uniform counterpart [19]. Also, as we show later, this leads to a set of important design considerations for a distributed worm monitoring system, especially as it relates to the location, number, and size of the monitors.
 |
In the following sections we use this extended model to estimate the detection time of different distributed monitor configurations.
Over the last few years, a number of research projects have proposed
the use of network monitors (also called telescopes [14] or
traffic sinks) for forensic analysis of worms, as well as for
estimating the prevalence of security events such as DDoS
attacks [13,21,23]. However, several questions regarding the
practicality of distributed monitoring and its pertinent design
considerations such as required number, size and deployment
considerations have been left unanswered. To answer such questions, we
introduce an observation model that measures the detection capability
of a distributed monitoring system. Specifically, the model computes
the probability, ![]() , that an instance of the worm is observed by
any monitor in the system. We then use this probability to derive a
detection metric that computes the expected time elapsed before the
monitoring system detects (with a certain confidence level) a worm
instance.
, that an instance of the worm is observed by
any monitor in the system. We then use this probability to derive a
detection metric that computes the expected time elapsed before the
monitoring system detects (with a certain confidence level) a worm
instance.
|
The notation we use is summarized in Table (4).
To facilitate computing ![]() , we organize monitors into a logical
hierarchy. Each layer in the hierarchy can ``see'' scans with a
certain probability according to its location in the address space
(relative to an infected host) and according to the worm preferential
scanning strategy. In the case of Nimda, the distributed
monitoring system can be logically divided into a three-tier
hierarchy. Figure 8 shows an example of this
logical hierarchy. In our example there are three monitors:
, we organize monitors into a logical
hierarchy. Each layer in the hierarchy can ``see'' scans with a
certain probability according to its location in the address space
(relative to an infected host) and according to the worm preferential
scanning strategy. In the case of Nimda, the distributed
monitoring system can be logically divided into a three-tier
hierarchy. Figure 8 shows an example of this
logical hierarchy. In our example there are three monitors:
![]() of size /9,
of size /9,
![]() of
size /22 and
of
size /22 and
![]() of size /24.
of size /24.
![]() and
and
![]() are located
in two different /16 subnets but have the same /8 prefix.
are located
in two different /16 subnets but have the same /8 prefix.
To derive the detection probability ![]() , we make the simplifying
assumption that a single scan is enough to classify a source as
malicious3. We also assume that any infected host is eventually detected
(i.e:
, we make the simplifying
assumption that a single scan is enough to classify a source as
malicious3. We also assume that any infected host is eventually detected
(i.e:
![]() ). Therefore,
). Therefore, ![]() is formally defined as
the probability that an infected host scans any monitor in the system
at least once. This probability is the
complement of the probability that the scanning host evades detection
by monitors in all logical layers. Therefore,
is formally defined as
the probability that an infected host scans any monitor in the system
at least once. This probability is the
complement of the probability that the scanning host evades detection
by monitors in all logical layers. Therefore, ![]() can be expressed
as follows:
can be expressed
as follows:
where ![]() is the index over the layers in the logical
monitor hierarchy (i.e. /8, /16, and /0).
is the index over the layers in the logical
monitor hierarchy (i.e. /8, /16, and /0). ![]() denotes the relevant monitor size in layer
denotes the relevant monitor size in layer ![]() relative to this host,
relative to this host,
![]() is the IP space scanned by the worm instance at that layer (
i.e. /8, /16 or /0), and
is the IP space scanned by the worm instance at that layer (
i.e. /8, /16 or /0), and
![]() is the probability
with which the worm scans layer
is the probability
with which the worm scans layer ![]() .
.
Then, for a non-uniform scanning worm with preferential scanning
probabilities ![]() and
and ![]() , Equation (7) can be
rewritten as:
, Equation (7) can be
rewritten as:
For a uniform scanning worm which scans the whole IP space with
uniform probability (ie:
![]() ,
,
![]() ,
,
![]() ),
), ![]() is simply expressed as:
is simply expressed as:
In the following section we use our observation model to compute the expected detection time of a distributed monitoring system.
Arguably, the most critical indicator of the effectiveness of a worm
monitoring system is its reaction time ![]() .
. ![]() is the
elapsed time from the instant an infected host sends its first scan up
to the point where at least one scan from that host is detected (with
a certain confidence) by any monitor in the distributed monitor
deployment [14]. Using Equation
(7) we define
is the
elapsed time from the instant an infected host sends its first scan up
to the point where at least one scan from that host is detected (with
a certain confidence) by any monitor in the distributed monitor
deployment [14]. Using Equation
(7) we define ![]() as the probability that the distributed
monitoring system has detected a new infected host by time
as the probability that the distributed
monitoring system has detected a new infected host by time
![]() . Equivalently,
. Equivalently, ![]() is the probability that any monitor in the
system observes at least one scan from that source by the detection
time
is the probability that any monitor in the
system observes at least one scan from that source by the detection
time ![]() . Therefore,
. Therefore, ![]() can be expressed as:
can be expressed as:
which can be simplified to:
The observant reader will note that Equation (10)
assumes that a monitor exists in all logical layers relative to an
infected host. However, in practice the deployment of distributed
monitors will not cover all such locations. For example, if we select
an infected host at random, the probability that this host scans
a monitored address using
![]() depends on having
a monitor placed within the same /16 address space as the infected
host (the same applies for the other preferential scanning
probabilities).
depends on having
a monitor placed within the same /16 address space as the infected
host (the same applies for the other preferential scanning
probabilities).
The probability that a monitor is placed near an infected host, denoted
![]() , is solely defined by the distributed
monitors' deployment strategy and the IP space coverage achieved by
that deployment. To accommodate for this probability, we can rewrite
Eq. (10) as:
, is solely defined by the distributed
monitors' deployment strategy and the IP space coverage achieved by
that deployment. To accommodate for this probability, we can rewrite
Eq. (10) as:
For the case of a non-uniform scanning worm with
preferential scanning probabilities ![]() and
and ![]() ,
, ![]() is
then given by:
is
then given by:
![\begin{eqnarray*}
P_{r} &= &1 - \Bigg[ \Big( 1- \frac{S^{\scriptscriptstyle (/16...
...ac{S}{2^{{32}}} \Big) ^{p_{\scriptscriptstyle 0}\,s t_d}
\Bigg]
\end{eqnarray*}](Pr.png)
where,
![]() is the probability
that a monitor exists in the /16 subnet of an infected
host. Similarly,
is the probability
that a monitor exists in the /16 subnet of an infected
host. Similarly,
![]() is the probability of
having a monitor within the /8 subnet of an infected host.
is the probability of
having a monitor within the /8 subnet of an infected host.
Our goal is to determine the expected time, ![]() , at which the
probability of detection is at a particular confidence level (e.g:
95%). Solving Eq.(11) for
, at which the
probability of detection is at a particular confidence level (e.g:
95%). Solving Eq.(11) for ![]() gives:
gives:
Now that we have an observation model and accompanying detection metric, we proceed to evaluate the parameters and design alternatives that directly affect the detection time of distributed monitoring systems.
Moore et al. have previously highlighted that a /8 monitor has a very different view of a Code Red infection (i.e. uniform scanning worm) compared to a /16 monitor [14]. Specifically, the /8 monitor was able to provide a timely view of the worm's actual propagation, while the view from the /16 monitor was significantly delayed.
In the distributed case however, the number (and location) of
monitors may be more important than aggregate size. In what follows,
we compute the expected detection time ![]() , of different monitor
sizes across various combinations. To do so, we explore several
deployment scenarios ranging from a total monitored address space of size
/8 (
, of different monitor
sizes across various combinations. To do so, we explore several
deployment scenarios ranging from a total monitored address space of size
/8 (![]() addresses) down to a total size of /16 (
addresses) down to a total size of /16 (![]() addresses). For simplicity, each aggregate size is broken into a
different number of
monitors of equal sizes 4.
addresses). For simplicity, each aggregate size is broken into a
different number of
monitors of equal sizes 4.
 |
First, we distribute monitors uniformly over the whole IP
space. In order to compute ![]() in Eq. (12) we first need to
compute
in Eq. (12) we first need to
compute
![]() for the different layers in the logical monitor
hierarchy. Since we distribute monitors uniformly, the probability
for the different layers in the logical monitor
hierarchy. Since we distribute monitors uniformly, the probability
![]() that a monitor exists at each layer, is simply equal to
the total number of monitors divided by all the possible locations
(prefixes) that these monitors can occupy.
that a monitor exists at each layer, is simply equal to
the total number of monitors divided by all the possible locations
(prefixes) that these monitors can occupy.
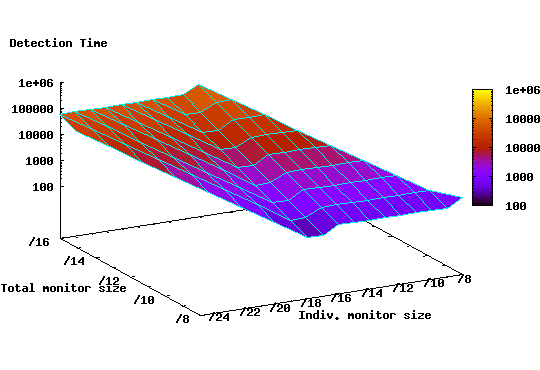
Figure 9 shows the expected detection time
![]() for different monitor configurations. It is clear from the graph
that there is a substantial improvement in detection time associated with
distributed monitoring configurations. For example, while a single /8
monitor yields a detection time of 940 time ticks, a distributed
deployment of 512 /17 monitors results in a detection time of 230
ticks. During the additional detection time of 710 seconds, a worm
instance can generate roughly 7100 more scans, thus infecting a
larger number of vulnerable hosts before being detected. Furthermore,
Figure 9 shows that configurations with a number
of monitors of a certain size perform equally well, or better, than other
configurations with larger total size. For instance, a
distributed monitor deployment of 512 /18 monitors (i.e. /9 aggregate
size) provides lower detection time (471 time ticks) than a single /8
monitor (940 time ticks).
for different monitor configurations. It is clear from the graph
that there is a substantial improvement in detection time associated with
distributed monitoring configurations. For example, while a single /8
monitor yields a detection time of 940 time ticks, a distributed
deployment of 512 /17 monitors results in a detection time of 230
ticks. During the additional detection time of 710 seconds, a worm
instance can generate roughly 7100 more scans, thus infecting a
larger number of vulnerable hosts before being detected. Furthermore,
Figure 9 shows that configurations with a number
of monitors of a certain size perform equally well, or better, than other
configurations with larger total size. For instance, a
distributed monitor deployment of 512 /18 monitors (i.e. /9 aggregate
size) provides lower detection time (471 time ticks) than a single /8
monitor (940 time ticks).
Unfortunately, deploying monitors randomly over the IP address space is still a resource consuming proposition. The minimum detection time (230 time ticks) comes at the cost of requiring an aggregate monitor size of /8, a considerable amount of unused address space. Next, we consider whether deploying monitors in a way that takes into account the vulnerable population density over the address space can substantially reduce detection time, and if so, to what degree.
In this section we investigate the effect of using the vulnerable population density to guide the placement of distributed monitors. To do so, we use the population distribution of sources attempting connections to port 80 inferred from the DShield data set (cf. Section 3). We understand that such information might not be available at a global scale. However, our focus here is to understand to what degree can detection time be improved given some level of knowledge about the vulnerable population.
First, we assume that we have full knowledge of the vulnerable
population density over the address space and so we can deploy
monitors in the most populated prefixes. In this scenario, the
probability ![]() of having a monitor at layer
of having a monitor at layer ![]() of the
hierarchy, is calculated in the following way: Let
of the
hierarchy, is calculated in the following way: Let ![]() be the
number of vulnerable hosts that have a monitor within their common
prefix at layer
be the
number of vulnerable hosts that have a monitor within their common
prefix at layer ![]() . Then,
. Then, ![]() is equal to
is equal to
![]() , where
, where ![]() is the size of the vulnerable population.
is the size of the vulnerable population.
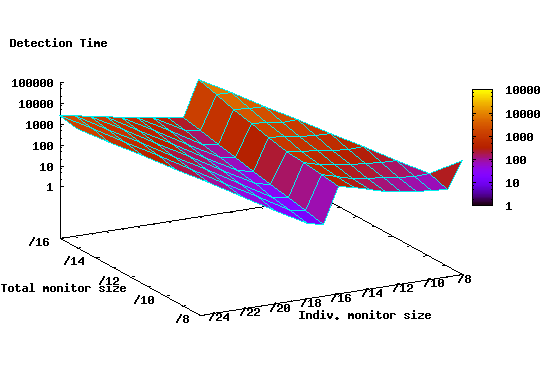 |
Given ![]() , for each size and number combination, we can compute
, for each size and number combination, we can compute
![]() directly from Equation (12).
Figure 10 shows the detection time for the
same set of configurations used in the previous section. It is evident
that the population density aware deployment strategy can
achieve significantly lower detection time. Indeed, under this
scenario, a number of points are worthy of further discussion:
directly from Equation (12).
Figure 10 shows the detection time for the
same set of configurations used in the previous section. It is evident
that the population density aware deployment strategy can
achieve significantly lower detection time. Indeed, under this
scenario, a number of points are worthy of further discussion:
While it would be impractical to deploy /17 monitors in the most densely populated /16 prefixes, we argue that there are a number of practical alternatives that can achieve better detection with less resource requirements. For example, one such strategy might be to place four /24 monitors, in each of the 512 networks owning the most populated /16 prefixes. In this case, it is possible to achieve detection time of 300 ticks compared to 7544 ticks for the same number and size combination under the random deployment strategy.
To explore the practicality of the strategy above, we calculate the number of Autonomous Systems (ASes) whose participation would be required in such a system. We use ASes since they represent the unit of administrative control in the Internet and therefore reflect the number of administrative entities (e.g. ISPs and enterprises) that will need to be involved in the distributed monitoring architecture. Clearly, the fewer the participants the easier it becomes to realize this architecture. To find the required number of ASes we map each of the 512 prefixes to its origin AS using the Routeviews [17] BGP table snapshots. Surprisingly, these prefixes fall into only 130 ASes, 50% of which are among the top 200 ASes in terms of the size of the advertised IP space.
These results imply that a well-planned deployment can achieve significantly lower detection time and at the same time have lower resource requirements in terms of monitored space. However, such a strategy can be practically viable, only if major ISPs participate in the monitoring infrastructure.
Our analysis in the previous section assumed prefect knowledge of the vulnerable population distribution -- a task that is arguably difficult to achieve especially at a global scale. For this reason, we investigate how approximate knowledge of the population density can be useful in reducing detection time. To do so, we explore a deployment strategy in which monitors are randomly deployed within the top 5,000 (out of a total of 12,000) /16 prefixes containing at least one host attempting connections to port 80. The selected 5000 prefixes are responsible for 90% of the total number of sources in our dataset. Furthermore, unlike previous cases where configurations with monitor sizes equal to, or greater than /16 were deployed in the top populated /8 prefixes, we deploy such monitors at random throughout the IP space.
The coverage provided by this strategy is reduced. For example, deploying 1024 /15 monitors achieves only 20% coverage of the /16 logical layer as opposed to 50% coverage when we assume full knowledge of the population density. This reduced coverage will potentially result in increased detection delay. The reason behind this reduction is that the vulnerable population distribution follows a power law and therefore the majority of vulnerable hosts are concentrated in a small number of prefixes.
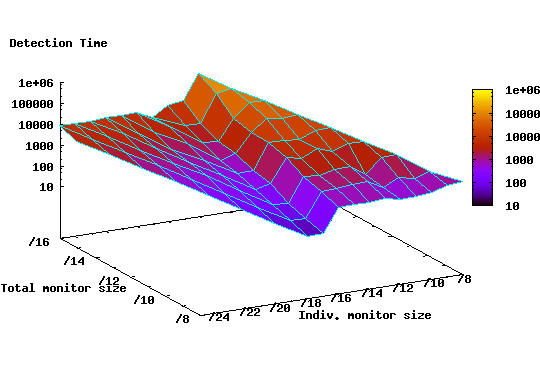 |
Figure 11 shows the detection time for different size and number configurations under this scenario. Observe that for deployments with monitor unit sizes less than /16, the detection time is still significantly lower than equivalent deployments where random placement is used (cf. Figure 9). Specifically, the minimum detection time is 33 time ticks compared to 230 time ticks for random deployments. Moreover, notice that the minimum detection time is close to the minimum detection time (9 ticks) when perfect knowledge of the population density is available. This is an encouraging result since it shows that even with partial knowledge of the vulnerable population distribution, one still can significantly enhance the detection capability of the monitoring scheme.
Monitoring unused IP space is an attractive approach for detecting security events such as active scanning worms. Recently, a number of research proposals have advocated the use of distributed network monitors to automatically detect worm outbreaks. Clearly, the effectiveness of such a monitoring system depends heavily on the monitors' ability to quickly detect new worm outbreaks. However, until now, a number of factors that have direct implications for the detection speed of distributed monitoring systems were left unanswered.
In this paper, we focus on the effect of three important factors, namely (i) the aggregate size of the monitored space, (ii) the number of monitors in the system, and (iii) the location of the monitors in the IP address space. Our results show that distributed monitors can have detection times that are 4 to 100 times faster when compared to single monitors of the same sizes. Additionally, we investigate whether information about the density of the vulnerable population can be used to improve detection speed, and our results show that even given partial knowledge the impact on detection is substantial; for some deployments the detection time is seven times as fast compared to analogous monitor configurations where monitors are deployed randomly in the IP space. While precise knowledge about the vulnerable population distribution is probably unattainable, particularly at a global scale, we contend that establishing incremental knowledge of population density by major service providers is not intractable.
As part of our future work, we plan to conduct a more in-depth evaluation of the locality and stationary of the vulnerable population, and how that impacts monitoring practices. Moreover, we plan to explore other challenges associated with distributed monitoring, particularly its resilience to monitor failures and misinformation, efficient strategies for information sharing, and appropriate communication protocols to support this task.
|
This paper was originally published in the
Proceedings of the 14th USENIX Security Symposium,
July 31–August 5, 2005, Baltimore, MD Last changed: 3 Aug. 2005 ch |
|