
Yin Wang ![]() Terence Kelly
Terence Kelly ![]() Manjunath Kudlur
Manjunath Kudlur ![]() Stéphane Lafortune
Stéphane Lafortune ![]() Scott Mahlke
Scott Mahlke ![]()
![]() EECS Department, University of Michigan
EECS Department, University of Michigan
![]() Hewlett-Packard Laboratories
Hewlett-Packard Laboratories
Deadlock is an increasingly pressing concern as the multicore revolution forces parallel programming upon the average programmer. Existing approaches to deadlock impose onerous burdens on developers, entail high runtime performance overheads, or offer no help for unmodified legacy code. Gadara automates dynamic deadlock avoidance for conventional multithreaded programs. It employs whole-program static analysis to model programs, and Discrete Control Theory to synthesize lightweight, decentralized, highly concurrent logic that controls them at runtime. Gadara is safe, and can be applied to legacy code with modest programmer effort. Gadara is efficient because it performs expensive deadlock-avoidance computations offline rather than online. We have implemented Gadara for C/Pthreads programs. In benchmark tests, Gadara successfully avoids injected deadlock faults, imposes negligible to modest performance overheads (at most 18%), and outperforms a software transactional memory system. Tests on a real application show that Gadara identifies and avoids both previously known and unknown deadlocks while adding performance overheads ranging from negligible to 10%.
Deadlock remains a perennial scourge of parallel programming, and hardware technology trends threaten to increase its prevalence: The dawning multicore era brings more cores, but not faster cores, in each new processor generation. Performance-conscious developers of all skill levels must therefore parallelize software, and deadlock afflicts even expert code. Furthermore, parallel hardware often exposes latent deadlocks in legacy multithreaded software that ran successfully on uniprocessors. For these reasons, the ``deadly embrace'' threatens to ensnare an ever wider range of programs, programmers, and users as the multicore era unfolds.
Our work addresses circular-mutex-wait deadlocks in conventional shared-memory multithreaded programs. Although alternative paradigms such as transactional memory and lock-free data structures attract increasing attention, mutexes will remain important in practice for the foreseeable future. One reason is that mutexes are sometimes preferable, e.g., in terms of performance, compatibility with I/O, or maturity of implementations. Another reason is sheer inertia: Enormous investments, unlikely to be abandoned soon, reside in existing lock-based programs and the developers who write them.
Decades of study have yielded several approaches to deadlock, but none is a panacea. Static deadlock prevention via strict global lock-acquisition ordering is straightforward in principle but can be remarkably difficult to apply in practice. Static deadlock detection via program analysis has made impressive strides in recent years [11,9], but spurious warnings can be numerous and the cost of manually repairing genuine deadlock bugs remains high. Dynamic deadlock detection may identify the problem too late, when recovery is awkward or impossible; automated rollback and re-execution can help [38], but irrevocable actions such as I/O can preclude rollback. Variants of the Banker's Algorithm [8] provide dynamic deadlock avoidance, but require more resource demand information than is often available and involve expensive runtime calculations.
Fear of deadlock distorts software development and diverts energy from more profitable pursuits, e.g., by intimidating programmers into adopting cautious coarse-grained locking when multicore performance demands deadlock-prone fine-grained locking. Deadlock in lock-based programs is difficult to reason about because locks are not composable: Deadlock-free lock-based software components may interact to deadlock a larger program [44]. Deadlock-freedom is a global program property that is difficult to reason about and difficult to coordinate across independently developed software modules. Non-composability therefore undermines the cornerstones of programmer productivity, software modularity and divide-and-conquer problem decomposition. Finally, insidious corner-case deadlocks may lurk even within single modules developed by individual expert programmers [9]; such bugs can be difficult to detect, and repairing them is a costly, manual, time-consuming, and error-prone chore. In addition to preserving the value of legacy code, a good solution to the deadlock problem will improve new code by allowing requirements rather than fear to dictate locking strategy, and by allowing programmers to focus on modular common-case logic rather than fragile global properties and obscure corner cases.
This paper presents Gadara, our approach to automatically enabling multithreaded programs to dynamically avoid circular-mutex-wait deadlocks. It proceeds in four phases: 1) compiler techniques extract a formal model from program source code; 2) Discrete Control Theory methods automatically synthesize control logic that dynamically avoids deadlocks in the model; 3) instrumentation embeds the control logic in the program where it monitors and controls relevant aspects of program execution; 4) run-time control logic compels the program to behave like the controlled model, thereby dynamically avoiding deadlocks. (Gadara is the Biblical place where a miraculous cure liberated a possessed man by banishing en masse a legion of demons.)
Gadara intelligently postpones lock acquisition attempts when necessary to ensure that deadlock cannot occur in a worst-case future. Sometimes the net effect is to alter the scheduling of threads onto locks; in other cases, a thread requesting a lock must wait to acquire it even though the lock is available. Gadara may thereby impair performance by limiting concurrency; program instrumentation is another potential performance overhead. Gadara strives to meddle as little as possible while guaranteeing deadlock avoidance, and Discrete Control Theory provides a rigorous foundation that helps Gadara avoid unnecessary instrumentation and concurrency reduction. In practice, we find that the runtime performance overhead of Gadara is typically negligible and always modest--at most 18% in all of our experiments. The computational overhead of Gadara's offline phases (modeling, control logic synthesis, and instrumentation) is similarly tolerable--no worse than the time required to build a program from source. Programmers may selectively override Gadara by disabling the avoidance of some potential deadlocks but not others, e.g., to improve performance in cases where they deem deadlocks highly improbable.
Gadara offers numerous benefits. It dynamically avoids both deterministic/repeatable and also nondeterministic deadlocks. It guarantees that all circular-mutex-wait deadlocks are eliminated from a program, and does not introduce new deadlocks or other liveness/progress bugs. It is safe and cannot cause a correct program to behave incorrectly. It performs control-synthesis computations offline, greatly reducing the overhead of online control. While it does impose performance overheads, it does not introduce a compulsory global performance bottleneck (e.g., a mandatory ``big global lock'' or analogous serialization); its control logic is decentralized, fine-grained, and highly concurrent. It works with legacy programs and also with existing programmers, requiring no retraining or conceptual reorientation. It neither forbids nor discourages unrestricted I/O. Finally, it relieves programmers of the burden of global reasoning about composability and corner-case deadlock faults.
We have implemented Gadara for C/Pthreads programs. Our experiments show that Gadara enables deadlock-prone software to avoid deadlock at runtime. Gadara furthermore imposes only modest performance overheads, which compare favorably with those of a software transactional memory system. This paper describes the Gadara methodology and our prototype implementation and presents experiments on benchmark software and on a real application, the OpenLDAP directory server. Additional technical details on the Discrete Control Theory techniques underlying Gadara and experiments on randomly generated programs are available in [47].
The remainder of this paper is organized as follows: Section 2 provides an overview of our approach and Section 3 introduces elements of Discrete Control Theory central to Gadara. Section 4 describes how we extract suitable models from program source code, Section 5 explains how Gadara synthesizes control logic from such models, and Section 6 describes Gadara's program instrumentation and run-time control. Section 7 presents our experimental results. Section 8 surveys related work, and Section 9 concludes.
Figure 1 shows the architecture of Gadara. The offline calculations depicted on the left involve three steps. First, Gadara automatically constructs a formal model from a whole-program Control Flow Graph (CFG) obtained at compile time. This step involves enhancing the standard CFG construction procedure and translating the enhanced graph into a formal model suitable for Discrete Control Theory (DCT) analysis and control logic synthesis. Second, Gadara synthesizes feedback control logic from the model by using DCT techniques. We improve the computational efficiency of standard DCT algorithms by supplementing them with special-purpose strategies that exploit the structure of the model. Third, the synthesized feedback control logic guides source code instrumentation. The key objective of this step is to minimize the online overhead of updating control-related state and implementing the control actions. Finally, online execution of the instrumented program proceeds according to the familiar observation-action paradigm of feedback control. In our problem, control logic delays lock acquisitions to ensure deadlock-free execution of the original program.
An important goal of Gadara's control synthesis phase is a property called ``maximally permissive control'' (MPC). In the present context, MPC means that the control logic will postpone a lock acquisition only if the program model indicates that deadlock might occur in the future execution of the program if the lock were granted immediately. In other words, control strives to avoid inhibiting concurrency more than necessary to guarantee deadlock avoidance. (One could of course ensure deadlock-freedom in many programs by serializing all threads, but that would defeat the purpose of parallelization.) We are able to make formal statements about MPC because Gadara employs a model-based approach and uses DCT algorithms that guarantee MPC.
Numerous challenges arise in the application of Gadara to real-world programs. We must enhance the standard CFG to obtain a formal model that more accurately captures program behavior; pointer analysis and related difficulties loom large in this area. Imperfections in the formal model can complicate the problem of achieving MPC during the control synthesis phase. Instrumentation must be tolerably lightweight to minimize runtime overhead. Subsequent sections discuss in detail how we address these challenges.
Gadara's limitations fall into two categories: those that are inherent in the problem domain, and those that are artifacts of our current prototype. A trivial example of the former is that Gadara cannot avoid inevitable deadlocks, e.g., due to repeatedly locking a nonrecursive mutex; Gadara issues warnings about such deadlocks. Another limitation inherent to the domain involves the undecidability of general static analysis [23]. It is well known that no method exists for statically determining with certainty any non-trivial dynamic/behavioral property of a program, including deadlock susceptibility. However, most real-world programs do admit useful static analysis. Gadara builds a program model for which synthesizing deadlock-avoidance control logic is decidable. The model is conservative in the sense that it causes control intervention when static analysis cannot prove that intervention is unnecessary. The net effect is that superfluous control logic sometimes harms performance through instrumentation overhead and concurrency reduction.

As with many existing program checkers, imperfect data flow analysis may cause unaided Gadara to identify large numbers of spurious potential deadlocks. We therefore introduce a novel style of programmer-supplied annotation that allows Gadara to eliminate many such ``false positives.'' A first pass of Gadara directs the programmer to problematic functions associated with large numbers of suspected potential deadlocks. The programmer may then annotate these functions to aid a second pass of Gadara, which typically identifies far fewer potential deadlocks by exploiting the annotations. In practice, it is not difficult to annotate real programs correctly and comprehensively. The number of functions that require inspection after the first pass is typically small and it is straightforward for the programmer to annotate them appropriately. Omitted annotations can reduce performance and incorrect annotations can prevent Gadara from avoiding deadlocks already present in the program, but neither compromise safety or correctness. Similarly, illegal pointer casts involving wrapper structures containing mutexes can confuse Gadara and void the guarantee of deadlock-freedom.
Gadara's model-based approach entails both benefits and challenges. Gadara requires that all locking and synchronization be included in its program model; Gadara recognizes standard Pthread functions but, e.g., homebrew synchronization primitives must be annotated. To be fully effective, Gadara must analyze and potentially instrument a whole program. Whole-program analysis can be performed incrementally (e.g., models of library code can accompany libraries to facilitate analysis of client programs), but instrumenting binary-only libraries with control logic would be more difficult. On the positive side, a strength of a model-based approach is that modeling tends to improve with time, and Gadara's modeling framework facilitates extensions. Petri nets model language features and library functions handled by our current Gadara prototype (calls through function pointers, gotos, libpthread functions) and also extensions (setjmp()/longjmp(), IPC). Some phenomena may be difficult to handle well in our framework, e.g., lock acquisition in signal handlers, but most real-world programming practices can be accommodated naturally and conveniently.
With a modicum of programmer assistance in the form of annotations, Gadara's run-time performance overhead ranges from negligible to modest. Section 7 presents experimental results that quantify these overheads. Before explaining the details of Gadara's phases, we review elements of DCT crucial to Gadara's operation.
Prior research has applied feedback control techniques to computer systems problems [14]. However, this research applied classical control to time-driven systems modeled with continuous variables evolving according to differential or difference equations. Classical control cannot model logical properties (e.g., deadlock) in event-driven systems. This is the realm of Discrete Control Theory, which considers discrete event dynamic systems with discrete state variables and event-driven dynamics. As in classical control, the paradigm of DCT is to synthesize a feedback controller for a dynamic system such that the controlled system will satisfy given specifications. However, the models and specifications that DCT addresses are completely different from those of classical control, as are the modeling formalisms and controller synthesis techniques. DCT is a mature and rigorous body of theory developed since the mid-1980s. This section briefly reviews the specific methods that Gadara employs; see Cassandras & Lafortune for a comprehensive graduate-level introduction to DCT [5].
Finite-state automata and Petri nets [32] are two common modeling formalisms used in DCT, and they are well suited for studying deadlock and other logical correctness properties of discrete event dynamic systems. Given a model of a system in the form of an automaton or a Petri net, DCT techniques can construct feedback controllers that will enforce logical specifications such as avoidance of deadlock, illegal states, and illegal event sequences. DCT is different from (but complementary to) model checking [6] and other formal analysis methods: DCT emphasizes automatically synthesizing a controller that provably achieves given specifications, as opposed to verifying that a given controller (possibly obtained in an ad hoc or heuristic manner) satisfies the specifications. DCT control is correct by construction, obviating the need for a separate verification step.
Wallace et al. [46] proposed the use of DCT in IT automation for scheduling actions in workflow management. We proposed a failure-avoidance system for workflows using DCT [48]. However, these prior efforts assume severely restricted programming paradigms. Gadara moves beyond these limitations and handles multithreaded C programs. DCT has not previously been applied in computer systems for deadlock avoidance in general-purpose software. The finite-automata models of our previous work [48] were adequate since the control flow state spaces of workflows are typically quite small. In the present context, however, automata models do not scale sufficiently for the large C programs that Gadara targets. Gadara therefore employs Petri net models.
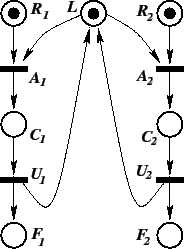
Arcs connecting places to a transition represent pre-conditions
of the event associated with the transition. For instance,
transition ![]() in our example can occur only if its input places
in our example can occur only if its input places
![]() and
and ![]() each contain at least one token; in this case, we say
that
each contain at least one token; in this case, we say
that ![]() is enabled. Similarly,
is enabled. Similarly, ![]() is enabled, but all
other transitions in the example are disabled. Here, one can think
of place
is enabled, but all
other transitions in the example are disabled. Here, one can think
of place ![]() as representing the status of a lock: if
as representing the status of a lock: if ![]() is empty,
the lock is not available; if
is empty,
the lock is not available; if ![]() contains a token, the lock is
available. Thus this Petri net models two threads, 1 and 2, that
each require the lock. Place
contains a token, the lock is
available. Thus this Petri net models two threads, 1 and 2, that
each require the lock. Place ![]() represents the request for
acquiring the lock for thread
represents the request for
acquiring the lock for thread ![]() ,
, ![]() , with transition
, with transition ![]() representing the lock acquisition event. The two lock requests are
in conflict: The lock can be granted to only one thread at a time.
If transition
representing the lock acquisition event. The two lock requests are
in conflict: The lock can be granted to only one thread at a time.
If transition ![]() fires, it consumes one token from
each input place
fires, it consumes one token from
each input place ![]() and
and ![]() and deposits one token in its output
place
and deposits one token in its output
place ![]() , which models the critical region of thread 1. In
general, the firing of a transition consumes tokens from each of its
input places and produces tokens in each of its output places; the
token count need not remain constant. After
, which models the critical region of thread 1. In
general, the firing of a transition consumes tokens from each of its
input places and produces tokens in each of its output places; the
token count need not remain constant. After ![]() fires,
fires, ![]() becomes disabled and must wait for
becomes disabled and must wait for ![]() to occur (lock release by
thread 1) before it becomes enabled again. Place
to occur (lock release by
thread 1) before it becomes enabled again. Place ![]() represents
that thread
represents
that thread ![]() has finished.
has finished.
DCT control logic synthesis techniques for Petri nets exploit the structure of Petri nets for computational efficiency, avoiding an enumeration of the state space (the set of all markings reachable from a given initial marking) [15]. This is a key advantage of Petri nets over automata, which by construction enumerate the entire state space and thus do not scale to large systems. In a Petri net, state information is distributed and ``encoded'' as the contents of the places.
Many of the techniques for analyzing the dynamic behavior of a Petri
net employ linear algebraic manipulations of matrix
representations [32]. In turn, these techniques underlie
the control synthesis methodology known as Supervision Based on Place
Invariants (SBPI); see [31,19] and references therein. Gadara uses SBPI for
control logic synthesis. In SBPI, the control synthesis problem is
posed in terms of a set of linear inequalities on the marking of the
Petri net. SBPI strategically adds control places, and tokens
in these, to the Petri net. These control places restrict the
behavior of the net and guarantee that the given linear inequalities
are satisfied at all reachable markings. Moreover, the control
actions provably satisfy the MPC property with respect to the given
control specification. In our example Petri net, one could interpret
place ![]() as a control place that ensures that the sum of tokens in
as a control place that ensures that the sum of tokens in
![]() and
and ![]() never exceeds 1. Given this Petri net without place
never exceeds 1. Given this Petri net without place
![]() and its adjacent arcs, and given the constraint that the total
number of tokens in
and its adjacent arcs, and given the constraint that the total
number of tokens in ![]() and
and ![]() cannot exceed 1, SBPI would
automatically add
cannot exceed 1, SBPI would
automatically add ![]() , its arcs, and its initial token. In SBPI, the
online control logic is therefore ``compiled'' offline in the form of
the augmented Petri net (with control places). During online
execution, the markings of the control places dictate control
actions. SBPI terminates with an error message if the system is
fundamentally uncontrollable with respect to the given
specifications. For Gadara, an example of an uncontrollable program
is one that repeatedly acquires a nonrecursive mutex.
, its arcs, and its initial token. In SBPI, the
online control logic is therefore ``compiled'' offline in the form of
the augmented Petri net (with control places). During online
execution, the markings of the control places dictate control
actions. SBPI terminates with an error message if the system is
fundamentally uncontrollable with respect to the given
specifications. For Gadara, an example of an uncontrollable program
is one that repeatedly acquires a nonrecursive mutex.
Gadara achieves deadlock avoidance by combining SBPI with siphon analysis [4]. A siphon is a set of places that never regains a token if it becomes empty. If a Petri net arrives at a marking with an empty siphon, no transition reached by the siphon's places can ever fire. We can therefore establish a straightforward correspondence between deadlocks in a program and empty siphons in its Petri net model.
Gadara employs SBPI to ensure that siphons corresponding to potential circular-mutex-wait deadlocks do not empty. The control places added by SBPI may create new siphons, so Gadara ensures that newly created siphons will never become empty by repeated application of SBPI. Gadara thus resolves deadlocks introduced by its own control logic offline, ensuring that no such deadlocks can occur at run time. We have developed strategies for siphon analysis that exploit the special structure of our Petri net models and employ recent results in DCT [27]. These strategies accelerate convergence of Gadara's iterative algorithm while preserving the MPC property.
In summary, siphon analysis and SBPI augment the program's Petri net model with control places that encode feedback control logic; this process does not enumerate the reachable markings of the net. The control logic is provably deadlock-free and maximally permissive with respect to the program model. Program instrumentation ensures that the online behavior of the program corresponds to that of the control-augmented Petri net. Gadara control logic and corresponding instrumentation are decentralized, fine-grained, and highly concurrent. Gadara introduces no global runtime performance bottleneck because there is no centralized allocator (``banker'') adjudicating lock-acquisition requests, nor is there any global lock-disposition database (``account ledger'') requiring serial modification.
We use the open source compiler OpenIMPACT [36] to construct an augmented control flow graph (CFG) for each function in the input program. Each basic block is augmented with a list of lock variables that are acquired (or released) and the functions that are called within the basic block.
Lock functions We recognize standard Pthreads functions and augment the basic blocks from which they are called. Recognized functions include the mutex, spin, and reader-writer lock/unlock functions and condition variable functions. Large scale software often uses wrapper functions for the primitive Pthread functions. It is beneficial to recognize these wrapper functions, which appear higher up in the call tree where more information is available about the lock involved (e.g., the structures that enclose it). We rely on programmer annotations to recognize wrapper functions. The programmer annotates the wrapper functions at the declaration site using preprocessor directives, along with the argument position that corresponds to the lock variable. Basic blocks that call wrapper functions are marked as acquiring/releasing locks.
Lock variables Every lock function call site in a basic block is also augmented with the lock variable it acquires/releases. Wrapper lock functions typically take wrapper structures as arguments, which ultimately embed the lock variable of the primitive type pthread_mutex_t. The argument position used in the annotation of a wrapper function automatically marks these wrapper structure types. We define a lock type as the type of the wrapper structure that encloses the primitive lock. Basic blocks are augmented with the names of the lock variables if the lock acquisition is directly through the ampersand on a lock variable (e.g., lock(&M)). If a pointer to a lock type is passed to the lock function at the acquisition site, then the basic block is annotated with the lock type.
Translation To Petri Nets Translating the CFG into a Petri net follows the methodology described in Section 3. A detailed discussion of modeling Pthread functions can be found in [21]. Here, we focus on practical issues related to modeling real-world programs.
We translate each function's CFG into a Petri net in which each transition has a single input place and a single output place. Each basic block in the function is represented by a place in the Petri net, and control transfer from one basic block to another is represented by a transition. Function calls are modeled by substituting into the call site a copy of the callee's Petri net model, i.e., our overall Petri net represents the program's global inlined CFG.
Recursion Recursive function calls are handled somewhat like loops when building the inlined CFG for control synthesis. For each function in a recursion, we inline exactly one copy of its Petri net in the model. The recursive call of the function is linked back to the Petri net representing the topmost invocation of the function in the call stack. Control synthesis need not distinguish these ``special'' loops from normal loops. For control instrumentation, when there are control actions associated with recursive functions, we need to correctly identify entry and return from the recursive call. We augment the function parameter to record the depth of the recursion.
Locks Each statically allocated lock is added to the net as a mutex place with one initial token. In addition, every unique lock type (i.e., wrapper structure type) has its own mutex place. An acquisition of a statically allocated lock is modeled as an arc from its corresponding mutex place to the transition corresponding to the lock acquisition. However, an acquisition through a lock pointer is conservatively approximated as an arc from the single place corresponding to the lock type to the corresponding transition. Note that this approximation does not miss any deadlock bugs, but could lead to conservative control. For example, a circular wait detected by Gadara may not be a real deadlock since the threads might be waiting on different lock instances of the same lock type. Section 5 revisits spurious deadlocks and shows how programmer annotations can help Gadara distinguish them.
Thread creation We model thread creation by marking the
input places of functions spawned by pthread_create() with
an infinite number of tokens. This models the scenario in which
any number of threads could be running concurrently, and
deadlock is detected for this scenario. In a real execution, if ![]() is the maximum number of threads that will ever be spawned, and
deadlock can occur only when the number of concurrent threads exceeds
is the maximum number of threads that will ever be spawned, and
deadlock can occur only when the number of concurrent threads exceeds
![]() , then Gadara will conservatively add control logic to address the
spurious deadlock; the runtime cost of this superfluous control is
typically a constant. We identify potential thread entry functions
in two ways: as statically resolvable pointers passed to
pthread_create(), and as entry points in the global
function call graph; programmer annotations can eliminate some of the
latter.
, then Gadara will conservatively add control logic to address the
spurious deadlock; the runtime cost of this superfluous control is
typically a constant. We identify potential thread entry functions
in two ways: as statically resolvable pointers passed to
pthread_create(), and as entry points in the global
function call graph; programmer annotations can eliminate some of the
latter.
Pruning the Petri net Real programs could result in a large Petri net, slowing offline control logic synthesis. However, logic unrelated to mutexes constitutes the vast majority of real programs. We therefore perform a correctness-preserving performance optimization for the offline control logic synthesis phase by removing such irrelevant areas of program logic from the Petri net model. We prune the original Petri net to a much smaller equivalent by removing functions that do not call lock-related functions directly or indirectly, and then by further reducing the representations of the functions that remain. Function removal involves straightforward analysis of the global function call graph, but function reduction is a more elaborate procedure; see [47] for the details. An important property of our pruning algorithm is that it preserves the mapping from Petri net places to basic blocks in the original program, which facilitates the online control implementation.
Gadara synthesizes maximally permissive control logic using specialized versions of standard Discrete Control Theory methods. This section explains the basics of our procedures; several correctness-preserving optimizations speed up control logic synthesis, as described in [47].
As explained in Section 3, control logic synthesis in Gadara
iteratively identifies siphons in a Petri net corresponding to
deadlocks in a real program and uses SBPI to add control places that
ensure deadlock avoidance. SBPI operates on a ![]() matrix
representation of the Petri net structure, where
matrix
representation of the Petri net structure, where ![]() and
and ![]() ,
respectively, are the number of places and transitions in our pruned
Petri net. The computational cost of a single iteration of SBPI is
,
respectively, are the number of places and transitions in our pruned
Petri net. The computational cost of a single iteration of SBPI is
![]() using naïve methods; Gadara's methods are usually
faster because they are specialized to sparse matrices, which are
common in practice. In the worst case, the cost of siphon detection
is exponential in the number of distinct lock types held by any
thread at any instant; better worst-case performance is unlikely
because MPC logic synthesis is NP-hard even in our special class of
Petri nets [39]. In practice, however, Gadara's
entire control logic synthesis phase typically terminates after a
single iteration. For a real program like OpenLDAP slapd, it is
more than an order of magnitude faster than running make
(seconds vs. minutes).
using naïve methods; Gadara's methods are usually
faster because they are specialized to sparse matrices, which are
common in practice. In the worst case, the cost of siphon detection
is exponential in the number of distinct lock types held by any
thread at any instant; better worst-case performance is unlikely
because MPC logic synthesis is NP-hard even in our special class of
Petri nets [39]. In practice, however, Gadara's
entire control logic synthesis phase typically terminates after a
single iteration. For a real program like OpenLDAP slapd, it is
more than an order of magnitude faster than running make
(seconds vs. minutes).
Deadlock faults may involve distinct lock types, or multiple instances of a single type. Gadara uses standard SBPI control synthesis procedures to identify the former and synthesize satisfactory control logic. Because Gadara's modeling phase substitutes lock types for lock instances, however, standard DCT techniques detect but cannot remedy deadlock faults involving multiple lock instances of the same lock type. This is not a shortcoming of DCT, but rather a consequence of a modeling simplification forced upon us by the difficulty of data flow analysis, as discussed in Section 4.
This approach guarantees deadlock avoidance, but may be deemed unnecessary by programmers: In practice, most real deadlock bugs involve different lock types [9,28], since it is relatively easy to ensure correct lock ordering within the same lock type. The programmer may therefore choose to disable Gadara's deadlock avoidance for deadlocks involving a single lock type (all such deadlocks, or individual ones).
The control logic that Gadara synthesizes is typically far more subtle than in the simple example discussed above. Most of the subtlety arises from three factors: complicated branching in real programs, the constraint that Gadara's run-time control logic may intervene only by postponing lock acquisitions, and the demand for MPC. We illustrate a more realistic example of deadlock-avoidance control logic using an actual OpenLDAP bug shown in Figure 2, to which we have added clarifying comments; Gadara instrumentation is shown in italics.
 |
Correct lock acquisition order is alphabetical in the notation of the
comments. Deadlock occurs if one thread reaches line 10 (holding
lock B and requesting A) while another reaches line 2 (holding A,
requesting B). Gadara's control logic addresses this fault as
follows: Let ![]() denote the first thread to reach line 1. Gadara
immediately forbids other threads from passing line 1 by postponing
this lock acquisition, even if lock A is available (e.g., if
thread
denote the first thread to reach line 1. Gadara
immediately forbids other threads from passing line 1 by postponing
this lock acquisition, even if lock A is available (e.g., if
thread ![]() is at line 6). If
is at line 6). If ![]() branches over the body of the
if on line 7, or if it executes line 13, Gadara knows that
branches over the body of the
if on line 7, or if it executes line 13, Gadara knows that
![]() cannot be involved in this deadlock bug and therefore permits
other threads to acquire the lock at line 1.
cannot be involved in this deadlock bug and therefore permits
other threads to acquire the lock at line 1.
We instrument the code as follows: we replace the boldface lock-acquisition call on line 1 of the original code with a call to wrapper function gadara_wlock_and_deplete(), which atomically depletes the token in the control place that Gadara has added to address this deadlock and calls the program's original lock function. Calls to gadara_replenish() restore the token to the control place when it is safe to do so, permitting other threads to pass the modified line 1. MPC guarantees that these replenish calls are inserted as soon as possible, while preserving deadlock-free control. The control place is implemented with a condition variable; the deplete function waits on this condition and the replenish function signals it.
This example shows that Gadara's control logic is lightweight, because it adds only a simple condition variable wait/signal to the code. It is also decentralized and therefore highly concurrent, because it affects only code that acquires or releases locks A and B; threads acquiring unrelated locks are completely unaffected by the control logic that addresses this deadlock fault, and no central allocator or ``banker'' is involved. Finally, Gadara's control logic is fine grained, because it addresses this specific fault with a dedicated control place; other potential deadlocks are addressed with control places of their own.
Annotations Like many state-of-the-art static analysis tools, Gadara's modeling and control logic synthesis phases do not analyze data flow. As noted in Section 2, false control flow paths lead directly to the detection of spurious deadlock potentials. Whereas a static analysis tool like RacerX [9] may strive to rank suspected deadlock bugs to aid the human analyst, Gadara is conservative and therefore treats all suspected deadlocks equally by synthesizing control logic to dynamically avoid them. Gadara encourages the programmer to add annotations that help rule out spurious deadlocks by showing where annotations are likely to be most helpful; annotations reduce runtime overhead by reducing instrumentation and control.
We found that function-level annotations can greatly reduce the false positive rate with modest programmer effort. Many false positives arise because Gadara believes that a lock type acquired within a function may or may not be held upon return; we call such functions ambiguous. Programmer annotations can tell Gadara that a particular lock type is always or never held upon return from a particular function, thereby disambiguating it. This is a local property of the function and is typically easy to reason about. In our experience, a person with little or no knowledge of a large real program such as OpenLDAP can correctly annotate a function in a few minutes. A first pass of Gadara uses lockset analysis [40] to identify ambiguous functions, which are not numerous even in large programs. After the programmer annotates these, Gadara's second pass exploits the annotations to reduce false positives.

The output of the control logic synthesis algorithm is an augmented version of the input Petri net, to which control places with incoming and outgoing arcs to transitions in the original Petri net have been added. An outgoing arc from a control place delays the target transition until a token is available in the control place; the token is consumed when the transition fires. An incoming arc from a transition to a control place replenishes the control place with a token when the transition fires. Outgoing arcs from control places always link to lock acquisition calls, which are the transitions that Gadara's runtime control logic controls. Incoming arcs originate at transitions corresponding to lock release calls or branches that the control logic must observe.
Gadara's runtime control consists of wrappers for lock-acquisition functions, a control logic state update function, and local variables inserted into the program during instrumentation. The wrappers handle control actions by postponing lock acquisitions; the update function observes selected runtime events and updates control state. Both the wrappers and the update function must correlate program execution state with the corresponding Petri net state. Because we inlined functions to create the Petri net, the runtime control logic requires more context than just the currently executing basic block in the function-level CFG. The extra information could be obtained by inspecting the call stack, but we instead instrument functions as necessary with additional parameters that encode the required context. In practice, the control logic usually needs only the innermost two or three functions on the stack, and we add exactly as much instrumentation as required to provide this. For real programs, only a handful of functions require such instrumentation.
As illustrated in Figure 2 and the accompanying discussion, we replace the native lock-acquisition functions with our wrappers only in cases where the corresponding transitions in the Petri net are controlled, i.e., transitions with incoming arcs from a control place. The wrapper function depletes a token from the control place and grants the lock to the thread. If the control place is empty, it waits on a condition variable that implements the control place, which effectively delays the calling thread. For transitions with an outgoing arc to a control place, we insert a control update function that replenishes the token and signals the condition variable of the control place. In certain simple cases, control places can be implemented with mutexes rather than condition variables. In all cases, control is implemented with standard Pthread functions. Gadara carefully orders the locks used in the implementation so that instrumentation itself introduces no deadlocks or other liveness/progress bugs.
The net effect of instrumentation and control is to compel the program's runtime behavior to conform to that of the controlled Petri net model. The control logic intervenes in program execution only by postponing lock acquisition calls. Runtime performance penalties are due to control state update overhead and concurrency reduction from postponing lock acquisitions. The former overhead for a given lock-acquisition function call is proportional to the number of potential deadlocks associated with the call. In practice, we found control update overhead negligible compared to the performance penalty of postponing lock acquisitions; MPC helps to mitigate the latter.
We conducted experiments to verify Gadara's dynamic deadlock avoidance capabilities, measure its performance overheads, and compare it with an alternative method of guaranteeing deadlock-free execution. Section 7.1 employs several variants of a benchmark application in experiments that exercise Gadara's ability to exorcise injected deadlock bugs, evaluate Gadara's impact on both throughput and response time, and compare Gadara with a software transactional memory (STM) implementation. Section 7.2 shows that Gadara automatically eliminates one known nondeterministic deadlock bug and two previously unreported potential deadlocks in OpenLDAP, and measures Gadara's performance overhead on OpenLDAP. The benchmark deadlock fault involves common-case code, but the OpenLDAP bug involves corner-case code. Section 7.3 briefly summarizes our experience applying Gadara to a deadlock-free program, Apache. Earlier experiments involving randomly generated ``dining philosophers'' programs are reported in [47].
We implemented in C/Pthreads a simple client-server publish-subscribe application, PUBSUB, to facilitate fault-injection experiments and comparisons with STM. At a high level, the main logic of the server resembles the ``listener pattern'' popularized by Miller [29] and Lee [26] to exemplify a simple, useful, and widespread programming pattern that is remarkably troublesome under concurrency. Our PUBSUB server supports three operations: clients may subscribe to channels, publish data to a channel, and request a snapshot of all of their current subscriptions.
The server maintains two data structures: a table of each client's subscription lists, indexed by client ID, and a table of channel state and subscriber lists, indexed by channel ID. Both are implemented as open hash tables. Subscribe operations atomically insert a client ID in a channel record and a channel ID in a client's subscription list, thus modifying both tables. Publish operations update the state of a channel and broadcast the result to all of its subscribers. Snapshots first copy the requesting client's list of subscriptions and then traverse the channel table, sending the client the current state of all channels on the list. The server employs a fixed-size pool of worker threads (12 in all of our experiments) and ensures consistent access to shared data via medium-grain locking: one mutex per hash table bucket. An additional mutex per network interface ensures atomicity of snapshot replies. A deadlock-free variant of the server acquires locks in a fixed global order; it is straightforward to inject deadlock faults by perturbing this order. We replaced locks with atomic { } blocks to obtain a variant suitable for the Intel C/C++ compiler's prototype STM extension [18,34].
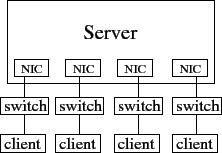
Each client machine emulates 1024 clients. Each emulated client first subscribes to 50 different randomly selected channels, then each client machine issues random publish/snapshot requests, with request type, client ID, and channel ID selected with uniform probability; each client machine issues a total of 250,000 requests. The client emulator carefully checks replies for evidence of server-end races, e.g., publication output interleaved with snapshot replies (the latter are supposed to be atomic); we saw no suspicious replies in our tests. The client emulator generates open-arrival requests, which allows us to control server load more readily [41], by using separate threads to issue requests and read replies. We test three variants of the PUBSUB server under two conditions: in heavy-load tests, clients issue requests as rapidly as possible; light-load tests add inter-request delays to throttle request rates to within server capacity.
The table below presents mean server-to-client bandwidths under heavy load and mean response times under light load measured at one of our four symmetric client machines (results on the other client machines are similar). These results are qualitatively representative of a wider range of experiments not reported in detail here.
| PUBSUB | Heavy Load | Light Load |
| variant | b/w (Mbit/s) | resp. time (ms) |
| DL-free | 94.25 | 10.83 |
| Gadarized | 76.88 | 10.52 |
| STM | 47.15 | 66.70
|
The deadlock-free variant of PUBSUB (DL-free) represents best-case performance for any deadlock-prone (but race-free) variant. Under heavy load it saturates all four dedicated Fast Ethernet connections to all four client machines, and it serves requests in roughly 11 ms under light load.
Due to the conservatism of Gadara's modeling--specifically, due to the absence of data flow analysis--Gadara cannot distinguish the original deadlock-free PUBSUB from variants containing injected deadlock faults, and Gadara treats both the same way (no annotations were added to PUBSUB, because they would not have helped). The ``Gadarized'' row in the table therefore represents performance in two scenarios: when Gadara successfully avoids real deadlock bugs, and also when it operates upon a deadlock-free PUBSUB. In the latter case Gadara can only harm performance. In our tests, the harm is moderate: an 18% reduction in throughput under heavy load, and essentially unchanged response times under light load.
The STM results in the last row of the table seem baffling. The optimistic concurrency of TM seems well-suited to the PUBSUB server's data structures and algorithms [25]. PUBSUB-STM should match the performance of the deadlock-free mutex variant under heavy load, and should achieve faster response times under light load. The Gadarized variant should (hopefully) perform acceptably, but might reasonably be expected to trail the pack.
The root cause of the TM performance problem lies in the interaction between I/O and the semantics of atomic { } blocks. At best, it is very difficult for a TM system to permit concurrency among atomic sections that perform I/O [49,42]. The Intel STM prototype permits I/O within atomic blocks, but it marks such blocks as ``irrevocable'' and serializes their execution [18]. Like many modern server and client applications [3], PUBSUB performs I/O in critical sections (to ensure that snapshot replies are atomic), and this leads to serialization in the STM variant of PUBSUB.
TM is widely touted as more convenient for the programmer, and less error-prone, than conventional mutexes. Our experience is partly consistent with this view, with several important qualifications. Defining atomic sections is indeed easier than managing locks. Our performance results show, however, that this convenience can carry a price: Mutexes are a more nuanced language for expressing I/O concurrency opportunities than atomic sections, and performance may suffer if the latter are used. If our goal is to exploit available physical resources fully, we would currently choose locks over TM; Gadara removes a major risk associated with this choice. The STM implementation that we used furthermore requires additional work from the programmer beyond defining atomic sections, e.g., function annotations; the total amount of programmer effort required to STM-ify PUBSUB was greater than that of using Gadara. Moreover, some of the extra work requires great care: incorrect STM function annotations can yield undefined behavior [18], whereas omitted or incorrect Gadara annotations have less serious consequences.
OpenLDAP is a popular open-source implementation of the Lightweight Directory Access Protocol (LDAP). The OpenLDAP server program, slapd, is a high-performance multithreaded network server. We applied Gadara to slapd in version 2.2.20, which has a confirmed deadlock bug [37]. The bug was fixed in 2.2.21 but returned in 2.3.13 when new code was added.
The slapd program has 1,795 functions, of which 456 remain after pruning. Control flow graph generation and Gadara's modeling phase took roughly as long as a full build of the slapd program; two passes of control logic synthesis each took far less time (a few seconds).
In addition to standard Pthreads lock functions, we annotated six pairs of lock and unlock functions that operate upon file or database locks or call Pthreads lock functions through pointers. OpenLDAP contains 41 lock types, i.e., distinct types of wrapper structures that contain locks. After model translation and reduction, the model contains two separate Petri nets that may potentially deadlock, one with two lock types and the other with 15 lock types. The model contains separate Petri nets because different modules of the program use different subsets of locks. We apply Gadara to each separate net independently, which reduces the computational complexity of control logic synthesis without changing the resulting control logic. Gadara's first pass completed in a few seconds and reported 25 ambiguous functions (i.e., the set of locks held on return was ambiguous). We manually inspected these functions and annotated 21; ambiguities in the remaining four functions were genuine. A programmer not deeply familiar with the source code required a little over an hour to disambiguate slapd's functions.
Disambiguation allows Gadara's second pass to construct a more accurate model with fewer false execution paths and fewer spurious deadlock potentials. The second-pass model of slapd contains four separate Petri nets that may deadlock, three with two lock types and one with four. Each separate Petri net contains one siphon. It was easy to confirm manually that the known deadlock bug corresponds to one of these siphons. Of the remaining three siphons, one was clearly a false positive; it was a trivial variant of the false paths pattern in Section 2 that spans two functions and that our current prototype does not weed out, even after disambiguation. The last two siphons correspond to genuine deadlock faults. We disabled Gadara control for the obvious false positive and allowed Gadara to address the three genuine faults. The control synthesis algorithm terminated in a few seconds, after a single iteration.
We first tested whether the Gadarized slapd successfully avoids the known deadlock bug, which resides among database cache functions that participate in insertion and eviction operations on the slapd application-level cache. The bug is nondeterministic and hard to reproduce, but we were able to reliably trigger it after inserting four sched_yield() calls immediately before a thread requests an additional lock while holding a particular lock. We configured slapd with a small cache size to trigger frequent cache evictions. After these changes, we were able to reproduce the deadlock bug reliably within one minute or less with a workload consisting of a mixture of add, delete and modify requests. An otherwise-identical Gadarized version of the same slapd, however, successfully serves the same workload indefinitely without deadlock or other difficulty.
Our next experiments compare performance between original and Gadarized slapd variants (neither containing the sched_yield() calls inserted for our deadlock-avoidance test above). Our OpenLDAP clients submit three different workloads to a slapd that contains a simulated ``employee database'' directory: search workloads perform lookups on indexed fields of randomly selected directory entries; modify workloads alter the contents of randomly selected entries by adding new field and deleting a field; and add/delete workloads create and remove randomly generated entries. We vary the number of clients between 1 and 16, and we locate the client emulators on the same server as slapd to make it easier to overload the latter.
Preliminary tests showed that Gadara overhead is negligible when slapd is configured normally, because performance is disk bound and because the deadlock faults that Gadara addressed involve code paths that execute infrequently. We therefore took extraordinary measures to ensure that slapd is not disk bound and that the faulty code of the known bug executes frequently: we used a small directory (100 entries), disabled database synchronization, and configured slapd to serve replies from in-memory data via the ``dirtyread'' directive. This configuration is highly atypical but is required to trigger any Gadara overhead at all for the OpenLDAP deadlock bug.
Figures 3, 4, and 5 present average response time and throughput measurements for our three workloads. In terms of both performance metrics, Gadara imposes overheads of 3-10% for the Modify and Add/delete workloads; overhead is negligible for the Search workload. The difference occurs because the Gadara instrumentation and control logic are triggered only in functions that add and delete items from the slapd application-level cache. Modify and Add/delete workloads cause cache insertions and deletions, and therefore incur Gadara overhead. The Search workload, however, performs only cache lookups, and therefore avoids Gadara overhead.
We applied Gadara to Apache httpd version 2.2.8. The program has 2,264 functions and 12 distinct lock types. The first pass of Gadara identifies 28 ambiguous functions. Almost all ambiguities involve error checking in lock/unlock functions (if the attempt to acquire a lock fails, return immediately) so it was easy to disambiguate these functions. After we appropriately annotate them, Gadara reports no circular-mutex-wait deadlock, and therefore Gadara inserts no control logic instrumentation. In Apache, most functions acquire at most one lock and release it before returning. This lock usage pattern is restrictive, but makes it relatively easy to write deadlock-free programs. Gadara's analysis of httpd is consistent with the Apache bug database, which reports no circular-mutex-wait deadlocks in any 2.x version of Apache. Two reported deadlocks in the bug database involve inter-process communication, not mutexes [28].
Our experience shows that Gadara handles large real programs, and it is easier to Gadarize a program than migrate it to atomic sections. Experiments with our prototype implementation show that Gadara successfully avoids deadlocks in deadlock-prone programs with little or no adverse impact on performance. As illustrated by our OpenLDAP results, Gadara works particularly well for corner-case deadlock faults in infrequently-executed code; Gadara eliminates such faults with modest programmer effort and with low performance overhead even under adverse conditions. Our benchmark tests show that the performance overhead may be tolerable even when Gadara corrects deadlock faults in common-case code paths. The history of the OpenLDAP bug furthermore shows that Gadara may be a reasonable alternative to the straightforward approach of manually fixing deadlock faults--the latter was done for the slapd deadlock we discuss, but the bug returned many versions later. The cost of running Gadara to eliminate corner-case deadlocks in each new version may compare favorably with the cost of repeated manual repair.
There are four basic approaches to dealing with deadlock in multithreaded programs that employ locks: static prevention, static detection, dynamic detection, and dynamic avoidance. Static deadlock prevention by acquiring locks in a strict global order is straightforward but rarely easy. Experience has shown that it is cumbersome at best to define and enforce a global lock acquisition order in complex, modular, multi-layered software. Lock ordering can become untenable in software developed by independent teams separated in both time and geography. Indeed, corner-case lock-order bugs arise even in individual modules written by a single expert programmer [9]. Our contribution is to perform systematic global reasoning in the control logic synthesis phase of Gadara, relieving programmers of this burden.
Static detection uses program analysis techniques to identify potential deadlocks. Examples from the research literature include the Extended Static Checker (ESC) [11] and RacerX [9]; commercial tools are also available [43]. Adoption, however, is far from universal because spurious bug reports are common for real-world programs, and it can be difficult to separate the wheat from the chaff. Repair of real defects identified by static analysis remains manual and therefore time-consuming, error-prone, and costly. By contrast, Gadara automatically repairs deadlocks.
Dynamic detection does not suffer from false positives, but by the time deadlock is detected, recovery may be awkward or impossible. Automated rollback and re-execution can eliminate the burden on the programmer and guarantee safety in a wider range of conditions [38], but irrevocable actions such as I/O may preclude rollback. Dynamic detection of potential deadlocks (inconsistent lock acquisition ordering) can complement static deadlock detection [2,1].
Dijkstra's ``Banker's Algorithm'' dynamically avoids resource deadlocks by postponing requests, thereby constraining a set of processes to a safe region from which it is possible for all processes to terminate [7,22,13] (mutex deadlocks call for different treatment because, unlike units of resources, mutexes are not fungible). Holt [16,17] improved the efficiency of the original algorithm and introduced a graphical understanding of its operation. While the classic Banker's Algorithm is sometimes used in real-time computing, its usefulness in more general computing is limited because it requires knowledge of a program's dynamic resource consumption that is difficult to specify. The Banker's Algorithm has been applied to manufacturing systems under assumptions and system models inappropriate for our domain [45,39].
Generalizations of the Banker's Algorithm address mutex deadlocks, and some can exploit (but do not provide) models of program behavior of varying sophistication [12,33,30,10,50,24]. Gadara differs in several respects. First, it both generates and exploits models of real programs with greater generality and fidelity. More importantly, Gadara's online computations are much more efficient. In contrast to the Banker's Algorithm's expensive online safety checks, Discrete Control Theory allows Gadara to perform most computation offline, greatly reducing the complexity of online control. Finally, Banker-style schemes employ a central allocator whose ``account ledger'' must be modified whenever resources/locks are allocated. In an implementation, such write updates may be inherently serial, regardless of the concurrency control mechanisms that ensure consistent updates (conventional locks, lock-free/wait-free approaches, or transactional memory). For example, in the classic single-resource Banker's Algorithm, updates to the ``remaining units'' variable are necessarily serial. As a consequence, performance suffers doubly: acquisitions are serialized, and each acquisition requires an expensive safety check. By contrast, Gadara's control logic admits true concurrency because it is decentralized; there is no central controller or global state, and lock acquisitions are not globally serialized.
Nir-Buchbinder et al. describe a two-stage ``exhibiting/healing'' scheme that prevents previously observed lock discipline violations from causing future deadlocks [35]. The ``exhibiting'' phase attempts to trigger lock discipline violations during testing by altering lock acquisition timing. ``Healing'' then addresses the potential deadlocks thus found by adding gate locks to ensure that they cannot cause deadlocks in subsequent executions. The production runtime system detects new lock discipline violations and also deadlocks caused by gates; it recovers from the latter by canceling the gate, and ensures that similar gate-induced deadlocks cannot recur. As time goes on, programs progressively become deadlock-free as both native and gate-induced deadlocks are healed. The runtime checks of the healing system require time linear in the number of locks currently held and requested; lower overhead is possible if deadlock detection is disabled. Jula & Candea describe a deadlock ``immunization'' scheme that dynamically detects specific deadlocks, records the contexts in which they occur, and dynamically attempts to avoid recurrences of the same contexts in subsequent executions [20]. This approach dynamically performs lock-acquisition safety checks on an allocation graph; the computational complexity of these checks is linear, polynomial, and exponential in various problem size parameters. Like healing, immunization can introduce deadlocks into a program.
Gadara differs from healing and immunization in several respects: Whereas these recent proposals perform centralized online safety checks involving graph traversals, Gadara's control logic is much less expensive because DCT enables it to perform most computation--including the detection and remediation of avoidance-induced deadlocks--offline. Healing and immunity tell the user what deadlocks have been addressed, but not whether any deadlocks remain. By contrast, Gadara guarantees that all deadlocks are eliminated at compile time, ensuring that they never occur in production. Whereas the computational complexity of the safety checks in healing and immunity depend on runtime conditions, in Gadara the dynamic checks associated with a lock acquisition (i.e., the control places incident to a lock acquisition transition) are known statically; programmers may therefore choose to manually repair deadlock faults that entail excessive control logic and allow Gadara to address the deadlocks that require little control logic. Whereas healing's guard locks essentially coarsen a program's locking, Gadara's maximally permissive control logic synthesis allows more runtime concurrency. The price Gadara pays for its advantages is the need for whole-program analysis, reliance on programmer annotations to improve performance, and the possibility of performance degradation due to superfluous control logic for spurious deadlock faults detected during offline analysis.
To the best of our knowledge, Gadara is the first approach to circular-mutex-wait deadlock that does all of the following: Leverages deep knowledge of applications; safely eliminates all circular-mutex-wait deadlocks; places no major new burdens on programmers; remains compatible with the installed base of compilers, libraries, and runtime systems; imposes modest performance overheads on real programs serving realistic workloads; and liberates programmers from fear of deadlock, empowering them to implement more ambitious locking strategies. In Gadara, compiler technology supplies deep whole-program analysis that yields a global model of all possible program behaviors, including corner-cases likely to evade testing. Discrete Control Theory combines the strengths of offline analysis and control synthesis with online observation and control to dynamically avoid deadlocks in concurrent programs. Thanks to DCT, Gadara's control logic is lightweight, decentralized, fine-grained, and highly concurrent. Gadara exploits the natural synergy between the strengths of DCT and compiler technology to solve one of the most formidable problems of concurrent programming. Gadara is set apart from alternative approaches in that it provides a whole-program model for analyzing and managing concurrency.
The research of Wang, Lafortune, and Mahlke is supported in part by NSF grants ECCS-0624821, CCF-0819882, and CNS-0615261, and by an HP Labs Open Innovation award. We thank Marcos Aguilera, Eric Anderson, Hans Boehm, Dhruva Chakrabarti, Peter Chen, Pramod Joisha, Xue Liu, Mark Miller, Brian Noble, and Michael Scott for encouragement, feedback, and valuable suggestions. Ali-Reza Adl-Tabatabai answered questions about the Intel STM prototype. We are grateful to Kumar Goswami and Norm Jouppi for funding, to Laura Falk and Krishnan Narayan for IT support, to Kelly Cormier and Cindy Watts for administrative and logistical assistance, and to Shan Lv and Soyeon Park for sharing details concerning [28]. Finally we thank our shepherd, Remzi Arpaci-Dusseau, and the anonymous OSDI reviewers for many helpful suggestions.
This document was generated using the LaTeX2HTML translator Version 2008 (1.71)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 -show_section_numbers -local_icons -no_navigation gadara_osdi.tex
The translation was initiated by Manjunath V Kudlur on 2008-10-08