
OSDI '06 Paper
Pp. 103–116 of the Proceedings


CRAMM: Virtual Memory Support for Garbage-Collected Applications
| Ting Yang |
Emery D. Berger |
Scott F. Kaplan |
J. Eliot B. Moss |
| tingy@cs.umass.edu |
emery@cs.umass.edu |
sfkaplan@cs.amherst.edu |
moss@cs.umass.edu |
| Dept. of Computer Science |
 Dept. of Mathematics and Computer Science Dept. of Mathematics and Computer Science |
| University of Massachusetts Amherst |
Amherst College |
| Amherst, MA 01003-9264 |
Amherst, MA 01002-5000 |
Abstract:
Existing virtual memory systems usually work well with applications
written in C and C++, but they do not provide adequate support for
garbage-collected applications. The performance of garbage-collected
applications is sensitive to heap size. Larger heaps reduce the
frequency of garbage collections, making them run several times
faster. However, if the heap is too large to fit in the available RAM,
garbage collection can trigger thrashing. Existing Java virtual
machines attempt to adapt their application heap sizes to fit in RAM,
but suffer performance degradations of up to 94% when subjected to
bursts of memory pressure.
We present CRAMM (Cooperative Robust Automatic Memory Management), a
system that solves these problems. CRAMM consists of two parts: (1) a
new virtual memory system that collects detailed reference information
for (2) an analytical model tailored to the underlying garbage
collection algorithm. The CRAMM virtual memory system tracks recent
reference behavior with low overhead. The CRAMM heap sizing model uses
this information to compute a heap size that maximizes throughput
while minimizing paging. We present extensive empirical results
demonstrating CRAMM's ability to maintain high performance in the face
of changing application and system load.
1 Introduction
The virtual memory (VM1) systems in today's
operating systems provide relatively good support for applications
written in the widely-used programming languages of the 80's and 90's,
such as C and C++. To avoid the high overhead of heavy page swapping,
it is sufficient for these applications to fit their working sets in
physical memory [16]. VM systems typically
manage physical memory memory with an approximation of a global LRU
policy [12,13,15,16,22], which works reasonably
well for legacy applications.
However, garbage-collected languages are now increasingly
prevalent, ranging from general-purpose languages like
Java and C# to scripting languages like Python and Ruby. Garbage
collection's popularity derives from its many software engineering
advantages over manual memory management, including the elimination of
dangling pointer errors and a drastic reduction of memory leaks.
The performance of garbage-collected applications is highly sensitive
to heap size. A smaller heap reduces the amount of memory referenced,
but requires frequent garbage collections that hurt performance. A
larger heap reduces the frequency of collections, thus improving
performance by up to 10x. However, if the heap cannot fit in
available RAM, performance drops off suddenly and sharply. This is
because garbage collection has a large working set (it touches the
entire heap) and thus can trigger catastrophic page swapping that
degrades performance and increases collection pauses by orders of
magnitude [18]. Hence, heap size and main memory
allocation need to be coordinated to achieve good performance.
Unfortunately, current VM systems do not provide sufficient support
for this coordination, and thus do not support garbage-collected
applications well.
Choosing the appropriate heap size for a garbage-collected
application--one that is large enough to maximize throughput but
small enough to avoid paging--is a key performance challenge. The
ideal heap size is one that makes the working set of garbage
collection just fit within the process's main memory
allocation. However, an a priori best choice is impossible in
multiprogrammed environments, since the amount of main memory allocated
to each process constantly changes. Existing garbage-collected
languages either ignore this problem, allowing only static heap sizes,
or adapt the heap size dynamically using mechanisms that are only
moderately effective. For example, Figure 1 shows the
effect of dynamic memory pressure on an industrial-strength Java
virtual machine, BEA's JRockit [7], running a variant of
the SPECjbb2000 benchmark. The solid line depicts program execution
when given a fixed amount of RAM, while the dashed line shows
execution under extra periodic bursts of memory pressure. This memory
pressure dilates overall execution time by a factor of 220%, and
degrades performance by up to 94%.
Figure 1:
Impact of bursts of memory pressure on the performance on the
JRockit Java virtual machine, which degrades throughput by as much as
94%.
|
The problem with these adaptive approaches is not that their
adaptivity mechanism is broken, but rather that they are
reactive. The only way these systems can detect whether the
heap size is too large is to grow the heap until paging occurs, which
leads to unacceptable performance degradation.
Contributions: This paper makes the following contributions. It
presents CRAMM (Cooperative Robust Automatic Memory Management), a
system that enables garbage-collected applications to predict
an appropriate heap size, allowing the system to maintain high
performance while adjusting dynamically to changing memory pressure.
CRAMM consists of two parts; Figure 2 presents an
overview. The first part is the CRAMM VM system that dynamically
gathers the working set size (WSS) of each process, where we
define the WSS as the main memory allocation that yields a
trivial amount of page swapping. To accomplish this, CRAMM VM
maintains separate page lists for each process and computes an
LRU reference histogram [25,27] that captures
detailed reference information while incurring little overhead (around
1%).
The second part of CRAMM is its heap sizing model, which
controls application heap size and is independent of any particular
garbage collection algorithm. The CRAMM model correlates the WSS
measured by the CRAMM VM to the current heap size. It then uses this
correlation to select a new heap size that is as large as possible
(thus maximizing throughput) while yielding little or no page faulting
behavior. We apply the CRAMM model to five different garbage
collection algorithms, demonstrating its generality.
Figure 2:
The CRAMM system. The CRAMM VM system efficiently gathers
detailed per-process reference information, allowing the CRAMM heap
size model to choose an optimal heap size dynamically.
|
We have implemented the CRAMM VM system in the Linux kernel and the
CRAMM heap sizing model in the Jikes RVM research Java virtual
machine [3]. We present the results of an extensive
empirical evaluation of CRAMM, including experimental measurements
across 20 benchmarks and 5 garbage collectors, as well as comparison
with two industrial Java implementations. These results demonstrate
CRAMM's effectiveness in maintaining high performance in the face of
changes in application behavior and system load.
This work builds on our previous study that introduced an early
version of the CRAMM heap sizing model [28]. That
study presented a model that was evaluated only in the context of
trace-driven simulations. This paper builds on the previous study
significantly. It refines the heap sizing model to take into account
copying and non-copying regions (required to handle generational
collectors), provides more accurate startup adjustment, and more
effectively adapts to dynamic memory allocation by polling the
underlying VM between collections. Furthermore, it is implemented in
a fully functional kernel and JVM, introduces implementation
strategies that make its overhead practical, has more efficient
overhead control mechanisms, and presents extensive empirical results.
In addition to serving the needs of garbage-collected applications,
the CRAMM VM system is the first system to our knowledge to provide
per-process and per-file page management while efficiently gathering
detailed reference histograms. This information can be used to
implement a wide range of recently proposed memory management systems
including compressed caching [27], adaptive LRU policies
like EELRU [25], and informed
prefetchers [20,24].
The remainder of this paper is organized as follows.
Section 2 presents an overview of garbage collection
algorithms and terminology used in this paper.
Section 3 derives the CRAMM heap sizing model, which
relates application working set size to heap size.
Section 4 describes the CRAMM VM system, which gathers
detailed statistics allowing it to compute the precise current process
working set size. Section 5 presents empirical
results, comparing static and previous adaptive approaches to CRAMM.
Section 6 presents work most closely related to ours,
and Section 7 concludes.
2 GC Behavior and Terminology
A garbage collector (GC) periodically and
automatically finds and reclaims heap-allocated objects that a program
can no longer possibly use. We now sketch how, and when, a GC may do this
work, and along the way introduce GC terminology and concepts
critical to understanding CRAMM.
Garbage collectors operate on the principle that if an object is
unreachable via any chain of pointers starting from
roots--pointers found in global/static variables and on thread
stacks--then the program cannot possibly use the object in the future, and
the collector can reclaim and reuse the object's space.
Through a slight abuse of terminology, reachable objects are often called
live and unreachable ones dead.
Reference counting collectors determine (conservatively) that an object is
unreachable when there are no longer any pointers to it. Here, we focus
primarily on tracing collectors, which actually trace through pointer
chains from roots, visiting reachable objects.
The frequency of collection is indirectly determined by the heap
size: the maximum virtual memory space that may be consumed by
heap-allocated objects. When allocations have consumed more than some
portion of the heap size (determined by the collection algorithm), collection
is invoked. Thus, the smaller
the heap size, the more frequently GC occurs, and the more CPU time is
spent on collection.
GC algorithms divide the heap into one or more regions.
A non-generational GC collects all regions during every collection,
triggering collection when some percentage of the entire heap space is filled
with allocated objects. A non-generational GC may have only one region.
In contrast,
generational GCs partition the regions into groups, where each group of
regions, called a generation, contains objects of a similar age. Most
commonly, each group consists of a single region. When some percentage of the
space set aside for a generation has been filled, that generation, and all
younger ones, are collected. Additionally, live
objects that survive the collection are generally promoted to the next
older generation. New objects are typically allocated into a
nursery region. This region is usually small, and thus is
collected frequently, but quickly (because it is small). The generational
configurations that we consider here have
two generations, a nursery and a mature
space. Because nursery collection generally filters out a large volume of
objects that die young, mature space grows more slowly--but when it fills,
that triggers a full heap collection.
Orthogonal to whether a collector is generational is how it reclaims
space. Mark-sweep (MS) collection marks the reachable objects,
and then sweeps across the allocation region to reclaim the unmarked
ones. MS collection is non-copying in that it does not move
allocated objects. In contrast, copying collectors proceed by
copying reachable objects to an empty copy space, updating pointers to
refer to the new copies. When done, it reclaims the previous
copy space. We do not consider here collectors that compact in place
rather than copying to a new region, but our techniques would work
just as well for them. Notice that collectors that have a number of
regions may handle each region differently. For example, a given GC
may collect one region by copying, another by MS, and others it may never
collect (so-called immortal spaces).
Finally, allocation and collection are intertwined. When allocating
into an MS-managed region, the allocator may use free lists to find available
chunks of space. When allocating into a copying region, it typically
increments a free space pointer through the initially empty space. For
generational collection, the nursery is usually a copy-collected space,
thus allowing fast allocation. The
mature space, however, may be a copying- or a non-copying-collected
region, depending on the particular collector.
3 CRAMM Heap Sizing Model
The goal of the CRAMM heap sizing model is to relate heap size and
working set size, so that, given a current real memory allocation, we
can determine a heap size whose working set size just fits in the allocation.
The working set size (WSS) for a GCed
application is determined almost entirely by what happens during full
collections, because full collections touch every reachable heap
object.
Since live and
dead objects are generally mixed together, the working set includes all heap
pages used for allocated objects. It also includes the space needed for copied
survivors of copying regions. Thus, each non-copying region contributes its
size to the working set, while each copying region adds its size plus the
volume of copied survivors, which can be as much as the size of the copying
region in the worst case.
Figure 3:
The effect of heap size on performance and working set size (the
number of pages needed to run with at most a 5% slowdown from paging).
|
Several properties of GCed applications are important here. First,
given adequate real memory, performance varies with heap size. For
example, Figure 3 depicts the effect of different
amounts of memory (the size of the garbage-collected heap) on
performance. This graph is for a particular benchmark and garbage
collector (the SPECjvm98 benchmark javac with a mark-sweep
garbage collector), but it is typical. On the left-hand side, where the
heap is barely large enough to fit the application, execution time is
high. As the heap size increases, execution time sharply drops,
finally running almost 250% faster. This speedup occurs because a larger heap
reduces the number of collections, thus reducing GC overhead.
The execution time graph has a 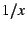 shape,
with vertical and horizontal asymptotes. shape,
with vertical and horizontal asymptotes.
However, the working set size--here given as the amount of
memory required to run with at most 5% elapsed time added for paging--has a
linear shape. The heap size determines the working set
size, as previously described. Our earlier work explores this in more
detail [28]. The key observation is that working set
size is very nearly linear in terms of heap size.
3.1 GC Working Set Size and Heap Sizing Model
We define heap size, 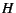 , as the maximum amount of space allowed to
contain heap objects (and allocation structures such as free lists) at one
time.
If non-copy-collected regions use , as the maximum amount of space allowed to
contain heap objects (and allocation structures such as free lists) at one
time.
If non-copy-collected regions use 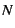 pages and
copy-collected regions allocate objects into pages and
copy-collected regions allocate objects into 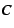 pages, then pages, then
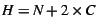 . We must reserve up to . We must reserve up to 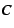 pages into which to copy survivors from the
original pages into which to copy survivors from the
original 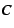 space, and the collector needs both copies until it is done.
The total WSS for the heap during full collection is determined by the pages
used for copied survivors, CS: space, and the collector needs both copies until it is done.
The total WSS for the heap during full collection is determined by the pages
used for copied survivors, CS:
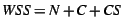 . Thus, heap WSS varies from . Thus, heap WSS varies from 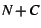 to to 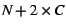 . .
As a program runs,
its usage of non-copying and copying space may vary, but it is reasonable to assume that
the balance usually does not change rapidly from one full collection to the next. We
call the ratio of allocable space (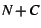 ) to heap size ( ) to heap size (
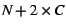 ) the
heap utilization, ) the
heap utilization, 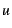 . It varies from 50% for . It varies from 50% for 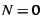 to 100% for to 100% for
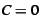 . Given an estimate of . Given an estimate of 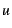 , we can determine , we can determine 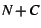 from from 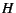 , but to
determine WSS, we also need to estimate CS. Fortunately, CS
is a property of the application (volume of live objects in copy-collected regions), not
of the heap size. As with , but to
determine WSS, we also need to estimate CS. Fortunately, CS
is a property of the application (volume of live objects in copy-collected regions), not
of the heap size. As with 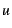 , we can reasonably assume that CS does
not change too rapidly from one full collection to the next. , we can reasonably assume that CS does
not change too rapidly from one full collection to the next.
When adjusting the heap size, we use this equation as our model:
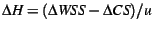 .
Notice that .
Notice that
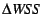 is just our target WSS (i.e., the
real memory allocation the OS is willing to provide) minus our current
WSS. The CRAMM VM provides both of these values to the heap size
manager. is just our target WSS (i.e., the
real memory allocation the OS is willing to provide) minus our current
WSS. The CRAMM VM provides both of these values to the heap size
manager.
Starting out: Once the JVM reaches the point where it needs
to calculate an initial heap size, it has touched an initial
working set of code and data. Thus, the space available for the heap is
exactly the volume of free pages the VM system is willing to grant us (call that
Free). We wish to set our heap size so that our worst case heap
WSS during the first full collection will not exceed Free. But
the worst heap WSS is exactly the heap size, so we set 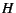 to the minimum of
Free and the user-requested initial heap size. to the minimum of
Free and the user-requested initial heap size.
Tracking the parameters: To determine the heap utilization 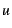 , we
simply calculate it at the end of each collection, and assume that the near
future will be similar.
Estimating , we
simply calculate it at the end of each collection, and assume that the near
future will be similar.
Estimating
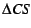 is more involved. We track the maximum
value for CS that we have seen so far, maxCS, and we also
track the maximum increment we have seen to CS,
maxCSInc. If, after a full collection, CS exceeds maxCS,
we assume CS is increasing and estimate is more involved. We track the maximum
value for CS that we have seen so far, maxCS, and we also
track the maximum increment we have seen to CS,
maxCSInc. If, after a full collection, CS exceeds maxCS,
we assume CS is increasing and estimate
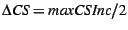 , i.e., that it will grow by 1/2 of the largest
increment. Otherwise we estimate , i.e., that it will grow by 1/2 of the largest
increment. Otherwise we estimate
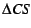 as as
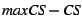 , i.e., that CS for the next
full collection will
equal maxCS. After calculating , i.e., that CS for the next
full collection will
equal maxCS. After calculating
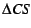 , we decay
maxCS, multiplying it by 0.98 (a conservative policy to maintain stable maxCS), and maxCSInc,
multiplying it by 0.5 (a more rapidly adjusting policy so that maxCSInc decays away quickly once
maxCS reaches its stable state). , we decay
maxCS, multiplying it by 0.98 (a conservative policy to maintain stable maxCS), and maxCSInc,
multiplying it by 0.5 (a more rapidly adjusting policy so that maxCSInc decays away quickly once
maxCS reaches its stable state).
Handling nursery collections: Because nursery collections do not
process the whole heap, their CS value underestimates survival from
future full collections. So, if the nursery size is less than 50% of
allocable space, we do not update 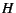 . For larger nurseries, we estimate . For larger nurseries, we estimate
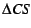 by multiplying the size of uncollected copying space
times by multiplying the size of uncollected copying space
times  , where , where 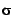 is the survival rate of the nursery
collection, i.e., is the survival rate of the nursery
collection, i.e.,
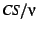 , where , where 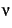 is the size of the nursery. is the size of the nursery.
This model is a straightforward generalization of our previous one
[28], taking into account copying and non-copying regions and
modeling startup effects, and eliminates the overhead (8% - 23%) caused
by inaccurate startup adjustment in our previous model. Tracking of maxCS and
maxCSInc also helps avoid paging. We periodically request the
current Free value on allocation slow path, when the allocator tries to request
a new chunk of memory from the VM (128KB for MS and 1MB for others). Once Free
is less than maxCS, we trigger an immediate collection and resize the
heap. This new polling mechanism allows us to adapt to bursts of memory pressure more quickly and effectively than our previous model.
4 VM System Design and Implementation
We now present the CRAMM VM system. We first describe why standard VM
systems are insufficient for predictively adaptive heap sizing. We
then describe the structure of the CRAMM VM system, followed by detailed
discussions of how it calculates working set sizes and how it
controls histogram collection overhead.
Given the heap sizing model presented in Section 3.1, the
underlying VM system must provide to a GC-based process both its working
set size (WSS) and its main memory allocation,2thus allowing the GC to choose a proper heap size. Unfortunately, we
cannot easily obtain this information from standard VM systems,
including the Linux VM.
Linux uses a global page replacement policy that manages each physical
page within a single data structure for all processes and files.
Linux thus has only ordinal information about all pages, giving
each page a ranking among the total pool of pages. It has no
cardinal information about the reference rates, nor any
separation of pages according to process or file. Consequently, it
cannot track the LRU reference histogram--the distribution of
memory references to pages managed by an LRU queue--which is needed
to determine the WSS for each process. Furthermore, it cannot predict
how much it could reduce the allocations of files and other processes
without inducing heavy page faulting. It therefore cannot wisely
choose a main memory allocation to offer to a GC-based process.
Finally, even if it chose to reduce the allocations for some files or
other processes, global page replacement cannot guarantee that it will
replace the pages of those processes first.
The CRAMM VM system addresses these limitations.
Figure 2 gives an overview of the CRAMM VM structure
and interface. For each file and process, it keeps separate page
lists and an LRU reference histogram. It also tracks the mean cost of
a major page fault (one that requires disk I/O) so that, along with
the histogram and a desired maximum fault rate, it can compute the WSS
of a process.
Its ability to compute the WSS of each file and process allows the
CRAMM VM to calculate new allocations to each without causing
thrashing by assigning too small an allocation. When an allocation is
reduced, the separate page lists allow the VM to prefer reclaiming
pages from those files and processes that are consuming more than
their allocation.
A garbage collector communicates with the CRAMM VM through system
calls. First, the collector registers itself as a cooperative process
with the CRAMM VM at initialization time. The VM responds with the
current amount of free memory, allowing the collector to pick a
reasonable initial heap size. Second, after each heap collection, the
collector requests a WSS estimate and a main memory allocation from
the VM. The collector then uses this information to select a new heap
size. If it changes its heap size, it calls on the VM to clear its
old histogram, since the new heap size will exhibit a
different reference pattern.
Last, the collector periodically polls the VM for an estimate of the
free memory--the main memory space that could be allocated to
the process without causing others to thrash. If this value is
unexpectedly low, then memory pressure has suddenly increased. Either
some other system activity is aggressively consuming memory
(e.g. the startup of a new process), or this process has more
live data (increased heap utilization), and thus is using more memory
than expected. The collector responds by pre-emptively collecting the
heap and selecting a new heap size.
4.1 CRAMM VM Structure
The CRAMM VM allocates a data structure, called mem_info,
for each address space (an inode for files or an mm_struct for processes). This structure comprises a list of pages,
an LRU reference histogram, and some additional control fields.
Figure 4:
Segmented queue page lists for one address space (file or
process).
|
Figure 4 shows the page list structure of a
process. The CRAMM VM manages each address space (the space of
a file or a process) much like the Linux VM manages its global queue.
For the in-memory pages of each address space, it maintains a
segmented queue (SEGQ) structure [5], where
the active list contains the more recently used pages and the
inactive list contains those less recently used. When a new
page is faulted into memory, the VM places it at the head of the
active list. If the addition of this page causes the active list to
be too large, it moves pages from the tail of the active list to the
head of the inactive list. When the process exceeds its main memory
allocation, the VM removes a page from the tail of the inactive list
and evicts it to disk. This page is then inserted at the head of a
third segment, the evicted list. When an address space's WSS
exceeds its main memory allocation, the evicted list's histogram data allows
the VM to project
how large the allocation must be to capture the working set.
The active list is managed using a CLOCK algorithm. The inactive list
is ordered by each page's time of removal from the active list. The
relative sizes of these two lists is controlled by an adaptive
mechanism described in Section 4.3. Like a
traditional SEGQ, all inactive pages have their access
permissions removed, forcing any reference to an inactive page to
cause a minor page fault. When such a page fault occurs, the VM
restores the page's permissions and promotes it into the active list,
and then updates the address space's histogram. The insertion of a
new page into the active list may force other pages out of the active
list. The VM manages the evicted list similarly; the only difference
is that a reference to an evicted page triggers disk activity.
Replacement algorithm: The CRAMM VM places each
mem_info structure into one of two lists: the unused
list for the address spaces of files for which there are no open file
descriptors, and the normal list for all other address spaces.
When the VM must replace a page, it preferentially selects a
mem_info from the unused list and then reclaims a page from
the tail of that inactive list. If the unused list is empty, the VM
selects a mem_info in a round robin manner from the normal
list, and then selects a page from the tail of its inactive list.
As Section 5.2 shows, this eviction algorithm is less
effective than the standard Linux VM replacement algorithm. However,
the CRAMM VM structure can support standard replacement policies and
algorithms while also presenting the possibility of new policies that
control per-address-space main memory allocation explicitly.
Available Memory: A garbage collector will periodically
request that the CRAMM VM report the available memory--the
total main memory space that could be allocated to the process.
Specifically, the CRAMM VM reports the available memory
(available) as the sum of the process's resident set size
(rss), the free main memory (free), and the total number
of pages found in the unused list (unused). There is also
space reserved by the VM (reserved) to maintain a minimal pool
of free pages that must be subtracted from this sum:
This value is useful to the collector because the CRAMM VM's
per-address-space structure allows it to allocate this much space to a
process without causing any page swapping. Standard VM systems that
use global memory management (e.g., Linux) cannot identify the unused
file space or preclude the possibility of page swapping as memory is
re-allocated to a process.
4.2 Working Set Size Calculation
The CRAMM VM tracks the current working set size of each process.
Recall that the WSS is the smallest main memory allocation for
which page faulting degrades process throughput by less than 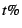 .
If .
If  , space may be wasted by caching pages that receive very
little use. When , space may be wasted by caching pages that receive very
little use. When 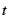 is small but non-zero, the WSS may be
substantially smaller than for is small but non-zero, the WSS may be
substantially smaller than for  , yet still yield only trivial
page swapping. In our experiments, we chose , yet still yield only trivial
page swapping. In our experiments, we chose 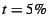 . .
In order to calculate the WSS, the VM maintains an LRU reference
histogram 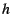 [25,27] for each process. For each
reference to a page at position [25,27] for each process. For each
reference to a page at position 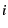 of the process's page lists, the
VM increments of the process's page lists, the
VM increments ![$h[i]$](img34.png) .3 This histogram
allows the VM to calculate the number of page faults that would occur
for each possible memory allocation. The VM also monitors the mean
cost of a major fault (majfc) and the time .3 This histogram
allows the VM to calculate the number of page faults that would occur
for each possible memory allocation. The VM also monitors the mean
cost of a major fault (majfc) and the time 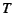 that each
process has spent on the CPU. To calculate the WSS, it scans the
histogram backward to find the allocation at which the number of page
faults is just below that each
process has spent on the CPU. To calculate the WSS, it scans the
histogram backward to find the allocation at which the number of page
faults is just below
 . .
Page list position: When a page fault occurs, the referenced
page is found within the page lists using a hash map. In order to
maintain the histograms, the CRAMM VM must determine the position of
that page within the page lists. Because a linear traversal of the
lists would be inefficient, the VM attaches an AVL tree to each page list.
Figure 4 shows the structure that the VM uses
to calculate page list positions in logarithmic time. Specifically,
every leaf node in the AVL tree points to a linked list of up to 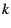 pages,
where pages,
where 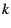 depends on the list into which the node points. Every
non-leaf node is annotated with the total number of pages in its
subtree; additionally, each non-leaf node is assigned a capacity that
is the depends on the list into which the node points. Every
non-leaf node is annotated with the total number of pages in its
subtree; additionally, each non-leaf node is assigned a capacity that
is the 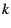 -values of its children. The VM puts newly added pages into
a buffer, and inserts this buffer into the AVL tree as a leaf node
when that buffer points to -values of its children. The VM puts newly added pages into
a buffer, and inserts this buffer into the AVL tree as a leaf node
when that buffer points to 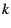 pages. Whenever a non-leaf node drops
to half full, the VM merges its children and adjusts the tree shape
accordingly. pages. Whenever a non-leaf node drops
to half full, the VM merges its children and adjusts the tree shape
accordingly.
When a page is referenced, the VM first searches linearly to find the
page's position in the containing leaf node. It then walks up the AVL
tree, summing the pages in leaf nodes that point to earlier portions
of the page list. Thus, given that 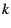 is constant and small,
determining a page's list position is performed in time proportional to the
height of the AVL tree. is constant and small,
determining a page's list position is performed in time proportional to the
height of the AVL tree.
Because the CRAMM VM does not track references to pages in the active
list, one leaf node contains pointers to all pages in the active list,
and for this leaf node,  . For leaf nodes that point to
inactive and evicted pages, . For leaf nodes that point to
inactive and evicted pages, 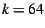 -- a value chosen to balance the
work of linear search and tree traversal. The AVL trees have low
space overhead. Suppose an application has -- a value chosen to balance the
work of linear search and tree traversal. The AVL trees have low
space overhead. Suppose an application has 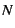 4KB pages, and our AVL
node structure is 24 bytes long. Here, the worst case space overhead
(all nodes half full, total number of nodes double the number of leaf
node) is: 4KB pages, and our AVL
node structure is 24 bytes long. Here, the worst case space overhead
(all nodes half full, total number of nodes double the number of leaf
node) is:
On average, we observe that the active list contains a large portion
(more than half) of the pages used by a process, and thus the overhead
is even lower.
LRU histogram: Keeping one histogram entry for every
page list position would incur a large space overhead. Instead, the
CRAMM VM groups positions into bins. In our implementation,
every bin corresponds to 64 pages (256 KB given the page size of 4
KB). This granularity is fine enough to provide a sufficiently
accurate WSS measurement while reducing the space overhead
substantially.
Furthermore, CRAMM dynamically allocates space for the histogram in
chunks of 512 bytes. Given that a histogram entry is 8 bytes in size,
one chunk corresponds to histogram entries for 16 MB of pages.
Figure 4 shows the data structure for a
histogram. We see that, when a process or file uses less than 64
pages (256 KB), it uses only  . This
approach optimizes space for the common case of small
processes and files. Any process or file that requires more than 256
KB but less than 16MB memory uses the level_1 histogram. Larger
ones use the level_2 histogram. The worst-case histogram space
overhead occurs when a process uses exactly 65 pages. Here, the
histogram will need about 0.2% of the memory consumed by the
process. In common cases, it is about 8 bytes per 64 pages, which is
less than 0.004%. . This
approach optimizes space for the common case of small
processes and files. Any process or file that requires more than 256
KB but less than 16MB memory uses the level_1 histogram. Larger
ones use the level_2 histogram. The worst-case histogram space
overhead occurs when a process uses exactly 65 pages. Here, the
histogram will need about 0.2% of the memory consumed by the
process. In common cases, it is about 8 bytes per 64 pages, which is
less than 0.004%.
Major fault cost: Calculating WSS requires tracking the
mean cost of a major page fault. The CRAMM VM keeps a single,
system-wide estimate majfc of this cost. When the VM initiates
a swap-in operation, it marks the page with a time-stamp. After the
read completes, the VM calculates the time used to load the page.
This new time is then used to update majfc.
4.3 Controlling Histogram Collection Overhead
Because the CRAMM VM updates a histogram entry at every reference to
an inactive page, the size of the inactive list determines the
overhead of histogram collection. If the inactive list is too large,
then too much time will be spent handling minor page faults and
updating histogram entries. If the inactive list is too small, then
the histogram will provide too little information to calculate an
accurate WSS. Thus, we want the inactive list to be as large as
possible without inducing too much overhead.
The VM sets a target for minor fault overhead, expressed as a
percentage increase in running time for processes, and dynamically
adjusts the inactive list size according to this target. For each
process, the VM tracks its CPU time 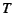 and a count of its minor page
faults and a count of its minor page
faults 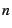 . It also maintains a system-wide minor fault cost
minfc using the same approach as with majfc. It uses
these values to calculate the minor fault overhead as . It also maintains a system-wide minor fault cost
minfc using the same approach as with majfc. It uses
these values to calculate the minor fault overhead as
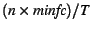 . It performs this calculation
periodically, after which it resets both . It performs this calculation
periodically, after which it resets both 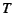 and and 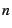 . Given a target
of . Given a target
of 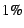 and a constant threshold for deviation from that target of and a constant threshold for deviation from that target of
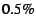 , one of three cases may apply: , one of three cases may apply:
- If the overhead exceeds
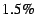 , the VM decreases the
inactive list size. , the VM decreases the
inactive list size.
- If the overhead is less than
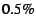 , it increases
the inactive list size. , it increases
the inactive list size.
- If there are no minor faults during this period, and if the
inactive list is not full, then it moves pages from the active to the
inactive list (refilling the inactive list).
This simple adaptive mechanism, set to a 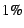 overhead target and a overhead target and a
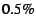 deviation threshold, successfully keeps the overhead low while
yielding sufficient histogram information for WSS calculations. deviation threshold, successfully keeps the overhead low while
yielding sufficient histogram information for WSS calculations.
Size adjustment calculations: CRAMM assigns each process a target
inactive size, initially 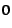 . When CRAMM adjusts the inactive list
size, it is really setting this target size. Assume that a process
has . When CRAMM adjusts the inactive list
size, it is really setting this target size. Assume that a process
has 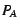 pages in the active list and pages in the active list and 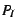 in the inactive list.
Depending on the overhead's relationship to its threshold, the new
target will be: in the inactive list.
Depending on the overhead's relationship to its threshold, the new
target will be:
- Increase:
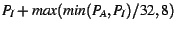
- Decrease:
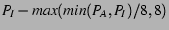
- Refill:
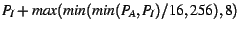
By choosing the smaller of 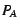 and and 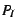 in these equations, we make
the adjustments small if either list is small, thus not changing the
target too drastically. These formulas also ensure that at least some
constant change is applied to the target, ensuring a change that will
have some effect. We also put an upper bound on the refilling
adjustment to prevent flushing too many pages into the inactive list
at a time. Finally, we decrease the target inactive list size more
aggressively than we increase it because low overhead is a more
critical and sensitive goal than accurate histogram information. We
also refill more aggressively than we increase because an absence of minor
faults is a strong indication of an inadequate inactive list size. in these equations, we make
the adjustments small if either list is small, thus not changing the
target too drastically. These formulas also ensure that at least some
constant change is applied to the target, ensuring a change that will
have some effect. We also put an upper bound on the refilling
adjustment to prevent flushing too many pages into the inactive list
at a time. Finally, we decrease the target inactive list size more
aggressively than we increase it because low overhead is a more
critical and sensitive goal than accurate histogram information. We
also refill more aggressively than we increase because an absence of minor
faults is a strong indication of an inadequate inactive list size.
Whenever a page is added to the active list, the VM checks the
current inactive list size. If it is less than its target, then the
VM moves several pages from the active list to the inactive list (8
pages in our implementation). When an adjustment triggers refilling,
the VM immediately forces no more than 256 pages into the inactive list to match its
new target.
As this adjustment only resets the target size and usually does not move
pages immediately, the algorithm is largely insensitive to the values of these parameters.
Adaptivity triggers: In the CRAMM VM, there are two events
that can trigger an inactive list size adjustment. The first,
adjust_interval, is based on running time, and the second,
adjust_count, is based on the number of minor faults.
For every new process, its adjust_interval is initialized to a
default value (
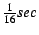 ). Whenever a process
is scheduled, if its running time since the last adjustment exceeds
its adjust_interval value, then the VM adjusts the inactive
list size. ). Whenever a process
is scheduled, if its running time since the last adjustment exceeds
its adjust_interval value, then the VM adjusts the inactive
list size.
The adjust_count variable is initialized to be
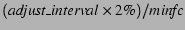 . If a process suffers this number of minor
faults before adjust_interval CPU time has passed, then its
overhead is well beyond the acceptable level. At each minor fault,
the VM checks whether the number of minor faults since the last
adjustment exceeds adjust_count. If so, it forces an
adjustment. . If a process suffers this number of minor
faults before adjust_interval CPU time has passed, then its
overhead is well beyond the acceptable level. At each minor fault,
the VM checks whether the number of minor faults since the last
adjustment exceeds adjust_count. If so, it forces an
adjustment.
5 Experimental Evaluation
We now evaluate our VM implementation and heap size
manager. We first compare the performance of the CRAMM VM with the original
Linux VM. We then add the heap size manager to several collectors
in Jikes RVM, and evaluate their performance under both static and dynamic
real memory allocations. We also compare them with the JRockit [7] and
HotSpot [19] JVMs under similar conditions. Finally, we run two
concurrent instances of our adaptive collectors under memory pressure to
see how they interact with each other.
5.1 Methodology Overview
We performed all measurements on a 1.70GHz Pentium 4 Linux machine
with 512MB of RAM and 512MB of local swap space. The processor has
12KB I and 8KB D L1 caches and a
256KB unified L2 cache. We installed both the ``stock''
Linux kernel (version 2.4.20) and our CRAMM kernel. We ran each of our
experiments six times in single-user mode, and always report the mean
of the last five runs. In order to simulate memory pressure, we used
a background process to pin a certain volume of pages in memory using
mlock.
Application platform: We used Jikes RVM
v2.4.1 [3] built for Linux x86 as our
Java platform. We optimized the system images to the highest
optimization level to avoid run-time compilation of those components.
Jikes RVM uses an adaptive compilation system, which invokes
optimization based on time-driven sampling. This makes executions
non-deterministic. In order to get comparable deterministic
executions, we took compilation logs from 7 runs of each benchmark
using the adaptive system, and directed the system to compile methods
according to the log from the run with the best performance. This is called
the replay system. It is deterministic and highly similar
to typical adaptive system runs.
Collectors: We evaluate five collectors from the
MMTk memory management toolkit [9] in Jikes RVM: MS (mark-sweep), GenMS
(generational mark-sweep), CopyMS (copying mark-sweep), SS
(semi-space), and GenCopy (generational copying). All of these collectors have
a separate non-copying region for large objects (2KB or more), collected with the
Treadmill algorithm [6]. They also use separate non-copying
regions for meta-data and immortal objects.
We now describe the other regions each collector uses for ordinary
small objects.
MS is non-generational with a single MS region. GenMS is generational with a
copying nursery and MS mature space. CopyMS is non-generational with two
regions, both collected at every GC. New objects go into a copy region, while
copy survivors go into an MS region. SS is non-generational with a single
copying region. GenCopy is generational with copying nursery and mature
space. Both generational collectors (GenMS and GenCopy) use Appel-style
nursery sizing [4] (starts large and shrinks as mature space grows).
Benchmarks: For evaluating JVM performance, we ran all benchmarks from
the SPECjvm98 suite (standard and widely used), plus those benchmarks from the
DaCapo suite [10] (an emerging standard
for JVM GC evaluation) that run
under Jikes RVM, plus ipsixql (a publicly available XML database
program) and pseudojbb (a variant of the standard, often-used SPECjbb
server benchmark with a fixed workload (140,000 transactions) instead of fixed
time limit). For evaluating general VM performance, we used the standard
SPEC2000 suite.
Presented: Many results are similar, so to save space we present
results only from some
representative collectors and benchmarks. For collectors, we chose SS,
MS, and GenMS to cover copying, non-copying, and generational variants.
For benchmarks, we chose javac, jack, pseudojbb,
ipsixql, jython, and pmd.
5.2 VM Performance
For the CRAMM VM to be practical, its baseline
performance (i.e., while collecting useful histogram/working set size
information) must be competitive when physical RAM is plentiful. We
compare the performance of the CRAMM VM to that of
the stock Linux kernel across our entire benchmark suite.4 For each benchmark, we use the input that
makes it runs longer than 60 seconds.
Figure 5 summarizes the results, which are
geometric means across all benchmarks: SPEC2000int, SPEC2000fp, and
all the Java benchmarks (SPECjvm98, DaCapo, pseudojbb, and ipsixql)
with five different garbage collectors. While the inactive list size
adjustment mechanism effectively keeps the cost of collecting
histogram data in the desired range (e.g., 0.59% for SPEC2Kint and
1.02% for SPEC2Kfp), the slowdown is generally about 1-2.5%. We
believe this overhead is caused by CRAMM polluting the cache when handling
minor faults as it processes page lists and AVL trees. This, in turn,
leads to extra cache misses for the application. We verified that
at the target minor fault overhead, CRAMM incurs enough minor
faults to calculate the working set size accurately with respect to our 5% page
fault threshold.
Figure 5:
Virtual memory overhead (% increase in execution time) without paging, across all benchmark suites and garbage collectors.
|
CRAMM's performance is generally somewhat poorer on the Java
benchmarks, where it must spend more time handling minor faults caused
by the dramatic working set changes between the mutator and collector
phases of GCed applications. However, the fault handling overhead
remains in our target range. Overall, CRAMM collects the necessary information
at very low overhead in most cases, and its performance is
competitive to that of the stock kernel.
5.3 Static Memory Allocation
To test our adaptive mechanism, we run the benchmarks over a
range of requested heap sizes with a fixed memory allocation. We select memory
allocations that reveal the effects of large heaps in small
allocations and small heaps in large allocations. In particular, we
try to evaluate the ability of our mechanism to grow and shrink the
heap. We run the non-adaptive collectors (which simply use the requested heap size) on
both the stock and CRAMM kernels, and the adaptive collectors on the
CRAMM kernel, and compare performance.
Figure 6:
Static Memory Allocation: MarkSweep
|
Figure 7:
Static Memory Allocation: GenMS
|
Figure 6 and Figure 7 show execution time for
benchmarks using MS and GenMS collectors respectively with a static memory allocation.
For almost every
combination of benchmark and requested heap size, our adaptive collector
chooses a heap size that is nearly optimal. It reduces total
execution time dramatically, or performs at least as well as the
non-adaptive collector. At the leftmost side of each curve, the non-adaptive
collector runs at a heap size that does not consume the entire
allocation, thus under-utilizing available memory, collecting too frequently
and inducing high GC overhead. The adaptive collector
grows the heap size to reduce the number of collections without
incurring paging. At the smallest requested heap sizes, this adjustment
reduces execution time by as much as 85%.
At slightly larger requested heap sizes, the non-adaptive collector performs
fewer collections, better utilizing available memory. One can
see that there is an ideal heap size for the given benchmark and
allocation. At that heap size, the non-adaptive collector performs well--but the
adaptive collector often matches it, and is never very much worse.
The maximum slowdown we observed is 11% across all the benchmarks.
(Our working set size calculation uses a page fault
threshold of 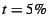 , so we are allowing a trivial amount of paging--while
reducing the working set size substantially.) , so we are allowing a trivial amount of paging--while
reducing the working set size substantially.)
Once the requested heap size goes slightly beyond the ideal, non-adaptive
collector performance drops dramatically. The working set size
is just slightly too large for the allocation, which induces enough paging to
slow execution by as much as a factor of 5 to 10.
In contrast, our adaptive collector shrinks the heap so that
the allocation completely captures the working set size. By performing
slightly more frequent collections, the adaptive collector consumes a
modest amount of CPU time to avoid a lot of paging,
thus reducing elapsed time by as much as 90%. When the requested
heap size becomes even larger, the performance of our adaptive
collector remains the same. However, the execution time of the non-adaptive
collector decreases gradually. This is because it does fewer collections, and
it is collections that cause most of the paging.
Interestingly, when we disable adaptivity, the CRAMM VM exhibits worse paging performance than the
stock Linux VM. LRU-based eviction algorithm turns out to be a poor fit for
garbage collection's memory reference behavior.
Collectors typically exhibit loop-like behavior
when tracing live objects, and LRU is notoriously bad in handling large loops.
The Linux VM instead uses an eviction algorithm
based on a combination of CLOCK and a linear scan over the program's
address space, which happens to work better in this case.
5.4 Dynamic Memory Allocation
The results given so far show that our adaptive mechanism
selects a good heap size when presented with an unchanging memory
allocation. We now examine how CRAMM performs when the memory allocation changes dynamically.
To simulate dynamic memory pressure, we use a background process that
repeatedly consumes and releases memory. Specifically, it consists of
an infinite loop, in which it sleeps for 25 seconds, mmap's
50MB memory, mlock's it for 50 seconds, and then unlocks and
unmaps the memory. We also modify how we invoke benchmarks so that they run
long enough (we give pseudojbb a large transaction number, and
iterate javac 20 times).
Table 1:
Dynamic Memory Allocation: Performance of Adaptive vs. Non-Adaptive Collectors
|
Benchmark |
Collector |
Enough Memory |
Adaptive Collector |
Non-Adaptive Collector |
Adaptive |
|
(Memory) |
(Heap Size) |
T(sec) |
MF |
T(sec) |
cpu |
MF |
T(sec) |
cpu |
MF |
Yes/No |
|
pseudojbb |
SS |
(160M) |
297.35 |
1136 |
339.91 |
99% |
1451 |
501.62 |
65% |
24382 |
0.678 |
|
(160M) |
MS |
(120M) |
336.17 |
1136 |
386.88 |
98% |
1179 |
928.49 |
36% |
47941 |
0.417 |
|
|
GenMS |
(120M) |
296.67 |
1136 |
302.53 |
98% |
1613 |
720.11 |
48% |
39944 |
0.420 |
|
javac |
SS |
(150M) |
237.51 |
1129 |
259.35 |
94% |
1596 |
455.38 |
68% |
24047 |
0.569 |
|
(140M) |
MS |
(90M) |
261.63 |
1129 |
288.09 |
95% |
1789 |
555.92 |
47% |
25954 |
0.518 |
|
|
GenMS |
(90M) |
249.02 |
1129 |
263.69 |
95% |
2073 |
541.87 |
50% |
33712 |
0.487 |
|
Figure 8:
Dynamic Memory Allocation (pseudojbb): Heap Adjustment and Throughput
|
Table 1 summarizes the performance of both non-adaptive
and adaptive collectors under this dynamic memory pressure.
The first column gives the benchmarks and their initial memory
allocation. The second column gives the collectors and their requested
heap sizes respectively. We set the requested heap size so that
the benchmark will run gracefully in the initial memory
allocation. We present the total elapsed time (T), CPU utilization (cpu),
and number of major faults (MF) for each
collector. We compare them against the base case, i.e., running the
benchmark at the requested heap size with sufficient memory. The
last column shows adaptive execution time relative to non-adaptive.
We see that for each collector the adaptive mechanism adjusts the
heap size in response to memory pressure, nearly eliminating
paging. The adaptive collectors show very high CPU utilization and
dramatically reduced execution time.
Figure 8 illustrates how our adaptive
collectors change the heap size while running pseudojbb under
dynamic memory pressure. The graphs in the first row
demonstrate how available memory changes over time, and
the corresponding heap size chosen by each adaptive collector. We see that
as available memory drops, the adaptive collectors
quickly shrink the heap to avoid paging. However, if our adaptive collectors
do not periodically polling for current available memory and collect before
the heap is filled up, the CPU utilization falls below 80% and can be as low as 53%.
Likewise, they grow the heap
responsively when there is more available memory.
One can also see that the difference between the maximum and
minimum heap size is approximately the amount of memory change divided
by heap utilization 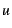 , consistent with our working set size model
presented in Section 3.1. , consistent with our working set size model
presented in Section 3.1.
Figure 9:
Running Two Instances of Adaptive Collectors.
|
We also compare the throughput of the adaptive and non-adaptive collectors
(the second row in Figure 8), by printing
out the number of transactions finished as time elapses for pseudojbb. These curves
show that memory pressure has much less impact on throughput when
running under our adaptive collectors. It causes only a small
disturbance and only for a short period of time. The total execution time of
our adaptive collectors is a little longer than that of the base case,
simply because they run at a much smaller heap size (and thus collect more often) when there is
less memory. The non-adaptive collectors experience significant paging
slowdown when under memory pressure.
As previously mentioned, JRockit and HotSpot do not adjust heap size
well in response to changing memory allocation.
Figure 10 compares the throughput of our adaptive
collectors with that of JRockit and HotSpot. We carefully choose the
initial memory allocation so that the background process imposes the
same amount of relative memory pressure as for our adaptive
collectors. However, being an experimental platform, Jikes RVM's
compiler does not produce as efficient code as these commercial
JVMs. We thus normalize the time for each of them to the total
execution time that each JVM takes to run when given ample
physical memory. The results show that both JRockit and HotSpot experience a
large relative performance loss. The flat regions on their throughput
curves indicate that they make barely any progress when available
memory suddenly shrinks to less than their working set. Meanwhile,
our adaptive collector changes the heap size to fit in available
memory, maintaining high performance.
Figure 10:
Throughput under dynamic memory pressure, versus JRockit and HotSpot.
|
Finally, we examine how our adaptive collectors interact with each other.
We started two instances using adaptive collectors with a certain
memory allocation (220MB), and let them adjust their heap sizes
independently. We explored several combinations of collector and
benchmark: the same collector and benchmark, the same collector and
different benchmarks, and different collectors with different
benchmarks. The experiments show that, for all these combinations, our
adaptive collectors keep CPU utilization at least 91%.
Figure 9 shows the amount of available memory
observed by each collector and their adapted heap size over time.
We see that, after bouncing around a little, our adaptive collectors tend to
converge to heap sizes that give each job a fair share of available memory,
even though each works
independently.
The curves of GenMS in the
third graph show how filtering out small nursery collections
helps to stabilize heap size.
This experiment still focus on how each JVM adapts to dynamic memory
allocation. Although our mechanism effectively prevents each of them
from paging, the memory allocation to each JVM may still be unfair.
We leave to future work how best to divide memory among
multiple competing JVMs.
6 Related Work
Table 2:
A comparison of approaches to dynamic heap sizing.
|
Grows |
Shrinks |
Static |
Dynamic |
Collector |
Needs OS |
|
|
Heap |
Heap |
Allocation |
Allocation |
Neutral |
Support |
Responds to |
|
Alonso et al.[2] |
|
 |
 |
 |
|
 |
memory allocation |
|
Brecht et al.[11] |
 |
|
 |
|
|
|
pre-defined rules |
|
Cooper et al.[14] |
 |
|
 |
|
|
|
user
supplied target |
|
BC [18] |
|
 |
 |
 |
|
 |
page swapping |
|
JRockit [7] |
 |
 |
 |
|
 |
|
throughput or pause time |
|
HotSpot [19] |
 |
 |
 |
|
|
|
throughput and pause time |
|
MMTk [9] |
 |
 |
 |
|

|
|
live ratio and GC load |
|
CRAMM/AHS [28] |
 |
 |
 |
 |
 |
 |
memory allocation |
|
We now discuss the work most closely related to CRAMM, first
discussing work related to the CRAMM VM and then addressing GC-based
approaches to sizing the heap.
The CRAMM VM computes stack distances, which were originally
designed for trace analysis. Mattson et al. introduced a one-pass
algorithm, based on stack distances, that analyzes a reference trace
and produces cache misses for caches of any
size [22]. This algorithm was later adapted by
Kim and Hsu to handle highly-associative caches [21].
However, these algorithms compute a stack distance
in linear time, making them too slow to
use inside a kernel. Subsequent work on analyzing reference traces
used more advanced dictionary data
structures [1,8,17,23,26].
These algorithms calculate a stack distance in logarithmic time, but do
not maintain underlying referenced blocks in order. This order is
unnecessary for trace processing but crucial for page eviction
decisions. The CRAMM VM maintains pages in a list that preserves
potential eviction order, and uses a separate AVL tree to calculate
a stack distance in logarithmic time.
Zhou et al. present a VM system that also tracks LRU reference curves
inside the kernel [29]. They use Kim and Hsu's
linear-time algorithm to maintain LRU order and calculate stack
distances. To achieve reasonable efficiency, this algorithm requires
the use of large group sizes (e.g., 1024 pages) that significantly
degrade accuracy. They also use a static division between the active
and inactive lists, yielding an overhead of 7 to 10%. The CRAMM VM
computes the stack distance in logarithmic time, and can
track reference histograms at arbitrary granularities. Furthermore,
its inactive list size adjustment algorithm allows it to collect
information accurately from the tail of miss curves while limiting
reference histogram overhead to 1%.
Researchers have proposed a number of heap sizing approaches for
garbage collection; Table 2 provides a summary. The
closest work to CRAMM is by Alonso and Appel, who also exploit VM
system information to adjust the heap
size [2]. Their collector periodically queries the
VM for the current amount of available memory and adjusts the heap
size in response. CRAMM differs from this work in several key
respects. While their approach shrinks the heap when memory pressure
is high, it does not expand and thus reduce GC frequency when pressure
is low. It also relies on standard interfaces to the VM system that
provide a coarse and often inaccurate estimate of memory pressure. The
CRAMM VM captures detailed reference information and provides reliable
values.
Brecht et al. adapt Alonso and Appel's approach to control heap
growth via ad hoc rules for two given static memory
sizes [11]. Cooper et al. dynamically adjust the heap
size of an Appel-style collector according to a user-supplied
memory usage target [14]. If the target matches the
amount of free memory, their approach adjusts the heap to make full
use of it. However, none of these approaches can adjust to dynamic
memory allocations. CRAMM automatically identifies an optimal heap
size using data from the VM. Furthermore, the CRAMM model captures
the relationship between working set size and heap size, making its
approach more general and robust.
Our research group previously presented the bookmarking collector
(BC), a garbage-collection algorithm that guides a lightly modified VM
system to evict pages that do not contain live objects and installs
``bookmarks'' in pages in response to eviction
notifications [18]. These bookmarks allow BC to
collect the heap without touching already evicted pages, which CRAMM
must. One shortcoming of BC is that it currently cannot grow the heap
because it responds only to page eviction notifications. CRAMM both
shrinks and grows the heap to fit, and can be applied to a wide range
of existing garbage collection algorithms.
7 Conclusion
We present CRAMM, a new system designed to support
garbage-collected applications. CRAMM combines a new virtual memory
system with a garbage-collector-neutral, analytic heap sizing model to
dynamically adjust heap sizes. In exchange for modest overhead
(around 1-2.5% on average), CRAMM improves performance dramatically by
making full use of memory without incurring paging. CRAMM allows
garbage-collected applications to run with a nearly-optimal heap size
in the absence of memory pressure, and adapts quickly to dynamic
memory pressure changes, avoiding paging while providing high CPU
utilization.
This material is based upon work supported by the National Science
Foundation under grant number CCR-0085792 and CAREER Award
CNS-0347339. Any opinions, findings, conclusions, or recommendations
expressed in this material are those of the authors and do not
necessarily reflect the views of the NSF.
- 1
-
G. Almasi, C. Cascaval, and D. A. Padua.
Calculating stack distances efficiently.
In ACM SIGPLAN Workshop on Memory System Performance, pages
37-43, Berlin, Germany, Oct. 2002.
- 2
-
R. Alonso and A. W. Appel.
An advisor for flexible working sets.
In Proceedings of the 1990 SIGMETRICS Conference on
Measurement and Modeling of Computer Systems, pages 153-162, Boulder, CO,
May 1990.
- 3
-
B. Alpern, C. R. Attanasio, J. J. Barton, M. G. Burke, P. Cheng, J.-D. Choi,
A. Cocchi, S. J. Fink, D. Grove, M. Hind, S. F. Hummel, D. Lieber,
V. Litvinov, M. F. Mergen, T. Ngo, V. Sarkar, M. J. Serrano, J. C. Shepherd,
S. E. Smith, V. C. Sreedhar, H. Srinivasan, and J. Whaley.
The Jalepeño virtual machine.
IBM Systems Journal, 39(1):211-238, Feb. 2000.
- 4
-
A. Appel.
Simple generational garbage collection and fast allocation.
Software: Practice and Experience, 19(2):171-183, Feb. 1989.
- 5
-
O. Babaoglu and D. Ferrari.
Two-level replacement decisions in paging stores.
IEEE Transactions on Computers, C-32(12):1151-1159, Dec.
1983.
- 6
-
H. G. Baker.
The Treadmill: Real-time garbage collection without motion
sickness.
ACM SIGPLAN Notices, 27(3):66-70, March 1992.
- 7
-
BEA WebLogic.
Technical white paper JRockit: Java for the enterprise.
https://www.bea.com/content/news_events
/white_papers/BEA_JRockit_wp.pdf.
- 8
-
B. T. Bennett and V. J. Kruskal.
LRU stack processing.
IBM Journal of R & D, 19(4):353-357, 1975.
- 9
-
S. M. Blackburn, P. Cheng, and K. S. McKinley.
Oil and Water? High Performance Garbage Collection in Java with
MMTk.
In 26th International Conference on Software Engineering, pages
137-146, May 2004.
- 10
-
S. M. Blackburn, R. Garner, C. Hoffman, A. M. Khan, K. S. McKinley, R. Bentzur,
A. Diwan, D. Feinberg, D. Frampton, S. Z. Guyer, M. Hirzel, A. Hosking,
M. Jump, H. Lee, J. E. B. Moss, A. Phansalkar, D. Stefanovic,
T. VanDrunen, D. von Dincklage, and B. Wiedermann.
The DaCapo benchmarks: Java benchmarking development and
analysis.
In OOPSLA '06: Proceedings of the 21st annual ACM SIGPLAN
conference on Object-Oriented Programing, Systems, Languages, and
Applications, New York, NY, USA, Oct. 2006. ACM Press.
- 11
-
T. Brecht, E. Arjomandi, C. Li, and H. Pham.
Controlling garbage collection and heap growth to reduce the
execution time of Java applications.
In Proceedings of the 2001 ACM SIGPLAN Conference on
Object-Oriented Programming, Systems, Languages & Applications, pages
353-366, Tampa, FL, June 2001.
- 12
-
R. W. Carr and J. L. Henessey.
WSClock - a simple and effective algorithm for virtual memory
management.
In Proceedings of the Eighth ACM Symposium on Operating Systems
Principles (SOSP), pages 87-95, Dec. 1981.
- 13
-
W. W. Chu and H. Opderbeck.
The page fault frequency replacement algorithm.
In AFIPS Conference Proceedings, volume 41(1), pages 597-609,
Montvale, NJ, 1972. AFIPS Press.
- 14
-
E. Cooper, S. Nettles, and I. Subramanian.
Improving the performance of SML garbage collection using
application-specific virtual memory management.
In Conference Record of the 1992 ACM Symposium on Lisp and
Functional Programming, pages 43-52, San Francisco, CA, June 1992.
- 15
-
P. J. Denning.
The working set model for program behavior.
In Proceedings of the ACM Symposium on Operating System
Principles, pages 15.1-15.12, Jan. 1967.
- 16
-
P. J. Denning.
Working sets past and present.
IEEE Transactions on Software Engineering, SE-6(1):64-84, Jan.
1980.
- 17
-
C. Ding and Y. Zhong.
Predicting whole-program locality through reuse distance analysis.
In ACM SIGPLAN 2003 Conference on Programming Language Design
and Implementation, pages 245-257, San Diego, CA, June 2003.
- 18
-
M. Hertz, Y. Feng, and E. D. Berger.
Garbage collection without paging.
In Proceedings of the 2005 ACM SIGPLAN Conference on Programming
Language Design and Implementaton, pages 143-153, Chicago, IL, June 2005.
- 19
-
JavaSoft.
J2SE 1.5.0 documentation: Garbage collector ergonomics.
https://java.sun.com/j2se/1.5.0/docs/guide/vm/ gc-ergonomics.html.
- 20
-
S. F. Kaplan, L. A. McGeoch, and M. F. Cole.
Adaptive caching for demand prepaging.
In Proceedings of the 2002 International Symposium on Memory
Management, pages 114-126, June 2002.
- 21
-
Y. H. Kim, M. D. Hill, and D. A. Wood.
Implementing stack simulation for highly-associative memories.
In Proceedings of the 1991 SIGMETRICS Conference on
Measurement and Modeling of Computer Systems, pages 212-213, San Diego, CA,
1991.
- 22
-
R. L. Mattson, J. Gecsei, D. R. Slutz, and I. L. Traiger.
Evaluation techniques for storage hierarchies.
IBM Systems Journal, 9(2):78-117, 1970.
- 23
-
F. Olken.
Efficient methods for calculating the success function of fixed space
replacement policies.
Technical Report LBL-12370, Lawrence Berkeley Laboratory, 1981.
- 24
-
R. H. Patterson, G. A. Gibson, E. Ginting, D. Stodolsky, and J. Zelenka.
Informed prefetching and caching.
In Proceedings of the Fifteenth ACM Symposium on Operating
Systems Principles, pages 79-95, New York, NY, USA, 1995. ACM Press.
- 25
-
Y. Smaragdakis, S. F. Kaplan, and P. R. Wilson.
The EELRU adaptive replacement algorithm.
Performance Evaluation, 53(2):93-123, July 2003.
- 26
-
R. A. Sugumar and S. G. Abraham.
Efficient simulation of caches under optimal replacement with
applications to miss characterization.
In Measurement and Modeling of Computer Systems, pages 24-35,
Santa Clara, CA, 1993.
- 27
-
P. R. Wilson, S. F. Kaplan, and Y. Smaragdakis.
The case for compressed caching in virtual memory systems.
In Proceedings of The 1999 USENIX Annual Technical Conference,
pages 101-116, Monterey, California, June 1999. USENIX Association.
- 28
-
T. Yang, M. Hertz, E. D. Berger, S. F. Kaplan, and J. E. B. Moss.
Automatic heap sizing: Taking real memory into account.
In Proceedings of the ACM SIGPLAN International Symposium on
Memory Management, pages 61-72, Vancouver, Canada, Oct. 2004.
- 29
-
P. Zhou, V. Pandy, J. Sundaresan, A. Raghuraman, Y. Zhou, and S. Kumar.
Dynamic tracking of page miss ratio curves for memory management.
In Proceedings of the 11th International Conference on
Architectural Support for Programming Languages and Operating Systems, pages
177-188, Boston, MA, Oct. 2004.
CRAMM: Virtual Memory Support for Garbage-Collected Applications
This document was generated using the
LaTeX2HTML translator Version 2002 (1.62)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 -show_section_numbers -local_icons autoheapsizing.tex
The translation was initiated by Ting Yang on 2006-09-05
Footnotes
- ... (VM1
- We use VM to denote
virtual memory throughout this paper.
- ... allocation,2
- The
main memory allocation is not the same as the resident
set size. The latter is the amount of main memory currently consumed
by a process, while the former is the amount of main memory that the
VM system is willing to let the process consume before evicting its pages.
- ....3
- Notice that we refer to the histogram
as an LRU reference histogram, but that our page lists are not
in true LRU order, and so the histogram is really a
SegQ reference histogram. Also, note that only references to
the inactive and evicted lists are applicable here, since references
to active pages occur without kernel intervention.
- ... suite.4
- We
could not compile and run some SPEC2000 Fortran programs, so we omit
some of the FP benchmarks.



Ting Yang
2006-09-05
|
