
OSDI '06 Paper
Pp. 161–176 of the Proceedings
From Uncertainty to Belief: Inferring the Specification Within |
|
Ted Kremenek, Stanford University
Paul Twohey, Stanford University
Godmar Back, Virginia Tech
Andrew Ng, Stanford University
Dawson Engler, Stanford University
|
Abstract:
Automatic tools for finding software errors require a set of
specifications before they can check code: if they do not know what to
check, they cannot find bugs. This paper presents a novel framework
based on factor graphs for automatically inferring specifications
directly from programs. The key strength of the approach is that it
can incorporate many disparate sources of evidence, allowing us to
squeeze significantly more information from our observations than
previously published techniques.
We illustrate the strengths of our approach by applying it to the
problem of inferring what functions in C programs allocate and release
resources. We evaluated its effectiveness on five codebases: SDL,
OpenSSH, GIMP, and the OS kernels for Linux and Mac OS X (XNU). For
each codebase, starting with zero initially provided annotations, we
observed an inferred annotation accuracy of 80-90%, with often near
perfect accuracy for functions called as little as five times. Many
of the inferred allocator and deallocator functions are functions for
which we both lack the implementation and are rarely called — in
some cases functions with at most one or two callsites.
Finally, with the inferred annotations we quickly found both missing
and incorrect properties in a specification used by a commercial
static bug-finding tool.
1 Introduction
Many effective tools exist for finding software
errors [15, 5, 28, 8, 4, 33, 18].
While different in many respects, they are identical in one: if they
do not know what to check, they cannot find bugs.
In general, tools require specifications that document what a
program should do in order for the tool to discern good program
behavior from bad. Undetected errors due to missing specifications
are a serious form of false negatives that plague sound
and unsound bug-finding tools alike. From our own experience with
developing such tools, we believe that legions of bugs remain
undetected in systems previously “vetted” by checking tools simply
because they lack the required specifications, and not because tools
lack the necessary analysis precision.
Furthermore, checking tools generally operate without safety nets.
There is no mechanism to discover when bugs in the checking tool lead
to missed errors in checked code. Analysis bugs are a source of false negatives; while an unsound tool may have false
negatives by design, even a sound tool can have false negatives due to
implementation bugs. In our experience this is a serious concern: if
an analysis bug does not cause a false positive, the only way to catch
it is by comparison against regression runs.
The result of all these factors is that checking tools miss many
bugs they could catch.
Unfortunately, acquiring accurate specifications can be daunting at
best. Even with state-of-the-art annotation systems, the manual labor
needed to specify high-level invariant properties for large programs
can be overwhelming [12, 35]. Further, in
large, evolving codebases with many developers, interfaces may change
rapidly as functions are added and removed. This churn
exacerbates the problem of keeping a specification, if there is one,
current.
Fortunately, there are many sources of knowledge, intuitions, and
domain-specific observations that can be automatically leveraged to
help infer specifications from programs directly.
First and foremost, the behavior of programs is well-structured, with
recognizable patterns of behavior implying high-level roles for the
objects in a program. For example, functions that allocate and
release resources (such as file handles and memory)
vary widely in their implementations, but
their interfaces are used nearly identically.
In essence, the behavior of a program reflects what the programmer
intended it to do, and the more we observe that one or more objects
appear to interact in a recognizable role, the more we believe
that role reflects their true purpose. More plainly, the more
something behaves like an X the more we believe it is an X. Thus,
leveraging such information has the desired property that the amount
of evidence garnered about a program's specification grows in the
amount of code analyzed.
In addition, we often have a volume of valuable, non-numeric ad hoc
information such as domain-specific naming conventions (e.g.,
a function name containing the word “alloc” often implies the
function is an allocator).
This paper presents a novel, scalable, and customizable framework for
automatically inferring specifications from programs. The
specifications we infer come in the form of annotations, which are
able to describe many kinds of important program properties. The key
strength of our approach is that it tightly binds together many
disparate sources of evidence. The result is that any information
about one object becomes indirect information about related objects,
allowing us to squeeze significantly more information from our
observations than previously published approaches. Our framework can
incorporate many sources of information: analysis results from
bug-finding tools, ad hoc knowledge, and already known annotations
(when available). Moreover, because the technique is built upon a
probabilistic model called a factor
graph [36, 21], it is fully
capable of fusing multiple sources of information to
infer specifications while handling the inherent uncertainty in our
information sources and the often noisy relationships
between the properties we wish to infer.
Further, inferred annotations can be immediately employed to
effectively find bugs even before the annotations are inspected
by a user.
This last feature makes our framework pragmatic even for rapidly
evolving codebases: the process of inferring annotations and using
those annotations to check code with automated tools can be integrated
into a nightly regression run. In the process of the daily inspection
of bug reports generated by the nightly run, some of
the inferred annotations will be inspected by a user. These now known
annotations can subsequently be exploited on the next nightly regression to
better infer the remaining uninspected annotations. Thus, our
framework incrementally accrues knowledge about a project
without a huge initial investment of user labor.
This paper makes the following contributions.
We present Annotation Factor Graphs (AFGs), a group of probabilistic
graphical models that we have architected specifically for inferring
annotations.
We illustrate how information from program analysis as well as
different kinds of ad hoc
knowledge can be readily incorporated into an AFG.
We reduce the process of inferring annotations with an
AFG to factor graph inference and describe important
optimizations specific to incorporating
information from static program analysis into an AFG.
We provide a thorough evaluation of the technique using the
example of inferring resource management functions, and illustrate
how our technique scales to large codebases with high accuracy.
Further, we show that with our results we have found both missing
and incorrect properties in a specification used by a commercial
bug-finding tool (Coverity
Prevent [7]).
Section 2 presents a complete example of
inferring specifications from a small code fragment, which introduces
the key ideas of our approach.
Section 3 uses the example to lay
the theoretical foundations, which
Section 4 further formalizes.
Section 5 refines the approach and shows more advanced
AFG modeling techniques.
Section 6 discusses the computational mechanics
of our inference technique.
We evaluate the effectiveness of our approach in
Section 7, discuss related work in
Section 8, and then conclude.
2 Motivating Example
We now present a complete example of inferring specifications from a
small code fragment. This example, along with the solution presented
in the next section, serves to introduce many of the core ideas
of our technique.
2.1 Problem: Inferring Ownership Roles
Application and systems code manages a myriad of resources such as
allocated heap objects, file handles, and database
connections. Mismanagement of resources can lead to bugs such as
resource leaks and use-after-release errors. Although
tools exist to find such
bugs [32, 18, 17, 28],
all require a list of functions that can allocate
and release resources (allocators and deallocators).
Unfortunately, systems code often employs non-standard APIs to manage
resources, causing tools to miss bugs.
A more general concept that subsumes knowing allocation and deallocation
functions is knowing what functions return or claim ownership of
a resource. Many C programs use the ownership idiom: a resource has
at any time
exactly one owning pointer, which must release the resource.
Ownership can be transferred from a pointer by storing it
into a data structure or by passing it to a function that claims it.
A function that returns an owning pointer has the annotation ro
(returns ownership)
associated with its interface. A function that claims a pointer
passed as an argument has the property co (claims ownership)
associated with the corresponding formal parameter. In this model,
allocators are ro functions, while deallocators are co functions.
Many ro functions have a contract similar to an allocator, but
do not directly allocate resources.
For example, a function that
dequeues an object from a linked list and returns it to the caller.
Once the object is removed from the list, the caller must ensure the object
is fully processed. A similar narrative applies to co functions.
FILE * fp = fopen("myfile.txt","r");
fread( buffer, n, 1000, fp );
fclose( fp );
Figure 1: Simple example
involving
a C file handle: fopen “allocates” the
handle, fread uses it, and fclose releases it.
Consider the task of inferring what functions in a program return
and claim ownership of resources. For example, assume we are given the code
fragment in Figure 1 and are asked to determine
if fopen is an ro and if either fread or fclose
are co's. Without prior knowledge about these functions, what
can we conclude by looking at this fragment alone?
While we cannot reach a definitive conclusion, simple intuition
renders some possibilities more likely than others. Because programs
generally behave correctly, a person might first make the assumption
that the code fragment is likely to be bug-free. This
assumption elevates the likelihood of two conclusions over all others.
First, fopen may be an ro, fread a
function that uses fp but does not claim ownership of the
resource (¬co), and fclose a co.
For this case, the code fragment can be logically rewritten as:
fp = ro(); ¬co(fp); co(fp)
This conclusion follows if we assume the code fragment
is correct. If fopen is an ro, then this assignment is the
only one to all three functions that does not induce a bug.
To avoid a resource-leak,
either fread or fclose must be a co. To avoid a
use-after-release error, however, fread cannot be a co.
This leaves fclose being a co.

Figure 2: DFA summarizing basic ownership rules.
A pointer returned from a
function call enters either the Owned or ¬ Owned state
depending on whether the called function has the property ro or
¬ ro respectively. Function calls involving the pointer cause
the DFA to transition states based on the co or ¬ co property
associated with the called function. An “end-of-path” indicates no
further uses of the pointer within the function. The two final states
for the DFA indicate correct ( OK)
or incorrect use of the pointer ( Bug).
Here we have assumed that an owned pointer cannot be used
after being claimed. This strict interpretation of the
ownership idiom assumes that all co's are
deallocators.
For now, the correctness rules for ownership that we use are
summarized by the DFA in Figure 2, and we
discuss refinements in Section 5.1
Continuing, the second likely assignment of ownership roles to these functions
is that fopen is an ¬ro, with both
fread and fclose as ¬co's:
fp = ¬ro(); ¬co(fp); ¬co(fp);
We reach this conclusion using similar reasoning as before.
If fopen is an ¬ro, we no longer have the
opportunity to leak an allocated resource, but as
Figure 2 shows, it is now a bug to pass fp
to a co.
Consequently, from simple reasoning
we can infer
much about these functions.
Note that we are not certain of anything; we only
believe that some conclusions are more likely than others.
Further, we may be able to infer more about these functions by
incorporating additional intuitions and knowledge. In the next section
we discuss how to precisely formulate such reasoning.
| Annotations |
|
Factor Values |
Factor Product |
Probability |
| fopen:ret |
fread:4 |
fclose:1 |
DFA |
f< check > |
f< ro >(fopen:ret) |
f< co >(fread:4) |
f< co >(fclose:1) |
Π f |
1/ZΠ f |
| ro |
¬co |
co |
52 |
0.9 |
0.8 |
0.7 |
0.3 |
0.151 |
0.483 |
| ¬ro |
¬co |
¬co |
52 |
0.9 |
0.2 |
0.7 |
0.7 |
0.088 |
0.282 |
| ro |
¬co |
¬co |
56 |
0.1 |
0.8 |
0.7 |
0.7 |
0.039 |
0.125 |
| ro |
co |
¬co |
56 |
0.1 |
0.8 |
0.3 |
0.7 |
0.017 |
0.054 |
| ro |
co |
co |
56 |
0.1 |
0.8 |
0.3 |
0.3 |
0.007 |
0.023 |
| ¬ro |
¬co |
co |
56 |
0.1 |
0.2 |
0.7 |
0.3 |
0.004 |
0.013 |
| ¬ro |
co |
¬co |
56 |
0.1 |
0.2 |
0.3 |
0.7 |
0.004 |
0.013 |
| ¬ro |
co |
co |
56 |
0.1 |
0.2 |
0.3 |
0.3 |
0.002 |
0.006 |
Table 1: Table depicting intermediate
values used to compute
P(fopen:ret,fread:4,fclose:1).
Specifications are sorted by their probabilities. The
value Z is a normalizing constant computed by summing the
column Πf.
By summing the values in the last column when
fopen:ret=ro we compute
P(fopen:ret=ro)≈0.7. The
marginal probabilities
P(fread:4=¬co)≈0.9
and P(fclose:1=co)≈0.52
are similarly computed.
3 The Big Picture
This section gives
a crash course in our inference approach, tying it to
the example just presented. By its end, the reader will
have a basic arsenal for inferring annotations, which the next sections
extend.
Our goal is to provide a framework
(a probabilistic model)
that (1) allows users to easily express every intuition and
domain-specific observation they have that is useful for inferring
annotations and then (2) reduces such knowledge in a
sound way to meaningful probabilities. In
the process, the framework squeezes out all available information
about the annotations we are inferring.
The inference framework must solve two common challenges.
First, it must robustly handle noise. Otherwise its brittleness will
prevent the exploitation of many observations that are only “often”
true rather than always true (e.g., an observation that an annotation obeys
a feature 51% of the time). Second, it must soundly combine
uncertain information. Treated independently, a fact of which we are only
partially certain is only marginally useful. However,
aggregated with other sources of knowledge, one fact can be the
missing link in a chain of evidence we would not otherwise be able to
exploit.
Our annotation inference has three steps:
Define the set of possible annotations to infer.
Model domain-specific knowledge and intuitions
in our probabilistic model.
Compute annotation probabilities using the model.
These probabilities are then used to rank, from most-to-least
probable: entire specifications, individual annotations, or errors.
We now apply these three steps to our motivating example. In general,
annotations are implicitly defined by a correctness property
that we wish to check in a program; we briefly describe
it for our example (§ 3.1). We then
describe the fundamental mechanics of our probabilistic model
(§ 3.2), and how
to model two basic properties: (1) the fact that the more something
behaves like an X the more likely it is an X
(§ 3.3) and (2) domain-specific prior beliefs
(§ 3.4). We finish the section by
computing the probabilities for the annotations in our example.
3.1 Defining the Annotations to Infer
We use annotation variables to denote the program objects to
which annotations bind. The example has three such variables:
fopen:ret, fread:4 and
fclose:1. The variable fopen:ret
corresponds to the possible annotations for the return value of
fopen, and has the domain { ro, ¬ ro }. The variables
fread:4 and fclose:1 (where “:i”
denotes the ith formal parameter) have the domain { co, ¬ co
}.
We have 23=8 combinations of values for these variables, and
each represents a joint specification of the roles of all three
functions.
(For this paper, an annotation and its negation are mutually exclusive.)
We denote the set of annotation variables as
A. In our example, A = { fopen:ret,
fread:4, fclose:1 }. Further, the notation
A=a means that a is some concrete assignment of
values to all the variables in A. Thus a
represents one possible complete specification, which in our example
specifies ownership roles for all three functions.
Table 1 lists all possible specifications for
Figure 1, and displays the
intermediate values used to compute probabilities for each specification.
We use this table throughout the remainder of this section.
The “DFA” column indicates, for each specification, the
final state of the DFA from Figure 2 when applied to
the code example.
3.2 Modeling Beliefs for Annotations
The rest of the section shows how to express domain-insights in our
inference framework in terms of user-defined mathematical functions,
called factors. The framework uses these
factors to compute annotation probabilities, e.g. the probability
P(fopen:ret=ro) that the return value of
fopen has the annotation ro.
Factors are
relations mapping the possible values of one or more annotation
variables to non-negative real numbers. More precisely, each factor
fi is a map from the possible values of a set of variables Ai (Ai ⊆ A) to [ 0, ∞ ).
Factors “score” an assignment of values to a group of
related annotation variables, with higher values indicating more
belief in an assignment. Although not required, for many
factors the mapped values we specify are probabilities
(i.e. sum to 1) because probabilities are intuitive to specify by hand.
Suppose we know that
functions in a codebase that return a value of type FILE*
have a higher chance of returning ownership (ro). We can express
this tendency using a factor that, given the annotation label for the
return value of a function with a FILE* return type, returns
slightly higher weights for ro annotations than ¬ro
annotations. For example, making fFILE*(fopen:ret=ro)=0.51 and fFILE*(fopen:ret=¬ro)=0.49. Note that the
magnitude of the values is not important, but rather their relative
odds. We could have used 51 and 49 instead,
implying an odds of 51:49 to prefer ro over ¬ro
annotations. While trivial, this example illustrates a couple of
recurrent themes. First, the observations we want to exploit for
inference are often tendencies and not laws — as long as these
tendencies are right more often than wrong, they
convey useful information. The ratio that their associated factor
returns reflects the reliability of a tendency — big ratios
for very reliable tendencies, smaller ratios for mildly reliable ones.
Second, factors work well in our domain since (1) they let the
user express any computable intuition in terms of a custom function
and (2) inference intuitions naturally reduce to preferences over
the possible values for different groups of annotation variables.
Factors thus provide a way to reduce disparate observations to a common
currency.
Once we represent individual beliefs with factors, we combine
a group of
factors { fi } into a single probability model
by multiplying their values together and normalizing:
The normalizing constant Z causes the scores to define a probability
distribution over the values of A, which directly translates into
a distribution over specifications.
One way to view Equation 1 is as a specific case of
Hinton's concept of a Product of Experts [19]. From this
view, each factor represents an “expert” with some specific
knowledge which serves to constrain different dimensions in a
high-dimensional space. The product of these experts will then
constrain all of the dimensions. In this case, the dimensions
represent the space of possible specifications, and the most probable
specifications are those that most “satisfy”
the combined set of constraints.
Note that because factors can share inputs their values are not
independent; such correlation gives the model much expressive power.
As stated previously (§ 2.1), annotations may
be correlated (e.g., if fopen is an ro, then fclose is
likely a co). We capture this correlation by having the
probabilistic model represent a probability distribution
P(A) over the values of all
the annotation variables A.
The simplicity of Equation 1 is deceptive. It is
trivial to define an ad hoc scoring function that in a deep sense
means nothing. This function is not one of those. It subsumes the
expressive power of both Bayesian networks and Markov Random Fields,
two widely used methods for modeling complex probabilistic domains,
because both can be directly mapped to it. In our experience it is
also simpler and easier to reason about.
We defer discussion of its mathematical foundation
(see [36]) — but for our purposes, it has the
charm of being understandable, general enough to express a variety
of inference tricks, and powerful enough to make them mean something.
We now show how to use factors by defining two common types
of factors for our example: behavioral signatures and prior beliefs.
3.3 Behavioral Signatures
“Behavior is the mirror in which everyone shows
their image.”
— Johann Wolfgang von Goethe
In general, the more something behaves like an X, the more probable it
is an X. In our context, programmers often use
program objects that should have a given annotation in idiomatic
ways. Such behavioral signatures provide a good source of data that
we can automatically extract from code (e.g., by using static analysis),
which gives a nice mechanical way to get
large data samples. As with any statistical analysis,
the more data we have the more information we can extract.
The most common behavioral signature for any annotation is that
programs generally behave correctly and that errors are rare. Thus,
correct annotations (typically!) produce fewer errors than incorrect
ones. We measure how much a behavioral signature
is exhibited in a program by using a behavioral
test. A behavioral test works as follows: for every location in a
program where a behavioral signature may apply, we conduct a
check to see if a given set of annotations matches that
signature. Because the behavior may involve reasoning about the
semantics of different execution paths in the program (either intra-
or inter-procedurally), this check is implemented using a static
analysis checker.
The checker we use in this paper is an intra-procedural static
analysis that simulates the DFA in Figure 2 on
paths through functions stemming from callsites where a pointer is
returned.
In principle, however, checks can employ program analysis of arbitrary
complexity to implement a behavioral test, or even be done with
dynamic analysis.
The output of the checker indicates whether
or not the annotation assignment ai to the set of annotation
variables Ai matched with one (or more) behavioral signatures.
We can capture this belief for our example with a single check factor,
f< check
>(fopen:ret,fread:4,fclose:1):
|
f< check >(...)
= |
⎧
⎨
⎩ |
| θ<ok > |
: |
if DFA
= OK |
| θ<bug> |
: |
if DFA =
Bug |
|
|
1. FILE * fp1 = fopen( "myfile.txt", "r" );
2. FILE * fp2 = fdopen( fd, "w" );
3. fread( buffer, n, 1, fp1 );
4. fwrite( buffer, n, 1, fp2 );
5. fclose( fp1 );
6. fclose( fp2 );
Figure 3: Code example that would produce two
distinct checks, one for fp1 and fp2 respectively.
Observe that both fopen and fdopen return ownership of
a resource that must be claimed by fclose.
Check factors easily correlate annotation variables.
In this case, f< check > correlates
fopen:ret, fread:4, and fclose:1
since its value depends on them.
In general there will be one “f< check >” for each
location in the program where a distinct bug could occur.
Figure 3 gives an example with two callsites where
two file handles are acquired by calling fopen and
fdopen respectively. These two cases constitute separate
checks (represented by two factors) based on the reasoning that the
programmer made a distinct decision in both cases in how the returned
handles were used. Observe in this case that the variable
fclose:1 is associated with two checks, and consequently
serves as input to two check factors. Thus the more a function is
used the more evidence we acquire about the function's behavior
through additional checks.
3.4 Prior Beliefs: Small Sample Inference
As in any data analysis task, the less data we have the harder
inference becomes. In our domain, while a large number of callsites
are due to a few functions, a large number of functions have few
callsites. As already discussed, AFGs partially counter this
problem by explicitly relating different functions together, thus
information from one annotation can flow and influence others. An
additional approach that cleanly melds into our framework is the use
of priors to indicate initial preferences (biases). We attach
one prior factor to each annotation variable to bias its value. Having one
prior factor per annotation variable, rather than per callsite, means
it provides a constant amount of influence that can be gradually
overwhelmed as we acquire more evidence.
For example, a completely useless specification for a
codebase is that all functions have either ¬ro or ¬co
annotations. This specification generates no bugs since nothing is
ever allocated or released, but is vacuous because we are interested
in identifying allocators and deallocators.
One counter to this problem (we discuss an additional method later in
§ 5.1) is to encode a slight bias towards
specifications with ro's and co's. We encode this bias with two
sets of factors. The first is to bias towards ro annotations with
the factor f< ro >:
|
f< ro >(X)
= |
⎧
⎨
⎩ |
| θ< ro > |
: |
if X = ro |
| θ< ¬ro > |
: |
if X = ¬ro |
|
|
The addition of f< ro >(fopen:ret) biases
us towards ro annotations, but may cause us to be overly aggressive
in annotating some formal parameters as co in order to minimize the
number of bugs flagged by the checker (thereby maximizing the value of
the f< check > factors).
To bias against co annotations, we define f< co >
in an analogous manner to f< ro >. We set
θ< co > = 0.3 and θ< ¬co
> = 0.7, which makes our bias away from co annotations
slightly weaker than our bias for ro annotations. In our example,
we add two co factors: f< co >(fread:4)
and f< co >(fclose:1). These two
factors, while distinct, share the same values of θ< co
> and θ< ¬co >.
In general, we use priors when we have some initial insights that can
be overcome given enough data. Further, when we do not know enough to
specify their values, they can be omitted entirely.
3.5 Computing Probabilities
Equipped with four factors to encode beliefs for the three functions,
we now employ Equation 1 to compute final probabilities
for the possible specifications.
We first multiply the values of the factors (shown in column “Π
f” of Table 1) and then normalize those values
to obtain our final probabilities. From Table 1,
we can see that for the specification < ro, ¬co, co
> (first row) the product of its individual factor values
is 0.9×0.8×0.7×0.3=0.151.
After normalizing, we have a probability of 0.483, making it the most
probable specification. Observe that because of our bias towards ro
annotations, the second most probable specification, < ¬ro,
¬ co, ¬co >, has a probability of 0.282 (almost half
as likely).
Further, we can use the table to compute the probabilities
of individual annotations. To compute P(
fopen:ret=ro ), we sum the probabilities in the last column
for each row where fopen:ret = ro.
These probabilities match our intuitive reasoning. The probability
P( fopen:ret = ro )≈0.7
indicates that we are confident, but not completely certain, that
fopen could be an ro, while P(
fread:4 = ¬co )≈0.9 shows that we have a
strong belief that fread is ¬co. For fclose, we
are left with a modest probability that
P(fclose:1=co)≈0.52. While this
number seems low, it incorporates both our bias towards ro
annotations and our bias against co annotations. Observe that if we
rank the possible co's by their probabilities (in this case only
two), fclose is at the top. The more locations where
fclose is used in a similar manner the more confidently we
believe it is a co.
3.6 How to Handle Magic Numbers?
By now, the reader may feel uneasy. Despite dressing them in
formalisms, factors simply map annotation values to magic numbers.
(Or, in formal newspeak, the parameters of the model.) As with all
uses of magic numbers two questions immediately surface:
(1) where do they come from? and (2) how hard are they to get right?
For our experiments, even crudely-chosen parameter values (as we have
done so far) work well. This robustness seems to be due to two
features: (1) the large amount of data that inference can work with
and (2) the strong behavioral patterns evident in code. Further, these
numbers seem portable across codebases. In a separate
paper [20], when we took the parameters learned on one
codebase A and used them for inference on another codebase B the
results were imperceptible compared to learning
them directly on B from a perfect set of known annotations. (We
discuss the mechanics of learning in § 6.3.)
However, assume a hypothetical case where neither approach works.
Fortunately, the way annotations get consumed provides algorithmic
ways to converge to good parameter values. First, we commonly run
inference repeatedly over a codebase as it evolves over time — thus,
there will be significant numbers of known annotations from previous
runs. Because our approach easily incorporates known information (in
this case previously validated annotations), users can (1) apply
machine learning to refine parameter values, (2) recompute annotation
probabilities, or (3) do both simultaneously. In all cases results
will improve.
The same approach works even when applying inference to a codebase
for the first time. Annotations either get consumed directly or get fed
to an error checking tool. In both cases we can sort the annotations
or errors (based on the probabilities of their underlying annotations)
from most-to-least probable, and inspect them by going down the list
until the number of inference mistakes becomes annoying. We then rerun
inference using the validated annotations as discussed above.
Second, it is generally clear how to conservatively bias parameters
towards higher precision at the expense of lower recall. For example,
assume we feed inferred annotations to a checker that flags storage
leaks (ro without a subsequent co). We can strongly bias against
the ro annotation to the extent that only a function with a very low
error rate can get classified as an ro. While this misses errors
initially, it ensures that the first round of inspections has high
quality errors. Rerunning learning or inference will then yield a
good second round, etc.
4 Annotation Factor Graphs
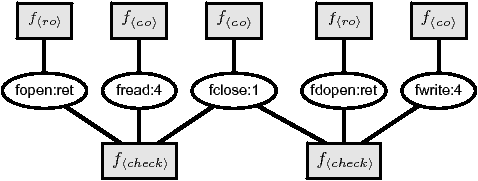
Figure 4: Factor graph for the code example in
Figure 3. Rectangular nodes represent factors
and round node represent annotation variables. The top factors
represent factors for prior beliefs (§ 3.4), while
the bottom factors represent behavioral tests (checks)
(§ 5.1).
While Equation 1 is the formal backbone of our
framework, in practice we operate at a higher level with its
corresponding visual representation called a factor graph. A factor
graph is an undirected, bipartite graph where one set of nodes
represent the variables A and the other set of nodes represent
the factors { fj }.
We call the factor graphs we construct for annotation inference
Annotation Factor Graphs (AFGs).
Figure 4 depicts an AFG for the code example
in Figure 3. Depicted are nodes for annotation
variables, factors for prior beliefs (§ 3.4), and
factors that represent two distinct checks of the code fragment. Each
factor node (square) maps to a distinct factor multiplicand in
Equation 1, each variable node (oval) maps to an
annotation variable,
and an edge exists between a factor node and variable node if the variable
is an input to the given factor.
Further, beliefs about one variable can influence another if there is
a path between them in the graph. For example, observe that the
AFG in Figure 4 explicitly illustrates the
indirect correlation between fopen and fdopen through
their relationship to fclose. If we believe that fopen
is an ro, this belief propagates to the belief that fclose is
a co because of the check for fp1. This belief then
propagates to the belief that fdopen is an ro because of the
check for fp2. While the AFG illustrates this flow of
correlation, the underlying machinery is still
Equation 1. Thus AFGs meet our criteria for an
inference framework capable of combining, propagating, and reasoning
about imperfect information.
A benefit of factor graphs is that they more compactly represent
P(A) than the table in
Section 3, which scales exponentially in the
number of possible annotations. The inference algorithm we use to
infer probabilities for annotations (§ 6.2)
operates directly on the AFG, forgoing the need to build a
table and exploiting the graphical structure to determine which
features influence others.
5 Advanced Inference Techniques
Building on our concept of AFGs, this section goes beyond the
basic inference techniques of Section 3 to more
advanced themes. We keep our discussion concrete by exploring how to
build factors for the ownership problem that incorporate multiple,
differently-weighted behavioral tests (§ 5.1),
exploit ad hoc naming conventions (§ 5.2), and
handle a function that may have no good labeling for a specification
because it grossly violates the ownership idiom
(§ 5.3). Our experiments (§ 7)
evaluate an AFG with all of these features. While we discuss
these points in terms of the ownership problem, they readily apply to
other inference tasks.
5.1 Multiple Behavioral Tests
The properties we wish to infer almost always have multiple behavioral
signatures. For signatures that are mutually exclusive (i.e., only
one behavior can be exhibited at once) we can define a single check
factor that weighs the different observed behaviors. For non-exclusive
behaviors, we can simply define different factors as we have done so far.
We thus focus on the former. We illustrate the technique by refining
the checker in Figure 2 from a checker which reduced
all behaviors to two mutually exclusive states ({ Bug, OK }) to
one which captures more nuanced behavior with five final states,
given in Figure 5. The five signatures it accepts are:
Deallocator: a ro's returned pointer reaches
a single matching co that occurs at the end of the trace.
Ownership: a ro's returned pointer
reaches a single matching co
that does not occur at the end of the trace (i.e., is followed
by one or more ¬co functions).
Contra-Ownership: a ¬ro's returned
pointer only reaches ¬cos.
Leak: an error where
a ro's returned pointer does not reach a co.
Invalid use: an error, includes all
misuses besides Leak.
We assign weights to these outcomes as follows. First, we bias away
from the promiscuous assignment of ¬ro-¬co (accepted
by Contra-Ownership) and towards ro-co (accepted by
Deallocator) by giving Deallocator twice the weight
of Contra-Ownership. Since Deallocator is the harshest
test, we use it as a baseline, giving it the weight 1.0 and, thus,
Contra-Ownership the weight 0.5. The other non-error case,
Ownership, is the least intuitive (and we arrived at it after some
experimentation): we weigh it slightly less than Contra-Ownership
since otherwise the AFG over-biases towards ro-co annotations.
As before, we weight error states less than non-error states
because of the assumption that programs generally behave correctly
(§ 2.1). Thus, for errors we assign a low score:
0.1 for leaks and 0.01 for all other bugs (the latter occurring
very rarely in practice). (Note that even if a codebase had no
errors we would still assign these outcomes non-zero values since static
analysis imprecision can cause the checker to falsely flag “errors.”)
Although all of these weights were specified with simple heuristics,
we show in Section 7 that they provide
respectable results. Moreover, such weights are amenable to automatic
tuning (§ 6.3).
| Extended-DFA State |
f< check > |
Reason for weight |
| Deallocator |
1.0 |
Baseline |
| Contra-Ownership |
0.5 |
Weight half as much as Deallocator |
| Ownership |
0.3 |
Slightly less than Contra-Ownership |
| Leak |
0.1 |
Low weight: errors are rare |
| Invalid Use |
0.01 |
Such errors are very rare |
Table 2: Values of f< check
> for the behavioral signatures for the ownership idiom.
Observe that for this factor the values do not sum to 1, but instead
are based reasoning about relative “reward.”

Figure 5: Complete DFA used by a static checker to
implement behavioral tests for Ownership. Shaded nodes are error
states.
5.2 Ad Hoc Knowledge: Naming Conventions
Ad hoc knowledge captures information such as biases for certain
annotations, naming conventions, and other heuristics. We further
illustrate how to express such features by using factors to model naming
conventions.
Given a list of keywords suggestive of an ro annotation (e.g.,
“alloc”, “open”), we construct a factor f< keyword, ro > for each function whose name
contains the keyword as a substring:
|
f< keyword, ro >(A)
= |
⎧
⎨
⎩ |
| θ< keyword, ro > |
: |
A = ro |
| θ< keyword, ¬ro > |
: |
A = ¬ro |
|
|
For co variables, the construction is similar, except that instead
of the factor being associated with one ro annotation variable, it
is associated with all the co annotation variables for a function.
If any of those variables have the value co, then the factor
maps to θ< keyword, co > and to θ<
keyword, ¬co > otherwise. Our reasoning is that naming
conventions imply that at least one of the parameters should have
a co annotation.
We only construct such factors if the function
contains the keyword; in our experience while the presence of a
keyword may suggest a function's role, the
absence of a keyword usually provides no additional information.
5.3 Does the Model Fit?
The ownership idiom only approximates how developers use resources.
Thus, there will be functions that do not fit it (e.g., byzantine uses
of reference counting).
If a function is far enough outside the ownership model,
then no matter what annotation(s) we assign it, ro or ¬ro,
co or ¬co, the checker will flag a proliferation of
“errors.” This problem arises in many inference contexts: the property
we want to infer assumes some structure of how code behaves, and when
those assumptions are wrong, the resultant noise can hurt inference
dramatically. AFGs let us tackle this problem by simply
modeling the possibility that a function may not fit the ownership. We discuss two ways to do so.
The first way just adds another annotation ¬fit
to the domain of our annotation variables and models “not fitting” as
yet another behavioral signature (as in § 5.1).
We modify the checker described in Section 5.1 so
that if it encounters a ¬fit annotation while
checking it transitions to a special end-state Outside Model.
For the ownership idiom, this increases the number of end-states in
the checker DFA from five to six. We then change f< check
> to assign Outside Model a value slightly above
those for errors but below that of acceptable states (e.g., 0.2).
Thus, if all values for an annotation variable cause many errors, we
will overcome our bias against the ¬fit value
and classify the variable as not fitting the model. Once an annotation
variable is classified as ¬fit, all behavioral
tests involving that function are effectively discarded since the
outcomes of those checks will always be Outside Model. Thus,
Outside Model represents a state where the checker accepts
any behavior, regardless of the annotation values.
The second way treats the not-fit property more globally: if the
annotation variables for a function's return value or any of its
formal parameters cause it to not fit, we remove the entire function
from our checks. Implementing this requires correlating annotation
variables in the AFG in a new way by adding a
“meta-annotation” for each function whose corresponding annotation
variable has the domain { fit,
¬fit }. For example, for the function
fopen we would create the variable fopen:fit.
Similarly as above, we modify the checker to include an
Outside Model state, but because the not-fit property is now
shared by all of the function's annotation variables, the checker
consults the fit-variable for a function immediately prior to
consulting the values of any of the function's regular annotation
variables. As before, when the value is ¬fit the checker
transitions to Outside Model; otherwise execution continues
as normal by consulting the regular annotation variable and taking the
usual transition in the DFA. Consequently, a function's fit-variable
serves as an additional input to each check factor that involves at
least one of the function's regular annotation variables. As before,
we state a strong bias toward a value of fit by attaching a
prior belief factor to the fit-variable.
Thus, if all values for any of a function's
annotation variables lead to many errors, we overcome our bias against
the ¬fit value and classify the function as not
fitting the model.
As described in Section 7.3, this second
construction found aspects of Linux that proved noisome for inference.
Moreover, neither approach is specific to the ownership idiom and can
be applied to other annotation inference domains.
6 Implementation
We now discuss our implementation, including the
details of the actual checker and how probabilities are
computed in practice from the AFG.
6.1 The Checker
Our program analysis is built on CIL [27]
and is similar to xgcc [15]: unsound, but
efficient and reasonably effective. The analysis engine, written in
OCaml, is partially derived from the version of
xgcc as described in Chou's thesis [6].
Our entire factor graph implementation is written in OCaml as well.
For the ownership checker, beyond constructing checks for every
callsite that returns a pointer, we track the use of string constants
within the function and treat them as if they were returned by a
¬ro. Pointer dereferences are modeled as implicit calls to a
¬co function to monitor if an owning pointer is used in any way
after it is claimed. We also perform minor alias tracking: when
tracking a pointer p and we observe the expression q = p
(where q is a local variable) we add q to p's
alias set. We do not model ownership transfer from p to
q (unlike [18]) and simply treat q as
another name for p since both pointers are local variables
(i.e., the reference has not escaped the function). Further, when a
tracked pointer is involved in a return statement, we consult
the corresponding ro (¬ro) annotation of the enclosing
function and treat it essentially as a co (¬co) annotation
except that for error conditions we always transition to the
Invalid Use state. This follows from the intuition that
while programmers may accidentally leak resources on unforeseen paths,
when implementing a function they reason very consciously about the
properties of the function's return value. Hence ownership errors at
return sites are considered very rare. This allows the
AFG to model a form of inter-procedural reasoning that handles
idioms such as wrapper functions.
Because the checker analyzes multiple paths stemming from a single
pointer returning callsite, we summarize the results over all analyzed
paths by reporting the most pessimistic DFA state found:
Invalid Use, followed by Leak, Ownership,
Contra-Ownership, and finally
Deallocator. The idea is to penalize annotations that induce
errors, and reward annotations that completely obey our strictest
behavioral signatures.
Finally, there are paths the checker does not analyze because they are
beyond its limited reasoning capability. We abort the analysis of
paths where a tracked pointer is stored either into a global or the
field of a structure. If all the paths for a given check would be
discarded (this is determined when the AFG is constructed) the
check is not included in the AFG. While this leads to some
selection bias in the paths we observe, our decision was to focus on
paths that would provide the cleanest evidence of different behavioral
signatures. Accurately modeling the heap shape of systems programs
statically is an important open problem that we (fortunately) did not
need to solve in order to infer properties of many functions.
6.2 Probabilistic Inference
In theory it is possible to compute probabilities for
annotations by directly using Equation 1, but this
requires enumerating an exponential number of combinations for the
values of annotation variables. Instead, we estimate probabilities
using
Gibbs sampling [13], which generates
approximate samples from the distribution P(A).
Abstractly this algorithm simulates a random walk through a Markov
chain. Theory shows that once the chain is run long enough it
converges to its stationary distribution (equilibrium), and sampling
from that distribution is equivalent to drawing samples from
P(A).
0.51ex
| ▷ A: annotation variables, known: known annotations |
| GibbsSample(A, known) |
|
a = {} |
|
▷ initial random values |
|
for v ∈ A, v ∉known |
|
|
a[v] = RandomValue(Domain(v)) |
|
▷ burn in the sample |
|
for j = 1 to 1000 |
|
|
for v ∈ PermuteVariables(A), v ∉known |
|
|
|
N = 0.0 |
|
|
|
▷ compute all scores that rely on v's annotation |
|
|
|
for d ∈ Domain(v) |
|
|
|
|
scores = {} |
|
|
|
|
a[v]= d |
|
|
|
|
scores[d] = FactorsScore(v, a) |
|
|
|
|
N = N + score[d] |
|
|
|
▷ normalize scores |
|
|
|
for d ∈ Domain(v) |
|
|
|
|
scores[d] = scores[d] / N |
|
|
|
a[v] = DistributionSample(scores) |
|
return a
|
.51ex
Figure 6: Pseudocode for Gibbs sampling from P( A).
While the full details of Gibbs sampling are beyond the scope of this
paper, the pseudocode for generating samples is depicted in
Figure 6. Gibbs sampling has two key advantages over
other algorithms: (1) it treats the checker implementation as a black
box and (2) at all times there is a complete assignment of values (in
a) to all the variables in the AFG. The upshot is that we
always run the checker with a full set of annotations.
To generate a single sample, we
perform “burn-in,” a process of iteratively adjusting the values
of the variables to drift them towards a configuration consistent with
being drawn from P(A). Determining the
minimum number of iterations for the burn-in is generally
perceived as a black art; we have chosen a large number (1000) that
has yielded consistently reliable results.
Each iteration of the burn-in visits each variable v in the
AFG in random order. To generate a new value for v, for
each of its possible values we call FactorsScore to compute the
product of all the factors in the AFG that share an
edge with v.
This computation will re-run
the checker for every check in which v appears. The result
is a single non-negative score for each value d of v.
The scores are then normalized to create a probability distribution over
v's values, and finally a new value for v is sampled from this
distribution.
After the burn-in completes, we take a snapshot of the values of
all variables and store it as a single sample from
P(A). From these samples we estimate
probabilities for annotations. For example, to estimate the
probability that an annotation has the value ro, we simply count the
fraction of samples where it had the value ro.
This naďve description is subject to numerous well-known
improvements.
First, all computations are done in log-space to avoid problems with
arithmetic roundoff. Second, we apply standard “annealing”
tricks to improve convergence of the simulated Markov chain.
Our most important optimization (which we devised specifically for
AFG inference), involves the execution of the
checker. Because the checker will be executed many times, we
cache checker results for each check by recording what values in
a the checker consulted and storing the outcome of the
check in a trie. This memoization is agnostic to the details of the
checker itself, and leads to a two orders of
magnitude speedup. The caches tend to be fairly well populated after
generating 3-5 samples for the AFG, and is the primary reason
the algorithm scales to analyzing real codebases.
6.3 Learning Parameters
If some annotations are known for a codebase, the parameters of an
AFG can be learned (or tuned) by applying
machine learning. The general approach to learning parameters
for factor graphs is to apply gradient ascent to maximizing the
likelihood function, where in this case the data is the set of
known annotations. At a high level, gradient ascent iteratively tunes
the parameters of the AFG to maximize the probability that the
known annotations would be predicted using Equation 1.
Full derivation of the gradient and the specific details for getting
gradient ascent to work for AFGs is beyond the scope of this
paper, but complete details can be found in [20].
Section 7.4 discusses our experience with
parameter learning for leveraging codebase naming conventions.
7 Evaluation
We applied our technique to five open source codebases: SDL, OpenSSH,
GIMP, XNU, and the Linux kernel. Table 3 gives
the size of each codebase and its corresponding AFG. For each
codebase's AFG we generated 100 samples using Gibbs sampling
to estimate probabilities for annotations. We sort annotations from
most-to-least probable based on these annotation probabilities. Note,
we provided no “seed” annotations to the inference engine (e.g., did not include malloc, free).
Since ro and co represent two distinct populations of annotations,
we evaluate their accuracy separately. For our largest AFG
(Linux), Gibbs sampling took approximately 13 hours on a 3 GHz dual-core Intel
Xeon Mac Pro, while for the smallest AFG (SDL) sampling finished
in under 5 minutes. Unless otherwise noted, the AFGs we evaluate
include the factors for modeling prior biases (§ 3.4)
and for multiple behavioral tests (§ 5.1).
Table 3 gives the breakdown of the “test set”
of annotations we manually classified for each codebase. We selected
the test set by: (1) automatically extracting a list of
all functions involved in a check, (2) randomly picking n functions (100
≤ n ≤ 200) from this list, and (3) hand classifying these n functions.
Note that this method produces a very harsh test set for inference because
it picks functions with few callsites as readily as those with many.
A seemingly innocent change produces a drastically easier test set:
pick n functions from a list of all callsites. The selected test set
would inflate our inference abilities since the probability of picking a
function scales with the number of callsites it has. As a result, most
functions in the test set would have many callsites, making inference
much easier. In aggregate, we manually classified around 1,000 functions,
giving a very comprehensive comparison set.
We first measure the accuracy of inferred annotations
(§ 7.2). We then discuss
the model's resilience to unanticipated coding idioms
(§ 7.3).
We next discuss our experience extending the core AFG
model with keyword factors
(§ 7.4). Finally we discuss
using inferred annotations as safety nets for
bug-finding tools (§ 7.5) and for finding bugs
(§ 7.6).
| |
|
AFG Size |
Manually Classified Annotations |
| Codebase |
Lines (103) |
|A| |
# Checks |
ro |
¬ro |
ro/¬ro |
co |
¬co |
co/¬co |
Total |
| SDL |
51.5 |
843 |
577 |
35 |
25 |
1.4 |
16 |
31 |
0.51 |
107 |
| OpenSSH |
80.12 |
717 |
3416 |
45 |
28 |
1.6 |
10 |
108 |
0.09 |
191 |
| GIMP |
568.3 |
4287 |
21478 |
62 |
24 |
2.58 |
7 |
109 |
0.06 |
202 |
| XNU |
1381.1 |
1936 |
9169 |
35 |
49 |
0.71 |
17 |
99 |
0.17 |
200 |
| Linux |
6580.3 |
10736 |
92781 |
21 |
31 |
0.67 |
19 |
93 |
0.20 |
164 |
Table 3: Quantitative
breakdown for each codebase of: (1) the size of the codebase, (2)
the size of constructed AFG, and (3) the composition of the
test set used for evaluating annotation accuracy. For the
AFG statistics, |A| denotes the number of annotation
variables.
7.1 Codebases
We evaluated our technique on important, real-world applications and
systems based on both their size and their disparate
implementations. We strove for project diversity in coding idioms and
resource management.
The smallest project, SDL, is a
challenge for inference because most functions have few callsites
(most are called fewer than four times). Further, because it
was originally developed for porting games from
Windows to Linux, it employs uncommonly-used resource management
functions from external libraries such as XLib. Thus, inferring these
functions is not only challenging but also useful. As our results
show, the AFG model readily infers correct ro and co
annotations for functions in SDL that have as few as one or two
callsites.
OpenSSH and the GIMP are widely-employed applications with
modest to large source code size.
The GIMP
image manipulation program uses custom memory management functions and
a plug-in infrastructure where plug-ins are loaded and unloaded on
demand and where leaking plug-in memory is not considered an error
because of their short lifetime. Despite such noise, our AFG
worked well, and discovered several memory leaks in the GIMP core.
XNU (the kernel for Mac OS X)
contains many specialized routines for managing kernel resources.
Our results are mostly for the core kernel because much of the
rest of XNU is written in C++,
which our front-end does not handle.
Inferred annotations for XNU immediately led to the discovery of bugs.
The Linux 2.6.10 kernel is a strong test because it is
huge and its code frequently breaks the ro-co idiom due to
sporadic use of (among other things) reference-counting
and weird pointer mangling.
Despite these challenges, our AFG
successfully analyzed Linux
with a reasonable annotation accuracy.
Note that AFG size scales with the number of checks, which
only roughly correlates with code size: we ignore functions not
involved in at least one check and (by necessity) skip function
implementations our C front-end had difficultly parsing.
7.2 Annotation Accuracy
| |
|
Inspections by P(ro) |
Inspections by P(co) |
| Codebase |
Inspections |
ro's |
¬ro's |
co's |
¬co's |
| SDL |
10 |
10 |
0 |
9 |
1 |
| |
20 |
20 |
0 |
17 |
3 |
| OpenSSH |
10 |
10 |
0 |
10 |
0 |
| |
20 |
19 |
1 |
16 |
4 |
| GIMP |
10 |
10 |
0 |
9 |
1 |
| |
20 |
20 |
0 |
16 |
4 |
| XNU |
10 |
9 |
1 |
9 |
1 |
| |
20 |
16 |
4 |
17 |
3 |
| Linux |
10 |
8 |
2 |
9 |
1 |
| |
20 |
17 |
3 |
18 |
2 |
Table 4: Absolute number of ro (co)
annotations found within the first 10 and 20 inspections for each
codebase.
This section measures the accuracy of our inferred specifications.
Our first experiment, shown in Table 4, gives
a feel for the initial accuracy of inferred annotations. It presents
the results from the first 10 and 20 inspections of the highest
probability annotations for each codebase. These are selected from
all the annotation variables in the AFG. The table
assumes that the ro and co annotations are inspected separately,
although this need not be the case in practice. The first few
inspections are important as they represent our most confident
annotations and will be the basis of a user's initial impression of
the results. These top ranked annotations have near perfect accuracy for ro's and
co's on all codebases.
[SDL: ro] 
[SDL: co] 
[OpenSSH: ro] 
[OpenSSH: co] 
[GIMP: ro] 
[GIMP: co] 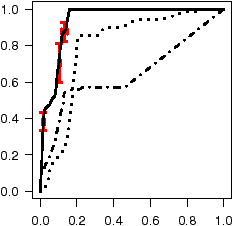
[XNU: ro] 
[XNU: co] 
[Linux: ro] 
[Linux: co] 
Figure 7: ROC curves depicting accuracy of inferred annotations.
Results are averaged over 10 runs where we add Gaussian
noise to AFG parameters. Error bars (shown at the
classification probability thresholds of 0.95, 0.7, and 0.4) depict
standard deviations.
We then more thoroughly measure annotation accuracy by comparing inferred
annotations to the entire test set for each codebase (from
Table 3). We also compare the accuracy of our base
AFG against two ablated (i.e., broken) ones: AFG−NoFPP,
which measures the effect of decreasing checker power, and
AFG−Rename, which measures the effect of decreased correlation.
Figure 7 shows the annotation accuracy of all three models for
each codebase test set using Receiver Operating Characteristics
(ROC) curves [11]. The ROC curve for ro annotations
plots the classification accuracy as the classification probability
threshold t slides from 1 to 0. Any annotation with a probability
P(A=ro) ≥ t is classified as ro, and ¬ro otherwise.
The x-axis depicts, for each value of t, the cumulative fraction of all
the ¬ro's in the test set that were mistakenly classified as ro
(the false positive rate, or FPR). The y-axis depicts
the cumulative fraction of all the ro's in the test set that were
correctly classified as ro (the true
positive rate, or TPR). Perfect annotation inference would
yield a 100% TPR with a 0% FPR (visually a step, with a line segment
from (0,0) to (0,1) and another from (0,1) to (1,1)), as all the
ro's appear before all of the ¬ro's when the annotations are
sorted by their probabilities. Random labeling yields a diagonal line
from ( 0, 0 ) to ( 1, 1 ). With ROC curves we can easily compare
accuracy across code bases since they are invariant to test set size and
the relative skew of ro's to ¬ro's and co's to ¬co's.
Basic AFG: as can be seen in the figure, the AFG model
has very high accuracy for all codebases except Linux, where accuracy is
noticeably lower but still quite good. SDL, had both the least code
and the highest annotation accuracy, with a nearly perfect accuracy
for co's. Further, 35% of all ro's for SDL are found without
inspecting a single ¬ro. For OpenSSH we observe around a 90%
TPR with a FPR of 10% or less. Both GIMP and XNU observe an 80%
or better TPR for both ro's and co's with a 20% FPR.
| |
# Callsites per Function |
% of Functions with … |
| Codebase |
Mean |
Median |
≥ 5 Callsites |
≥ 10 Callsites |
| SDL |
4.51 |
2 |
22.4 |
9.3 |
| OpenSSH |
7.41 |
2 |
23.0 |
11.5 |
| GIMP |
13.11 |
2 |
32.6 |
21.2 |
| XNU |
9.19 |
2 |
24.0 |
11.5 |
| Linux |
4.22 |
2 |
20.7 |
9.7 |
Table
5: Summary statistics
of the number of callsites per function (only for callsites that are
consulted by at least one check). Since the mean number of callsites
per function is much higher than the median, the number of callsites
has a long-tailed distribution.
Accuracy appears to decrease with increased codebase size. While
inspecting results, we observed that larger codebases frequently violate
the ro-co idiom and have a lot of code beyond the reasoning power of our
checker. However, even the hardest codebase, Linux, had decent accuracy:
we were able to infer 70% (62%) of ro (co) functions with
a 30% FPR.
While Figure 7 depicts overall codebase accuracy (with an
aggregate annotation accuracy of 80-90% on the first four codebases,
assuming a classification probability threshold of 0.5), in truth
these numbers are highly pessimistic. First, as shown in
Table 4, the accuracy of both ro and co
annotations for the top ranked inspections (from the set of all
inferred annotations) is near-perfect across all codebases. Thus,
users will almost always see valid annotations when inspecting the
highest confidence results.
More importantly, we observe on all codebases that the distribution of
the number of callsites per function is highly skewed
(Table 5), with a little over 50% of all functions
being called at most twice, and only 20-30% being called five times
or more. Assuming we classify, using a probability threshold of
0.5, the annotations for functions that are called five or more
times, we observe on all codebases (including Linux) an 80-95%
accuracy for both ro and co annotations, and an overall accuracy
of 90%. While annotation accuracy for single callsite functions is
important, correctly inferring annotations for functions that are
called at least a few times often has much higher practical impact
because those annotations will be used throughout a codebase (and
often provide the greatest traction for bug-finding tools). Moreover,
our annotation accuracy for single callsite functions is far
better than random labeling. For such functions, on Linux
the AFG model
correctly infers around twice as many ro and co
annotations as
random labeling for the same number of inspected false positives.
AFG-NoFPP: reduces the checker's analysis precision by
disabling false path pruning [6] (FPP), which eliminates
many bogus paths through the code that static analysis would otherwise
believe existed. In practice FPP reduces false error messages by
recognizing many control-dependent branches such as:
if( x == 1 ) p = malloc();
...
if( x == 1 ) free(p);
Disabling FPP will cause the checker to believe that there are
four possible paths instead of two. Consequently, removing FPP generates
significant noise in the checker's results (the next section provides
more detail). Unsurprisingly, for all codebases, AFG−NoFPP has
significantly reduced accuracy for co annotations due to false paths.
The main way false paths cause problems for ro-co inference is that they
make it appear that some functions claim a resource when in reality they
are never called in this manner. While this always has a negative impact
on co accuracy, because of the large ratio of ro's to ¬ro's
for GIMP (Table 3) this over-inflates the evidence
for ro annotations and leads to increased ro accuracy while still
having poor co accuracy. AFG−NoFPP performs very poorly
on XNU and Linux (to the degree that random labeling does better) as the
use of many resources in these codebases are highly control-dependent.
AFG-Rename: evaluates the benefit of exploiting
inter-correlation between annotations by systematically destroying it.
We do so by “renaming,” for each callsite, the called function
so that each callsite refers to a distinct function. This causes
AFG−Rename to have an annotation for each callsite of a
function. We compute probabilities for these annotations as normal,
but then compute probabilities for the original function annotations
(non-renamed) by averaging the probabilities across the per-callsite
annotations. The end result is that by we can see how much correlation
helps inference by contrasting the performance of AFG−Rename
to AFG.
The curves for AFG−Rename perform closest to AFG on
the smallest codebases, and gradually diverges (especially for co
accuracy) as we look at larger codebases. This is largely due to the
increased amount of correlation in the larger codebases. The accuracy
of AFG−Rename diverges significantly from AFG for
codebases larger than OpenSSH so that co performance degenerates to
that produced by AFG−NoFPP. (Note that for OpenSSH and GIMP, an
apparent bump in co accuracy of AFG−Rename over AFG
in the tail of the ROC curve is due a single co annotation, and is
within the margin of noise induced by the test set size.)
Sensitivity to magic numbers. As part of this experiment we also
measured our earlier claim that even rough guesses of AFG
parameters generate acceptable (initial) results by doing the
following sensitivity analysis. We perturb each AFG parameter
by a randomly generated amount of Gaussian noise (σ2 = 0.02),
which maintains the relative ordering between parameter values, but
skews their values slightly and thus their relative odds. We generate
10 sets in this manner, use them to infer annotations, and then report
averages and standard deviations (depicted as error bars in
Figure 7) across all runs.
In general, as the figure
shows, the error bars for AFG are quite small, illustrating
that our inference results were robust to small perturbations in parameter
values. While we believe the parameters are amendable to tuning, the
choice of numbers is not so brittle as to cause violent changes in
results when perturbed slightly.
7.3 Detecting Unanticipated Coding Idioms
Initially, classifications for Linux were slightly worse than the
other codebases because its ownership model is more subtle than the
one we attempt to infer. Using the fit model variables discussed in
Section 5.3, we quickly identified a corner case in
Linux that we needed to explicitly model in our checker. A common
practice in Linux is to conflate the values of pointers and to store
error codes in them instead of memory addresses. Since the kernel
resides in a restricted address space, error codes can be mangled into
pointer values that lie outside this region.
Such pointers are frequently tested as follows:
p = foo( ... );
if( IS_ERR_PTR(p) ) { /* error path */ }
On the true branch of such tests the reference to p appears
to be lost, when in reality it was not a valid pointer. This
causes serious problems because IS_ERR_PTR is far outside
our simple ro-co model. Because it appears hundreds of times,
inference computed a probability of 0.99 that this function did
not fit (¬fit) the ro-co model and
all checks involving IS_ERR_PTR were
effectively removed as evidence.
We immediately noticed the highly probable ¬fit value for IS_ERR_PTR
and modified our checker to
recognize the function and prune analysis of paths where
its return value for a tracked pointer is true, allowing
us to glean evidence from these checks.
7.4 Additional Information
Our last experiment for annotation accuracy looks at how overall
annotation accuracy for XNU improves as inference is given additional
information. We use (1) a set of 100 known good function annotations
to serve as a training set — in practice these would be harvested as
a checking tool is repeatedly run over a code base, and (2) a list of
substrings a programmer feels might be relevant to the labeling of a
function. We provided a relatively small set of 10 strings such as
“alloc” and “get,” but there is nothing to keep a motivated user
from listing all interesting strings from their problem domain. We
applied parameter learning to train the parameters for the keyword
factors based on a training set (as described in [20]), and
tested the classification accuracy on the remaining 100. We set the
classification probability threshold at 0.5 to indicate whether an
annotation was ro or ¬ro (co or ¬co) to get a
measure of overall accuracy.
For XNU, the baseline aggregate accuracy (inference without knowing
the training set) was 81.2%, and with the addition of knowing the
annotations in the training set accuracy of the test set increased to
84.2%. Knowledge of the training set during inference simulates
already knowing some of the annotations. Equipped with the keyword
information alone accuracy was 89.1%, with the addition of knowing
the annotations in the training set the accuracy was 90.1%. This
experiment demonstrates the power of our technique: we are able to
easily incorporate additional information and have that information
improve the accuracy of our results.
We also benchmarked these results against an AFG that only
included keyword and prior belief factors. While the top
ranked ro and co inferred annotations from this model were usually
correct, very quickly accuracy degrades as annotations are inspected.
Overall, ro and co accuracy is 22-33% worse when using keyword
information alone.
7.5 Safety Nets for Bug-Finding Tools
| |
Function |
Param. |
Label |
Sites |
Prob. |
| |
XAllocWMHints |
ret |
ro |
1 |
0.99 |
| X11 |
XFree |
1 |
co |
9 |
0.98 |
| API |
XGetVisualInfo |
ret |
ro |
1 |
0.97 |
| |
XListPixmapFormats |
ret |
ro |
1 |
0.97 |
| |
X11_CreateWMCursor |
ret |
ro |
1 |
0.95 |
| |
XOpenDisplay |
ret |
ro |
2 |
0.86 |
| |
XGetModifierMapping |
ret |
ro |
1 |
0.86 |
| |
XCreateGC |
ret |
ro |
2 |
0.84 |
| |
XFreeGC |
2 |
co |
2 |
0.82 |
| |
XFreeModifierMap |
1 |
co |
1 |
0.79 |
| |
XCloseDisplay |
1 |
co |
2 |
0.76 |
| |
dlopen |
ret |
ro |
1 |
0.95 |
| C |
opendir |
ret |
ro |
1 |
0.87 |
| Standard |
setmntent |
ret |
ro |
1 |
0.74 |
| Library |
closedir |
1 |
co |
1 |
0.73 |
| |
endmntent |
1 |
co |
1 |
0.58 |
Table 6:
A selection of correctly inferred labels for external functions
inferred from analyzing SDL and not in the Coverity Prevent “root
set.” “Sites” is the number of callsites for the given function
utilized by the program analysis and used for inference.
We evaluate our classifications by comparing the inferred ro and
co functions classifications for SDL against the allocator and
deallocator functions used by Prevent [7].
Coverity Prevent is a commercial static
analysis tool that contains several analyses to detect resource errors.
It performs an
unsound relaxation analysis through the call-graph to identify functions
that transitively call “root” allocators and deallocators such as
malloc and free. Prevent's analysis is geared to find as many
defects as possible with a low false error rate.
The set of allocators and deallocators yielded by our inference and
Prevent (respectively) perform a synergistic cross-check. Prevent
will miss some allocators because they do not transitively call known
allocators, and static analysis imprecision may inhibit the diagnosis
of some functions that do. On the other hand, Prevent can classify some
functions we miss since it analyzes more code than we do, has better alias
tracking and better path-sensitivity. It found four classifications that
our inference missed. We inspected each of the four and all were due
to the fact that our static analysis made mistakes rather than a flaw
in the inference algorithm.
Our belief that manual specifications will have holes was born out.
Inference found over 40 allocator and deallocator functions that
Prevent missed. Table 6 gives a representative
subset. Prevent missed the bulk of these because SDL uses obscure
interfaces which were not annotated and which were not part of the
SDL source code (and therefore it could not analyze them).
It is unclear what caused some of the omissions, though analysis
mistakes are the plausible candidate. This experiment shows that even
highly competent, motivated developers attempting to annotate all
relevant functions in a “root set” easily miss many candidates.
Finally, our inference found an annotation misclassified by Prevent's
relaxation. The function SDL_ConvertSurface returns a pointer
obtained by calling SDL_CreateRGBSurface. This function, in
turn, returns a pointer from malloc, a well-known allocator
function. Prevent misclassifies the return value of
SDL_ConvertSurface as ¬ro, an error likely due to the
complexity of these functions. Our checker also had problems
understanding the implementation of these functions, but correctly
inferred an ro annotation for its return value based on the context
of how SDL_ConvertSurface was used. We reported this
case to Coverity developers and they confirmed it was a misclassified
annotation.
void gimp_enum_stock_box_set_child_padding (...) {
GList *list;
...
for( list = gtk_container_get_children(...); list;
list = g_list_next(list) ) { ... }
}
Figure 8: [BUG] gtk_container_get_children returns a newly
allocated list. The pointer to the head of the list is lost after the
first iteration of the loop.
GList* gtk_container_get_children (GtkContainer *container) {
GList *children = NULL;
/* gtk_container_foreach performs a copy of
the list using an iterator interface and
a callback to perform an element copy. */
gtk_container_foreach (container,
gtk_container_children_callback,
&children);
/* The list "children" is reversed. The last pointer
in the list is now the owning pointer. */
return g_list_reverse (children);
}
Figure 9:
Source code from the Gtk+ library of
gtk_container_get_children. The function performs a complicated
copy and reversal of a linked list. Inference labels the return value
(correctly) as ro without analyzing the implementation.
7.6 Defect Accuracy
Using our inference technique, we diagnosed scores of resource bugs
(most of them leaks) in all five codebases, but since our focus was on
annotation accuracy, we did not perform an exhaustive evaluation on
all codebases of the quantity of bugs our tool found. All diagnosed
bugs were discovered by ranking errors by the probabilities of the
annotations involved, and for each codebase led to the
discovery of bugs within minutes.
One particular bug found in GIMP highlights the inferential power of
AFGs.
Figure 8 shows an incorrect use of
the function gtk_container_get_children (whose
return value we correctly annotate as ro) in the core GIMP code and
illustrates the power of being able to infer the annotation for a
function based on the context in which it is used. This function
returns a freshly allocated linked list, but in this code fragment a
list iteration is performed and the head of the list is immediately
lost. We did not analyze the source of the Gtk+ library when
analyzing GIMP; this annotation was inferred solely from how the
function was used.
The implementation of gtk_container_get-_children,
excerpted in Figure 9,
shows how the list
is created by performing a complicated element-wise copy (involving a
custom memory allocator) after which the list is reversed, with the new
head being the “owning” pointer of the data structure. Even if the
implementation were available, understanding this
function would pose a strenuous task for classic program analysis.
8 Related Work
Most existing work on inferring specifications from code looks for
rules of the form “do not perform action a before action b” or
“if action a is performed then also perform action b.” The
inferred rules are captured in (probabilistic) finite-state
automata (FSAs and PFSAs).
Engler et al [9] infer a variety of properties from
template rules, including a-b pairs in systems code.
Examples include inferring whether
malloc is paired with free, lock with unlock,
whether or not a null pointer check should always be
performed on the return value of a function, etc. The
intuition is that frequently occurring patterns are likely to be
rules, while deviant behavior of strongly observed patterns are
potential bugs.
Our work can be viewed as a natural generalization of this earlier
work to leverage multiple sources of information and exploit
correlation.
Weimer and Necula [30] observed that
API rule violations occur frequently on “error paths” such as
exception handling code in Java programs. Consequently, they
weight observations on these paths differently from regular code.
We observe similar mistakes in systems code, although there identifying
an error path is not always trivial. This poses a potential
form of indirect correlation to exploit for inferring
annotations. High confidence specifications can be used to infer
error paths, which in turn can be used to infer other specifications.
Li and Zhou [22] and Livshits and Zimmerman [25]
look for generalized a-b patterns in code.
Li and Zhou look for patterns across a codebase, whereas Livshits and
Zimmerman look at patterns that are correlated through version control
edits. While general, these approaches are based on data mining
techniques that often require large amounts of data to derive
patterns, meaning it is unlikely they will be able to say anything
useful about infrequently called functions. It is also unclear how to
extend them to incorporate domain specific knowledge.
Ammons et al [2] have a dynamic analysis to learn
probabilistic finite-state automatons (PFSAs)
that describe the dependency relationship between a series of function
calls with common values passed as arguments.
Concept analysis is then used to aid the user, somewhat successfully,
in the daunting task of debugging the candidate
PFSAs [3]. Their method suffers from the usual code
coverage hurdles inherent in a run-time analysis, making it difficult
for such methods to infer properties about rarely executed code. They
also assume program traces that illustrate perfect compliance of the
rules being inferred (i.e., all traces are “bug-free”). This
limitation is overcome by Yang et al [34],
but unlike AFGs, their mechanism for handling noise and
uncertainty is specific to the patterns they infer.
In addition, it is unclear how to extend either method to
incorporate domain specific knowledge in a flexible and natural way.
Whaley et al [31]
derive interface specifications of the form
“a must not be followed by b” for Java method calls.
Their technique relies on static analysis of a method's implementation
to find out if calling b after a would produce a runtime error.
Alur et al [1] extend their method using
model checking to handle sequences of calls σ and to provide
additional soundness.
Although powerful, these techniques examine the implementation of
methods rather than the context in which they are used. The results
of such techniques are thus limited by the ability of the analysis to
reason about the code, and may not be able to discover some of the
indirectly correlated specifications our approach provides.
Hackett et al [14] partially automate the
task of annotating a large codebase in order to find buffer overflows.
Their method is used in an environment with significant user input
(over a hundred thousand user annotations) and is specific to their
problem domain. Further, it is unclear how to extend their technique
to leverage additional behavioral signatures.
Ernst and his collaborators developed Daikon
[10, 29], a system that infers program
invariants via run-time monitoring. Daikon finds simple
invariants specifying relational properties such as a ≥ b and x ≠ 0,
although conceivably inferring other properties is possible.
Their method is not statistical, and invariants inferred require
perfect compliance from the observed program.
More distantly related are techniques that tackle the inverse problem
of “failure inference” for postmortem debugging. The goal is to
diagnose the cause of a fail-stop error such as an assertion failure
or segmentation fault. Both pure static analysis [26] and
statistical debugging techniques have been employed with inspiring
results [16, 23, 24].
Although specification inference and failure inference have different
goals, we believe that many of the ideas presented in this paper could
be readily applied in that domain.
9 Conclusion
This paper presented a novel specification inference framework based
on factor graphs whose key strength is the ability to combine
disparate forms of evidence, such as those from behavioral signatures,
prior beliefs, and ad hoc knowledge, and reason about them in the
common currency of factors and probabilities. We evaluated the
approach for the ownership problem, and achieved high annotation
accuracy across five real-world codebases. While our checker was
primitive, with inferred annotations we immediately discovered
numerous bugs, including those that would impossible to discover with
state-of-the-art program analysis alone.
10 Acknowledgements
This research was supported by NSF grants CNS-0509558,
CCF-0326227-002, NSF CAREER award CNS-0238570-001, and the Department
of Homeland Security.
We would like to thank Andrew Sakai and Tom Duffy for their help in
sorting out XNU bugs. We are grateful to our shepherd Peter Druschel
for his help, and Cristian Cadar, Junfeng Yang, Can Sar, Peter
Pawlowski, Ilya Shpitser, and Ashley Dragoman for their helpful
comments.
0.1
References
- [1]
-
R. Alur, P. Cerný, P. Madhusudan, and W. Nam.
Synthesis of interface specifications for java classes.
In Proceedings of the 32nd ACM SIGPLAN-SIGACT symposium on
Principles of programming languages, 2005.
- [2]
-
G. Ammons, R. Bodík, and J. R. Larus.
Mining specifications.
In Proceedings of the 29th ACM SIGPLAN-SIGACT symposium on
Principles of programming languages, pages 4–16, New York, NY, USA, 2002.
- [3]
-
G. Ammons, D. Mandelin, R. Bodík, and J. R. Larus.
Debugging temporal specifications with concept analysis.
In PLDI '03: Proceedings of the ACM SIGPLAN 2003 conference on
Programming language design and implementation, pages 182–195, New York,
NY, USA, 2003. ACM Press.
- [4]
-
W. Bush, J. Pincus, and D. Sielaff.
A static analyzer for finding dynamic programming errors.
Software: Practice and Experience, 30(7):775–802, 2000.
- [5]
-
H. Chen and D. Wagner.
MOPS: an infrastructure for examining security properties of
software.
In Proceedings of the 9th ACM conference on Computer and
communications security, pages 235 – 244. ACM Press, 2002.
- [6]
-
A. Chou.
Static Analysis for Finding Bugs in Systems Software.
PhD thesis, Stanford University, 2003.
- [7]
-
Coverity Prevent.
http://www.coverity.com.
- [8]
-
M. Das, S. Lerner, and M. Seigle.
Path-sensitive program verification in polynomial time.
In ACM SIGPLAN 2002 Conference on Programming Language Design
and Implementation, Berlin, Germany, June 2002.
- [9]
-
D. Engler, D. Chen, S. Hallem, A. Chou, and B. Chelf.
Bugs as deviant behavior: A general approach to inferring errors in
systems code.
In Eighteenth ACM Symposium on Operating Systems Principles,
2001.
- [10]
-
M. Ernst, J. Cockrell, W. Griswold, and D. Notkin.
Dynamically discovering likely program invariants to support program
evolution.
In IEEE Transactions on Software Engineering, Feb. 2001.
- [11]
-
T. Fawcett.
ROC Graphs: Notes and practical considerations for data mining
researchers.
Technical Report HPL-2003-4, Intelligent Enterprise Technologies
Laboratory, HP Laboratories Palo Alto, January 2003.
- [12]
-
C. Flanagan, K. Leino, M. Lillibridge, G. Nelson, J. Saxe, and R. Stata.
Extended static checking for Java.
In PLDI 2002, pages 234–245, 2002.
- [13]
-
W. R. Gilks, S. Richardson, and D. J. Spiegelhalter, editors.
Markov Chain Monte Carlo in Practice.
Chapman and Hall/CRC, 1996.
- [14]
-
B. Hackett, M. Das, D. Wang, and Z. Yang.
Modular checking for buffer overflows in the large.
In L. J. Osterweil, H. D. Rombach, and M. L. Soffa, editors, ICSE, pages 232–241. ACM, 2006.
- [15]
-
S. Hallem, B. Chelf, Y. Xie, and D. Engler.
A system and language for building system-specific, static analyses.
In ACM SIGPLAN 2002 Conference on Programming Language Design
and Implementation, 2002.
- [16]
-
S. Hangal and M. S. Lam.
Tracking down software bugs using automatic anomaly detection.
In International Conference on Software Engineering, May 2002.
- [17]
-
R. Hastings and B. Joyce.
Purify: Fast detection of memory leaks and access errors.
In Proceedings of the Winter USENIX Conference, Dec. 1992.
- [18]
-
D. L. Heine and M. S. Lam.
A practical flow-sensitive and context-sensitive C and C++ memory
leak detector.
In ACM SIGPLAN 2003 conference on Programming language design
and implementation, 2003.
- [19]
-
G. E. Hinton.
Products of experts.
Technical report, Gatsby Computational Neuroscience Unit, University
College London.
- [20]
-
T. Kremenek, A. Ng, and D. Engler.
A factor graph model for software bug finding.
Technical report, Stanford University, 2006.
- [21]
-
F. R. Kschischang, B. J. Frey, and H. A. Loeliger.
Factor graphs and the sum-product algorithm.
IEEE Transactions on Information Theory, 2001.
- [22]
-
Z. Li and Y. Zhou.
PR-Miner: Automatically extracting implicit programming rules and
detecting violations in large software code.
In 13th ACM SIGSOFT International Symposium on Foundations of
Software Engineering, Sept. 2005.
- [23]
-
B. Liblit, A. Aiken, A. X. Zheng, and M. I. Jordan.
Bug isolation via remote program sampling.
In ACM SIGPLAN 2003 Conference on Programming Language Design
and Implementation, San Diego, CA USA, 2003.
- [24]
-
B. Liblit, M. Naik, A. X. Zheng, A. Aiken, and M. I. Jordan.
Scalable statistical bug isolation.
In PLDI '05: Proceedings of the 2005 ACM SIGPLAN conference on
Programming language design and implementation, pages 15–26, New York, NY,
USA, 2005. ACM Press.
- [25]
-
B. Livshits and T. Zimmermann.
Dynamine: finding common error patterns by mining software revision
histories.
In 13th ACM SIGSOFT international symposium on Foundations of
software engineering, pages 296–305, New York, NY, USA, 2005. ACM Press.
- [26]
-
R. Manevich, M. Sridharan, S. Adams, M. Das, and Z. Yang.
PSE: explaining program failures via postmortem static analysis.
In Proceedings of the 12th ACM SIGSOFT twelfth international
symposium on Foundations of software engineering, pages 63–72, New York,
NY, USA, 2004.
- [27]
-
G. C. Necula, S. McPeak, S. Rahul, and W. Weimer.
CIL: Intermediate language and tools for analysis and
transformation of c programs.
In Proceedings of Conference on Compilier Construction, 2002.
- [28]
-
N. Nethercote.
Dynamic Binary Analysis and Instrumentation.
PhD thesis, University of Cambridge, 2004.
- [29]
-
J. H. Perkins and M. D. Ernst.
Efficient incremental algorithms for dynamic detection of likely
invariants.
In 12th ACM SIGSOFT twelfth international symposium on
Foundations of software engineering, 2004.
- [30]
-
W. Weimer and G. Necula.
Mining temporal specifications for error detection.
In 11th International Conference on Tools and Algorithms For The
Construction And Analysis Of Systems, 2005.
- [31]
-
J. Whaley, M. C. Martin, and M. S. Lam.
Automatic extraction of object-oriented component interfaces.
In Proceedings of the 2002 ACM SIGSOFT international symposium
on Software testing and analysis, 2002.
- [32]
-
Y. Xie and A. Aiken.
Context- and path-sensitive memory leak detection.
In 13th ACM SIGSOFT international symposium on Foundations of
software engineering, pages 115–125, New York, NY, USA, 2005.
- [33]
-
Y. Xie and A. Aiken.
Scalable error detection using boolean satisfiability.
In Proceedings of the 32nd ACM SIGPLAN-SIGACT symposium on
Principles of programming languages, pages 351–363, New York, NY, USA,
2005.
- [34]
-
J. Yang, D. Evans, D. Bhardwaj, T. Bhat, and M. Das.
Perracotta: mining temporal api rules from imperfect traces.
In 28th international conference on Software engineering, pages
282–291, New York, NY, USA, 2006.
- [35]
-
J. Yang, T. Kremenek, Y. Xie, and D. Engler.
MECA: an extensible, expressive system and language for statically
checking security properties.
In 10th ACM conference on Computer and communications security,
2003.
- [36]
-
J. S. Yedidia, W. T. Freeman, and Y. Weiss.
Understanding belief propagation and its generalizations.
In Exploring Artificial Intelligence in the New Millennium,
pages 239–269. Morgan Kaufmann Publishers Inc., 2003.
This document was translated from LATEX by
HEVEA.
|
