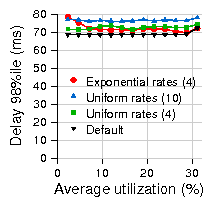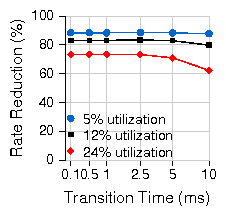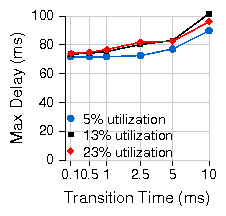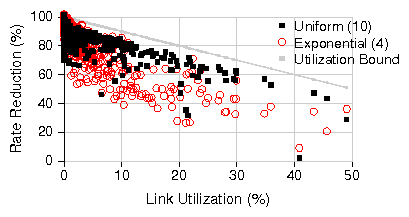
 |
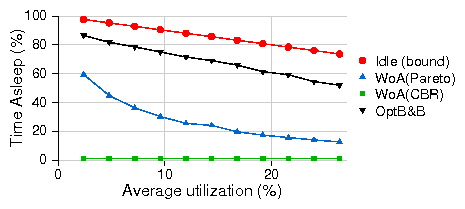
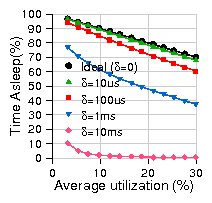
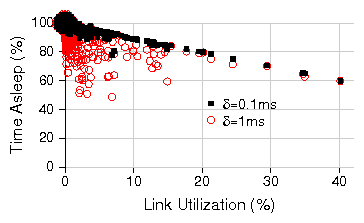
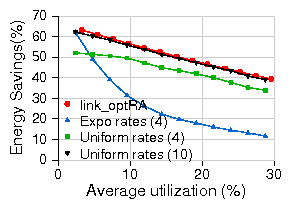
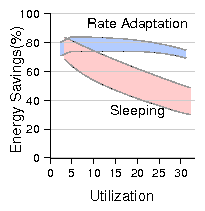
Figure 14: Comparison of energy savings between sleep and rate adaptation.
Support for dynamic voltage scaling.
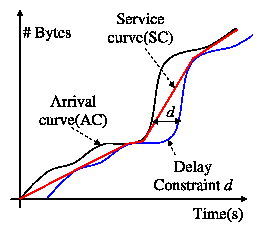
For further insight on what determines the boundary utilization, we
consider the scenario of a single idealized link. The sleep-mode
energy consumption of such an idealized link can be viewed as:
|
Esleep = pa(rmax) mT + ps(1-m)T |
| (7) |
Similarly, the idealized link with rate adaptation is one that
runs with an average rate of mrmax for an energy
consumption of:
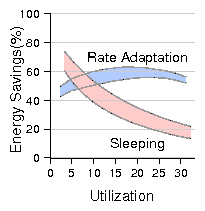
Figure 15 represents the boundary utilization for
this idealized link as a function of C. In this idealized scenario, the dominant
parameter is C because the link is never idle and therefore β has only
a small, indirect effect on ps. The gray zone in the figure
represents the spread in boundary utilization obtained by varying β
between 0.1 and 0.9.
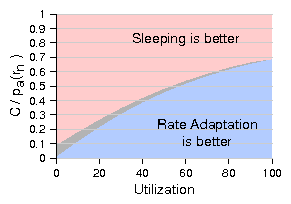 Figure 15: Sleeping vs. rate-adaptation
With frequency scaling alone: f(r)=O(r)
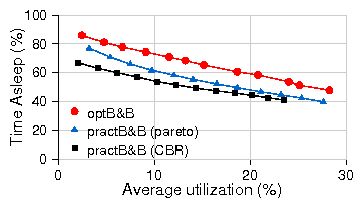
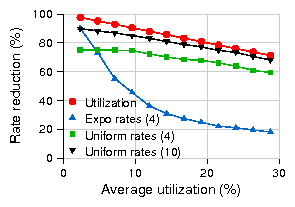
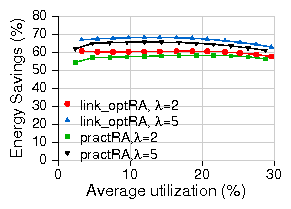
Figures 16 plots the overall energy savings for practRA and
practB&B for the different test scenarios in the more pessimistic scenario where
voltage scaling is not supported. Due to lack of space, we only plot the
comparison for the first two test scenarios where C=0.1; at C=0.3, the
savings show a similar scaling trend but with significantly poorer
performance for rate-adaptation and hence add little additional information.
The primary observation is that the savings from rate adaptation are significantly
lower than in the previous case with DVS and, in this case, sleeping outperforms rate adaptation
more frequently.
We also see that - unlike the DVS case - network utilization impacts energy savings in
a similar manner for both sleeping and rate-adaptation (i.e., the overall "slope" of the
savings-vs-utilization curves is similar with both sleeping and rate-adaptation
while they were dramatically different with DVS - see Fig. 14).
Once again, we obtain insight on this by studying the
the highly simplified case of a single idealized link.
For this idealized scenario with f(r)=O(r), we find that the
boundary condition that determines whether to use sleep or rate adaptation
is in fact independent of network utilization.
Instead, one can show that sleep is superior to rate-adaptation if the
following inequality holds:
Figure 15: Sleeping vs. rate-adaptation
With frequency scaling alone: f(r)=O(r)
Figures 16 plots the overall energy savings for practRA and
practB&B for the different test scenarios in the more pessimistic scenario where
voltage scaling is not supported. Due to lack of space, we only plot the
comparison for the first two test scenarios where C=0.1; at C=0.3, the
savings show a similar scaling trend but with significantly poorer
performance for rate-adaptation and hence add little additional information.
The primary observation is that the savings from rate adaptation are significantly
lower than in the previous case with DVS and, in this case, sleeping outperforms rate adaptation
more frequently.
We also see that - unlike the DVS case - network utilization impacts energy savings in
a similar manner for both sleeping and rate-adaptation (i.e., the overall "slope" of the
savings-vs-utilization curves is similar with both sleeping and rate-adaptation
while they were dramatically different with DVS - see Fig. 14).
Once again, we obtain insight on this by studying the
the highly simplified case of a single idealized link.
For this idealized scenario with f(r)=O(r), we find that the
boundary condition that determines whether to use sleep or rate adaptation
is in fact independent of network utilization.
Instead, one can show that sleep is superior to rate-adaptation if the
following inequality holds:
Otherwise, rate adaptation is superior.
In practice, network utilization does play a role (as our results clearly
indicate) because the various practical constraints due to delay bounds
and transition times prevent our algorithms from fully exploiting
all opportunities to sleep or change rates.
In summary, we find that both sleeping and rate-adaptation are useful,
with the tradeoff between them depending primarily on the power profile
of hardware capabilities and network utilization.
Results such as those presented here can guide operators in deciding how to best run their
networks. For example, an operator might choose to run the network with rate
adaptation during the day and sleeping at night based on where the boundary
utilization intersects diurnal behavior, or identify components of the network
with consistently low (or high) utilization to be run with sleeping (or
rate-adaptation).
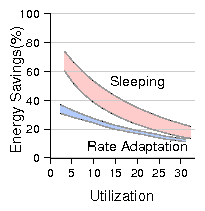
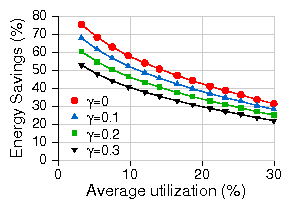
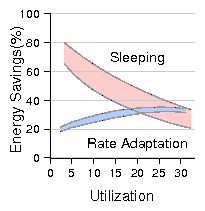
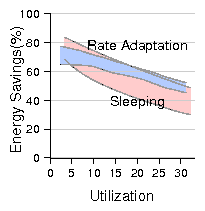 Figure 16: Energy savings of sleep vs. rate adaptation, β = 0.1, frequency scaling alone.
Figure 16: Energy savings of sleep vs. rate adaptation, β = 0.1, frequency scaling alone.
6 Related Work
There is a large body of work on power management in contexts complementary to ours.
This includes power provisioning and load balancing in data centers[5,8],
and OS techniques to extend battery lifetimes in mobiles[9,30].
Perhaps the first to draw attention to the problem of saving overall energy in the network
was an early position paper by Gupta et al. [12]. They use data from
the US Department of Commerce to detail the growth in
network energy consumption and argue the case for energy-saving
network protocols, including the possibility of wake-on-arrival in wired routers.
In follow-on work they evaluate the
application of opportunistic sleeping in a campus LAN environment [22,11].
Other recent work looks at powering-down redundant access points (APs) in enterprise
wireless networks [17]. The authors propose that a central server collect AP connectivity and utilization information
to determine which APs can be safely powered down. This approach is
less applicable to wired networks that exhibit much less redundancy.
Sleeping has also been explored in the context of 802.11 to save client power, e.g., see [2]. The 802.11 standard itself includes two schemes (Power-Save Poll and Automatic Power Save Delivery) by which access points may buffer packets so that clients may sleep for short intervals. In some sense, our proposal for bunching traffic to improve
sleep opportunities can be viewed as extending this idea deep into the network.
Finally, the IEEE Energy Efficient Ethernet Task Force has recently started to
explore both sleeping and rate adaptation for energy savings. Some initial
studies consider individual links and are based on synthetic traffic and
infinite buffers [3].
In the domain of sensor networks, there have been numerous efforts to design energy efficient
protocols. Approaches investigated include putting
nodes to sleep using TDMA-like techniques to coordinate transmission and
idle times (e.g., FPS [14]), and distributed algorithms for sleeping (e.g.,S-MAC [28]).
This context differs from ours in many ways.
7 Conclusion
We have argued that power management states that slow down links and put
components to sleep stand to save much of the present energy expenditure of
networks.
At a high-level, this is apparent from the facts that while network
energy consumption is growing networks continue to operate at low average
utilizations.
We present the design and evaluation of simple power management algorithms
that exploit these states for energy conservation and show that -
with the right hardware support - there is the potential for saving much
energy with a small and bounded impact on performance, e.g., a few milliseconds of delay.
We hope these preliminary results will encourage the development of hardware support for
power saving as well as algorithms that use them more effectively to realize
greater savings.
Aknowledgments
We thank Robert Hays, Bob Grow, Bruce Nordman, Rabin Patra and Ioan Bejenaru for their suggestions.
We also thank the anonymous reviewers and our shepherd Jon Crowcroft for their
useful feedback.
.90
References
- [1]
-
Power and Thermal Management in the Intel Core Duo Processor.
In Intel Technology Review, Volume 10, Issue 2, Section 4.
2006.
- [2]
-
Y. Agarwal, R. Chandra, et al.
Wireless wakeups revisited: energy management for voip over wi-fi
smartphones.
In ACM MobiSys. 2007.
- [3]
-
C. Gunaratne and K. Christensen and B. Nordman and S. Suen.
Reducing the energy consumption of Ethernet with Adaptive Link Rate
(ALR).
In IEEE Transactions on Computers. April, 2008.
- [4]
-
J. Chabarek, J. Sommers, et al.
Power awareness in network design and routing.
In INFOCOM 2008. 2008.
- [5]
-
J. S. Chase, D. C. Anderson, et al.
Managing energy and server resources in hosting centers.
In ACM SOSP. 2001.
- [6]
-
Cisco Systems.
NetFlow services and applications.
White Paper, 2000.
- [7]
-
X. Fan, C. S. Ellis, et al.
Memory Controller Policies for DRAM Power Management.
In International Symposium on Low Power Electronics and
Design. 2003.
- [8]
-
X. Fan, W.-D. Weber, et al.
Power provisioning for a warehouse-sized computer.
In ACM ISCA. 2007.
- [9]
-
J. Flinn and M. Satyanarayanan.
Energy-aware adaptation for mobile applications.
In ACM SOSP. 1999.
- [10]
-
C. Gunaratne, K. Christensen, et al.
Managing Energy Consumption Costs in Desktop PCs and LAN Switches
with Proxying, Split TCP Connections, and Scaling of Link Speed.
In International Journal of Network Management. October 2005.
- [11]
-
M. Gupta, S. Grover, et al.
A feasibility study for power management in lan switches.
In ICNP. 2004.
- [12]
-
M. Gupta and S. Singh.
Greening of the internet.
In ACM SIGCOMM, Karlsruhe, Germany. August 2003.
- [13]
-
R. Hays.
Active/Idle Toggling with Low-Power Idle,
http://www.ieee802.org/3/az/public/jan08/hays_01_0108 .pdf.
In IEEE 802.3az Task Force Group Meeting. 2008.
- [14]
-
B. Hohlt, L. Doherty, et al.
Flexible power scheduling for sensor networks.
In IEEE and ACM Third International Symposium on Information
Processing in Sensor Networks (IPSN). April 2004.
- [15]
-
IEEE 802.3 Energy Efficient Ethernet Study Group.
http://grouper.ieee.org/groups/802/3/eee_study/.
- [16]
-
Ipmon Sprint.
The Applied Research Group. http://ipmon.sprint.com/.
- [17]
-
A. Jardosh, G. Iannaccone, et al.
Towards an Energy-Star WLAN Infrastructure.
In HOTMOBILE. 2007.
- [18]
-
S. Kandula, D. Katabi, et al.
Walking the tightrope: Responsive yet stable traffic engineering.
In ACM SIGCOMM 2005.
- [19]
-
M. Lin and Y. Ganjali.
Power-efficient rate scheduling in wireless links using computational
geometric algorithms.
In IWCMC. 2006.
- [20]
-
J. Lorch.
Operating systems techniques for reducing processor energy
consumption.
In Ph.D. Thesis, University of California, Berkeley. 1994.
- [21]
-
M. Mandviwalla and N.-F. Tzeng.
Energy-efficient scheme for multiprocessor-based router linecards.
In IEEE SAINT. 2006.
- [22]
-
Maruti Gupta and Suresh Singh.
Dynamic Ethernet Link Shutdown for Energy Conservation on Ethernet
Links.
In IEEE ICC. 2007.
- [23]
-
E. Miranda and L. McGarry.
Power/thermal impact of networking computing.
In Cisco System Research Symposium, August, 2006.
- [24]
-
S. Nedevschi.
Reducing network energy consumption via sleeping and
rate-adaptation, http://www.ieee802.org/3/az/public/jan08/nedevschi_01
_0108.pdf.
In IEEE 802.3az Task Force Group Meeting. 2008.
- [25]
-
B. Nordman.
Energy Efficient Ethernet, Outstanding Questions.
2007.
- [26]
-
K. W. Roth, F. Goldstein, et al.
Energy Consumption by Office and Telecommunications Equipment in
Commercial Buildings - Volume I: Energy Consumption Baseline.
Tech. Rep. 72895-00, Arthur D. Little, Inc, Jan. 2002.
- [27]
-
The Abilene Observatory. http://abilene.internet2.edu/.
observatory.
- [28]
-
W. Ye, J. Heidemann, et al.
An energy-efficient mac protocol for wireless sensor networks.
In ACM INFOCOM. 2002.
- [29]
-
Yin Zhang's AbileneTM,http://www.cs.utexas.edu/ yzhang.
/research/AbileneTM.
- [30]
-
W. Yuan and K. Nahrstedt.
Energy-efficient soft real-time cpu scheduling for mobile multimedia
systems.
In ACM SOSP. 2003.
- [31]
-
M. Yuksel, B. Sikdar, et al.
Workload generation for ns simulations of wide area networks and the
internet.
In Communication Networks and Distributed Systems Modeling and
Simulation Conference. 2000.
- [32]
-
B. Zhai, D. Blaauw, et al.
Theoretical and practical limits of dynamic voltage scaling.
In DAC. 2004.
Notes:
1
In reality the energy savings using rate-adaptation will depend on
the distribution of operating rates over time and the
corresponding power consumption at each rate. For simplicity, we
initially use the average rate of operation as an indirect measure of savings in
Section 4 and then consider the complete distribution of operating
rates in Section 5 when we compute energy savings.
|