|
NSDI '05 Paper
[NSDI '05 Technical Program]
Decentralized, Adaptive Resource Allocation for Sensor
Networks
Geoffrey Mainland, David C. Parkes, and Matt Welsh
Division of Engineering and Applied Sciences
Harvard University
This paper addresses the problem of resource allocation in sensor
networks. We are concerned with how to allocate limited energy,
radio bandwidth, and other resources to maximize the value of each
node's contribution to the network. Sensor networks present a novel
resource allocation challenge: given extremely limited resources,
varying node capabilities, and changing network conditions, how can
one achieve efficient global behavior? Currently, this is accomplished
by carefully tuning the behavior of the low-level sensor program
to accomplish some global task, such as distributed event detection
or in-network data aggregation. This manual tuning is difficult,
error-prone, and typically does not consider network dynamics such
as energy depletion caused by bursty communication patterns.
We present Self-Organizing Resource Allocation (SORA), a
new approach for achieving efficient resource allocation in sensor
networks. Rather than manually tuning sensor resource usage, SORA defines a
virtual market in which nodes sell goods (such as sensor readings
or data aggregates) in response to prices that are established by
the programmer. Nodes take actions to maximize their profit, subject
to energy budget constraints. Nodes individually adapt their
operation over time in response to feedback from payments, using
reinforcement learning. The behavior of the network is determined
by the price for each good, rather than by directly specifying
local node programs.
SORA provides a useful set of primitives for controlling the
aggregate behavior of sensor networks despite variance of
individual nodes. We present the SORA paradigm and a sensor network
vehicle tracking application based on this design, as well as
an extensive evaluation demonstrating that SORA realizes an efficient
allocation of network resources that adapts to changing network
conditions.
Sensor networks, consisting of many low-power, low-capability devices
that integrate sensing, computation, and wireless communication,
pose a number of novel systems problems. They raise new challenges
for efficient communication protocols [13,44],
distributed algorithm design [11,24],
and energy management [1,5].
While a number of techniques have been proposed
to address these challenges, the general problem of resource
allocation in sensor networks under highly volatile network conditions
and limited energy budgets remains largely unaddressed.
Current programming models require that global
behavior be specified in terms of the low-level actions of individual
nodes. Given varying node locations, capabilities, energy budgets,
and time-varying network conditions, this approach makes it
difficult to tune network-wide resource usage.
We argue that new techniques are required to bridge the gap
from high-level goals to low-level implementation.
In this paper, we present a novel approach to adaptive resource
allocation in sensor networks, called
Self-Organizing Resource Allocation (SORA).
In this approach, individual sensor nodes are modeled as
self-interested agents that attempt to maximize their ``profit''
for performing local actions in response to globally-advertised
price information. Sensor nodes run a very simple cost-evaluation
function, and the appropriate behavior is induced by
advertising prices that drives nodes to react.
Nodes adapt their behavior by learning their utility for each potential
action through payment feedback. In this way, nodes dynamically
react to changing network conditions, energy budgets, and external
stimuli. Prices can be set to meet systemwide goals of lifetime,
data fidelity, or latency based on the needs of the system designer.
Consider environmental
monitoring [9,28] and distributed
vehicle tracking [23,45], which are two oft-cited
applications for sensor networks. Both applications require nodes to
collect local sensor data and relay it to a central base station,
typically using a multihop routing scheme. To reduce bandwidth
requirements, nodes may need to aggregate their local sensor data with
that of other nodes. In-network detection of distributed phenomena,
such as gradients and isobars, may require more sophisticated cross-node
coordination [15,41,47].
Two general challenges emerge in implementing these applications. First,
nodes must individually determine the ideal rate for sampling,
aggregating, and sending data to operate within some fixed energy
budget. This rate affects overall lifetime and the accuracy of
the results produced by the network.
Each node's ideal schedule is based on its physical location, position
in the routing topology, and changes in environmental stimuli. Many
current applications use a fixed schedule for node actions,
which is suboptimal when nodes are differentiated in this way. Second,
the system may wish to tune these schedules in response to changes in
the environment, such as the target vehicle's location and velocity,
to meet goals of data rate and latency. More complex adaptations
might involve selectively activating nodes that are expected to be
near some phenomenon of interest. Currently, programmers have to
implement these approaches by hand and have few tools to help
determine the ideal operating regime of each node.
Rather than defining a fixed node schedule, SORA causes nodes to
individually tune their rate of operation using techniques from
reinforcement learning [37]. Nodes receive virtual
payments for taking ``useful'' actions that contribute to the
overall network goal, such as listening for incoming radio messages
or taking sensor readings. Each node learns which actions
are profitable based on feedback from receiving payments for past
actions. Network retasking is accomplished by adjusting prices,
rather than pushing new code to sensor nodes. Network lifetime is controlled
by constraining nodes to take actions that meet a local energy budget.
In this paper, we focus on a specific challenge application, vehicle
tracking, which provides a rich space of problems in terms of managing
latency, accuracy, communication overhead, and task decomposition. The
SORA model is not specifically tailored to tracking, however, and can
be readily adopted for other problem domains. We present a thorough
evaluation of the SORA approach using a realistic sensor network
simulator. Our results demonstrate that, using SORA, resource allocation
within the sensor network can be controlled simply by advertising prices,
and that nodes self-organize to take the set of actions that make the
greatest contribution to the global task under a limited energy budget.
This paper expands on our previous workshop paper [18]
on SORA, presenting a thorough evaluation of the approach.
We show that SORA achieves more efficient allocation than static node
scheduling (the most commonly-used approach currently in use), and
outperforms a dynamic scheduling approach that accounts for changes in
energy availability. In addition, SORA makes it straightforward to
differentiate node activity by assigning price vectors that influence
nodes to select certain actions over others.
The rest of this paper is organized as follows. In
Section 2 we present the background for the SORA
approach, specific goals, and related work. Section 3
presents the Self-Organizing Resource Allocation model in detail, and
Section 4 describes the use of SORA in our vehicle
tracking application. Section 5 presents our implementation
of SORA in a realistic sensor network simulator, as
well as evaluation in terms of network
behavior and node specialization as prices, energy budgets, and other
parameters are tuned. Finally, Section 6 describes
future work and concludes.
Motivation and Background
Sensor networks consist of potentially many nodes with very limited
computation, sensing, and communication capabilities. A typical
device is the UC Berkeley Mica2 node, which consists of a
7.3 MHz ATmega128L processor, 128KB of code memory, 4KB of
data memory, and a Chipcon CC1000 radio capable of 38.4 Kbps
and an outdoor transmission range of approximately 300m. The node
measures 5.7cm 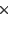 3.1cm 3.1cm 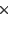 1.8cm and is typically powered
by 2 AA batteries with an expected lifetime of days to
months, depending on application duty cycle. The limited memory and
computational resources of this platform make an interesting design
point, as software layers must be tailored for this restrictive
environment.
The Mica2 node uses a lean, component-oriented operating system, called
TinyOS [16], and an unreliable message-passing
communication model based on Active Messages [38]. 1.8cm and is typically powered
by 2 AA batteries with an expected lifetime of days to
months, depending on application duty cycle. The limited memory and
computational resources of this platform make an interesting design
point, as software layers must be tailored for this restrictive
environment.
The Mica2 node uses a lean, component-oriented operating system, called
TinyOS [16], and an unreliable message-passing
communication model based on Active Messages [38].
To begin, we outline the distributed resource allocation problem
that arises in the sensor network domain. We highlight several prior
approaches to this problem and make the case for market-based
techniques as an attractive solution.
Sensor networks have been proposed for a wide range of novel
applications. Examples include instrumenting buildings,
bridges, and other structures to measure response to seismic
events [8,20],
monitoring environmental conditions and wildlife
habitats [9,28], tracking of
vehicles along a road or in an open area [43], and
real-time monitoring of patient vital signs for emergency and disaster
response [25,33].
One of the core challenges of sensor application design is
balancing the resource usage of individual nodes with the global behavior
desired of the network. In general, the sequence of actions taken by
a node affects local energy consumption, radio bandwidth availability,
and overall quality of the results. However, tuning the resource usage
of individual sensor nodes by hand is difficult and error-prone.
Although TinyOS [16] and other systems provide
interfaces for powering down
individual hardware devices such as the radio and CPU, using these
interfaces in a coordinated fashion across the network requires careful
planning. For example, if a node is sleeping, it cannot receive or
route radio messages.
The typical approach to scheduling sensor operations is
to calculate a static schedule for all nodes in the network.
For example, query-based systems such as TinyDB [26]
and Cougar [46] allow the user to specify a
query epoch that drives periodic sampling, aggregation,
and data transmission. Other programming models, such as
directed diffusion [12,17], abstract
regions [41], or Hoods [43], either
assume periodic data collection or leave scheduling to higher-level
code. However, an application that uses a fixed schedule for every node
will exhibit very different energy consumption rates across the
network. For example, nodes responsible for routing messages
will consume more energy listening for and sending radio
messages. Likewise, nodes on the network periphery may not
need to route radio messages at all.
Another solution is to compute, offline, the optimal schedule for each node
based on a model of radio connectivity, node location, and physical
stimuli that induce network activity. For example, Adlakha et
al. [1] describe a design-time recipe for tuning
aspects of sensor networks to achieve given accuracy, latency, or
lifetime goals. However, this approach assumes a statically-configured
network where resource requirements are known in advance, rather than
allowing the network behavior to be tuned at runtime (say, in response
to increased activity).
Other systems have attempted to address the node scheduling problem
for specific applications or communication patterns.
For example, Liu et al. [24] describe an approach to
tracking a moving half-plane shadow through a sensor network that can be
used to selectively activate nodes along the frontier of the shadow.
STEM [34] is a protocol that dynamically
wakes nodes along a routing path to trade energy consumption for
latency. LEACH [13] is a cluster-based routing scheme that
rotates the local clusterhead to distribute energy load across multiple
nodes. These techniques point to more general approaches to adapting the
behavior of sensor networks to maximize lifetime.
Providing application control over resource usage is often desirable when
designing high-level programming abstractions for sensor networks.
Abstract regions [41]
focuses on the ability to tune the communication layer to trade off energy
for accuracy. Likewise, TinyDB provides a lifetime keyword that
scales the query sampling and transmission period of individual nodes to
meet a user-supplied lifetime target [27]. Both of these
approaches provide a means for nodes to ``self-tune'' their behavior to
meet specific systemwide resource and accuracy targets. However, the
general problem of adaptive resource allocation in sensor networks
has not been adequately addressed.
AI-based approaches to resource allocation
The SORA approach draws on the areas of reinforcement learning
and economic theory to yield new techniques for decentralized
optimization in sensor networks.
In reinforcement
learning [37], an agent attempts to maximize
its ``reward'' for taking a series of actions.
Whether or not a node receives a reward is defined by the success of
the action; for example, whether a radio message is received while
the node is listening for incoming messages.
The agent's goal is to maximize its reward,
subject to constraints on resource usage, such as energy.
The reward for each successful action can be modeled as a price in a
virtual market. By applying ideas from economic theory, SORA attempts
to achieve efficient resource allocation in a decentralized
fashion. Economics has been used as an inspiration for solving
resource-management problems in many computational systems,
such as network bandwidth allocation [35],
distributed database query optimization [36],
and allocating resources in distributed systems such as
clusters, Grids, and peer-to-peer
networks [3,4,7,10,39].
Much of this prior work has been concerned with resource arbitration
across multiple self-interested
users, which may attempt to cheat or otherwise hoard resources in the
system for their own advantage. In the sensor network context,
however, we assume that nodes are well-behaved and program them
to behave as the classic economic actors of microeconomic theory.
Thus, we use markets as a programming paradigm, not
because we are concerned with self-interested behavior of sensor
nodes. We need not model complex game-theoretic behavior, but can
instead focus on nodes that (by design) are classic price-taking
economic agents.
SORA is inspired by Wellman's seminal work on market-oriented
programming [30,40], which uses
market equilibrium to solve statically-defined distributed
optimization problems. We believe that SORA is the first
serious attempt to use market-oriented methods to provide complete
runtime control for a real distributed system. This systems focus
leads us to consider continuous, real-time resource allocation, while
Wellman's work was concerned with solving a static allocation problem.
Other recent work has applied economic ideas to specific
sensor network problems. For instance, market-inspired methods
have been suggested for the problems of ad hoc routing [2] and information-directed query
processing [47]. Our goal in SORA is not to
provide a point solution but to address the general issue of
adaptive resource allocation.
Self-Organizing Resource Allocation
In Self-Organizing Resource Allocation (SORA),
sensor nodes are programmed to maximize their
``profit'' by taking actions subject to energy constraints.
Actions that contribute to the network's overall goal, such as
taking useful sensor readings or forwarding radio messages, result in a
payment to the node taking the action. By setting the price for each
action, the network's global behavior can be tuned by the system designer.
Nodes continuously learn a model for which actions are profitable,
allowing them to adapt to changing conditions.
The essential problem that SORA addresses is that of determining
the set of local actions to be taken by each sensor node to meet some
global goals of lifetime, latency, and accuracy for the data produced by
the network as a whole. Each node can take a set of local actions
(such as data sampling, aggregation, or routing), each with varying
energy costs and differing contributions to the global task of the
network. Through self-scheduling, nodes independently determine
their ideal behavior (or schedule) subject to constraints on local
energy consumption. Self-scheduling in SORA meets three key goals:
Differentiation:
Nodes in a sensor network are heterogeneous in terms of their
position in the network topology, resource availability, and
proximity to phenomena of interest. Through self-scheduling, nodes
differentiate their behavior based on this variance. For example, nodes
closer to phenomena of interest should acquire and transmit more
sensor readings than those nodes that are further away.
Adaptivity:
Differentiation in nodal behavior should also vary with time,
as external stimuli move, nodes join and leave the network, energy
reserves are depleted, and network connectivity shifts.
Such adaptation permits a more efficient use of
network resources. For example, nodes will consume energy only when
it is worthwhile to do so based on current network conditions, rather
than as dictated by an a priori schedule.
Control:
Finally, a system designer should have the ability to express
systemwide goals and effect control over the behavior of the network
despite uncertainty in the exact state, energy reserves, and physical
location of sensor nodes. For example, if the data rate being generated
by the network is insufficient for the application's needs, nodes should
be instructed to perform sampling and routing actions more frequently.
This goal differs from internal adaptation by nodes,
since it requires external observation and manipulation.
In the SORA model, each sensor node acts as an agent that attempts to maximize its profit for taking a
series of actions.
Each action consumes
some amount of energy and produces one or more goods that have
an associated price. Nodes receive payments by producing goods
that contribute value to the network's overall operation.
For example, a node may be paid for transmitting a sensor reading that
indicates the proximity of a target vehicle, but not be paid if the
vehicle is nowhere nearby. Reacting to this payment feedback is the
essential means of adaptivity in SORA.
Prices are determined by the
client of the sensor network, which can be thought of as an
external agent that receives data produced by the network and sets
prices to induce network behavior.
The local program executed by each node is simple and avoids
high communication overhead in order to operate efficiently.
In the SORA approach, nodes operate using primarily local
information about their state, such as energy availability.
The only global information shared by nodes is the current set
of prices, which are defined by the sensor network client.
To minimize overhead, prices should be updated infrequently (for
example, to effect large changes in the system's activity)
and can be propagated to nodes through a variety of efficient gossip or
controlled-flooding protocols [22].
The actions that sensor
nodes can take depend on the application, but typically include
sampling a sensor, aggregating multiple sensor readings, or broadcasting
a radio message. An action may be unavailable if the node does not
currently have enough energy to perform the action. In addition,
production of one good may have dependencies on the availability of
others. For example, a node cannot aggregate sensor readings until
it has acquired multiple readings.
Taking an action may or may not produce a good of value to the sensor
network as a whole. For example, listening for incoming radio messages
is only valuable if a node hears a transmission from another node.
Likewise, transmitting a sensor reading is only valuable if the
reading has useful informational content.
We assume that nodes can determine locally whether a given action
deserves a payment. This works well for the simple
actions considered here, although more complex actions (e.g., computing
a function over a series of values) may require external notification
for payments.
A node's energy budget constrains the actions that it can take.
We assume that nodes are aware of how much energy each
action takes, which is straightforward to measure offline. The energy
budget can be modeled in a number of different
ways. A simple approach is to give each node a fixed budget that
it may consume over an arbitrary period of time.
In this case, however, nodes may rapidly deplete their energy
resources by taking many energy-demanding actions, resorting to
less-demanding actions only when reserves get low.
To capture the desire for nodes to consume energy at a regular rate,
we opt to use a token bucket model for the budget. Each node has a
bucket of energy with a maximum capacity of 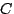 Joules, filling
at a rate Joules, filling
at a rate 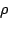 that represents the average desired rate of
energy usage (e.g., 1000 J per day).
When a node takes an action, the appropriate amount of energy is deducted
from the bucket. If a node cannot take any action because its bucket is
too low, it must sleep, which places the node in the lowest-possible
energy state. that represents the average desired rate of
energy usage (e.g., 1000 J per day).
When a node takes an action, the appropriate amount of energy is deducted
from the bucket. If a node cannot take any action because its bucket is
too low, it must sleep, which places the node in the lowest-possible
energy state.
The capacity 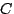 represents the total amount of energy
that a node can consume in one ``burst.'' If represents the total amount of energy
that a node can consume in one ``burst.'' If 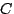 is set to the size of the
node's battery, the node is able to consume its entire energy
reserves at once. By limiting is set to the size of the
node's battery, the node is able to consume its entire energy
reserves at once. By limiting 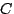 , one can bound the total
amount of energy used by a node over a short time interval. , one can bound the total
amount of energy used by a node over a short time interval.
Given a set of actions, goods produced by those actions,
prices for each good, and energy cost for each action,
each agent operates as follows. A node simply monitors its local state
and the global price vector, and periodically selects the action that
maximizes its utility for each action.
Upon taking that action, the node's energy budget
is reduced by the appropriate amount, and the node may or may not receive
a payment depending on whether its action produced a valuable good.
We define the utility function 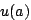 for an action for an action 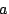 to be: to be:
where  is the current price for action is the current price for action 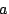 ,
and ,
and 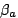 is the estimated probability of
payment for that action, which is learned by nodes as
described below. An action may be unavailable if either the
current energy budget is too low to take the action, or other
dependencies have not been met (such as lack of sensor readings to
aggregate). is the estimated probability of
payment for that action, which is learned by nodes as
described below. An action may be unavailable if either the
current energy budget is too low to take the action, or other
dependencies have not been met (such as lack of sensor readings to
aggregate).
In essence, the utility function represents the expected profit for
taking a given action. The parameter 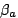 is continuously estimated
by nodes over time in response to the success of taking each action.
This is a form of reinforcement learning [37].
After taking an action is continuously estimated
by nodes over time in response to the success of taking each action.
This is a form of reinforcement learning [37].
After taking an action 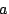 , the new value , the new value 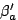 is calculated
based on whether the action received a payment: is calculated
based on whether the action received a payment:
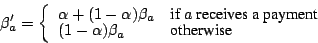
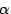 represents the sensitivity of the EWMA filter (in our
experiments, represents the sensitivity of the EWMA filter (in our
experiments, 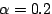 ).
In this way, nodes learn which actions are likely to
result in payments, leading to a natural self-organization
depending on the node's location in the network or intrinsic capabilities.
For example, a node that has the opportunity to route messages
for other nodes will be paid for listening for incoming radio messages;
nodes on the edges of the network will learn that this action is rarely
(if ever) profitable. ).
In this way, nodes learn which actions are likely to
result in payments, leading to a natural self-organization
depending on the node's location in the network or intrinsic capabilities.
For example, a node that has the opportunity to route messages
for other nodes will be paid for listening for incoming radio messages;
nodes on the edges of the network will learn that this action is rarely
(if ever) profitable.
The expected profit for an action will vary over time
due to price adjustments and changing environmental conditions.
Therefore, it is important that nodes periodically ``take risks'' by choosing
actions that have a low payment probability 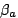 . We employ
an . We employ
an 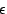 -greedy action selection policy.
That is, with probability -greedy action selection policy.
That is, with probability 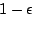 (for some small (for some small 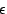 ; we
currently use ; we
currently use
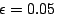 ), nodes
select the ``greedy'' action that maximizes the utility ), nodes
select the ``greedy'' action that maximizes the utility 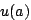 .
However, with probability .
However, with probability 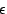 a node will select an (available)
action from a uniform distribution.
In effect, this ignores the value of a node will select an (available)
action from a uniform distribution.
In effect, this ignores the value of 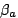 and allows a node to explore for new opportunities for profit.
Such exploration prevents a node from never electing to take an action
because it has not recently been paid to do so [37]. and allows a node to explore for new opportunities for profit.
Such exploration prevents a node from never electing to take an action
because it has not recently been paid to do so [37].
Our current reinforcement learning scheme does not take into
consideration other aspects of a node's state, such as the sequence of
past actions or the state of neighboring nodes, which may lead to more
efficient solutions. However, these techniques involve considerable
complexity, which goes against our goals of simplicity and limiting
per-node state. We intend to explore alternative learning algorithms
as part of future work.
Price selection and adjustment
In SORA, the global behavior of the network is controlled by the client
establishing prices for each good.
Prices are propagated to sensor nodes through an efficient global
data dissemination algorithm, such as SPIN [14] or
Trickle [22]. The client can also adjust prices as the
system runs, for example, to affect coarse changes in system activity.
There is a complex relationship between prices and agent behavior.
Raising the price for a good will not necessarily induce more nodes
to produce that good; the dynamics of maximizing expected profits may
temper a node's desire to take a given action despite a high price.
Our experiments in Section 5 demonstrate the effect of
varying prices. As it turns out, subtle changes to prices do not
have much impact on global network behavior. This is because each
node's operation is mostly dictated by its adaptation to
coarse-grained changes in the local state, such as whether sampling
sensors or listening for incoming radio messages is currently
profitable. Prices serve to differentiate behavior only when
a node has multiple profitable actions to choose between. Even when
one action has a much higher price than others, nodes will still
take a mixture of actions due to continual exploration of the
state space through the 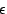 -greedy learning policy. -greedy learning policy.
The best approach to selecting optimal price settings in SORA is
still an open problem. Given the complexities of agent operations and unknown
environmental conditions, analytically solving for prices to obtain a
desired result is not generally possible. In a stationary system, it
is possible to search for optimal prices by slowly adjusting each
price and observing its effect on network behavior; this approach is
used by the WALRAS system [40].
A better approach is to determine prices empirically based on an
observation of the network's behavior at different price points.
For example, a system designer can experiment with a testbed deployment
or simulation to understand the effect of differing prices on
overall behavior. Prices can be readily tuned after deployment, since
broadcasting a new price vector to an active network is not expensive.
This process could be automated by an external controller that
observes the network behavior over time and adjusts prices accordingly.
One approach to
setting prices, based on economic principles, is to
establish a competitive equilibrium, where
the supply of goods produced by the network equals the demand for those
goods expressed by the client. This model is attractive when there are
multiple users programming the sensor network to take different sets of
actions on their behalf, since equilibrium prices ensure that network
resources are shared in an optimal manner. However, computing
equilibrium prices often requires continuous information on the
network's supply of goods, which may lag pricing updates.
A detailed discussion of this technique is beyond the scope of this
paper, but we return to this problem in Section 6.
Application Example: Vehicle Tracking
Figure 1:
Energy consumed for each sensor action.
 |
As a concrete example of using SORA to manage resource allocation in a
realistic sensor network application, we consider tracking a moving
vehicle through a field of sensors. We selected vehicle tracking
as a ``challenge application'' for SORA because it raises a number
of interesting problems in terms of detection accuracy and latency,
in-network aggregation, energy management, routing, node specialization,
and adaptivity [6,43,45].
Vehicle tracking can
be seen as a special case of the more general data collection problem
also found in applications such as environmental and structural
monitoring [20,28].
In the tracking application, each sensor is equipped with a magnetometer
capable of detecting local changes in magnetic field, which indicates
the proximity of the vehicle to the sensor node. One node acts as a
fixed base station, which collects readings from the other sensor nodes
and computes the approximate location of the vehicle based on the data
it receives. The systemwide goal is to track the location of the moving
vehicle as accurately as possible while meeting a limited energy
budget for each node.
Each sensor node can take the following set of actions: sample a local
sensor reading, send data towards the base station, listen for
incoming radio messages, sleep for some interval, and aggregate
multiple sensor readings into a single value. Each node maintains a
fixed-length LIFO buffer of sensor readings, which may be sampled locally or
received as a radio message from another node. Each entry in the buffer
consists of a tuple containing a vehicle location estimate weighted by a
magnetometer reading. The sample action appends a local reading to the buffer,
and the listen action may add an entry if the node receives a message from
another node during the listen interval.
Aggregation is used to limit communication bandwidth by combining readings from
multiple nodes into a single value representing the ``best'' sensor reading. The
aggregate action replaces the contents of the sample buffer with a single
weighted position estimate, ignoring any sample older than a programmer-defined
constant (10 sec in our simulations).
The sleep action represents the lowest-energy state of a node
which is entered when energy is unavailable for other actions, or
no other action is deemed profitable.
Figure 1 summarizes
the energy requirements for each action, based on
measurements of the Mica2 sensor node.
All radio transmissions route messages towards the base station using a multihop
routing protocol. Nodes are not assumed to be within a single radio hop of the
base. The choice of routing algorithm is not essential; we use a simple
greedy geographic routing protocol, similar to GPSR [19]
but without any face routing, although other routing algorithms can be
used [44,17]. Messages are forwarded to the
neighboring node that is both physically closer to the destination
(always the base station, in this case) and is currently executing the
listen action. This protocol assumes a CTS-RTS MAC layer that
allows a node to send a message to any one of its next-hop neighbors
that are currently listening. In this way,
as long as any closer neighbor is currently listening, the message will be
forwarded. This approach meshes well with the stochastic nature of node actions
in SORA and does not require explicit coscheduling of senders and receivers.
SORA naturally leads to an efficient allocation
of network resources. Individual nodes
are constrained to operate within their energy budget, and the
schedule for each node may vary over time depending on network
conditions and external stimuli. Nodes continuously learn which
actions are most profitable and thereby have the most value to the
sensor network as a whole. This emergent behavior is more effective
at allocating limited network resources than traditional schemes
based on static schedules.
The SORA approach captures a number of design tradeoffs that are worth
further discussion. One advantage of this model is that the nodal
program is simple: nodes simply take actions to maximize
their expected profit. Nodes do not reason directly about
dependencies or consequences of a series of actions, ordering, or
the rate
at which actions are taken.
Because nodes learn the payoff probabilities 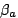 ,
they adapt to changing network conditions over time, and different nodes will
take different sets of actions depending on their utility functions. ,
they adapt to changing network conditions over time, and different nodes will
take different sets of actions depending on their utility functions.
Adjusting prices gives the client of the network control over
the behavior of the system, allowing the network to be readily retasked
simply by advertising a new price vector.
However, because nodes operate to
maximize their expected profit, an equilibrium arises that
balances the actions taken by different nodes in the network.
For example, increasing the price of the listen action might
substantially reduce the number of nodes that choose to sample or send
sensor readings. However, since listening nodes are only paid when other
nodes send data, the proportion of sending and listening nodes is
kept in balance. This is a valuable aspect of
self-scheduling and does not require explicit coordination across
nodes; this equilibrium arises naturally from the feedback of
payments. We demonstrate this aspect of SORA in Section 5.
SORA can be viewed as a general approach to decentralized resource
allocation in sensor networks, and is not specifically tailored for data
collection and vehicle tracking. However, it is worth keeping in mind that
many sensor network applications operate by routing (and possibly
aggregating) data towards a single base station, as evidenced by much
prior work in this
area [5,11,17,26,46].
It seems clear that the SORA approach could be readily applied to this
broad class of systems; for example, SORA could be used to control
the execution of query operators in TinyDB [26].
Extending SORA to other applications involves two basic steps: first,
identifying the set of primitive actions and goods that the system
should expose, and second, measuring the associated energy costs for
each action. For example, exposing a complex operation such as
``compute the sum-reduce of sensor readings over a node's 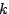 nearest
neighborhood'' [41] would be straightforward to wrap
as an SORA action. One requirement for actions is that data dependencies
be made explicit. For example, the send and aggregate
actions depend on the sensor reading buffer being non-empty. More complex
actions might have a richer set of dependencies that must be met in
order to fire. This suggests that nodes should be able to reason about
taking a sequence of actions to produce some (highly-valued) good;
this is another interesting avenue for future work. nearest
neighborhood'' [41] would be straightforward to wrap
as an SORA action. One requirement for actions is that data dependencies
be made explicit. For example, the send and aggregate
actions depend on the sensor reading buffer being non-empty. More complex
actions might have a richer set of dependencies that must be met in
order to fire. This suggests that nodes should be able to reason about
taking a sequence of actions to produce some (highly-valued) good;
this is another interesting avenue for future work.
Experiments and Evaluation
Figure 2:
Actions and energy budget for a single node.
This figure shows the actions taken, the energy budget, and the
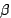 values for the listen and sample actions for node 31, which is
along the path of the vehicle. values for the listen and sample actions for node 31, which is
along the path of the vehicle.
|
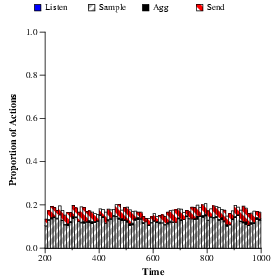
Figure 3:
Actions taken and energy use over time.
This graph shows (a) the proportion of non-sleep
actions taken by all nodes in the network and (b)
the total energy consumed over time. Over 60% of the actions taken by
the network are sleep.
 |
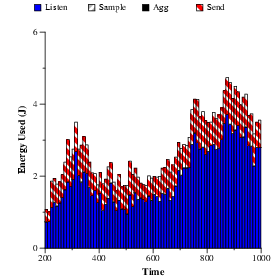 |
| (a) Non-sleep actions taken |
(b) Energy use |
|
To demonstrate the use of Self-Organizing Resource Allocation
in a realistic
application setting, we have implemented the SORA-based vehicle tracking
system in a sensor network simulator. This simulator captures
a great deal of detail, including hardware-level sensor operations
and a realistic radio communication model based on traces of packet
loss statistics in an actual sensor network. We have also implemented
the SORA-based tracking application in TinyOS [16]
using the TOSSIM [21] simulator environment. However, due
to performance limitations in TOSSIM, the results below are based on
our custom simulator that runs roughly an order of magnitude faster.
This performance gain is accomplished primarily by eliminating the
high overhead associated with the TOSSIM GUI, as well as eliding
hardware-level details of node actions that are not relevant to the
SORA approach. We have verified that the two simulators produce
nearly identical results.
The SORA code can be readily ported to run on actual sensor nodes, and we
are currently planning to take measurements on our building-wide sensor
network testbed [42].
Our evaluation of SORA has three basic goals. First, we show that SORA
allows nodes to self-schedule their actions to achieve an efficient
allocation of network resources. Second, we show that SORA achieves
much greater energy efficiency than traditional scheduling
techniques without sacrificing data fidelity.
Third, we show that SORA allows the system designer to differentiate
node actions by varying energy budgets and price vectors.
We compare the use of SORA to several other
implementations of vehicle tracking that use different
scheduling techniques. These include the
commonly-used static scheduling technique, a dynamic energy-aware
scheduling scheme, and a tracking application
based on the Berkeley NEST design as described in [43].
These systems are described in detail below.
We simulated a network of 100 nodes distributed semi-irregularly in a
100x100 meter area.
The base station (to which all nodes route their messages) is
located near the upper-left corner of this area. The energy cost for
each action is shown in Figure 1.
The simulated vehicle moves in a circular path of radius 30 m at a
rate of 1.5 m/sec. Moving the vehicle through such a path causes
nodes in different areas of the network to detect the vehicle and
route sensor readings towards the base station. The strength of
each sensor reading depends on the distance to the vehicle; sensors
cannot detect the vehicle when it is more than 11 meters away.
Unless otherwise noted, the energy budget for each node is
1000 J/day, corresponding to a node lifetime of
30.7 days.1 The prices for all actions
were set to an identical value, so nodes have no bias towards
any particular action. The exploration probability 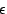 is set
to 0.05, and the learning parameter is set
to 0.05, and the learning parameter 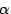 is set to 0.2.
We demonstrate the effect of varying these parameters in
Section 5.7 and 5.8. is set to 0.2.
We demonstrate the effect of varying these parameters in
Section 5.7 and 5.8.
To compare the use of SORA with more traditional approaches to sensor
network scheduling, we implemented three additional versions
of the tracking
system. The first employs static scheduling, in which
every node uses a fixed schedule for sampling, aggregating, and
transmitting data to the base station. This is the most common approach
to designing sensor network applications, typified
by fixed sampling periods in TinyDB [26] and directed
diffusion [17].
The static schedule is computed based on the energy budget. Given a daily
budget of 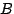 joules, a node calculates the rate for performing each
round of actions (sample, listen, aggregate, transmit, and sleep) in
order to meet its budget.
For example, given a daily budget of 1000 J, the data collection sequence
can be performed once every 0.4 sec. This schedule is conservative,
since not all nodes will actually detect the vehicle or transmit data
during each period.
The same schedule is used for every
node in the network, so nodes do not learn which actions they should
perform, nor adapt their sampling rate to stimuli such as the approach
of the vehicle. joules, a node calculates the rate for performing each
round of actions (sample, listen, aggregate, transmit, and sleep) in
order to meet its budget.
For example, given a daily budget of 1000 J, the data collection sequence
can be performed once every 0.4 sec. This schedule is conservative,
since not all nodes will actually detect the vehicle or transmit data
during each period.
The same schedule is used for every
node in the network, so nodes do not learn which actions they should
perform, nor adapt their sampling rate to stimuli such as the approach
of the vehicle.
The second approach employs dynamic scheduling in which nodes
continuously adjust their processing rate based on their current
energy budget. In this way, nodes that do not consume energy aggregating
or transmitting data can recycle that energy to increase their
sampling rate accordingly.
The third and final approach, the Hoods tracker, is based on the
tracking system implemented using the Hoods communication
model [43]. It is largely similar
to the dynamically-scheduled tracker, except in the way that nodes
calculate the target location. Each node that detects the vehicle
broadcasts its sensor reading to its neighbors.
The node then listens for some period of time, and if its own reading
is the maximum of those it has heard, computes the centroid of the readings
(based on the known locations of neighboring nodes) as the estimated
target location. This location estimate is then routed towards
the base station. We implemented the Hoods tracker to emulate the
behavior of a previously-published tracking system for direct comparison
with the SORA approach.
We begin by demonstrating the operation of the sensor network over
time, as nodes learn which actions receive payments.
Figure 2 depicts the actions taken, energy budget,
and 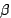 values for node 31, which is along the path of the vehicle.
As the vehicle approaches along its circular path at time values for node 31, which is along the path of the vehicle.
As the vehicle approaches along its circular path at time
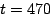 , the node determines that it will be paid to sample,
aggregate, and send sensor readings. As the vehicle departs around
time , the node determines that it will be paid to sample,
aggregate, and send sensor readings. As the vehicle departs around
time 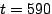 , the node returns to its original behavior.
At certain times (e.g., at , the node returns to its original behavior.
At certain times (e.g., at 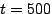 and and 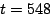 ),
the node receives messages
from other nodes and routes them towards the base station, explaining
the increase in ),
the node receives messages
from other nodes and routes them towards the base station, explaining
the increase in 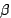 for the listen action.
When the vehicle is not nearby,
the node mostly sleeps, since no interesting samples or
radio messages are received. The energy bucket fills during this time
accordingly; the bucket capacity for the listen action.
When the vehicle is not nearby,
the node mostly sleeps, since no interesting samples or
radio messages are received. The energy bucket fills during this time
accordingly; the bucket capacity 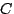 is set arbitrarily to 115 mJ, which
requires the node to sleep for 20 seconds to fill the bucket
entirely. is set arbitrarily to 115 mJ, which
requires the node to sleep for 20 seconds to fill the bucket
entirely.
Observe that the node performs listen and sample
actions even when its utility for doing so is low (even zero).
This is because the node has enough energy to perform these actions,
and the 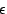 -greedy action selection policy dictates that it
will explore among these alternatives despite negligible utility. -greedy action selection policy dictates that it
will explore among these alternatives despite negligible utility.
Figure 3 shows the proportion of (non-sleeping) actions
and energy use by the network over time. As the graph shows, over 60%
of the actions taken by nodes during the run are sleep.
Listen and send consume far more
energy than other actions. The variation in network activity
arises due to the movement of the vehicle. For example, at time 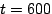 ,
the vehicle is closest to the base station, so only those nodes close to
the base are sampling and routing data, while the rest of the network
is dormant. ,
the vehicle is closest to the base station, so only those nodes close to
the base are sampling and routing data, while the rest of the network
is dormant.
Figure 4:
Tracking accuracy.
This figure is a CDF of the tracking position error over
a run of 1000 sec for each of the tracking systems. The static and dynamic
schedulers are the most accurate, since they operate periodically,
while SORA has slightly higher error due to its probabilistic operation.
Disabling aggregation in SORA causes accuracy to suffer since more
readings are delivered to the base station.
These three tracking schemes outperform the Hood-based
tracker with the same energy budget.
|
To compare SORA with the other scheduling techniques, we are interested
in two metrics: tracking accuracy and energy efficiency.
We do not expect SORA to be more accurate than the other
scheduling approaches, however, it is important that it performs in
the same ballpark in order to be viable.
Figure 4 compares the accuracy of the SORA tracker
with the other three scheduling techniques. For each position estimate
received by the base station, the tracking error is measured as the
difference between the estimated and true vehicle position at
the time that the estimate is received. This implies that position
estimate messages that are delayed in the network will increase tracking
error, since the vehicle may have moved in the interim.
As the figure shows, SORA achieves an 80th percentile tracking
error of 3.5 m, only slightly higher than the static and dynamic
trackers.
The Hood tracker performs poorly due to its different
algorithm for collecting and aggregating sensor data.
Figure 5 shows a scatterplot of position
estimates received at the base station for each tracking technique.
Hood delivers far fewer position estimates and exhibits wider variation
in accuracy. Also, disabling aggregation in SORA (by setting the price
for the aggregate action to 0) causes more position estimates
to be delivered that exhibit greater variation than the aggregated
samples.
Figure 5:
Tracking accuracy scatterplots.
These scatterplots show the set of readings delivered to the base
station by each tracking system over time. Hood performs poorly and
delivers far fewer vehicle position estimates. The effect of disabling
aggregation in SORA can be seen clearly.
|
Figure 6:
Tracking accuracy and energy efficiency.
This figure shows (a) the mean tracking error and (b) overall
system energy efficiency as the energy budget is varied.
 |
 |
| (a) Mean tracking error |
(b) Energy efficiency |
|
By allowing nodes to self-schedule their operation in response to
external stimuli and energy availability, SORA achieves an
efficient allocation of energy across the network. For each of the
scheduling techniques, we measure the efficiency of
resource allocation in terms of the energy cost to acquire each position
estimate in proportion to the total amount of ``wasted'' energy in the
network.
For each position estimate received by the base station, we
measure the ``useful'' energy cost of acquiring and routing that
data. This includes the sum energy cost of sampling, (optional) aggregation,
radio listening, and transmission of the data along each hop.
In the case of estimates with aggregated values, we count both the
total energy cost for each sensor reading in the estimate, as well
as the number of sensor readings represented. Because aggregation
amortizes communication overhead across multiple readings, we expect
aggregation to reduce the overall per-sample energy cost.
The total amount of useful energy consumed by the network is the
sum of the energy cost for all position estimates produced during a
run of the tracking system.
All other energy consumed by the network is wasted in the sense that it
does not result in data being delivered to the base. In a perfect
system, with a priori knowledge of the vehicle location and
trajectory, communication patterns, and so forth, there would be
no wasted energy. In any realistic system, however, there is some
amount of waste. For example, nodes may listen for incoming radio
messages or take sensor readings that do not result in position
estimates. We define efficiency as the ratio of the
total useful energy consumed by the network to the total energy consumed
(useful plus wasted energy).
It is important to note that the statically-scheduled and
dynamically-scheduled trackers do not make any attempt to
save energy beyond their energy budget. Nodes are programmed to
operate at a rate that consumes the local energy budget, despite
local network conditions. In SORA, however, many nodes may
conserve energy by sleeping when they have zero utility for
any potential action (e.g., because they are in a quiescent area
of the network). The use of reinforcement learning in SORA allows
nodes to tune their duty cycle in response to local conditions,
significantly extending lifetime.
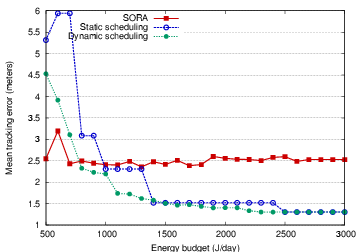
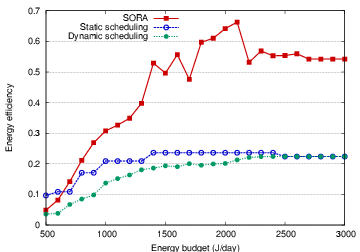
Figure 6 summarizes the accuracy and
efficiency of each
scheduling technique as the energy budget is varied.
Each system varies in terms of its overall tracking accuracy
as well as the amount of energy used.
While SORA has a somewhat higher tracking error compared to the
other scheduling techniques, it
demonstrates the highest efficiency, exceeding 66% for an energy
budget of 2100 J. The static and dynamic schedulers achieve an
efficiency of only 22%.
In SORA, most nodes use far less energy than the budget allows.
The ability of SORA to ``learn'' the duty cycle on a per-node basis
is a significant advantage for increasing network lifetimes.
Varying learning parameters
Apart from the energy budgets and prices, two parameters that
strongly affect node behavior in SORA are  ,
the exploration probability, and ,
the exploration probability, and  , the EWMA gain for
learning action success probabilities. By varying , the EWMA gain for
learning action success probabilities. By varying  , we
can trade off increased energy waste (for exploring the action
space) for faster response to changing network conditions.
By varying , we
can trade off increased energy waste (for exploring the action
space) for faster response to changing network conditions.
By varying  , the system reacts more or less quickly to
changes in success probabilities; higher values of , the system reacts more or less quickly to
changes in success probabilities; higher values of 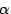 cause a node to bias action selection towards more-recently
profitable actions.
cause a node to bias action selection towards more-recently
profitable actions.
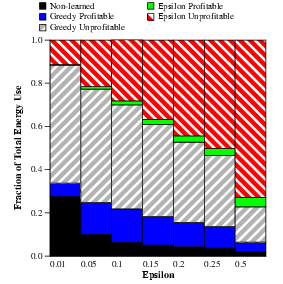
Figure 7:
Effect of varying exploration and learning
parameters. (a) 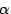 is held constant at 0.2 and the probability of
taking a random action is held constant at 0.2 and the probability of
taking a random action 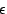 is varied.
(b) is varied.
(b) 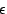 is held constant at 0.05 and the EWMA filter
gain is is held constant at 0.05 and the EWMA filter
gain is 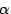 is varied. is varied.
 |
 |
(a) Varying exploration probability 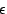 |
(b) Varying EWMA filter gain 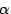 |
|
Figure 7(a) shows the effect of varying 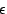 from 0.01 to 0.5. As the probability of taking a random action
increases, the proportion of energy wasted taking those actions
also increases. However, the proportion of energy wasted taking
the ``greedy'' action (the action with the highest expected
probability of success) decreases, since nodes learn more
rapidly which actions are profitable by exploring the action
space.
from 0.01 to 0.5. As the probability of taking a random action
increases, the proportion of energy wasted taking those actions
also increases. However, the proportion of energy wasted taking
the ``greedy'' action (the action with the highest expected
probability of success) decreases, since nodes learn more
rapidly which actions are profitable by exploring the action
space.
Figure 7(b) shows a similar result for varying 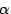 .
When .
When 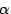 is increased, nodes react very quickly to changes in
action success. When is increased, nodes react very quickly to changes in
action success. When 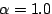 , if an action is successful once,
the node will immediately prefer it over all others. Likewise, the node
will immediately ignore a potentially profitable action the first time
it is unsuccessful. As a result, the
proportion of energy used on successfully choosing the greedy action
decreases. Also, since the node's action selection policy is
increasingly myopic, nodes spend more time sleeping. As a result,
a greater proportion of energy is spent on exploratory
actions since few ``greedy'' actions are considered worthwhile. , if an action is successful once,
the node will immediately prefer it over all others. Likewise, the node
will immediately ignore a potentially profitable action the first time
it is unsuccessful. As a result, the
proportion of energy used on successfully choosing the greedy action
decreases. Also, since the node's action selection policy is
increasingly myopic, nodes spend more time sleeping. As a result,
a greater proportion of energy is spent on exploratory
actions since few ``greedy'' actions are considered worthwhile.
Heterogeneous energy budgets and prices
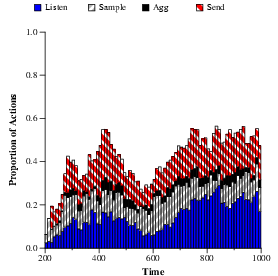
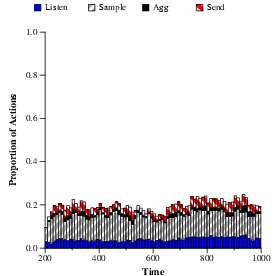
Figure 8:
Exploiting heterogeneous energy budgets.
Here, 20% of the nodes are given a large energy budget of
3000 J/day (a), where the rest of the nodes use a smaller energy budget
of 500 J/day (b). The large energy budget nodes automatically take on a
greater proportion of the energy load in the system, choosing to
perform a far greater number of listen and send actions than the low-energy
nodes.
 |
 |
| (a) Large energy budget |
(b) Small energy budget |
|
SORA allows nodes to be differentiated with respect to their
energy budgets, as well as the prices under which they operate.
For example, certain nodes may have access to a large power supply and
should be able to perform more power-hungry operations than nodes
operating off of small batteries.
Likewise, advertising different price vectors to
different nodes allows them to be customized to take certain actions.
Figure 8 shows the behavior of the tracking
system where 20% of the nodes are given a large energy budget of
3000 J/day, effectively allowing them to ignore energy constraints for
the purpose of selecting actions. The large energy budget nodes
automatically elect to perform a greater number of listen and send
actions, while the other nodes mostly perform sample actions, which
consume far less energy overall. Identical prices are used
throughput the network, showing that differences in energy
budget have a profound effect on resource allocation.
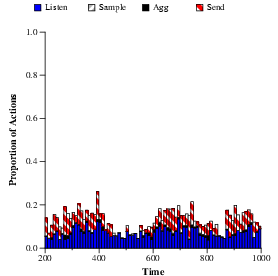
Figure 9:
Specialization through pricing.
Here, 20% of the nodes are configured as ``routers'' (left) using
prices for listening, aggregation, and sending. The other 80% of the
nodes are configured as ``sensors'' (right) and only have prices for sampling
and sending. As the figure shows the proportion of actions taken by
each group of nodes differs greatly according to the prices.
 |
 |
| (a) Routers |
(b) Sensors |
|
Advertising different price vectors to different sets of nodes is another
way to specialize behavior in SORA. Figure 9 shows a
case where 20% of the nodes are configured as ``routers'' with all prices set
to 0, except for listening, aggregation, and sending.
The other nodes act as ``sensors'' with nonzero prices only for sampling and
sending. As the figure shows, each group of nodes exhibits very
different behavior over the run, with sensor nodes performing a large
number of sampling and send actions, while router nodes primarily listen
and transmit.
Routers spend a great deal of time sleeping because most
actions (e.g., aggregation and sending) are unavailable, and listening
consumes too much energy to perform continually.
Future Work and Conclusions
The design of sensor network applications is complicated by the extreme
resource limitations of nodes and the unknown, often time-varying,
conditions under which they operate. Current approaches to
resource management are often extremely low-level, requiring that
the operation of individual sensor nodes be specified manually.
In this paper, we have presented an
technique for resource allocation in sensor networks
in which nodes
act as self-interested agents that select actions to maximize profit,
subject to energy limitations. Nodes self-schedule their local actions
in response to feedback in the form of payments. This allows nodes to
adapt to changing conditions and specialize their behavior according to
physical location, routing topology, and energy reserves.
Exploiting techniques from reinforcement learning and economic theory
yields new insights into the allocation of scarce resources in an adaptive,
decentralized fashion. Our initial work on SORA raises a number
of interesting questions that we wish to explore in future work. These
are described in summary below.
Equilibrium pricing:
As discussed earlier, a system is in competitive equilibrium (Pareto
optimal) when prices are selected such that supply of goods equals demand.
This is an attractive model for allowing multiple users to allocate
and share sensor network resources in an optimal fashion.
However, such an approach
raises a number of practical problems that must be addressed before
it can be applied to sensor networks.
The traditional tâtonnement approach [29] is to
increase prices on undersupplied goods (and vice versa for oversupplied
goods) until reaching equilibrium, and execute trade only after prices
have been selected. A real system must depart from this approach in that
it operates continuously. As a result, since supply and demand may
lag price adjustments, true equilibrium may never be reached.
In addition, calculating equilibrium prices generally requires clients
to have global information on the supply provided by each sensor
node at the currently-proposed prices. We are exploring techniques in
which aggregate supply information is collected and piggybacked on other
transmissions to the base station. However, clients must then operate
on incomplete and out-of-date supply information. Another approach is
to collect supply information at several price points simultaneously,
allowing the client to adjust prices based on the resulting gradient
information.
Richer pricing models:
More complex pricing schemes can be used to induce sophisticated
behaviors in the network. For example, rather than pricing only those
goods that result from single actions, we can price sequences of
actions. Consider aggregating multiple sensor readings into a single
value for transmission. Rather than price the final aggregate value
and requiring an agent to reason about a sequence of actions to
achieve that result, we can establish prices for each step in the
sequence and introduce control or data dependencies between actions.
Another question is that of location-based prices, in which goods
are priced differently in different areas of the network.
This can be used to establish a ring of ``sentry nodes''
around the perimeter of the network that wake other nodes in the
interior when the entrance of a vehicle is detected.
New application domains:
We intend to explore other applications for the SORA technique.
As discussed earlier, this requires that nodes be programmed with
new actions and corresponding energy consumption models. One application
that we are actively investigating involves sensor networks for emergency
medical care and disaster response [25]. This scenario
involves establishing multicast communication pathways between multiple
vital sign sensors worn by patients and handheld devices carried by
rescuers and doctors. We envision SORA providing a mechanism for
efficient bandwidth and energy allocation in this environment.
Integration with programming languages:
Finally, our broader research agenda for sensor networks involves
developing high-level macroprogramming languages
that compile down to local behaviors of
individual nodes. SORA presents a suite of techniques for scheduling node
actions and managing energy that could be integrated into such a
language. For example, TinyDB's SQL-based query language could be
implemented using SORA to control the execution of query operators on
each node, rather than the current model of relying on a static
schedule.
We have completed
the initial design of a functional macroprogramming language for sensor
networks that compiles down to a simple per-node state machine that could
be readily implemented using a SORA-based
model [31,32].
The authors wish to thank our shepherd, Amin Vahdat, as well as the
anonymous reviewers for their comments on this paper.
- 1
-
S. Adlakha, S. Ganeriwal, C. Schurgers, and M. B. Srivastava.
Density, accuracy, latency and lifetime tradeoffs in wireless sensor
networks - a multidimensional design perspective.
In review, 2003.
- 2
-
L. Anderegg and S. Eidenbenz.
Ad hoc-VCG: a truthful and cost-efficient routing protocol for
mobile ad hoc networks with selfish agents.
In Proc. MOBICOM'03, September 2003.
- 3
-
A. AuYoung, A. C. Snoeren, A. Vahdat, and B. Chun.
Resource allocation in federated distributed computing
infrastructures.
In Proc. First Workshop on Operating System and Architectural
Support for the on demand IT InfraStructure, October 2004.
- 4
-
M. Balazinska, H. Balakrishnan, and M. Stonebraker.
Contract-based load management in federated distributed systems.
In Proc. First Symposium on Networked Systems Design and
Implementation (NSDI '04), March 2004.
- 5
-
A. Boulis, S. Ganeriwal, and M. B. Srivastava.
Aggregation in sensor networks: An energy - accuracy tradeoff.
In Proc. IEEE workshop on Sensor Network Protocols and
Applications, 2003.
- 6
-
R. Brooks, P. Ramanathan, and A. Sayeed.
Distributed target classification and tracking in sensor networks.
Proceedings of the IEEE, November 2003.
- 7
-
R. Buyya.
Economic-based Distributed Resource Management and Scheduling
for Grid Computing.
PhD thesis, Monash University, April 2002.
- 8
-
Center for Information Technology Research in the Interest of Society.
Smart buildings admit their faults.
https://www.citris.berkeley.edu/applications/disaster_response/smartbuildings.html, 2002.
- 9
-
A. Cerpa, J. Elson, D. Estrin, L. Girod, M. Hamilton, and J. Zhao.
Habitat monitoring: Application driver for wireless communications
technology.
In Proc. the Workshop on Data Communications in Latin America
and the Caribbean, Apr. 2001.
- 10
-
S. H. Clearwater, editor.
Market-Based Control: A Paradigm for Distributed Resource
Allocation.
World Scientific, 1996.
- 11
-
D. Ganesan, B. Greenstein, D. Perelyubskiy, D. Estrin, and J. Heidemann.
An evaluation of multi-resolution search and storage in
resource-constrained sensor networks.
In Proc. the First ACM Conference on Embedded Networked Sensor
Systems (SenSys 2003), November 2003.
- 12
-
J. S. Heidemann, F. Silva, C. Intanagonwiwat, R. Govindan, D. Estrin, and
D. Ganesan.
Building efficient wireless sensor networks with low-level naming.
In Proc. the 18th SOSP, Banff, Canada, October 2001.
- 13
-
W. Heinzelman, A. Chandrakasan, and H. Balakrishnan.
Energy-efficient communication protocol for wireless microsensor
networks.
In Proc. the 33rd Hawaii International Conference on System
Sciences (HICSS), January 2000.
- 14
-
W. Heinzelman, J. Kulik, and H. Balakrishnan.
Adaptive protocols for information dissemination in wireless sensor
networks.
In Proc. the 5th ACM/IEEE Mobicom Conference, August 1999.
- 15
-
J. M. Hellerstein, W. Hong, S. Madden, and K. Stanek.
Beyond average: Towards sophisticated sensing with queries.
In Proc. the 2nd International Workshop on Information
Processing in Sensor Networks (IPSN '03), March 2003.
- 16
-
J. Hill, R. Szewczyk, A. Woo, S. Hollar, D. E. Culler, and K. S. J. Pister.
System architecture directions for networked sensors.
In Proc. the 9th International Conference on Architectural
Support for Programming Languages and Operating Systems, pages 93-104,
Boston, MA, USA, Nov. 2000.
- 17
-
C. Intanagonwiwat, R. Govindan, and D. Estrin.
Directed diffusion: A scalable and robust communication paradigm
for sensor networks.
In Proc. International Conference on Mobile Computing and
Networking, Aug. 2000.
- 18
-
L. Kang, S. Lahaie, G. Mainland, D. C. Parkes, and M. Welsh.
Using virtual markets to program global behavior in sensor networks.
In Proc. 11th ACM SIGOPS European Workshop, Leuven, Belgium,
September 2004.
- 19
-
B. Karp and H. T. Kung.
GPSR: Greedy perimeter stateless routing for wireless networks.
In Proc. the Sixth Annual ACM/IEEE International Conference on
Mobile Computing and Networking (MobiCom 2000), Boston, MA, August 2000.
- 20
-
V. A. Kottapalli, A. S. Kiremidjian, J. P. Lynch, E. Carryer, T. W. Kenny,
K. H. Law, and Y. Lei.
Two-tiered wireless sensor network architecture for structural health
monitoring.
In Proc. the SPIE 10th Annual International Symposium on Smart
Structures and Materials, San Diego, CA, March 2000.
- 21
-
P. Levis, N. Lee, M. Welsh, and D. Culler.
TOSSIM: Accurate and scalable simulation of entire TinyOS
applications.
In Proc. the First ACM Conference on Embedded Networked Sensor
Systems (SenSys 2003), November 2003.
- 22
-
P. Levis, N. Patel, S. Shenker, and D. Culler.
Trickle: A self-regulating algorithm for code propagation and
maintenance in wireless sensor networks.
In Proc. the First USENIX/ACM Symposium on Networked Systems
Design and Implementation (NSDI), 2004.
- 23
-
D. Li, K. Wong, Y. H. Hu, and A. Sayeed.
Detection, classification and tracking of targets in distributed
sensor networks.
IEEE Signal Processing Magazine, 19(2), March 2002.
- 24
-
J. Liu, P. Cheung, L. Guibas, and F. Zhao.
A dual-space approach to tracking and sensor management in wireless
sensor networks.
In Proc. First ACM International Workshop on Wireless Sensor
Networks and Applications, September 2002.
- 25
-
K. Lorincz, D. Malan, T. R. F. Fulford-Jones, A. Nawoj, A. Clavel, V. Shnayder,
G. Mainland, S. Moulton, and M. Welsh.
Sensor Networks for Emergency Response: Challenges and
Opportunities.
IEEE Pervasive Computing, Oct-Dec 2004.
- 26
-
S. Madden, M. J. Franklin, J. M. Hellerstein, and W. Hong.
TAG: A Tiny AGgregation Service for Ad-Hoc Sensor Networks.
In Proc. the 5th OSDI, December 2002.
- 27
-
S. Madden, M. J. Franklin, J. M. Hellerstein, and W. Hong.
The design of an acquisitional query processor for sensor networks.
In Proc. the ACM SIGMOD 2003 Conference, June 2003.
- 28
-
A. Mainwaring, J. Polastre, R. Szewczyk, D. Culler, and J. Anderson.
Wireless sensor networks for habitat monitoring.
In ACM International Workshop on Wireless Sensor Networks and
Applications (WSNA'02), Atlanta, GA, USA, Sept. 2002.
- 29
-
A. Mas-Colell, M. D. Whinston, and J. R. Green.
Microecononmic Theory.
Oxford University Press, 1995.
- 30
-
T. Mullen and M. P. Wellman.
Some issues in the design of market-oriented agents.
In W. et al., editor, Intelligent Agents: Theories,
Architectures and Languages, volume 2. Springer-Verlag, 1996.
- 31
-
R. Newton, Arvind, and M. Welsh.
Building up to macroprogramming: An intermediate language for sensor
networks.
In Proc. Fourth International Conference on Information
Processing in Sensor Networks (IPSN'05), April 2005.
- 32
-
R. Newton and M. Welsh.
Region streams: Functional macroprogramming for sensor networks.
In Proc. the First International Workshop on Data Management for
Sensor Networks (DMSN), Toronto, Canada, August 2004.
- 33
-
S. Rhee and S. Liu.
An ultra-low power, self-organizing wireless network and its
applications to noninvasive biomedical instrumentation.
Proc. IEEE/Sarnoff Symposium on Advances in Wired and Wireless
Communications, March 2002.
- 34
-
C. Schurgers, V. Tsiatsis, S. Ganeriwal, and M. Srivastava.
Topology management for sensor networks: Exploiting latency and
density.
In Proc. MobiHoc, 2002.
- 35
-
S. Shenker.
Fundamental design issues for the future Internet.
IEEE Journal on Selected Areas in Communications, 13(7),
September 1995.
- 36
-
M. Stonebraker, R. Devine, M. Kornacker, W. Litwin, A. Pfeffer, A. Sah, and
C. Staelin.
An economic paradigm for query processing and data migration in
Mariposa.
In Proc. the 3rd International Conference on Parallel and
Distributed Information Systems, September 1994.
- 37
-
R. S. Sutton and A. G. Barto.
Reinforcement Learning: An Introduction.
MIT Press, Cambridge, MA, 1998.
- 38
-
T. von Eicken, D. E. Culler, S. C. Goldstein, and K. E. Schauser.
Active messages: a mechanism for integrating communication and
computation.
In Proc. the 19th Annual International Symposium on Computer
Architecture, pages 256-266, May 1992.
- 39
-
C. A. Waldspruger, T. Hogg, B. A. Huberman, J. O. Kephart, and S. Stornetta.
Spawn: A Distributed Computational Economy.
IEEE Transactions on Software Engineering, 18(2):103-177,
February 1992.
- 40
-
M. P. Wellman.
Market-oriented programming: Some early lessons.
In S. Clearwater, editor, Market-Based Control: A Paradigm for
Distributed Resource Allocation. World Scientific, 1996.
- 41
-
M. Welsh and G. Mainland.
Programming sensor networks using abstract regions.
In Proc. the First USENIX/ACM Symposium on Networked Systems
Design and Implementation (NSDI '04), March 2004.
- 42
-
G. Werner-Allen, P. Swieskowski, and M. Welsh.
Motelab: A wireless sensor network testbed.
In Proc. Fourth International Conference on Information
Processing in Sensor Networks (IPSN'05), Special Track on Platform Tools and
Design Methods for Network Embedded Sensors (SPOTS), April 2005.
- 43
-
K. Whitehouse, C. Sharp, E. Brewer, and D. Culler.
Hood: A neighborhood abstraction for sensor networks.
In Proc. the International Conference on Mobile Systems,
Applications, and Services (MOBISYS `04), June 2004.
- 44
-
A. Woo, T. Tong, and D. Culler.
Taming the underlying challenges of reliable multihop routing in
sensor networks.
In Proc. the First ACM Conference on Embedded Networked Sensor
Systems (SenSys 2003), November 2003.
- 45
-
Y. Xu and W.-C. Lee.
On localized prediction for power efficient object tracking in sensor
networks.
In Proc. 1st International Workshop on Mobile Distributed
Computing, May 2003.
- 46
-
Y. Yao and J. E. Gehrke.
The Cougar approach to in-network query processing in sensor
networks.
ACM Sigmod Record, 31(3), September 2002.
- 47
-
F. Zhao, J. Liu, J. Liu, L. Guibas, and J. Reich.
Collaborative signal and information processing: An information
directed approach.
Proc. the IEEE, 91(8):1199-1209, 2003.
|

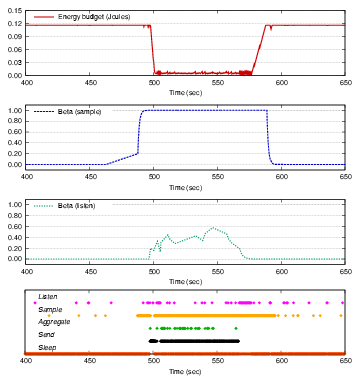
![]() is set
to 0.05, and the learning parameter
is set
to 0.05, and the learning parameter ![]() is set to 0.2.
We demonstrate the effect of varying these parameters in
Section 5.7 and 5.8.
is set to 0.2.
We demonstrate the effect of varying these parameters in
Section 5.7 and 5.8.
![]() joules, a node calculates the rate for performing each
round of actions (sample, listen, aggregate, transmit, and sleep) in
order to meet its budget.
For example, given a daily budget of 1000 J, the data collection sequence
can be performed once every 0.4 sec. This schedule is conservative,
since not all nodes will actually detect the vehicle or transmit data
during each period.
The same schedule is used for every
node in the network, so nodes do not learn which actions they should
perform, nor adapt their sampling rate to stimuli such as the approach
of the vehicle.
joules, a node calculates the rate for performing each
round of actions (sample, listen, aggregate, transmit, and sleep) in
order to meet its budget.
For example, given a daily budget of 1000 J, the data collection sequence
can be performed once every 0.4 sec. This schedule is conservative,
since not all nodes will actually detect the vehicle or transmit data
during each period.
The same schedule is used for every
node in the network, so nodes do not learn which actions they should
perform, nor adapt their sampling rate to stimuli such as the approach
of the vehicle.
![]() values for node 31, which is along the path of the vehicle.
As the vehicle approaches along its circular path at time
values for node 31, which is along the path of the vehicle.
As the vehicle approaches along its circular path at time
![]() , the node determines that it will be paid to sample,
aggregate, and send sensor readings. As the vehicle departs around
time
, the node determines that it will be paid to sample,
aggregate, and send sensor readings. As the vehicle departs around
time ![]() , the node returns to its original behavior.
At certain times (e.g., at
, the node returns to its original behavior.
At certain times (e.g., at ![]() and
and ![]() ),
the node receives messages
from other nodes and routes them towards the base station, explaining
the increase in
),
the node receives messages
from other nodes and routes them towards the base station, explaining
the increase in ![]() for the listen action.
When the vehicle is not nearby,
the node mostly sleeps, since no interesting samples or
radio messages are received. The energy bucket fills during this time
accordingly; the bucket capacity
for the listen action.
When the vehicle is not nearby,
the node mostly sleeps, since no interesting samples or
radio messages are received. The energy bucket fills during this time
accordingly; the bucket capacity ![]() is set arbitrarily to 115 mJ, which
requires the node to sleep for 20 seconds to fill the bucket
entirely.
is set arbitrarily to 115 mJ, which
requires the node to sleep for 20 seconds to fill the bucket
entirely.
![]() -greedy action selection policy dictates that it
will explore among these alternatives despite negligible utility.
-greedy action selection policy dictates that it
will explore among these alternatives despite negligible utility.
![]() ,
the vehicle is closest to the base station, so only those nodes close to
the base are sampling and routing data, while the rest of the network
is dormant.
,
the vehicle is closest to the base station, so only those nodes close to
the base are sampling and routing data, while the rest of the network
is dormant.
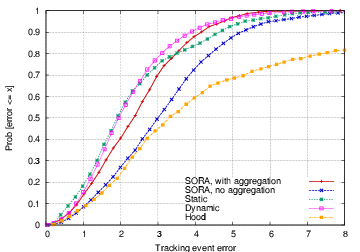
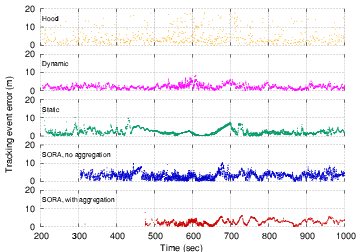
![]() ,
the exploration probability, and
,
the exploration probability, and ![]() , the EWMA gain for
learning action success probabilities. By varying
, the EWMA gain for
learning action success probabilities. By varying ![]() , we
can trade off increased energy waste (for exploring the action
space) for faster response to changing network conditions.
By varying
, we
can trade off increased energy waste (for exploring the action
space) for faster response to changing network conditions.
By varying ![]() , the system reacts more or less quickly to
changes in success probabilities; higher values of
, the system reacts more or less quickly to
changes in success probabilities; higher values of ![]() cause a node to bias action selection towards more-recently
profitable actions.
cause a node to bias action selection towards more-recently
profitable actions.
![]() from 0.01 to 0.5. As the probability of taking a random action
increases, the proportion of energy wasted taking those actions
also increases. However, the proportion of energy wasted taking
the ``greedy'' action (the action with the highest expected
probability of success) decreases, since nodes learn more
rapidly which actions are profitable by exploring the action
space.
from 0.01 to 0.5. As the probability of taking a random action
increases, the proportion of energy wasted taking those actions
also increases. However, the proportion of energy wasted taking
the ``greedy'' action (the action with the highest expected
probability of success) decreases, since nodes learn more
rapidly which actions are profitable by exploring the action
space.
![]() .
When
.
When ![]() is increased, nodes react very quickly to changes in
action success. When
is increased, nodes react very quickly to changes in
action success. When ![]() , if an action is successful once,
the node will immediately prefer it over all others. Likewise, the node
will immediately ignore a potentially profitable action the first time
it is unsuccessful. As a result, the
proportion of energy used on successfully choosing the greedy action
decreases. Also, since the node's action selection policy is
increasingly myopic, nodes spend more time sleeping. As a result,
a greater proportion of energy is spent on exploratory
actions since few ``greedy'' actions are considered worthwhile.
, if an action is successful once,
the node will immediately prefer it over all others. Likewise, the node
will immediately ignore a potentially profitable action the first time
it is unsuccessful. As a result, the
proportion of energy used on successfully choosing the greedy action
decreases. Also, since the node's action selection policy is
increasingly myopic, nodes spend more time sleeping. As a result,
a greater proportion of energy is spent on exploratory
actions since few ``greedy'' actions are considered worthwhile.