|
| |||||||||||||||||||||||||||||||||||||||||||||||||||

| ||||||||||||||||||||||||||||||||||||||||||||||||||||
|
NSDI '04 Paper
[NSDI '04 Technical Program]
Programming Sensor Networks Using Abstract RegionsMatt Welsh and Geoff Mainland Harvard University {mdw,mainland}@eecs.harvard.edu
AbstractWireless sensor networks are attracting increased interest for a wide range of applications, such as environmental monitoring and vehicle tracking. However, developing sensor network applications is notoriously difficult, due to extreme resource limitations of nodes, the unreliability of radio communication, and the necessity of low power operation. Our goal is to simplify application design by providing a set of programming primitives for sensor networks that abstract the details of low-level communication, data sharing, and collective operations.We present abstract regions, a family of spatial operators that capture local communication within regions of the network, which may be defined in terms of radio connectivity, geographic location, or other properties of nodes. Regions provide interfaces for identifying neighboring nodes, sharing data among neighbors, and performing efficient reductions on shared variables. In addition, abstract regions expose the tradeoff between the accuracy and resource usage of communication operations. Applications can adapt to changing network conditions by tuning the energy and bandwidth usage of the underlying communication substrate. We present the implementation of abstract regions in the TinyOS programming environment, as well as results demonstrating their use for building adaptive sensor network applications.
|
|
Our algorithm is based on a pruned Yao graph [23] and is
depicted in Figure 2.
First, each node discovers a ![]() -nearest radio region of candidate
nodes. When
-nearest radio region of candidate
nodes. When ![]() neighbors have been accumulated, each node forms the
Yao graph by dividing space around
it into
neighbors have been accumulated, each node forms the
Yao graph by dividing space around
it into ![]() equal-sized sectors of angle
equal-sized sectors of angle
![]() and selecting the nearest node within each sector
as a potential neighbor. Next, each node uses a single-hop broadcast
to advertise its selected outedges.
Upon reception of an edge advertisement, each node tests
whether the given edge crosses one of its own outedges, and if so sends
an invalidation message to the source, causing it to prune the offending
edge from its set. Nodes do not select additional neighbors beyond
the initial candidates, so a node may end up with fewer than
and selecting the nearest node within each sector
as a potential neighbor. Next, each node uses a single-hop broadcast
to advertise its selected outedges.
Upon reception of an edge advertisement, each node tests
whether the given edge crosses one of its own outedges, and if so sends
an invalidation message to the source, causing it to prune the offending
edge from its set. Nodes do not select additional neighbors beyond
the initial candidates, so a node may end up with fewer than ![]() outedges. Nodes perform several rounds of edge set broadcasts and wait
for some time before settling on a final set of neighbors.
Both the number of broadcasts and the timeout settings can be tuned by
the application, as discussed below in Section 3.3.
Changes in the underlying
outedges. Nodes perform several rounds of edge set broadcasts and wait
for some time before settling on a final set of neighbors.
Both the number of broadcasts and the timeout settings can be tuned by
the application, as discussed below in Section 3.3.
Changes in the underlying ![]() -nearest-neighbor set initiates selection
of new Yao neighbors.
Data sharing and reduction are implemented using the same components as
in the radio neighborhood, as all neighbors are one radio hop away.
-nearest-neighbor set initiates selection
of new Yao neighbors.
Data sharing and reduction are implemented using the same components as
in the radio neighborhood, as all neighbors are one radio hop away.
We have also implemented planar regions based on the Relative Neighborhood Graph and Gabriel Graph, and an implementation of GPSR [19] based on them. This is described in Section 5.4.
Spanning trees are useful for aggregating values within the sensor network at a single point, as demonstrated by systems such as TinyDB [25] and directed diffusion [18]. Our spanning tree implementation provides the same programmatic interface as other regions, although the semantics of the shared variable and reduction operations have been augmented to support global communication through the routing topology provided by the spanning tree. The shared variable put operation at the root floods the shared value to all nodes in the tree, while a put at a non-root node propagates the value to the root. Reduction operations cause data to propagate up the tree, causing each node to aggregate its local value with that of its children.
The spanning tree implementation adapts to changing network conditions, as nodes attempt to select a parent in the spanning tree to maximize the link quality and minimize the message hopcount to the root. Each node maintains an estimate of the link quality to its parent, measured in terms of the fraction of successful message transmissions to the parent and the fraction of messages successfully received from other nodes, using a simple sequence number counting scheme.
The tree is formed by broadcasting messages indicating the source node ID and number of hops from the root; nodes rebroadcast received advertisements with their own ID as the source and the hopcount incremented by 1. Nodes initially select a parent in the tree based on the lowest hopcount advertisement they receive, but may select another parent if the link quality estimate falls below a certain threshold. This estimate is smoothed with an exponentially weighted moving average (EWMA) to avoid rapid parent reselections. Our goal in this work has not been to develop the most robust tree formation algorithm, but rather to demonstrate that spanning trees fit within the programming interface provided by abstract regions. It would be straightforward to replace the tree construction algorithm with another, such as that described in [36], and layer the abstract regions interface over it.
The collective operations provided by abstract regions are inherently unreliable. The quality of region discovery, the fraction of nodes contacted during a reduction operation, and the reliability of shared variable operations all depend on the number of messages used to perform those operations. Generally, increasing the number of messages (and hence, energy usage) improves communication reliability and the accuracy of collective operations. However, given a limited energy or bandwidth budget, the application may wish to perform region operations with reduced fidelity.
Abstract regions expose this tradeoff between resource consumption and the accuracy or yield of collective operations. This is in contrast to most existing approaches to sensor network communication, which hide these resource tradeoffs from the application. As a concrete example of such a tradeoff, the communication layer may tune the number and frequency of message retransmissions to obtain a given degree of reliability from the underlying radio channel. Similarly, nodes may vary the rate at which they broadcast location advertisements to neighboring nodes, affecting the quality of region discovery.
Abstract regions provide feedback to the application in the form of a
quality measure that represents the completeness or accuracy of
a given operation. For member discovery,
the quality measure represents the fraction of candidate nodes that
responded to the discovery request. For example, when discovering
one-hop neighbors within distance ![]() , the quality measure represents the
fraction
of one-hop nodes that responded to the region formation request.
For reduction, the quality measure represents the fraction of nodes
in the region that participated in the reduction. In addition, each
operation supports a timeout mechanism, in which the operation will fail
if it has not completed within a given time interval. For example, when
performing a shared variable get operation, a timeout indicates
that the data could not be retrieved from the requested node.
, the quality measure represents the
fraction
of one-hop nodes that responded to the region formation request.
For reduction, the quality measure represents the fraction of nodes
in the region that participated in the reduction. In addition, each
operation supports a timeout mechanism, in which the operation will fail
if it has not completed within a given time interval. For example, when
performing a shared variable get operation, a timeout indicates
that the data could not be retrieved from the requested node.
Applications can use this quality feedback to affect resource consumption of collective operations through a tuning interface. The tuning interface allows the application to specify low-level parameters of the region implementation, such as the number of message broadcasts, amount of time, or number of candidate nodes to consider when forming a region. Likewise, region operations perform message retransmission and acknowledgment to increase the reliability of communication; the depth of the transmit queue and number of retransmission attempts can be tuned by the application.
In our current implementation, the set of parameters exposed by the tuning interface is somewhat low-level and in many cases specific to the particular region implementation. Many of these parameters are straightforward to tune, although their effect on resource consumption may not be immediately evident, as it is highly dependent on application behavior. In general, an application designer will need to study the impact of the relevant tuning parameters on resource usage and application performance.
Exposing tuning knobs and quality feedback greatly impacts the programming model supported by abstract regions. Rather than hiding performance tradeoffs within a generic communication library with no knowledge of application requirements, the tuning interface enables applications to adapt to changing environments, network conditions, node failure, and energy budget. For example, this interface can be used to implement adaptive control mechanisms that automatically tune region parameters to meet some quality or resource usage target. In Section 6, we demonstrate an adaptive controller that tunes the maximum retransmission count to achieve a target yield for reduction operations.
We are currently working on a resource-centric tuning mechanism that allows the programmer to express an energy, radio bandwidth, or latency budget for each operator, and which maps these constraints onto the appropriate low-level parameter settings. This approach shields the programmer from details of the low-level interface and enables adaptivity using higher-level resource constraints. This is discussed further in Section 7.
In this section we detail the implementation and programming interface for abstract regions on TinyOS [17], a small operating system for sensor nodes. Unlike the event-driven, asynchronous concurrency model provided by TinyOS, abstract regions provide a blocking, synchronous interface, which greatly simplifies application logic. This is accomplished using a lightweight, thread-like abstraction called fibers, described below.
Traditional concurrency mechanisms, such as threads, are too heavyweight to implement on extremely resource-constrained devices such as motes. TinyOS employs an event-driven concurrency model, in which long-running operations are not permitted to block the application, but rather using a split-phase approach. An initial request for service is invoked through a command, and when the operation is complete, an event (or callback) is invoked on the original requesting component. For example, to take a sensor reading, an application invokes the getData() command on the sensor hardware component, which later invokes the dataReady() callback supplying the sensor reading.
The TinyOS concurrency model requires each concurrent ``execution context'' to be implemented manually by the programmer as a state machine, with execution driven by the sequence of commands and events invoked on each software component. If an application is performing multiple concurrent tasks, these operations must be carefully interleaved. In addition, each split-phase operation requires that the application code be broken across multiple disjoint segments of code. The programmer must manually maintain continuation state across each split-phase operation, adding significant complexity to the code. While the logical program may be quite simple, the lack of blocking operations in TinyOS requires that the application be broken into multiple tasks and event handlers.
A key observation is that a broad class of sensor network applications can be represented by a small number of concurrent activities: for example, a core application loop that periodically performs some sensing and communication operations, as well as a reactive context that responds to external events (e.g., incoming messages). Providing blocking operations in TinyOS does not require a full-fledged threads mechanism, but rather the means to support a limited range of blocking operations along with event-driven code to handle asynchronous events.
We have implemented a lightweight, thread-like concurrency model for TinyOS, supporting a single blocking execution context alongside the default, event-driven context provided by TinyOS. We use the term fibers to refer to each execution context.1 The default system fiber is event-driven and may not block, while the application fiber is permitted to block. Because there is only one blocking context, both the system and application fibers can share a single stack. The overhead for each fiber, therefore, consists of a saved register set, which on the ATmega128L is 24 bytes. The runtime overhead for a context switch is just 150 instructions. Apart from the single blocking context, applications may employ additional concurrency through TinyOS's event-driven concurrency model.
The application fiber may block by saving its register set and jumping to the system fiber. The system fiber restores its registers, but resumes execution on the application stack. An event, such as a timer interrupt or message arrival, may wake up the application fiber, causing its register state to be restored once the event handler has completed. The system fiber maintains no live state on the stack after the application fiber is resumed.
Fibers allow blocking and event-driven concurrency to be freely mixed in an application, and different components can use different concurrency models depending on their requirements. In general, the central sense-process-communication loop of an application may employ blocking for simplicity, while the bulk of the TinyOS code remains event-driven.
The abstract regions programming interface is shown in Figure 3. The use of blocking interfaces, provided by fibers, greatly simplifies application design. Rather than breaking application logic across a set of disparate event handlers, a single, straight-line loop can be written. Apart from considerably shortening the code, this approach avoids common programming errors, such as maintaining continuation state incorrectly.
Without blocking calls, the object tracking application described in Section 5.1 is 369 lines of nesC code, consisting of 5 event handlers and 11 continuation functions. The corresponding blocking version (shown in pseudocode form in Section 5.1) is 134 lines of code and consists of a single main loop. All application state is stored in local variables within the loop, rather than being marshaled into and out of global continuations for each split-phase call.
Abstract regions themselves are implemented using event-driven concurrency, due to the number of concurrent activities that the region must perform. For example, the spanning tree region is continually updating routing tables based on link quality estimates received from neighboring nodes; the reactive nature of this activity is better suited to an event-driven model. A wrapper component is used to provide a blocking, fiber-based interface to each abstract region implementation, and applications can decide whether to invoke a region through the blocking or the split-phase interface.
To demonstrate the effectiveness of regions, in this section we describe four sensor network applications that are greatly simplified by their use. These include tracking an object in the sensor field, finding spatial contours, distributed event detection using directed diffusion [18], and geographic routing using GPSR [19].
Object tracking is an oft-cited application for sensor networks [5,22,37]. In its simplest form, tracking involves determining the location of a moving object by detecting changes in some relevant sensor readings, such as magnetic field.
Our version of object tracking uses a simple algorithm based on the DARPA NEST demonstration software, described in [35]. Each node takes periodic magnetometer readings and compares them to a threshold value. Nodes above the threshold communicate with their neighbors and elect a leader node, which is the node with the largest magnetometer reading. The leader computes the centroid of its neighbors sensor readings, and transmits the result to a base station.
The following pseudocode shows this application expressed in terms of
abstract regions:2
location = get_location();
/* Get 8 nearest neighbors */
region = k_nearest_region.create(8);
while (true) {
reading = get_sensor_reading();
/* Store local data as shared variables */
region.putvar(reading_key, reading);
region.putvar(reg_x_key, reading * location.x);
region.putvar(reg_y_key, reading * location.y);
if (reading > threshold) {
/* ID of the node with the max value */
max_id = region.reduce(OP_MAXID, reading_key);
/* If I am the leader node ... */
if (max_id == my_id) {
/* Perform reductions and compute centroid */
sum = region.reduce(OP_SUM, reading_key);
sum_x = region.reduce(OP_SUM, reg_x_key);
sum_y = region.reduce(OP_SUM, reg_y_key);
centroid.x = sum_x / sum;
centroid.y = sum_y / sum;
send_to_basestation(centroid);
}
}
sleep(periodic_delay);
}
The program performs essentially all communication through the abstract
regions interface, in this case the ![]() -nearest-neighbor region.
Nodes store their local sensor reading and the reading scaled by the
-nearest-neighbor region.
Nodes store their local sensor reading and the reading scaled by the
![]() and
and ![]() dimensions of their location as shared variables. Nodes
above the threshold perform a reduction to determine the node with the
maximum sensor reading, which is responsible for calculating the centroid
of its neighbors' readings. A series of sum-reductions is performed over the
shared variables which are used to compute the centroid:
dimensions of their location as shared variables. Nodes
above the threshold perform a reduction to determine the node with the
maximum sensor reading, which is responsible for calculating the centroid
of its neighbors' readings. A series of sum-reductions is performed over the
shared variables which are used to compute the centroid:
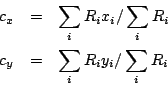
The use of regions greatly simplifies application design. The programmer need not be concerned with the details of routing, data sharing, or identifying the appropriate set of neighbor nodes for performing reductions. As a result the application code is very concise. As described earlier, our actual implementation is just 134 lines of code, of which 70 lines comprise the main application loop above. The rest consists of variable and constant declarations as well as initialization code.
As a rough approximation of the linecount for a ``hand coded'' version of
this application, without the benefit of the abstract regions interface,
consider the combined size of the nonblocking object tracking code
(369 lines) and the ![]() -nearest-neighbor region code (247 lines).
This total of 616 lines, compared with 134 lines for the abstract
region version, suggests that this programming abstraction captures a
great deal of the complexity of sensor applications.
-nearest-neighbor region code (247 lines).
This total of 616 lines, compared with 134 lines for the abstract
region version, suggests that this programming abstraction captures a
great deal of the complexity of sensor applications.
Another typical sensor network application is detecting contours or edges in the set of sensor readings [16,24]. Contour finding involves determining a set of points in space that lie along, or close to, an isoline in the gradient of sensor readings. Contours might represent the boundary of a region of interest, such as a group of sensors with an interesting range of readings. Contour finding is a valuable spatial operation as it compresses the per-node sensor data into a low-dimensional surface. This primitive could be used for detecting thermoclines or tracking the flow of contaminants through soil [6].
|
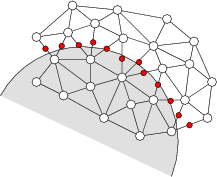
An implementation of contour finding using abstract regions is depicted in Figure 4, and is expressed in pseudocode as:
location = get_location();
/* Form approximate planar mesh */
region = apmesh_region.create();
region.putvar(loc_key, location);
while (true) {
reading = get_sensor_reading();
region.putvar(reading_key, reading);
if (reading > threshold) {
foreach (nbr in region.get_neighbors()) {
/* Fetch neighbor's reading */
rem_reading = region.getvar(reading_key, nbr);
if (rem_reading <= threshold) {
rem_loc = region.getvar(loc_key, nbr);
contour_point = midpoint(location, rem_loc);
send_to_basestation(contour_point);
}
}
}
sleep(periodic_delay);
}
Nodes first form an approximate planar mesh region, as described in
Section 3.
Each node stores its location and sensor reading as a
shared variable. Nodes that are above the sensor threshold of interest
fetch the readings and locations of their neighbors. For each neighbor
that is below the threshold, the node computes a contour point as the
midpoint between itself and its neighbor, and sends the result to the
base station.
The use of the approximate planar mesh region ensures that few edges will cross, and that nodes will generally select neighbors that are geographically near. These properties are vital for our contour finding algorithm as it is based on pairwise comparisons of sensor readings, and values are computed along edges in the mesh. As with the object tracking application, abstract regions shield the programmer from details of mesh formation and data sharing; the application code is very straightforward. It is only 118 lines of nesC code, 56 lines of which are devoted to the main application loop.
|
As discussed in Section 2,
directed diffusion [18] has been proposed as a
mechanism for distributed event detection in sensor networks. The idea
is to flood interests for named data throughout the network (such
as ``all nodes with sensor readings greater than threshold ![]() ''),
as shown in Figure 5. Nodes that match some
interest report their local value to the
sink that generated the interest. Here, we show that abstract
regions can be used to implement the directed diffusion mechanism,
demonstrating their value for building higher-level
communication abstractions.
''),
as shown in Figure 5. Nodes that match some
interest report their local value to the
sink that generated the interest. Here, we show that abstract
regions can be used to implement the directed diffusion mechanism,
demonstrating their value for building higher-level
communication abstractions.
The directed diffusion programming interface consists of two
operations: broadcastInterest and publishData.
Sink nodes invoke broadcastInterest with an
operator (such as ![]() ,
, ![]() , or
, or ![]() ) and a comparison
value. Our current implementation supports interests in the form of
simple binary operator comparisons; it would be straightforward to
extend this to support more general interest specifications.
Nodes call publishData to provide local data, which is
periodically compared against
all received interests. When the local data matches an interest,
the node routes an event report to the corresponding sink.
When the sink receives an event report, a dataReceived
event handler is invoked with the corresponding node address and value.
) and a comparison
value. Our current implementation supports interests in the form of
simple binary operator comparisons; it would be straightforward to
extend this to support more general interest specifications.
Nodes call publishData to provide local data, which is
periodically compared against
all received interests. When the local data matches an interest,
the node routes an event report to the corresponding sink.
When the sink receives an event report, a dataReceived
event handler is invoked with the corresponding node address and value.
Our directed diffusion layer is implemented using the spanning tree abstract region. Data sinks first form an adaptive spanning tree, and publish an interest record by inserting it into the tuplespace associated with that region. Recall that in the spanning tree region, the tuplespace put operation, when invoked at the root, broadcasts the entry to all nodes in the tree. Nodes periodically check for interest records using the tuplespace get operation, and compare their current value (provided by publishData()) with all received interests. If the value matches, it is inserted into the tuplespace of the corresponding spanning tree, which propagates the value to the root.
Nearly all of the complexity of broadcasting interests and propagating data to the sink is captured by the spanning tree region and its tuplespace implementation. The directed diffusion layer is responsible only for representing interests and matching data values as tuplespace entries, allowing the spanning tree region to handle the details of maintaining routes between data sources and sinks. One drawback with our current implementation is that multiple sinks receiving the same data must form separate spanning trees, causing nodes with matching data to send multiple copies. However, it would be straightforward to optimize the spanning tree region by suppressing duplicate packets being sent along the same network path. The directed diffusion layer is only 188 lines of nesC code, of which 66 lines handle initialization and definitions. In contrast, the spanning tree region code is 937 lines.
Geographic routing protocols use the locations of nodes in the network to make packet forwarding decisions. Rather than maintaining distance vectors or link state at each node, a node only needs to know the geographic positions of its immediate neighbors. One such protocol is Greedy Perimeter Stateless Routing (GPSR) [19], which operates in two modes: greedy routing, in which the message is routed to the neighboring node that is closest to the destination, and face routing, which is used when no neighbor is closer to the destination than the current node. Face routing requires a planar mesh to ensure that these local minima can be traversed.
We have implemented GPSR using both our radio neighborhood region (for greedy routing mode) and approximate planar mesh regions (for face routing mode). The abstract regions code handles all aspects of constructing the appropriate graphs, greatly simplifying the GPSR code itself. There are three types of approxiate planar mesh: the pruned Yao graph (PYG), Relative Neighborhood Graph (RNG), and Gabriel Graph (GG). Each of these graphs has slightly different rules for determining inclusion of an edge using only local information about the immediate neighbors of each node. Our GPSR implementation provides a scalable ad hoc routing framework for sensor networks, although space limitations prevent us from presenting detailed results.
In this section, we evaluate the abstract region primitives and demonstrate their ability to support tuning of resource consumption to achieve targets of energy usage and reliability. We investigate five scenarios: adaptive shared variable reduction, construction of an approximate planar mesh, object tracking, contour finding, and event detection using directed diffusion. In each case, we explore the use of the tuning interface to adjust resource usage and evaluate its effect on the accuracy of region operations.
|
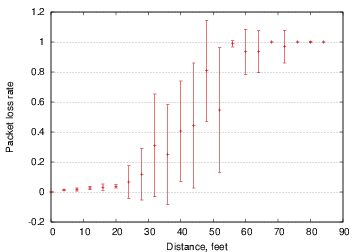
These results were obtained using TOSSIM [21], a simulation environment that executes TinyOS code directly; our abstract region code can either run directly on real sensor motes or in the TOSSIM environment. TOSSIM incorporates a realistic radio connectivity model based on data obtained from a trace gathered from Berkeley MICA motes in an outdoor setting, as shown in Figure 6. This loss probability captures transmitter interference during the original trace that yielded the model. More detailed measurements would be required to capture the full range of transmission characteristics, although experiments have shown the model to be highly accurate [21]. We simulate a network of 100 nodes distributed semi-irregularly in a 20x20 foot area. Because TOSSIM does not currently simulate the energy consumption of nodes, we report the number of radio messages sent as a rough measure of energy consumption, which is reasonable given that on the MICA platform, radio communication dominates CPU energy usage by several orders of magnitude.
|
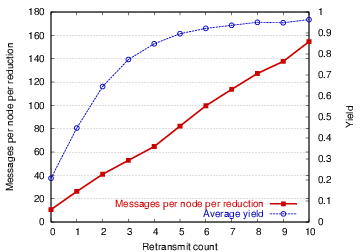
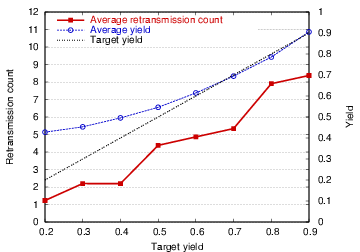
By performing reduction over a subset of neighbors in a region, nodes can trade off energy consumption for accuracy. As described earlier, the reduction operator provides quality feedback in the form of the fraction of nodes that responded to the reduce operation. Over an unreliable radio link, this fraction is directly related to the number of retransmission attempts made by the underlying transport layer, as shown in Figure 7. Moreover, the appropriate retransmission count to meet a given yield target is a function of the local network density and channel characteristics, which vary both across the network and over time.
|
We implemented a simple adaptive reduction algorithm that attempts to
maintain a target reduction yield by dynamically adjusting the maximum
number of retransmission attempts made by the transport layer.
Pseudocode is shown in Figure 9,
and illustrates the use of the regions tuning interface.
Nodes form a ![]() -nearest-neighbor region (
-nearest-neighbor region (![]() ) and
repeatedly perform a max-reduce over a local sensor reading.
An additive-increase/additive-decrease controller is used, which
takes an exponentially-weighted moving average (EWMA) of the yield
of each reduction operation. If the yield is 10% greater than
the target, the maximum retransmission count is reduced by one;
if it is 10% less than the target, the count is
increased by one.
) and
repeatedly perform a max-reduce over a local sensor reading.
An additive-increase/additive-decrease controller is used, which
takes an exponentially-weighted moving average (EWMA) of the yield
of each reduction operation. If the yield is 10% greater than
the target, the maximum retransmission count is reduced by one;
if it is 10% less than the target, the count is
increased by one.
This simple algorithm is very effective at meeting a given yield target, as shown in Figure 8. Note that for targets below 0.5, the controller overshoots the target somewhat. This is mainly because most nodes are well-connected, and even a low retransmission count will result in a good fraction of messages getting through. Another interesting metric is the average number of messages exchanged for each reduction operation (not shown in the figure). Reductions are implemented by the root sending a request message to each neighbor in the region, which replies with the value of the requested shared variable. Therefore, with no message loss, two messages are exchanged per node. As the yield target scales, this number ranges from 3 (for a yield target of 0.2) to about 10.5 (for a target of 0.9), which gives an indication of the additional overhead for achieving a target reliability.
|
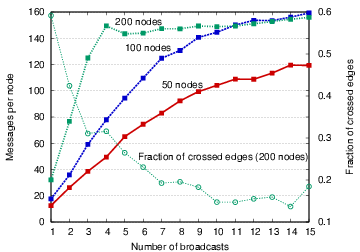
Constructing an approximate planar mesh is a tradeoff between the number of messages sent and the quality of the resulting mesh, which we measure in terms of the fraction of crossing edges. Given the unreliable nature of the communication channel, our pruned Yao graph algorithm cannot guarantee that the mesh will be planar. For many applications, a perfect mesh is not necessary, since planarity is impossible to guarantee if there is measurement error in node localization. As we will see in the next subsection, the quality of the planar mesh has a direct influence on the accuracy of contour detection.
In our implementation, the fraction of crossed edges in the mesh
depends primarily on the number of broadcasts made by each node
to advertise its location. These advertisements are used to form the
![]() -nearest-neighbor region, the first step in the planar mesh
construction. Intuitively, hearing from a greater number of radio
neighbors allows the
-nearest-neighbor region, the first step in the planar mesh
construction. Intuitively, hearing from a greater number of radio
neighbors allows the ![]() -nearest-neighbor region to select the closest
neighbors from this set. Missing an advertisement may cause nodes to
select more distant neighbors, leading to a larger proportion of crossed
edges.
-nearest-neighbor region to select the closest
neighbors from this set. Missing an advertisement may cause nodes to
select more distant neighbors, leading to a larger proportion of crossed
edges.
Figure 10 shows the cost in terms of the number of messages sent per node, as well as the fraction of crossed edges, as the number of node advertisements is increased. Note that the message overhead does not grow linearly with the broadcast count; this is because we are counting all messages involved in mesh construction, including exchanging location information, outedge advertisements, and edge invalidation messages. There is a clear relationship between increased communication, and hence increased bandwidth and energy usage, and the quality of the mesh. As in the case of reduction, applications can tune the number of broadcasts to meet a given target resource budget or mesh quality.
The effect of increasing network density is also shown in the figure. In all cases, nodes are distributed over a fixed geographic area. As density increases, so does the message overhead, since nodes have more neighbors to consider during graph construction.
Next, we evaluate the contour finding application, described in Section 5, in terms of the quality of the underlying approximate planar mesh. We characterize the accuracy of contour finding as the mean error between each computed contour point and the actual contour location. Crossed edges in the mesh are likely to introduce error in the contour calculation, as they generally connect two nodes that may not be closest to the actual contour.
We simulated a linear contour passing through the center of the sensor field that rotates by an angle of 0.1 radians every 5 sec. Nodes take local sensor readings once a second and those that are above the sensor threshold compute new contour points. This scenario stresses the contour finding application and causes all areas of the network to eventually calculate contour points as the frontier rotates. In each case we ran the application for 100 simulated seconds.
Figure 11 shows the error in contour detection as the number of broadcasts used to construct the planar mesh is increased. There is a clear relationship between the overhead of mesh formation and the accuracy of contour detection. Also shown is the fraction of crossed edges, following a pattern similar to that in Figure 10.
|
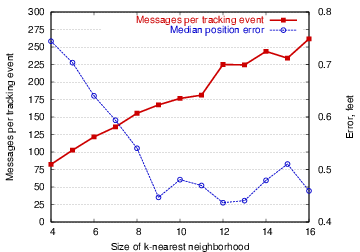
Next, we evaluate the accuracy of the object tracking application described in Section 5. The application tracks a simulated object moving in a circular path of radius 6 feet at a rate of 0.6 feet every 2 sec. As with contour finding, moving the object in a circular path causes nodes in different regions of the network to detect and track the object. Nodes take sensor readings once a second, the value of which scales linearly with the node's distance to the object, with a maximum detection range of 5 feet. In each case we run the application for 100 simulated seconds and average over three runs.
The resource tuning parameter in question is the size of the ![]() -nearest
neighbor region. A smaller number of neighbors reduces communication
requirements, but yields a less accurate estimate of the object
location. Note that increasing the neighborhood size beyond a certain
point will not increase tracking accuracy, as more distant nodes are
less likely to respond to the reduction request due to packet loss.
-nearest
neighbor region. A smaller number of neighbors reduces communication
requirements, but yields a less accurate estimate of the object
location. Note that increasing the neighborhood size beyond a certain
point will not increase tracking accuracy, as more distant nodes are
less likely to respond to the reduction request due to packet loss.
Figure 12 shows
the accuracy of the tracking application as we vary the number of
neighbors in each region. For each time step, we calculate the
distance between the simulated object and the value reported by the sensor
network. As the figure shows, as the size of the neighborhood increases,
so does the accuracy, as well as the number of messages sent
(network-wide) per tracking event.
Above about ![]() , the increase in the neighborhood
size does not improve performance appreciably, in part because the
additional nodes are further from the target object and may not detect
its presence. Also, the more distant nodes may have poor radio
connectivity to the root, as described above.
, the increase in the neighborhood
size does not improve performance appreciably, in part because the
additional nodes are further from the target object and may not detect
its presence. Also, the more distant nodes may have poor radio
connectivity to the root, as described above.
Finally, we evaluate the use of directed diffusion, implemented using the spanning tree region, to detect the presence of a moving object through the sensor field. The base station, located in the upper-left corner of the sensor field, forms a spanning tree region and floods interests to the network through the directed diffusion interface. Rather than computing the location of the object, nodes with a local sensor reading over a fixed threshold (corresponding to an object distance of 2.5 feet) route an event report back to the base. We compute the total number of messages as well as the fraction of event reports received at the base station as the number of retransmission attempts is scaled.
Figure 13 presents the results in terms of the number of messages transmitted per detected event, as well as the fraction of events received by the base station. As with the other examples, scaling the maximum retransmission count increases the number of messages, and has a corresponding effect on the reliability if event delivery to the base. In all of these cases, the core benefit of the abstract regions interface is the ability to tune the underlying communication substrate to achieve resource management and accuracy goals.
As sensor networks become more common, better tools are needed to aid the development of applications for this challenging domain. We believe that programmers should be shielded from the details of low-level radio communication, addressing, and sharing of data within the sensor network. At the same time, the communication abstraction should yield control over resource usage and make it possible for applications to balance the tradeoff between energy/bandwidth consumption and the accuracy of collective operations.
The abstract region is a fairly general primitive that captures a wide range of communication patterns within sensor networks. The notion of communicating within, and computing across, a neighborhood (for a range of definitions of ``neighborhood'') is a useful concept for sensor applications. Similar concepts are evident in other communication models for sensor networks, although often exposed at a much higher level of abstraction. For example, directed diffusion [18] and TinyDB [25] embody similar concepts but lump them together with additional semantics. Abstract regions are fairly low-level and are intended to serve as building blocks for these higher-level systems.
We have described several abstract region implementations, including geographic and radio neighborhoods, an approximate planar mesh, and spanning trees. The implementation of abstract regions in the TinyOS environment relies on fibers, a lightweight concurrency primitive that greatly simplifies application design. Finally, we have evaluated the use of abstract regions for four typical sensor network applications: object tracking, contour finding, distributed event detection, and geographic routing. Our results show that abstract regions are able to provide flexible control over resource consumption to meet a given latency, accuracy, or energy budget.
In the future, we intend to explore how far the abstract region concept addresses the needs of sensor network applications. We are currently completing a suite of abstract region implementations and are developing several applications based on them. We also intend to provide a set of tools that allow application designers to understand the resource consumption and quality tradeoffs provided by abstract regions. These tools will provide developers with a view of energy consumption, communication overheads, and accuracy for a given application. Our goal is to allow designers to express tolerances (say, in terms of a resource budget or quality threshold) that map onto the tuning knobs offered by abstract regions. This process cannot be performed entirely off-line, as resource requirements depend on activity within the network (such as the number of nodes detecting an event). Runtime feedback between the application and the underlying abstract region primitives will continue to be necessary.
Our eventual goal is to use abstract regions as a building block for a high-level programming language for sensor networks. The essential idea is to capture communication patterns, locality, and resource tradeoffs in a high-level language that compiles down to the detailed behavior of individual nodes. Shielding programmers from the details of message routing, in-network aggregation, and achieving a given fidelity under a fixed resource budget should greatly simplify application development for this new domain.
The authors wish to thank Ion Stoica for his excellent advice in shepherding this paper, as well as the comments by the anonymous reviewers. Nelson Lee and Phil Levis provided much of the simulation framework used in the analyses. We also wish to thank Kamin Whitehouse and Cory Sharp for their comments on the neighborhood abstraction, as well as the tracking application upon which our algorithm is based.
|
This paper was originally published in the
Proceedings of the First Symposium on Networked Systems Design and Implementation,
March 29–31, 2004, San Francisco, CA, USA Last changed: 22 March 2004 ch |
|