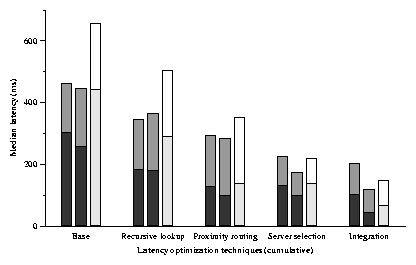|
NSDI '04 Paper
[NSDI '04 Technical Program]
Designing a DHT for low latency and high throughput
Frank Dabek, Jinyang Li, Emil Sit, James Robertson, M. Frans Kaashoek, Robert Morris
1
MIT Computer Science and Artificial Intelligence Laboratory
fdabek, jinyang, sit, jsr, kaashoek, rtm@csail.mit.edu
Abstract
Designing a wide-area distributed hash table (DHT) that provides
high-throughput and low-latency network storage is a challenge.
Existing systems have explored a range of solutions, including
iterative routing, recursive routing, proximity routing and neighbor
selection, erasure coding, replication, and server selection.
This paper explores the design of these techniques and their
interaction in a complete system, drawing on the measured performance
of a new DHT implementation and results from a
simulator with an accurate Internet latency model.
New techniques that resulted from this
exploration include use of latency predictions based on synthetic
coordinates, efficient integration of lookup routing and data
fetching, and a congestion control mechanism suitable for fetching
data striped over large numbers of servers.
Measurements with 425 server instances running on 150 PlanetLab and
RON hosts show that the latency optimizations
reduce the time required to locate and fetch data by a factor of
two. The throughput optimizations result in a sustainable bulk read
throughput related to the number of DHT hosts times the capacity of the
slowest access link; with 150 selected PlanetLab hosts, the peak
aggregate throughput over multiple clients is 12.8 megabytes per
second.
1 Introduction
The Internet has transformed communication for distributed
applications: each new system need not implement its own network, but
can simply assume a shared global communication infrastructure. A
similar transformation might be possible for storage, allowing
distributed applications to assume a shared global storage
infrastructure. Such an infrastructure would have to name and find
data, assure high availability, balance load across available servers,
and move data with high throughput and low latency.
Distributed hash tables (DHTs) are a promising path towards a global storage
infrastructure, and have been used as the basis for
a variety of wide-area file and content
publishing systems [13,26,34,38].
Good performance, however, is a challenge:
the DHT nodes holding the data may be far away in
the network, may have access link capacities that vary by orders of
magnitude, and may experience varying degrees of congestion and packet
loss.
This paper explores design choices for DHT read and write algorithms.
Existing work has investigated how to make the
lookup of keys in DHTs scalable, low-latency, fault-tolerant, and secure, but less attention has been paid
to the efficiency and robustness with which DHTs read and store
data.
This paper considers a range of design options for efficient
data handling in the context of a single DHT, DHash++.
The decisions are evaluated
in simulation and in an implementation of
DHash++ on the PlanetLab [29] and RON [2] test-beds.
To bound the discussion of design decisions, we have made a number of
assumptions. First, we assume that all nodes cooperate; the
algorithms for reading and writing are likely to be more expensive if
they have to defend against malicious nodes. Second, we assume that
lookups are routed using one of the O(logN)-style schemes, instead of
using the recently proposed O(1) schemes [14,17,18,44]. Finally, we assume that the DHT stores
small blocks (on the order of 8192 bytes). Relaxing these
assumptions will result in different DHT designs with different
latency and throughput properties, which we hope to explore in the
future.
The paper makes the following contributions.
Recursive lookups take about 0.6
times as long as iterative; the reason why the reduction is not a factor
of two is the cost of the final return trip. The latency of the last
few hops in a lookup acts as a lower bound on the performance of Proximity
Neighbor Selection [37,16], which approximates 1.5
times the average round trip time in the underlying network. This
result holds regardless of the number of DHT nodes (and thus
regardless of the number of hops). Replicated data allows for
low-latency reads because there are many choices for server selection,
while erasure-coded data reduces bandwidth consumption for writes at
the expense of increased read latency. Integration of key lookup and
data fetch reduces the lower bound imposed by the last few lookup
hops. Finally, using an integrated transport protocol rather than TCP
provides opportunities for efficiency in alternate routing after
timeouts and allows the DHT freedom to efficiently contact many nodes.
The rest of this paper is structured as follows.
Section 2 outlines the complete system
that surrounds the specific mechanisms detailed in the paper.
Section 3 describes the methods behind the paper's
measurements and quantitative evaluations.
Section 4 discusses design decisions that
affect latency, and Section 5 discusses
throughput.
Section 6 describes related work.
We conclude in Section 7.
2 Background
For concreteness, this evaluates design decisions in the
context of a complete DHT called DHash++.
This section
describes the parts of DHash++ that are needed to understand the rest
of the paper.
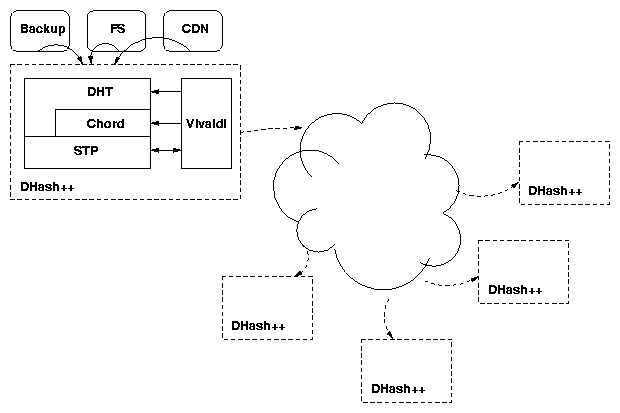 Figure 1: DHash++ system overview.
DHash++ uses the Chord lookup algorithm to help it find
data [42]. Chord provides a
function lookup(key) → set-of-IP, which maps a 160-bit key to
the set of IP addresses of the nodes responsible for that key. Each node
has a 160-bit identifier, and Chord designates the s nodes whose
identifiers immediately follow a key as responsible for that key;
these are the key's successors. To provide reliable lookup even
if half of the nodes fail in a 216-node network, the number of successors, s, is 16 in the
Chord implementation. The ID space wraps around, so that zero
immediately follows 2160−1.
The base Chord lookup algorithm (which will be modified in subsequent
sections) works as follows. Each Chord node maintains a
finger table, consisting of the IP addresses and IDs of nodes that
follow it at power-of-two distances in the identifier space. Each
node also maintains a successor list referring to its s
immediate successors. When a node
originates a lookup, it consults a sequence of
other nodes, asking each in turn which node to talk to next. Each
node in this sequence answers with the node from its finger table
with highest ID still less than the
desired key. The originating node will find the key's
predecessor node after O(logN) consultations; it then asks the
predecessor for its successor list, which is the result of the lookup.
This style of lookup is called iterative, since the originating
node controls each step of the lookup. All of the communication
uses UDP RPCs.
Figure 1: DHash++ system overview.
DHash++ uses the Chord lookup algorithm to help it find
data [42]. Chord provides a
function lookup(key) → set-of-IP, which maps a 160-bit key to
the set of IP addresses of the nodes responsible for that key. Each node
has a 160-bit identifier, and Chord designates the s nodes whose
identifiers immediately follow a key as responsible for that key;
these are the key's successors. To provide reliable lookup even
if half of the nodes fail in a 216-node network, the number of successors, s, is 16 in the
Chord implementation. The ID space wraps around, so that zero
immediately follows 2160−1.
The base Chord lookup algorithm (which will be modified in subsequent
sections) works as follows. Each Chord node maintains a
finger table, consisting of the IP addresses and IDs of nodes that
follow it at power-of-two distances in the identifier space. Each
node also maintains a successor list referring to its s
immediate successors. When a node
originates a lookup, it consults a sequence of
other nodes, asking each in turn which node to talk to next. Each
node in this sequence answers with the node from its finger table
with highest ID still less than the
desired key. The originating node will find the key's
predecessor node after O(logN) consultations; it then asks the
predecessor for its successor list, which is the result of the lookup.
This style of lookup is called iterative, since the originating
node controls each step of the lookup. All of the communication
uses UDP RPCs.
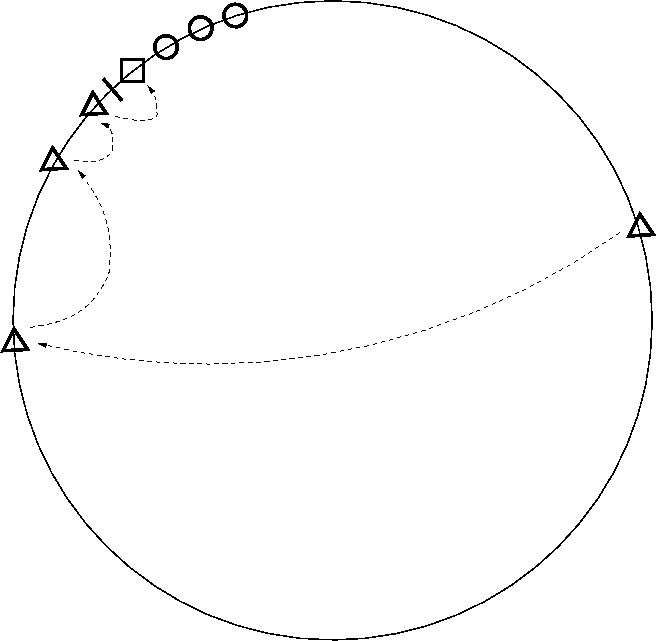 Figure 2: An illustration of a Chord identifier ring. The tick mark
denotes the position of a key in ID space. The square shows the key's
successor node, and the circles show the nodes in the successor's
successor list. The triangles and arrows show a lookup path. The last
node before the tick mark is the key's
predecessor.
Figure 2 shows a Chord ring with a key, its
successor, the successor's successor list, and a lookup path;
this picture is helpful to keep in mind since much of the discussion
appeals to the ring geometry.
Although this paper explores optimizations over base Chord, we believe
that these optimizations also apply to other DHTs that route in ID
spaces using an O(logN) protocol.
Figure 2: An illustration of a Chord identifier ring. The tick mark
denotes the position of a key in ID space. The square shows the key's
successor node, and the circles show the nodes in the successor's
successor list. The triangles and arrows show a lookup path. The last
node before the tick mark is the key's
predecessor.
Figure 2 shows a Chord ring with a key, its
successor, the successor's successor list, and a lookup path;
this picture is helpful to keep in mind since much of the discussion
appeals to the ring geometry.
Although this paper explores optimizations over base Chord, we believe
that these optimizations also apply to other DHTs that route in ID
spaces using an O(logN) protocol.
2.2 DHash++
DHash++ stores key/value pairs (called blocks) on a set of
servers. The DHash++ client API consists of key ← put(value) and
get(key) → value. DHash++ calculates the key to be
the SHA-1 hash of the value, and uses Chord to decide which server
should store a given block; each server runs both Chord and DHash++
software. As well as finding and moving data for client applications,
DHash++ authenticates the data and moves it from server to server as
nodes join, leave, and fail [7].
2.3 Synthetic coordinates
Many of the techniques described in this paper use synthetic
coordinates to predict inter-node latencies without having to perform
an explicit measurement to determine the latency. A number of
synthetic coordinate systems have been
proposed [10,24,27,30,33,39].
We chose to use Vivaldi [12], because its
algorithm is decentralized, which makes it suitable for use in
peer-to-peer systems. Furthermore, the Vivaldi algorithm is
lightweight, since it can piggy-back on DHash++'s communication patterns to
compute coordinates.
Whenever one Chord or DHash++ node communicates directly with
another, they exchange Vivaldi coordinates. Nodes store these
coordinates along with IP addresses in routing tables and successor
lists. The result of a lookup for a key carries the coordinates of the
nodes responsible for the key as well as their IP addresses. Thus the
requesting node can predict the latencies to each of the responsible
nodes without having to first communicate with them.
3 Evaluation methods
The results in this paper are obtained through simulations and
measurements on the PlanetLab and RON test-beds. The measurements
focus on DHT operations that require low latency or high throughput.
3.1 Evaluation infrastructure
DHT performance depends on the detailed
behavior of the servers and the underlying network.
The test-bed measurements in Section 4
were taken from a DHash++ implementation deployed on the PlanetLab and
RON test-beds. 180 test-bed hosts were used, of
which 150 were in the United States and 30 elsewhere. 105 of the hosts
are on the Internet2 network; the rest have connections via DSL, cable
modem, commercial T1 service, or are at co-location centers. Each
host runs three independent DHash++ processes, or virtual nodes,
in order to improve load balance and to ensure
that the total number of nodes is large compared to the size of the
Chord successor list. The measurements in Section 5
were taken on the 27-node RON test-bed alone.
The test-bed measurements are augmented with simulation results to
explore large configurations, to allow easy testing of alternate
designs, and to allow analytic explanations of behavior in a
controlled environment.
The simulated network models
only packet delay. One input to the simulator is a full matrix of the
round-trip delays between each pair of simulated hosts.
This approach
avoids having to simulate the Internet's topology, a currently open
area of research; it requires only the measurement of actual pair-wise
delays among a set of hosts. The simulator can produce useful
speed-of-light delay results, but cannot be used to predict throughput
or queuing delay.
The simulator's delay matrix is derived from Internet measurements using
techniques similar to those described by Gummadi et
al. [15]. The measurements involved 2048 DNS servers
found with inverse DNS lookups on a trace of over
20,000 Gnutella clients.
For each pair of these servers, a measuring
node sends a query to one server that requires it to contact the other
server. Subtracting the delay between the measuring node and the first
server from the total delay yields the delay between the two
servers. In order to reduce the effects of queuing delay, the minimum
delay from five experiments is used. In this paper the results are
called the King data-set. All the simulations in this paper
involve 2048 DHT nodes using King delay matrix unless otherwise mentioned.
Figure 3 shows the CDF of
the King data-set round-trip times; the median is 134 milliseconds,
while the average is 154 milliseconds. The graph also shows the
minimum delay of five pings between each pair of PlanetLab hosts for
comparison. The main difference between the two curves is the longer
tail on the King distribution, which is likely caused by the
larger sample of nodes.
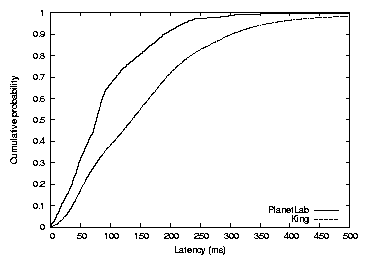 Figure 3: Round-trip latency distribution over all pairs of PlanetLab
and King dataset hosts. The median and average King dataset latencies are
134 and 154 milliseconds respectively. The median and
average PlanetLab latencies are 76 and 90 milliseconds respectively.
Figure 3: Round-trip latency distribution over all pairs of PlanetLab
and King dataset hosts. The median and average King dataset latencies are
134 and 154 milliseconds respectively. The median and
average PlanetLab latencies are 76 and 90 milliseconds respectively.
3.2 Application workload
The design of a DHT must incorporate assumptions about probable
application behavior, and a DHT evaluation must also involve either
applications or models of application behavior. The application
aspects that most affect performance are the mix of read and write
operations, the degree to which operations can be pipelined,
and the size of the data records.
DHash++ is designed to support read-heavy applications that demand
low-latency and high-throughput reads as well as reasonably
high-throughput writes. Examples of such applications might include
the Semantic Free Referencing system (SFR) [45] and
UsenetDHT [40].
SFR is a naming system designed to replace
the use of DNS as a content location system. SFR uses a DHT to
store small data records representing name bindings.
Reads are frequent and should complete with low latency.
Writes are relatively
infrequent and thus need not be as high performance. SFR data blocks
are likely to be on the order hundreds of bytes.
UsenetDHT is a service aiming to reduce the total storage
dedicated to Usenet by storing all Usenet articles in a shared DHT.
UsenetDHT
splits large binary articles (averaging 100 KB) into small blocks for
load balance, but smaller text articles (typically 5 KB or less) are
stored as single blocks. While readership patterns vary, UsenetDHT
must support low-latency single article reads, as well as
high-throughput pipelined article fetches.
These systems are unlikely to be deployed on high-churn
networks-these systems are all server-class. The target environment
for them is a network with relatively reliable nodes that have good
Internet access.
4 Designing for low latency
This section investigates five design choices that affect DHT
get latency. The naive algorithm against which these choices are
judged, called base DHash++, operates as follows. Each
8192-byte block is stored as 14 1171-byte erasure-coded fragments, any
seven of which are sufficient to reconstruct the block, using the IDA
coding algorithm [31]. The 14 fragments are stored at the
14 immediate successors of the block's key. When an application calls
get(key), the originating node performs an iterative Chord
lookup, which ends when the key's predecessor node returns the key's
16 successors; the originating node then sends seven parallel requests
the first seven successors asking them each to return one fragment.
Figure 4 gives a preview of the results of this
section. Each pair of bars shows the median time to fetch a block on
the PlanetLab test-bed after cumulatively applying each design
improvement. The design improvements shown are recursive rather than
iterative routing, proximity neighbor selection, fetching of data from
the closest copy, and integration of lookup routing and data fetching.
These design improvements together reduce the total
fetch latency by nearly a factor of two.
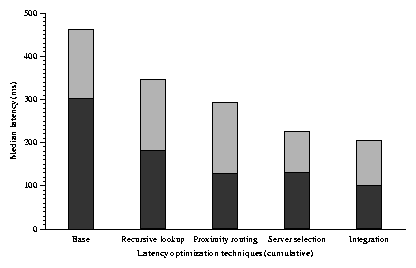 Figure 4: The cumulative effect of successive optimizations
on the latency of a DHash++ data fetch. Each bar shows the median
time of 1,000 fetches of a randomly chosen 8192-byte data block from a
randomly chosen host. The dark portion of each bar shows the lookup
time, and the light portion shows the time taken to fetch the
data. These data are from the implementation running on PlanetLab.
This paper uses a log(N) protocol for routing lookups. An
optimization that isn't explored in this paper is an increase in the base
to reduce the number of hops, or the use of a constant-hop
protocols. These optimizations would reduce latency under low churn, because
each node would know about many other nodes. On the other hand, in high
churn networks, these optimizations might require more bandwidth to keep
routing tables up to date or experience more timeouts because routing
tables might contain recently-failed nodes. The paper's evaluation
infrastructure isn't adequate to explore this design decision in
detail. We hope
to explore this issue in future work. We do explore the extent to which
proximity routing can reduce the impact of the number of hops on the lookup
latency.
Figure 4: The cumulative effect of successive optimizations
on the latency of a DHash++ data fetch. Each bar shows the median
time of 1,000 fetches of a randomly chosen 8192-byte data block from a
randomly chosen host. The dark portion of each bar shows the lookup
time, and the light portion shows the time taken to fetch the
data. These data are from the implementation running on PlanetLab.
This paper uses a log(N) protocol for routing lookups. An
optimization that isn't explored in this paper is an increase in the base
to reduce the number of hops, or the use of a constant-hop
protocols. These optimizations would reduce latency under low churn, because
each node would know about many other nodes. On the other hand, in high
churn networks, these optimizations might require more bandwidth to keep
routing tables up to date or experience more timeouts because routing
tables might contain recently-failed nodes. The paper's evaluation
infrastructure isn't adequate to explore this design decision in
detail. We hope
to explore this issue in future work. We do explore the extent to which
proximity routing can reduce the impact of the number of hops on the lookup
latency.
4.1 Data layout
The first decision to be made about where a DHT should store data is
whether it should store data at all. A number of DHTs provide only a
key location service, perhaps with a layer of indirection, and let
each application decide where (or even whether) to store
data [20,28]. The choice is a question of
appropriate functionality rather than performance, though
Section 4.5 describes some performance benefits of
integrating the DHT lookup and data storage functions. The approach
taken by DHash++ is appropriate for applications that wish to view
the DHT as a network storage system, such as our motivating examples
SFR and UsenetDHT.
For DHTs that store data, a second layout decision is the size of the
units of data to store. A DHT key could refer to a disk-sector-like
block of data [13], to a complete file [38], or to an
entire file system image [11].
Large values reduce the amortized cost of each DHT lookup.
Small blocks spread the load of serving popular large files.
For these reasons, and because some applications such as SFR
require the DHT to store small blocks, DHash++ is optimized
with blocks of 8 KB or less in mind.
A third layout decision is which server should store each block of
data (or each replica or coded fragment). If a given block is likely
to be read mostly by hosts in a particular geographic area, then it
would make sense to store the data on DHT servers in that area.
Caching is one way to achieve this kind of layout.
On the other hand, geographic concentration may make the data
more vulnerable to network and power failures,
it may cause the load to be less evenly balanced across all nodes,
and is difficult to arrange in general without application hints.
At the other extreme, the DHT could distribute data uniformly
at random over the available servers; this design would be reasonable
if there were no predictable geographic locality in the originators of
requests for the data, or if fault-tolerance were important. DHash++
uses the latter approach: a block's key is essentially random (the
SHA-1 of the block's value), node IDs are random, and a block's
replicas or fragments are placed at its key's successor nodes. The
result is that blocks (and load) are uniformly spread over the DHT
nodes, and that a block's replicas or fragments are widely scattered
to avoid correlated failure.
Given a DHT design that stores blocks on randomly chosen servers, one
can begin to form some expectations about fetch latency. The lower
bound on the total time to find and fetch a block is the round trip
time from the originator to the nearest replica of the block, or the
time to the most distant of the closest set of fragments required to
reconstruct the block.
For the typical block this time is determined by
the distribution of inter-host delays in the Internet, and by the
number of choices of replicas or fragments. The DHT lookup required
to find the replicas or fragments will add to this lower bound, as
will mistakes in predicting which replica or fragments are closest.
Most of the design choices described in subsequent subsections have to do
with taking intelligent advantage of choices in order to reduce
lookup and data fetch latency.
4.2 Recursive or iterative?
The base Chord and Kademlia algorithms are iterative: the originator
sends an RPC to each successive node in the lookup path, and waits for
the response before proceeding [25,42]. Another possibility is
recursive lookup [6,47]: each node in the
lookup path directly forwards the query to the next node, and when the
query reaches the key's predecessor, the predecessor sends its
successor list directly back to the originator [42].
Recursive lookup, which many DHTs use, might eliminate half the
latency of each hop since each intermediate node can immediately
forward the lookup before acknowledging the previous hop.
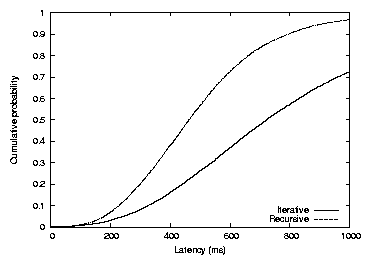 Figure 5: The cumulative distributions of lookup time for Chord
with recursive and iterative lookup. The recursive median and average
are 461 and 489 milliseconds; the iterative median and average
are 720 and 822 milliseconds. The numbers are from simulations.
Figure 5 shows the effect of using recursive rather
than iterative lookup in the simulator with the 2048-node King data set.
For each technique, 20,000
lookups were performed, each from a random host for a random key. The
average number of hops is 6.3. Recursive lookup takes on average 0.6
times as long as iterative. This decrease is not quite the expected
factor of two: the difference is due to the extra one-way hop of (on
average) 77 milliseconds to return the result to the originator.
While recursive lookup has lower latency than iterative, iterative is
much easier for a client to manage. If a recursive lookup elicits no response,
the originator has no information about what went wrong and how to
re-try in a way that is more likely to succeed. Sometimes a simple
re-try may work, as in the case of lost packets. If the problem is
that each successive node can talk to the next node, but that Internet
routing anomalies prevent the last node from replying to the
originator, then re-tries won't work because only the originator
realizes a problem exists. In contrast, the originator knows which
hop of an iterative lookup failed to respond, and can re-try that hop
through a different node in the same region of the identifier space.
On the the other hand, recursive communication may make congestion
control easier (that is, it is it may make it more feasible to rely on
TCP). We will show in Section 5 that the
performance of a naive TCP transport can be quite poor.
DHash++ uses recursive lookups by default since they are faster, but
falls back on iterative lookups after persistent failures.
Figure 5: The cumulative distributions of lookup time for Chord
with recursive and iterative lookup. The recursive median and average
are 461 and 489 milliseconds; the iterative median and average
are 720 and 822 milliseconds. The numbers are from simulations.
Figure 5 shows the effect of using recursive rather
than iterative lookup in the simulator with the 2048-node King data set.
For each technique, 20,000
lookups were performed, each from a random host for a random key. The
average number of hops is 6.3. Recursive lookup takes on average 0.6
times as long as iterative. This decrease is not quite the expected
factor of two: the difference is due to the extra one-way hop of (on
average) 77 milliseconds to return the result to the originator.
While recursive lookup has lower latency than iterative, iterative is
much easier for a client to manage. If a recursive lookup elicits no response,
the originator has no information about what went wrong and how to
re-try in a way that is more likely to succeed. Sometimes a simple
re-try may work, as in the case of lost packets. If the problem is
that each successive node can talk to the next node, but that Internet
routing anomalies prevent the last node from replying to the
originator, then re-tries won't work because only the originator
realizes a problem exists. In contrast, the originator knows which
hop of an iterative lookup failed to respond, and can re-try that hop
through a different node in the same region of the identifier space.
On the the other hand, recursive communication may make congestion
control easier (that is, it is it may make it more feasible to rely on
TCP). We will show in Section 5 that the
performance of a naive TCP transport can be quite poor.
DHash++ uses recursive lookups by default since they are faster, but
falls back on iterative lookups after persistent failures.
4.3 Proximity neighbor selection
Many DHTs decrease lookup latency by choosing nearby nodes as routing
table
entries [6,16,25,42,43,47],
a technique often called proximity neighbor selection (PNS). The
reason this is possible is that there are usually few constraints in
the choice of routing entries: any node in the relevant portion of the
identifier space is eligible. A DHT design must include an algorithm
to search for nearby nodes; an exhaustive search may improve lookup
latency, but also consume network resources. This subsection builds on
the work of Gummadi et al. [16] in two ways: it explains why
PNS approximates 1.5 times the average round trip time in the
underlying network and shows that this result holds regardless of the
number of DHT nodes (and thus regardless of the number of hops).
Following Gummadi et al. [16], define PNS(x) as follows.
The ith Chord finger table entry of the node with ID a properly
refers to the first node in the ID-space range a + 2i to a +2i+1 − 1. The PNS(x) algorithm considers up to the first x nodes in
that range (there may be fewer than x), and routes lookups through
the node with lowest latency. Ideal PNS refers to PNS(x) with
x equal to the total number of nodes, so that every finger table
entry points to the lowest-latency node in the entire allowed ID-space
range. The simulator simply chooses the lowest-latency of the x
nodes, while the real implementation asks each proper finger entry for
its successor list and uses Vivaldi to select the closest node.
This means that the real implementation requires that x ≤ s (the
number of successors).
What is a suitable value for x in PNS(x)? Figure 6
shows the simulated effect of varying x on lookup latency. For each x
value, 20,000 lookups were issued by randomly selected hosts for
random keys. Each lookup is recursive, goes to the
key's predecessor node (but not successor),
and then directly back to the originator.
The graph plots the median, 10th percentile, and 90th percentile of
latency.
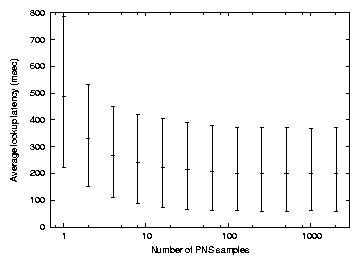 Figure 6:
Average lookup latency as a function of the number of PNS samples. The bar at each
x value shows the 10th, average, and 90th percentile of the latencies
observed by 20,000 recursive lookups of random keys from random nodes
using PNS(x). The measurements are from the simulator with 2048 nodes.
Figure 6:
Average lookup latency as a function of the number of PNS samples. The bar at each
x value shows the 10th, average, and 90th percentile of the latencies
observed by 20,000 recursive lookups of random keys from random nodes
using PNS(x). The measurements are from the simulator with 2048 nodes.
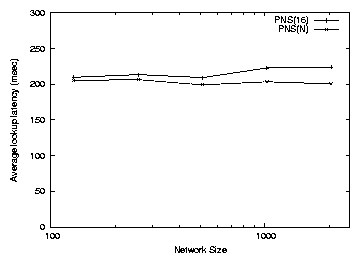 Figure 7:
Average lookup latency of PNS(16) and PNS(N) as a function of the
number of nodes in the system, N.
The simulated network sizes consist of 128, 256, 512, 1024, 2048 nodes.
Figure 6 shows that PNS(1) has a simulated average latency of
489 ms, PNS(16) has an average latency of 224 ms, and PNS(2048) has an
average latency of 201 ms.
The latter is ideal PNS, since the neighbor choice is over all nodes
in the simulation.
PNS(16) comes relatively close to the ideal, and is convenient to
implement in the real system with successor lists.
Why does ideal PNS show the particular improvement that it does?
The return trip from the predecessor to the originator has the same
median as the one-way delay distribution of the nodes in the network,
δ. For the King data set, δ = 67ms.
The last hop (to the predecessor) has only one candidate, so its
median latency is also δ.
Each preceding hop has twice as many candidate nodes to choose
from on average, since the finger-table interval involved is twice as large
in ID space.
So the second-to-last hop is the smaller of two randomly chosen
latencies, the third-to-last is the smallest of four, etc. The minimum
of x samples has its median at the 1 − 0.5[1/x]
percentile of the original distribution, which can be approximated as
the [1/x] percentile for large x. Doubling the
sample size x will halve the percentile of the best sample.
Assuming a uniform latency distribution,
doubling the sample size halves the best sampled latency.
Therefore, the latencies incurred at successive lookup hops with ideal PNS can
be approximated by a geometric series with the final lookup hop to the key's
predecessor being the longest hop. The lookup process includes
an additional final hop to the originator. If we use the per-hop median latency as
a gross approximation of the average per-hop latency, the total average lookup latency
is thus approximated as: δ+ (δ+ [δ/2]+ [δ/4] + ... ) = δ+ 2δ = 3δ. For the
King data set, this gives 201 ms. This is coincidentally the ideal PNS simulation
result of 201 ms.
The fact that the average lookup latency of PNS(N) can be approximated
as an infinite geometric series whose sum converges quickly
suggests that despite the fact that the number of lookup
hops scales as log(N), the total average lookup latency will stay
close to 3δ. Figure 7 shows the simulated average
lookup latency as a function of the number of nodes in the system. As
we can see, there is indeed little increase in average lookup latency
as the network grows.
Figure 7:
Average lookup latency of PNS(16) and PNS(N) as a function of the
number of nodes in the system, N.
The simulated network sizes consist of 128, 256, 512, 1024, 2048 nodes.
Figure 6 shows that PNS(1) has a simulated average latency of
489 ms, PNS(16) has an average latency of 224 ms, and PNS(2048) has an
average latency of 201 ms.
The latter is ideal PNS, since the neighbor choice is over all nodes
in the simulation.
PNS(16) comes relatively close to the ideal, and is convenient to
implement in the real system with successor lists.
Why does ideal PNS show the particular improvement that it does?
The return trip from the predecessor to the originator has the same
median as the one-way delay distribution of the nodes in the network,
δ. For the King data set, δ = 67ms.
The last hop (to the predecessor) has only one candidate, so its
median latency is also δ.
Each preceding hop has twice as many candidate nodes to choose
from on average, since the finger-table interval involved is twice as large
in ID space.
So the second-to-last hop is the smaller of two randomly chosen
latencies, the third-to-last is the smallest of four, etc. The minimum
of x samples has its median at the 1 − 0.5[1/x]
percentile of the original distribution, which can be approximated as
the [1/x] percentile for large x. Doubling the
sample size x will halve the percentile of the best sample.
Assuming a uniform latency distribution,
doubling the sample size halves the best sampled latency.
Therefore, the latencies incurred at successive lookup hops with ideal PNS can
be approximated by a geometric series with the final lookup hop to the key's
predecessor being the longest hop. The lookup process includes
an additional final hop to the originator. If we use the per-hop median latency as
a gross approximation of the average per-hop latency, the total average lookup latency
is thus approximated as: δ+ (δ+ [δ/2]+ [δ/4] + ... ) = δ+ 2δ = 3δ. For the
King data set, this gives 201 ms. This is coincidentally the ideal PNS simulation
result of 201 ms.
The fact that the average lookup latency of PNS(N) can be approximated
as an infinite geometric series whose sum converges quickly
suggests that despite the fact that the number of lookup
hops scales as log(N), the total average lookup latency will stay
close to 3δ. Figure 7 shows the simulated average
lookup latency as a function of the number of nodes in the system. As
we can see, there is indeed little increase in average lookup latency
as the network grows.
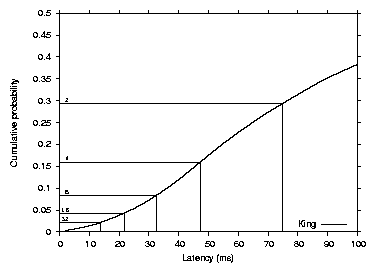 Figure 8: The median of the minimum latency taken from x samples out of
the all-pairs empirical latency distribution of the King dataset. The boxes
correspond to 2,4,8,16,32 samples starting from the right.
Why are there diminishing returns in Figure 6 beyond
roughly PNS(16)? First, the King delay distribution is not uniform,
but has a flat toe. Thus increasing the number of samples produces smaller
and smaller decreases in minimum
latency. Figure 8 shows this effect for various
sample sizes. Second, for large x, the number of samples is
often limited by the allowed ID-space range for the finger in
question, rather than by x; this effect is more important in the
later hops of a lookup.
One lesson from this analysis is that the last few hops of a lookup
dominate the total latency. As a lookup gets close to
the target key in ID space, the number of remaining nodes that are
closer in ID space to the key decreases, and thus the latency to the
nearest one increases on average. Section 4.5 shows how to
avoid this problem.
Figure 8: The median of the minimum latency taken from x samples out of
the all-pairs empirical latency distribution of the King dataset. The boxes
correspond to 2,4,8,16,32 samples starting from the right.
Why are there diminishing returns in Figure 6 beyond
roughly PNS(16)? First, the King delay distribution is not uniform,
but has a flat toe. Thus increasing the number of samples produces smaller
and smaller decreases in minimum
latency. Figure 8 shows this effect for various
sample sizes. Second, for large x, the number of samples is
often limited by the allowed ID-space range for the finger in
question, rather than by x; this effect is more important in the
later hops of a lookup.
One lesson from this analysis is that the last few hops of a lookup
dominate the total latency. As a lookup gets close to
the target key in ID space, the number of remaining nodes that are
closer in ID space to the key decreases, and thus the latency to the
nearest one increases on average. Section 4.5 shows how to
avoid this problem.
4.4 Coding versus replication
Once the node originating a fetch acquires the key's predecessor's
successor list, it knows which nodes hold the block's
replicas [13,38] or fragments of an erasure-coded
block [8,3,22,19].
In the case of replication, the originator's strategy should be to
fetch the required data from the successor with lowest latency. The
originator has more options in the case of coded fragments, but a
reasonable approach is to fetch the minimum required number of
fragments from the closest successors. The technique of fetching the
data from the nearest of a set of candidate nodes is typically called
server selection.
The design choice here can be framed as choosing the coding parameters
l and m, where l is the total number of fragments stored on
successors and m is the number required to reconstruct the
block. Replication is the special case in which m = 1, and l is
the number of replicas. The rate of coding, r = [l/m],
expresses the amount of redundancy. A replication scheme with three
replicas has m = 1, l = 3, and r = 3, while a 7-out-of-14 IDA
coding scheme has m = 7, l = 14, and r = 2.
The choice of parameters m and l has three main effects. First,
it determines a block's availability when nodes
fail [46]. If the probability that any given DHT node is available is
p0, the probability that a block is still available is [4]:
|
pavail = |
l
∑
i=m
|
|
l!
l!(l−i)!
|
p0i (1−p0)l−i |
| (1) |
Second, increasing r
is likely to decrease fetch latency, since that provides the
originator more choices from which to pick a nearby node. Third,
increasing r increases the amount of communication required to write
a block to the DHT. These performance aspects of erasure coding have
not been considered previously.
Figure 9 illustrates the relationship between
total fetch latency and block availability. The probability p0 that each node
is available is kept constant at 0.9. Each line represents a different
rate r, and the points on the line are obtained by varying m and
setting l = r ×m. Each point's x-axis value indicates the
probability that a block is available as calculated by
Equation 1. Each point's y-axis value is the
average latency from 20,000 simulations of fetching a random block from
a random originating node. The originator performs a lookup to obtain
the list of the desired key's successors, then issues parallel RPCs to
the m of those successors that have lowest latency, and waits for
the last of the RPCs to complete. The y-axis values include only
the data fetch time.
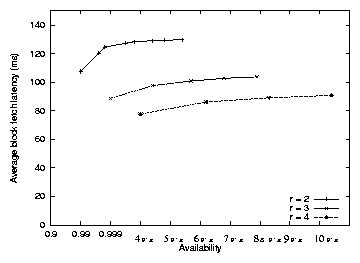 Figure 9: The relationship between read latency and block availability.
The different lines correspond to different redundancy factors of r = 2, 3, 4. The data points on each line (starting from the left)
correspond to reading m = 1, 2, 3... fragments out of r ×m total
fragments. The x-axis value is computed from Equation 1
with the per-node availability p0 set to 0.9, while
the y-axis value is the simulated block fetch time (not including lookup time).
The left-most point on each line corresponds to replication; that
point on the different lines corresponds to 2, 3, and 4 replicas. For
each line, the points farther to the right indicate coding schemes in
which smaller-sized fragments are placed onto larger numbers of nodes.
For each redundancy rate r, replication provides the lowest latency
by a small margin. The reason is easiest to see for r=2: choosing
the nearest k of 2k fragments approaches the median as k grows,
while choosing the nearest replica of two yields a latency
considerably below the median. Replication also provides the least
availability because the redundant information is spread over fewer
nodes. The lower lines correspond to larger amounts of redundant
information on more nodes; this provides a wider choice of nodes from
which the originator can read the data, which increases the
probability that it can read from nearby nodes, and lowers the fetch
latency.
The best trade-off between replication and coding is dependent on the
workload: a read-intensive workload will experience lower latency with
replication, while a write-intensive workload will consume less
network bandwidth with coding.
DHash++ uses IDA coding with m=7 and l=14. The number seven is
selected so that a fragment for an 8 KB block will fit in a single
1500-byte packet, which is important for UDP-based transport.
The originator uses Vivaldi
(Section 2.3) to predict the latency to the successors.
Figure 9: The relationship between read latency and block availability.
The different lines correspond to different redundancy factors of r = 2, 3, 4. The data points on each line (starting from the left)
correspond to reading m = 1, 2, 3... fragments out of r ×m total
fragments. The x-axis value is computed from Equation 1
with the per-node availability p0 set to 0.9, while
the y-axis value is the simulated block fetch time (not including lookup time).
The left-most point on each line corresponds to replication; that
point on the different lines corresponds to 2, 3, and 4 replicas. For
each line, the points farther to the right indicate coding schemes in
which smaller-sized fragments are placed onto larger numbers of nodes.
For each redundancy rate r, replication provides the lowest latency
by a small margin. The reason is easiest to see for r=2: choosing
the nearest k of 2k fragments approaches the median as k grows,
while choosing the nearest replica of two yields a latency
considerably below the median. Replication also provides the least
availability because the redundant information is spread over fewer
nodes. The lower lines correspond to larger amounts of redundant
information on more nodes; this provides a wider choice of nodes from
which the originator can read the data, which increases the
probability that it can read from nearby nodes, and lowers the fetch
latency.
The best trade-off between replication and coding is dependent on the
workload: a read-intensive workload will experience lower latency with
replication, while a write-intensive workload will consume less
network bandwidth with coding.
DHash++ uses IDA coding with m=7 and l=14. The number seven is
selected so that a fragment for an 8 KB block will fit in a single
1500-byte packet, which is important for UDP-based transport.
The originator uses Vivaldi
(Section 2.3) to predict the latency to the successors.
4.5 Integrating routing and fetching
So far the design of the DHT lookup algorithm and the design of the
final data server-selection have been considered separately. One
problem with this approach is that obtaining the complete list of a
key's s successors requires that the originator contact the key's
predecessor, which Section 4.3 observed was expensive
because the final lookup steps can take little advantage of proximity
routing. However, of the s successors, only the first l immediate
successors store the fragments for the key's data block. Furthermore,
fragments from any m of these successors are sufficient to
reconstruct the block. Each of the s − m predecessor nodes of the
key has a successor list that contains m successors. Thus the lookup
could stop early at any of those predecessors, avoiding the expensive
hop to the predecessor; Pastry/PAST uses a similar
technique [38].
However, this design choice decreases the lookup time at the expense
of data fetch latency, since it decreases the number of successors
(and thus fragments) that the originator can choose from. Once the
recursive lookup has reached a node n1 whose successor list overlaps
the key, n1 is close enough to be the penultimate hop in the routing.
By forwarding the
query to the closest node n2 in its successor list that can return
enough nodes, n1 can ensure that the next hop will be the last hop.
There are two cases - if n2 is past the key, then n1 must directly
retrieve n2's successor list and merge it with its own overlapping
nodes to avoid overshooting. Otherwise, n1 can simply hand-off the
query to n2 who will have enough information to complete the request.
Figure 10 shows the
pseudo-code for this final version of the DHash++ lookup algorithm.
The d argument indicates how many successors the caller would
like. d must be at least as large as m, while setting d to l
retrieves the locations of all fragments.
a.lookup(q, k, d):
overlap = { n′ | n′ ∈ succlista ∧n′ > k }
if |overlap| ≥ d
return overlap to the originator q
elsif overlap ≠ ∅
t = { the s−d nodes in succlista immediately preceding k } ∪overlap
b = ti ∈ t s.t. dist(a, ti) is minimized
if b ∈ overlap
t = b.get_succlist()
u = merger of t and overlap to produce k first d successors
return u to the originator q
else
return b.lookup(q, k, d)
else
b = closestpred(lookupfinger, k)
return b.lookup(q, k, d)
Figure 10: Recursive lookup that returns at least d fragments of key k
to sender q. Each node's successor list contains s nodes.
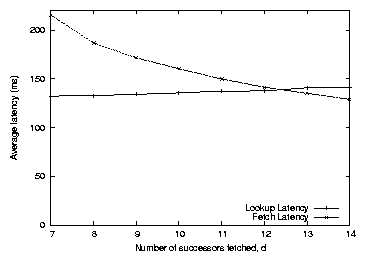 Figure 11: Simulated lookup and fetch time as a function of the d
parameter in Figure 10. Larger d causes the
lookup to take more hops and gather more successors; the extra
successors decrease the fetch latency by providing more choice
of nodes to fetch from. For comparison, the average
lookup and fetch times that result from always contacting the
predecessor are 224 and 129 milliseconds, respectively.
The final latency design decision is the choice of d. A large value
forces the lookup to take more hops, but yields more choice for the
data fetch and thus lower fetch latency; while a small d lets the
lookup finish sooner but yields higher fetch latency.
Figure 11 explores this tradeoff. It turns out that
the cost of a higher d is low, since the lookup algorithm in
Figure 10 uses only nearby nodes as the final hops,
while the decrease in fetch time by using larger d is relatively
large. Thus setting d = l is the best policy.
Figure 11: Simulated lookup and fetch time as a function of the d
parameter in Figure 10. Larger d causes the
lookup to take more hops and gather more successors; the extra
successors decrease the fetch latency by providing more choice
of nodes to fetch from. For comparison, the average
lookup and fetch times that result from always contacting the
predecessor are 224 and 129 milliseconds, respectively.
The final latency design decision is the choice of d. A large value
forces the lookup to take more hops, but yields more choice for the
data fetch and thus lower fetch latency; while a small d lets the
lookup finish sooner but yields higher fetch latency.
Figure 11 explores this tradeoff. It turns out that
the cost of a higher d is low, since the lookup algorithm in
Figure 10 uses only nearby nodes as the final hops,
while the decrease in fetch time by using larger d is relatively
large. Thus setting d = l is the best policy.
4.6 Summary
Figure 12 summarizes the cumulative effect of the
design decisions explored in this section. The leftmost bar in each
triple shows the median time on our PlanetLab implementation (copied from
Figure 4). The middle bar was produced by the
simulator using a latency matrix measured between PlanetLab hosts.
The dark portion of each bar shows the lookup time, and the light
portion shows the time taken to fetch the data. Although the
simulator results do not match the PlanetLab results exactly, the
trends are the same. The results differ because the simulator uses
inter-host delays measured between a slightly different set of
PlanetLab nodes than were used for the implementation experiments, and
at a different time.
The rightmost bar corresponds to simulations of 2048 nodes using the
King latency matrix. The absolute numbers are larger than for the
PlanetLab results, and perhaps more representative of the Internet as
a whole, because the King data set includes a larger and more diverse
set of nodes. Again, the overall trends are the same.
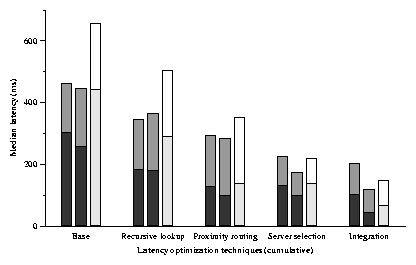 Figure 12: The cumulative effect of successive performance optimizations
on the median latency of a DHash++ data fetch. The leftmost bar in each
triple shows the time on our PlanetLab implementation (copied from
Figure 4). The middle bar
was produced by the simulator using a latency matrix
measured between PlanetLab hosts. The rightmost bar corresponds to
simulations of 2048 nodes using the King latency matrix. The dark
portion of each bar shows the lookup time, and the light portion shows
the time taken to fetch the data.
Figure 12: The cumulative effect of successive performance optimizations
on the median latency of a DHash++ data fetch. The leftmost bar in each
triple shows the time on our PlanetLab implementation (copied from
Figure 4). The middle bar
was produced by the simulator using a latency matrix
measured between PlanetLab hosts. The rightmost bar corresponds to
simulations of 2048 nodes using the King latency matrix. The dark
portion of each bar shows the lookup time, and the light portion shows
the time taken to fetch the data.
5 Achieving high throughput
Some applications, such as Usenet article storage, need to store or
retrieve large amounts of data in a DHT. If data movement is to be
fast, the DHT must make efficient use of the underlying network
resources. The DHT must keep enough data in flight to cover the
network's delay-bandwidth product, stripe data over multiple slow
access links in parallel, and recover in a timely fashion from
packet loss. The DHT must also provide congestion
control in order to avoid unnecessary re-transmissions and to avoid
overflowing queues and forcing packet loss. These goals are similar to those of
traditional unicast transport protocols such as TCP [21], but
with the additional requirement that the solution function well when the
data is spread over a large set of servers.
This section presents two different designs, then compares their
efficiency when implemented in DHash++ on the RON test-bed.
We focus here on bulk fetch operations rather than insert
operations.
5.1 TCP transport
Perhaps the simplest way for a DHT to manage its consumption of
network resources is to use TCP.
Because TCP imposes a start-up latency, requires
time to acquire good timeout and congestion window size estimates, and
consumes host state that limits the number of simultaneous
connections, it makes the most sense for a DHT to maintain a
relatively small number of long-running TCP connections to its
neighbors and to arrange that communication only occur between
neighbors in the DHT overlay.
This arrangement
provides congestion control without burdening the DHT with its
implementation. Several systems use this
approach (e.g., [34]), some with slight modifications to avoid
exhausting the number of file descriptors. For example, Tapestry uses
a user-level re-implementation of TCP without in-order
delivery [47].
Restricting communication to the overlay links means that all lookups
and data movement must be recursive: iterative lookups or direct
movement of data would not be able to use the persistent
inter-neighbor TCP connections. Section 4.2 showed
that recursive lookups work well. However, recursive data movement
requires that each block of data be returned through the overlay
rather than directly. This recursive return of data causes it to be
sent into and out of each hop's Internet access link, potentially increasing
latency and decreasing useful throughput. In addition, hiding the
congestion control inside TCP limits the options for the design of the
DHT's failure recovery algorithms, as well as making it hard for the
DHT to control its overall use of network resources.
Section 5.3 shows performance results that may help in
deciding whether the convenience of delegating congestion control to
TCP outweighs the potential problems.
DHash++ allows the option to use TCP as the transport. Each node
keeps a TCP connection open to each of its fingers, as well as a
connection to each node in its successor list. DHash++ forwards a
get request recursively through neighbors' TCP connections until the
request reaches a node whose successor list includes a sufficient
number of fragments (as in Section 4.5). That node
fetches fragments in parallel over the connections to its successors,
trying the most proximate successors first. It then re-constructs the
block from the fragments and sends the block back through the reverse
of the route that the request followed. Pond [34] moves
data through the Tapestry overlay in this way.
5.2 STP transport
At the other extreme, a DHT could include its own specialized
transport protocol in order to avoid the problems with TCP transport
outlined above. This approach allows the DHT more freedom in which
nodes it can contact, more control over the total load it places on
the network, and better integration between the DHT's failure handling
and packet retransmission.
DHash++ allows the option to use a specialized transport
called the Striped
Transport Protocol (STP). STP allows nodes to put and get data
directly to other nodes, rather than routing the data through multiple
overlay hops.
STP does not maintain any per-destination
state; instead, all of its decisions are based on aggregate
measurements of recent network behavior, and on Vivaldi
latency predictions.
STP's core mechanism is a TCP-like congestion window controlling
the number of concurrent outstanding RPCs.
While STP borrows many ideas from TCP, DHT data transfers differ in
important ways from the unicast transfers that TCP is designed for.
Fetching a large quantity of DHT data involves sending lookup and get
requests to many different nodes, and receiving data fragments from
many nodes. There is no steady "ACK clock" to pace new data, since
each RPC has a different destination. The best congestion window size
(the number of outstanding RPCs to maintain) is hard to define,
because there may be no single delay and thus no single
bandwidth-delay product. Quick recovery from lost packets via fast
retransmit [41] may not be possible because RPC replies are
not likely to arrive in order. Finally, averaging RPC round-trip
times to generate time-out intervals may not work well because each
RPC has a different destination.
The rest of this section describes the design of STP.
5.2.1 STP window control
Each DHash++ server controls all of its network activity with a
single instance of STP.
STP maintains a window of outstanding UDP RPCs: it only issues a new
RPC when an outstanding RPC has completed.
STP counts both DHT lookup and data movement RPCs in the
window.
STP maintains a current window size w in a manner similar to that of
TCP [21,9]. When STP receives an RPC reply, it increases
w by 1/w; when an RPC times out, STP halves w.
STP actually keeps 3w RPCs in flight, rather than w. Using w
would cause STP to transfer data significantly slower than a single
TCP connection: lookup RPCs carry less data than a typical TCP packet,
STP has nothing comparable to TCP's cumulative acknowledgments to mask
lost replies, STP's retransmit timers are more conservative than
TCP's, and STP has no mechanism analogous to TCP's fast retransmit.
The value 3 was chosen empirically to cause STP's network use to match
TCP's.
5.2.2 Retransmit timers
Lost packets have a large negative impact on DHash++ throughput because
each block transfer is preceded by a multi-RPC lookup; even a modest
packet loss rate may routinely stall the advancement of the window.
Ideally STP would choose timeout intervals slightly larger than the
true round trip time, in order to to waste the minimum amount of
time. This approach would require a good RTT predictor. TCP predicts the RTT
using long-term measurements of the average and standard deviation of
per-packet RTT [21]. STP, in contrast, cannot count on sending
repeated RPCs to the same destination to help it characterize the
round-trip time. In order for STP to perform well in a large DHT, it
must be able to predict the RTT before it sends even one packet to a
given destination.
STP uses Vivaldi
latency predictions to help it choose the
retransmit time-out interval for each RPC.
However, Vivaldi tends to under-predict
network delays because it does not immediately
account for current network queuing
delays or CPU processing time at each end. Since under-predicting the
latency of an RPC is costly (a spurious loss detection causes a
halving of the current window) STP adjusts the Vivaldi prediction
before using it. STP characterizes the errors that Vivaldi makes
by keeping a moving average of the difference between each successful
RPC's round-trip time and the Vivaldi prediction. STP keeps this
average over all RPCs, not per-destination. STP chooses an RPC's
retransmission interval in milliseconds as follows:
where v is the Vivaldi-predicted round trip time to the destination and
α is the average error. The weight on the α term was chosen
by analyzing the distribution of RPC delays seen by a running node; the chosen
timers
produce less than 1 percent spurious retransmissions with
approximately three times less over-prediction in the case of a loss
than a conservative (1 second) timer.
This formula assumes that Vivaldi's errors are normally
distributed; adding a constant times the error corresponds to sampling
a low percentile of the error distribution.
The constant α plays a part similar to the measured RTT deviation in the
TCP retransmit timer calculation.
The constant term in Equation 2 (15 ms) is necessary to avoid
retransmissions to other virtual nodes on the same host;
Vivaldi predicts
small latencies to the local node, but under high load
the observed delay is as much as 15 ms. This term prevents those
retransmissions without adding significantly to over-prediction
for distant nodes.
5.2.3 Retransmit policy
When an STP retransmit timer expires, STP notifies the application
(DHash++) rather than re-sending the RPC. This gives DHash++ a
chance to re-send the RPC to a different destination. DHash++
re-sends a lookup RPC to the finger that is next-closest in ID space,
and re-sends a fragment fetch RPC to the successor that is
next-closest in predicted latency. This policy helps to avoid wasting
time sending RPCs to nodes that have crashed or have overloaded access
links.
DHash++ uses a separate background stabilization process to decide
whether nodes in the finger table or successor list have crashed; it
sends periodic probe RPCs and decides a node is down only when it
fails to respond to many probes in a row.
5.3 Performance comparison
This section presents measurements comparing the latency and throughput of
the TCP transport
implementation to the STP implementation when run on the RON test-bed.
We used 26 RON nodes, located in the United States and Europe. Each
physical RON node is located in a different machine room and ran 4
copies of DHash++. The average inter-node round-trip time is 75 ms,
and the median is 72 ms
(these reflect the multiple copies of DHash++ per host).
5.3.1 Fetch latency
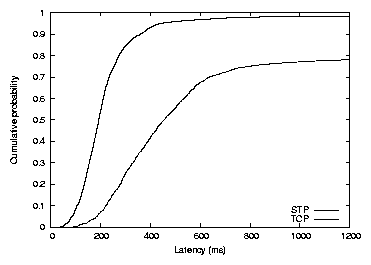 Figure 13: Distribution of individual
8192-byte fetch latencies on RON.
Figure 13 shows the distribution of
individual block fetch latencies on RON. The numbers are derived from
an experiment in which each node in turn fetched a sequence of
randomly chosen blocks; at any given time only one fetch was
active in the DHT. The median fetch time was 192 ms
with STP and 447 ms with TCP. The average number of hops required to
complete a lookup was 3.
The STP latency consists of approximately 3 one-way latencies to take
the lookup to the predecessor, plus one one-way latency to return the
lookup reply to the originator.
The parallel fetch of the closest seven fragments is limited by the
latency to the farthest fragment, which has median
latency (see Section 4.4). Thus the total expected time is roughly
4 ×37.5+72=222; the actual median latency of 192 ms is
probably less due to proximity routing of the lookup.
The TCP latency consists of the same three one-way latencies to reach
the predecessor, then a median round-trip-time for the predecessor to
fetch the closest seven fragments, then the time required to send the
8 KB block over three TCP connections in turn. If the connection
uses slow-start, the transfer takes 2.5 round trip times (there's no
need to wait for the last ACK); if not, just half a round-trip time. A
connection only uses slow-start if it has been idle for a second or
more. The connection from the first hop back to the originator is
typically not idle, because it has usually been used by a recent fetch
in the experiment; the other connections are much more likely to use
slow start. Thus the latency should range from 340 ms if
there was no slow-start, to 600 ms if two of the hops used
slow-start. The measured time of 447 ms falls in this range. This
analysis neglects the transmission time of an 8 KB block (about 131
ms at 1 Mb/s).
Figure 13: Distribution of individual
8192-byte fetch latencies on RON.
Figure 13 shows the distribution of
individual block fetch latencies on RON. The numbers are derived from
an experiment in which each node in turn fetched a sequence of
randomly chosen blocks; at any given time only one fetch was
active in the DHT. The median fetch time was 192 ms
with STP and 447 ms with TCP. The average number of hops required to
complete a lookup was 3.
The STP latency consists of approximately 3 one-way latencies to take
the lookup to the predecessor, plus one one-way latency to return the
lookup reply to the originator.
The parallel fetch of the closest seven fragments is limited by the
latency to the farthest fragment, which has median
latency (see Section 4.4). Thus the total expected time is roughly
4 ×37.5+72=222; the actual median latency of 192 ms is
probably less due to proximity routing of the lookup.
The TCP latency consists of the same three one-way latencies to reach
the predecessor, then a median round-trip-time for the predecessor to
fetch the closest seven fragments, then the time required to send the
8 KB block over three TCP connections in turn. If the connection
uses slow-start, the transfer takes 2.5 round trip times (there's no
need to wait for the last ACK); if not, just half a round-trip time. A
connection only uses slow-start if it has been idle for a second or
more. The connection from the first hop back to the originator is
typically not idle, because it has usually been used by a recent fetch
in the experiment; the other connections are much more likely to use
slow start. Thus the latency should range from 340 ms if
there was no slow-start, to 600 ms if two of the hops used
slow-start. The measured time of 447 ms falls in this range. This
analysis neglects the transmission time of an 8 KB block (about 131
ms at 1 Mb/s).
5.3.2 Single-client fetch throughput
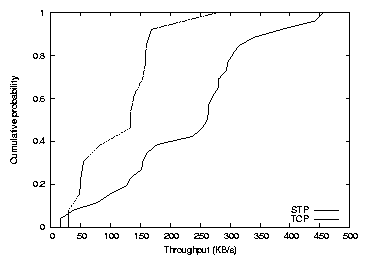 Figure 14: Distribution of average throughput
obtained by different RON nodes
during 4 megabyte transfers.
Figure 14 shows the distribution of fetch
throughput achieved by different RON nodes when each fetches a long
sequence of blocks from DHash++. The application maintains 64 one-block
requests outstanding to its local DHash++ server,
enough to avoid limiting the size of STP's congestion window.
Using TCP transport, the median node achieved a throughput of
133 KB/s. The minimum and maximum throughputs were 29 and 277 KB/s.
Both the median throughput and the range of individual node throughputs are
higher when using STP: the median was 261 KB/s, and throughputs ranged
from 15 to 455 KB/s. The TCP transport has lower throughput because
it sends each block back through each node on the recursive route,
and thus is more likely than STP to send a block through a slow
access link. About half of
the three-hop routes pass through one of the RON sites with sub-one-megabit
access links. STP sends coded fragments directly to the node originating
the request, and thus each fragment encounters fewer slow links.
To characterize the effectiveness of STP in utilizing available
resources we consider the expected throughput of a DHash++
system.
Assuming an STP window large enough to keep all links busy,
a node can fetch data at a rate equal to the slowest access link
times the number of nodes, since the blocks are spread evenly
over the nodes.
The slowest site access link in RON has a capacity of about
0.4 Mb/s. With 26 nodes one would expect 0.4 ×26 = 10.4
Mb/s or 1.3 MB/s total throughput for a fetching site not limited
by its own access link.
STP achieves less than half of this throughput at the fastest
site. The reason appears to be that STP has difficulty maintaining a large window in
the face of packet loss, which averages about 2 percent in these tests.
Figure 14: Distribution of average throughput
obtained by different RON nodes
during 4 megabyte transfers.
Figure 14 shows the distribution of fetch
throughput achieved by different RON nodes when each fetches a long
sequence of blocks from DHash++. The application maintains 64 one-block
requests outstanding to its local DHash++ server,
enough to avoid limiting the size of STP's congestion window.
Using TCP transport, the median node achieved a throughput of
133 KB/s. The minimum and maximum throughputs were 29 and 277 KB/s.
Both the median throughput and the range of individual node throughputs are
higher when using STP: the median was 261 KB/s, and throughputs ranged
from 15 to 455 KB/s. The TCP transport has lower throughput because
it sends each block back through each node on the recursive route,
and thus is more likely than STP to send a block through a slow
access link. About half of
the three-hop routes pass through one of the RON sites with sub-one-megabit
access links. STP sends coded fragments directly to the node originating
the request, and thus each fragment encounters fewer slow links.
To characterize the effectiveness of STP in utilizing available
resources we consider the expected throughput of a DHash++
system.
Assuming an STP window large enough to keep all links busy,
a node can fetch data at a rate equal to the slowest access link
times the number of nodes, since the blocks are spread evenly
over the nodes.
The slowest site access link in RON has a capacity of about
0.4 Mb/s. With 26 nodes one would expect 0.4 ×26 = 10.4
Mb/s or 1.3 MB/s total throughput for a fetching site not limited
by its own access link.
STP achieves less than half of this throughput at the fastest
site. The reason appears to be that STP has difficulty maintaining a large window in
the face of packet loss, which averages about 2 percent in these tests.
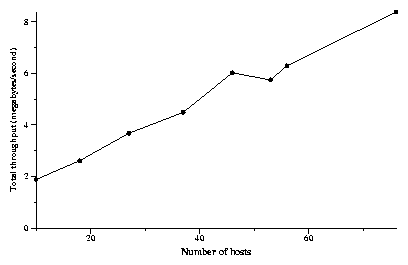 Figure 15: The effect of system size on total
throughput obtainable. Each point represents an
experiment with DHash++ running at x sites on the RON and PlanetLab
test-beds. Each site reads 1000 8 KB blocks; the
aggregate throughput of the system in steady state is reported. This
throughput increases as additional capacity (in the form of additional
sites) is added to the system.
This section evaluates the ability of STP and DHash++ to take advantage
of additional resources.
As the number of nodes grows, more network
capacity (in the form of additional access links) is added to the
system. Figure 15 shows the total
throughput for an N-node DHT when all N nodes simultaneously
read a large number of blocks, as a function of N.
The experiments were run on the combined PlanetLab and RON test-beds.
The slowest access link was that of a node in Taiwan, which was able
to send at 200 KB/s to sites in the US. The observed
throughput corresponds to our throughput prediction:
the total throughputs scales with the number of sites.
The first data point
consists of ten sites experiencing an aggregate of ten times the
bandwidth available at the slowest site.
A similar experiment run using 150 machines but at 70 unique sites
(many PlanetLab sites are home to more than one node) produces a peak
throughput of 12.8 MB/s. As more machines and DHash++ nodes are added
to each site, that site gains a proportionally greater share of that
site's link bandwidth and the system's aggregate bandwidth increases.
Figure 15: The effect of system size on total
throughput obtainable. Each point represents an
experiment with DHash++ running at x sites on the RON and PlanetLab
test-beds. Each site reads 1000 8 KB blocks; the
aggregate throughput of the system in steady state is reported. This
throughput increases as additional capacity (in the form of additional
sites) is added to the system.
This section evaluates the ability of STP and DHash++ to take advantage
of additional resources.
As the number of nodes grows, more network
capacity (in the form of additional access links) is added to the
system. Figure 15 shows the total
throughput for an N-node DHT when all N nodes simultaneously
read a large number of blocks, as a function of N.
The experiments were run on the combined PlanetLab and RON test-beds.
The slowest access link was that of a node in Taiwan, which was able
to send at 200 KB/s to sites in the US. The observed
throughput corresponds to our throughput prediction:
the total throughputs scales with the number of sites.
The first data point
consists of ten sites experiencing an aggregate of ten times the
bandwidth available at the slowest site.
A similar experiment run using 150 machines but at 70 unique sites
(many PlanetLab sites are home to more than one node) produces a peak
throughput of 12.8 MB/s. As more machines and DHash++ nodes are added
to each site, that site gains a proportionally greater share of that
site's link bandwidth and the system's aggregate bandwidth increases.
6 Related work
The primary contribution of this paper is exploring a large set of
design decisions for DHTs in the context of a single, operational
system. This exploration of design decisions emerged from an effort to
understand a number of recent DHT-like systems with different designs,
including
OceanStore/Pond [22,34,43],
CFS [13], Overnet [28,32],
PAST [6,37,38]
FarSite [1], and Pastiche [11].
Rhea et al. did a black-box comparison of the implementations of
several structured lookup systems (Chord, Pastry, Tapestry) and found
that the use of proximity information reduced lookup latency,
especially for lookups destined to nearby hosts [36].
Gummadi et al. studied the impact of routing geometry
on resilience and proximity [16]. They found that
flexibility in the routing geometry in general improved the ability of
the system to find good neighbors. We extend their findings with
additional analysis in simulation and with actual measurements to
better understand the performance gains seen when using proximity.
A number of recent papers discuss design ideas related to networks
with churn [5,23,35], some of which are used by
DHash++. These ideas include integrated transport systems that
quickly detect node failure and use alternate routes after
timeouts.
7 Conclusions and future work
This paper has presented a series of design decisions faced by DHTs
that store data, discussed the design options and how they interact,
and compared a number of variant designs using simulations and
measurements of an implementation running on PlanetLab and RON.
The paper proposed techniques that taken together together reduce fetch
latency by a factor of two and allow efficient bulk throughput.
The list of design decisions is not exhaustive, and future work will
analyze a wider range of DHT designs and behavior such as the relationship between lookup robustness and
performance, the latency and throughput of DHT writes, the handling of
data movement required when nodes join and leave, data
layout policies, the effects of block size, and the
tradeoffs involved in use of constant-hop-count lookup protocols.
The simulator and DHash++ are publically available from
https://project-iris.net.
Acknowledgements
We would like to thank Chuck Blake for his help with data analysis,
Thomer Gil, Jeremy Stribling
and Russ Cox
for their help writing the simulator, Peter Druschel
and the anonymous reviewers for their helpful comments,
and David Andersen and the PlanetLab project for the
RON and PlanetLab test-beds.
This paper is dedicated to the memory of Josh Cates.
References
- [1]
-
Adya, A., Bolosky, W. J., Castro, M., Cermak, G., Chaiken, R., Douceur,
J. R., Howell, J., Lorch, J. R., Theimer, M., and Wattenhofer, R. P.
Farsite: Federated, available, and reliable storage for an
incompletely trusted environment.
In Proc. of the 5th OSDI (Dec. 2002).
- [2]
-
Andersen, D., Balakrishnan, H., Kaashoek, M. F., and Morris, R.
Resilient overlay networks.
In Proc. of the 18th ACM SOSP (Chateau Lake Louise,
Banff, Canada, October 2001).
- [3]
-
Anderson, R. J.
The eternity service.
In Proc. of the 1996 Pragocrypt (1996).
- [4]
-
Blake, C., and Rodrigues, R.
High availability, scalable storage, dynamic peer networks: Pick two.
In Proc. of the 9th Workshop on Hot Topics in Operating
Systems (May 2003).
- [5]
-
Castro, M., Costa, M., and Rowstron, A.
Performance and dependability of structured peer-to-peer overlays.
Tech. Rep. MSR-TR-2003-94, Microsoft Research, December 2003.
- [6]
-
Castro, M., Druschel, P., Hu, Y. C., and Rowstron, A.
Exploiting network proximity in peer-to-peer overlay networks.
Tech. Rep. MSR-TR-2002-82, Microsoft Research, June 2002.
- [7]
-
Cates, J.
Robust and efficient data management for a distributed hash table.
Master's thesis, Massachusetts Institute of Technology, May 2003.
- [8]
-
Chen, Y., Edler, J., Goldberg, A., Gottlieb, A., Sobti, S., and Yianilos,
P.
A prototype implementation of archival intermemory.
In Proceedings of the 4th ACM Conference on Digital libraries
(Berkeley, CA, Aug. 1999), pp. 28-37.
- [9]
-
Chiu, D.-M., and Jain, R.
Analysis of the increase and decrease algorithms for congestion
avoidance in computer networks.
Computer Networks and ISDN Systems 17 (1989), 1-14.
- [10]
-
Costa, M., Castro, M., Rowstron, A., and Key, P.
PIC: Practical Internet coordinates for distance estimation.
In 24th International Conference on Distributed Computing
Systems (Tokyo, Japan, March 2004).
- [11]
-
Cox, L. P., and Noble, B. D.
Pastiche: making backup cheap and easy.
In Proc. of the 5th OSDI (Dec. 2002).
- [12]
-
Cox, R., Dabek, F., Kaashoek, F., Li, J., and Morris, R.
Practical, distributed network coordinates.
In Proc. of the Second workshop on Hot Topics in Networks
(HotNets-II) (Nov. 2003).
- [13]
-
Dabek, F., Kaashoek, M. F., Karger, D., Morris, R., and Stoica, I.
Wide-area cooperative storage with CFS.
In Proc. of the 18th ACM SOSP (Oct. 2001).
- [14]
-
Ganesh, A., Kermarrec, A.-M., and Massoulie, L.
HiSCAMP: self-organising hierarchical membership protocol.
In Proc. of the 10th European ACM SIGOPS workshop (Sept.
2002).
- [15]
-
Gummadi, K., Saroiu, S., and Gribble, S. D.
King: Estimating latency between arbitrary Internet end hosts.
In Proc. of the 2002 SIGCOMM Internet Measurement Workshop
(Marseille, France, Nov. 2002).
- [16]
-
Gummadi, K. P., Gummadi, R., Gribble, S., Ratnasamy, S., Shenker, S., and
Stoica, I.
The impact of DHT routing geometry on resilience and proximity.
In Proc. of the 2003 ACM SIGCOMM (Karlsruhe, Germany, Aug.
2003).
- [17]
-
Gupta, A., Liskov, B., and Rodrigues, R.
One hop lookups for peer-to-peer overlays.
In Proc. of the Ninth Workshop on Hot Topics in Operating
Systems (May 2003).
- [18]
-
Gupta, I., Birman, K., Linga, P., Demers, A., and van Renesse, R.
Kelips: Building an efficient and stable P2P DHT through
increased memory and background overhead.
In Proc. of the 2nd IPTPS (Feb. 2003).
- [19]
-
Hand, S., and Roscoe, T.
Mnemosyne: Peer-to-peer steganographic storage.
In Proc. of the 1st IPTPS (Mar. 2001).
- [20]
-
Iyer, S., Rowstron, A., and Druschel, P.
Squirrel: A decentralized, peer-to-peer web cache.
In Proc. 21st Annual ACM Symposium on Principles of Distributed
Computing (PODC). (July 2002).
- [21]
-
Jacobson, V.
Congestion avoidance and control.
In Proc. of the ACM SIGCOMM (Aug. 1988).
- [22]
-
Kubiatowicz, J., Bindel, D., Chen, Y., Czerwinski, S., Eaton, P., Geels,
D., Gummadi, R., Rhea, S., Weatherspoon, H., Weimer, W., Wells, C., and Zhao,
B.
OceanStore: An architecture for global-scale persistent storage.
In Proceeedings of the Ninth International Conference on
Architectural Support for Programming Languages and Operating Systems (ASPLOS
2000) (Boston, MA, Nov. 2000), pp. 190-201.
- [23]
-
Li, J., Stribling, J., Morris, R., Kaashoek, M. F., and Gil, T.
DHT routing tradeoffs in networks with churn.
In Proc. of the 3rd IPTPS (Feb. 2004).
- [24]
-
Lim, H., Hou, J., and Choi, C.-H.
Constructing an Internet coordinate system based on delay
measurement.
In Proc. of the 2003 SIGCOMM Internet Measurement Conference
(Oct. 2003).
- [25]
-
Maymounkov, P., and Mazieres, D.
Kademlia: A peer-to-peer information system based on the XOR
metric.
In Proc. of the 1st IPTPS (Mar. 2002).
- [26]
-
Muthitacharoen, A., Morris, R., Gil, T. M., and Chen, B.
Ivy: A read/write peer-to-peer file system.
In Proc. of the 5th OSDI (Dec. 2002).
- [27]
-
Ng, T. S. E., and Zhang, H.
Predicting Internet network distance with coordinates-based
approaches.
In Proc. of the 2002 IEEE Infocom (June 2002).
- [28]
-
Overnet.
https://www.overnet.com/.
- [29]
-
Peterson, L., Anderson, T., Culler, D., and Roscoe, T.
A blueprint for introducing disruptive technology into the
Internet.
In Proc. of HotNets-I (October 2002).
https://www.planet-lab.org.
- [30]
-
Pias, M., Crowcroft, J., Wilbur, S., Harris, T., and Bhatti, S.
Lighthouses for scalable distributed location.
In Proc. of the 2nd IPTPS (Feb. 2003).
- [31]
-
Rabin, M.
Efficient dispersal of information for security, load balancing, and
fault tolerance.
Journal of the ACM 36, 2 (Apr. 1989), 335-348.
- [32]
-
Ranjita Bhagwan, S. S., and Voelker, G.
Understanding availability.
In Proc. of the 2nd IPTPS (Feb. 2003).
- [33]
-
Ratnasamy, S., Handley, M., Karp, R., and Shenker, S.
Topologically-aware overlay construction and server selection.
In Proceedings of Infocom 2002 (2002).
- [34]
-
Rhea, S., Eaton, P., Geels, D., Weatherspoon, H., Zhao, B., and
Kubiatowicz, J.
Pond: the OceanStore prototype.
In Proc. of the 2nd USENIX Conference on File and Storage
Technologies (FAST) (Apr. 2003).
- [35]
-
Rhea, S., Geels, D., Roscoe, T., and Kubiatowicz, J.
Handling churn in a DHT.
Tech. Rep. UCB/CSD-3-1299, UC Berkeley, Computer Science Division,
Dec. 2003.
- [36]
-
Rhea, S., Roscoe, T., and Kubiatowicz, J.
Structured peer-to-peer overlays need application-driven benchmarks.
In Proc. of the 2nd IPTPS (Feb. 2003).
- [37]
-
Rowstron, A., and Druschel, P.
Pastry: Scalable, distributed object location and routing for
large-scale peer-to-peer systems.
In Proceedings of the 18th IFIP/ACM International Conference on
Distr ibuted Systems Platforms (Middleware 2001) (Nov. 2001).
- [38]
-
Rowstron, A., and Druschel, P.
Storage management and caching in PAST, a large-scale, persistent
peer-to-peer storage utility.
In Proc. of the 18th ACM SOSP (Oct. 2001).
- [39]
-
Shavitt, Y., and Tankel, T.
Big-bang simulation for embedding network distances in Euclidean
space.
In Proc. of IEEE Infocom (April 2003).
- [40]
-
Sit, E., Dabek, F., and Robertson, J.
UsenetDHT: A low overhead usenet server.
In Proc. of the 3rd IPTPS (Feb. 2004).
- [41]
-
Stevens, W. R.
RFC2001: TCP slow start, congestion avoidance, fast retransmit,
and fast recovery algorithms.
Tech. rep., Internet Assigned Numbers Authority, 1997.
- [42]
-
Stoica, I., Morris, R., Karger, D., Kaashoek, M. F., and Balakrishnan, H.
Chord: A scalable peer-to-peer lookup service for Internet
applications.
In Proc. of the ACM SIGCOMM (San Diego, Aug. 2001).
An extended version appears in ACM/IEEE Trans. on Networking.
- [43]
-
Stribling, J.
Optimizations for locality-aware structured peer-to-peer overlays.
In Proc. of the 1st IRIS Student Workshop (Cambridge, MA,
Aug. 2003).
- [44]
-
Voulgaris, S., and van Steen., M.
An epidemic protocol for managing routing tables in very large
peer-to-peer networks.
In Proc. of the 14th IFIP/IEEE Workshop on Distributed Systems:
Operations and Management (DSOM 2003) (Oct. 2003).
- [45]
-
Walfish, M., Balakrishnan, H., and Shenker, S.
Untangling the web from DNS.
In Proc. of the 1st NSDI (Mar. 2004).
- [46]
-
Weatherspoon, H., and Kubiatowicz, J. D.
Erasure coding vs. replication: A quantitative comparison.
In Proc. of the 1st IPTPS (Mar. 2002).
- [47]
-
Zhao, B. Y., Huang, L., Stribling, J., Rhea, S. C., Joseph, A. D., and
Kubiatowicz, J. D.
Tapestry: A resilient global-scale overlay for service deployment.
IEEE Journal on Selected Areas in Communications 22, 1 (Jan.
2004).
Footnotes:
1
This research was conducted as part of the IRIS project (https://project-iris.net/), supported by the National Science
Foundation under Cooperative Agreement No. ANI-0225660.
File translated from
TEX
by
TTH,
version 3.59.
On 3 Mar 2004, 22:33.
|