

| Pp. 139-146 of the Proceedings |  |
The open-source software RRDtool and Cricket provide a solution to the problem of collecting, storing, and visualizing service network time series data for the real-time monitoring task. However, simultaneously monitoring all service network time series of interest is an impossible task even for the accomplished network technician. The solution is to integrate a mathematical model for automatic aberrant behavior detection in time series into the monitoring software. While there are many such models one might choose, the primary goal should be a model compatible with real-time monitoring. At WebTV, the solution was to integrate a model based on exponential smoothing and Holt-Winters forecasting into the Cricket/RRDtool architecture. While perhaps not optimal, this solution is flexible, efficient, and effective as a tool for automatic aberrant behavior detection.
Real time management of a service network infrastructure at the IAP/ISP level is not a trivial task. First, there is the sheer quantity of data generated on a minute-by-minute basis. The WebTV production service infrastructure consists of tens of switches and routers, hundreds of host computers, and thousands of application daemon instances to support a subscriber base of over 1 million users. Second, there is great variety in the types of data collected. The WebTV production service monitors SNMP counters over network links, host statistics such as CPU load and I/O operations, and event logs for application daemons. Every variable monitored, whether byte traffic on a switch port, CPU load of a host machine, or requests handled by a cookie daemon, generates a time series. All of these time series reflect some part of the overall service network health.
The first challenge therefore, is to collect, store, and provide real-time access to this vast and diverse data. The open-source software RRDtool [6] and Cricket [1, 2] meet this first challenge. Using a web browser, a network technician can quickly navigate to and view a time series graph for a target and variable of interest.
The network technician is likely to be interested in aberrant behavior; that is, changes in the short-term behavior of a time series (on the order of minutes or hours) that are inconsistent with past history. Long-term trends (on the order of weeks or months) are not of interest from the service monitoring perspective because one expects a time series to evolve in a dynamic environment. Aberrant behavior may indicate a performance bottleneck, application component failure, or system downtime. In some cases, aberrant behavior is anticipated; other times it is not (see section ``Defining Aberrant Behavior'').
The second challenge of network monitoring is to automatically identify aberrant behavior in the midst of thousands of service network time series. Once such behavior is identified, an alert can be triggered to bring the technician's attention to the potential problem. Existing software tools provide some of this functionality, but these solutions usually rely on simple rules or thresholds (i.e., memory utilization should be below 80%). These rules and thresholds are sufficient for many applications, but they can't detect more subtle changes in behavior and they apply a static criteria to detect aberrant behavior rather than a dynamic one.
This paper describes a partial solution to this second challenge of network monitoring at the IAP/ISP level. Section ``Description of the Model'' discusses the aberrant behavior detection algorithm, with a focus on understanding the algorithm parameters. The bulk of the software implementation is in RRDtool, which is the focus of section ``Enhancements to RRDtool.'' Section ``Enhancements to Cricket'' discusses details relevant for Cricket. The conclusion lists availability of the software.
Suppose a statistical model exists that describes the behavior of a time series (or at least the characteristics of interest). With such a model, one can define aberrant behavior as behavior that does conform to the model (or is not well described by the model).
Of course, aberrant behavior with respect to a statistical model may or may not reflect a real event of interest for the technician. In the case that it does not, it is a false positive. Obviously, the ideal is to minimize the rate of false positives while identifying all events of real interest. However, this ideal can rarely be achieved. In most detection systems, there is a trade off between selectivity (avoiding false positives; also referred to as specificity and precision) and sensitivity (ability to detect true positives; also referred to as recall). While it is important to remain cognizant of these issues, they become less important if one perceives a statistical model for aberrant behavior as a screening mechanism rather than a surrogate for the expert judgement of a network technician.
Note that this definition treats each time series independently of all others. No doubt there is much to be gained by leveraging the relationships between service network variables, but that is not addressed in this paper.
Many service network variable time series exhibit the following regularities (characteristics) that should be accounted for by a model:
In addition to modeling time series regularities, model design must consider the real-time monitoring context. Complicated statistical models are unlikely to be understood by network technicians and unlikely to be feasible computationally in a real-time context.
Aberrant behavior detection is decomposed into three pieces, each building on its predecessor:
The proposed model is an extension of Holt-Winters Forecasting, which supports incremental model updating via exponential smoothing. The following sections discuss the model in some detail and require some mathematical notation. Let y1 ... yt-1, yt, yt+1 ... denote the sequence of values for the time series observed at some fixed temporal interval (recall RRDtool maps an irregular time series to a regular interval). Let m denote the period of the seasonal trend (i.e., the number of observations per day).
Exponential smoothing [3] is a simple algorithm for predicting the
next value in a time series given the current value and the current
prediction. Let
 denote the predicted value for time
t+1, then:
denote the predicted value for time
t+1, then:

The prediction is actually a weighted average of all past observations in the time series. The premise of exponential smoothing is that the current value is most informative for prediction of the next value, and that the weight of older observation decays exponentially as the observation moves further into the past. It is an incremental algorithm because the next prediction is obtained by updating the current prediction with the current observed value.
 is the model parameter and 0 <
is the model parameter and 0 <  < 1. It
determines the rate of decay (1 -
< 1. It
determines the rate of decay (1 -  ) and the weight the
current value is given during the incremental update.
) and the weight the
current value is given during the incremental update.
Holt-Winters Forecasting [3] is a more sophisticated algorithm that builds upon exponential smoothing. Holt-Winters Forecasting rests on the premise that the observed time series can be decomposed into three components: a baseline, a linear trend, and a seasonal effect. The algorithm presumes each of these components evolves over time and this is accomplished by applying exponential smoothing to incrementally update the components.
The prediction is the sum of the three components:


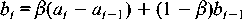

 ,
,  ,
,  ). Recall m is the period of the
seasonal cycle; so the seasonal coefficient at time t references the
last computed coefficient for the same time point in the seasonal
cycle.
). Recall m is the period of the
seasonal cycle; so the seasonal coefficient at time t references the
last computed coefficient for the same time point in the seasonal
cycle.
The new estimate of the baseline is the observed value adjusted by the best available estimate of the seasonal coefficient (ct-m). As the updated baseline needs to account for change due to the linear trend, the predicted slope is added to the baseline coefficient. The new estimate of the slope is simply the difference between the new and old baseline (as the time interval between observations is fixed, it is not relevant). The new estimate of the seasonal component is the difference between the observed value and the corresponding baseline.
 ,
,  , and
, and  are the adaptation
parameters of the algorithm and 0 <
are the adaptation
parameters of the algorithm and 0 <  ,
,
 ,
,  < 1.
Larger values mean the algorithm adapts faster and predictions reflect
recent observations in the time series; smaller values means the
algorithm adapts slower, placing more weight on the past history of the
time series.
< 1.
Larger values mean the algorithm adapts faster and predictions reflect
recent observations in the time series; smaller values means the
algorithm adapts slower, placing more weight on the past history of the
time series.
Note that the update formulas imply an implementation need only to store the current values of the slope and intercept, and a single period of seasonal coefficients, as these stored values are replaced at each iteration.
Holt-Winters Forecasting can also predict a time series further than a single time step in the future [3]. This multi-step prediction provides a mechanism to handle missing data.
Confidence bands measure deviation for each time point in the seasonal cycle; this mechanism models seasonal variability. The measure of deviation is a weighted average absolute deviation, updated via exponential smoothing:
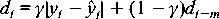
 . The
confidence band is simply the collection of intervals
. The
confidence band is simply the collection of intervals

 and
and
 are scaling factors for the width
of the confidence band. Often, a symmetric confidence band is desired
and
are scaling factors for the width
of the confidence band. Often, a symmetric confidence band is desired
and  . In this case, denote the common
parameter
. In this case, denote the common
parameter  . Given some assumptions and statistical distribution
theory, sensible values of
. Given some assumptions and statistical distribution
theory, sensible values of  are between 2 and 3 [7].
are between 2 and 3 [7].
A simple mechanism to detect an anomaly is to check if an observed value of the time series falls outside the confidence band. However, this mechanism often yields a high number of false positives. A more robust mechanism is to use a moving window of a fixed number of observations [7]. If the number of violations (observations that fall outside the confidence band) exceeds a specified threshold, then trigger an alert for aberrant behavior. Formally, define a violation as an observation yt that falls outside the interval:

As discussed thus far, each component of the seasonal coefficients vector is determined independently. It seems reasonable to assume that the seasonal effect is a smooth function over the period, not a discontinuous series of points. A similar argument applies to the seasonal deviations. Note that exponential smoothing performs smoothing across seasonal cycles, but does not perform temporal smoothing within a seasonal cycle.
At a cost of adding some additional overhead to the implementation, the model performs temporal smoothing within a cycle for the seasonal coefficients and deviations. The smoother used is an equal-weight moving average, with a window of 0.05m.
The model parameters need to be set and tuned for the model to work well. There is no single optimal set of values, even restricted to data for a single variable. This is due to the interplay between multiple parameters in the model.
For example, consider two observations in sequence,
yt and yt+1. The intercept (a),
slope (b), and seasonal (c) coefficients all `absorb' some
part of the difference between yt and
yt+1 during the exponential smoothing update. It is
safe to assume some of the difference is noise, so updates to the
coefficients need not account for all of the difference between
yt and yt+1. The values of  ,
,  , and
, and  determine the relative share of the difference
assigned to a changing baseline, a changing linear trend, and a changing
seasonal coefficient.
determine the relative share of the difference
assigned to a changing baseline, a changing linear trend, and a changing
seasonal coefficient.
Here are some common sense guidelines for setting parameters:
 : At least one of
: At least one of  ,
,
 , and
, and  should
allow adaptation in a short time frame. As seasonal updates occur
infrequently for each coefficient (once per cycle), and the goal of
should
allow adaptation in a short time frame. As seasonal updates occur
infrequently for each coefficient (once per cycle), and the goal of
 is to capture a slowly changing linear
trend, the most logical choice is
is to capture a slowly changing linear
trend, the most logical choice is  . Use
exponential smoothing weights to make an educated choice for
. Use
exponential smoothing weights to make an educated choice for  . The sum of the most recent n weights is 1 -
(1 -
. The sum of the most recent n weights is 1 -
(1 -  )n and of course the sum
of all weights is 1 (ignoring initialization, see section
``Initialization''). These facts can be manipulated to choose
)n and of course the sum
of all weights is 1 (ignoring initialization, see section
``Initialization''). These facts can be manipulated to choose  using the formula:
using the formula:

 = 0.28. This formula can be
rearranged using simple algebra to compute either the total weights as
a percentage or the number of time points (elapsed time). For example,
if
= 0.28. This formula can be
rearranged using simple algebra to compute either the total weights as
a percentage or the number of time points (elapsed time). For example,
if  = 0.1, then the most recent hour of
observations at five minute intervals (12 time points) accounts for 75%
of the baseline prediction.
= 0.1, then the most recent hour of
observations at five minute intervals (12 time points) accounts for 75%
of the baseline prediction.
 : As the purpose of
: As the purpose of  is to capture a linear trend longer than one
seasonal cycle, it is logical to choose
is to capture a linear trend longer than one
seasonal cycle, it is logical to choose  such that one seasonal cycle does not account
for a majority of the exponential smoothing weights. The formula
discussed previously applies with
such that one seasonal cycle does not account
for a majority of the exponential smoothing weights. The formula
discussed previously applies with  replacing
replacing  . For example, if the period of the cycle is one day
at one observation every five minutes (288 per day), then setting
. For example, if the period of the cycle is one day
at one observation every five minutes (288 per day), then setting
 = 0.0024 will guarantee that observations within the last day
account for less than 50% of the smoothing weights.
= 0.0024 will guarantee that observations within the last day
account for less than 50% of the smoothing weights.
 : The seasonal adaptation parameter can also be selected using
exponential smoothing weights using a variation of the previous
formula. Note this single parameter controls both seasonal
coefficient and deviation adaptation, on the assumption that seasonal
trend and variability evolve together over time at roughly the same
rate.
: The seasonal adaptation parameter can also be selected using
exponential smoothing weights using a variation of the previous
formula. Note this single parameter controls both seasonal
coefficient and deviation adaptation, on the assumption that seasonal
trend and variability evolve together over time at roughly the same
rate.
 : As noted in confidence bands section, the
scaling factor of the confidence bands can be chosen by appealing to
statistical distribution theory. Reasonable values fall in the interval
[2, 3]. Choose 2 to detect more failures (which may just mean a higher
rate of false positives).
: As noted in confidence bands section, the
scaling factor of the confidence bands can be chosen by appealing to
statistical distribution theory. Reasonable values fall in the interval
[2, 3]. Choose 2 to detect more failures (which may just mean a higher
rate of false positives).
The model requires initial values for the intercept, slope, seasonal coefficients, and deviations (seasonal variability). These could be set arbitrarily, computed from a long history of past data, or bootstrapped from data as it becomes available. The implementation in RRDtool is to bootstrap the algorithm from a cold start.
Initial values exert
influence for some time. The analysis of exponential smoothing weights
in the previous section assumes that influence of initial values has
become negligible. For the intercept coefficient, the weight of the
initial value in exponential smoothing for observation t is
(1 -  )t-1.
Similar formulas hold for
)t-1.
Similar formulas hold for  and
and  . These formulas can
be used to calculate the influence of initial values. For example, if
the seasonal period is one day, 10 days have elapsed since
initialization, and
. These formulas can
be used to calculate the influence of initial values. For example, if
the seasonal period is one day, 10 days have elapsed since
initialization, and  = 0.1, then the weight of
the initial value in the predicted seasonal coefficient is 0.39. In
contrast, the weight of the most recent observation (which in the long
run is the most influential) is only 0.1.
= 0.1, then the weight of
the initial value in the predicted seasonal coefficient is 0.39. In
contrast, the weight of the most recent observation (which in the long
run is the most influential) is only 0.1.
While the model is designed to meet several goals, it is not
optimal. The proposed algorithm lacks a formalism found in some other
models. It is certainly true that there is no uniformly superior
forecasting algorithm for all time series, but consider the comments
of researcher Richard Lawton [5]:
The Holt-Winters method is one of the best known forecasting
techniques which allows the seasonal pattern to adapt over time...
When compared with other methods the technique has been found to
perform relatively well and it has the merit of being understood
by users who lack a statistical background without sacrificing the
ability to adapt to changing patterns in the data.
RRD is the acronym for Round Robin Database. RRD is a system to store and display time-series data [6]. It stores the data compactly, minimizes I/O operations for real-time updates, and presents useful graphs by processing the data at different temporal resolutions.
This section describes the implementation and usage of aberrant behavior detection in RRDtool. Some familiarity with the internals of the current release (1.0.x) of RRDtool is assumed, as this section makes reference to the pre-existing architecture.
There are several reasons why support for aberrant behavior detection is integrated within RRDtool, as opposed to implemented as a standalone program. These include:
On disk, the round robin database (RRD) is organized into sequential sections, round robin archives (RRA). Within each RRA is a section for each of the data sources (variables) stored in this RRD. Each RRA is defined by a consolidation function which maps primary data points (PDP) to consolidated data points (CDP). At another level, an RRA is just an array of data values that is updated in sequence according to some function at some fixed time interval.
On its face, the aberrant behavior detection algorithm needs at least two arrays, one to store the forecast values corresponding to each primary data point, and a second to store the predicted deviation corresponding to each PDP. As implemented, the seasonal coefficients and deviations that are used to calculate the forecast and predicted deviations are stored in a second pair of RRAs. These arrays have length equal to the seasonal period and are updated once for each PDP. Failures are tracked by a fifth RRA, which determines violations and failures on each update.
The intercept and slope coefficients required for the forecast are updated for every primary data point and are unique for each data source. As only the most recent value of each is required (see ``The Holt-Winters Forecasting Algorithm''), these parameters are stored in a temporary buffer in the header allocated for each RRA-data source combination in the RRD (the CDP buffer). This buffer is flushed back to disk on every call to RRD update.
The adaptation parameters are the same for all data sources within that RRA. They are stored in the RRA parameter buffer, which is read only during RRD update.
Therefore, implementation of the aberrant behavior algorithm adds five new `consolidation functions' to RRDtool
This section illustrates how to use the aberrant behavior detection algorithm in RRDtool through an example. The monitoring target will be a router interface on a link between two data centers in the WebTV production service network. The variable will be the outgoing bandwidth rate (in Mbps). Bandwidth usage follows a daily cycle and SNMP is polled at five minute intervals.
The first step is to create a RRD for this target with aberrant behavior detection enabled. In order to simplify the creation for the novice user, in addition to supporting explicit creation the HWPREDICT, SEASONAL, DEVPREDICT, DEVSEASONAL, and FAILURES RRAs, the RRDtool create command supports implicit creation of the other four when HWPREDICT is specified alone. To take advantage of this, use the following syntax:
RRA:HWPREDICT:<row count>:
<alpha>:<beta>:<period>
Where:
Here is an example of the create command, using this syntax:
rrdtool create monitor.rrd -s 300 \ DS:ifOutOctets:COUNTER:1800:0:4294967295 \ RRA:AVERAGE:0.5:1:2016 \ RRA:HWPREDICT:1440:0.1:0.0035:288After creation parameters can be changed using the tune command. RRDtool supports several new tune flags:
--alpha --beta --gamma --window-length --failure-threshold --deltapos --deltanegEach of these flags takes a single argument that corresponds to parameters discussed in section ``Choosing Model Parameters.'' The gamma flag will reset the adaptation parameter for both the SEASONAL and DEVSEASONAL RRAs (setting both to the same value). Both deltapos and deltaneg set the scale parameter for the upper and lower confidence band respectively, the default value for both is 2.
For example, suppose the technician is unhappy with the default window length and threshold for the FAILURES RRA implicitly created by the previous command. Issue the command:
rrdtool tune monitor.rrd \
--window-length 5 \
--failure-threshold 3
The remainder of the example uses the default window length of 9 and
the default threshold of 7.
Other options of the create command, including syntax and details of the explicit creation of the new RRAs, are discussed in a detailed implementation document [4] and the RRDtool manual [6].
The aberrant behavior detection algorithm requires nothing unusual for the RRDtool update command; the collection mechanism (i.e., Cricket invoking SNMP) will run normally. Now suppose some time has passed and the network technician is monitoring outgoing bandwidth at the router interface. He can view a graph of daily activity, including confidence bands and any failures, with the command in Listing 1.
rrdtool graph example.gif \ DEF:obs=monitor.rrd:ifOutOctets:AVERAGE \ DEF:pred=monitor.rrd:ifOutOctets:HWPREDICT \ DEF:dev=monitor.rrd:ifOutOctets:DEVPREDICT \ DEF:fail=monitor.rrd:ifOutOctets:FAILURES \ TICK:fail#ffffa0:1.0:"Failures Average bits out" \ CDEF:scaledobs=obs,8,* \ CDEF:upper=pred,dev,2,*,+ \ CDEF:lower=pred,dev,2,*,- \ CDEF:scaledupper=upper,8,* \ CDEF:scaledlower=lower,8,* \ LINE2:scaledobs#0000ff:"Average bits out" \ LINE1:scaledupper#ff0000:"Upper Bound Average bits out" \ LINE1:scaledlower#ff0000:"Lower Bound Average bits out"
TICK is a new graphing option in RRDtool. For every non-zero value in the DEF or CDEF argument, it plots a tick mark. The length of the mark (line) is specified by the third argument (after the color code) as a decimal percentage of the y-axis. 1.0 is 100% of the length of the y-axis, so the tick mark becomes a vertical line on the graph.
Figure 1 is an example of this daily graph generated on Wed, May 31, 2000 for the router target described previously. The thin lines are the confidence bands and the vertical bars represent failures (actually multiple failures in sequence - once the observed value strays outside the confidence bands it remains outside the bands for roughly a two hour period in both cases). The TICK graph option generates the bars from the FAILURES RRA.

The graph suggests that bandwidth on this outgoing link is increasing faster than expected by the model (past history). It is up to the network technician to decide if this represents aberrant behavior of interest. One approach the technician might take is to view the time series for this router interface over a longer time period.
With hindsight, it is easy to demonstrate something unusual is going on and the aberrant behavior detection model is catching it in real time. Figure 2 is the time series for the week and half period from May 24, 2000 to June 2, 2000. It is clear that Wed, May 31, is unusual. Bandwidth increases in two steps: once in the early morning and again in the early afternoon. In this case, the dip to 0 in the early morning hour and the subsequent jump can be attributed to a scheduled downtime for the service network. Perhaps the remainder of bandwidth activity on Wed has the same cause, in which case aberrant behavior detected is a false positive in the eyes of the network technician.

As alluded to in the previous initialization section, the implementation is designed to use bootstrap initialization. The intercept coefficient is initialized to the first observed value. The slope is initialized to 0, predicated on the assumption the linear trend over time is close to 0. If this is not the case, the time required for the Holt-Winters algorithm to gravitate away from 0 will depend on the seasonal adaptation parameter, gamma. During the first seasonal cycle of observed values, seasonal coefficients are initialized. During the second seasonal cycle of observed values, seasonal deviations are initialized. Unknown values during the first two seasonal cycles can complicate initialization. Basically, the implementation initializes any coefficients it can at the earliest opportunity; refer to the detailed implementation document [4].
Cricket is a front-end to RRDtool [1, 2]. Cricket manages multiple time series via RRDtool in a target configuration hierarchy. The configuration hierarchy (or config tree) is a flexible approach to grouping targets with common time series variables, graphing characteristics, and other properties. The Cricket collector provides built-in and extensible mechanisms for gathering data and feeding it to RRDtool. The collector manages SNMP calls and reads application event logs. The Cricket grapher generates time series graphs using the capabilities of RRDtool in real-time and serves them up as web pages. The graphs are organized via directory pages generated to match the config tree.
RRDtool has no mechanism for raising alerts, while Cricket does. Cricket provides several types of monitor-thresholds, which are defined in the config tree in a target dictionary section. Each monitor-threshold entry can contain multiple monitors. The basic functionality of a Cricket monitor-threshold is to fetch the most recent value from one of the RRAs of the target RRD file, check some criteria, and take some user-defined action if the criteria fails.
For efficiency and simplicity, Cricket 1.1 includes a new type of monitor-threshold specific for aberrant behavior detection. This monitor, failures, joins the existing Cricket monitors relation, value, and hunt. The general Cricket 1.1 monitor-threshold syntax permits a comma- delimited list of monitors. The syntax of each monitor is:
<data source>:<monitor type>: <monitor args>:<action>:<action args>The failures monitor does not take any arguments. For example, to send an SNMP trap whenever a failure is recorded for the ifOutOctets data source used in the example, the network technician adds the following entry to the appropriate target dictionary section:
my-monitor-threshold =
"IfOutOctets:failures::SNMP"
Note that currently in Cricket 1.1, SNMP actions do not require any
arguments, but the tag trap-address must be defined in
the target dictionary. This may change in the future as
Cricket 1.1 is still under development.
The failures monitor searches for a FAILURES RRA in the RRD file for the specified data source and if successful fetches the most recent value. If this value is 1, indicating a failure, it triggers the specified action. Through this mechanism, a network technician can easily be notified when the algorithm identifies something of interest.
Note that while the aberrant behavior detection RRAs, if created, apply to all data sources in the RRD file, the monitoring mechanism can be enabled for specific data sources or none at all.
Given the complexity of the RRDtool graph command, the Cricket 1.1 implementation provides a simple mechanism to view graphs relevant to aberrant behavior detection.
Cricket generates HTML navigation links to graphs using the new RRAs if it detects the string `HoltWinters' in the name of the view. The view must consist of a single data source that is not multi- target. It verifies these restrictions before enabling the navigation links. There are three navigation links added:
There is a need to meet the second challenge of networking monitoring: automatic aberrant behavior detection. The model and software outlined here are a solid approach to the problem, working within the architecture of the existing open-source solutions RRDtool and Cricket. There is ample room for future work, especially in a solution that exploits not only the past history of a service network variable, but the relationships between service network variables.
The RRDtool implementation is available as a patch to the current release of RRDtool at https://cricket.sourceforge.net/aberrant. This web site also includes the more detailed reference document [4] on the implementation in RRDtool. The Cricket enhancements are part of Cricket 1.1, available at https://cricket.sourceforge.net/.
Jake Brutlag is a statistician with the network operations group at Microsoft WebTV. He obtained an MS degree in statistics from the University of Washington in 1999. He can be reached via email at jakeb@corp.webtv.net or U.S. mail at Microsoft WebTV; 1065 La Avenida; Mountain View, CA 94043.