Queuing Models for Peer-to-peer Systems

Taoyu Li$^*$ $^\dagger$   Minghua Chen$^\dagger$   Dah-Ming Chiu$^\dagger$   Maoke Chen$^*$

$^*$ Tsinghua University, Beijing, China. {taoyu,cmk}@ns.6test.edu.cn
$^\dagger$ The Chinese University of Hong Kong, Shatin, Hong Kong. {tyli,minghua,dmchiu}@ie.cuhk.edu.hk

Abstract:

Recent development of peer-to-peer (P2P) services (e.g. streaming, file sharing, and storage) systems introduces a new type of queue systems not studied before. In these new systems, both job and server arrive and depart randomly. The server dynamics may or may not correlate to the job dynamics. Motivated by these observations, we develop queuing models for P2P service systems and a taxonomy for different variations of these queueing models. For several basic classes of these systems, we show that they are stable, i.e. all arriving job will be served and cleared in finite time, if the average workload does not exceed the average system service capacity. Numerical experiments verify our results, and indicate that higher server dynamics lead to less time a job spends in the system on average.

1 Introduction

Classical queueing theory models systems where jobs arrive randomly at static service stations of given service capacities, and provides analysis of the system's properties, such as waiting time and stability. Queueing theory has wide application in many scenarios of operations research. In particular, its application in studying computer networks and operating systems led to a generalization of queueing theory to model a network of queues and many different service policies [1,2].

Recently, the modeling of peer-to-peer (P2P) systems is pointing to a new kind of queueing system not studied before. In this new model, jobs still arrive randomly, but the service stations also arrive randomly, possibly correlated to the arrival of jobs. Like classical queueing theory, this new kind of model can also help answer some fundamental questions in the design of (P2P) systems. For example, what are the necessary or sufficient conditions to guarantee the stability of a P2P system? And what would be the performance for a given workload and service parameters?

One of the first dynamic P2P models was introduced by Qiu and Srikant [3] to model BitTorrent, a P2P file sharing system. The model is simple, but very inspiring. Although they did not mention queueing theory, they implicitly modeled randomly arriving service stations (which are peers themselves) providing an effective service (file sharing) rate. Subsequently, Fan, Chiu and Lui [4] modeled and studied the tradeoff between different service rate allocations in a dynamic P2P system similar to the Qiu-Srikant model. Clevenot, Nain and Ross [5] generalized the Qiu-Srikant model fluid model to describe more realistic cases. The authors in [6] and [7] also used randomly arriving peers with certain service rate to model P2P streaming systems. There are many other examples of dynamic P2P system models, yet there has not been a unifying analysis in terms of an generalized queueing theory.

In this paper, we first develop a taxonomy and a family of notations similar to that in [1] for different variations of queueing models with server dynamics (Section II). For several basic classes of these systems, we derive the stability conditions and compare them to those results in the classical queueing theory (Section III). Next, to demonstrate the application of a P2P queueing model to real systems, we study a P2P storage system known as Wuala [8] (Section IV). We present some numerical simulation results in Section V, and conclude the work in Section VI.

2 Queuing Model for Peer-to-Peer Systems

The key notations we use in this paper are listed in Table I. Throughout this paper, we assume servers are homogeneous and each has a unit service capacity. The case of heterogeneous servers can be handled by modeling multiple classes of homogeneous servers in the system, each class having different service capacity.

Table I: Key Notation

Notation	Definition
A	job arrival process.
B	job service time distribution.
s	number of servers (used in traditional queuing model).
C	server arrival process.
E	server life time distribution.
POLICY	the service policy assumed.
$1/\lambda_c$	average interarrival time between two job arrivals.
$1/\mu_c$	average job service time.
$\rho_c=\lambda_c /\mu_c$	job load demand of the system.
$1/\lambda_s$	average interarrival time between two server arrivals.
$1/\mu_s$	average server life time.
$\rho_s=\lambda_s /\mu_s$	service capacity of the system.
$n_c(t)$	the number of jobs in the system at time $t$ .
$n_s(t)$	the number of servers in the system at time $t$ .

In classical queuing theory, Kendall's notation [1], i.e., A$/$B$/$s$/$POLICY , is widely used to represent queuing model for static service systems where servers are static.

To represent new queuing models for P2P service systems in which both job and server dynamically arrive and depart, we use the following notation

$$/ /( / )/ .$$ (1)

This notation extends Kendall's notation, by using two additional terms (C and E) to represent the server dynamics in P2P queuing models.

To represent systems with different job and server dynamics, some notations we use for arrival processes (A or C) and distributions (B or E) are 1) $M$ for a Memoryless process (e.g. Poisson process), or an exponential distribution. 2) $D$ for a deterministic process, or a deterministic distribution. 3) $G$ for a process with general independent arrivals, or arbitrary distribution.

Notice that for $C$ or $E$ , it may be the case that server arrival and lifetime distribution has correlation with job arrival and job service time distribution. We use notation `$-$ ' for $C$ or $E$ in the case that server arrival and lifetime distribution is identical to the job arrival and job service time distribution. We use notation $+M/+G$ for $E$ in the case that server lifetime equals to the summation of job service time and an extra period of time following exponential or arbitrary distribution, respectively.

Similarly, notations we use for service policy (POLICY) include 1) $FCFS$ (First-Come-First-Served), which means jobs are served in their arrival order, each by all the servers currently in the system. 2) $PS(k)$ ($k$ -Processor-Sharing), which means all jobs in the system are served, each by no more than $k$ servers simultaneously. In real systems, this constraint is often due to downlink capacity limitation of end users. Furthermore, we assume the job-server allocation is efficient so that the number of busy servers (also the total service capacity, since each server has a unit service capacity) at time $t$ is exactly the maximum allowed value $\min(kn_c(t), n_s(t))$ .

We discuss several classes of P2P service systems as follows.

1 $M/M/(M/M)/FCFS$ Systems

This type of systems has independent Poisson job and server arrivals, and independent exponentially-distributed job service time and server life time. The service policy allows only the first job in the queue to get served, by all servers simultaneously.

2 $M/M/(M/M)/PS(k)$ Systems

This type of systems is the same as the $M/M/(M/M)/FCFS$ systems, except the service policy allows all jobs to get served simultaneously, each by no more than $k$ servers. In practice, some P2P online storage systems may belong to this type of systems. We would model a real P2P online storage system in Section IV.

3 $M/M/(-/-)$ Systems

In this type of systems, job dynamics and server dynamics are identical and full correlated, and we have $n_s(t)=n_c(t)$ for all $t$ . Whenever a job joins (leaves) the system, a server also joins (leaves) the system and vice versa. In practice, this corresponds to P2P systems where a peer provides service to others only during the time period it is being served.

4 $M/M/(-/+G)$ Systems

In this type of systems, job and server arrive in a pair (i.e. they are peers themselves). For each job-server pair, the server stays for additional random amount of time after the job leaves the system. In practice, this corresponds to P2P file downloading systems where peers may remain in the system for a while to serve others after they finish their own downloads. Note that Qiu-Srikant model[3] can be modeled as an M/M/(-/+M) model in a similar way.

3 Stability of Peer-to-peer Service Systems

To facilitate the discussions, we first give the definition of stability for the P2P queuing system.

Definition 1 (Stability)   A P2P service system is stable if its corresponding job-server process $\left\{ n_{c}(t),n_{s}(t)\right\} _{t}$ is positive recurrent, so that a stationary distribution exists.

Note that if the Markov process $\left\{ n_{c}(t),n_{s}(t)\right\} _{t}$ is stable, then not only it has a stationary distribution, but also the states $(n_c=0, n_s=j), (0\leq j)$ , will be visited within finite amount of time. Practically, this means that all arriving jobs will be served and cleared by the P2P service system in finite time.

1 Stability of M/M/(M/M)/FCFS Systems

The job-server process $\{n_c(t), n_s(t)\}_t$ of this type of systems is a two-dimension birth-death process with infinite states. Its transition rate is given in Table II. Since at any time $t$ one job is served by $n_s(t)$ servers, the job departure rate is $n_s(t)\mu_c$ , as shown in the third row in Table II. The server dynamics, on the other hand, does not depend on the number of jobs in the system, and can be studied by an $M/M/\infty$ queue.

Table II: Transition rate of the job-server Markov process in $M/M/(M/M)/FCFS$ systems.

From	To	Rate
$(n_c,n_s)$	$(n_c+1,n_s)$	$\lambda_c$	for $n_c\geq 0$
$(n_c,n_s)$	$(n_c-1,n_s)$	$n_s\mu_c$	for $n_c\geq 1$
$(n_c,n_s)$	$(n_c,n_s+1)$	$\lambda _s$	for $n_s \geq 0$
$(n_c,n_s)$	$(n_c,n_s-1)$	$n_s\mu_s$	for $n_s \geq 1$

A routine way to derive the stability condition is to solve the balance equations. However, for the above process, applying this approach involves solving infinite number of balance equations, each having four unknown variables. Observing that the approach is very challenging, we thus re-interpret the job-server process as a quasi-birth-death (QBD) one and proceed with a matrix-analytical method.

Definition 2 (QBD process[9])   A QBD process is a continuous time Markov process satisfies that:

1. It has a two-dimensional state space $\bigcup_{n\geq 0}\ell(n)$ , where $\ell(n)$ is called level, and is given by

   $$\ell(n) = \left\{ \begin{array}{ll} \{(0,1),(0,2),\ldots,(0,m')\}... ...n=0$;} \ \{(n,1),(n,2),\ldots,(n,m)\}, & \hbox{$n\geq 1$.} \end{array} \right.$$ (2)

   
   
   where $m$ and $m'$ are two positive constants and can be infinity.
2. A transition from $(n,i)$ to $(n',j)$ is not possible if $\vert n'-n\vert\geq 2$ .

Further, the QBD is called homogeneous if it also satisfies that:

3)

For $n \geq 1$ , the instantaneous transition rate between two states in the same level $\ell(n)$ or between two states in the levels $\ell(n)$ and $\ell(n\pm 1)$ is independent of $n$ .

Otherwise the QBD is called non-homogeneous.

It is not difficult to verify that a $M/M/(M/M)/FCFS$ system is a homogeneous QBD process, and its transition matrix, denoted by $Q_A$ , is given by:

$$Q_A=\left[ \begin{array}{ccccc} V & P_0 & & & \ P_2 & P_1 & P_0 ... ...1 & P_0 & \ & & P_2 & \ddots & \ddots \ & & & \ddots & \ \end{array} \right]$$ (3)

where $P_0$ ,$P_1$ , and $P_2$ are square matrices given by $P_0=$diag$(\lambda_c)$ , $P_2=$diag$(0,\mu_c,2\mu_c,\cdots)$ ,

$$P_1 = (-\lambda_c,-\lambda_c-\mu_c,-\lambda_c-2\mu_c,\cdots )+$$

$$\left[ \begin{array}{ccccc} -\lambda_s & \lambda_s & & & \\ \... ...& & & m\cdot\mu_s & -\lambda_c-m\cdot\mu_c-m\cdot\mu_s\\ \end{array} \right],$$ (4)

and

$$V = (-\lambda_c)$$

$$+\left[ \begin{array}{ccccc} -\lambda_s & \lambda_s & & & \\ ... ...& & & m\cdot\mu_s & -\lambda_c-m\cdot\mu_c-m\cdot\mu_s\\ \end{array} \right].$$ (5)

The stability condition of a homogeneous QBD process is given in [9] as follows.

Lemma 3 (Stability condition for homogeneous QBD[9])   If the homogeneous QBD process is irreducible, and if Markov process corresponding to transition matrix $P=P_0+P_1+P_2$ is irreducible and positive recurrent, then the QBD process is positive recurrent if and only if

$$\boldsymbol{\pi}P_0{\mathbf 1} <\boldsymbol{\pi}P_2{\mathbf 1},$$ (6)

where ${\mathbf 1}$ is a value-one vector and $\boldsymbol{\pi}$ is a stationary probability vector satisfying $\boldsymbol{\pi}P=\boldsymbol{\pi}$ and $\boldsymbol{\pi} \cdot {\mathbf 1}=1$ .

Using Lemma 3, we derive the stability condition for $M/M/(M/M)/FCFS$ systems and summarize it in the following theorem.

Theorem 4 (Stability for $M/M/(M/M)/FCFS$ systems)   A $M/M/(M/M)/FCFS$ queuing system is stable if and only if

$$\rho_c<\rho_s.$$ (7)

Proof. By interpreting the $M/M/(M/M)/FCFS$ system as a QBD process, we can get matrix $P$ as

$$P = \left[\begin{array}{ccccc} -\lambda_{s} & \lambda_{s}\\ \mu_... ...2\mu_{s} & \lambda_{s}\\ & & \ddots & \ddots & \ddots\\ \end{array}\right].$$

It is not difficult to verify $P$ is the transition matrix of an $M/M/\infty$ queuing process, which is irreducible and positive recurrent. Furthermore, by solving balance equations, the corresponding stationary distribution $\boldsymbol{\pi}$ is given by

$$\pi_i = \left\{ \begin{array}{ll} e^{-\rho_s}, & \hbox{if $i=0$;} \\ e^{-\rho_s}\rho_s^i/i!, & \hbox{if $i\geq 1$.} \end{array} \right.$$

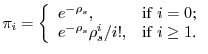
The average queue length in the stationary state is $\sum_{i=0}^{\infty}\pi_i\cdot i = \rho_s$ .

Since $P_0=$   diag$(\lambda_c)$ , we have $\boldsymbol{\pi}P_0 \mathbf{1} = \lambda_c$ . With $P_2=$diag$(0,\mu_c,2\mu_c,\cdots)$ , we can derive $\boldsymbol{\pi}P_2 \mathbf{1} = \mu_c\sum_{i=0}^{\infty}\pi_i\cdot i = \mu_c \rho_s$ .

Combining above observations and applying Lemma 3, we conclude that $\rho_c <\rho_s$ is the stability condition for $M/M/(M/M)/FCFS$ systems. $\qedsymbol$

Remarks: Recall the server dynamics of this type of systems can be modeled by a $M/M/\infty$ queue. In stationary state, the average service capacity, i.e. the average number of servers, is $\rho _s$ . Therefore, Theorem 4 states that a $M/M/(M/M)/FCFS$ P2P service system is stable if and only if the average workload $\rho_c$ does not exceed the average service capacity $\rho _s$ . This result is consistent with stability conditions of classical static service systems, e.g. $\rho_c<1$ for $M/M/1$ systems and $\rho_c<s$ for $M/M/s$ systems.

2 Stability of $M/M/(M/M)/PS(k)$ Systems

As compared to $M/M/(M/M)/FCFS$ systems, in $M/M/(M/M)/PS(k)$ systems, a job can only get served by at most $k$ servers. Its job-server process $\{n_c(t), n_s(t)\}_t$ can still be modeled as an irreducible and aperiodic two-dimensional birth-death process with infinity number of states, but with a different set of transition rate given in Table III.

Table III: Transition rate of the job-server Markov process in $M/M/(M/M)/PS(k)$ systems.

From	To	Rate
$(n_c,n_s)$	$(n_c+1,n_s)$	$\lambda_c$	for $n_c\geq 0$
$(n_c,n_s)$	$(n_c-1,n_s)$	$\min(k n_c, n_s)\cdot\mu_c$	for $n_c\geq 1$
$(n_c,n_s)$	$(n_c,n_s+1)$	$\lambda _s$	for $n_s \geq 0$
$(n_c,n_s)$	$(n_c,n_s-1)$	$n_s\mu_s$	for $n_s \geq 1$

It is not difficult to verify that an $M/M/(M/M)/PS(k)$ system is a non-homogeneous QBD, and its transition matrix $Q_B$ is given by

$$Q_B=\left[ \begin{array}{ccccc} V & P_0 & & & \ P_2^{(1)} & P_1^... ...0 & \ & & P_2^{(3)} & \ddots & \ddots \ & & & \ddots & \ \end{array} \right]$$ (8)

where $P_0=$diag$(\lambda_c)$ , $P_2^{(i)}=$diag$(\min(k i, j)\cdot\mu_c,0 \leq j)$ , for $i\geq 1$ describing the job departure rate when there is $i$ job within the system. $V$ is as given by (5), and $P_1^{(i)}$ satisfies $(P_0 + P_1^{(i)}+P_2^{(i)})\cdot\mathbf{1} = 0$ and is given by

$$P_1^{(i)} = (-\lambda_c-\min(k i,j)\cdot\mu_c,0 \leq j))+$$

$$\left[ \begin{array}{ccccc} -\lambda_s & \lambda_s & & & \\ \... ...& & & m\cdot\mu_s & -\lambda_c-m\cdot\mu_c-m\cdot\mu_s\\ \end{array} \right],$$ (9)

By building a series of homogeneous QBD and applying Lemma 3, we have the stability condition for $M/M/(M/M)/PS(k)$ systems as follows.

Theorem 5 (Stability for $M/M/(M/M)/PS(k)$ systems)   A $M/M/(M/M)/PS(k)$ queuing system is stable if and only if

$$\rho_c<\rho_s.$$ (10)

Proof. We first prove the necessity of the condition. Suppose $\rho_c\geq\rho_s$ , then applying Lemma 3, we can verify the homogeneous QBD with transition matrix $Q_A$ given by (3) is unstable: Note the departure rate in $Q_B$ given in (8) is less than or equals to that of $Q_A$ given in (3) for every state. Therefore, if the QBD process associated with $Q_A$ is unstable, so is the job-server process associated with $Q_B$ . This completes the proof of necessity.

We now show the sufficiency of the condition. We first construct two series of QBD processes, whose transition matrices are given as: for all $i\geq 0$ ,

$$Q^{(i)}=\left[ \begin{array}{cccccccc} V & P_0 & & & \\ P_2^{... ...^{(i)} & P_0 \\ & & & & & \ddots& \ddots & \ddots \\ \end{array} \right],$$

and

$$Q'^{(i)}=\left[ \begin{array}{ccccc} V & P_0 & & & \\ P_2^{(i... ...& & P_2^{(i)} & \ddots & \ddots \\ & & & \ddots & \\ \end{array} \right],$$

respectively.

For any $i$ , the two QBD processes associated with $Q^{(i)}$ and $Q'^{(i)}$ respectively will have the same stability since their transition rates are only different in the first finite levels. Since the QBD processes associated with $Q'^{(i)}, (i\geq 0),$ are homogeneous, their stability conditions are simply $\rho_c<F_i$ according to Lemma 3, where

$$F_i=\sum_{j=0}^{ki}\pi_j\cdot j+ \sum_{j=ki+1}^{\infty}\pi_j\cdot ki$$

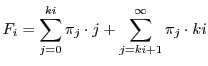
is a constant depending on the stationary distribution $\boldsymbol{\pi}$ .

Notice that sequence $\{F_i\}_i$ is increasing and has a limit of $\rho_s=\sum_{j=0}^{\infty}\pi_j\cdot j$ . Thus if we have $\rho_c <\rho_s$ , there must exists a $t$ that $\rho_c<F_t$ . Therefore the QBD process associated with $Q'^{(t)}$ is stable, and so is the QBD process associated with $Q^{(t)}$ .

Now we compare $Q^{(t)}$ and $Q_B$ given in (8). Observing the departure rate in $Q$ is larger than or equals to that in $Q^{(t)}$ for every state, we conclude the job-server process associated with $Q_B$ is stable. This completes the proof of sufficiency. $\qedsymbol$

Remarks: Theorem 5 states that for $M/M/(M/M)$ systems, using $PS(k)$ or $FCFS$ policy leads to the same stability condition. Intuitively, this is because these two policies both allow full utilization of the system service capacity when the number of jobs is large (i.e. when the system is crowded), and differ only when the number of jobs is small. Since the stability is determined by the service capacity utilization when the system is crowded, it is not surprising that these two policies leads to the same stability condition.

3 Stability of $M/M(-/-)$ and $M/M/(-/+G)$ Systems

In $M/M(-/-)$ systems, every job arrival (departure) also brings in (takes away) a server. So it is sufficient to describe only the job dynamics to represent the entire system.

Table IV: Transition rate of the job process in $M/M/(-/-)$ systems.

From	To	Rate
$n_c$	$n_c+1$	$\lambda_c$	for $n_c\geq 0$
$n_c$	$n_c-1$	$n_c\mu_c$	for $n_c\geq 1$

The job process $\{n_c(t)\}_t$ is a one-dimension birth-death process with transition rate given in Table IV, which is exactly same with the job process associated with a classical $M/M/\infty$ system. Since $M/M/\infty$ systems are always stable, so are $M/M/(-/-)$ systems.

For $M/M/(-/+G)$ systems, since peers may stay in the system for a while to serve others after its job has been finished, the total number of servers would always be larger than the total number of jobs.

In practical P2P file downloading systems, this result indicates that as long as every joining peer brings in some service capability with it, the system is always stable.

4 Modeling Peer-to-peer Storage Systems

Let us consider Wuala [8] as an example of a P2P storage system. Wuala allows users to store and share files online. Instead of relying purely on centralized (and deployed) servers, Wuala relies on peers to contribute their disk space to help provide the service. These peers may be users of the system or may be pure storage sellers who only contribute to (without using) the service. For the purpose of this modeling exercise, we assume the requests for files are independent from the peers providing the storage, who are referred to as storage peers.

To store a file into the system, Wuala encrypts it, erasure codes it into fragments, and stored the coded fragments at different storage peers. To retrieve a file from the system, Wuala first locates the fragments using a distributed hash table (DHT), then downloads fragments from multiple storage peers simultaneously. After sufficient fragments are downloaded, the file can be decoded and restored. This approach not only saves the deployment (and maintenance) costs of centralized servers, but can also provide better download rate for users, since it utilizes the upload bandwidth of multiple peers instead of sharing the upload bandwidth of a centralized server.

In studying the performance of systems based on centralized servers, we may apply classical queueing theory to determine the number of servers needed to support a certain workload. For a P2P storage system such as Wuala, there is a corresponding question of what type of online behavior of the storage peers is necessary to ensure the download request rates can be satisfied, which is exactly the kind of questions that can be addressed by the P2P queueing model proposed in Section II.

Table V: Key Parameters for Modeling P2P Storage Systems

Notation	Definition
$t_{\text{ON}}$	average online time of a storage peer.
$t_{\text{OFF}}$	average offline time of a storage peer.
$r_u$	upload bandwidth of each storage peer.
$r_d$	download bandwidth of each downloading peer.
$L$	average file length in the system.
$\gamma$	file download request arrival rate.

In modeling Wuala as a queueing system, we assume the availability of the file is not an issue, as it can be taken care of by sufficient redundancy. The key performance problem would be whether there is sufficient bandwidth to support the download requests.

The key parameters used in modeling a P2P storage system are listed in Table V.

If we assume server online/offline time and file length to follow exponential distributions, and the arrival of file download requests to follow a Poisson process, then such a P2P storage system can be modeled by an $M/M/(M/M)/PS(k)$ model, where

$$\lambda_s=1/t_{\text{OFF}} , \mu_s=1/t_{\text{ON}},$$ (11)

$$\lambda_c=\gamma , \mu_c = r_u/L,$$ (12)

$$k=r_d/r_u .$$ (13)

Applying Theorem 5, we know that stability does not depend on $k$ , and the stability condition $\rho_c <\rho_s$ reduces to

$$\frac{t_{\text{ON}}}{t_{\text{OFF}}}r_u>\gamma L,$$ (14)

The left hand side represents the total supply (of uplink bandwidth) whereas the right hand side represents the total demand of downloading requests. The insight from this result is the relationship between storage peers' online/offline time ratio and the system's capacity. The online behavior of storage peers can be adjusted by the policy for rewarding them, thus the system capacity could be controlled.

In the next section we show some simulation results which may give more insights on building P2P storage systems.

5 Simulation Result

In this section, we run numerical experiments to verify the stability conditions we derive in Section III for different types of systems, and explore other system performance metrics. The value of time and parameter $\lambda_c,\lambda_s,\mu_c$ and $\mu_s$ are normalized so we omit the unit of them when showing the results.

1 Verification of stability condition

In this experiment, we verify the stability conditions for $M/M/(M/M)/FCFS$ and $M/M/(M/M)/PS(k)$ systems given in Theorem 4 and Theorem 5. We fix $\rho _s$ by fixing $\lambda _s$ and $\mu_s$ , vary $\rho_c$ by fixing $\mu_c$ and changing $\lambda_c$ , and see how the time a job spends in the system change. In particular, we simulate 20000 arriving jobs and record the time each of them spends in the system. The initial value of $n_c$ and $n_s$ is 0 and $\rho _s$ respectively.

We also evaluate the stability of a system with general service time distribution, i.e. an $M/G/(M/M)/FCFS$ system. We use a service time distribution which is converted from a file size distribution measured from practical P2P file sharing system[10].

We fix $\lambda_s=0.005$ , $\mu_s=0.0005$ and $\mu_c=0.006$ , adjust $\lambda_c$ so that $\rho_c/\rho_s=0.85$ , $0.95$ , $1.05$ , $1.15$ , and $1.25$ respectively, and the result is shown in Fig.1. From the result, it can be inferred that when $\rho_c/\rho_s<1$ , the total time a job spends in the system is bounded. However, if $\rho_c/\rho_s>1$ , the time a job spends in the system has a trend of increasing unboundedly by time. This verifies that the stability condition $\rho_c/\rho_s>1$ holds for $M/M/(M/M)/FCFS$ and $M/M/(M/M)/PS(k)$ systems, as well as for $M/G/(M/M)/FCFS$ systems.

Figure 1: The time job spends in the systems with different $\rho _c/\rho _s$ .

2 Impact of Server Dynamics

It would be interesting to compare the performance of P2P service systems with same average service capacity (i.e. same $\rho _s$ ) but different server dynamics (i.e. different $\lambda _s$ and $\mu_s$ ).

In this experiment, we fix $\rho_s=10$ , and adjust the value of $\lambda _s$ and $\mu_s$ proportionally to form several systems with different server dynamics. All systems have the same $\lambda_c$ and $\mu_c$ ; hence, they have the same average workload.

We simulate the systems with $10^6$ job arrivals, and record the cumulative percentage of time a job spends in the system. The initial value of $n_c$ and $n_s$ is 0 and $\rho _s$ , respectively. The results of $\lambda _s$ equal to $0.1$ , $0.01$ , $0.001$ and $0.0001$ are shown in Fig.2. The average and standard deviation of the time a job spends in different systems are summarized in Table VI.

Figure 2: Cumulative percentages for time a job spends in systems with constant $\rho _s$ but different $\lambda _s$ .

Table VI: Average and standard deviation of total time spent

$\lambda _s$	0.1	0.01	0.001	0.0001
average	104	331	2030	29030
standard deviation	114	453	3630	38001

These results indicate that with fixed average service capacity, a job would spend less time in systems with high server dynamics than in systems with low server dynamics, averagely. To explain this, we first define the system is in ``surplus stage'' if the service capacity is no less than workload $\rho_c$ , and is in ``deficiency stage'' otherwise. Compared to high server dynamics, low server dynamics lead to longer stay in a stage each time the system enters it but less frequent switches between stages.

In a system with low server dynamics, the queue builds up when the system is in ``deficiency stage'' before it gets clear after the system switches to ``surplus stage''. Thus the queued-up jobs spend longer time in the system. On the contrary, in a system with high server dynamics, the switching between stages is more frequent. Consequently, less jobs get queued up in the ``deficiency stage'' before the system switches stage, resulting in less time in the system in average.

Consider the P2P storage system we modeled in Section IV. Remembering that we have $\lambda_s=1/t_{\text{ON}}$ and $\mu_s=1/t_{\text{OFF}}$ , the simulation result indicates that, a system in which servers get online/offline more frequently would have a better performance, by shorter average file downloading time.

6 Discussion and future work

In this paper, we extend classical queuing models to represent P2P service systems where both job and server arrive and depart randomly. We develop a taxonomy for different variations of these queueing models, and study the stability conditions for several classes of the models.

For $M/M/(-/-)$ models where job and server dynamics are identical, we show that the system is always stable. This confirms the observations in practical P2P streaming systems.

For $M/M/(M/M)$ models where job and server arrive independently, we show that the system is stable if its average service capacity is larger than the average workload. This stability condition is similar to that of static service systems. The limitation of that a single job can get service from only limited number of servers has no effect on this stability condition.

As shown in our numerical experiments, the service dynamics in the P2P service systems helps to reduce the time a job spends in the system. We plan to further characterize this effect in future work.

Since this paper is an exordial study of applying queueing model to P2P systems, we believe that there is lots of possible further work in the area. Future work directions includes study of $M/G/(M/M)$ systems with general service time distribution, system with different classes of service policy, system with different type of job/server correlation, and system with heterogeneous servers. It would also be interesting to derive more analytical results than just stability. An example would be average queue length. Applying Little's Law[1], the study on average queue length would obtain the result on average service time, which may give us more insight on the performance of P2P systems.

Bibliography

1

L. Kleinrock, Queueing systems. Vol. 1, Theory. Wiley NewYork, 1975.

2

F. Baskett, K. Chandy, R. Muntz, and F. Palacios, ``Open, closed, and mixed networks of queues with different classes of customers,'' J. Assoc. Comput. Mach, vol. 22, no. 2, pp. 248每260.

3

D. Qiu and R. Srikant, ``Modeling and performance analysis of BitTorrent-like peer-to-peer networks,'' in Proceedings of SIGCOMM 2004, New York, NY, USA, 2004, pp. 367每378.

4

B. Fan, D. Chiu, and J. Lui, ``The Delicate Tradeoffs in BitTorrentlike File Sharing Protocol Design,'' in Proceedings of ICNP 2006, Washington, DC, USA, 2006, pp. 239每248.

5

F. Clevenot, P. Nain, and K. W. Ross, ``Multiclass P2P Networks: Static Resource Allocation for Bandwidth for Service Differentiation and Bandwidth Diversity,'' Performance Evaluation, vol. 62, pp. 32每49, 2005.

6

R. Kumar, Y. Liu, and K. W. Ross, ``Stochastic Fluid Theory for P2P Streaming Systems,'' in Proceedings of IEEE Infocom, 2007.

7

D. Wu, Y. Liu, and K. W. Ross, ``Queueing Network Models for Multi- Channel P2P Live Streaming Systems,'' in Proceedings of IEEE Infocom, 2009.

8

``Wuala, the social online storage,'' http://www.wuala.com.

9

G. Latouche and V. Ramaswami, Introduction to Matrix Analytic Methods in Stochastic Modeling. SIAM, 1999.

10

S. Saroiu, K. Gummadi, R. Dunn, S. Gribble, and H. Levy, ``An analysis of Internet content delivery systems,'' ACM SIGOPS Operating Systems Review, vol. 36, pp. 315每327, 2002.

About this document ...

Queuing Models for Peer-to-peer Systems

This document was generated using the LaTeX2HTML translator Version 2008 (1.71)

Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999, Ross Moore, Mathematics Department, Macquarie University, Sydney.

The command line arguments were:
latex2html -split 0 -show_section_numbers -local_icons -no_navigation p2pqueuing.tex

The translation was initiated by 3P1C on 2009-03-25

Footnotes

... {tyli,minghua,dmchiu}@ie.cuhk.edu.hk

This work was supported by a Competitive Earmarked Research Grant (Project Number 2150572) established under the University Grant Committee of the Hong Kong Special Administrative Region, China, the Direct Grant (Project Number 2050397) of The Chinese University of Hong Kong, and a gift grant from Cisco.