On the Accuracy of Embeddings for Internet Coordinate Systems
On the Accuracy of Embeddings for Internet Coordinate Systems
Eng Keong Lua, Timothy Griffin, Marcelo Pias, Han Zheng, Jon Crowcroft
University of Cambridge, Computer Laboratory
Email: {eng.keong-lua, timothy.griffin, marcelo.pias, han.zheng,
jon.crowcroft}@cl.cam.ac.uk
Abstract
Internet coordinate systems embed Round-Trip-Times (RTTs) between
Internet nodes into some geometric space so that unmeasured RTTs can
be estimated using distance computation in that space. If accurate,
such techniques would allow us to predict Internet RTTs without
extensive measurements. The published techniques appear to work very
well when accuracy is measured using metrics such as
absolute
relative error. Our main observation is that absolute relative
error tells us very little about the
quality of an embedding
as experienced by a user. We define several new accuracy metrics
that attempt to quantify various aspects of user-oriented
quality. Evaluation of current Internet coordinate systems
using our new metrics indicates that their quality is not as high as
that suggested by the use of absolute relative error.
1 Introduction and Motivation
An Internet coordinate system starts with a collection of nodes and
measured Round-Trip-Times (RTTs) between some pairs of these nodes.
It then
embeds the nodes into a geometric space by associating
each node with a point in that space. The goals of such an embedding
are twofold. First, the embedding should be
accurate in the
sense that the geometric distance between embedded nodes should, in
some sense, closely approximate their RTTs. Second, the methods
should remain accurate even when the input is a small subset of all
possible RTT measurements. That is, a node's coordinates should
allow even the unmeasured RTTs to be estimated accurately.
Many Internet coordinate systems have been described in the
literature. Accuracy is typically assessed using metrics similar to
absolute relative error, which forms an average over every
pair of nodes of the absolute value of the difference between their
embedded distance and their original distance. Note that an
embedding technique does not require a full mesh of RTT
measurements, but assessing its accuracy surely does. The main
conclusion of this paper is that by itself an accuracy metric such
as absolute relative error tells us very little about the
quality of an embedding as experienced by a user.
Our own experiences and experiments with Internet coordinate systems
have been disappointing in several respects. First, distance
estimation results are often
unpredictable in the sense that
many nodes obtain good estimates while a few obtain extremely bad
results. In a real-world setting it seems that nodes cannot
determine the
quality of their estimates without performing
exactly the full probing that coordinate systems are intended to
eliminate. Second, we observed that the
quality of an
embedding often varied considerably with small changes to the
topology of the underlying network - something which would be
beyond the control of most users of a coordinate system. Third, we
observed that the
quality of embeddings often varies
considerably as the number of participating nodes changed, even when
the underlying topology remains fixed. In short, these observations
suggest that it is very hard to predict when a coordinate system
will work well at any given node.
Highly aggregated accuracy metrics, such as absolute relative error,
seem to give little indication of these types of
quality
problems. This experience led us to question the usefulness of
metrics such as absolute relative error, at least in isolation from
other means of assessing
quality. This paper presents several
new accuracy metrics that attempt to capture more
application-centric notions of
quality. The first is called
relative rank loss at node A (
rrl at node A), and is
intended to be useful for applications used by nodes that need to
know only their
relative distance of other nodes. That is,
node A needs to answer question such as "Which node is closer to me,
B or C?"
- which we will call A's proximity query for nodes B and C.
The metric
rrl at node A is defined as a type of
swap
distance and takes values between 0 (all proximity queries at A
are correctly estimated) and 1 (none of the proximity queries at A
are correctly estimated). For example, an
rrl at node A of 0.5
tells us that node A has a 50 percent chance of getting the
correct answer to a proximity query. We then define aggregate
versions of
rrl such as the average
rrl over all nodes, and the
maximal
rrl value over all nodes. The other new metric we define
is
closest neighbors loss at node A (
cnl at node A). This
metric is intended to be useful to nodes using applications that are
interested only in determining which nodes are
closest. The
value of
cnl at node A is 0 if the nodes closest to A remain
closest in the embedding, and 1 otherwise. Again, we then define
aggregate versions of
cnl such as the average global
cnl over
all nodes. For example, an average global
cnl value of 0.5 would
tell us that 50 percent of the nodes have a different set of
closest neighbors in the original space than they have in the
embedded space.
When we compare the accuracy of embedding techniques using our new
metrics the results can be very poor, even in simple tree and
hub-and-spoke networks. Our new metrics capture and quantify, at
least partially, some of our disappointment with the
quality
of the embedding techniques. However, it remains that no single
accuracy metric can capture the
quality of an embedding
technique. It seems better to develop a collection of accuracy
metrics that are each designed to quantify a specific aspect of
user-oriented
quality. By no means do we want to suggest that
our new metrics represent a complete or definitive set - they are
simply an initial attempt at exploring this space.
This paper is complementary to the work presented
in [
23], which shows that RTT violations of the
triangle inequality are a common, persistent, and widespread
consequence of Internet routing policies. We strongly suspect that
such violations will degrade
every embedding technique with
respect to
any accuracy metric, at least when the embedding
maps into a geometric space where the triangle inequality does hold.
The results of the current paper and those of [
23] are
not very encouraging, to say the least. On the positive side, we
feel that research is always improved with a better understanding of
the fundamentals. In this case, we believe an improved understanding
suggests a new and potentially interesting line of research, which
we will call Embeddable Overlay Networks (EONs). An EON is an
overlay where routing nodes have been
selected to avoid
violations of the triangle inequality (for overlay forwarding)
and the overlay topology has been
selected to embed
with high accuracy with respect to multiple useful accuracy metrics.
To do this well will require new insights and new algorithms.
Paper Outline. Section
2 presents a short
survey of the embedding techniques described in the literature.
Section
3 presents the basic terminology of network
embeddings and our new accuracy metrics. In
Section
4 we present an embedding experiment using
our data collected on PlanetLab. We use a
full Lipschitz
embedding technique which makes use of all nodes as the landmarks
(reference nodes) without any dimensionality reduction, and evaluate
the results with our new metrics. In Section
5, we
conducted experiments using our PlanetLab data sets and new accuracy
metrics, but on other techniques that are based on numerical
minimization - Vivaldi [
8] and Big Bang Simulation
(BBS) [
18,
19,
20]. In
Section
6, we revisit these previously published
experiments and use their data sets to re-evaluate their accuracy
with our new accuracy metrics. Section
7 concludes with
some topics for future work.
2 A Brief Survey of Embedding Techniques
Among the recently described Internet coordinate systems are the
Global Network Positioning (GNP) [
16],
Lighthouses [
17], Virtual Landmarks [
21], Internet
Coordinate System (ICS) [
11], Matrix Factorization
[
15], Practical Internet Coordinates
(PIC) [
7], Vivaldi [
8], Big Bang Simulation
(BBS) in Euclidean space [
18], and BBS in Hyperbolic space
[
19,
20]. Basically, Internet coordinate
systems comprise of
two categories of network embeddings of
finite metric space into low dimensional Euclidean or non-Euclidean
(e.g. Hyperbolic) space, namely,
numerical minimization of
some defined objective distance error functions for
nodes-to-landmarks distances; and initial Lipschitz embedding with
some form of dimensionality reduction using
distance matrix
factorization (which is a form of mathematical optimization and
minimization techniques of error functions).
ICS and Virtual Landmarks systems are based on Lipschitz embedding
of a finite metric space into Euclidean space and use the Principal
Component Analysis (PCA) to reduce dimensionality. Typically, the
accuracy of such embeddings is studied
only after some type
of dimensionality reduction technique has been applied. Matrix
factorization based on Singular Value Decomposition (SVD) is of the
form
D=
USVT, where
D is the distance matrix,
U and
V are
orthogonal matrices and
S is an diagonal matrix with nonnegative
elements arranged in decreasing order which measure the significance
of the contribution from each principal component. This is related
to PCA on the distance matrix row vectors in ICS and Virtual
Landmarks, where the first
d rows of the matrix
U are used as
coordinates for the network nodes. The Matrix Factorization
embedding uses the distance matrix whose rows are not linearly
independent (has rank strictly less than
n where
n is the number
of nodes). It is expressed as the product of two smaller matrices of
A and
B (through SVD or Nonnegative Matrix Factorization (NMF)
algorithms), which contain the outgoing and incoming vectors
respectively for each node. Estimated distances between nodes are
derived from the dot product of these
two vectors.
Lighthouses technique makes use of multiple local bases
L together
with a transition matrix in vector space, to allow flexibility for
any node to determine coordinates relative to any set of landmarks
provided it maintains a transition matrix for global basis
G. It
uses linear matrix factorization such as the
QR decomposition
(Gram-Schmidt orthogonalization).
For techniques involving minimization of some defined objective
distance error functions, many algorithms are proposed to compute
the coordinates of the network nodes. For example, GNP and PIC
systems use the Simplex Downhill to minimize the objective distance
error function: sum of relative errors. The problems of using the
Simplex Downhill method is the slow convergence, sensitive to the
initial coordinates or position of the network nodes, and the
potential of getting stuck in the local minima. This leads to the
eventual assignment of different coordinates for the same node
depending on the minimization process (e.g. selection of the initial
position). So, methods that are clever to converge to the global
minimum are required. Both Vivaldi and BBS (Euclidean and Hyperbolic
spaces) algorithms are based on the numerical minimization of sum of
distance error functions that are related to the problem of
minimizing the potential energy of newtonian mechanics principles.
Vivaldi system is constantly adjusting the coordinates of the nodes
because each node contacts a random set of nodes in a decentralized
manner. Each node cannot find a global minimum fit, and it cannot
guarantee that a given error function minimization does not increase
the global error, although Vivaldi ensures nodes always decrease the
local error. Hence, the error term in each small time-step is
monitored to derive the optimal sets of coordinates selected.
The Big-Bang Simulation (BBS) (Euclidean and Hyperbolic) systems
model the network nodes as a set of particles, having a position in
Euclidean space. The nodes are traveling under the effect of the
potential force field which reduces the potential energy of the
nodes. This is related to the total embedding distance error of all
node pairs in Euclidean space. Each node pair is effected by the
field force induced between them depending on their node pair's
embedding distance error, i.e. the embedding distance error of the
distance between the node pair. The node is also affected by
simulated friction force. BBS systems have the advantage over
conventional gradient minimization schemes, such as steepest descent
and Simplex Downhill, due to the kinetic energy accumulated by the
moving nodes which enable them to escape the local minima.
Hyperbolic geometric space is the target embedding space for the BBS
(Hyperbolic) system. A distance decreases as it moves away from the
origin. Similar to Euclidean line distance, the Hyperbolic distance
line between two nodes is defined as the parametric curve,
connecting between the nodes, over which the integral of the arc
length is minimized. Unlike Euclidean line distance, a Hyperbolic
line distance bents towards the origin point. The extent to which
the bend depends on the curvature of the Hyperbolic space. The
bending becomes larger when space curvature increases, and thus,
Hyperbolic distance between two nodes increases. There are three
embedding methods in BBS systems:
All Pairs (AP) embedding
- Embedding is done for
full mesh of the
n nodes of the
network topology comprising of [(
n(
n-1))/2] distance pairs
(
n is the number of network nodes).
Two Phases (TP)
embedding - Embedding is done using landmarks similar to GNP,
where the landmarks are embedded first and the coordinates of the
other nodes are calculated from the distance to
several
chosen
closest landmarks through minimization of the
symmetric distortion in these node-to-landmark pairs. Specifically,
TP embedding requires
k+1 landmarks' measurements for
k-dimensional coordinate vectors.
Log-Random and Neighbors
(LRN) embedding [
20] - It aims to increase neighbor
distances accuracy. The LRN embedding concurrently embed nodes
through minimization of objective error function of
n nodes and
LRN subset, which comprises of the node pairs whose distance is
below a certain threshold, i.e. the threshold is selected so that
the number of distance pairs that are below the threshold is
O(
n.log
n), and together with a set of randomly sampled
distance pairs that are selected uniformly at random with
probability [(log
n)/(
n)]. The number of randomly sampled
distance pairs is equivalent to
n.log
n. The LRN algorithm
embeds all the
n nodes concurrently. The objective function is the
sum of embedding errors for all
n nodes in the system, and the
embedding error of one node is the error of distance from that node
to the LRN subset of nodes.
3 Embeddings and Their Accuracy
This section rigourously defines several accuracy metrics for
embeddings. We use the Lipschitz embedding as a running example to
illustrate and motivate our metric definitions.
A
metric space is a pair
M = (
X,
d) where
X is a set
equipped with the distance function
d :
X ® R+ - for each
a,
b Î X the
distance between a
and b is given by the function
d(
a,
b). We require that for
all
a,
b,
c Î X,
- (anti-reflexivity)
- d(a, b) = 0 if and only if a=b,
- (symmetry)
- d(a, b) = d(b, a),
- (triangle inequality)
- d(a, b) £ d(a, c) + d(c, b).
Note that we will ignore the fact that in reality, violations of the
triangle inequality exist for Internet RTTs ([
23]).
Suppose that
M1 = (
X1,
d1) and
M2 = (
X2,
d2) are metric spaces.
Every one-to-one function
f from
X1 to
X2
naturally defines a metric space called
the embedding of M1 in M2 under f,
defined as
f(
M1) = (
f(
X1),
d2).
We normally abuse terminology and simply say that
f embeds
X1 into
X2,
leaving the distance functions to be inferred from the context.
If
f embeds
X1 in
X2 and
Z is a subset of
X1,
then
f also defines an embedding of
Z in
X2 in the natural way.
One simple case is where
X1 is a finite set,
X2 is
Rn with the standard notion of Euclidean distance,
d2(
x,
y) =
||x - y|| =
Ö{
å1 £ i £ n(
xi - yi)
2}.
If
L = {
l1,
l2,
¼,
lm}
Í X, then we can map each
a Î X to a point in
Rm as
fL(
a) = (
d(
a,
l1),
d(
a,
l2),
¼,
d(
a,
lm)).
This is called the
Lipschitz embedding of X using landmarks
L. If
L =
X, we refer to
fX =
f as the
full Lipschitz embedding.
Figure 1: A binary tree
of depth 2.
We illustrate the
full Lipschitz embedding with a simple
example. Any weighted undirected graph
G = (
V,
E,
w) naturally
gives rise to a metric space
M(
G) = (
V,
d), where
d(
a,
b) is
the length of a shortest path between nodes
a and
b.
Figure
1 presents one example - a simple binary
tree of depth 2, where each edge represents a distance of 1, and
gives rise to the following distance matrix:
| | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1 | 0 | 1 | 2 | 2 | 1 | 2 | 2 |
| 2 | 1 | 0 | 1 | 1 | 2 | 3 | 3 |
| 3 | 2 | 1 | 0 | 2 | 3 | 4 | 4 |
| 4 | 2 | 1 | 2 | 0 | 3 | 4 | 4 |
| 5 | 1 | 2 | 3 | 3 | 0 | 1 | 1 |
| 6 | 2 | 3 | 4 | 4 | 1 | 0 | 2 |
| 7 | 2 | 3 | 4 | 4 | 1 | 2 | 0
|
Note that this distance matrix itself can be viewed as a
full Lipschitz embedding into a
R7 by reading
each row as the 7-dimensional coordinate of the associated node.
For example, (0, 1, 2, 2, 1, 2, 2)
are the coordinates of node 1.
3.1 Relative Error
We seek embeddings that are
accurate. There are several ways
to capture this formally, and in the context of Internet coordinate
systems the most appropriate notion may depend on the needs of an
application. Some applications require that the distances in the
embedding accurately reflect the original distances. Note that with
the binary tree example above distances are not well preserved -
we can calculate the distance between
f(1) and
f(7) = (2, 3, 4, 4, 1, 2, 0) as approximately 4.47, yet it is only 2
in the original metric space.
If we multiply each coordinate
f(
x) by a scalar value
b,
and redefine the embedding as
f¢(
x) =
bf(
x), we could
improve this notion of accuracy. As in [
21], we choose
b to minimize the
absolute relative error for all pairs
of nodes, given by
åx, y Î X [( |
||f¢(
x)
-f¢(
y)
|| - d(
x,
y) | )/(
d(
x,
y))]. For the example above, this
gives a value for
b of approximately 0.5, which reduces the
distance between the embeddings of nodes 1 and 7 to
approximately 2.3. The
average absolute relative error is
obtained by dividing the absolute relative error with
n(
n-1),
where
n is the total number of nodes. The
maximum local
absolute relative error is the maximal
absolute relative
error over all nodes.
A similar accuracy metric is
stress, defined as
[(
åx ¹ y Î X (
||f¢(
x)
- f¢(
y)
|| - d(
x,
y))
2)/(
åx ¹ y Î X d(
x,
y)
2)].
Note that both stress and relative error quantify the magnitude of the differences between original
distances and embedded distances.
If stress (or relative error) is 0, then we have an embedding that preserves distances exactly (an isometry).
3.2 Distortion
In the theoretical literature on embeddings (for example, [
12,
14,
13,
10])
the most common notion of accuracy is captured by
distortion.
This measure is invariant under scalar multiplication.
That is,
distortion(
f) =
distortion(
af), for all
a ¹ 0 -
and so provides a notion of accuracy that is independent of the absolute values of distances.
Distortion measures the worst-case change in the
relative distances of the embedding.
First, define the ratio
r(
f,
x,
y) = [(
||f(
x)
- f(
y)
||)/(
d(
x,
y))].
The
expansion of f,
expansion(
f), is the maximum value of
r(
f,
x,
y) as
x and
y range over
X (
x ¹ y).
The
contraction of f,
contraction(
f), is the minimum value of
r(
f,
x,
y) as
x and
y range over
X (
x ¹ b).
The
distortion of f is defined as the ratio
distortion(
f) = [(
expansion(
f))/(
contraction(
f))].
Note that the
distortion(
f) is always greater than or equal to 1.
The equality holds only when there exists a constant
a such that
r(
f x,
y) =
a for every
x,
y.
In this case
f¢(
x) =
f(
x)/
a is an isometry.
One way to gain intuition for the meaning of distortion is to imagine that
contraction(
f) = 1
(which could always be achieved with scalar multiplication).
In this case there is no contraction in the embedding, only expansion, and the largest expansion is achieved by some pair
x,
y, where
the distance between
x and
y in the embedding is
expansion(
f) times the original distance
d(
x,
y).
Note that distortion is a global worst-case measure, which may be
relevant to applications (such as mapping) that require a global
picture of the entire embedding. However, most Internet coordinate
applications will be interested only in
local distortion -
the amount of distortion seen from any one node. For a fixed
x, we
define
expansion(
f,
x), to be the maximum value of
r(
f,
x,
y) as
y range over
X (
x ¹ y), and
contraction(
f,
x), to be the minimum value of
r(
f,
x,
y) as
y range over
X (
x ¹ y). Then the local distortion is defined to be
distortion(
f,
x) = [(
expansion(
f,
x))/(
contraction(
f,
x))]. The
maximum local distortion is
the maximal
distortion(
f,
x) over all
x.
3.3 A New Metric: Relative Rank Loss (rrl)
Many applications only need to know the
relative distance of
other nodes. They need to answer question such as Ïs A closer than
B?" What is important for such applications is that the
relative rankings of distances is not lost. For this
notion of accuracy we define
relative rank loss (
rrl) to be
between 0 (for no loss of relative order) and 1 (for a complete
reversal of order). This is a slight generalization of
swap
distance, a well-known edit distance on strings. For example,
between strings
s1 =
abcd and
s2 =
acdb there is a swap
distance of 2. We need to generalize this slightly to account for
the fact that multiple nodes can be equidistant from a given node.
First, define the function
We say that
x and y are swapped w.r.t. z if
R(
d(
z,
x),
d(
z,
y))
¹ R(
||f(
z)
- f(
x)
||,
||f(
z)
- f(
y)
||)
and denote this as
swapped(
z,
x,
y).
That is, if
swapped(
z,
x,
y) holds, then
z's relative distance relationship
to
x and
y is different in the original and embedded spaces.
Define
P(
z), a subset of (
X - {
z})×(
X - {
z}), to be
|
{ (x, y) | x ¹ y and swapped(z, x, y)}. |
|
Finally, define the
local relative rank loss at z to be
where
s = [(( |
X |
- 1)( |
X |
- 2))/2].
Note that
rrl(
f,
z) is between 0 and 1.
It can be interpreted as the probability that the relationship between any two nodes in
(
X - {
z})×(
X - {
z}) will have a different relative order (from
z's point of view) in
the original and embedded spaces (assuming all pairs (
x,
y) have equal probability of
being chosen).
Define the
maximal local relative rank loss at z to be the
maximal value of
rrl(
f,
z) as
z ranges over
X.
The
average local relative rank loss at z, denoted
rrl(
f),
is defined as [(
åx Î X rrl(
f,
x))/( |
X | )].
3.4 A New Metric: Closest Neighbors Loss (cnl)
Some applications are interested only in determining which nodes are
closest, and so require that embeddings accurately preserve
the set of closest nodes. For a node
x, we define its local
closest neighbors loss to be 0 if the nodes closest to
x in
X
are mapped to the nodes closest to
f(
x), and 1 otherwise. We
denote this value by
cnl(
f,
x). If we take the average over
all nodes in
X, we denote the global value as
cnl(
f). We
often multiply this global
cnl by 100 and speak of the
percentage of nodes whose nearest neighbors are not preserved.
3.5 Examples of Inherent Inaccuracy - Topology Matters
We now apply the accuracy measures defined above to several simple
topologies. Figure
2 presents the relative error
and maximum local relative error measures for binary trees of depth
1 (3 nodes) through 8 (511 nodes). Note that it is not
obvious or intuitive how to interpret these (small) values. On the
other hand, Figure
3 presents the
scalar-independent measures for the same set of binary trees. The
plot for
cnl tells us that about 96 percent of the 511 nodes
in a tree of depth 8 have a different closest neighbors set in the
Lipschitz embedding. The plot for
rrl shows that on average nodes
see over 20 percent of their relative distance relationships
swapped. The plot for maximal local
rrl tells us that at least
one node saw over 30 percent of its relative distance
relationships swapped.
Figure
4 helps us to understand these inaccuracies.
This plot is from the perspective of a leaf node in a binary tree of
depth 4 (31 nodes). The signature plot marked with
*'s shows the distances of other nodes from this leaf, in
ascending order. The signature plot marked with
o's shows
the distances of the same nodes in the Lipschitz embedding. In the
original metric space, the parent of this leaf is the only node at
distance 1. But in the embedding, this node moves to a distance of
about 1.8. There were two nodes originally at distance 2 - the
leaf's sibling and its parent's parent. One of these (its sibling)
has moved closer (and is now closer than the leaf's parent), to a
distance just under 1, while the leaf's parent's parent moves out
to a distance of about 3.4. The local
rrl for this node is
17.2 percent. Note that it has lost its closest neighbor in the
embedding.
Some topologies show a very different relationship between
rrl and
cnl. For example, Figure
5 shows the
scalar-independent measures for a family of hub-and-spoke networks.
The graph have
n spokes and 1 root, where
n ranges from 1 to
30. Here we see a rising
cnl and a falling
rrl after
n=6.
The reason becomes clear when we look at the view from a leaf node,
as shown in Figure
6. We see that the root
nodes is
pushed away to a distance of about 3.3.
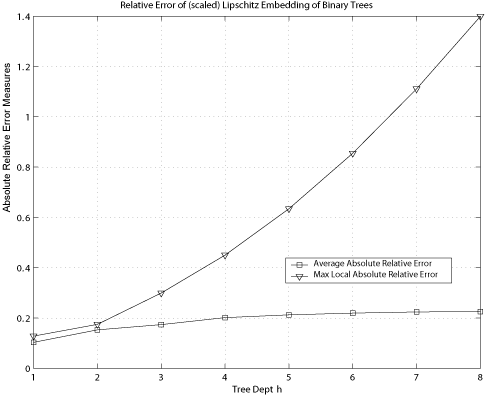
Figure 2: Absolute Relative Error measures for Lipschitz embedding on
binary trees, depth 1 to 8.
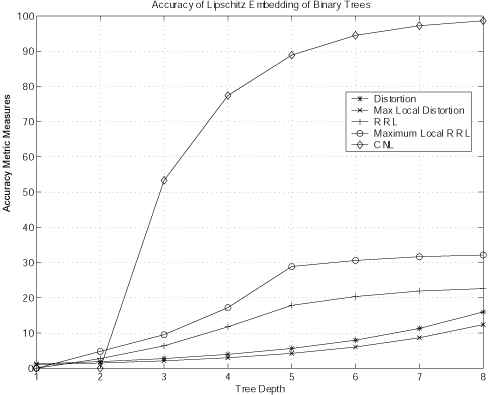
Figure 3: Scalar independent measures for Lipschitz embedding on
binary trees, depth 1 to 8.
Figure 4: The view from a leaf in a binary tree of depth
4.
Figure 5: Hub and Spoke accuracy.
Figure 6: The view from a leaf in a hub with 30 spokes.
3.6 The Scalability (Meta-) Metric
Suppose that a set of applications is only interested in a subset of
nodes, say just the North American sites. Would it be
better to use a coordinate system generated for all sites,
or one generated just from inter-site RTTs restricted to North
American sites? The answer to such questions will determine if
embeddings of coordinate
services could be
truly
scalable.
If
Y is a subset of
X, we
can obtain an embedding in one of two ways.
First, we could use the
embedding techniques to obtain
f(
X), and then restrict this to
the nodes in
Y, which we will denote as
f(
X)
¯ Y.
This is called
Superspace embedding.
Alternatively, we could
use the embedding techniques on
Y to get
f(
Y),
which we call the
Subspace embedding.
In general,
f(
X)
¯ Y and
f(
Y) may be
very different
embeddings and have
very different behaviors with different accuracy measures.
For example, consider again Figure
3. Let
X be
the binary tree of depth 8. We can consider each of the subtrees
of depths 1 to 7 as a Subspace
Y of
X. The figure shows the
scalar-independent accuracy measures for each full Lipschitz
embedding of Subspace
f(
Y). However, the full Lipschitz
embeddings derived from the Superspace,
f(
X)
¯ Y, will
in general inherit some of the inaccuracies of the Superspace
embedding
- that is the nodes outside of
Y in
X impact the way
Y is embedded.
4 An Experiment with the Lipschitz Embedding
Although data sets studied in previous research comprised large
number of measurements, some of them were not
full meshes.
The Skitter project [
3] used in Virtual
Landmarks [
21], for instance, makes RTT data available from
a small number of monitoring nodes
n to
m target nodes, where
m is in the order of hundreds of thousands. This yields an
asymmetric data set of
n ×
m where only estimated distances
between monitoring nodes and target nodes can be verified; distances
between target nodes cannot be determined. This issue can be
overcome with mesh data sets. We acknowledge the fact that finding
representative mesh data sets is not an easy task. However,
planetary-scale testbeds such as PlanetLab [
2]
provides a distributed platform not only for overlay-based services
but also for network measurements.
We used RTT data
1 collected
between all PlanetLab nodes from March 22
nd to March
28
th 2004. During this time period, there were over 150
participating sites with a total of over 370 hosted nodes
distributed in the Americas, Europe, Asia and Australia. We then
calculated the minimum RTT between each pair of nodes available
between those dates on consecutive 15-minute periods. Thus, for
each day in this period there were 96 matrices of RTT
measurements, and the size of each matrix was 325 ×325.
Therefore, over the seven days period, we obtained 672 such
matrices.
Since we wanted to perform this analysis only over our estimate of
propagation delays on the paths (and not the queueing and congestion
effects), we first constructed a single distance matrix
D, in
which each entry represented the minimum RTT between a pair of
PlanetLab nodes over the entire 7-day period. This avoided biases
in the results due to high variations in RTTs, e.g. during congested
periods. Our analysis of the data indicated that by taking the
minimum over a 7-day period, we can filter out congestion related
effects which have periodic weekly patterns.
Many PlanetLab sites had multiple nodes per site. For instance,
the Computer Laboratory (University of Cambridge) site hosted three
nodes
planetlab1,
planetlab2 and
planetlab3 under the domain
cl.cam.ac.uk. The
minimum RTTs between nodes within a site were very small, often of
the order of 1 ms. Examining RTTs between all pairs of nodes was
therefore wasteful and biased our results by the distribution of
nodes in PlanetLab sites and by the fact that there were missing
entries on the original 325 ×325 distance matrix. Thus, we
selected a representative node in each site so as to build a
site by site distance matrix
D¢, and then we removed rows
and columns that contained missing entries. This process reduced the
distance matrix to 69 ×69 RTTs between sites. Finally, we
used the classification proposed in [
5] to split
D¢
into three sub-matrices of different sizes based on the geographical
locations of PlanetLab sites:
North America (NA-PL): 44 ×44 distance matrix which contains RTTs between
PlanetLab sites located in North America. The majority of these
sites obtain inter-connectivity through the Abilene network.
Outside North America (ONA-PL): 25 ×25 distance matrix
with RTTs between
research and
commercial sites outside North America.
It includes sites in Australia, Europe, Latin America and Asia.
All sites (ALL-PL): the combination of NA-PL and ONA-PL data sets, of size 69 ×69.
We apply the
full Lipschitz embedding to the RTT distance
matrix of the 69 PlanetLab sites in
ALL-PL. Here are the
minimum, mean, and maximum values we found for local
rrl:
| Min | Mean | Max |
| rrl | 0.0887 | 0.1822 | 0.6058 |
Figure 7: PlanetLab site comet.columbia.edu with minimum
rrl using full Lipschitz embedding.
The difference between the maximum and minimum rrls is high
(51.71%). Figure 7 presents data
from the PlanetLab site comet.columbia.edu, which had the
minimum local rrl measure. The x-axis enumerates sites and the
y-axis shows the RTT distance of each site from
comet.columbia.edu (in milliseconds). The signature plot
marked with *'s indicates RTTs in the original distance
matrix, and the sites on the x-axis have been sorted to ensure
that this plot is in ascending order of RTTs. The signature
plot marked with o's is the geometric distances between
the same sites in the embedded geometric space. For these signature
plots, we have multiplied the Lipschitz embedding by a scaling
factor that minimizes relative error (as described in
Section 3). Of course, this does not impact the rrl
or cnl measures, but it helps us visualize the differences between
distances in the original and embedded spaces. Note that even in
this best case (at least with respect to local rrl), we see that
the relative ranking of many close nodes is reversed and
the list of close neighbors is not preserved. We saw
similar results for binary trees (Section 3), and we
suspect that many of the inaccuracies visible in
Figure 7 may be a consequence of the
inaccuracies inherent in the Lipschitz embedding for the underlying
network topology. Note that a user of this embedding at
comet.columbia.edu would conclude that nyu.edu was
about as far away as utexas.edu!
Figure 8: PlanetLab site planetlab1-pop-mg.mp.br
with maximum rrl using full Lipschitz embedding.
Figure
8 presents a signature plot for
the site with the maximum local
rrl measure, where the results
here are not very impressive - site
pop-mg.rnp.br has a
60.6% chance of swapping the relative distance of any two nodes.
It would appear from looking at this plot that using this embedding
at site
pop-mg.rnp.br would give very poor results.
Note that in these figures, the site has
lost its list of
neighbors' rankings in the embedding. In fact, the global
cnl
measure is 84.06%, for ALL-PL data set, so only about 15% of
the sites retain their closest neighbors in the embedding.
(a) North America (Lipschitz Superspace
embedding). PlanetLab site with maximum rrl.
(b) North America (Lipschitz Subspace
embedding). PlanetLab site with maximum rrl.
Figure 9: PlanetLab site with maximum rrl using full Lipschitz
Superspace and Subspace embeddings.
We proceed to explore scalability (meta-) metric of the Lipschitz
embedding with our PlanetLab site data. We used the data sets NA-PL
(North America) as a Subspace of the data set ALL-PL (All sites) of
size 69. We call
f(NA-PL) the
Subspace
embedding and
f(NA-ALL)
¯ NA-PL the
Superspace embedding of NA-PL. The minimum, mean, and
maximum local
rrl for the full
Lipschitz Superspace and
Subspace embeddings are shown in
Table
1. This is visualized in
Figure
9(a) and
Figure
9(b), which show the nodes
with the maximum
rrls for
Lipschitz Superspace and Subspace
embeddings. Note that the
Lipschitz Subspace embedding in
Euclidean space, is a
much better one. Figure
10
shows the CDFs of the local
rrl, for the
Lipschitz
f(ALL-PL),
f(NA-PL) (Subspace), and
f(NA-ALL)
¯ NA-PL (Superspace)
embeddings. It clearly shows that the
Lipschitz Subspace
embedding in
Euclidean space is
better than the
Lipschitz Superspace embedding, at least with respect to the
local
rrl measure of accuracy.
Table 1: Local rrl of Lipschitz
Subspace and Superspace embeddings using NA-ALL and ALL-PL PlanetLab sites.
| Embeddings | Min rrl |
Mean rrl | Max rrl |
|
| f(NA-PL) | 0.1141 | 0.1897 |
0.3023 |
| f(NA-ALL)¯ NA-PL | 0.1606 | 0.2916 |
0.4452
|
Figure 10: CDFs of Local rrl for Lipschitz
Subspace and Superspace embeddings in Euclidean Space.
5 Using Other Embeddings
We run experiments to apply our new accuracy metrics using Vivaldi
and BBS (Euclidean and Hyperbolic) systems and our PlanetLab sites
data. The
ALL-PL (All sites) data set of 69 sites
consisting of North America and Outside North America PlanetLab
sites, are selected for this experiments. We utilize the
p2psim simulator [
1] (which Vivaldi embedding
system is incorporated in), BBS (Euclidean) and BBS (Hyperbolic) TP
and LRN embeddings systems, to generate 3-dimensional coordinates
for our PlanetLab
ALL-PL (All sites) data set. We utilize
the TP embedding's parameters of
t=15 landmarks (the first 15 nodes
in the data set chosen as landmarks) and 15 node-to-landmark
measurements (each of the other nodes measure their distance to 15
landmarks for distortion minimization).
Table
2 shows the maximum, mean and
minimum
rrl and
cnl accuracy metrics for Vivaldi and BBS
(Euclidean and Hyperbolic spaces) embeddings using
ALL-PL
PlanetLab sites data.
Table 2: rrl and cnl accuracy metrics for Vivaldi and
BBS (Euclidean and Hyperbolic) embeddings using ALL-PL PlanetLab
sites
| Embeddings | Min rrl | Mean rrl | Max rrl | cnl (%) |
|
| Vivaldi | 0.0817 | 0.1476 | 0.3494 | 75.36 |
| BBS (Euclidean) | 0.0768 | 0.1263 | 0.2291 | 75.36 |
| BBS TP | | | | |
| (Hyperbolic) | 0.0382 | 0.2391 | 0.6286 | 72.46 |
| BBS LRN | | | | |
| (Hyperbolic) | 0.0680 | 0.1419 | 0.3670 | 68.12 |
Both BBS (Euclidean) and Vivaldi embeddings in Euclidean space have
the same cnl measure of 75.36%, but Vivaldi embedding
has a higher maximum rrl compared to BBS (Euclidean). The
BBS (Hyperbolic) TP embedding has a much higher maximum
rrl than BBS (Hyperbolic) LRN embedding, but its minimum rrl is
lower than BBS (Hyperbolic) LRN embedding. BBS (Hyperbolic)
LRN embedding has the lowest cnl measure of 68.12%,
compared to the other embeddings. On the other hand, BBS (Euclidean)
embedding has the lowest maximum rrl and BBS (Hyperbolic)
TP embedding has the largest maximum rrl compared to the
other embeddings. Figures 11 and
12 show the signature plots of the
PlanetLab node with maximum rrl for BBS (Hyperbolic) TP embedding
in Hyperbolic space and Vivaldi embedding in Euclidean space
respectively. Both graphs show their lists of close neighbors are
being pushed away in the embedded target geometric space.
Figure 11: BBS (Hyperbolic) TP embedding
using 69 PlanetLab ALL-PL (All sites) network topology
- Nodes with Maximum rrl.
Figure 12: Vivaldi embedding using 69 PlanetLab ALL-PL (All
sites) network topology
- Nodes with Maximum rrl.
Table 3: Local rrl for Vivaldi and BBS Subspace and
Superspace embeddings using NA-ALL and ALL-PL PlanetLab sites
| Embeddings | Min rrl | Mean rrl | Max rrl |
|
| Vivaldi |
| f(NA-PL) | 0.0853 | 0.1542 | 0.2625 |
| f(NA-ALL)¯ NA-PL | 0.1351 | 0.23 | 0.4507 |
|
| BBS (Euclidean) |
| f(NA-PL) | 0.0819 | 0.1407 | 0.2614 |
| f(NA-ALL)¯ NA-PL | 0.1440 | 0.2170 | 0.3544 |
|
| BBS (Hyperbolic) TP |
| f(NA-PL) | 0.0388 | 0.1512 | 0.3045 |
| f(NA-ALL)¯ NA-PL | 0.0410 | 0.1496 | 0.3101 |
|
| BBS (Hyperbolic) LRN |
| f(NA-PL) | 0.0864 | 0.1713 | 0.3167 |
| f(NA-ALL)¯ NA-PL | 0.0930 | 0.1504 | 0.2824 |
Similarly, we explore scalability (meta-) metric of the Vivaldi and
BBS embeddings with our PlanetLab site data. The Vivaldi and
BBS (Euclidean) Subspace and Superspace embeddings have the
same behavior as the Lipschitz Subspace and Superspace
embeddings, i.e. the Subspace embedding has better rrl
accuracy than the Superspace embedding in the Euclidean
space. However, in BBS (Hyperbolic) TP and BBS
(Hyperbolic) LRN Subspace and Superspace embeddings, the Subspace
embedding rrl accuracy is close to the Superspace
embedding as shown in the Table 3. For BBS
(Hyperbolic) TP embedding using the NA-PL site data set, we adopt
the same parameters as in the TP embedding for the ALL-PL, which is t=15 landmarks (the first 15 nodes in the data set chosen as the
landmarks), and 15 node-to-landmark measurements (each of the
other nodes measure their distance to 15 landmarks for distortion
minimization). Figure 13 shows the CDFs
of the local rrl for the BBS (Hyperbolic) TP and LRN
f(ALL-PL), f(NA-PL) (Subspace) and
f(NA-ALL)¯ NA-PL (Superspace)
embeddings. This results suggest that the Superspace embedding tends
to have a close or better rrl accuracy than the
Subspace embedding in the Hyperbolic space.
(a) CDFs of Local rrl for BBS (Hyperbolic) TP
Subspace and Superspace embeddings.
(a) CDFs of Local rrl for BBS (Hyperbolic) LRN
Subspace and Superspace embeddings.
Figure 13: CDFs of Local
rrl metrics for Subspace and Superspace embeddings in Hyperbolic
Space.
6 Revisiting Previous Work with New Accuracy Metrics
It will be interesting to apply our new accuracy metrics to Vivaldi
and BBS (Euclidean and Hyperbolic) systems (based on numerical
minimization techniques) on
their data sets that were used in
their work. We generate 3-dimensional coordinates for these
embeddings in our experiments. With reference to BBS
systems [
18,
19,
20], we utilize network
topologies from the TRACER placement method (the network topologies
chosen by selecting the first
n nodes in the
whole network)
for our experiments due to its suitability for geometric distance
experiments. We utilize the TP embedding's parameters of
t=10
landmarks and 6 node-to-landmark measurements: this means that
there are 10 landmarks chosen from the first 10 nodes in the
network topology and
only 6
closest measurements are
carried out by other nodes to these 10 landmarks.
There are
two data sets used in the Vivaldi [
8]
work.
PlanetLab RTT data of filtered nodes: This is
pair-wise minimum RTTs of 192 PlanetLab nodes over a certain
period of time (not specified in [
8]), from the PlanetLab
"ping" collection traces. It is filtered due to some nodes in
PlanetLab having security measures restricting "ping" connection
from other nodes.
King [9] data: This data set
contains 1740 Internet DNS servers RTT traces based on the King
collection method.
We selected the following data sets from the BBS (Euclidean)
[
18] work.
Waxman [22] Network
Topology: This data set contains undirected fixed network
topologies of 600 nodes and the edge weights are generated with
random uniform distribution in the range of [1,1000]. The edge
weights are taken as
ë10
E + 0.5
û, where
E is
randomly and uniformly distributed in the interval (0,3]. Based on
the 600 nodes' connectivity, a Dijkstra algorithm is performed to
find the shortest path distance matrix. Network topologies consist
of the first 50 nodes chosen among the 600 nodes in the Waxman
Network.
Barabási-Albert [4,6] (BA)
Network Topology (considered to follow the PowerLaw): This data set
consists of undirected fixed network topologies of 1000 network
nodes and the edge weights are generated with random uniform
distribution in the interval of [1,1000]. Based on the 1000
nodes' connectivity, a Dijkstra algorithm is performed to find the
shortest path distance matrix. Network topologies consist of the
first 15 nodes chosen among the 1000 nodes in the BA Network.
We used the following data sets from BBS (Hyperbolic)
[
19,
20] work.
Barabási-Albert
(BA) [4,6] Network Topology (considered to
follow the PowerLaw): This data set consists of undirected fixed
network topologies of 1000 nodes, and edge weights are generated
with random uniform distribution in the interval of [1,1000] (same
data set in BBS (Hyperbolic) work [
19]). Network
topologies consist of the first 150 nodes chosen among the 1000
nodes. A Dijkstra algorithm is performed to find the shortest path
distance matrix.
January 2000 AS Network Topology from
University of Oregon (RouteViews): This hierarchical tree network
topology consists of 6474 nodes, and edge weights are generated
with random uniform distribution in the interval of [1,1000] (same
data set in BBS (Hyperbolic) work [
19]). Network
topologies consist of the first 150 nodes chosen among the 6474
nodes. A Dijkstra algorithm is performed to find the shortest path
distance matrix.
March 2001 AS Network Topology from
University of Oregon (RouteViews): This data set is only used in
the BBS (Hyperbolic) LRN embedding work [
20]. It
consists of a hierarchical tree network topology of 10670 nodes
that are randomly weighted, with edge weights distributed uniformly
in the interval of [1,1000]. We extracted 200 weighted network
topology of nodes with lower degree, or stub ASes.
Table 4: rrl accuracy metric for Vivaldi and BBS
(Euclidean and Hyperbolic) embeddings
| Embeddings | Data sets | Min rrl | Mean rrl | Max rrl |
|
| Vivaldi | 192 PlanetLab filtered nodes | 0.0334 | 0.0894 | 0.2808 |
| Vivaldi | 1740 King nodes | 0.0633 | 0.1306 | 0.5667 |
| BBS (Euclidean) | Topology of 50 nodes chosen among 600 nodes in
Waxman Network
| 0.1310 | 0.2090 | 0.3639 |
| BBS (Euclidean) | Topology of 15 nodes chosen among 1000
nodes in BA Network | 0.0220 | 0.0982 | 0.2857 |
| BBS (Euclidean) | Topology of 150 nodes chosen among 6474 nodes
in
Jan 2000 AS Network | 0.3531 | 0.4553 | 0.6379 |
| BBS (Hyperbolic) TP with 10 landmarks and 6 measurements | Topology of 150 nodes chosen among 1000 nodes in BA
Network | 0.0892 | 0.2452 | 0.4995 |
| BBS (Hyperbolic) TP with 10 landmarks and 6 measurements | Topology of 150 nodes chosen among 6474 nodes in Jan 2000 AS Network | 0.3305 | 0.4636 | 0.6452 |
| BBS (Hyperbolic) TP with 10 landmarks and 6 measurements | Topology of 50 nodes chosen among 600 nodes in Waxman Network
| 0.1573 | 0.2647 | 0.4524 |
| BBS (Hyperbolic) TP with 15 landmarks and 15 measurements | Topology of 200 nodes with lower degree chosen among
10670 nodes in Mar 2001 AS Network | 0.0228 | 0.1419 | 0.2153 |
| BBS (Hyperbolic) LRN | Topology of 200 nodes with lower
degree chosen among 10670 nodes in Mar 2001 AS Network | 0.0802
| 0.1796 | 0.2389 |
(a) Node with Maximum rrl using network topology of 150 nodes chosen
from 1000 nodes in BA Network Topology.
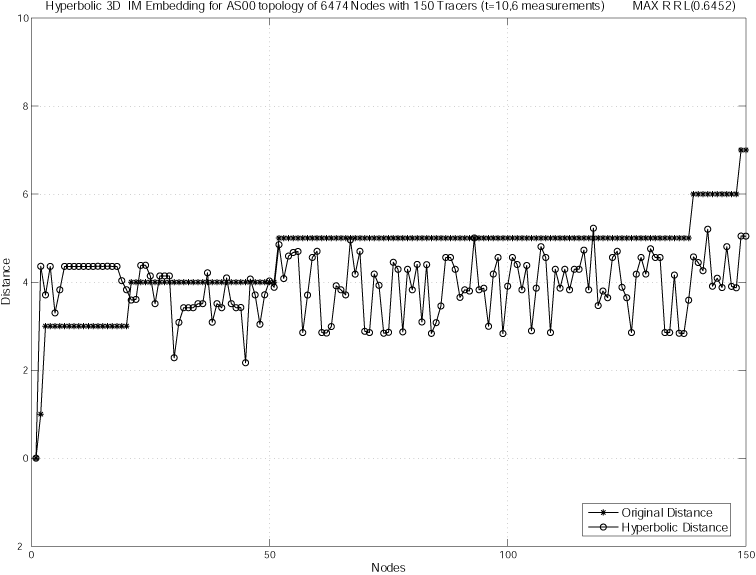
(b) Node with Maximum rrl using network topology of 150 nodes chosen
from 6474 nodes in Jan 2000 AS Hierarchical Tree Network Topology.
Figure 14: BBS (Hyperbolic) TP
embedding with 10 landmarks and 6 measurements
- Nodes with Maximum rrl.
Table
4 summarizes the maximum, mean and
minimum
rrl accuracy metric for Vivaldi and BBS (Euclidean and
Hyperbolic) embeddings using their data sets
[
8,
18,
19,
20]. The signature
plots of the nodes having maximum
rrl for BBS (Hyperbolic) TP
embedding in Hyperbolic space are shown in
Figure
14. Evidently, the result of
TP embedding in Hyperbolic space using AS Hierarchical Tree Network
Topology shows
similar rrl inaccuracy behavior as the
Lipschitz embedding in Euclidean space from the perspective of the
tree node in the synthetic binary trees which we have illustrated in
Section
3.5. This confirms that BBS (Hyperbolic)
TP embedding in
Hyperbolic space has the
similar
rrl inaccuracy behavior as
Lipschitz embedding in
Euclidean space for
tree-like network topology.
Also, from the BBS (Hyperbolic) TP embedding experiment using BA
Network Topology, it shows
similar rrl inaccuracy
behavior as the Lipschitz embedding using our PlanetLab site data.
All these experiments show that the lists of close neighbors are
being
pushed away in the target Euclidean and Hyperbolic
spaces.
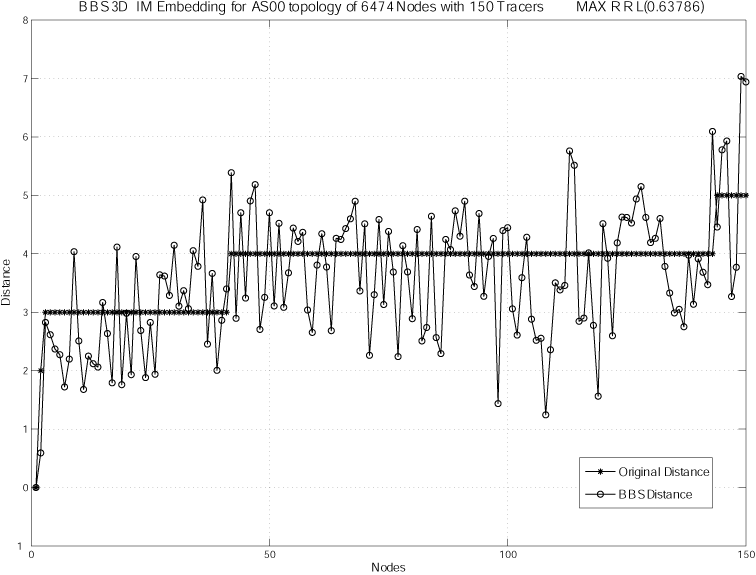
Figure 15: BBS (Euclidean) embedding using network topology of 150
nodes chosen from 6474 nodes in Jan 2000 AS Hierarchical Tree
Network Topology
- Node with Maximum rrl.
We attempt to make a comparison study of BBS (Euclidean) and BBS
(Hyperbolic) TP embeddings. The Jan 2000 AS Hierarchical Tree
Network Topology (RouteViews) data set is used for this comparison.
We examine the signature plot of nodes with the maximum rrl for
BBS (Hyperbolic) TP and BBS (Euclidean) embeddings, as illustrated
in Figure 14(b) and
Figure 15 respectively. For
hierarchical tree-like network graphs, both embeddings in Euclidean
and Hyperbolic spaces have sharp bi-modal rrl error
behaviors. Similarly, in Euclidean space, the rrl measure
for the BBS (Euclidean) embedding shows similar rrl
inaccuracy behavior as the Lipschitz embedding from the perspective
of the tree node in the synthetic binary trees, which we have
illustrated in Section 3.5.
We continue to run
rrl accuracy metric on BBS (Hyperbolic) LRN
embedding using the March 2001 AS Hierarchical Tree Network
Topology (RouteViews) data set. This is compared with BBS
(Hyperbolic) TP embedding's parameters of
t=15 landmarks, and 15
node-to-landmark measurements for distortion minimization. Figure
16 shows the signature plots of
the nodes with maximum
rrl for BBS (Hyperbolic) TP and LRN
embeddings. In LRN embedding, the list of close neighbors is being
pushed away very much further and it has a
higher
maximum
rrl compared to TP embedding. Both exhibit
similar
bi-polar rrl error behavior in Hyperbolic space.
(a) Node with Maximum rrl for BBS (Hyperbolic) TP
embedding.
(b) Node with Maximum rrl for BBS (Hyperbolic) LRN
embedding.
Figure 16: rrl Comparison
of BBS (Hyperbolic) TP embedding with 15 landmarks and 15
measurements and BBS (Hyperbolic) LRN embedding, using network
topology of 200 nodes with lower degree chosen from 10670 nodes
in Mar 2001 AS Hierarchical Tree Network Topology.
7 Discussion
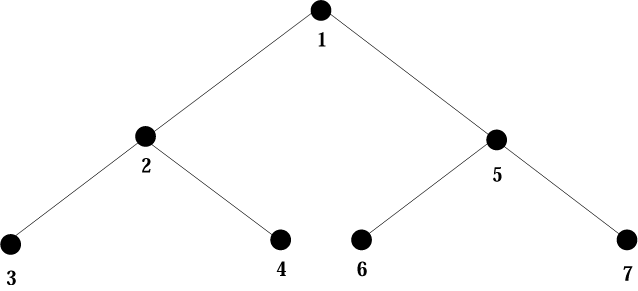
Our goal in this experimental work is to apply our new accuracy
metrics to study the
accuracy of estimated distances
predicted by Internet coordinate systems and to what extent it
varies among different pairs of nodes. The results of this initial
attempt are not very encouraging. However, it remains that no single
accuracy metric can capture the
quality of the embedding
techniques and it is worthwhile to develop a collection of accuracy
metrics that are able to quantify user-oriented
quality.
Another interesting open problem is: Can we characterize the impact
of network topologies that have good embeddings with respect to an
accuracy metric? We envisage to answer this through our newfound
future research on EONs and to discover its embeddability which aim
to give good
quality embeddings with respect to accuracy
metrics. We also note that the number of landmarks has some impact
on the accuracy of the embedding techniques: less information can
give
better accuracy results.
Figures
17
and
18 show the accuracy metrics (average
absolute relative error and
rrl) versus number of landmarks of the
embedding techniques for the binary tree of depth 2
(Figure
1). The landmarks are selected
sequentially and incrementally from the list of nodes in the binary
tree. The results of this simple experiment indicate that Lipschitz
plain embedding (without any scaling) gives
better average
relative absolute error and Vivaldi embedding gives
lower
rrl with small number of landmarks. Other embedding techniques
have similar observation. This contradicts the intuition that having
more landmarks (i.e. having more information) will give
better accuracy results. A complete understanding will
require the investigation of structural effects of the number of
landmarks and landmarks' selection with respect to accuracy metrics.
Figure 17: Average Absolute Relative Error Metric versus Number of
Landmarks.
Figure 18: rrl Error Metric versus Number of Landmarks.
8 Acknowledgments
Initial work for this paper was done while the first four authors
were with Intel Research, and we thank Derek McAuley for his
support. We also thank Yuval Shavitt, Tomer Tankel, Jinyang Li and
Frank Dabek for useful and helpful discussions of their systems and
data sets. Eng Keong Lua is sponsored by Microsoft Research Ph.D.
Studentship.
References
- [1]
-
p2psim: A simulator for peer-to-peer protocols.
http://www.pdos.lcs.mit.edu/p2psim/index.html.
- [2]
-
PlanetLab home page.
http://www.planetlab.org.
- [3]
-
Skitter home page.
http://www.caida.org/tools/measurement/skitter.
- [4]
-
Albert, R., and Barabási, A.-L.
Topology of evolving networks: Local events and universality.
Physical Review Letters (December 11 2000), 5234-5237.
- [5]
-
Banerjee, S., Griffin, T. G., and Pias, M.
The interdomain connectivity of planetlab nodes.
In Proceedings of the 5th International Workshop on Passive and
Active Network Measurement (Antibes Juan-les-Pins, France, April 2004).
- [6]
-
Barabási, A.-L., and Albert, R.
Emergence of scaling in random networks.
Science 286 (October 15 1999), 509-512.
- [7]
-
Costa, M., Castro, M., Rowstron, A., and Key, P.
Pic: Practical internet coordinates for distance estimation.
In Proceedings of the 24th IEEE International Conference on
Distributed Computing Systems (ICDCS' 04) (Tokyo, Japan, March 2004).
- [8]
-
Dabek, F., Cox, R., Kaashoek, F., and Morris, R.
Vivaldi: A decentralized network coordinate system.
In Proceedings of the ACM SIGCOMM 2004 (Portland, Oregon,
August 2004).
- [9]
-
Gummadi, K., Saroiu, S., and Gribble, S.
King: Estimating latency between arbitrary internet end hosts.
In Proceedings of the Internet Measurement Workshop (November
2002).
- [10]
-
Gupta, A.
Embedding tree metrics into low dimensional euclidean spaces.
In Proceedings of the 31st annual ACM symposium on Theory of
computing (1999), pp. 694-700.
- [11]
-
Lim, H., Hou, J., and Choi, C.
Constructing internet coordinate system based on delay measurement.
In Proceedings of the ACM SIGCOMM Internet Measurement
Conference (IMC 2003) (Miami, Florida, USA, October 2003).
- [12]
-
Linial, N., London, E., and Rabinovich, Y.
The geometry of graphs and some of its algorithmic applications.
Combinatorica 15 (1995), 215-245.
- [13]
-
Linial, N., Magen, A., and Saks, M.
Trees and euclidean metrics.
In Proceedings of the ACM Symposium on Theory of Computing
(STOC) (1998).
- [14]
-
Linial, N., and Saks, M.
The euclidean distortion of complete binary trees.
Discrete and Computational Geometry 29, 1 (2003), 19-21.
- [15]
-
Mao, Y., and Saul, L. K.
Modeling distances in large-scale networks by matrix factorization.
In Proceedings of the 4th ACM SIGCOMM conference on Internet
Measurement (2004), pp. 278-287.
- [16]
-
Ng, T. E., and Zhang, H.
Predicting internet network distance with coordinates-based
approaches.
In Proceedings of the IEEE INFOCOM 2002 (New York, USA, June
2002).
- [17]
-
Pias, M., Crowcroft, J., Wilbur, S., Harris, T., and Bhatti, S.
Lighthouses for scalable distributed location.
In Proceedings of the 2nd International Workshop on Peer-to-Peer
Systems (February 2003).
- [18]
-
Shavitt, Y., and Tankel, T.
Big-bang simulation for embedding network distances in euclidean
space.
In Proceedings of the IEEE INFOCOM 2003 (San Francisco,
California, April 2003).
- [19]
-
Shavitt, Y., and Tankel, T.
On the curvature of the internet and its usage for overlay
construction and distance estimation.
In Proceedings of the IEEE INFOCOM 2004 (Hong Kong, March
2004).
- [20]
-
Shavitt, Y., and Tankel, T.
On internet embedding in hyperbolic spaces for overlay construction
and distance estimation.
Submitted to a Journal,
http://www.eng.tau.ac.il/~tankel/pub/HypEmb05v2.pdf (2005).
- [21]
-
Tang, L., and Crovella, M.
Virtual landmarks for the internet.
In Proceedings of the ACM SIGCOMM Internet Measurement
Conference (IMC 2003) (Miami, Florida, USA, October 2003).
- [22]
-
Waxman, B.
Routing of multipoint connections.
IEEE JSAC (1988), 1617-1622.
- [23]
-
Zheng, H., Lua, E. K., Pias, M., and Griffin, T.
Internet routing policies and round-trip-times.
In Proceedings of the Passive Active Measurement 2005 (March
30 - April 1 2005).
-
Notes
1The all-pairs RTT
measurement data was being continuously collected by Jeremy Stribling and it
is available from
http://www.pdos.lcs.mit.edu/~strib/pl_app/
Need help?
