|
||||||||||||||
|
Sparse Approximations for High
Fidelity
Compression of Network Traffic Data
Abstract
An important component of traffic analysis and network monitoring is the ability to correlate events across multiple data streams, from different sources and from different time periods. Storing such a large amount of data for visualizing traffic trends and for building prediction models of ``normal'' network traffic represents a great challenge because the data sets are enormous. In this paper we present the application and analysis of signal processing techniques for effective practical compression of network traffic data. We propose to use a sparse approximation of the network traffic data over a rich collection of natural building blocks, with several natural dictionaries drawn from the networking community's experience with traffic data. We observe that with such natural dictionaries, high fidelity compression of the original traffic data can be achieved such that even with a compression ratio of around 1:6, the compression error, in terms of the energy of the original signal lost, is less than 1%. We also observe that the sparse representations are stable over time, and that the stable components correspond to well-defined periodicities in network traffic.1 Introduction
Traffic monitoring is not a simple task. Network operators have to deal with large volumes of data, and need to identify and respond to network incidents in real-time. The task is complicated even further by the fact that monitoring needs to be done on multiple dimensions and timescales. It is evident that network operators wish to observe traffic at finer granularities across different dimensions for a multitude of reasons that include: 1. real-time detection and response to network failures and isolating errant network segments, 2. real-time detection of network attacks such as DDoS and worms, and installation of filters to protect network entities, and 3. finer resolution root-cause analysis of the incidents and automated/semi-automated drill down of the incident. To meet these requirements, we must be able to generate and store traffic data on multiple resolution scales in space (network prefixes and physical network entities such as links, routers), and in time (storing the traffic aggregates at multiple time resolutions). Such requirements naturally translate into increased operational costs due to the increased storage requirement. We often transport large portions of the historical data across a network to individual operators, import pieces of data into statistical analysis and visualization software for modeling purposes, and index and run queries against various historical databases for data drill down. Thus the management overhead involved in handling such large data sets, and the computational overhead in accessing and processing the large volumes of historical data also increases. We must reduce the storage size of the data, not only for efficient management of historical traffic data, but also to accommodate fine data resolution across space and time. The compression techniques we investigate are ``lossy'' compression methods. For most network monitoring applications that utilize historical traffic data, it often suffices to capture salient features of the underlying traffic. We can thus afford some error by ignoring the low-energy stochastic components of the signal, and gain better compression using lossy compression techniques (as opposed to lossless compression methods such as gzip [11] which reduce the storage size of the data only and do not reduce the size of the input to monitoring applications). The overall goal of such compression techniques is to obtain high fidelity (i.e. low error) representations with as little storage as possible. In particular, we use a compression method called sparse representation over redundant dictionaries. A visual inspection of aggregated network traffic for many high volume ports reveals three components. First, there is a natural diurnal variation for many ports and/or other periodic variations as well. Second, there are spikes, dips, and other components of the traffic that appear to be the result of non-periodic events or processes. Finally, the traffic appears to be stochastic over small time scales with variance much smaller than the periodic variations for high volume ports. Representing a signal with all three components using a single orthonormal basis, such as a Fourier basis or a wavelet representation is not likely to yield good compression: a basis that represents periodic signals well will not represent non-periodic signals efficiently and vice versa. The methods presented in this paper allow us to use two or more orthonormal bases simultaneously. A set of two or more orthonormal bases is called a redundant dictionary. Hence, with an appropriate set of orthonormal bases as the redundant dictionary, the periodic and the significant non-periodic portions of the traffic time series can both be represented efficiently within the same framework. Sparse representation or approximation over redundant dictionaries does not make assumptions about the underlying distributions in the traffic time series. As a result, sparse approximation can guarantee high fidelity regardless of changes in the underlying distributions. In addition, there are highly efficient, provably correct algorithms for solving sparse approximation problems. These algorithms scale with the data and can be easily adapted to multiple sources of data. They are greedy algorithms, known as matching or orthogonal matching pursuit. The primary contribution of this paper is a rigorous investigation of the method of sparse representation over redundant dictionaries for the compression of network time series data. We propose and evaluate several redundant dictionaries that are naturally suited for traffic time series data. We conclude that these methods achieve significant compression with very high fidelity across a wide spectrum of traffic data. In addition, we also observe that the sparse representations are stable, not only in terms of their selection in the sparse representation over time but also in terms of the individual amplitudes in the representation. These stable components correspond to well-defined periodicities in network traffic, and capture the natural structure of traffic time series data. To the best of our knowledge, this is the first thorough application of sparse representations for compressing network traffic data. We discuss related work in Section 2, and present a overall motivation for compression in Section 3. In Section 4 we describe in more detail the framework of matching (greedy) pursuit over redundant dictionaries. Section 5 describes our traffic data set, derived from a large Internet provider. We evaluate the efficacy of our compression techniques in Section 6. Section 7 presents some network traffic monitoring applications that demonstrate the utility of the compression methods we used. Section 8 discusses the scope for improving the compression, before we conclude in Section 9.
2 Related Work
Statisticians concern themselves with subset selection in
regression [13]
and electrical engineers use sparse representations for the compression
and analysis of audio, image, and video signals (see [12,6,4] for several
example references). Lakhina, et al. [10,9] examine the
structure of network traffic using Principal Component Analysis (PCA).
The observations in our work provide similar insight into the structure
of network traffic. There are two compelling reasons for using sparse
approximations over redundant dictionaries, as opposed to PCA alone, for
obtaining similar fidelity-compression tradeoffs. First, the description
length for sparse approximation is much shorter than for PCA, since the
principal vectors require substantially more space to represent than
simple indices into a dictionary. Second, PCA like techniques may
capture and identify the (predominant) structure across all
measurements, but may not be adequate for representing subtle
characteristics on individual traffic aggregates. Barford, et al. [1] use pseudo-spline
wavelets as the basis wavelet to analyze the time localized normalized
variance of the high frequency component to identify signal anomalies.
The primary difference is our application of signal processing
techniques for compressing network traffic data, as opposed to using
signal decomposition techniques for isolating anomalies in time series
data. There are several methods for data reduction for generating
compact traffic summaries for specific real-time applications. Sketch
based methods [8]
have been used for anomaly detection on traffic data, while Estan et
al. [3]
discuss methods for performing multi-dimensional analysis of network
traffic data. While such approaches are appealing for real-time traffic
analysis with low CPU and memory requirements, they do not address the
problems of dealing with large volumes of historical data that arise in
network operations. A third, important method of reducing data is
sampling [2]
the raw data before storing historical information. However, in order
for the sampled data to be an accurate reflection of the raw data, one
must make assumptions regarding the underlying traffic distributions.
3 Compression
It is easy to (falsely) argue that compression techniques have
considerably less relevance when the current cost of (secondary) storage
is less than $1 per GB. Large operational networks indeed have the
unenviable task of managing many terabytes of measurement data on an
ongoing basis, with multiple data streams coming from different routers,
customer links, and measurement probes. While it may indeed be feasible
to collect, store, and manage such a large volume of data for small
periods of time (e.g. for the last few days), the real problem is in
managing large volumes of historical data. Having access to historical
data is a crucial part of a network operator's diagnostic toolkit. The
historical datasets are typically used for building prediction models
for anomaly detection, and also for building visual diagnostic aids for
network operators. The storage requirement increases not only because of
the need for access to large volumes of historical traffic data, but
also the pressing need for storing such historical data across different
spatial and temporal resolutions, as reference models for fine-grained
online analysis. It may be possible to specify compression and
summarization methods for reducing the storage requirement for specific
traffic monitoring applications that use historical data. However, there
is a definite need for historical reference data to be stored at fine
spatial and temporal resolutions for a wide variety of applications, and
it is often difficult to ascertain the set of applications and
diagnostic techniques that would use these datasets ahead of time. The
compression techniques discussed in this paper have the desirable
property that they operate in an application-agnostic setting, without
making significant assumptions regarding the underlying traffic
distributions. Since many traffic monitoring applications can tolerate a
small amount of error in the stored values, lossy compression
techniques that can guarantee a high fidelity representation with small
storage overhead are ideally suited for our requirements. We find that
our techniques provide very accurate compressed representations so that
there is only a negligible loss of accuracy across a wide spectrum of
traffic monitoring applications. The basic idea behind the compression
techniques used in this paper is to obtain a sparse representation of
the given time series signal using different orthonormal and redundant
bases. While a perfect lossless representation can be obtained by
keeping all the coefficients of the representation (e.g. using all
Fourier or wavelet coefficients), we can obtain a compressed (albeit
lossy) representation by only storing the high energy coefficients,
that capture a substantial part of the original time series signal.
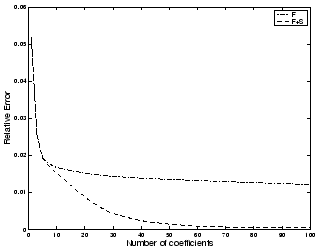
Suppose we have a given time series signal of length
4 Sparse Representations over Redundant Dictionaries
One mathematically rigorous method of compression is that of sparse
approximation. Sparse approximation problems arise in a host of
scientific, mathematical, and engineering settings and find greatest
practical application in image, audio, and video compression [12,6,4], to name a few.
While each application calls for a slightly different problem
formulation, the overall goal is to identify a good approximation
involving a few elementary signals--a sparse approximation.
Sparse approximation problems have two characteristics. First, the
signal vector is approximated with a linear model of elementary
signals (drawn from a fixed collection of several orthonormal bases).
Second, there is a compromise between approximation error (usually
measured with Euclidean norm) and the number of elementary signals in
the linear combination. One example of a redundant dictionary for
signals of length 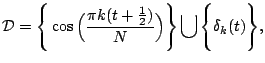
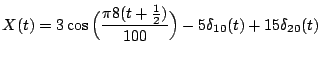
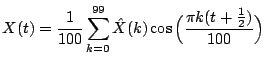
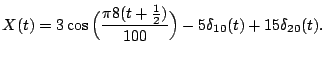
4.1 Greedy Pursuit Algorithms
A greedy pursuit algorithm at each iteration makes the best local improvement to the current approximation in hope of obtaining a good overall solution. The primary algorithm is referred to as Orthogonal Matching Pursuit (OMP), described in Algorithm 4.1. In each step of the algorithm, the current best waveform is chosen from the dictionary to approximate the residual signal. That waveform is then subtracted from the residual and added to the approximation. The algorithm then iterates on the residual. At the end of the pursuit stage, the approximation consists of a linear combination of a small number of basic waveforms. We fix some notation before describing the algorithm. The dictionaryINPUT:
- A
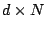 matrix
matrix 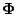
- A vector
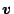 of measurements of length
of measurements of length 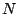
- The desired number of terms
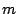 in the compressed
signal
in the compressed
signal
- A set of
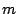 indices
indices 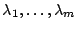
- An
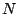 -dimensional residual
-dimensional residual 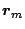
- Initialize the residual
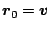 and the iteration counter
and the iteration counter 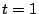 .
. - Find the index
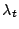 of the vector with the
largest dot product with the current residual
of the vector with the
largest dot product with the current residual
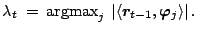
- Let
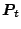 be the orthogonal projection onto
the span of the current vectors
be the orthogonal projection onto
the span of the current vectors 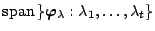 .
Calculate the new residual:
.
Calculate the new residual:
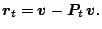
- Increment
 , and return to Step 2 if
, and return to Step 2 if  .
.
5 Data Description
The primary data set we have used for evaluating our methods consists
of traffic aggregates collected over a 20 week period (between January
and June 2004) at a large Tier-1 Internet provider's IP backbone
network. The dataset consists of traffic aggregates in terms of flow,
packet, and byte counts. The dimensions of interest over which the
aggregates are collected are:
- TCP Ports: Traffic to and from each of the 65535 TCP ports.
- UDP Ports: Traffic to and from each of the 65535 UDP ports.
- Aggregated Network Prefixes: Traffic to and from network prefixes aggregated at a set of predefined network prefixes.
The traffic aggregates were generated from flow records using traffic collection tools similar to Netflow [14], aggregated over multiple links in the provider's Internet backbone. In this particular data set, the traffic volume counts are reported on an hourly basis. For example, for each TCP port the data set contains the total number of flows, packets, and bytes on that port. The data set aggregates each metric (i.e., flows, packets, and bytes) for both incoming (i.e., traffic with this port was the destination port) and outgoing traffic (i.e., traffic with this port as the source port). Such per-port and per-prefix aggregates are routinely collected at many large ISPs and large enterprises for various traffic engineering and traffic analysis applications.
It is useful to note that such data sets permit interesting traffic analysis including observing trends in the traffic data, and detecting and diagnosing anomalies in the network data. For many types of network incidents of interest (outages, DoS and DDoS attacks, worms, viruses, etc.) the dataset has sufficient spatial granularity to diagnose anomalies. For example, the number of incoming flows into specific ports can be an indication of malicious scanning activity or worm activity, while the number of incoming flows into specific prefixes may be indicative of flash-crowds or DoS attacks targeted at that prefix.
For the following discussions, we consider the data in week long chunks, partly because a week appears to be the smallest unit within which constituent components of the signal manifest themselves, and also because a week is a convenient time unit from an operational viewpoint.
6 Results
In this section, we demonstrate how we can use sparse approximations to
compress traffic time series data. We look at the unidimensional
aggregates along each port/protocol pair and prefix as an independent
univariate signal. In the following sections, unless otherwise stated,
we work with the total number of incoming flows into a particular port.
We observe similar results with other traffic aggregates such as the
number of packets and the number of incoming bytes incoming on each
port, and for aggregated counts for the number of outgoing flows,
packets, bytes on each port--we do not present these results for
brevity. We present the results only for the TCP and UDP ports and note
that the compression results for aggregated address prefixes were
similar. Since an exhaustive discussion of each individual port would be
tedious, we identify 4 categories of ports, predominantly characterized
based on the applications that use these ports. For each of the
categories the following discussion presents results for a few canonical
examples.
- High volume, popular application ports (e.g., HTTP, SMTP, DNS).
- P2P ports (e.g., Kazaa, Gnutella, E-Donkey).
- Scan target ports (e.g., Port 135, Port 139) .
- Random low volume ports.
6.1 Fourier Dictionary
Our first attempt at selecting a suitable dictionary for compression
was to exploit the periodic structure of traffic time series data. A
well known fact, confirmed by several measurements [9,10,15], is the fact that
network traffic when viewed at sufficient levels of aggregation exhibits
remarkably periodic properties, the strongest among them being the
distinct diurnal component. It is of interest to identify these using
frequency spectrum decomposition techniques (Fourier analysis). It is
conceivable that the data can be compressed using a few fundamental
frequencies, and the traffic is essentially a linear combination of
these harmonics with some noisy stochastic component. To understand the
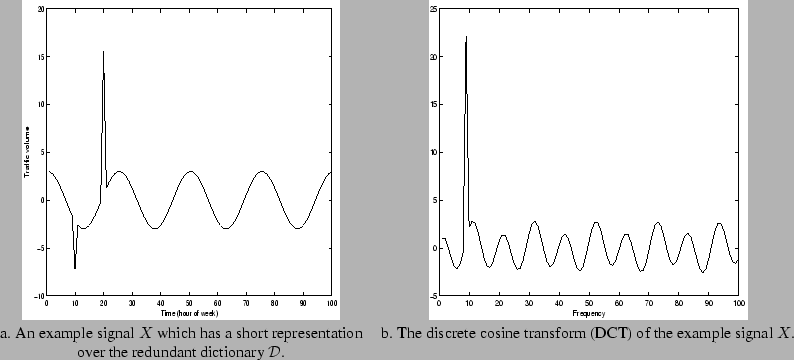
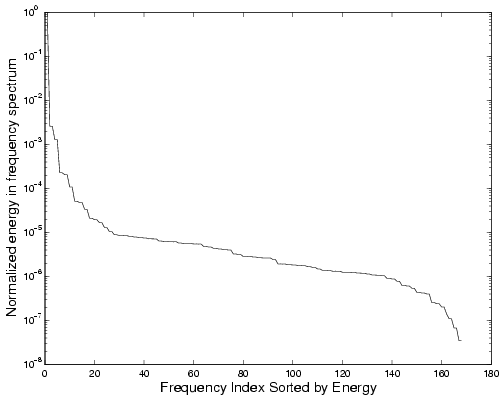
intuition behind using the frequency spectrum as a source of compression
we show in Figure 2 the
power spectrum of two specific ports for a single week. In each case
the power spectrum amplitudes are normalized with respect to the maximum
amplitude frequency for that signal (usually the mean or 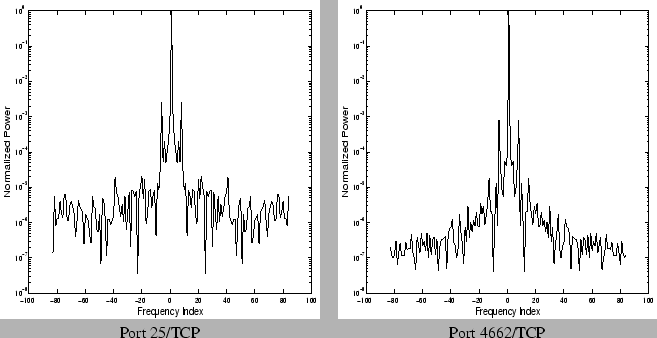 |
 |
 |
| Port 25/TCP |
Port 4662/TCP |
6.2 Using Redundant Dictionaries
Our choice of the Fourier dictionary was motivated by the observation that the traffic time-series when viewed at a reasonable level of aggregation possesses a significant periodic component. Therefore, using Fourier basis functions as part of the redundant dictionary seems a reasonable starting point. There are however, other interesting incidents we wish to capture in the compressed representation. Experience with traffic data indicates that interesting events with high volume (and hence high signal energy) include possibly anomalous spikes, traffic dips, and slightly prolonged high traffic incidents. Such isolated incidents, localized in time, cannot be succinctly captured using only a Fourier basis. Fortunately, these events can be modeled either using spike functions appropriately placed at different time indices, or using Haar wavelets (square waveforms) of different scales and all translations. The fully-translational Haar wavelets at all scales and all translations form a rich redundant dictionary of size| Port Type | Port Number | Relative error with different dictionaries | |||||||
| DF | DW | DS | DH | DF+S | DF+H | DF+H+S | DH+S | ||
| High Volume | 25 | 0.0005 | 0.0026 | 0.8446 | 0.0007 | 0.0004 | 0.0004 | 0.0004 | 0.0007 |
| 80 | 0.0052 | 0.0256 | 0.7704 | 0.0074 | 0.0052 | 0.0018 | 0.0018 | 0.0073 |
|
| P2P | 1214 | 0.0003 | 0.0036 | 0.0007 | 0.8410 | 0.0003 | 0.0001 | 0.0001 | 0.0007 |
| 6346 | 0.0009 | 0.0056 | 0.8193 | 0.0013 | 0.0009 | 0.0005 | 0.0005 | 0.0013 |
|
| Scan | 135 | 0.0016 | 0.0216 | 0.7746 | 0.0049 | 0.0015 | 0.0008 | 0.0008 | 0.0049 |
| 9898 | 0.0066 | 0.0143 | 0.7800 | 0.0036 | 0.0063 | 0.0032 | 0.0032 | 0.0036 |
|
| Random | 5190 | 0.0023 | 0.0280 | 0.7916 | 0.0040 | 0.0023 | 0.0010 | 0.0010 | 0.0039 |
| 114 | 0.5517 | 0.1704 | 0.0428 | 0.0218 | 0.0097 | 0.0218 | 0.0068 | 0.0068 |
|
Rather than try to optimize the basis selection for each specific port, we wish to use redundant dictionaries that can best capture the different components that can be observed across the entire spectrum of ports. Hence we use redundant dictionaries composed of Fourier, fully-translational Haar, and Spike waveforms and observe that we can extract the best compression (in terms of number of coefficients selected), across an entire family of traffic time series data. We compare three possible redundant dictionaries: Fourier+ Haar wavelets (referred to as
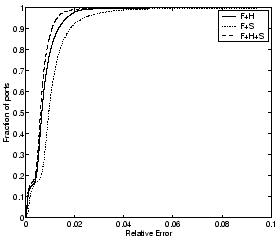 |
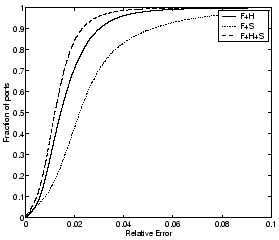 |
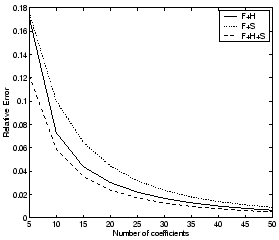 |
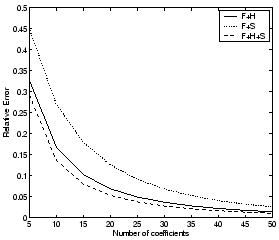 |
6.3 Analysis of Selected Modes
We proceed to analyze the set of dictionary components that are chosen
in the compressed representation using the redundant dictionaries for
different ports, along different spatial and temporal dimensions.
First, we are interested to see if there is substantial similarity in
the set of dictionary components selected in the compressed
representation across different ports. Second, we want to observe the
temporal properties of compression; i.e., for a fixed traffic dimension,
how does one week differ from another in terms of the components
selected from the redundant dictionary? Third, we want to identify
possible sources of correlation across the different traffic aggregates
(flows, packets, bytes, both to and from) on a particular port of
interest. Such analysis not only helps us to understand the nature of
the underlying constituent components that make up each traffic time
series but also enables us to identify possible sources of joint
compression, to further reduce the storage requirements. For the
discussion presented in this section, we use the dictionary 6.3.1 Spatial Analysis Across Ports
We observe that the majority of selected dictionary components are restricted to a small number of ports--this is expected as these modes capture the minor variations across different ports, and also represent traffic spikes that may be isolated incidents specific to each port. We also observe that there are a few components that are consistently selected across almost all the ports. These components that are present across all the ports under consideration include the mean (zero-th Fourier component), the diurnal/off-diurnal periodic components, and a few other periodic components which were found to be the highest energy components in the Fourier analysis presented in Section 6.1.
6.3.2 Temporal Analysis Across Multiple Weeks
We also analyze, for specific instances of ports as defined by our four
categories, the temporal stability of the set of components that are
selected across different weeks over the 20 week data set, using 30
modes per week. As before, we use 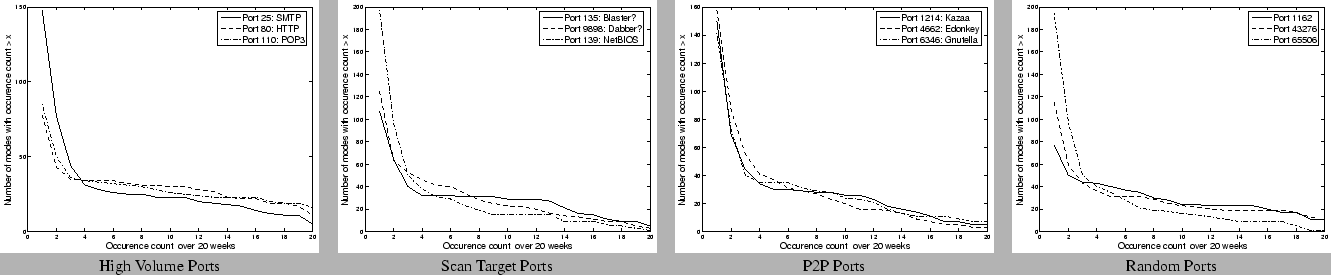 |
| Port Type | Port Number | All 20 weeks | 10-20 weeks | 0-10 weeks | |||
| Periodic | Spike | Periodic | Spike | Periodic | Spike | ||
| High Volume | 25 | 5 | 0 | 18 | 0 | 23 | 102 |
| 80 | 11 | 0 | 19 | 0 | 15 | 33 |
|
| P2P | 1214 | 5 | 0 | 21 | 0 | 20 | 104 |
| 6346 | 7 | 0 | 17 | 0 | 23 | 94 |
|
| Scan | 135 | 5 | 0 | 24 | 0 | 15 | 63 |
| 9898 | 3 | 0 | 20 | 0 | 35 | 67 |
|
| Random | 5190 | 11 | 0 | 10 | 0 | 27 | 73 |
| 65506 | 1 | 0 | 15 | 0 | 31 | 147 |
|
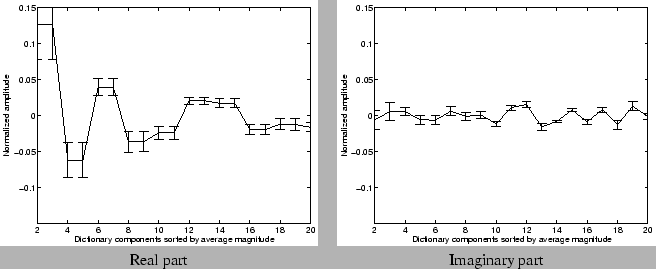
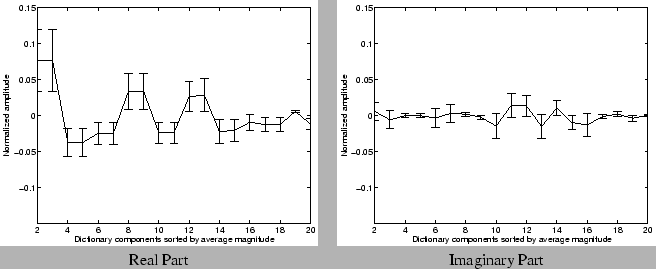
The stability of a component depends not only on the fact that it was selected in the compressed representation, but also on the amplitude of the component in the compressed representation. Hence, we also analyze the amplitudes of the frequently occurring components (that occur greater than 50% of the time) across the 20 week dataset. Figures 11 and 12 show the mean and deviation of the amplitudes returned by the greedy pursuit procedure for these frequently occurring components. For clarity, we show the amplitudes of the real and imaginary part of the Fourier (periodic) components separately. For each port, we first sort the components according to the average magnitude (i.e, the energy represented by both the real and imaginary parts put together) over the 20 week period. We normalize the values of the average amplitude in both real and imaginary parts, and the deviations by the magnitude of the mean (or zero-th Fourier) component. We observe that the amplitudes are fairly stable for many Fourier components across the different port types. These results suggest that these stable (Fourier) frequencies may indeed form fundamental components of the particular traffic time series. The relative stability of amplitudes in the compressed representation also indicates that it may be feasible to build traffic models, that capture the fundamental variations in traffic, using the compressed representations.
6.3.3 Spatial Analysis Across Traffic Metrics
The last component of our analysis explores the similarity in the
traffic data across different aggregates for a given port, within each
week. One naturally expects a strong correlation between the number of
flows, the number of packets, and the number of bytes for the same port,
and also reasonable correlation between the total incoming volume and
the total outgoing volume of traffic on the same port4.
Figure 13
confirms this natural intuition about the nature of the traffic
aggregates. We observe that for the high volume and P2P application
ports, more than two-thirds of the dictionary components are commonly
selected across all the different traffic aggregates and we also find
that more than 30 components are selected across at least 4 of the
traffic aggregates (bytes, packets, flows both to and from the port). We
found that such similarity in the selected components across the
different aggregates is less pronounced for the scan target ports and
the random ports under consideration. Our hypothesis is that the
distribution of packets per flow and bytes per packet are far more
regular for the high volume applications (for example most HTTP, P2P
packets use the maximum packet size to get maximum throughput) than on
the lesser known ports (which may be primarily used as source ports in
small sized requests).
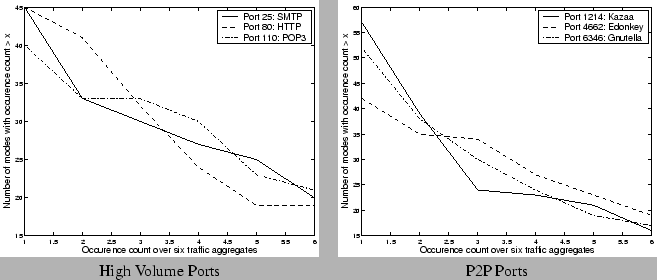 |
7 Applications
7.1 Visualization
One of the primary objectives of compression is to present to the
network operator a high fidelity approximation that captures salient
features of the original traffic metric of interest. Visualizing
historical traffic patterns is a crucial aspect of traffic monitoring
that expedites anomaly detection and anomaly diagnosis involving a
network operator, who can use historical data as visual aids. It is
therefore imperative to capture not only the periodic trends in the
traffic, but also the isolated incidents of interest (for example, a
post-lunch peak in Port 80 traffic, the odd spike in file sharing
applications, etc).
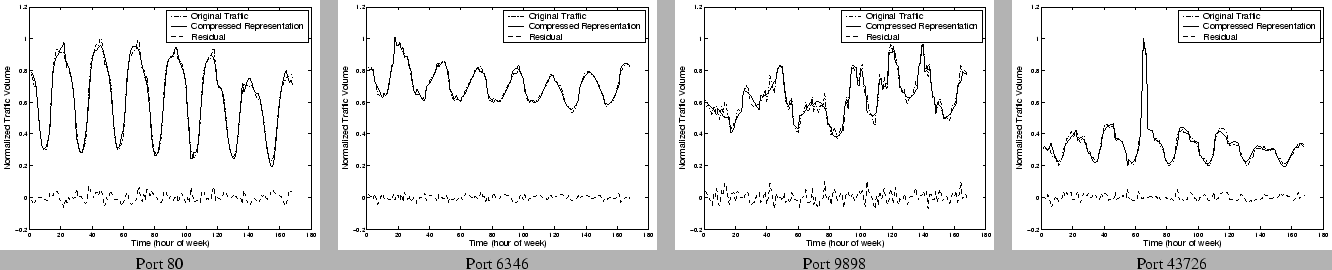
Figure 14 shows
some canonical examples from each of the four categories of ports we
described earlier. In each case we show the original traffic time series
over a week and the time series reconstructed from the compressed
representation using 1:6 compression with ![]() (Fourier +
Haar + Spike). We also show the residual signal, which is the point-wise
difference between the original signal and the compressed
reconstruction. The traffic values are normalized with respect to the
maximum traffic on that port observed for the week. We find that the
compressed representations provide a high fidelity visualization of the
original traffic data. Not surprisingly, the ports which exhibit the
greatest amount of regularity in the traffic appear to be most easily
compressible and the difference between the actual and compressed
representation is almost negligible for these cases. It is also
interesting to observe in each case that the compressed representation
captures not only the periodic component of the signal, but also traffic
spikes and other traffic variations.
(Fourier +
Haar + Spike). We also show the residual signal, which is the point-wise
difference between the original signal and the compressed
reconstruction. The traffic values are normalized with respect to the
maximum traffic on that port observed for the week. We find that the
compressed representations provide a high fidelity visualization of the
original traffic data. Not surprisingly, the ports which exhibit the
greatest amount of regularity in the traffic appear to be most easily
compressible and the difference between the actual and compressed
representation is almost negligible for these cases. It is also
interesting to observe in each case that the compressed representation
captures not only the periodic component of the signal, but also traffic
spikes and other traffic variations.
7.2 Traffic Trend Analysis
Analyzing trends in traffic is a routine aspect in network operations.
Operators would like to understand changes and trends in the application
mix that is flowing through the network (e.g. detecting a a new popular
file sharing protocol). Understanding traffic trends is also crucial for
traffic engineering, provisioning, and accounting applications. It is
therefore desirable that such trend analysis performed on the compressed
data yields accurate results when compared to similar trend analysis on
the raw (uncompressed) data. A simple method to extract trends over
long timescales is to take the weekly average, and find a linear fit
(using simple linear regression to find the slope of the line of best
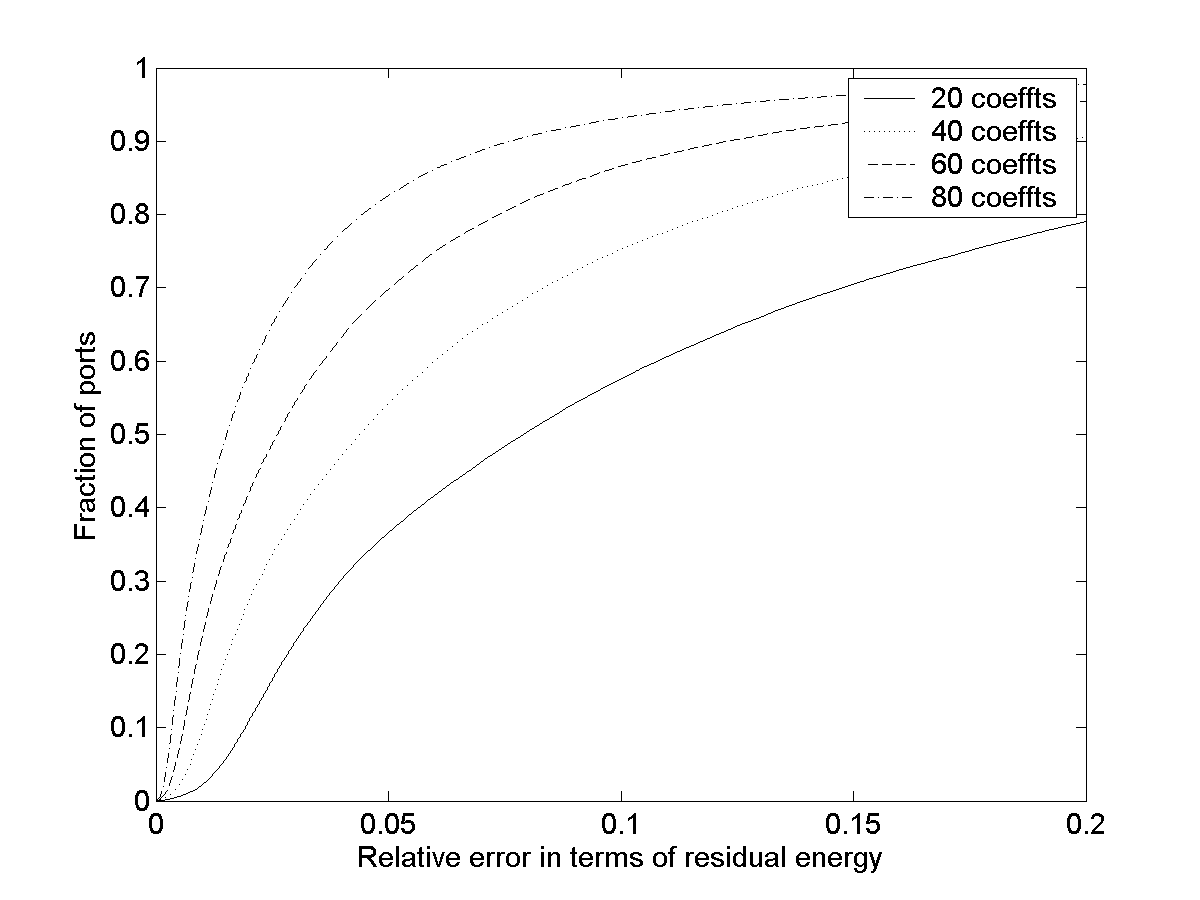
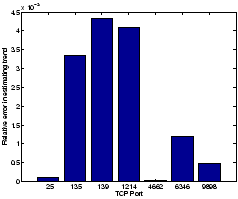
fit) to the weekly averages over multiple weeks of data. In Figure 15, we plot the
relative error in estimating such a linear trend. We estimate the trend
using 20 weeks of data for different ports, and in each case we
estimate the slope of the best linear fit on the raw data and on the
compressed data (using a 30 coefficient representation using
7.3 Modeling and Anomaly Detection
We observed in Section 6.3 that the underlying fundamental components are stable (both in terms of occurrence and their amplitudes) over time. It is conceivable that traffic models for anomaly detection can be learned on the compressed data alone. Our initial results suggest that traffic models [15] learned from compressed data have almost identical performance to models learned from uncompressed data, and hence compression does not affect the fidelity of traffic modeling techniques. Ongoing work includes evaluating different models for building prediction models for real-time anomaly detection using accurate yet parsimonious prediction models generated from the insights gained from the compression procedures.
8 Discussion
8.1 Stopping Criteria
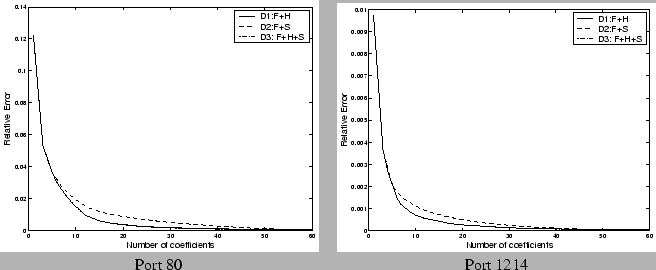
In our experiments, we fixed the number of coefficients across all ports. One can imagine a host of stopping criteria to apply. One particularly interesting observation is that in many of the cases, a few of which are depicted in Figure 16, we find that the residual energy has a distinct knee beyond which the rate of drop in the residual energy is significantly lower. Intuitively one can imagine as the knee corresponding to the stochastic noise component of the original signal, which cannot be efficiently represented using any fundamental component. Note that the anomalous incidents such as spikes or glitches are usually captured before we hit the knee of the curve, as observed in Section 7.1. This raises the possibility that we have a robust representation of the original signal--one that does not change with the addition of noise as there are diminishing returns for any added effort aimed at modeling the noise component, which are not necessarily of interest either from a visualization or modeling perspective. We have performed independent experiments with synthetic time series signals, similar to traffic time series (sinusoidal signals, with spikes and different noise patterns thrown in). We observe that in almost all the cases we observe a distinct knee in the redundant dictionary decomposition, once the fundamental high energy components get picked. We also find that the asymptotic slope of the curve of the residual energy beyond the knee has a unique signature that is characterized by the nature of the noise component (Gaussian or ``White'' vs. Power-law or ``Colored''), and the redundant dictionary used.
8.2 Smaller Scales
At an appropriate aggregation level, network traffic will exhibit some
periodicities. Traffic time series data from a variety of settings
(enterprise and university) also confirm this hypothesis. These data
typically represent the aggregate traffic at the border of a reasonably
large network with fairly high aggregation levels. We believe that the
methods for time-series compression using matching pursuit with
redundant dictionaries are still applicable to data even at slightly
lower scales of aggregation.
One of the objectives of compressing the time series is to enable
different scales of time resolution for anomaly detection. It is
imperative that the time scale for detecting traffic anomalies be less
than the minimum time required for a large network attack to saturate.
When the compression is applied to traffic aggregates at finer time
granularities (e.g. for each week if we had volume counts for each five
minute bin instead of hourly time bins), one expects that the effective
compression would be better. The rationale behind the intuition arises
from the fact that the high energy fundamental components correspond to
relatively low frequency components, and such pronounced periodicities
are unlikely to occur at finer time-scales. As a preliminary
confirmation of this intuition, we performed the same compression
procedures on a different data set, consisting of 5 minute traffic rates
collected from SNMP data from a single link. Note that with 5-minute
time intervals, we have ![]() data points per week. Figure 17 the relative error as
a function of the number of coefficients used in the compressed
representation (using
data points per week. Figure 17 the relative error as
a function of the number of coefficients used in the compressed
representation (using ![]() ). We observe that with
less than 40 ( = 2% of the original space requirement) coefficients we
are able to adequately compress the original time-series (with a
relative error of less than 0.005), which represents significantly
greater possible compression than those observed with the hourly
aggregates.
). We observe that with
less than 40 ( = 2% of the original space requirement) coefficients we
are able to adequately compress the original time-series (with a
relative error of less than 0.005), which represents significantly
greater possible compression than those observed with the hourly
aggregates.
8.3 Encoding Techniques
We observed that with larger dictionaries that include full-translation
wavelets, we can achieve better compression. There is, however, a
hidden cost in the effective compression with larger dictionaries as the
indices of a larger dictionary potentially require more bits to
represent than the indices of a smaller dictionary. One can imagine
better ways of encoding the dictionary indices (e.g., using Huffman
coding) to reduce the amount of space used up for storing the dictionary
indices in addition to the component amplitudes. Our work explored the
potential benefit of using signal processing methods for lossy
compression and we observed that there is a substantial reduction in the
storage requirement using just the methods presented in this paper. Many
compression algorithms use lossy compression techniques along with
efficient encoding techniques (lossless compression) to get the maximum
compression gain, and such combinations of lossy and lossless
compression methods can be explored further.
8.4 Joint Compression
We observe that there are multiple sources of correlation across the
different traffic dimensions that may be additionally utilized to
achieve better compression. The temporal stability of the compressed
representations (Section 6.3.2) suggests
there is scope for exploiting the similarity across different weeks for
the same traffic aggregate. For example, we could build a stable model
over The observations of the low dimensionality of network traffic data across different links also raises the possibility of using Principal Component Analysis (PCA) [10] for extracting better spatial compression, both across different traffic aggregates (e.g. different ports, across time) and across different measurements (e.g. across per-link, per-router counts). PCA like methods can be used to extract the sources of correlation before one applies redundant dictionary approaches to compress the traffic data. For example we can collapse the 20 week data set for a single port into a single matrix of traffic data, on which PCA like techniques can be applied to extract the first few common components, and the redundant dictionary can be applied on the residual (the projection on the non-principal subspace) to obtain a higher fidelity representation.
9 Conclusions
There is a pressing need for fine-grained traffic analysis at different
scales and resolutions across space and time for network monitoring
applications. Enabling such analysis requires the ability to store large
volumes of historical data across different links, routers, and
customers, for generating visual and diagnostic aids for network
operators. In this paper, we presented a greedy pursuit approach over
redundant dictionaries for compressing traffic time series data, and
evaluated them using measurements from a large ISP. Our observations
indicate that the compression models present a high fidelity
representation for a wide variety of traffic monitoring applications,
using less than 20% of the original space requirement. We also observe
that most traffic signals can be compressed and characterized in terms
of a few stable frequency components. Our results augur well for the
visualization and modeling requirements for large scale traffic
monitoring. Ongoing work includes evaluating and extracting sources of
compression across other spatial and temporal dimensions, and evaluating
the goodness of traffic models generated from compressed
representations.
Bibliography
-
- 1
- BARFORD, P., KLINE, J., PLONKA,D.,AND
RON,A.
A Signal Analysis of Network Traffic Anomalies.
In Proc. of ACM/USENIX Internet Measurement Workshop (2002). - 2
- DUFFIELD, N. G., LUND, C., AND
THORUP,M.
Charging From Sampled Network Usage.
In Proc. of ACM SIGCOMM Internet Measurement Workshop (2001). - 3
- ESTAN, C., SAVAGE, S., ANDVARGHESE,G.
Automatically Inferring Patterns of Resource Consumption in Network Traffic.
In Proc. of ACM SIGCOMM (2003). - 4
- FROSSARD, P., VANDERGHEYNST, P., I VENTURA,R.
M. F., AND KUNT, M.
A posteriori quantization of progressive matching pursuit streams.
IEEE Trans. Signal Processing (2004), 525-535. - 5
- GILBERT, A. C., MUTHUKRISHNAN, S.,AND
STRAUSS,M. J.
Approximation of functions over redundant dictionaries using coherence.
In Proc. of 14th Annual ACM-SIAM Symposium on Discrete Algorithms (2003). - 6
- GRIBONVAL, R., AND BACRY, E.
Harmonic decomposition of audio signals with matching pursuit.
IEEE Trans. Signal Processing (2003), 101-111. - 7
- INDYK, P.
High-dimensional computational geometry.
PhD thesis, Stanford University, 2000. - 8
- KRISHNAMURTHY, B., SEN, S., ZHANG,Y.,AND
CHEN,Y.
Sketch-based Change Detection: Methods, Evaluation, and Applications.
In Proc. of ACM/USEINX Internet Measurement Conference (2003). - 9
- LAKHINA, A., CROVELLA, M., AND
DIOT,C.
Diagnosing network-wide traffic anomalies.
In Proc. of ACM SIGCOMM (2004). - 10
- LAKHINA, A., PAPAGIANNAKI, K., CROVELLA,M.,
DIOT, C., KOLACZYK, E., AND TAFT,N.
Structural analysis of network traffic flows.
In Proc. of ACM SIGMETRICS (2004). - 11
- LEMPEL, A., AND ZIV, J.
Compression of individual sequences via variable-rate coding.
IEEE Transactions on Information Theory 24, 5 (1978), 530-536. - 12
- MALLAT, S., AND ZHANG, Z.
Matching pursuits with time frequency dictionaries.
IEEE Trans. Signal Processing 41, 12 (1993), 3397-3415. - 13
- MILLER, A. J.
Subset selection in regression, 2nd ed.
Chapman and Hall, London, 2002. - 14
- Cisco Netflow.
https://www.cisco.com/warp/public/732/Tech/nmp/netflow/index.shtml. - 15
- ROUGHAN, M., GREENBERG, A., KALMANEK,C.,
RUMSEWICZ, M., YATES, J., AND ZHANG,Y.
Experience in measuring internet backbone traffic variability: Models, metrics, measurements and meaning.
In Proc. of International Teletraffic Congress (ITC) (2003). - 16
- TROPP, J. A., GILBERT, A. C.,ANDSTRAUSS,M. J.
Algorithms for simultaneous sparse approximation part i: Greedy pursuit.
submitted (2004). - 17
- ZHUANG, Y., AND BARAS, J. S.
Optimal wavelet basis selection for signal representation.
Tech. Rep. CSHCN TR 1994-7, Institute for Systems Research, Univ. of Maryland, 1994.
Notes
- Typically, k is less than k, i.e. the magnitudes of the amplitudes of the dictionary components are less than the original time series.
- The slowest step in OMP is choosing the waveform which maximizes the dot product with the residual at each step. We can speed up this step with a Nearest Neighbors data structure [7] and reduce the time complexity for each iteration to N + polylog(d).
- Note that for each Fourier coefficient, we need to store both the real part and the imaginary part. It appears that we may actually need twice the space. However, the amplitudes for frequency f and frequency -f are the same (except that they are complex conjugates of one another), we can treat them as contributing only two coefficients to the compressed representation together in total as opposed to four coefficients.
- We however note that there may be certain exceptional situations
(e.g., worm or DDoS attacks that use substantially different packet and
byte types) where such stable correlations between the flow,
packet, and byte counts may not always hold.
Footnotes
- ... Aiello
- Majority of this work was done when the author was a member of AT & T Labs-Research
- ... Gilbert
- Majority of this work was done when the author was a member of AT & T Labs-Research. The author is supported by an Elizabeth Crosby Faculty Fellowship.
- ... Sekar
- Majority of this work was done when the author was a research intern at AT & T Labs-Research
|
Last changed: 22 Sept. 2005 aw |