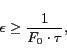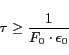To measure its own clock frequency, a digital system would typically feed its
clock to a counter and periodically compare its output with that of another
counter clocked by an accurate reference. The digital nature of the counting
process, however, limits the resolution of the measurement due to temporal
quantization. Thus, to obtain a high resolution frequency measurement, one must
either use a high nominal frequency or sample the counter over long intervals.
More formally, the resolution error 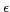 of a frequency measurement is bounded by
of a frequency measurement is bounded by
where, 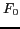 is the nominal frequency of the clock and
is the nominal frequency of the clock and 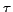 is the interval over which the counter is sampled.
In other words, if a system wants to know the frequency error with a resolution of
is the interval over which the counter is sampled.
In other words, if a system wants to know the frequency error with a resolution of 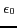 , then it needs to wait for at least
, then it needs to wait for at least
seconds. Numerically, a nominal clock frequency of 1MHz estimated to a resolution of 0.04ppm will require at least 25 seconds of contiguous counting. Power consumption is also related to nominal frequency through the linear relationship:
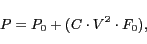 |
(1) |
where 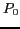 is the power lost due to leakage,
is the power lost due to leakage, 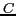 is the effective load capacitance and
is the effective load capacitance and 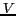 is the driving voltage.
Further, as energy consumed is
is the driving voltage.
Further, as energy consumed is 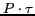 , there exists a strict tradeoff between the energy consumption and the achievable timing resolution.
Or in other words, if you lower the nominal frequency, you lower the power consumption, but at the same time decrease the achievable time resolution.
, there exists a strict tradeoff between the energy consumption and the achievable timing resolution.
Or in other words, if you lower the nominal frequency, you lower the power consumption, but at the same time decrease the achievable time resolution.
Thomas Schmid
2008-11-14

![]() of a frequency measurement is bounded by
of a frequency measurement is bounded by