|
|

|
Abstract This paper proposes to develop a system-wide energy consumption model for servers by making use of hardware performance counters and experimental measurements. We develop a real-time energy prediction model that relates server energy consumption to its overall thermal envelope. While previous studies have attempted system-wide modeling of server power consumption through subsystem models, our approach is different in that it uses a small set of tightly correlated parameters to create a model relating system energy input to subsystem energy consumption. We develop a linear regression model that relates processor power, bus activity, and system ambient temperatures into real-time predictions of the power consumption of long jobs and as result controlling their thermal impact. Using the HyperTransport bus model as a case study and through electrical measurements on example server subsystems, we develop a statistical model for estimating run-time power consumption. Our model is accurate within an error of four percent(4%) as verified using a set of common processor benchmarks. |
The upwardly spiraling operating costs of the infrastructure for enterprise-scale computing demand efficient power management in server environments. This is difficult to achieve in practice as a data center usually over-provisions its power capacity to address worst case scenarios. This often results in either waste of considerable power budget or severe under-utilization of capacity. Thus, it is critical to quantitatively understand the relationship between power consumption and thermal load at the system level so as to optimize the use of deployed power capacity in the data center.
This paper introduces a statistical model that provides run-time system-wide prediction of energy consumption on server blades. The model takes into account key thermal and system parameters such as ambient temperatures, die temperatures, and hardware performance counters as metrics for system energy consumption within a given power and thermal envelope.
A hardware performance counter (PeC) based relationship between server blade power consumption and the consequent thermal envelope is necessary to dynamically control the thermal footprint of large workloads. We construct a model for run-time system power estimation that dynamically correlates system-bus traffic with task activities, memory-access metrics and board-level power measurements. This work demonstrates that appropriate provision of additional PeCs beyond what are provided by a typical processor is required to obtain more accurate prediction of system-wide energy consumption.
Using the HyperTransport [1] bus model as a case study and through electrical measurements on an example server architecture, we develop our model to estimate run-time power consumption. Scheduler-based mechanisms are being developed to take advantage of this estimation model when dispatching jobs to confine server power consumption within a given power budget and thermal envelope while minimizing impact upon server performance. Their results will be reported separately at a later time.
Power management techniques developed for mobile and desktop computers have been applied with some success to managing the power consumption of microprocessors used in server hardware. The current generation of Intel and AMD processors use different techniques for processor-level power management including (1) per core clock gating, (2) multiple clock domains, (3) multiple voltage domains for cores, caches, and memory, (4) dynamic voltage and frequency scaling per core and processor, and (5) hardware support for virtualization techniques. In general, these techniques take advantage of the fact that application performance can be adjusted to utilize idle time on the processor for energy savings [2]
Extensive study has focused on limiting the power consumption of storage devices and main memory as these devices are the greatest energy consumers in the system after the processor. However, these approaches optimize only one part of the system. This is problematic because the system components interact with each other and focusing on just one piece of the energy consumption model may not be optimal from the complete system standpoint. An effective power model must take into account the impact of these interactions.
Processor power consumption is often modeled by the correlation of power consumption to phases of application execution using system-level metrics. The approaches used to define this mapping fall into two categories: determining the application phase from either the control flow of the application or performance counter signatures of the executed instructions or operating system metrics [2][3][4][5]. Attempts have been made to reconcile these approaches by mapping programs phases to events [6]. The most common technique used to associate PeCs and/or operating systems metrics to energy consumption use linear regression models to map the collected metrics to the energy consumed during the execution of a program [2][5][7].
The power model must also take thermal issues into account. Management of thermal issues is complicated by the existence of multiple cores per processor. Recent advances in processor design permit thermal management to occur on a per core and per processor basis. An analysis of the impact of multi-core processors can be found in [8].
Our model considers a single server blade as a closed black-box system. The black-box system model lets us converge upon an upper bound of the thermal, energy, and power envelopes of the system. We develop our model by measuring the energy input into the system as a function of the work done by the system in executing its computational tasks and residual thermal energy given off by the system in doing that work. It is important to note that we are trying to establish an energy relationship between the workload and the overall thermodynamics of the system.
We begin by considering the power supplied into the server at the output of the power supply unit. Having a measure of this input power gives us a handle over the total current distribution across various voltage domains and into the various sub-systems of the server. Current sensors with readable counters at the outputs of the power supply as performance counters would immensely aid in dynamically tracking DC power drawn into the system that varies according to the system load.
The DC power is delivered in the domains of +/-12 V, +/-5V, and +/- 3.3V [9]. Most power supplies limit the total power delivered through the 5V and 3.3V lines to about 20% of the rated power supply (PR). Now assuming each of the voltage lines vk(t) draws current ik(t), then each line draws an instantaneous power of pk(t) = vk(t) ⋅ ik(t). If a voltage domain has M DC lines as output, the board has N voltage domains and the total power delivered into the system in time interval t2 to t1 is:
| Edc | = ∫ t1t2 ∑ j=0N ∑ k=0Mjv k(t) ⋅ ik(t)dt | (1) |
This energy delivered to the system Edc = Esystem can be expressed as a sum of energy component contributed by the different sub-systems in the server blade. We define five energy consumption components within a system: (1) Eproc: Energy consumed in the processor due to all computations, (2) Emem: Energy consumed in the DDR SDRAM chips, (3) Eem: Energy consumed by the electromechanical components in the server blade, (4) Eboard: Energy consumed by peripherals that support the operation of the board., and (5) Ehdd: Energy consumed by the hard disk drive during the server’s operation. Note that Eem includes the fans and optical drives but Ehdd is separate as one can dynamically compute the HDD’s power consumption. Eboard includes all devices in the multiple voltage domains across the board, including chipset chips, voltage regulation, bus control chips, connectors, interface devices, and etc. Mostly these are covered in the 3.3V and 5V domains.
Our processor model aims to treat the processor as a black box, whose energy consumption is a function of its work load, and the work done manifests as the core die-temperature and system ambient temperature (measured at a system level by ipmitool through sensors in the path of the outgoing airflow from the processor). A practical issue with trying to estimate processor power using a large number of PeCs is that there are only a limited number of PeCs that tools like cpustat can track simultaneously. In order to track the energy-thermal load relationship for a job, we had to develop a model with the least number of PeCs that would accurately reflect the energy consumption-thermal load relationship.
Given the AMD Operton processor architecture connected in a dual core configuration shown in Figure 1, we consider traffic on the HyperTransport buses as representative of the processor work load and reflecting the amount of data being processed by a processor or any of its cores. The HT2 bus is non-coherent and connects one of the two processors to the Southbridge (whereas the Northbridge is inside the Opteron processor). Thus, traffic on the HT2 bus reflects hard-disk and network traffic. The model therefore scales when considering the effect of network traffic and heavy disk I/O based jobs. HT1 is a coherent bus between the two SMP processors and PeCs on that bus give an accurate reflection on the processing load of cores executing jobs. Per-core die temperature readings and, consequently, ambient temperature per processor are thus greatly affected by the number of transactions over the HT buses. We also include L2 cache misses as one of our variables (to be explained in Section 3.2).
Thus the total processor power consumption to reflect the thermal change due to workload can be expressed as:
| Pproc | = H ⋅ X | (2) |
= [β0 β10]T ⋅ [V ar
0 β10]T ⋅ [V ar
0 V ar10]T V ar10]T | (3) |
Energy consumed by the DRAM banks can be computed by a combination of measuring the counts of the highest level cache miss in the processor combined with the DRAM Read/Write power along with the DRAM background power(activation power). As illustrated in [10], DRAM background power and activation power can be obtained from the DRAM datasheets. For a single DRAM in our case, a total of 493mW would be consumed. However, given the number of L2 cache misses per second when a job is running on a certain core (over 22M / sec at the peak of bzip2 SPEC2006 benchmark), a significant amount of heat is generated from the DRAM chips. The thermal airflow proximity of the DRAM banks to their respective processors makes it possible for us to combine the energy consumption and the consequent thermal output of the memory banks with the processor ambient temperature. This value is reported by IPMI and we combine it into our regression model.
The energy consumed by the hard disk while operating, can be approximated to give an upper bound on the energy consumption of the hard disk using a combination of performance counters and drive ratings. In our server, Hitachi’s 7200 RPM, 250GB SATA hard disk [11] is used. We can achieve a crude but simple model based on the typical power consumption data of the hard disk and performance counters.
The utility iostat can be used to measure the number of read and writes per second to the disk as well as the kilobytes read from and written to the disk. Based on this performance counter, we can compute an approximate disk power consumption Ehdd value as :
| Ehdd | = Pspin-up × tsu + Pread ∑ Nr × tr | ||
| + Pwrite ∑ Nw × tw + ∑ Pidle × tidle | (4) |
The quantity Eem in our model takes into account the energy consumed by the cooling fans in the server as well as the optical drives. In our case, no performance counters are available for the optical drive energy measurements and they are obtained from measurements but could easily be obtained using current sensors at the DC output of the power supply. Power drawn by the fans for cooling can be given by the following equation [12]:
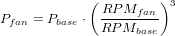 | (5) |
Pbase in this case defines the base of the unloaded system. In our system that is the power consumption of the system when running only the base operating system and no other jobs. That value is obtained experimentally by measuring the current drawn on the +12V and +5V lines, using a current probe and an oscilloscope. IPMI sensors [13] easily collect fan RPM data, and hence it is possible to quantify the electrical power consumption in the system. Thus,
| Eem | = ∑ Pfan × tipmi-slice + ∑ Poptical × t | (6) |
The quantity Eboard captures the energy required by the support chipsets and usually fall in the 3.3V and 5V power domains. In our case we obtain this value using current probe based measurements. However, as in earlier cases, current sensors for the power lines going into the board can provide instantaneous energy draw from the power supply. The processor, disk, fan, and optical-drive power lines are excluded here. For our server, at most 28 additional current sensors might be required for the entire blade [9]. Thus:
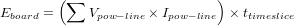 | (7) |
The total energy consumed by the system for a given computational workload is modeled as a function of these metrics as:
| Esystem | = α0(Eproc + Emem) + α1Eem | ||
| + α2Eboard + α3Ehdd | (8) |
|
The power model was calibrated to the SUT by executing eight benchmarks from the SPEC CPU2006 benchmark suite: bzip2, cactusadm, gromac, lbm, leslie3d, mcf, omnetpp, and perlbench [14]. The power consumed is measured with a WattsUP [15] power meter connected between the AC Main and System Under Test (SUT). The internal memory of the power meter is cleared at the start of the run and the measures collected during the run are downloaded after the run completes from the meter’s internal memory into a spreadsheet.
Current flow on the different voltage domains in the server is measured using an Agilent MSO6014A oscilloscope with one Agilent 1146A current probes per system power domain (12v, 5v, and 3.3v). This data is collected from the oscilloscope at the end of the execution of a benchmark and stored in a spreadsheet on the test host.
Five classes of metrics are sampled at 5 second intervals during the experiment: (1) CPU temperature for all processors in the system, (2) Ambient temperature in the computer case measured in one more locations using the sensors provided by server manufacturer, (3) the number of completed transactions processed through the system bus, (4) the number of misses that occur in the L2 cache associated with each CPU core in the system, and (5) the amount of data transferred to/from disk.
System data is collected from the system baseboard controller using the IPMI interface and the Solaris iostat utility. Processor performance counters are collected on a system-wide basis using the Solaris cpustat utility.
|
|
The collected data was consolidated using the arithmetic mean (average) and geometric means of the data sets. Trial models were constructed using each method and a statistical analysis of variance (ANOVA) was performed to determine which model generated the best fit to the collected data.The model was verified by examining the predicted results for each benchmark against the data collected in the calibration test (Fig. 2). A comparison between the predicted CPU power consumption and the ambient temperatures is shown in Fig. 3. The mean error per benchmark ranged from [1.35,2.30] Watts with median values in the range of [0.83,2.40] watts and standard deviation between [0.80,1.5] watts.
The consolidated model is attempting to predict for all benchmarks. Given the large volume of data generated thorough the different logging mechanisms, it is nearly impossible to discard bad data. Using the geometric mean as discussed in the previous section helps to smooth out some of the errors introduced in the cases. However, the diversity of the benchmarks used means that some discrepancies arise within variables where we expect to see tight correlations, This, the model predicts well in some cases and not in others. The worst error is no more than the four present reported above.
Also, the asymmetry of the β-coefficients for tightly correlated variables (HT1Scaled and HT2Scaled, for example) leads us to believe non-linear relationships may exist among these variables. Therefore, future work needs to consider the impact of use of non-linear regression models together with hardware performance counters.
Another observation from the model pertains to the placement of the temperature sensors in the server. Ambient_Temp0 reflects more of the hot air flow due to the server design. This illustrates that for different server designs the factors controlling the thermal envelope will be accurately reflected in the model. Thus, we would expect to see a more symmetric set of coefficients for Ambient_Temp0 and Ambient_Temp1 had the placement of the sensors been more balanced in the server.
In terms of measuring performance counters, we have used the Solaris 10 cpustat, iostat, and ipmitool utilities. Of these, iostat and ipmitool are available across all UNIX-based operating systems commonly used in data centers. cpustat is a Solaris specific utility but is already being ported to Linux. In future work, it is planned to use tools like dtrace and oprofile for more controllable and tunable performance parameters which have major impacts on system-wide and processor wide power consumption.
The computation methodology used in this paper can be extended to other architectures. For example, we would measure Xeon performance counters like BUS_TRANS_ANY, BUS_TRANS_MEM, and BUS_TRANS_BURST. Similar model development and coefficient extraction arguments would hold for dual and quad core Xeons in different processor configurations. Currently without data from the Intel processors it is hard to say whether the model is more accurate on a certain platform as compared to the other.
For a practical usage scenario the statistical coefficients need to be computed only once using the SPEC benchmarks for a given server architecture. They can be used as embedded constants available either through the system firmware or the operating system kernel.
The model developed in this paper is valid for any AMD Opteron dual-core/dual-processor system using the HyperTransport system bus. However, it is scalable to any quad-core dual processors Opteron system using HyperTransport. One would expect to see a slight difference or variation in the predicted power due to the greater or diminished affect of the die temperatures on the other parameters and the model would have to be adjusted accordingly. For a dual-core quad-processor system, the additional HT0 term would be introduced into the CPU power consumption term and the β coefficients would have to be recalculated and the CPU power equation will have more terms. For a quad-core quad processor system, similar recalculations would be required.
In this paper, we have introduced a comprehensive model which uses statistical methods to predict system-wide energy consumption on server blades. The model measures energy input to the system as a function of the work done for completing tasks being gauged and the residual thermal energy given off by the system as a result. Traffic on the system bus, misses in the L2 cache, CPU temperatures, and ambient temperatures are combined together using linear regression techniques to create a predictive model which can be employed to manage the processor thermal envelope.