No Title

Towards a Practical, Verified Kernel

Kevin Elphinstone¹, Gerwin Klein, Philip Derrin, Timothy Roscoe², Gernot Heiser ³
National ICT Australia⁴

Abstract

In the paper we examine one of the issues in designing, specifying, implementing and formally verifying a small operating system kernel - how to provide a productive and iterative development methodology for both operating system developers and formal methods practitioners.

We espouse the use of functional programming languages as a medium for prototyping that is readily amenable to formalisation with a low barrier to entry for kernel developers, and report early experience in the process of designing and building seL44: a new, practical, and formally verified microkernel.

1 Introduction

We describe our approach to constructing seL44 - a useful yet formally verified operating system kernel, by means of a novel development process which aims to reconcile the conflicting methodologies of kernel developers and formal methods practitioners.

Despite vigorous debate on the topic of microkernels versus virtual machine monitors[5,6,12], there is an emerging consensus on smaller and more trustworthy kernels (whether hypervisors or microkernels) at the core of larger software systems. We have argued that the small size of current kernels, and the increased power of interactive theorem proving environments, means that the time is right to attempt formal verification by proof of a real-world microkernel [14].

The end goal of such a project is to show that a working kernel implementation behaves as it is formally specified in an abstract model. Additionally, we would like properties such as spatial partitioning of processes to hold in both the model and implementation, together with useful properties such as guaranteed termination of system calls, and the kernel never throwing an internal exception.

Successful OS kernels have generally been the result of careful attention to performance issues, and repeatedly iterating bottom-up implementations of low-level functionality, in some cases changing high-level interfaces and functionality to accommodate implementation constraints and performance goals. This is, unfortunately, in conflict with formal methods, which typically work by top-down refining models of system properties, and rarely deal with low-level implementation features.

This paper describes our approach to resolving this tension, and reports on our experience so far in applying it to seL44. We use a high-level language (Literate Haskell) to simultaneously develop a specification of the kernel and a reference implementation for evaluation and testing. The implementation can be used in conjunction with a simulator such as QEMU for running real application binaries, while the specification generates input to an interactive theorem prover (Isabelle) for formal proof of properties. The use of a clean, high-level language allows rapid iterative prototyping of both the specification and reference implementation. Finally, a deployable kernel is constructed as a refinement of the reference implementation in a high-performance low-level language.

The rest of this paper is structured as follows. In the next section we look in more detail at the issues in achieving a verified kernel, based in part on our experience trying to formally verify L4. Section 3 describes our pragmatic approach to tackling the issues identified, and Section 4 reports on our experience so far with seL44. Section 5 concludes.

2 Background and Issues

There are many challenges in designing, specifying, implementing, and formally verifying a high-performance microkernel. In our view, the most significant of these (and our focus in this paper) is reconciling the approach taken by kernel developers when system building with that taken by formal methods practitioners in developing and verifying properties of a system.

Kernel developers tend to adopt a bottom-up approach. Required functionality is provided by iteratively developing a high-performance low-level implementation, and it is not unusual to modify the delivered functionality or its interface to facilitate efficient implementation.

In contrast, formal methods practitioners take a top-down approach, iteratively developing potential models of the system to possess the properties required, with secondary regard (if any) to low-level implementation details.

This characterization simplifies a rather complex problem, but it illustrates the need for a methodology that has a low barrier to entry for both teams, facilitates both working together, and enables both to efficiently iterate through the design, specification, implementation, and verification of the system.

Creating an assured and useful general-purpose OS kernel has been a goal for some time [16,1]. Recently, a number of approaches have been adopted.

A strawman approach is to create a natural-language specification and then iterate through the design of the system. Such a specification is easily written and read, but is prone to ambiguity and incompleteness. It often fails to expose design issues that may have a significant impact on performance, usability, and ease of implementation.

The VFiasco project [7] aims to verify an existing kernel (L4/Fiasco) directly by developing a formal semantics for the subset of C++ used to build it, in particular with a novel treatment of memory access. However, a formal semantics for a sufficiently rich subset of C++ is a large task, and it is unclear how much progress has been made since the project's inception in 2001.

The Coyotos team [13] take the different approach of defining a new low-level implementation language (BitC) with precise formal semantics, and hope to subsequently verify properties of the kernel they are building.

Although with less emphasis on high-level verification, the Singularity project also uses a type-safe imperative language (C#), but with additional compiler extensions to allow programmers and system architects to specify low-level checkable properties of the code, for example IPC contracts [3].

All these approaches iteratively develop a kernel in an imperative systems programming language (with varying degrees of safety), and then attempt to reason at a some level about the system as a whole. The challenge here is that it may be extremely difficult to extract an abstract model from the finished artifact, as the expected behavior is not made clear by the low-level code (especially since this code may contain bugs).

Furthermore, since it must be extracted from the implementation, such an abstract model cannot be used during the design process and is unlikely to be useful as a readable specification for developing a formal model of the system.

A final, and rarely acknowledged drawback with a bottom-up approach to verified kernel development is that many low-level details such as hardware interfacing must be implemented before any experience can be gained with the new design. The approach in section 3 allows a new design to be tried with real applications at an early stage.

In contrast, using formal specification at an abstract level to specify the design avoids ambiguity, but may not expose issues affecting performance and ease of implementation of the design until a much later stage. This is a particular problem for systems software, which is performance-critical and must operate in a relatively constrained environment. To a formal model, it makes little difference if a data type is implementable in four or five bytes, but to a kernel developer this can be critical to performance of an important code path in the system.

Also, it is difficult to evaluate the usability of a microkernel interface for building complete systems based on that interface, until such a system has actually been built.

Finally, the tools and techniques used for developing formal specifications are quite different to those typically used for systems software, so there is a high cost of entry for many kernel developers.

Implementation in a high-level language with well-defined and safe semantics is a good compromise between the previous two approaches. For example, the Osker kernel [4] is written in Haskell. The resulting implementation is easier to reason about than one in a low-level language but is typically limited by a high-level language's dependency on a complex runtime ill-suited to use in a stand-alone kernel. This may impose restrictions on the system that are not present when using low-level languages, such as a need for garbage collection of kernel memory.

In summary, there is a need for a development methodology that enables kernel developers to rapidly iterate through prototype kernels with sufficient access to low-level details to explore performance aspects of the design, while providing formal verification teams with the precise semantics of the system in a form suitable as input to a theorem proving environment.

We now describe our approach, which has produced a precisely specified kernel API, together with a usable reference implementation, and a formal model for the implementation in the Isabelle theorem prover.

3 Our Approach

In this section we describe the pragmatic approach we took to address the issues we identified earlier and unify our team of formal verification experts with our team of kernel developers. Referring to Figure 1, our approach revolves around "running the manual": We use Literate Haskell to develop both a specification document of the kernel, and at the same time, a reference implementation that can be used for evaluation and testing. The Haskell specification serves as the medium for iterative prototyping of the implementation as well as the system model for both the kernel and formal modelling teams, i.e. the Haskell specification forms a bridge between the teams improving the flow of ideas, with a low barrier of entry for both. In addition, the reference implementation, when coupled with a simulator, can be used to run native binaries.

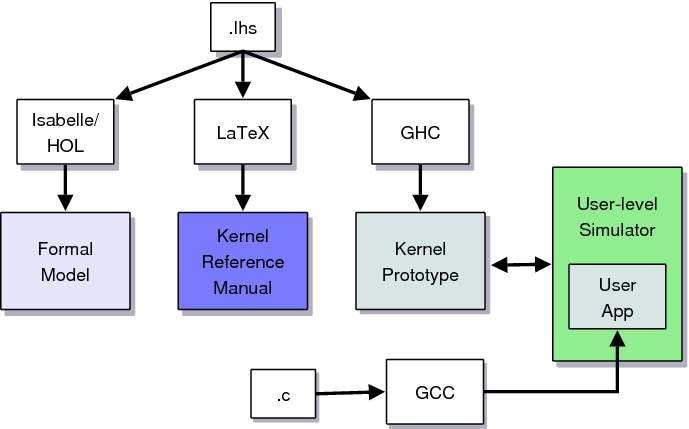Figure 1: Graphical representation of our approach using Literate Haskell (.lhs) as a basis for specification, implementation, and formalisation

3.1 Kernel Development

From the kernel development perspective, various designs and their implementation can be explored at a high level without the initial need to deal with the complexity of low-level hardware. However, given that the specification is an implementation, kernel developers are forced to think about implementation details that would be necessary for efficient implementation on real hardware. While the Haskell implementation is not suitable for quantifying the kernel's performance, it does provide valuable insights into the approximate performance of data structures and algorithms.

To explore the utility of the design from a user-level perspective, we have several approaches. From the kernel perspective, the hardware is an event generator (interrupts, exceptions, system calls). The Haskell prototype is set up as the recipient of an event stream, upon which it can process the events and return the results as if it were a real kernel. Early, simplistic, versions of the kernel used a simple event generator function which took embedded pseudo-assembly to exercise the kernel model. For more mature versions of the design, we coupled the kernel model with a simulator for the unprivileged part of a real processor's ISA. This enables running compiled native code just as on real hardware. We currently can link our kernel model with the M5 Alpha simulator[8], a home-grown ARM simulator, and the QEMU ARM simulator complete with emulated devices. In each case, the kernel model processes the incoming event stream, returning the results such that it appears to application code that it is running on raw hardware. Thus we have an environment that allows kernel developers to explore design and implementation of both the kernel itself and the applications intended to be supported.

3.2 Formal Modelling

One of the tasks of the formal verification team is to extract a formal model of the prototype in order to reason about it in the theorem proving environment.

Given the precise semantics of the Haskell language, and the lack of side-effects of functional languages in general, it is a much simpler task to extract a formal model of the kernel compared to typical low-level systems languages like C.

The translation from Haskell to a model in the theorem prover Isabelle/HOL [11] is mostly syntactic and can be automated. The exceptions worth noting are lazy evaluation and monadic computations (an example being computation that modifies global state). While Isabelle/HOL is not suitable for expressing the semantics of lazy evaluation as provided by Haskell, our goal is not to translate faithfully every language construct in Haskell to Isabelle. Instead, we only seek an accurate representation of the semantics of each function that occurs in the prototype, and thus we can avoid the issue by not making essential use of laziness in our Haskell specification. The type system of Isabelle/HOL is also not strong enough to express monads in the traditional abstract way, but it can express all the particular concrete monads that are used in the prototype. For more detailed coverage of the issues we encountered in the translation process, see [2].

Since Isabelle/HOL is a logic of total functions, we had to prove during the translation that all functions terminate. The translation of our Haskell kernel model into Isabelle thus already establishes one useful property of the kernel - system calls always terminate.

In our ongoing work on formally verifying the kernel we are currently showing that the Isabelle/HOL translation of the Haskell prototype conforms to a simplified, more abstract formal model of the kernel. This model is used to facilitate proofs of more complex safety and invariant properties of the kernel without going into implementation detail.

The process of formal refinement already requires us to show certain invariants of the kernel. The main part of these invariants resemble a strong typing system: capabilities always point to kernel objects of the right type (i.e. a thread capability always points to a valid TCB), capability tables are always of the correct size, references in kernel objects point to valid other kernel objects of the right type, etc. Note that the usual programming-language type systems are not strong enough to ensure these properties statically, even Haskell's very strong type system is insufficient.

Isabelle is an interactive theorem prover. This means that proof scripts are written manually with considerable creative input. The tool mechanically checks the proofs and assists in finding them by dealing with symbolic calculations, automatated proof tactics for certain classes of formulae etc, but it is not fully automatic.

The abstract specification is ca. 3.5k lines of Isabelle code, the translated Haskell prototype comes to about 7k lines of Isabelle code (this number is somewhat inflated due to the automated translation process), and the proof scripts to date to about 48k lines. The verification process so far lead to 109 changes in the abstract specification and 37 changes in the Haskell code. This supports the conclusion that executing the specification finds many small problems with relatively little effort early in the process.

Examples of the bugs we found range from cut & paste errors (e.g. using the wrong function on the AsyncEndpoint data type where the line directly above has the same pattern for Endpoint), over forgotten cases, to more conceptual issues like a complex, recursive delete function that was misbehaving in the case of circular pointer structures, or simply functions that were less general than believed and required more checks on user-supplied parameters (e.g. a capability move function that took the same arguments as the corresponding copy function, but would lead to security violations in some of the cases that worked for copy).

The next step in the verification will be connecting this prototype with a high performance C implementation of the seL44 API. Tuch et al [15] have demonstrated the technology for this step and have shown its feasibility for low-level C code in a case study on the L4 kernel memory allocator.

3.3 Overall

It should be clear that our approach makes some progress towards resolving the issues we have identified, but what might not be clear is how our approach relates to our original goal of producing a formally verified, high-performance microkernel - i.e. a kernel implemented in a more traditional systems language such as C.

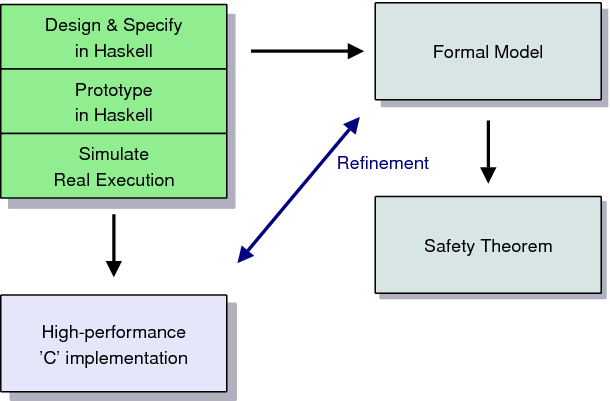Figure 2: Overall approach to eventual verification of a high performance kernel.

Figure 2 illustrates the end game. We are using the mature Haskell specification as a basis for both a formal abstract model of the system, and a high-performance C implementation. To achieve our original goal, we expect to then show that the C implementation is a refinement of the formal model. Details on our method for reasoning abstractly about low-level C code can be found in [15]. Together with the proof described here, this automatically gives us a proof that the abstract invariants also hold for the C implementation, and that the production kernel formally implements the abstract seL44 API as described previously [14]. As in the first verification step, we expect this second refinement to lead to a number of changes in the implementation - be they for performance or correctness reasons. For the final theorem to hold, these will be propagated back to the higher specifation levels and the proofs adjusted accordingly. Since the proofs are machine checked, we still get guaranteed consistency between all layers.

In principle, for the production kernel and its formal proof, the Haskell prototype could be thrown away; in the correctness sense it is redundant. For investigating new features and further developing the API, we expect it to be still useful, though, even when the production kernel exists. In any case, the Haskell kernel has already had an immense impact on overall productivity.

4 Experience

Despite the inevitable culture clash, experience with developing an OS kernel in this way has so far been positive. We describe our key learnings to date below.

4.1 Parallel Development

For us the most positive outcome of developing a kernel in a functional language has been having a medium in common for both kernel developers and formal modellers to cooperatively and iteratively develop a formally verified design and implementation of a small kernel.

The translation to Isabelle/HOL started relatively early, when the seL44 API was nearing a first stable point and first user-level binaries could be run through the machine simulator. The formal verification team, in translating the Haskell specification, found and fixed a number of problems. An illustrative example is an obscure corner case, where the execution time of the IPC send operation was unbounded. This was discovered when Isabelle demanded termination proofs for operations that were supposed to execute in constant time.

This shows that formalisation and the use of theorem proving tools is beneficial even if full verification is not yet performed. Thus far, the cost involved in formalisation has been significantly less than the design, implementation, and testing input by the kernel team, while the kernel team did not have to switch to completely new methods or notations. Additionally, the common medium has enabled the formal modellers to have input on the structure of the reference implementation in order to reduce the complexity of formalisation, with minimal effect on the kernel behaviour and performance.

The user-level simulation environment has enabled the porting of existing software to the new kernel design prior to its existence on bare metal. The experience gained by actual use of the new design has also led to the identification of issues requiring attention. For example, when attempting to implement a higher-level system upon the microkernel, we found that an atomic swap operation on a particular kernel object greatly simplified the implementation of higher-level system software. The missing operation was added in a matter of hours, and formalised soon afterwards.

Summarising, we have found our methodology has enabled the kernel developers, the formal modellers, and the higher-level system programmers to work more closely together, leading to faster and better results than we would expect if the phases had been sequential.

4.2 Precise Specification

Our choice of Literate Haskell as our modelling language has enabled us to produce a reference manual and implementation that is one and the same thing, providing rare but highly-welcome assurance that our reference manual and reference implementation are consistent. Our catch phrase is "we run the manual". While our hope is to produce a readily understandable reference manual describing each operation with the reference Haskell implementation as the definitive definition of each operation, structuring our code to avoid too much implementation detail (that would obscure the relevant details of the specification) has proved challenging. However, the document is improving with each iteration.

4.3 Hardware and Prototyping

We found that iteratively prototyping the system in a high-level language away from the pitfalls and traps of real hardware helped in maturing the design of a new system. Rather than spend time debugging low-level code from the beginning of prototyping, we could initially focus on design and implementation issues of the basic concepts behind the system. As the design evolves, we are bringing in hardware-related issues (such as dealing with pages table or TLBs) when we choose to tackle each particular aspect of the design.

However, we could still gain experience in using the new design as soon as it was mature enough to be coupled with various user-level simulators. We have ported the Iguana OS (an embedded OS personality for the L4 microkernel [10]) to our design and could understand the interaction between Iguana and our new design prior to any prototype existing on bare metal.

5 Conclusions

We found that using a very high-level language as a medium for concurrently prototyping the specification and design of a high-performance microkernel not only provided a convenient and highly productive fast prototyping environment. More importantly, it allowed us to design a high-performance kernel for formal verification, producing a model that can be translated automatically into the theorem prover, and that is suitable for proving system invariants as well as formal refinement. Specifically it provided the bridge that makes it feasible, even easy, for kernel developers and formal methods people to collaborate on the specification, design, implementation and formal verification of the kernel.

Overall, this has allowed us to take a new approach towards building an OS kernel that can be proven to operate correctly. Almost forty years ago, Needham and Hartley remarked [9]:

In designing an operating system one needs both theoretical insight and horse sense. Without the former, one designs an ad hoc mess; without the latter one designs an elephant in best Carrara marble (white, perfect, and immobile).

We believe that we have developed an approach to OS design that results in a highly productive synthesis of theoretical insight and horse sense.

References

[1]: William R. Bevier. Kit: A study in operating system verification. IEEE Transactions on Software Engineering, 15(11):1382-1396, 1989.
[2]: Philip Derrin, Kevin Elphinstone, Gerwin Klein, David Cock, and Manuel M. T. Chakravarty. Running the manual: An approach to high-assurance microkernel development. In ACM SIGPLAN Haskell WS, Portland, OR, USA, Sep 2006.
[3]: Manuel Fähndrich, Mark Aiken, Chris Hawblitzel, Orion Hodson, Galen C. Hunt, James R. Larus, and Steven Levi. Language support for fast and reliable message-based communication in Singularity OS. In Proc. of EuroSys2006, April 2006.
[4]: Thomas Hallgren, Mark P. Jones, Rebekah Leslie, and Andrew Tolmach. A principled approach to operating system construction in Haskell. In Proc. 10th ACM Int. Conf. on Functional Programming, 2005.
[5]: Steven Hand, Andrew Warfield, Keir Fraser, Evangelos Kottsovinos, and Dan Magenheimer. Are virtual machine monitors microkernels done right? In 10th HotOS, Sante Fe, NM, USA, Jun 2005. USENIX.
[6]: Gernot Heiser, Volkmar Uhlig, and Joshua LeVasseur. Are virtual-machine monitors microkernels done right? Operat. Syst. Rev., 40(1):95-99, Jan 2006.
[7]: Michael Hohmuth and Hendrik Tews. The VFiasco approach for a verified operating system. In Proc. 2nd ECOOP Workshop on Programm Languages and Operating Systems, Glasgow, UK, Oct 2005.
[8]: The M5 simulator system. , 2006.
[9]: R. M. Needham and D. F. Hartley. Theory and practice in operating system design. In 2nd SOSP, 1969.
[10]: Iguana. , 2007.
[11]: Tobias Nipkow, Lawrence Paulson, and Markus Wenzel. Isabelle/HOL - A Proof Assistant for Higher-Order Logic, volume 2283 of Lecture Notes in Computer Science. Springer Verlag, 2002.
[12]: Timothy Roscoe, Kevin Elphinstone, and Gernot Heiser. Hype and virtue. In 11th HotOS, San Diego, CA, USA, May 2007.
[13]: Jonathan Shapiro. Coyotos. , 2006.
[14]: Harvey Tuch, Gerwin Klein, and Gernot Heiser. OS verification - now! In 10th HotOS, pages 7-12, Santa Fe, NM, USA, Jun 2005. USENIX.
[15]: Harvey Tuch, Gerwin Klein, and Michael Norrish. Types, bytes, and separation logic. In Martin Hofmann and Matthias Felleisen, editors, 34th POPL, pages 97-108, Nice, France, Jan 2007.
[16]: Bruce Walker, Richard Kemmerer, and Gerald Popek. Specification and verification of the UCLA Unix security kernel. CACM, 23(2):118-131, 1980.

Footnotes:

¹Also at the University of New South Wales

²Now at ETH Zürich, Switzerland

³Also with Open Kernel Labs

⁴ National ICT Australia is funded by the Australian Government's Backing Australia's Ability initiative, in part through the Australian Research Council.

File translated from T_EX by T_TH, version 3.77.
On 11 Apr 2007, 20:12.