
Derek G. Murray and Steven Hand
Computer Laboratory
University of Cambridge
{Firstname.Lastname}@cl.cam.ac.uk
Spread-spectrum computation will use computation dispersal algorithms to add redundancy to computations, in order that they may tolerate a particular failure distribution. In this position paper, we introduce computation dispersal algorithms, providing examples of their implementation and applications.
Failure-tolerant computing is inefficient. Existing methods waste time by repeating partly-completed tasks [4,9]; computational resources by sending the same task to several hosts [1]; or storage by taking regular checkpoints [17]. However, machine failures are common [4], and we propose that it is both feasible and more efficient to deal with failures in advance of computation. Therefore, we propose spread-spectrum computation, which uses techniques from forward error-correction to add a controllable amount of redundancy to the inputs of an algorithm.
The aim of this work is to enlarge the scope of internet-scale distributed computing. Currently, such approaches are limited to solving embarrassingly-parallel problems - i.e. those in which the overall problem can trivially be divided into a large number of parallel tasks, with no dependencies between the tasks [1]. When the success of a computation depends on volunteer-provided resources, failure tolerance is critical: volunteered computers may crash or go offline at any time, and the internet connection may fail. Fortunately, since there is no dependency between the tasks, the simple failure-tolerance mechanisms (retry or send-to-many) work perfectly well.
Unfortunately, not all algorithms are embarrassingly parallel. An important class of problems can be solved using data-parallel algorithms, in which many parallel processors cooperate to solve a task by each processing a different piece of the input data [9]. There are dependencies between the processors at the beginning and end, when the data is respectively distributed and collected, and there may be dependencies during execution in order to exchange intermediate data (e.g. a halo-swap). Now, if a node fails, it could stall the entire computation.
A workable system must achieve three properties:
Here we concentrate on failure tolerance, and provide brief descriptions of the mechanisms for providing latency tolerance and decentralised management in Subsection 3.2.
We propose a spread-spectrum approach, because spread-spectrum techniques have a long history of improving robustness in communication [16] and - more recently - in storage [7]. A typical spread-spectrum approach involves each principal independently spreading its input across a pseudorandomly selected ensemble of resources - for communication, these would be frequencies; for storage, block addresses. The randomness can provide robustness and security, but some redundancy is required in case two principals randomly choose the same resource.
Spread-spectrum computation is a combination of two ideas: computation dispersal algorithms (CDAs) (Subsection 3.1) and distributed random scheduling (Subsection 3.2). In this paper, we concentrate more on the redundancy provided by CDAs, but include a discussion of scheduling for completeness. We also provide examples of algorithms to which spread-spectrum computation can be applied.
It is well accepted that large-scale distributed systems experience failures [4,9]. While they are online, however, the failing nodes provide a worthwhile computational resource. In this section, we present an analysis of data from the CoMon project, which records the state of all nodes on PlanetLab [11]. Although PlanetLab does not exactly model our target network of idle desktop computers, it represents a large distributed system that is affected by transient node failures and network outages.
In this paper, we are concerned about each node's availability, which
CoMon detects by pinging all nodes every five minutes. We also
consider load: CoMon reports the five-minute load average of each
node. In our system, when a node takes much longer to respond than
others, it is considered to have failed, and heavier-loaded nodes will
(modulo processor heterogeneity) tend to be slower. In each of our
analyses, we differentiate between a node simply being online, and
having a load average below a certain threshold (![]() ,
, ![]() and
and ![]() ,
respectively).
,
respectively).
We begin by looking at node availability for a period of four days,
from the
![]() to the
to the
![]() of May 2008,
inclusive. On these dates, the PlanetLab network comprised
of May 2008,
inclusive. On these dates, the PlanetLab network comprised ![]() nodes. Figure 1 shows how system-wide node
availability changes over time. The first thing to note is that the
number of online nodes is fairly steady (
nodes. Figure 1 shows how system-wide node
availability changes over time. The first thing to note is that the
number of online nodes is fairly steady (
![]() ,
,
![]() ). By comparison, looking only at nodes with a load average less
than
). By comparison, looking only at nodes with a load average less
than ![]() , far fewer nodes are available, and the availability shows
diurnal variations (
, far fewer nodes are available, and the availability shows
diurnal variations (
![]() ,
,
![]() ). These variations
suggest that the optimal amount of redundancy may be a function of the
time of day.
). These variations
suggest that the optimal amount of redundancy may be a function of the
time of day.
Now that we have established that some nodes do fail, we must show
that the set of failing nodes provides a useful computational resource
(when those nodes are transiently online). Figure 2
shows a rank distribution of node availability. For each series, we
can see that some nodes are always available (where ![]() ), some
nodes are never available (
), some
nodes are never available (![]() ), and some nodes are transiently
available (
), and some nodes are transiently
available (![]() ) - these are the nodes that our failure
tolerance mechanism attempts to harness. The interesting aspect of
Figure 2 is therefore the area under the sloping part
of each series.
) - these are the nodes that our failure
tolerance mechanism attempts to harness. The interesting aspect of
Figure 2 is therefore the area under the sloping part
of each series.
The benefit of failure tolerance is that it enables the
transiently-available nodes to participate usefully in computation. We
make the assumption that the effective computational capacity of a
node is directly proportional to the fraction of the time that it is
available, if we ignore processor heterogeneity. The effective
computational capacity, ![]() , of a set of nodes,
, of a set of nodes, ![]() , is defined as:
, is defined as:
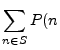 is available is available |
Table 1 summarises the effective capacity for
each scenario that we considered. For example, we see that the
effective computational capacity of the ![]() nodes that are
transiently online (with any load) is equivalent to
nodes that are
transiently online (with any load) is equivalent to ![]() always-on
computers. For nodes with a load average less than
always-on
computers. For nodes with a load average less than ![]() , this rises to
, this rises to
![]() effective nodes, which is
effective nodes, which is ![]() of the total system capacity.
of the total system capacity.
This preliminary study confirms that the transiently-available PlanetLab nodes comprise a substantial proportion of PlanetLab's total computational resource. A further concern is the effect of load on each node: Rhea et al. performed a more detailed study, and discovered that the latency of some operations could vary by more than two orders of magnitude [14]. Their solution of adding redundancy to improve performance agrees with our intuition about distributed random scheduling in §3.2.
Spread-spectrum computation takes a spread-spectrum approach to parallel computation. As stated in the introduction, its three main goals are failure tolerance, latency tolerance and decentralised management. These are fulfilled using two complementary techniques: computation dispersal algorithms (which provide failure tolerance), and distributed random scheduling (which provides decentralised management and latency tolerance). In this paper, we concentrate on the computation dispersal algorithms (Subsection 3.1), but give a brief description of distributed random scheduling (Subsection 3.2) for completeness.
Spread-spectrum computation uses a computation dispersal algorithm (CDA) to add redundancy to the inputs of an algorithm. It does this by adding encoding and decoding steps to an existing parallel algorithm (see Figure 3).
![\includegraphics[width=\linewidth]{dataflow-diagram}](img37.png)
|
We can define a CDA by analogy with Rabin's information dispersal
algorithm (IDA), which encodes a file of length ![]() into
into ![]() pieces,
each of length
pieces,
each of length ![]() , such that any
, such that any ![]() pieces are sufficient to
reconstruct the original file [13]. In effect, any subset
of the pieces with length totalling the original length of the file
can be used to reconstruct the original file. An optimal CDA, then,
encodes a computational input of size
pieces are sufficient to
reconstruct the original file [13]. In effect, any subset
of the pieces with length totalling the original length of the file
can be used to reconstruct the original file. An optimal CDA, then,
encodes a computational input of size ![]() into
into ![]() pieces, each of
size
pieces, each of
size ![]() , such that processing any
, such that processing any ![]() pieces is sufficient to
obtain the correct result.
pieces is sufficient to
obtain the correct result.
Borrowing from earlier work on algorithm-based fault
tolerance [8], we can show that an optimal CDA exists for the
problem of matrix-vector multiplication. Given
![]() and
and
![]() , we might calculate
, we might calculate
![]() by distributing each row,
by distributing each row,
![]() , of
, of
![]() to a processing node
to a processing node ![]() (where
(where
![]() ), which
calculates the dot product
), which
calculates the dot product
![]() .
.
If we wished to tolerate a single node failure, our CDA could
transform ![]() into
into
![]() such
that:
such
that:
![$\displaystyle \left[ \begin{array}{c} A \\ \boldsymbol{r}^T \end{array}\right]$](img52.png) |
|||
| where |
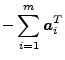 |
It is clear that:
![$\displaystyle A^\prime\boldsymbol{x} = \boldsymbol{y}^\prime = \left[ \begin{ar...
...{array}{c} \boldsymbol{y} \\ \boldsymbol{r}^T\boldsymbol{x} \end{array} \right]$](img55.png) |
To tolerate a single node failure, we distribute each of the ![]() rows of
rows of ![]() to processing node
to processing node ![]() (where
(where
![]() ). If node
). If node ![]() fails (where
fails (where
![]() ), we can compute the
missing
), we can compute the
missing ![]() by summing together all other
by summing together all other ![]() values. Chen and
Dongarra show that this approach generalises to tolerate
values. Chen and
Dongarra show that this approach generalises to tolerate ![]() failures,
by adding
failures,
by adding ![]() specially-weighted checksum rows [3].
specially-weighted checksum rows [3].
Obviously, if a CDA is to be useful, it must allow efficient encoding
and decoding. Constructing
![]() requires
requires ![]() additions, which
is relatively expensive compared to the cost of performing the
matrix-vector multiplication. However, many algorithms make it
possible to amortise the encoding cost, by reusing the encoded matrix
(see §4 for examples). More pertinently though, the
additions, which
is relatively expensive compared to the cost of performing the
matrix-vector multiplication. However, many algorithms make it
possible to amortise the encoding cost, by reusing the encoded matrix
(see §4 for examples). More pertinently though, the
![]() -failure-tolerant encoding procedure requires
-failure-tolerant encoding procedure requires
![]() operations to create the
operations to create the ![]() checksum rows [3].
checksum rows [3].
We therefore propose to use low-density parity-check (LDPC) codes
for use in this CDA, as they enable encoding and decoding in ![]() operations [15], which allows scaling to much larger
problem instances. An additional benefit of LDPC codes for this CDA is
that the checksum rows retain the sparseness of the data rows, unlike
the single-row example, which would generate a dense
operations [15], which allows scaling to much larger
problem instances. An additional benefit of LDPC codes for this CDA is
that the checksum rows retain the sparseness of the data rows, unlike
the single-row example, which would generate a dense
![]() ,
even for sparse
,
even for sparse ![]() . One disadvantage is that the LDPC code introduces
some overhead: if we begin with
. One disadvantage is that the LDPC code introduces
some overhead: if we begin with ![]() partial inputs, we require
partial inputs, we require ![]() (
(![]() ) encoded partial outputs to obtain the correct
result. However,
) encoded partial outputs to obtain the correct
result. However,
![]() as
as
![]() (and as
(and as
![]() ), and Plank and Thomason have observed that
the overhead can be made less than
), and Plank and Thomason have observed that
the overhead can be made less than ![]() (for
(for ![]() and
and ![]() ) [12].
) [12].
We have shown an example CDA for matrix-vector multiplication, but does this approach generalise? The checksum scheme adapts naturally to all linear transformations (i.e. those that satisfy the superposition property), which includes many other matrix operations and signal processing techniques. Huang and Abraham adapted algorithms for matrix multiplication and LU decomposition [8], which could lead to other CDAs. The search for further CDAs is the subject of our ongoing research.
Distributed random scheduling works in combination with computation dispersal algorithms to provide efficient, scalable and load-balanced scheduling across an internet-scale pool of idle desktop computers. In an internet-scale distributed system, it is not feasible to have a central scheduler that allocates parallel jobs to processing nodes. Any such scheduler would have to monitor the state of all processing nodes, and keep this information up-to-date. The use of redundancy gives us more flexibility in our scheduling mechanism.
Under distributed random scheduling, when a submitting node wishes to
submit a job to the system, it selects ![]() processing nodes at random,
and sends the encoded partial inputs to these nodes. This provides two
attractive properties. Firstly, if all submitters choose processing
nodes at random, the overall system load will be balanced, which
implies efficient resource utilisation. Moreover, in a heterogeneous
system using an
processing nodes at random,
and sends the encoded partial inputs to these nodes. This provides two
attractive properties. Firstly, if all submitters choose processing
nodes at random, the overall system load will be balanced, which
implies efficient resource utilisation. Moreover, in a heterogeneous
system using an ![]() -out-of-
-out-of-![]() CDA for failure tolerance, the
performance bottleneck will be the
CDA for failure tolerance, the
performance bottleneck will be the
![]() slowest
node, rather than the slowest node, which improves latency tolerance
and hence performance. This concurs with previous observations that
individual ``stragglers'' in a distributed system greatly affect the
performance of global computation [4,14]. The CDA
allows our system to produce a result after
slowest
node, rather than the slowest node, which improves latency tolerance
and hence performance. This concurs with previous observations that
individual ``stragglers'' in a distributed system greatly affect the
performance of global computation [4,14]. The CDA
allows our system to produce a result after ![]() responses, so the
slowest
responses, so the
slowest ![]() nodes do not delay the result.
nodes do not delay the result.
Obviously, if it is infeasible for a central node to maintain state information about all nodes, it is even more infeasible to expect each submitter to maintain such a list. We can achieve random selection by structuring the processing nodes as an expander graph, and performing a random walk on the resulting graph [10].
The best applications for the techniques described above will be those which require a large amount of data to be processed, such that it is infeasible to store the entire data set on a single processing node.
Initially, we are investigating large scale information retrieval tasks, such as PageRank calculation [2] and latent semantic indexing [5]. The PageRank of a collection of web pages may be computed as the principal eigenvector of the modified web page adjacency matrix, while latent semantic indexing involves calculating the singular value decomposition of the term-document matrix.
Calculating the principal eigenvector of a matrix can be achieved by power iteration [6]. The computationally-intensive part of this calculation is a repeated matrix-vector multiplication, for which we presented a CDA in Subsection 3.1. When used with web graphs, which form sparse matrices, the LDPC-based encoding scheme would be particularly appropriate. The singular value decomposition and full eigendecompositions can be calculated using Lanczos iteration [6], which is a more sophisticated version of this algorithm, but which is still based on iterative matrix-vector multiplication.
We are considering several other applications. The above CDA could also apply to boundary value problems, which may be solved iteratively using the conjugate gradient method. An adapted version of the CDA could also apply to multi-dimensional Fourier transforms, which have various applications in image analysis and molecular dynamics, amongst other areas.
In the volunteer-computing space, this work compares most directly with BOINC [1] and Condor [17], which represent different approaches to harnessing idle desktop computers. BOINC (on which projects such as SETI@Home are based) uses a task-farming approach to solving embarrassingly-parallel problems. Since every task is independent, it deals with failures simply by sending out multiple copies of each task to different processing nodes. Condor monitors when nodes in a local network become idle, and performs matchmaking between submitters and idle nodes. Wide-area distribution is made possible by ``flocking''. Condor supports process-level checkpointing for failure tolerance, although it does not generate consistent distributed snapshots for nodes executing in parallel. Moreover, although it has a rudimentary (failure intolerant) coscheduling feature, this is limited to the local network.
The data-parallel aspect of this work compares with MapReduce [4] and Dryad [9]. These respectively use functional programming and dataflow graph abstractions to process large-scale data sets. Both rely on re-execution as a failure tolerance method, which wastes wall-clock time, especially if tasks are long-lived. Furthermore, they are designed to work in large data centres, but not internet-scale distributed systems, so they rely on a centralised scheduler.
Our proposed system builds on algorithm-based fault tolerance (ABFT), which is intended for large-scale parallel computation [8]. ABFT introduced the idea of encoding the inputs to a parallel computation and computing with the encoded data, and our example CDA is based on the checksumming procedure that its authors describe. The focus of ABFT research has shifted to networks of workstations, and more advanced codes have been presented recently [3]. We intend to develop this work further by experimenting with more-efficient low-density codes, and deploying our system in a widely-distributed setting.
We have presented spread-spectrum computation: a set of novel techniques that aim to make data-parallel processing feasible on idle desktop computers. We plan to build and deploy our system in various widely-distributed settings, in order to investigate its real-world performance. In addition, we plan to study the failure characteristics of large-scale distributed systems, in order to model the appropriate redundancy parameters for efficient use of the system. Together, these projects will bring us to a point where idle-desktop computers can efficiently and dependably be used for data-parallel computation.
Thanks are due to our colleagues Jon Crowcroft, Theodore Hong, Tim Moreton, Henry Robinson, Amitabha Roy and Mark Williamson for their comments on earlier drafts of this paper. We would also like to thank the anonymous reviewers for their constructive comments and suggestions.