
Amitanand S. Aiyer, Eric Anderson, Xiaozhou Li, Mehul A. Shah, Jay J. Wylie
Hewlett-Packard Laboratories
1501 Page Mill Road, Palo Alto, CA 94304, USA
Date: September 26, 2008
Internet applications tend to stress availability rather than consistency, and so we believe it is important to be able to describe the trade-offs present for such applications. Towards that end, we introduce the notion of consistability which provides a way of describing how the consistency that a system provides may change during its execution. Our inspiration for consistability comes from the performability metric [20] that defined a unified metric for examining the fraction of time a system provides a given level of performance. Performability describes how often a system operates above some performance level. An example performability statement is that 90% of the time the system processes at least 1000 put requests per second and 99% of the time it processes at least 500. Performability captures the notion that a fault-tolerant system which degrades gracefully will offer different levels of performance, at different times, depending on the system's health. Performability also captures the notion that the system may be considered unavailable, or to have failed, if a certain minimum level of performance is not achieved. Our hope is that consistability will allow us to make similar statements about systems such as the following: The system offers linearizability 90% of the time, and eventual consistency (within two hours) 99.9% of the time.
The tension between strong consistency, availability, and partition-tolerance is well-known (e.g., [9]). However, it is possible to offer weak consistency with good availability and partition-tolerance (e.g., [6,7,5]). Unfortunately, there is a dearth of language with which to precisely describe such weakly consistent systems. Whereas we can describe how performance and availability of a system degrade in the face of failures, we cannot describe the consistency of a system that is usually consistent.
Consistency definitions provide worst-case guarantees. Such guarantees fail to capture the possibility that during failure-free periods the system can provide stronger guarantees. Beyond this, the normal language of consistency does not allow us to describe the fact that a system may achieve better consistency than the worst-case guarantee. We want to be able to describe and understand a system that provides distinct consistency classes throughout its execution, and that offers different applications distinct, appropriate consistency guarantees.
Part of our motivation for defining consistability comes from our experience in
specifying and designing a global-scale key-value storage (KVS) system.
By key we mean some client-specified unique string, by
value we mean a client-specified binary object of arbitrary
size, and by store we mean it offers a
![]() -
-
![]() interface.
The design goals for the KVS, in order, are as follows: low-cost,
availability, reliability (including disaster-tolerance), performance, and as
strong consistency as possible.
To achieve disaster-tolerance, the KVS must necessarily span multiple
data centers.
The design goal of availability is in tension with the goals of
disaster-tolerance and strong consistency.
Effectively, we want the KVS to provide best effort consistency: i.e.,
strong consistency in the face of most failures, and weaker consistency during
a network partition or other large correlated failure.
interface.
The design goals for the KVS, in order, are as follows: low-cost,
availability, reliability (including disaster-tolerance), performance, and as
strong consistency as possible.
To achieve disaster-tolerance, the KVS must necessarily span multiple
data centers.
The design goal of availability is in tension with the goals of
disaster-tolerance and strong consistency.
Effectively, we want the KVS to provide best effort consistency: i.e.,
strong consistency in the face of most failures, and weaker consistency during
a network partition or other large correlated failure.
The definition of consistability and approach to evaluating consistability that we describe in this position paper is an initial step towards developing a language capable of precisely evaluating usually consistent systems. As a metric, consistability offers an avenue by which to compare and contrast different techniques for implementing similar weak consistency guarantees. Consistability has helped us understand the affect of failures on the distinct consistency guarantees that the KVS can offer. This is especially useful to us since we intend the KVS to support many distinct client applications, each with slightly different consistency requirements; consistability will allow us to understand which applications can be supported with what availability.
We focus our discussion of related work on consistency guarantees that we considered during the design of the KVS. We discuss other additional related systems in the case studies section §4 and in the discussion section §5.
Lamport's definition of atomic registers provides the basis of most definitions of strong consistency [15]. Atomic registers guarantee that all reads and writes to a single object can be ordered, in a manner consistent with their relative orderings, such that reads always return the value of the latest completed write. Linearizability [11] and transactions [10] define strong consistency of operations that affect multiple objects. In this paper, we limit our discussion of consistability to an individual object. Lamport also defines regular and safe registers that have weaker consistency [15]. Regular registers allow a read operation concurrent to write operations to return the value from any concurrent write, or the previous completed write. Safe registers allow a read operation concurrent to write operations to return any value.
There are many forms of weak and eventual consistency; we discuss
some examples of each to provide context for consistability.
In the TACT project, Yu and Vahdat propose three axis along which consistency
can be weakened to improve availability: numerical-error, order-error, and
staleness [25].
PRACTI [3] also offers tunable consistency levels.
The bounded ignorance techniques of Krishnakumar and
Bernstein [14] permits concurrent transactions to
complete while being ignorant of some bounded number of other concurrent
transactions.
K-atomic registers, proposed by Aiyer et al. [1],
bound the number of distinct recently completed writes that may be returned by a
read operation.
Malkhi et al. proposed probabilistic quorums [19]
with which Lee and Welch have shown how to build a ![]() -randomized
register [17] whose staleness follows probability distribution
function
-randomized
register [17] whose staleness follows probability distribution
function ![]() .
.
In eventually consistent systems, a write operation may return before its value
propagates throughout the system; in such systems, once all transient failures
have been resolved, and no further writes are issued, replicas converge to a
consistent state [23].
Examples of research on weak consistency in the presence of network partitions
include the following: Davidson et al. [6] survey
partition-aware database techniques, Babaoglu et al. developed
partition-aware systems [2], and Pleisch et al. have clarified
the partitionable group membership problem [22].
The definitions of ![]() -registers,
-registers, ![]() -registers, and conits in TACT, do
not explicitly guarantee best-case consistency in well-conditioned executions.
These definitions therefore lack the sense that as concurrency, or latency, or
the number of failures increase, the consistency provided gracefully approaches
the worst-case guarantee.
-registers, and conits in TACT, do
not explicitly guarantee best-case consistency in well-conditioned executions.
These definitions therefore lack the sense that as concurrency, or latency, or
the number of failures increase, the consistency provided gracefully approaches
the worst-case guarantee.
We define consistability for a single object in three steps. First, we define consistency classes and failure scenarios. Then we describe how to map failure scenarios to consistency classes. Finally, we describe how to calculate consistability given this mapping.
To define consistability, all of the possible consistency classes achievable
must be enumerated.
Let
![]() be the set of all consistency classes the system can
provide.
A consistency class is a definition of some form of consistency, for
example, atomic/regular/safe [15],
linearizable [11], or some weaker variants (e.g., [25]).
be the set of all consistency classes the system can
provide.
A consistency class is a definition of some form of consistency, for
example, atomic/regular/safe [15],
linearizable [11], or some weaker variants (e.g., [25]).
The consistency classes in
![]() can be partially ordered.
For example, atomicity is stronger than
regularity [15],
can be partially ordered.
For example, atomicity is stronger than
regularity [15], ![]() -atomicity is weaker than
atomicity [1], but
-atomicity is weaker than
atomicity [1], but ![]() -atomicity and regularity are not
comparable.
Figure 1 provides an illustrative example of a lattice of
consistency classes that includes the traditional register consistency classes,
the recent
-atomicity and regularity are not
comparable.
Figure 1 provides an illustrative example of a lattice of
consistency classes that includes the traditional register consistency classes,
the recent ![]() -variants of those classes, and some eventual consistency
guarantees based on time in seconds.
In this example lattice, none of the consistency classes for traditional and
-variants of those classes, and some eventual consistency
guarantees based on time in seconds.
In this example lattice, none of the consistency classes for traditional and
![]() registers are comparable with any of the consistency classes for eventual
guarantees.
registers are comparable with any of the consistency classes for eventual
guarantees.
Let
![]() be the set of all possible failure scenarios.
A failure scenario is a description of a specific failure pattern;
failure scenarios are, by definition, disjoint.
Examples of failure scenarios include ``no failures,'' ``all failures of a
single server and no other failures,'' ``a network partition and no other
failures,'' and ``all failures of a single server and a network partition.''
be the set of all possible failure scenarios.
A failure scenario is a description of a specific failure pattern;
failure scenarios are, by definition, disjoint.
Examples of failure scenarios include ``no failures,'' ``all failures of a
single server and no other failures,'' ``a network partition and no other
failures,'' and ``all failures of a single server and a network partition.''
To calculate consistability, every failure scenario must be mapped to some subset of all of the consistency classes:
Given a failure scenario,
We say that a consistency class
![]() is maximal for a failure
scenario
is maximal for a failure
scenario
![]() , if there is no consistency class in
, if there is no consistency class in
![]() that is stronger than
that is stronger than
![]() .
Based on the partial order among the consistency classes, one could define the
mapping from failure scenarios to the set of maximal consistency classes which
are achievable.
For such an alternative mapping, if there is a total order among all consistency
classes in
.
Based on the partial order among the consistency classes, one could define the
mapping from failure scenarios to the set of maximal consistency classes which
are achievable.
For such an alternative mapping, if there is a total order among all consistency
classes in
![]() then each failure scenario would map to exactly one
(maximal) consistency class.
then each failure scenario would map to exactly one
(maximal) consistency class.
Consistability is the expected portion of time that a system provides each
consistency class.
To provide such an expectation, like reliability and performability metrics do,
we need probability distributions over the failure scenarios.
Let
![]() denote the probability that the system is in a
given failure scenario.
We compute the probability of providing a consistency class,
denote the probability that the system is in a
given failure scenario.
We compute the probability of providing a consistency class,
![]() , by summing the probabilities of each failure class
which maps to the consistency class:
, by summing the probabilities of each failure class
which maps to the consistency class:
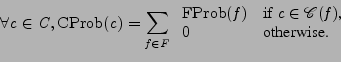
Because failure scenarios are disjoint,
![]() .
However,
.
However,
![]() .
This is because the mapping from a failure scenario to a consistency class can
be one-to-many.
.
This is because the mapping from a failure scenario to a consistency class can
be one-to-many.
There is no need to include every possible consistency class in
![]() :
only the ones that a client may care about, that an application can effectively
use, or that the system may actually provide are of interest.
Once
:
only the ones that a client may care about, that an application can effectively
use, or that the system may actually provide are of interest.
Once
![]() is decided, the system designer may be able to define a single
appropriate failure scenario for each consistency class.
I.e., figuring out the appropriate members of
is decided, the system designer may be able to define a single
appropriate failure scenario for each consistency class.
I.e., figuring out the appropriate members of
![]() and
and
![]() may be
an iterative process.
To account for correlated failures, failure scenarios must be defined that
include many different failures and the probability distribution over failure
scenarios must capture this correlation.
may be
an iterative process.
To account for correlated failures, failure scenarios must be defined that
include many different failures and the probability distribution over failure
scenarios must capture this correlation.
We expect that the practice of mapping failure scenarios to consistency classes will help designers better understand all of the capabilities of their distributed systems and protocols. Unfortunately, it requires significant effort to produce an actual consistability measure because it is difficult to determine the probability distributions over all failure scenarios. This is similar to the situation designers are in when they work with fault tolerance and reliability today: the former is easy to quantify and reason about during design; whereas the latter is difficult to evaluate and measure, and applies only narrowly to a specific, actual system instance.
In this section, we present a key-value store system that we are building as a case study to illustrate the various consistability concepts presented in the previous section. We also discuss other prior systems that make interesting consistability choices.
Figure 2 illustrates the system model for our key-value store (KVS). It shows three data centers (X, Y, Z) with their respective storage and proxies. It also shows six clients (a to f) that usually access the system through their closest proxy. In this position paper we ignore the design decisions about metadata (i.e., how clients determine which storage nodes host fragments for some key), but we do discuss whether the metadata service is available or not.
For the sake of availability, the KVS must allow
![]() and
and
![]() operations
during a network partition and handle reconciliations when the network
reconnects.
To cost-effectively achieve reliability, values are erasure-coded across
multiple data centers in such a manner so that each data center has sufficient
erasure-coded fragments to recover the value.
The
operations
during a network partition and handle reconciliations when the network
reconnects.
To cost-effectively achieve reliability, values are erasure-coded across
multiple data centers in such a manner so that each data center has sufficient
erasure-coded fragments to recover the value.
The
![]() operation offers best effort consistency and
disaster-tolerance. Once the metadata service selects the storage
nodes for a particular operation, that operation will not complete until
it has written to or timed out on all the selected nodes.
The
operation offers best effort consistency and
disaster-tolerance. Once the metadata service selects the storage
nodes for a particular operation, that operation will not complete until
it has written to or timed out on all the selected nodes.
The
![]() operation offers best effort availability: if it cannot retrieve the
latest version of the value
operation offers best effort availability: if it cannot retrieve the
latest version of the value
![]() into the system, it attempts to retrieve
prior versions until a value is returned (or all prior versions have been
tried).
There is a clear tension between the availability and disaster-tolerance
requirements.
Roughly speaking, we have designed a protocol that is usually consistent, and
only degrades to worst-case consistency when specific failures occur.
into the system, it attempts to retrieve
prior versions until a value is returned (or all prior versions have been
tried).
There is a clear tension between the availability and disaster-tolerance
requirements.
Roughly speaking, we have designed a protocol that is usually consistent, and
only degrades to worst-case consistency when specific failures occur.
For the KVS, we consider the following failure scenarios:
(1) There are at most
![]() disks unavailable (and the erasure code tolerates
up to
disks unavailable (and the erasure code tolerates
up to
![]() disk failures).
(2) More than
disk failures).
(2) More than
![]() disks are unavailable.
(3) A data center has failed catastrophically.
(4) The data centers are partitioned into multiple groups.
(5) The metadata service is unavailable.
For the sake of brevity, we do not discuss composite failure scenarios (e.g.,
failure scenarios (2) and (4) occurring simultaneously).
disks are unavailable.
(3) A data center has failed catastrophically.
(4) The data centers are partitioned into multiple groups.
(5) The metadata service is unavailable.
For the sake of brevity, we do not discuss composite failure scenarios (e.g.,
failure scenarios (2) and (4) occurring simultaneously).
Failure scenario (1) is effectively the ``no failures'' scenario because the
erasure code tolerates up to
![]() disk failures.
Failure scenarios (1) and (3) map to the regular consistency class.
In both cases, a
disk failures.
Failure scenarios (1) and (3) map to the regular consistency class.
In both cases, a
![]() operation concurrent to a
operation concurrent to a
![]() operation will return some
value being
operation will return some
value being
![]() concurrently, or the most recent completed
concurrently, or the most recent completed
![]() value.
For case (1), the
value.
For case (1), the
![]() operation will return either the prior value or the
value being
operation will return either the prior value or the
value being
![]() concurrently, depending on message ordering at each server.
For case (3), regularity is achieved because each data center has sufficient
erasure-coded fragments to recover a value and so the most recently
concurrently, depending on message ordering at each server.
For case (3), regularity is achieved because each data center has sufficient
erasure-coded fragments to recover a value and so the most recently
![]() value
is available after such a catastrophe.
Even though only regularity can be provided in these failure scenarios, there
are many executions that will achieve atomicity.
For example, if every client preferentially selects the same node for metadata
services, then the operations will achieve atomicity.
value
is available after such a catastrophe.
Even though only regularity can be provided in these failure scenarios, there
are many executions that will achieve atomicity.
For example, if every client preferentially selects the same node for metadata
services, then the operations will achieve atomicity.
Failure scenarios (2) and (4) map to the same consistency class:
![]() -regularity, a
-regularity, a
![]() returns one of the
returns one of the ![]() most recent values
most recent values
![]() [1].
In both scenarios, some recently
[1].
In both scenarios, some recently
![]() values may be lost because too few
erasure-coded fragments are available for
values may be lost because too few
erasure-coded fragments are available for
![]() to recover them.
Unfortunately, without bounding the number of new, or concurrent,
to recover them.
Unfortunately, without bounding the number of new, or concurrent,
![]() operations,
operations, ![]() .
For failure scenario (4), given a bound of
.
For failure scenario (4), given a bound of ![]() incomplete
incomplete
![]() operations, and
operations, and
![]() data centers, we can set
data centers, we can set
![]() , as each data center could be in its
own partition.
, as each data center could be in its
own partition.
Failure scenario (5) maps to the null set. In general, mapping to the null set means that the system is either unavailable or inconsistent. For failure scenario (5), the system is simply unavailable since no operations can complete.
We do not have probability distributions for the possible failure scenarios and
so cannot compute the overall consistability of the KVS system.
Instead, our current focus is on showing that for each of the failure
scenarios, the KVS protocol does indeed map to the consistency class we have
identified.
We first use the TLC [16] model-checker to verify that the
consistency class semantics are obeyed for small instances of the protocol, and
then use hand-proofs to prove that the consistency class is satisfied.
We have described the KVS protocol along with some consistency classes and
failure scenarios in TLA+ and model-checked them using TLC.
Our success in model checking the specification has been limited by the size of
the system.
For the failure-free case with a single data center, we have verified that
![]() and
and
![]() operations are atomic.
However, verifying the extended specification for multiple data centers with
distributed metadata service takes too long to check all possible states.
We have used TLC to verify that failure scenarios (1) and (3) map to
regularity, and used hand-proofing to prove it.
For failure scenarios (2) and (4) we hand-proved that the protocol only provides
operations are atomic.
However, verifying the extended specification for multiple data centers with
distributed metadata service takes too long to check all possible states.
We have used TLC to verify that failure scenarios (1) and (3) map to
regularity, and used hand-proofing to prove it.
For failure scenarios (2) and (4) we hand-proved that the protocol only provides
![]() regular consistency class, unless the number of disconnected
regular consistency class, unless the number of disconnected
![]() operations are bounded.
Further, we hand-proved that by using failure detectors, or by restricting the number
of disconnected
operations are bounded.
Further, we hand-proved that by using failure detectors, or by restricting the number
of disconnected
![]() operations, the KVS protocol provides
operations, the KVS protocol provides ![]() -regularity for
an appropriately chosen value of
-regularity for
an appropriately chosen value of ![]() .
.
There are other systems that try to offer best-effort consistency and so provide better consistency when networks are mostly-connected and responsive than when failures are present, or believed to be present. Unfortunately, the worst-case nature of most weak consistency guarantees discourages discussion of how much consistency a system provides in the common case.
Dynamo [7] uses a hinted handoff mechanism to tolerate temporary node or network failures. If one of the nodes responsible for storing an object (say A) is unavailable, data is stored at a different node (say B). B will later attempt to deliver the object to A, when it sees that A has recovered. In the meanwhile, if a reader attempts to read the object from A, before A receives the updated version from B, the reader can get an out-of-date value. We believe that the failure-free scenario in Dynamo maps to an atomic consistency class. The failure scenario involving a bounded number of node failures/unavailability maps to regular consistency class. Finally, the failure scenario involving a number of node failures that exceeds the bound leads to unavailability.
PNUTS [5] explicitly exposes the consistency classes it offers
via an extensive storage interface:
![]() -
-
![]() ,
,
![]() -
-
![]() ,
,
![]() -
-
![]() ,
,
![]() ,
and
,
and
![]() -
-
![]() -
-
![]() -
-
![]() .
In PNUTS, applications implicitly specify portions of their consistability
requirements via their use of the storage interface.
The failure scenarios that map to each consistency class and that ensure the
availability of certain storage interfaces depends on how PNUTS is configured
and used.
.
In PNUTS, applications implicitly specify portions of their consistability
requirements via their use of the storage interface.
The failure scenarios that map to each consistency class and that ensure the
availability of certain storage interfaces depends on how PNUTS is configured
and used.
Two recent Byzantine fault tolerant (BFT) systems provide interesting
consistability.
Li and Mazieres [18] developed BFT2F, which is a BFT
protocol that offers different guarantees depending on whether fewer
than one third of the replicas are faulty (linearizability), or if
fewer than two thirds of the replicas are faulty (fork![]() consistency).
Similarly, Chun et al. [4] developed Attested Append-only Memory
(A2M).
A2M provides safety and liveness if fewer than one third of the replicas are
faulty, but only safety if fewer than two thirds of the replicas are faulty.
Liveness in this sense could be thought of as performability requirement.
The set of failure scenarios are the same for both of these systems, but the
mapping to consistency classes for a single failure scenario differs.
consistency).
Similarly, Chun et al. [4] developed Attested Append-only Memory
(A2M).
A2M provides safety and liveness if fewer than one third of the replicas are
faulty, but only safety if fewer than two thirds of the replicas are faulty.
Liveness in this sense could be thought of as performability requirement.
The set of failure scenarios are the same for both of these systems, but the
mapping to consistency classes for a single failure scenario differs.
An open problem with consistability is how to reason about the consistency
classes provided as the system transitions between failure scenarios.
It is simple to reason about all operations that occur during a specific
failure scenario because the consistency class remains constant.
If, for example, a
![]() operation occurs during some failure scenario involving
a network partition, and then a
operation occurs during some failure scenario involving
a network partition, and then a
![]() operation occurs immediately after the
network merges, then which consistency class applies?
If the consistency classes are comparable, then the weaker class should apply.
If the consistency classes are not comparable, then it is unclear what should
happen.
operation occurs immediately after the
network merges, then which consistency class applies?
If the consistency classes are comparable, then the weaker class should apply.
If the consistency classes are not comparable, then it is unclear what should
happen.
Beyond understanding which consistency class applies after a transition, we need to better understand when the consistency class does in fact apply. We expect that a system which transitions to a worse failure scenario immediately switches to a consistency class which maps to that failure scenario. However, we expect that a system which transitions to a better failure scenario experiences a transition period during which increasingly more objects achieve the better consistency class.
One of the benefits of consistability is that clients can more precisely articulate their requirements. Consistability simply complements any performability measure (i.e., consistability is not a generalization of performability). Given models of system performance in each failure scenario and a model of the workload, we believe it is possible to develop a unified measure of performance, consistency, and availability. By combining failure frequency information with the consistability achieved by a system, a client could write a service level agreement (SLA) that would allow them to articulate the value they place on achieving ``more consistency, more often''. Unfortunately, both clients and servers need to be able to verify that an SLA is being met. Ideally, a system can tell a client which consistency class it provides, and potentially, what consistency class it is currently achieving (if it is offering better than worst-case consistency). We refer to this ability as introspection.
We believe that prior work on adaptive protocols may provide some guidance on how to implement introspection. For example, Hiltunen et al. developed methods for adaptive fault tolerance [13] and customizable failure models [12]. The fail-awareness work of Mishra, Fetzer, and Cristian [8,21] is also adaptive in nature since servers trigger an exception that clients catch if the server detects that it is not operating under normal conditions. Introspection and adaptive protocols may complicate the specification and evaluation of a system's consistability.
In this position paper, we argued that there is a need for a richer language with which to discuss the consistency of usually consistent systems. Traditionally, understanding of consistency is limited to the worst-case guarantees provided to clients. We introduced the concept of consistability to facilitate describing and understanding systems that can provide or achieve better than worst-case consistency under some conditions. Consistability is based on mapping possible failure scenarios to consistency classes that the system can provide during the failure scenario. Our motivation for enriching the language with which to reason about consistency was our ongoing effort to design a global-scale key-value store (KVS). A key design goal is for the KVS is to offer best effort consistency during failure-free periods and in the face of network partitions, data center catastrophes, and correlated failures. Consistability allows us to compare techniques and discuss trade-offs more precisely. We used the consistability definition to understand that mapping of failure scenarios to consistency classes for the KVS and other recent distributed systems such as Dynamo [7], PNUTS [5], BFT2F [18], A2M [4]. Finally, we discussed open problems with consistability. For example, understanding the mapping of failure scenario transitions to consistency classes, and if it is possible, via introspection, to determine that the consistency class achieved exceeds the worst-case consistency class.