
Yin Wang1
University of Michigan
Terence Kelly
Hewlett-Packard Laboratories
Stéphane Lafortune
University of Michigan
Information technology (IT) administration is increasingly automated. Workflows--concurrent programs written in very-high-level languages--are an increasingly popular IT automation technology. Like multi-threaded programming, workflow programming is notoriously difficult and error prone. Concurrency, resource contention, race conditions, and similar issues lead to subtle bugs that can survive testing undetected. Static workflow analysis provides a reliable offline way to validate IT administrative actions before they are performed [2], complementary to dynamic validation and post-mortem root cause localization. Static analysis, however, merely detects defects; repair remains manual, time-consuming, error-prone, and costly. Manually-corrected workflows are less natural, less readable, and less efficient than the flawed originals.
This paper shows how discrete control theory can allow safe execution of unmodified flawed workflows by dynamically avoiding undesirable execution states, e.g., states that violate dependability requirements. By externally enforcing compliance with some dependability requirements, our approach allows programmers to write straightforward workflows instead of perfect ones; by partially decoupling workflow software from dependability requirements, it reduces the need to alter the former when the latter change. Classical control theory has recently been applied to several performance-related IT problems [1]. Discrete control employs very different methods and modeling formalisms [3] and is better suited to safety and dependability problems. Discrete control has been applied in domains ranging from manufacturing to telecommunications. However it has never before been implemented for any IT automation or CS systems problem.
Whereas classical control deals with continuous-state systems whose
dynamics are described by differential equations, discrete control
theory considers discrete-state systems with event-driven dynamics.
Discrete control requires a model of the system to be controlled. We
use a finite state automaton ![]() representing all execution states
reachable from the initial state, and we automatically generate
representing all execution states
reachable from the initial state, and we automatically generate
![]() from a workflow. Undesirable behaviors are specified as
sublanguages of the regular language associated with automaton
from a workflow. Undesirable behaviors are specified as
sublanguages of the regular language associated with automaton
![]() . A simpler mode of specification is to define forbidden
states representing undesirable execution states. The goal of
discrete control is to ensure that the system reaches satisfactory
termination without entering forbidden states, even if worst-case
sequences of uncontrollable state transitions occur. This goal is
achieved in two stages: First, an offline control synthesis
stage uses the system model
. A simpler mode of specification is to define forbidden
states representing undesirable execution states. The goal of
discrete control is to ensure that the system reaches satisfactory
termination without entering forbidden states, even if worst-case
sequences of uncontrollable state transitions occur. This goal is
achieved in two stages: First, an offline control synthesis
stage uses the system model ![]() and the specification of terminal
and forbidden states to automatically synthesize a discrete
controller. Then during online dynamic control the
controller selectively disables controllable transitions based on
the current execution state.
and the specification of terminal
and forbidden states to automatically synthesize a discrete
controller. Then during online dynamic control the
controller selectively disables controllable transitions based on
the current execution state.
The synthesized controller should have two properties: First, it
should be minimally restrictive, disabling transitions only when
necessary to avoid forbidden states and livelock/deadlock. Second,
it must not prevent successful termination. A controller with these
properties restricts the system to its maximally permissive
controllable non-blocking sublanguage, and existing methods can
synthesize such a controller [3]. Control
synthesis requires time quadratic in the size of ![]() in the worst
case. However, control synthesis is an offline operation; in the
workflow domain, it does not increase execution time.
in the worst
case. However, control synthesis is an offline operation; in the
workflow domain, it does not increase execution time.
Figure 1 depicts our workflow control system architecture. We
begin with a workflow consisting of atomic tasks organized via
control-flow structures. Typical structures include sequence,
iteration, AND-forks to spawn parallel executions, OR-forks to
select a branch, and AND/OR joins to ``reconnect'' flow after a
fork. First, a translator converts the workflow into an automaton
that models its control flow and reachable state space. Transitions
in the automaton represent task invocation/completion, control
structure entrance/exit, and resource acquisition/release; states
represent the results of these transitions. The translator
identifies uncontrollable transitions by high-level workflow
features and can automatically detect livelock/deadlock states. The
programmer may define additional application-specific forbidden
states. Next, a discrete control synthesis algorithm uses the
automaton to generate control logic that specifies which
controllable transitions should be disabled as a function of current
execution state. Both workflow
![]() automaton translation and control
synthesis are offline operations. At run time, the workflow
execution engine tracks execution state and refrains from executing
controllable transitions that the control logic disables in the
current state. The result is that the system will avoid forbidden
states whenever possible, regardless of uncontrollable transitions
that may occur during execution.
automaton translation and control
synthesis are offline operations. At run time, the workflow
execution engine tracks execution state and refrains from executing
controllable transitions that the control logic disables in the
current state. The result is that the system will avoid forbidden
states whenever possible, regardless of uncontrollable transitions
that may occur during execution.
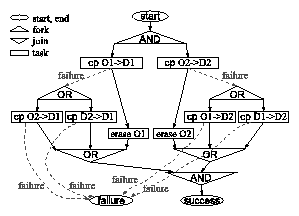
(a) Workflow diagram. 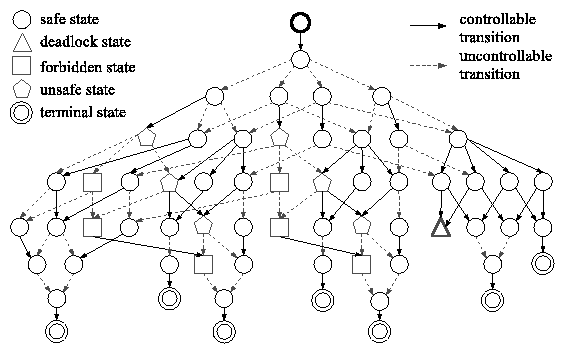 State-space automaton for workflow of Figure 2(a). Deadlock state corresponds to double failure. Forbidden states contain neither two origin nor two destination copies. Unsafe states may reach forbidden states via sequences of uncontrollable transitions. |
Figure 2(a) shows a simplified data migration workflow that moves two
original copies of a data set, O1 and O2, to destinations D1 and D2.
The two branches of the AND-fork represent concurrent copy-erase
operations. Uncontrollable ``failure'' transitions model the
possibility that copy operations may fail. If the O1
![]() D1 copy in
the left branch fails, the workflow will retry from O2 or D2.
However the workflow does not specify which; this decision is made
by the execution engine. If the second attempt to create D1 also
fails, the workflow will end in global failure. The right branch,
responsible for creating D2, is symmetric. Tasks require exclusive
access to copies of data.
D1 copy in
the left branch fails, the workflow will retry from O2 or D2.
However the workflow does not specify which; this decision is made
by the execution engine. If the second attempt to create D1 also
fails, the workflow will end in global failure. The right branch,
responsible for creating D2, is symmetric. Tasks require exclusive
access to copies of data.
The problem with this workflow is that if both O1
![]() D1 and O2
D1 and O2
![]() D2
tasks fail, and if the response to these failures are attempts to
copy D2
D2
tasks fail, and if the response to these failures are attempts to
copy D2
![]() D1 and D1
D1 and D1
![]() D2 respectively, then the workflow deadlocks
with each branch waiting for the other to complete. Static analysis
alone can detect this problem, requiring a programmer to repair the
flaw manually. Discrete control allows us to safely execute the
flawed workflow without modification. The controller will avoid the
deadlock state by disabling either D2
D2 respectively, then the workflow deadlocks
with each branch waiting for the other to complete. Static analysis
alone can detect this problem, requiring a programmer to repair the
flaw manually. Discrete control allows us to safely execute the
flawed workflow without modification. The controller will avoid the
deadlock state by disabling either D2
![]() D1 or D1
D1 or D1
![]() D2 if both
O1
D2 if both
O1
![]() D1 and O2
D1 and O2
![]() D2 fail. Figure 2(b) depicts the state-space
automaton for our example workflow. There is one deadlock state
corresponding to the above double failure.
D2 fail. Figure 2(b) depicts the state-space
automaton for our example workflow. There is one deadlock state
corresponding to the above double failure.
Suppose a new requirement is imposed: At any instant in time, either
both origin or both destination copies must exist. The workflow
does not satisfy this new requirement because it may erase O1 before
the O2
![]() D2 copy completes. With discrete control, the new
requirement can be satisfied simply by forbidding states that
violate it and then synthesizing a new controller. The controller
satisfies the new requirement by appropriately postponing erase
operations. This scenario shows that discrete control can
accommodate new requirements without modifying workflows.
D2 copy completes. With discrete control, the new
requirement can be satisfied simply by forbidding states that
violate it and then synthesizing a new controller. The controller
satisfies the new requirement by appropriately postponing erase
operations. This scenario shows that discrete control can
accommodate new requirements without modifying workflows.
In conclusion, we have described how discrete control methods can synthesize controllers from workflows and declarative specifications. These controllers add negligible run-time overhead, and they prevent undesirable behavior while otherwise restricting execution as little as possible. Extensive tests on real workflows bundled with Oracle BPEL Designer and on randomly-generated workflows demonstrate that offline control synthesis scales to workflows of practical size.
This document was generated using the LaTeX2HTML translator Version 2002-2-1 (1.70)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 -show_section_numbers -local_icons hotdep06.tex
The translation was initiated by Yin Wang on 2006-09-21