Traditional caching policies are known to perform poorly for storage server caches. One promising approach to solving this problem is to use hints from the storage clients to manage the storage server cache. Previous hinting approaches are ad hoc, in that a predefined reaction to specific types of hints is hard-coded into the caching policy. With ad hoc approaches, it is difficult to ensure that the best hints are being used, and it is difficult to accommodate multiple types of hints and multiple client applications. In this paper, we propose CLient-Informed Caching (CLIC), a generic hint-based policy for managing storage server caches. CLIC automatically interprets hints generated by storage clients and translates them into a server caching policy. It does this without explicit knowledge of the application-specific hint semantics. We demonstrate using trace-based simulation of database workloads that CLIC outperforms hint-oblivious and state-of-the-art hint-aware caching policies. We also demonstrate that the space required to track and interpret hints is small.
Multi-tier block caches arise in many situations. For example, running a database management system (DBMS) on top of a storage server results in at least two caches, one in the DBMS and one in the storage system. The challenges of making effective use of caches below the first tier are well known [15,19,22]. Poor temporal locality in the request streams experienced by the second-tier caches reduces the effectiveness of recency-based replacement polices [22], and failure to maintain exclusivity among the contents of the caches in each tier leads to wasted cache space [19].
Many techniques have been proposed for improving the performance of second-tier caches. Section 7 provides a brief survey. One promising class of techniques relies on hinting: the application that manages the first-tier cache generates hints and attaches them to the I/O requests that it directs to the second tier. The cache at the second tier then attempts to exploit these hints to improve its performance. For example, an importance hint [6] indicates the priority of a particular page to the buffer cache manager in the first-tier application. Given such hints, the second-tier cache can infer that pages that have high priority in the first tier are likely to be retained there, and can thus give them low priority in the second tier. As another example, a write hint [11] indicates whether the first tier is writing a page to ensure recoverability of the page, or to facilitate replacement of the page in the first-tier cache. The second tier may infer that replacement writes are better caching candidates than recovery writes, since they indicate pages that are eviction candidates in the first tier.
Hinting is valuable because it is a way of making application-specific information available to the second (or lower) tier, which needs a good basis on which to make its caching decisions. However, previous work has taken an ad hoc approach to hinting. The general approach is to identify a specific type of hint that can be generated from an application (e.g., a DBMS) in the first tier. A replacement policy that knows how to take advantage of this particular type of hint is then designed for the second tier cache. For example, the TQ algorithm [11] is designed specifically to exploit write hints. The desired response to each possible hint is hard-coded into such an algorithm.
Ad hoc algorithms can significantly improve the performance of the second-tier cache when the necessary type of hint is available. However ad hoc algorithms also have some significant drawbacks. First, because the response to hints is hard-coded into an algorithm at the second tier, any change to the hints requires changes to the cache management policy at the second-tier server. Second, even if change is possible at the server, it is difficult to generalize ad hoc algorithms to account for new situations. For example, suppose that applications can generate both write hints and importance hints. Clearly, a low-priority (to the first tier) replacement write is probably a good caching candidate for the second tier, but what about a low-priority recovery write? In this case, the importance hint suggests that the page is a good candidate for caching in the second tier, but the write hint suggests that it is a poor candidate. One response to this might be to hard code into the second-tier cache manager an appropriate behavior for all combinations of hints that might occur. However, each new type of hint will multiply the number of possible hint combinations, and it may be difficult for the policy designer to determine an appropriate response for each one. A related problem arises when multiple first-tier applications are served by a single cache in the second tier. If different applications generate hints, how is the second tier cache to compare them? Is a write hint from one application more or less significant than an importance hint from another?
In this paper, we propose CLient-Informed Caching (CLIC), a generic technique for exploiting application hints to manage a second-tier cache, such as a storage server cache. Unlike ad hoc techniques, CLIC does not hard-code responses to any particular type of hint. Instead, it is an adaptive approach that attempts to learn to exploit any type of hint that is supplied to it. Applications in the first tier are free to supply any hints that they believe may be of value to the second tier. CLIC analyzes the available hints and determines which can be exploited to improve second-tier cache performance. Conversely, it learns to ignore hints that do not help. Unlike ad hoc approaches, CLIC decouples the task of generating hints (done by applications in the first tier) from the task of interpreting and exploiting them. CLIC naturally accommodates applications that generate more than one type of hint, as well as scenarios in which multiple applications share a second-tier cache.
The contributions of this paper are as follows. First, we define an on-line cost/benefit analysis of I/O request hints that can be used to determine which hints provide potentially valuable information to the second-tier cache. Second, we define an adaptive, priority-based cache replacement policy for the second-tier cache. This policy exploits the results of the hint analysis to improve the hit ratio of the second-tier cache. Third, we use trace-based simulation to provide a performance analysis of CLIC. Our results show that CLIC outperforms ad hoc hinting techniques and that its adaptivity can be achieved with low overhead.
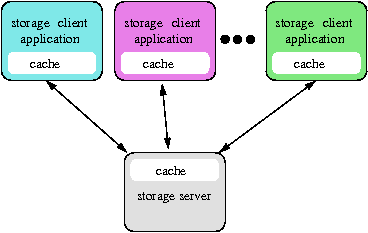
We assume a system in which multiple storage server client applications generate requests to a storage server, as shown in Figure 1. We are particularly interested in client applications that cache data, since it is such applications that give rise to multi-tier caching.
The storage server's workload is a sequence of block I/O requests from the various clients. When a client sends an I/O request (read or write) to the server, it may attach hints to the request. Specifically, each storage client may define one or more hint types and, for each such hint type, a hint value domain. When the client issues an I/O request, it attaches a hint set to the request. Each hint set consists of one hint value from the domain of each of the hint types defined by that client. For example, we used IBM DB2 Universal Database (DB2 Universal Database is a registered trademark of IBM) as a storage client application, and we instrumented DB2 so that it would generate five types of hints, as described in the first five rows of Figure 2. Thus, each I/O request issued by DB2 will have an attached hint set consisting of 5 hint values: a pool ID, an object ID, an object type ID, a request type, and a DB2 buffer priority.
CLIC does not require these specific hint types. We chose these particular types of hints because they could be generated easily from DB2, and because we believed that they might prove useful to the underlying storage system. Each application can generate its own types of hints. CLIC itself only assumes that the hint value domains are categorical. It neither assumes nor exploits any ordering on the values in a hint value domain. Each storage client application may have its own hint types. In fact, even if two storage clients are instances of the same application (e.g., two instances of DB2) and use the same hint types, CLIC treats each client's hint types as distinct from the hint types of all other clients.
Every I/O request, read or write, represents a caching opportunity
for the storage server.
The storage server must decide whether
to take advantage of each such opportunity by caching the requested page.
Our approach is to base these caching decisions on the hint sets
supplied by the client applications with each I/O request.
CLIC associates each possible hint set 
with a numeric
priority,
.
When an I/O request (read or write) for page 
with attached
hint set arrives at the server, the server uses
to decide whether to cache .
Cache management at the server will be described in more
detail in Section 4, but the essential
idea is simple: the server caches if there is some page 
in
the cache that was requested with a hint set 
for which
.
We expect that some hint sets may signal pages that are likely to be re-used quickly, and thus are good caching candidates. Other hint sets may signal the opposite. Intuitively, we want the priority of each hint set to reflect these signals. But how should priorities be chosen for each hint set? One possibility is to assign these priorities, in advance, based on knowledge of the client application that generates the hint sets. Most existing hint-based caching techniques use this approach. For example, the TQ algorithm [11], which exploits write hints, understands that replacement writes likely indicate evictions in the client application's cache, and so it gives them high priority.
CLIC takes a different approach to this problem. Instead of predefining hint priorities based on knowledge of the storage client applications, CLIC assigns a priority to each hint set by monitoring and analyzing I/O requests that arrive with that hint set. Next, we describe how CLIC performs its analysis.
We will assume that each request that arrives at the server
is tagged (by the server) with a sequence number.
Suppose that the server gets a request 
, meaning
a request (read or a write)
for a page with an attached hint set , and
suppose that this request is assigned sequence number 
.
CLIC is interested in whether and when page will be
requested again after .
There are three possibilities to consider:
in the request stream is a write request occurring with
sequence number 
(
).
In this case, there would have been no benefit whatsoever to caching
at time . A cached copy of would
not help the server handle the subsequent write request any more
efficiently. A cached copy of may be of benefit for
requests for that occur after , but in that case the server
would be better off
caching at rather than at .
Thus, the server's caching opportunity at is best ignored.
in the request stream is read request at time .
If the server caches at time and keeps in the cache
until , it will benefit by being able to serve the read request
at from its cache.
For the server to obtain this benefit, it must allow to
occupy one page ``slot'' in its cache during the interval 
.
is never requested again
after . In this case, there is clearly no benefit to
caching at .
on an analysis of previous
requests with hint set .
Specifically, CLIC tracks
three statistics for each hint set :
:.
:
that result in a read re-reference (rather than a write re-reference
or no re-reference).
: that result in
read re-references, the average number of requests that occur
between the request and the read re-reference.
Using these three statistics, CLIC performs a simple benefit/cost
analysis for each hint set , and assigns higher priorities to
hint sets with higher benefit/cost ratios.
Suppose that the server receives a request and that
it elects to cache .
If a read re-reference subsequently occurs while is
cached, the server will
have obtained a benefit from caching .
We arbitrarily assign a value of 
to this benefit (the
value we use does not affect the relative priorities of pages).
Among all previous requests with hint set , a fraction
 |
(1) |
the read hit rate of hint set .
Since the value of a read re-reference is ,
can be interpreted as the expected benefit of caching
and holding pages that are requested with hint set .
Conversely,
can be interpreted as
the expected cost of caching such pages, as it measures how long
such pages must occupy space in the cache before the benefit is
obtained.
We define the caching priority of hint set as:
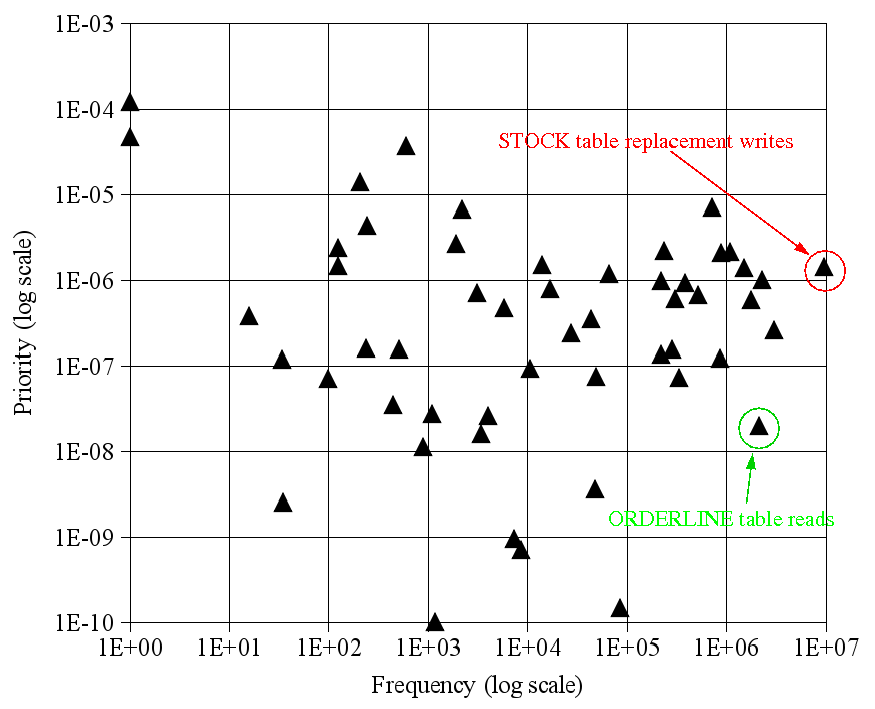
Figure 3 illustrates the results of this analysis for a trace of I/O requests made by DB2 during a run of the TPC-C benchmark. Our workload traces will be described in more detail in Section 6. Each point in Figure 3 represents a distinct hint set that is present in the trace, and describes the hint set's caching priority and frequency of occurrence. All hint sets with non-zero caching priority are shown. Clearly, some hint sets have much higher priorities, and thus much higher benefit/cost ratios, than others. For illustrative purposes, we have indicated partial interpretations of two of the hint sets in the figure. For example, the most frequently occurring hint set represents replacement writes to the STOCK table in the TPC-C database instance that was being managed by the DB2 client. We emphasize that CLIC does not need to understand that this hint represents the STOCK table, nor does it need to understand the difference between a replacement write and a recovery write. Its interpretation of hints is based entirely on the hint statistics that it tracks, and it can automatically determine that a request with the STOCK table hint set is a better caching opportunity than a request with the ORDERLINE table hint set.
 |
To track hint set statistics, CLIC maintains
a hint table with one entry for each distinct hint
set that has been observed by the storage server.
The hint table entry for records the current values
of the statistics
,
and
.
When the server receives a request , it increments
.
Tracking
and
is somewhat more involved, as CLIC
must determine whether a read request for page is a
read re-reference.
To determine this, CLIC records two pieces of information for
every page that is cached:
, which is the sequence number of the most recent request for ,
and
, which is the hint set that was
attached to the most recent request for .
In addition, CLIC records
and
for a
fixed number (
) of additional, uncached pages
This additional information is recorded in a
data structure called the outqueue.
is a CLIC parameter
that can be used to bound the amount of space required for tracking
read re-references.
When the server receives a read request for page with sequence
number 
, it checks both the cache and the outqueue for
information about the most recent previous request, if any,
for . If it finds
and
from a previous
request, then it knows that the current request is a read re-reference
of . It increments
and it updates
using the re-reference distance
.
When a page is evicted from the cache, an entry for is
inserted into the outqueue.
An entry is also placed in the outqueue for any requested
page that CLIC elects not to cache.
(CLIC's caching policy is described in Section 4.)
If the outqueue is full when a new entry is to be inserted,
the least-recently inserted entry is evicted from the outqueue
to make room for the new entry.
Since CLIC only records
and
for a limited
number of pages, it may fail to recognize that a new
read request is actually a read re-reference for .
Some error is inevitable unless CLIC were to record
information about all requested pages.
However, CLICs approach to tracking page
re-references has several advantages.
First, since CLIC tracks the most recent reference to all pages that
are in the cache, we expect to have accurate re-reference distance estimates
for hint sets that are believed to have the highest priorities,
since pages requested with those hint sets will be cached.
If the priority of such hint sets drops, CLIC should be able to detect this.
Second, by evicting the oldest entries from the outqueue when
eviction is necessary, CLIC will tend to miss read re-references that
have long re-reference distances.
Conversely, read re-references that happen quickly are likely
to be detected.
These are exactly the type of re-references that lead to high
caching priority.
Thus, CLIC's statistics tracking is biased in favor of
read re-references that are likely to lead to high caching priority.
To accommodate time-varying workloads, CLIC divides the
request stream into non-overlapping windows,
with each window consisting of
requests.
At the end of each window, CLIC adjusts the
priority for each hint set using the statistics collected
during that window. The adjusted priority will be used
to guide the caching policy during the next window.
It then clears
the statistics (
,
,
)
for all hint sets in the hint table so that it can
collect new statistics during the next window.
Let
represent the priority of that
is calculated after the 
th window, and that is
used by CLIC's caching policy during window 
.
Priority
is calculated as follows
represents the priorities
that were calculated using the statistics collected during the th
window (and Equation 2),
and
(
) is a CLIC parameter.
The effect of Equation 3 is that the impact
of statistics gathered
during the th window decays exponentially with each new window,
at a rate that is controlled by
. Setting
causes CLIC to base its priorities entirely on the statistics collected
during the most recently completed window. Lower values of
cause CLIC to give more weight to older statistics.
For all of the experiments reported in this paper, we have set
and
.
In the previous section, we described how
CLIC assigns a caching priority to each hint set .
In this section, we describe how the server uses these priorities
to manage the contents of its cache.
Figure 4 describes CLIC's priority-based
replacement policy.
This policy evicts a lowest priority page from the
cache if the newly requested page has higher priority.
The priority of a page is determined by the priority
of the hint set with which that page
was last requested.
Note that if a page that is cached after being requested with
hint set is subsequently requested with hint set ,
its priority changes from
to
.
The most recent request for each cached page
always determines its caching priority.
 |
The policy described in Figure 4 can be
implemented to run in constant expected time.
To do this, CLIC maintains a heap-based priority queue of
the hint sets.
For each hint set in the heap, all pages
with
are recorded in a doubly-linked list that
is sorted by
.
This allows the victim page to be identified
(Figure 4, lines 7-11)
in constant time.
CLIC also maintains a hash table of all cached pages
so that it can tell which pages are cached
(line 1)
and find a cached page in its hint set list in constant expected time.
Finally, CLIC implements the hint table as a hash table so that it can
look up
(line 12)
in constant expected time.
As described in Section 3.2, CLIC adjusts
hint set priorities after every window of
requests.
When this occurs, CLIC rebuilds its hint set priority queue
based on the newly adjusted priorities.
Hint set priorities do not change except at window
boundaries.
As described in Section 3.1, CLIC's hint table records statistical information about every hint set that the server has observed. Although the amount of statistical information tracked per hint set is small, the number of distinct hit sets from each client might be as large as the product of the cardinalities of that client's hint value domains. In our traces, the number of distinct hit sets is small. For other applications, however, the number of hint sets could potentially be much larger. In this section, we propose a simple technique for restricting the number of hint sets that CLIC must consider, so that CLIC can continue to operate efficiently as the number of hint sets grows.
All of the hint types in our workload traces exhibit frequency skew. That is, some values in the hint domain occur much more frequently than others. As a result, some hint sets occur much more frequently than others. To reduce the number of hints that CLIC must consider, we propose to exploit this skew by tracking statistics for the hint sets that occur most frequently in the request stream and ignoring those that do not. Ignoring infrequent hint sets may lead to errors. In particular, we may miss a hint set that would have had high caching priority. However, since any such missed hint set would occur infrequently, the impact of the error on the server's caching performance is likely to be small.
The problem with this approach is that we must determine,
on the fly, which hint sets occur frequently, without actually
maintaining a counter for every hint set.
Fortunately, this frequent item problem arises in
a variety of settings, and numerous methods have been proposed to solve it.
We have chosen one of these methods: the so-called Space-Saving algorithm
[14], which has recently been shown to outperform other frequent
item algorithms [7].
Given a parameter 
, this algorithm tracks the frequency of
different hint sets, among
which it attempts to include as many of the actual most frequent
hint sets as possible.
It is an on-line algorithm which scans the sequence of hint sets attached
to the requests arriving at the server. Although different hint
sets are tracked at once, the specific hint sets that are
being tracked may vary over time, depending on the request
sequence.
After each request has been processed, the algorithm can
report the hint sets that it is currently tracking, as well
as an estimate of the frequency (total number of occurrences) of each
hint set
and an error indicator which bounds the error in the frequency estimate.
By analyzing the frequency estimates and error indicators, it is
possible to determine which of the currently-tracked hint
sets are guaranteed to be among the actual top- most frequent
hint sets and which are not. However, for our purposes this
is not necessary.
We adapted the Space-Saving algorithm slightly so that it tracks the additional information we require for our analysis. Specifically:
: that is tracked by
the Space-Saving algorithm, we use the frequency estimate produced
by the algorithm, minus the estimation error bound reported by the
algorithm, as
.
: that is
currently being tracked. This counter is initialized to zero
when the algorithm starts tracking , and it is incremented
for each read re-reference involving that occurs while
is being tracked. We use the value of this counter as
.
: that occur while is
being tracked, i.e., those read re-references that are included
in
.
that are not currently tracked by the algorithm,
we take
to be zero, and hence
to be zero
as well.
In general,
will be
be an underestimate of the true frequency of hint set .
Since
is only incremented
while is being tracked, it too will in general
underestimate the true frequency of read re-references involving .
As a result of these underestimations,
, which is calculated as
the ratio of the
to
, may be inaccurate.
However, because we take the ratio of
to
,
the two underestimations may at least partially cancel one another,
leading to a more accurate
.
In addition,
the higher the true frequency of , the more time
will spend being tracked and the more accurate we expect our
estimates to be.
To account for time-varying workloads, we restart the Space-Saving
algorithm from scratch for every window of
requests.
Specifically, at the end of each window we use the Space-Saving
algorithm to estimate
,
, and
for each hint set that is tracked by the algorithm,
as described above.
These statistics are used to calculate
, which
is then used in Equation 3 to calculate
the hint set's caching priority (
) to be used during
the next request window.
Once the
have been calculated, the Space-Saving
algorithm's state is cleared in preparation for the next window.
The Space-Saving algorithm requires two counters for each tracked
hint-set, and we added several additional counters for the sake of
our analysis. Overall, the space required is proportional to .
Thus, this parameter can be used to limit the amount of space
required to track hint set statistics.
With each new request, the data structure used by the Space-Saving
algorithm can be updated in constant time [14], and the statistics
for the tracked hint sets can be reported, if necessary, in time
proportional to .
Objectives: We used trace-driven simulation to evaluate our proposed mechanisms. The goal of our experimental evaluation is to answer the following questions:
Simulator: To answer these questions, we implemented a simulation of the storage server cache. In addition to CLIC, the simulator implements the following caching policies for purpose of comparison:
The simulator accepts a stream of I/O requests with associated hint sets, as would be generated by one or more storage clients. It simulates the caching behavior of one of the five supported cache replacement policies (CLIC, OPT, LRU, ARC and TQ) and computes the read hit ratio for the storage server cache. The read hit ratio is the number of read hits divided by the number of read requests.
 |
Workloads: In this paper, we use DB2 Universal Database (version 8.2) and the MySQL (MySQL is a registered trademark of MySQL AB in the United States, the European Union and other countries) database system (Community Edition, version 5.0.33) as our storage system clients. DB2 is a widely-used commercial relational database system to which we had access to source code, and MySQL is a widely-used open source relational database system. We instrumented DB2 and MySQL so that they would generate I/O hints and dump them into an I/O trace. The types of hints generated by these two systems are described in Figure 2.
To generate our traces, we ran TPC-C and TPC-H workloads on DB2 and a TPC-H workload on MySQL. TPC-C and TPC-H are well-known on-line transaction processing (TPC-C) and decision support (TPC-H) benchmarks. We ran TPC-C at scale factor 25. At this scale factor, the TPC-C database initially occupied approximately 600,000 4KB blocks, or about 2.3 GB, in the storage system. The TPC-C workload inserts new items into the database, so the database grows during the TPC-C run. For the TPC-H experiments, the database size was approximately 3.2 GB for the DB2 runs, and 5 GB for the MySQL runs. The DB2 TPC-H workload consisted of the 22 TPC-H queries and the two refresh updates. The workload for MySQL was similar except that it did not include the refresh updated and we skipped one of the 22 queries (Q18) because of excessive run-time on our MySQL configuration.
On each run, we controlled the size of the database system's internal buffer cache. We collected traces using a variety of different buffer cache sizes for each DBMS. We expect the buffer cache size to be a significant parameter because it affects the temporal locality in the I/O request stream that is seen by the underlying storage server. Figure 5 summarizes the I/O request traces that were used for the experiments reported here.
In our first experiment, we compare the cache read hit ratio of CLIC to
that of
other replacement policies that we consider (LRU, ARC, TQ, and OPT).
We varied the size of the storage server buffer cache, and we present
the read hit ratio as a function of the server's buffer cache size
for each workload.
For these experiments, we set
and
the size of CLIC's outqueue (
)
to 5 entries per page in the storage server's cache.
If the cache holds
pages, this means that CLIC tracks
the most recent reference for
pages, since it tracks
this information for all cached pages, plus those in the outqueue.
For each tracked page, CLIC records a sequence number and a hint set.
If each of these is stored as a 4-byte integer, this represents
a space overhead of roughly 
.
To account for this, we reduced the server cache size by 1% for
CLIC only, so that the total space used by CLIC would be the same
as that used by other policies.
ARC also employs a structure similar to CLIC's outqueue for tracking
pages that are not in the cache. However, we did not reduce
ARC's cache size. As a result, ARC has a small space advantage in
these experiments.
Figure 6 shows the results of this experiment for the DB2 TPC-C traces. All of the algorithms have similar performance for the DB2_C60 trace. That trace comes from the DB2 configuration with the smallest buffer cache, and there is a significant amount of temporal locality in the trace that was not ``absorbed'' by DB2's cache. This temporal locality can be exploited by the storage server cache. As a result, even LRU performs reasonably well. Both of the hint-based algorithms (TQ and CLIC) also do well.
The performance of LRU is significantly worse on the other two TPC-C traces, as there is very little temporal locality. ARC performs better than LRU, as expected, though substantially worse than both of the hint-aware policies. CLIC, which learns how to exploit the available hints, does about as well as TQ, which implements a hard-coded response to one particular hint type on the DB2_C300 trace, and both policies' performance approaches that of OPT. CLIC outperforms TQ on the DB2_C540 trace, though it is also further from OPT. The DB2_C540 trace comes from the DB2 configuration with the largest buffer cache, so it has the least temporal locality of all traces and therefore presents the most difficult cache replacement problem.
Figures 7 and 8 show the results for the TPC-H traces from DB2 and for the MySQL TPC-H traces, respectively. Again, CLIC generally performs at least as well as the other replacement policies that we considered. In some cases, e.g., for the DB2_H400 trace, CLIC's read hit ratio is more than twice the hit ratio of the best hint-oblivious alternative. In one case, for the DB2_H80 trace with a server cache size of 300K pages, both LRU and ARC outperformed both TQ and CLIC. We are uncertain of the precise reason for this inversion. However, this is a scenario in which there is a relatively large amount of residual locality in the workload (because the DB2 buffer cache is small) and in which the storage server cache may be large enough to capture it.
In this experiment, we study the effect of tracking only the most frequently
occurring hint sets using the top- algorithm described in
Section 5.
In our experiment
we vary , the number of hint
sets tracked by CLIC, and measure the server cache hit ratio.
Figure 9 shows some of the results of this experiment.
The top graph in Figure 9 shows the results for the DB2 TPC-C
traces, with a server cache size of 180K pages.
We obtained similar results with the DB2 TPC-C traces for other server
cache sizes. In all cases, tracking the 20 most frequent hints (i.e.,
setting 
) was sufficient to achieve a read hit ratio close to
what we could obtain by tracking all of the hints in the trace.
In many cases, tracking fewer than 10 hints sufficed.
The curve for the DB2_C540 trace illustrates that the Space Saving
algorithm that we use to track frequent hint sets can sometimes
suffer from some instability, in the sense that larger values
of may result in worse performance than smaller .
This is because hint sets reported by the Space Saving
algorithm when 
are not guaranteed to be reported by
the space saving algorithm when 
.
We only observed this problem occasionally, and only
for very small values of .
The lower graph in Figure 9 shows the results for
the DB2 TPC-H traces, with a server cache size of 180K pages.
For all of the DB2 TPC-H traces and all of the cache sizes that we
tested, 
was sufficient to obtain
performance close to that obtained by tracking all hint sets.
For the MySQL TPC-H traces (not shown in Figure 9), which
contained fewer distinct hint sets, 
was sufficient to obtain
good performance.
Overall, we found the top- approach to be very effective
at cutting down the number of hints to be considered by CLIC.
In the previous experiment, we studied the effectiveness of the
top- approach at reducing the number of hints that must be
tracked by CLIC.
In this experiment, we consider a similar question, but from a
different perspective.
Specifically, we consider a scenario in which CLIC is subjected
to useless ``noise'' hints, in addition to the useful hints
that it has exploited in our previous experiments.
We limit the number of hint sets that CLIC is able to track
and increase the level ``noise''.
Our objective is to determine whether the top- approach is
effective at ignoring the noise, and focusing the limited space
available for hint-tracking on the most useful hints.
In practice, we hope that storage clients will not generate lots of useless hints. However, in general, clients will not be able to determine how useful their hints are to the server, and some hints generated by clients may be of little value. By deliberately introducing a controllable level of useless hints in the his experiment, we hope to test CLIC's ability to tolerate them without losing track of those hints that are useful..
For this experiment we used our DB2 TPC-C traces, each of which
contains 5 real hint types, and added 
additional
synthetic hint types.
In other words, each request will have 
hints associated with it,
the five original hints plus additional synthetic hints.
Each injected synthetic hint is chosen randomly from a domain of 
possible
hint values. A particular value from the domain is selected using
a Zipf distribution with skew parameter 
. When 
, each
injected hint value is chosen independently of the other injected hints
for the same record.
Since the injected hints are chosen at random, we do not expect them
to provide any information that is useful for server cache management.
This injection procedure potentially increases the number of distinct
hint sets in a trace by a factor 
.
For our experiments, we chose 
, and we varied , which controls
the amount of ``noise''.
Figure 10 shows the read hit ratios in a
server cache of size 180K pages as a function of .
We fixed 
for the top- algorithm, so the number of
hints tracked by CLIC remains fixed at 100 as the number of
useless hints increases.
As goes from 
to 
, the total number of distinct
hint sets in each trace increases from just over 
(the number of distinct hint sets each TPC-C trace),
to about 
when 
, and to more than 
when 
.
Ideally, the server cache read hit ratio would remain unchanged
as the number of ``noise'' hints is increased.
In practice, however, this is not the case.
As shown in Figure 10, CLIC fares reasonably
well for the DB2_C60 trace, suffering mild degradation in performance
for 
.
However, for the other two traces, CLIC experienced more
substantial degradation, particularly for .
The cause of the degradation is that high-priority hint sets from
the original trace get ``diluted'' by the additional noise hint
types. For example, with and 
, each original hint
set is split into as many as 
distinct hint sets because
of the additional noise hints that appear with each request.
Since CLIC has limited space for tracking hint sets, the dilution
eventually overwhelms its ability to track and identify the
useful hints.
This experiment suggests that it may be necessary to tune or
modify CLIC to ensure that it operates well in situations in
which the storage clients provide too many low-value hints.
One way to address this problem is to increase as the
number of hints increases, so that CLIC is not overwhelmed
by the additional hints. Controlling this tradeoff of
space versus accuracy is an interesting tuning problem for
CLIC.
An alternative approach is to add an additional mechanism
to CLIC that would allow it to group similar hint sets together,
and then track re-reference statistics for the groups rather
than the individual hint sets.
We have explored one technique for doing this, based on
decision trees.
However, both the decision tree technique and the tuning
problem are beyond the scope of this paper, and we leave
them as subjects for future work.
One desirable feature of CLIC is that it should be capable of accommodating hints from multiple storage clients. The clients independently send their different hints to the storage server without any coordination among themselves, and CLIC should be able to effectively prioritize the hints to get the best overall cache hit ratio.
To test this, we simulated a scenario in which multiple instances of DB2 share a storage server. Each DB2 instance manages its own separate database, and represents a separate storage client. All of the databases are housed in the storage server, and the storage server's cache must be shared among the pages of the different databases. To create this scenario, we create a multi-client trace for our simulator by interleaving requests from several DB2 traces, each of which represents the requests from a single client. We interleave the requests in a round robin manner, one from each trace. We truncate all traces to the length of the shortest trace being interleaved to eliminate bias towards longer traces. We treat the hint types in each trace as distinct, so the total number of distinct hint sets in the combined trace is the sum of the number of distinct hint sets in each individual trace.
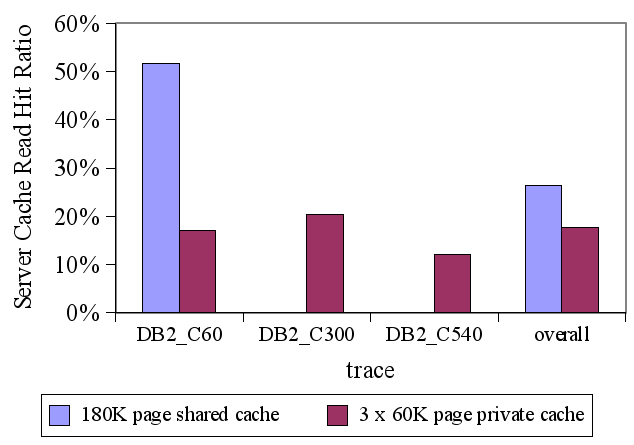
Figure 11 shows results for the trace generated by
interleaving the DB2_C60, DB2_C400, and DB2_C540 traces. The
server cache size is 180K pages, and CLIC uses top- filtering with
.
The figure shows the read hit ratio for the requests from each
individual trace that is part of the interleaved trace. The figure
also shows the overall hit ratio for the entire interleaved trace.
For comparison, the figure shows the hit ratios for the full-length
(untruncated) traces when they use independent caches of size 60K
pages each (i.e., the storage server cache is partitioned equally
among the clients). The figure shows a dramatic improvement in hit
ratio for the DB2_C60 trace and also an improvement in the overall
hit ratio as compared to equally partitioning the server cache among
the traces. CLIC is able to identify that the DB2_C60 trace presents the
best caching opportunities (since it has the most temporal locality),
and to focus on caching pages from this trace. This illustrates that
CLIC is able to accommodate hints from multiple storage clients and
prioritize them so as to maximize the overall hit ratio.
Note that it is possible to consider other objectives when managing the shared server cache. For example, we may want to ensure fairness among clients or to achieve certain quality of service levels for some clients. This may be accomplished by statically or dynamically partitioning the cache space among the clients. In CLIC, the objective is simply to maximize the overall cache hit ratio without considering quality of service targets or fairness among clients. This objectives results in the best utilization of the available cache space. Our experiment illustrates that CLIC is able to achieve this objective, although the benefits of the server cache may go disproportionately to some clients at the expense of others.
 |
Many replacement policies have been proposed to improve on LRU, including MQ [22], ARC [13], CAR [3], and 2Q [10]. These policies use a combination of recency of use and frequency of use to make replacement decisions. They can be used to manage a cache at any level of a cache hierarchy, though some, like MQ, were explicitly developed for use in second-tier caches, for which there is little temporal locality in the workload. ACME [1] is a mechanism that can be used to automatically and adaptively choose a good policy from among a pool of candidate policies, based on the recent performance of the candidates.
There are also caching policies that have been proposed explicitly for second (or lower) tier caches in a cache hierarchy. Chen et al [6] have classified these as either hierarchy-aware or aggressively collaborative. Hierarchy-aware methods specifically exploit the knowledge that they are running in the second tier, but they are transparent to the first tier. Some such approaches, like X-RAY [2], work by examining the contents of requests submitted by a client application in the first tier. By assuming a particular type of client and exploiting knowledge of its behavior, X-RAY can extract client-specific semantic information from I/O requests. This information can then be used to guide caching decisions at the server. X-RAY has been proposed for file system clients [2] and DBMS clients [17].
Aggressively collaborative approaches require changes to the first tier. Examples include PROMOTE [8] and DEMOTE [19], both of which seek to maintain exclusivity among caches, and hint-based techniques, including CLIC. Although all aggressively collaborative techniques require changes to the first tier, they vary considerably in the intrusiveness of the changes that are required. For example, ULC [9] gives complete responsibility for management of the second tier cache to the first tier. PROMOTE [8] prescribes a replacement policy that must be used by all tiers, including the first tier. This may be undesirable if the first tier cache is managed by a database system or other application which prefers an application-specific policy for cache management. Among the aggressively collaborative techniques, hint-based approaches like CLIC are arguably the least intrusive and least costly. Hints are small and can be piggybacked onto I/O requests. More importantly, hint-based techniques do not require any changes to the policies used to manage the first tier caches.
Several hint-based techniques have been proposed, including importance hints [6] and write hints [11], which have already been described. In their work on informed prefetching and caching, Patterson et al [16] distinguished hints that disclose from hints that advise, and advocated the former. Most subsequent hint-based techniques, including CLIC, use hints that disclose. Informed prefetching and caching rely on hints that disclose sequential access to entire files or to portions of files. Karma [21] relies on application hints to group pages into ``ranges'', and to associate an expected access pattern with each range. Unlike CLIC, all of these techniques are they are designed to exploit specific types of hints. As was discussed in Section 1, this makes them difficult to generalize and combine.
A previous study [6] suggested that aggressively collaborative approaches provided little benefit beyond that of hierarchy-aware approaches and thus, that the loss of transparency implied by collaborative approaches was not worthwhile. However, that study only considered one ad hoc hint-based technique. Li et al [11] found that the hint-based TQ algorithm could provide substantial performance improvements in comparison to hint-oblivious approaches (LRU and MQ) as well as simple hint-aware extensions of those approaches.
There has also been work on the problem of sharing a cache among multiple competing client applications [5,12,18,20]. Often, the goal of these techniques is to achieve specific quality-of-service objectives for the client applications, and the method used is to somehow partition the shared cache. This work is largely orthogonal to CLIC, in the sense that CLIC can be used, like any other replacement algorithm, to manage the cache contents in each partition. CLIC can also used to directly control a shared cache, as in Section 6.4, but it does not include any mechanism for enforcing quality-of-service requirements or fairness requirements among the competing clients.
The problem of identifying frequently-occurring items in a data stream occurs in many situations. Metwally et al [14] classify solutions to the frequent-item problem as counter-based techniques or sketch-based techniques. The former maintain counters for certain individual items, while the latter collect information about aggregations of items. For CLIC, we have chosen to use the Space-Saving algorithm [14] as it is both effective and simple to implement. A recent study [7] found the Space-Saving algorithm to be one of the best overall performers among frequent-item algorithms.
We have presented CLIC, a technique for managing a storage server cache based on hints from storage client applications. CLIC provides a general, adaptive mechanism for incorporating application-provided hints into cache management. We used trace-driven simulation to evaluate CLIC, and found that it was effective at learning to exploit hints. In our tests, CLIC learned to perform as well as or better than TQ, an ad hoc hint based technique. In many scenarios, CLIC also performed substantially better than hint-oblivious techniques such as LRU and ARC. Our results also show that CLIC, unlike TQ and other ad hoc techniques, can accommodate hints from multiple client applications.
A potential drawback of CLIC is the space overhead that is required learning which hints are valuable. We considered a simple technique for limiting this overhead, which involves identifying frequently-occurring hints and tracking statistics only for those hints. In many cases, we found that it was possible to significantly reduce the number of hints that CLIC had to track with only minor degradation in performance. However, although tracking only frequent hints is a good way to reduce overhead, the overhead is not eliminated and the space required for good performance may increase with the number of hint types that CLIC encounters. As part of our future work, we are using decision trees to generalize hint sets by grouping related hint sets together into a common class. We expect that this approach, together with the frequency-based approach, can enable CLIC to accommodate a large number of hint types.
We are grateful to Martin Kersten and his group at CWI for their assistance in setting up TPC-H on MySQL, and to Aamer Sachedina and Roger Zheng at IBM for their help with the DB2 modifications and trace collection. Thanks also to our shepherd, Liuba Shrira, and the anonymous referees for their comments and suggestions. This work was supported by the Ontario Centre of Excellence for Communication and Information Technology and by the Natural Sciences and Engineering Research Council of Canada.
