|
USENIX '05 Paper
[USENIX '05 Technical Program]



Attrition Defenses for a Peer-to-Peer Digital
Preservation System
TJ Giuli
Stanford University, CA
Petros Maniatis
Intel Research, Berkeley, CA
Mary Baker
HP Labs, Palo Alto, CA
David S. H. Rosenthal
Stanford University Libraries, CA
Mema Roussopoulos
Harvard University, Cambridge, MA
In peer-to-peer systems, attrition attacks
include both traditional, network-level denial of service attacks as
well as application-level attacks in which malign peers conspire to waste
loyal peers' resources.
We describe several defenses for the LOCKSS peer-to-peer digital
preservation system that help ensure that application-level attrition attacks even
from powerful
adversaries are less effective than simple network-level attacks, and that
network-level attacks must be intense, widespread, and prolonged to
impair the system.
1 Introduction
Denial of Service (DoS) attacks are among the most difficult for
distributed systems to resist.
Distinguishing legitimate requests for service from the attacker's requests
can be tricky,
and devoting substantial effort to doing so can easily be self-defeating.
The term DoS was introduced by Needham [34] with
a broad meaning but over time it has come to mean high-bit-rate
network-level flooding attacks [23] that
rapidly degrade the usefulness of the victim system.
In addition to DoS, we use the term attrition
to include also moderate- or low-bit-rate
application-level attacks that impair the victim system.
The mechanisms described in this paper are aimed at
equipping the LOCKSS (LOCKSS is a trademark of Stanford University --
it stands for "Lots Of Copies Keep Stuff Safe")
peer-to-peer (P2P) digital preservation
system to resist attrition attacks. The system is in use at
about 80 libraries worldwide; publishers of about 2000 titles
have endorsed its use. Cooperation among peers reduces the cost
and increases the reliability of preservation, eliminates the
need for backup, and greatly reduces other operator interventions.
A loyal (non-malign) peer participates in the LOCKSS system for two reasons:
to achieve regular reassurance that its content
agrees with the consensus of the peers holding copies of the same content,
and if it does not, to obtain the needed repair.
The goal of an attrition adversary is to prevent
loyal peers from successfully determining the consensus of their
peers or from obtaining requested repairs for so
long that undetected storage problems such as
natural ``bit rot'' or human error corrupt their
content. Other types of resource waste may be inconvenient
but have no lasting effect on this system.
In prior work [30] we
defended
LOCKSS peers against
attacks seeking to corrupt their content.
That system, however, remained vulnerable
to application-level attrition;
about 50 malign peers could abuse the protocol to prevent a network of
1000 peers from auditing
and repairing their content.
We have developed a set of defenses,
some adapted from other systems, whose
combination in a P2P context provides novel and effective protection against
attrition. These defenses
include admission control, desynchronization,
and redundancy.
Admission control, effected via rate limitation, first-hand
reputation, and effort balancing, ensures that legitimate requests can
be serviced even during malicious request floods.
Desynchronization ensures that progress continues even if
some suppliers of a needed service are currently too busy.
Redundancy ensures that the
attacker cannot incapacitate the system by targeting only few peers
at a time.
Our defenses may not all be immediately applicable
to all P2P applications, but we believe that many systems may benefit
from a subset of these defenses, and that our analysis of the
effectiveness of these defenses is more broadly useful.
This paper presents a new design of the LOCKSS protocol that makes four contributions.
First, we demonstrate via simulation how our new design ensures that
application-level attrition, no matter
how powerful the attacker, is less effective than simple network
flooding. We do this while retaining our previous resistance against
other adversaries.
Second, we show that
even network-level flooding attacks that continuously prevent all
communication among a majority of the peers must last for months
to affect the system significantly.
Such attacks are orders of
magnitude more powerful than those
observed in practice [33].
Third, since resource management lies at the
crux of attrition attacks and their defenses,
we extend our prior evaluation [30] to
deal with numerous concurrently preserved archival units of content
competing with each other for resources.
Finally, resource over-provisioning is essential in defending against
attrition attacks. We show that with a
practical amount of over-provisioning we can
defend the LOCKSS system from an arbitrarily powerful attrition adversary.
In the rest of this paper, we first describe our application. We
continue by outlining how we would like this application to behave
under different levels of attrition attack. We give an overview of the LOCKSS
protocol, describing how it incorporates each of our attrition defenses.
We then
explain the results of a systematic exploration of simulated attacks
against the resulting design,
showing that it successfully defends against attrition attacks
at all layers, from the network level up through the application protocol.
Finally, we describe how the new LOCKSS
protocol compares to our previous work, as well as other related work.
2 The Application
In this section, we provide an overview of the digital preservation
problem for academic publishing.
We then present and justify the set of design goals required of
any solution to this problem, setting the stage for the LOCKSS approach in
subsequent sections.
Academic publishing has migrated to the Web [46],
placing society's scientific and cultural heritage at a variety of
risks such as confused provenance,
accidental editing by the publisher,
storage corruption, failed backups,
government or corporate censorship, and
vandalism.
The LOCKSS system was designed [39] to
provide librarians with the tools they need to preserve
their community's access to journals and other Web materials.
Any solution must meet six stringent
requirements. First, since under U.S. law copyrighted Web content can only
be preserved with the owner's permission [16], the solution must accommodate
the publishers' interests. Requiring publishers, for example, to offer perpetual no-fee access or
digital signatures on content makes them reluctant to give that permission.
Second, a solution must be extremely cheap in terms of
hardware, operating cost, and human expertise.
Few libraries could afford [3] a solution involving handling
and securely storing off-line media, but most can afford the few cheap
off-the-shelf PCs that provide sufficient storage for tens of thousands of
journal-years. Third, the existence of cheap, reliable storage cannot
be assumed; affordable storage is unreliable [22,38].
Fourth, a solution must have a long time horizon.
Auditing content against stored digital signatures,
for example, assumes not only that the cryptosystem will remain unbroken,
but also that the secrecy, integrity, and availability of the keys are guaranteed
for decades. Fifth,
a solution must anticipate adversaries capable of powerful attacks
sustained over long periods; it must withstand these attacks, or at
least degrade slowly and gracefully while providing unambiguous
warnings [37]. Sixth, a solution must not require a central locus of control
or administration, if it is to withstand concentrated
technical or legal attacks.
Two different architectures have been proposed for preserving Web
journals. The centralized architecture of a ``trusted third party'' archive requires publishers
to grant a third party permission, under certain circumstances, to
republish their content. Obtaining this permission involves formidable
legal and business obstacles [5]. In contrast, the
distributed architecture of the
LOCKSS system consists of many individual archives at subscribing
(second party) libraries. Readers only access their local library's copy,
whose subscription already provides them access to the publisher's copy.
Most publishers see this as less of a risk to their business, and are
willing to add this permission to the subscription agreement. It is thus
important to note that our goal is not to minimize the number of replicas
consistent with content safety. Instead, we strive to minimize the
per-replica cost of maintaining a large number of replicas. We trade extra
replicas for fewer lawyers, an easy decision given their relative costs.
The LOCKSS design is extremely conservative, making few
assumptions about the infrastructure. Although we believe this is
appropriate for a digital preservation system, less conservative assumptions
are certainly possible. Increasing risk
can increase the amount of content that can be preserved with given
computational power. Limited amounts
of reliable, write-once memory would allow audits against local
hashes, a reliable public key infrastructure might
allow publishers to sign their content and peers to audit against the
signatures, and so on. Conservatively, the assumptions underlying such
optimizations could be violated without warning at any time;
the write-once memory might be corrupted or mishandled,
or a private key might leak. Thus,
these optimizations still require a distributed audit
mechanism as a fallback.
The more a peer operator can do to avoid local failures
the better the system works,
but our conservative design principles lead us to focus on mechanisms
that minimize dependence on these efforts.
With the application of digital preservation for academic publishing in
mind,
we tackle the ``abstract'' problem of
auditing and repairing replicas of distinct archival units or AUs
(a year's run of an on-line journal, in our target application) preserved by a population of peers
(libraries) in
the face of attrition attacks. For each AU it preserves, a peer starts out with its own,
correct replica
(obtained from the publisher's Web site), which it can only use
to satisfy local read requests (from local patrons) and to
assist other peers with replica repairs. In the rest of this
paper we refer to AUs, peers, and replicas, rather than journals and libraries.
3 System Model
In this section we present the adversary we model, our security goals
and the framework for our defenses.
3.1 Adversary Model
Our conservative design philosophy leads us to assume a powerful
adversary with several important abilities.
Pipe stoppage is his ability to prevent communication with
victim peers for extended periods by flooding links with garbage packets
or using more sophisticated
techniques [26]. Total information
awareness allows him to control and monitor all of
his resources instantaneously. He has unconstrained identities in that
he can purchase or spoof unlimited network identities.
Insider information provides him
complete knowledge of victims' system parameters and
resource commitments. Masquerading means that loyal peers cannot
detect him, as long as he follows the
protocol. Finally, he has unlimited computational resources,
though he is polynomially bounded in his computations (i.e., he cannot invert
cryptographic functions).
The adversary employs these capabilities in effortless and
effortful attacks. An effortless attack requires no measurable
computational effort from the attacker and includes traditional DoS
attacks such as pipe stoppage. An effortful
attack requires the attacker to invest in the system
with computational effort.
3.2 Security Goals
The overall goals of the LOCKSS system are that, with high probability,
the consensus of peers reflects the correct AU, and readers access good data.
In contrast, an attrition
adversary's goal is to decrease significantly the probability of these events by
preventing peers from auditing their replicas for a long time, long
enough for undetected storage problems such as ``bit rot'' to occur.
Severe but narrowly focused pipe stoppage attacks in the wild last for days or
weeks [33]. Our goal is to ensure that, in the very
least, the LOCKSS system withstands or degrades gracefully with even
broader such attacks sustained over months.
Beyond pipe stoppage, attackers must use protocol messages to some
extent. We seek to ensure the following three conditions. First, a peer manages
its resources so as to prevent exhaustion no matter how much effort is
exerted by however many identities requesting service. Second, when
deciding which requests to service, a peer gives preference to requests
from those likely to behave properly (i.e., ``ostensibly legitimate'').
And third, at every stage of a protocol exchange, an ostensibly
legitimate attacker expends commensurate effort to that which he imposes
upon the defenders.
3.3 Defensive Framework
We seek to curb the adversary's success by modeling a peer's processing
of inbound messages as a series of filters, each costing a certain
amount to apply. A message rejected by a filter has no further effect
on the peer, allowing us to estimate the cost of eliminating whole
classes of messages from further consideration. Each filter increases
the effort a victim needs to defend itself, but limits the effectiveness
of some adversary capability. The series of filters as a whole is
sound if the cost of applying a filter to the input stream passed
through its preceding filter is low enough to permit the system to make
progress. The filters include a volume filter, a reciprocity
filter, and a series of effort filters.
The volume filter models a peer's network connection. It
represents the physical limits on the rate of inbound messages that an
adversary can force upon the peer. It is an unavoidable filter; no
adversary can push data through a victim's network card at a rate
greater than the card's throughput. Soundness requires
the volume filter to restrict the volume of messages enough
that processing costs at the next filter downstream are low. This
condition can be enforced either through traffic shaping or via the
low-tech choice of configuring peers with low-bandwidth network cards.
The reciprocity filter takes inbound messages at the
maximum rate exported by the volume filter and further limits them by
rejecting those sent from peers who appear to be misbehaving. A peer's
reciprocity filter favors those of its peers who engage it with
requests at the same average rate as it engages them. The filter
further penalizes those peers it has not known for long enough to
evaluate their behavior. In this sense, the reciprocity
filter implements a self-clocking invariant, by which
inbound traffic exiting the filter mirrors in volume traffic originated at the
peer. Thus on average the number of requests passed to the next
filter matches the number of requests inflicted by the peer upon others.
The effort filters focus on the balance of effort
expended by the peer and a correspondent peer while the two are
cooperating on
an individual content audit request. These filters ensure that the
computational effort imposed upon a
potential victim peer by its ostensibly legitimate correspondent is
matched by commensurate effort borne by that correspondent. For
example, an attacker can only trick its victim peer into cryptographically
hashing large amounts of data by first performing the same hash
itself (or other effort equivalent to the same hash). As a result,
these filters enforce the invariant that ostensible legitimacy costs the
attacker as much as it allows the attacker to inflict on its victim. Furthermore, the effort
filters ensure that a peer can detect at a low cost that an
attacker has abandoned ostensible legitimacy.
In summary, these filters take an input stream of protocol messages and
reduce it to levels consistent with legitimate traffic in terms of
volume (volume filter), then in number of individual messages per
source (reciprocity filter), and then in effort induced per
message (effort filters).
Malicious interactions that pass
all filters can ultimately affect the victim peer adversely, but are
ensured to
impose no more than manageable additional burden on the victim peer
and are guaranteed to cost the attacker as much burden in
the process.
The former guarantee is essential for the correct
operation of good peers in all cases, whereas the latter is only
meaningful when the adversary is resource-constrained.
We show in Section 7.4 that the most effective strategy
for effortful attacks is to emulate legitimacy,
and that even this
has minimal effect on the utility of the system. Effortless attacks,
such as traditional distributed DoS (DDoS) attacks, are more effective but
must be maintained for a long time against most of the peer
population to
degrade the system significantly (Section 7.2).
4 The LOCKSS Replica Auditing and Repair Protocol
The LOCKSS audit process is a sequence of ``opinion polls''
conducted by every peer on each of its AU replicas. At intervals,
typically every 3 months, a peer (the poller) picks a
random sample of peers that it knows to be
preserving an AU, and invites those peers as voters into a poll.
Each voter individually hashes a poller-supplied nonce and its replica
of the AU to produce a fresh vote, which the poller tallies. If the
poller is outvoted in a landslide (e.g., it disagrees with 80% of the
votes), it assumes its replica is corrupt and repairs it from a
disagreeing voter. The roles of poller and voter are distinct, but
every peer plays both.
Figure 1:
A timeline of a poll,
showing the message exchange between the poller and a voter.
|
The general structure of a poll follows the timeline of
Figure 1. A poll consists of two phases:
vote solicitation and evaluation.
In the vote solicitation phase the poller requests and obtains
votes from as many voters in its sample of the population as possible.
Then the poller begins the evaluation phase,
during which it compares these votes to its own replica,
one hashed content block at a time,
and tallies them.
If the hashes disagree the poller may request repair blocks from its
voters and reevaluate the block.
If in the eventual tally, after any repairs, the poller agrees with the landslide majority,
it sends a receipt to each of its voters and immediately starts a new
poll.
Peers interleave progress on their own polls with voting in other
peers' polls, spreading each poll over a period chosen so
that polls on a given AU occur at a rate much higher than
that of undetected storage errors.
4.1 Vote Solicitation
The outcome of a poll is determined by the votes of the inner circle
peers, chosen at the start of the poll by the poller from its
reference list for the AU.
The reference list contains mostly peers that have agreed with the poller in
recent polls on the AU, and a few peers from its static friends list,
maintained by the poller's operator.
A poll is considered successful if its result is based on a minimum
number of inner circle votes, the quorum, which is
typically 10, but may change according to the application's needs for
fault tolerance. To ensure that a poll is likely to succeed, a poller
invites into its poll a larger inner circle than the quorum (typically,
twice as large). If at first try an inner circle peer fails to
respond to an invitation, or refuses it, the poller
contacts a different inner circle voter,
retrying the reluctant peer later in the same vote solicitation phase.
An individual vote solicitation consists of four messages (see
Figure 1): Poll, PollAck,
PollProof, and Vote. For the duration of a poll, a
poller establishes an encrypted TLS session with each voter
individually, via an anonymous Diffie-Hellman key exchange. Every
protocol message is conveyed over this TLS session, either keeping
the same TCP connection from message to message, or resuming the
TLS session over a new one.
The Poll message invites a voter to participate in a poll on an
AU. The invited peer
responds with a PollAck message, indicating either a refusal to
participate in the poll at the time, or an acceptance
of the invitation, if it can compute a vote within a predetermined time
allowance. The voter commits and reserves local resources to that
effect. The PollProof message supplies the voter with a random
nonce to be used during vote construction. To
compute its vote, the voter uses a cryptographic hash function
to hash the nonce supplied by the poller,
followed by its replica of the AU, block by block. The vote consists of the running hashes
produced at each block boundary. Finally, the voter sends its vote back
to the poller in a Vote message.
These messages also contain proofs of computational
effort, such as those introduced by Dwork et al. [15],
sufficient to ensure that, at every protocol stage, the requester of a service
has more invested in the exchange than the supplier of the service (see
Section 5.1).
4.2 Peer Discovery
The poller uses the vote solicitation phase of a poll not only to obtain
votes for the current poll, but also to discover new peers for its
reference list from which it can solicit inner circle votes in
future polls.
Discovery is effected via nominations included in
Vote messages. A voter
picks a random subset of its current reference list, which it
includes in the Vote message. The poller
accumulates these nominations. When it concludes
its inner circle solicitations, it chooses a random sample of these nominations
as its outer circle. It proceeds to
solicit regular votes from these outer circle peers in a manner identical
to that used for inner circle peers.
The purpose of the votes obtained from outer circle voters is to show
the ``good behavior'' of newly discovered peers. Those who perform
correctly, by supplying votes that agree with the prevailing outcome
of the poll, are added into the poller's reference list at the
conclusion of the poll; the outcome of the poll is
computed only from inner-circle votes.
4.3 Vote Evaluation
Once the poller has accumulated all votes it could obtain from
inner and outer circle voters, it begins the poll's evaluation phase.
During this phase, the poller computes, in parallel, all block
hashes that each voter should have computed, if that voter's replica
agreed with the poller's. A vote agrees with the
poller on a block if the hash in the vote and that computed by the
poller are the same.
For each hash computed by the poller for an AU block, there are three
possibilities: first, the landslide majority of inner-circle votes
(e.g., 80%) agree with the poller; in this case, the poller considers
the audit successful up to this block and proceeds with the next block.
Second, the landslide majority of inner-circle votes disagree with the
poller; in this case, the poller regards its own replica of the AU as
damaged, obtains a repair from one of the
disagreeing voters (via the RepairRequest and Repair
messages), and reevaluates the block hoping to find itself in the
landslide majority, as above. Third, if there is no landslide majority of
agreeing or disagreeing votes, the
poller deems the poll inconclusive, raising an alarm that requires
attention from a human operator.
Throughout the evaluation phase, the poller may also decide to obtain a
repair from a random voter, even if one is not required (i.e., even if
the corresponding block met with a landslide agreement). The purpose of such
frivolous repairs is to prevent targeted free-riding via the
refusal of repairs; voters are expected to supply a small number of
repairs once they commit to participate in a poll, and are penalized
otherwise (Section 5.1).
If the poller hashes all AU blocks without raising an alarm, it
concludes the poll by sending an evaluation receipt to each
voter (with an EvaluationReceipt message), containing
cryptographic proof that it has evaluated received votes. The poller
then updates its
reference list by removing all voters whose votes determined the poll
outcome and by inserting all agreeing outer-circle voters and some
peers from the friends list (for details
see [30]).
The poller then restarts a
poll on the same AU, scheduling it to conclude one interpoll interval
into the future.
5 LOCKSS Defenses
Here we outline the attrition defenses of the LOCKSS protocol: admission
control, desynchronization, and redundancy. These defenses raise system
costs for both
loyal peers and attackers, but favor ostensible legitimacy.
Given a constant amount of over-provisioning, loyal peers continue
to operate at the necessary rate regardless of the attacker's power.
Many systems over-provision resources to protect performance from
known worst-case behavior (e.g.,
the Unix file system [31]).
In prior work [30] we applied some of
these defenses (such as redundancy and some aspects of admission control,
including rate limitation and effort balancing) to combat powerful attacks
aiming to modify content without detection or to discredit the intrusion
detection system with false alarms.
In this work, we combine these previous defenses with new ones
to defend against attrition attacks as well.
5.1 Admission Control
The purpose of the admission control defense is to ensure that a peer
can control the rate at which it considers poll invitations from
others, favoring invitations from those who operate at roughly the same
rate as itself and penalizing others.
We implement admission control using three mechanisms: rate limitation,
first-hand reputation, and effort balancing.
Rate Limitation: Without limits on the rate at which they attempt
to service requests,
peers can be overwhelmed by floods of ostensibly valid requests.
Rate Limitation suggests that peers should initiate and
satisfy requests no faster than necessary rather than as
fast as possible. Because readers access only their local LOCKSS peer,
the audit and repair protocol is not subject to end-users'
unpredictable request patterns. The protocol can proceed at its own pace,
providing an interesting test case for rate limitation.
We identify three possible attacks based on deviation from the
necessary rate of polling.
A poll rate adversary seeks to trick victims into either
decreasing (e.g., through back-off behavior) or increasing (e.g.,
through recovery from a failed poll) their rate of calling
polls.
A poll flood adversary seeks,
under a multitude of identities, to invite victims into as many frivolous
polls as possible to crowd out the legitimate poll requests
and thereby reduce the ability of loyal peers to audit and repair their
content.
A vote flood adversary seeks to supply as many bogus votes
as possible to exhaust loyal pollers' resources in useless
but expensive proofs of invalidity.
Peers defend against all these adversaries by
setting their rate limits autonomously, not varying them in response
to other peers' actions.
Responding to adversity (inquorate polls or perceived contention)
by calling polls more frequently could aggravate the problem;
backing off to a lower rate of polls would achieve the adversary's
aim of slowing the detection and repair of damage. Kuzmanovic et
al. [26] describe a similar attack in the context
of TCP retransmission timers.
Because peers do not react, the poll rate adversary has no
opportunity to attack. The price of this fixed rate of operation is that,
absent manual intervention, a peer may
take several interpoll intervals to recover from a catastrophic storage
failure.
The poll flood adversary tries to get victims to over-commit their
resources or at least to commit excessively to the adversary.
To prevent over-commitment, peers maintain a task schedule of their
promises to perform effort, both to generate votes for others and
to call their own polls. If the effort of computing the
vote solicited by an incoming Poll message
cannot be accommodated in the schedule, the invitation is refused.
Furthermore, peers limit the rate at which they even consider poll
invitations (i.e., establishing a secure session, checking their
schedule, etc.). A peer sets this rate limit for considering
poll invitations according to the rate of poll
invitations it sends out to others; this is essentially a
self-clocking mechanism. We explain how this rate limit is enforced
in the first-hand reputation description below.
We evaluate our defenses against poll flood strategies in
Section 7.3.
The vote flood adversary is hamstrung by the fact that votes
can be supplied only in response to an invitation by the putative
victim poller, and pollers solicit votes at a fixed rate. Unsolicited votes are ignored.
First-hand reputation: A peer locally maintains and uses
first-hand reputation (i.e., history) for other peers. For each
AU it preserves,
each peer 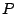 maintains a known-peers list containing an entry for every
peer
maintains a known-peers list containing an entry for every
peer 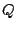 that that 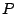 has encountered in the
past, tracking has encountered in the
past, tracking 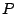 's exchange of votes with 's exchange of votes with 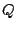 .
The entry holds a reputation grade for .
The entry holds a reputation grade for 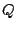 , which takes one of
three values: debt, even, or credit. A debt
grade means that , which takes one of
three values: debt, even, or credit. A debt
grade means that 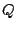 has supplied has supplied 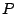 with fewer votes than with fewer votes than 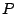 has supplied
has supplied 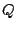 . A credit grade means . A credit grade means 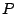 has supplied has supplied 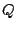 with
fewer votes than with
fewer votes than 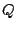 has supplied has supplied 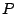 . An even grade means that . An even grade means that
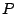 and and 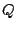 are even in their recent exchanges of votes.
Entries in the known-peers list ``decay'' with time toward the
debt grade. are even in their recent exchanges of votes.
Entries in the known-peers list ``decay'' with time toward the
debt grade.
In a protocol interaction, the poller and a voter each modify
the grade assigned to the other depending on their
respective behaviors. If the voter supplies a valid vote and valid repairs
for any blocks the poller requests, then the poller increases the grade it
assigns to the voter (from debt to even, from even to credit, or from
credit to credit) and the voter correspondingly decreases the grade it
assigns to the
poller. If either
the poller or the voter misbehave (e.g., the voter commits to supplying a
vote but does
not, or the poller does not send a valid evaluation receipt), then the other
peer decreases its grade to debt.
This is similar to the reciprocative strategy of Feldman et al. [17],
in that it penalizes peers who do not reciprocate.
This reputation system
thus reduces free-riding, as it is not possible for a peer to maintain an even
or credit grade without providing valid votes.
Peers randomly drop some poll invitations arriving from previously
unknown peers and from known pollers with a debt grade.
To discourage identity whitewashing the drop probability imposed on unknown
pollers is higher than that imposed on known indebted pollers.
Invitations from known pollers with an even or credit grade are not dropped.
Invitations from unknown or indebted pollers are subject to a
rigid rate limit; after it admits one such invitation for
consideration, a voter enters a refractory period. Like
the known-peers list, refractory periods are maintained on a per AU
basis. During a refractory period, a voter
automatically rejects all invitations from unknown or indebted pollers.
Consequently, during every refractory period, a voter admits at most one
invitation from unknown or indebted peers, plus at most one invitation from
each of its fellow peers with a credit or even grade.
Since credit and even
grades decay with time, the total ``liability'' of a peer in the number
of invitations it can admit per refractory period is limited to a small
constant number. The duration of the
refractory period is thus inversely proportional to the rate limit imposed by
the peer on the per AU poll invitations it considers.
If a victim peer's clock could be sped up over several poll intervals then
the refractory period could be shortened,
increasing the effectiveness of poll flood attacks.
The victim would call polls at a faster rate,
indebting the victim to its peers and making its invitations less likely to
be accepted.
However, halving the refractory period
from 24 to 12 hours has little effect (see Section 7.4).
Doubling the rate of issuing invitations does not affect other peers
significantly since the invitations are not accepted.
Further, an attack via the Network Time Protocol [32] that
doubles a victim's clock rate for months on end would be easy to detect.
Continuous triggering of the refractory period can stop a victim voter
from accepting invitations from unknown peers who are loyal; this can
limit the choices of voters a poller has to peers that know
the poller already. To reduce this impediment to diversity, we
institute the concept of peer introductions. A peer may
introduce to others those peers it considers loyal;
peers introduced this way bypass random drops and refractory
periods. Introductions are bundled along with nominations during
the regular discovery process (Section 4.2).
Specifically, a poller randomly partitions the peer identities in a
Vote message into outer circle nominations and
introductions.
A poll invitation from an introduced peer is
treated as if coming from a known peer with
an even grade. This unobstructed
admission consumes the introduction such that at
most one introduction is honored per (validly voting) introducer, and
unused introductions do not accumulate. Specifically, when consuming the
introduction of peer  by peer by peer  for AU for AU  ,
all other introductions of other
introducees by
peer ,
all other introductions of other
introducees by
peer  for AU for AU  are ``forgotten,'' as are all introductions of peer
are ``forgotten,'' as are all introductions of peer  for for  by
other introducers. Furthermore, introductions by peers who have
entered and left the reference list are also removed, and the maximum
number of outstanding introductions is capped. by
other introducers. Furthermore, introductions by peers who have
entered and left the reference list are also removed, and the maximum
number of outstanding introductions is capped.
Effort Balancing: If a peer expends more effort to react to
a protocol message than did the sender of that message to generate and
transmit it, then an attrition attack need consist only of a flow of
ostensibly valid protocol messages, enough to exhaust the victim peer's
resources.
Real-world attackers may be very powerful but their resources are finite;
markets have arisen to allocate pools of compromised machines to competing
uses [19].
Raising the computational cost of attacking one target system both
absolutely and relative to others will reduce the
frequency of attacks. Our simulations are conservative;
the unconstrained adversary has ample power for any attack.
But our design is more realistic.
It adapts the ideas of pricing via processing [15]
to discourage attacks from resource-constrained adversaries
by effort balancing our protocol.
We inflate the cost of a request by requiring it to include
a proof of computational effort sufficient to ensure that the
total cost of generating the request exceeds that imposed on the receiver
both for verifying the effort proof and for satisfying the request.
We favor Memory-Bound Functions
(MBF) [14] rather than CPU-bound schemes
such as ``client puzzles'' [12] for this purpose, because the
spread in memory system performance is smaller than that
of CPU performance [13].
Applying an effort filter at each step of a multi-step protocol
defends
against three attack patterns: first, desertion strategies in
which the attacker stops taking part some way through the protocol, having
spent less effort in the process than the effort inflicted upon his
victim; second, reservation strategies that cause the victim to
commit resources the attacker does not use,
making those resources unavailable to other, useful tasks; and, third, wasteful strategies
in which service is obtained but the result is not ``consumed'' by the
requester as expected by the
protocol, in an attempt to minimize the attacker's total expended effort.
Figure 2:
The effects of the
logical filters on the incoming stream of poll invitations at a single
peer. Rectangles represent poll
invitation streams from the different peers 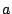 , , 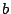 , , 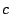 , etc.,
during the same time interval , etc.,
during the same time interval ![$[0,t]$](img4.png) . We show the streams as shaped by the
combination of filters, adding one filter at a time, to illustrate
each filter's incremental effect.
Within a peer's poll invitation stream,
vertical gray bands represent individual invitation requests. . We show the streams as shaped by the
combination of filters, adding one filter at a time, to illustrate
each filter's incremental effect.
Within a peer's poll invitation stream,
vertical gray bands represent individual invitation requests.
|
Pollers could mount a desertion attack by cheaply soliciting
an expensive vote.
To discourage this, the poller must include
provable effort in its vote solicitation
messages (Poll and PollProof) that in total
exceeds,
by at least an amount described in the next paragraph,
the effort required by the voter to verify that effort
and to produce the requested vote.
Producing a vote amounts to
fetching an AU replica from disk, hashing it, and shipping back to the
poller one hash per block in the Vote message.
Voters could mount a desertion attack by cheaply generating a bogus
vote in response to an expensive solicitation,
returning garbage instead of block hashes to
waste not merely the poller's solicitation effort but also its effort
to verify the hashes.
Because the poller evaluates the vote one block at a time, it
costs the effort of hashing one block to detect that the
vote disagrees with its own AU replica, which may mean
either that the vote is bogus, or that the poller's and voter's
replicas of the AU differ in that block.
The voter must therefore include in the Vote message
provable effort sufficient to cover the cost of hashing a
single block and of verifying this effort.
The extra effort in the solicitation messages referred to above
is required to cover the generation of this provable effort.
Pollers could mount a reservation attack by sending a valid Poll
message to cause a voter to reserve time for computing a vote in
anticipation of a PollProof message the poller never sends.
When a voter accepts a poller's invitation, it reserves a block of time
in the future to compute the vote. When it is time to begin voting,
the voter sets a timeout and waits for the poller to send a
PollProof if it has not done so already. If the timeout expires,
the voter can reschedule the remainder of the block of time as it
pleases. The attack exploits the voter's inability to reallocate the
timeout period to another operation by asking for a vote and then never
sending a PollProof. To discourage this, pollers must include
sufficient introductory effort in Poll messages to match
the opportunity cost the voter experienced while waiting for the
timeout.
Pollers could mount a wasteful attack by soliciting expensive
votes and then discarding them unevaluated.
To discourage this we require the poller,
after evaluating a vote,
to supply the voter with an unforgeable evaluation receipt
proving that it evaluated the vote.
Voters generate votes and pollers evaluate them using very
similar processes: generating or validating effort proofs and hashing
blocks of the local AU replica. Conveniently, generating a proof
of effort using our chosen MBF mechanism also generates
160 bits of unforgeable byproduct. The voter remembers the byproduct;
the poller uses it as the evaluation receipt to send to the voter.
If the receipt matches the voter's remembered byproduct the voter
knows the poller performed the necessary effort, regardless of whether the
poller was loyal or malicious.
Section 7.4 shows how effort
balancing fares against all three types of attacks mounted by
pollers. We omit the evaluation of these attacks by voters,
since they are rendered ineffective by the rate limits described above.
The Filters Revisited: Figure 2 illustrates how
the defenses of rate
limitation, first-hand reputation, and effort balancing, enforced as
serial filters over incoming traffic (see
Section 3.3),
can protect LOCKSS peers from
attrition attackers. Among the peers with an initially good standing (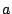 through
through 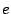 ), ), 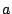 and and 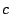 maintain a steady balance of requested votes
throughout the time interval maintain a steady balance of requested votes
throughout the time interval 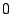 to to  .
Note that .
Note that 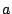 asks for two votes in
close succession; this is an instance of a peer expending its ``credit.''
In contrast, asks for two votes in
close succession; this is an instance of a peer expending its ``credit.''
In contrast,
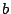 requests many more votes in close succession than justified by its
grade and is downgraded to the debt
grade by the reciprocity filter,
eventually becoming subject to the refractory period. requests many more votes in close succession than justified by its
grade and is downgraded to the debt
grade by the reciprocity filter,
eventually becoming subject to the refractory period. 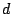 behaves with ostensible legitimacy with regards to the rate of
invitations it sends, but misbehaves by deserting (e.g., by not
supplying correct effort proofs) and, as a result, is
downgraded to the debt grade by the effort filter.
behaves with ostensible legitimacy with regards to the rate of
invitations it sends, but misbehaves by deserting (e.g., by not
supplying correct effort proofs) and, as a result, is
downgraded to the debt grade by the effort filter.
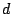 's subsequent invitations are subject to the refractory period. 's subsequent invitations are subject to the refractory period.
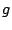 is initially unknown and therefore
subject to the refractory period, but behaves ostensibly legitimately
and is upgraded to even or credit grade, freeing itself
from the refractory period. Peers is initially unknown and therefore
subject to the refractory period, but behaves ostensibly legitimately
and is upgraded to even or credit grade, freeing itself
from the refractory period. Peers 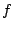 , , 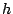 , ,  , and , and 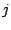 request many
more votes than reasonable and occasionally send simultaneous
traffic
spikes which exceed link capacity; they are thinned out
by the volume
filter along with other peers' traffic. These peers,
as well as misbehaving peers request many
more votes than reasonable and occasionally send simultaneous
traffic
spikes which exceed link capacity; they are thinned out
by the volume
filter along with other peers' traffic. These peers,
as well as misbehaving peers 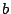 and and 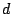 , share
the same refractory period and therefore only one invitation from them
can be accepted per refractory period. , share
the same refractory period and therefore only one invitation from them
can be accepted per refractory period.
5.2 Desynchronization
The desynchronization defense avoids the kind of
inadvertent synchronization observed in many distributed systems,
typically by randomization.
Examples include TCP sender windows at bottleneck routers,
clients waiting for a busy server,
and periodic routing messages [18].
Peer-to-peer systems in which a peer requesting service must find
many others simultaneously available to supply that service
(e.g., in a read-one-write-many fault-tolerant
system [28])
may encounter this problem.
If they do, even
absent an attack, moderate levels of peer busyness can prevent the
system from delivering services. In this situation, a poll flood attacker may
only need to increase peer busyness slightly to have a large effect.
Simulations of poll flood attacks on an earlier version of the
protocol [29] showed this effect.
Loyal pollers suffered because they needed to find a quorum of
voters who could simultaneously vote on an AU.
They had to be chosen at random to make directed subversion hard
for the adversary. They also needed to have free resources at the specified
time, in the face of resource contention from other peers
competing for voters on the same or other AUs.
Malign peers had no such constraints,
and could invite victims one by one into futile polls.
Peers avoid this problem
by soliciting votes individually rather
than synchronously, extending the period during which a quorum
of votes can be collected before they are all evaluated.
A poll is thus a sequence of two-party interactions rather than
a single multi-party interaction.
5.3 Redundancy
If the survival of, or access to, an AU relied only on a few replicas,
an attrition attack could focus on those replicas, cutting off the
communication between them needed for audit and repair.
Each LOCKSS peer preserving an AU maintains its own replica and serves it
only to its local clients. This massive redundancy helps resist
attacks in two ways.
First, it ensures that a successful attrition attack must target most
of the replicas, typically a large number of peers.
Second, it forces the attrition attack to suppress the communication
or activity of the targeted peers continuously for a long period.
Unless the attack does both, the targeted peers recover by
auditing and repairing themselves from the untargeted peers, as shown in
Section 7.2.
This is because massive redundancy allows peers at each poll
to choose a sample of their reference list that is bigger
than the quorum and continue to solicit votes from them
at random times for the entire duration of a poll (typically 3 months) until
the voters accept.
Further, the margin between the rate at which
peers call polls and the rate at which they suffer undetected damage provides
redundancy in time. A single failed poll has little effect on the safety
of its caller's replica.
6 Simulation
In this section we give details about the simulation environment and the
metrics we use to evaluate the system's effectiveness in meeting its goals.
6.1 Evaluation Metrics
We measure the effectiveness of our defenses
against the attrition adversary using four metrics:
Access failure probability: To measure the success of an
attrition adversary at increasing the probability that a reader obtains
a damaged AU replica, we compute the access failure probability as
the fraction of all replicas in the system that are damaged, averaged over
all time points in the experiment.
Delay ratio: To measure the degradation an attrition adversary
achieves, we compute the delay ratio as the mean time between successful polls at loyal
peers with the system under attack divided by the same measurement without
the attack.
Coefficient of friction: To measure the cost of an attack to loyal
peers, we measure the coefficient of friction, defined as the
average effort expended by loyal peers per successful poll during an attack divided by their
average per-poll effort absent an attack.
Cost ratio: To compare the cost of an effortful attack to the
adversary and to the defenders, we compute the cost ratio, which is the ratio of the
total effort expended by the attackers during an attack to that of the defenders.
We run our experiments using Narses [20],
a discrete-event simulator that
provides facilities for modeling computationally expensive operations,
such as computing MBF efforts and
hashing documents. Narses allows experimenters to pick from a range of
network models that trade off speed for accuracy.
A simplistic network model that accounts for
network delays but not congestion, except for the side-effects
of a pipe stoppage adversary's artificial congestion,
suffices for our current focus on application-level effects.
Peers' link bandwidths are
uniformly distributed
among three choices: 1.5, 10, and 100 Mbps, and latencies are
uniformly distributed between 1 and 30 ms.
Nodes in the system are divided into two categories: loyal
peers and the adversary's minions. Loyal peers are uncompromised peers that execute
the protocol correctly. Adversary minions are nodes that collaborate to
execute the adversary's attack strategy.
We conservatively simulate the adversary as a cluster of
nodes with as many IP addresses and as much compute power as he needs.
Each adversary minion has complete and instantaneous knowledge of all
adversary state and has a magically incorruptible copy of all AUs.
Other assumptions about our adversary that are less relevant to attrition can be
found in [30].
To distill the cost of an attack from other efforts the adversary might
have to shoulder (e.g., to masquerade as a loyal peer), in these
experiments he is completely outside of the network of loyal peers.
Loyal peers never ask his minions to vote in polls and he
only asks loyal peers to vote in his polls. This differs
from LOCKSS adversaries we have studied before [30].
6.3 Simulation Parameters
We evaluate the preservation of a collection of AUs distributed among a
population of loyal peers. For simplicity in this stage of our
exploration, we assume that each AU is 0.5 GBytes (a large AU in
practice). Each peer maintains 50 to 600 AUs.
All peers have replicas of all AUs; we do not yet simulate the
diversity of local collections we expect will evolve over time.
These simplifications allow us to focus our attention on the common
performance of our attrition resistance machinery, ignoring for the time
being how that performance varies when AUs vary in size and
popularity.
Note that our 600 simulated AUs total about 10% of the
size of the annual AU intake of a large journal collection such
as that of Stanford University
Libraries. Adding the equivalent of 10 of today's low-cost PCs per year
and consolidating them as old
PCs are rendered obsolete is an affordable
deployment scenario for such a library.
We set
all costs of primitive operations (hashing, encryption, L1 cache and RAM
accesses, etc.) to match the capabilities of a low-cost PC.
All simulations have a constant loyal peer population of 100 nodes and
run for 2 simulated years,
with 3 runs per data point. Each peer runs
a poll on each of its AUs on average every 3 months. Each poll uses a
quorum of 10 peers and considers landslide agreement as having a maximum
of 3 disagreeing votes. These parameters were empirically
determined from previous iterations of the deployed beta protocol. We
set the fixed drop probability to be 0.90 for unknown peers and 0.80 for
indebted peers.
We set the fixed drop probability for indebted peers and the cost of verifying
an introductory effort so that the cumulative introductory effort
expended by an effortful
attack on dropped invitations is more than the
voter's effort to consider the adversary's eventually admitted
invitation. Since an adversary has to try with indebted identities on
average 5 times to be admitted (thanks to the  admission
probability), we set the introductory effort to be 20% of the total
effort required of a poller; by the time the adversary has gotten his
poll invitation admitted, even if he defects for the rest of the poll,
he has already expended on average 100% of the effort he would have, had he
behaved well in the first place. admission
probability), we set the introductory effort to be 20% of the total
effort required of a poller; by the time the adversary has gotten his
poll invitation admitted, even if he defects for the rest of the poll,
he has already expended on average 100% of the effort he would have, had he
behaved well in the first place.
Memory limits in the Java Virtual Machine prevent Narses from simulating
more than about 50 AUs/peer in a single run. We simulate 600-AU collections
by layering 50 AUs/peer runs,
adding the tasks caused by one layer's 50 AUs to the
task schedule for each peer accumulated during the preceding
layers.
In effect, layer 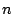 is a simulation of 50 AUs on peers already
running a realistic workload of is a simulation of 50 AUs on peers already
running a realistic workload of 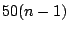 AUs.
The effect is to over-estimate the peer's busyness for AUs in higher
layers and under-estimate it for AUs in lower layers;
AUs in a layer compete for the resources left over by lower layers,
but AUs in lower layers are unaffected by the resources used in
higher layers.
We have validated this technique against unlayered simulations in
smaller collections, as well as against simulations in which inflated per-AU preservation
costs cause similar levels of peer load; we found negligible differences. AUs.
The effect is to over-estimate the peer's busyness for AUs in higher
layers and under-estimate it for AUs in lower layers;
AUs in a layer compete for the resources left over by lower layers,
but AUs in lower layers are unaffected by the resources used in
higher layers.
We have validated this technique against unlayered simulations in
smaller collections, as well as against simulations in which inflated per-AU preservation
costs cause similar levels of peer load; we found negligible differences.
We are currently exploring the parameter space but use the following
heuristics to help determine parameter values. The
refractory period of one day
allows for 90 invitations from unknown or indebted peers to be accepted
per 90-day interpoll interval; in contrast, a peer requires an
average of 30 votes per poll and, because of self-clocking,
should be able to accept at least an average of 30 poll
invitations per interpoll interval. Consequently, the one-day
refractory period allows up to a
total of 120 invitations per poll period,
four times the rate of poll invitations that should be expected
in the absence of attacks.
7 Results
The probability of access failure summarizes the success of an
attrition attack.
We start by establishing a baseline rate of
access failures absent an attack.
We then assess the effectiveness against this baseline of the
effortless attacks we consider:
network-level flooding attacks on the volume filter in Section 7.2,
and Sybil attacks on the reciprocity filter in Section 7.3.
Finally, in Section 7.4
we assess against this baseline each of the effortful attacks
corresponding to each effort filter.
In each case we show the effect of increasing scales of attack on
the access failure probability, and relevant supporting graphs including
the delay ratio, the coefficient of friction, and for effortful attacks the
cost ratio.
Our mechanisms for defending against an attrition adversary raise
the effort required per loyal peer.
To achieve a bound on access failure probabilities, one must
be willing to over-provision the system to accommodate the extra effort.
Over-provisioning the system by a
constant factor defends it against application-level attrition attacks
of unlimited power (Sections 7.3 and
7.4).
7.1 Baseline
Figure 3:
Mean access failure probability (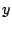 axis in
log scale) for increasing interpoll intervals ( axis in
log scale) for increasing interpoll intervals (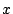 axis)
at variable mean times between storage failure (from 1 to 5 years
per disk), absent an attack. We show results for
collection sizes of 50 AUs (points only) and of 600 AUs (lines and points).
We show minimum and maximum values for the
2-year data set; this variance is representative of all measurements,
which we omit for clarity. axis)
at variable mean times between storage failure (from 1 to 5 years
per disk), absent an attack. We show results for
collection sizes of 50 AUs (points only) and of 600 AUs (lines and points).
We show minimum and maximum values for the
2-year data set; this variance is representative of all measurements,
which we omit for clarity.
|
The LOCKSS polling process is intended to detect and recover from
storage damage that is not detected locally, from causes
such as ``bit rot,'' human error and
attack. Our simulated peers suffer such damage at rates
of one block in 1 to 5 disk years (50 AUs per disk). This is an aggressively
inflated rate of undetected damage, given that, for instance, it is
125-400% the rate of detected failures in Talagala's
study of IDE drives in a large disk farm [45].
Experience with the IDE drives in deployed LOCKSS peers covers about
10 times as many disk years but with less
reliable data collection; it suggests much lower detected failure rates.
Figure 3 plots access failure
probability versus the interpoll interval. It shows that as the
interpoll
interval increases relative to the mean interval between storage
failures, access failure probability increases because damage
takes longer to detect and repair. The access failure probability is
similar for a 50-AU collection all the way up to a 600-AU collection
(we omit intermediate collection sizes for clarity).
For comparison purposes in the rest of the experiments, the baseline
access failure probability of
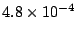 for a 50-AU collection
and of for a 50-AU collection
and of
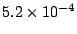 for a 600-AU collection correspond to our
interpoll interval of 3 months and a storage damage rate of one block
per 5 disk years. With these parameters, a machine preserving 600 AUs
has an average load of 9%, and a machine preserving 50 AUs
has a 0.7% average load. for a 600-AU collection correspond to our
interpoll interval of 3 months and a storage damage rate of one block
per 5 disk years. With these parameters, a machine preserving 600 AUs
has an average load of 9%, and a machine preserving 50 AUs
has a 0.7% average load.
Figure 4:
The access failure probability (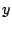 axis in log scale) observed
during repeated pipe stoppage attacks of varying duration ( axis in log scale) observed
during repeated pipe stoppage attacks of varying duration (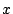 axis in log
scale), covering between 10 and 100% of the peers. axis in log
scale), covering between 10 and 100% of the peers.
|
7.2 Targeting the Volume Filter
The ``pipe stoppage'' adversary models packet flooding and more
sophisticated attacks [26]. This adversary
suppresses all communication between some proportion of the total peer
population (its coverage) and other LOCKSS peers. During a
pipe-stoppage attack, local readers may still access content. The
adversary subjects a victim to a period of pipe stoppage lasting between
1 and 180 days. Each attack is followed by a 30-day recuperation
period, during which communication is restored to the victim; this
pattern is repeated for the entire experiment. To lower the probability
that a recuperating peer can contact another peer, the adversary
schedules his attacks such that there is little overlap in peers'
recuperation periods. We performed experiments with an adversary that
schedules his attacks so that all victims' recuperation periods
completely overlap, but found that the low-overlap adversary caused
more damage, so we present results from the low-overlap adversary.
Figure 4 plots the access
failure probability versus the attack duration for varying coverage
values (10 to 100%). As expected, the access failure probability
increases as the coverage of the attack increases, though the attack
covering 70% of the peer population is almost as effective as the 100%
attack. In the extreme, the 180 day attack over 100% of the 600-AU
collection raises the access failure probability to
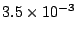 ; this is within tolerable limits for services open to the
Internet. ; this is within tolerable limits for services open to the
Internet.
For attacks between 20% and 60% coverage,
the access failure probability peaks at
an attack duration of 60 days and decreases for larger durations. The 180
day attack is less damaging for these coverage values because, while
the adversary focuses on a smaller number of peers for a longer time,
the rest of the peers continue polling. The 30 to 60 day attacks cycle
across more victims and interrupt more polls, wasting peers' time and
tarnishing their reputations, while 1 to 10 day attacks are
too short to interrupt many polls. As the attack coverage grows
from 70%, the 180 day attack disables such a significant portion of
the network that the peers free of attack have great difficulty finding
available peers and the access failure probability increases beyond the
60 day attack.
Figure 5:
The delay ratio (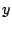 axis in log scale) imposed by repeated pipe
stoppage attacks of varying duration ( axis in log scale) imposed by repeated pipe
stoppage attacks of varying duration (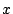 axis in log scale)
and coverage of the population. Absent an
attack, this metric has value 1. axis in log scale)
and coverage of the population. Absent an
attack, this metric has value 1.
|
Figure 6:
The coefficient of friction (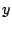 axis in log scale) imposed by
pipe stoppage attacks of varying duration ( axis in log scale) imposed by
pipe stoppage attacks of varying duration (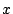 axis in log scale)
and coverage of the population. axis in log scale)
and coverage of the population.
|
Figures 5
and 6 plot the delay ratio and
coefficient of friction, respectively, versus attack duration.
We find that attacks must last longer than 30 days to
raise the delay ratio by an order of magnitude. Similarly, the
coefficient of friction during repeated attacks that last less than a
few days each is negligibly greater than 1. For very long attacks that
completely shut down the victim's Internet, the
coefficient can reach 6700, making pipe stoppage the most cost-effective
strategy for the attrition adversary.
As attack durations grow to 30 days and beyond, the adversary succeeds
in decreasing the total number of successful polls. For example,
attacks against 100% of the population with a 30 day duration reduce the
number of successful polls to 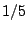 the number absent attack.
However, the average machine load during
recuperation remains within 2 to 3 times the baseline load -- a result
of designing the protocol to limit increases in resource consumption
while under attack. Fewer successful polls and nearly constant
resource consumption for increasing attack durations drives up the
average cost of a successful poll, and with it the coefficient of
friction. the number absent attack.
However, the average machine load during
recuperation remains within 2 to 3 times the baseline load -- a result
of designing the protocol to limit increases in resource consumption
while under attack. Fewer successful polls and nearly constant
resource consumption for increasing attack durations drives up the
average cost of a successful poll, and with it the coefficient of
friction.
Figure 7:
The access failure probability (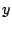 axis in log scale) for
attacks of increasing duration ( axis in log scale) for
attacks of increasing duration (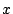 axis in log scale) by the admission
control adversary over 10 to 100% of the peer population. The scale
and size of the graph match
Figures 3 and
4 to facilitate comparison. axis in log scale) by the admission
control adversary over 10 to 100% of the peer population. The scale
and size of the graph match
Figures 3 and
4 to facilitate comparison.
|
7.3 Targeting the Reciprocity Filter
The reciprocity adversary attacks our admission control defenses aiming
to reduce the likelihood of a
victim admitting a loyal
poll request by triggering that victim's refractory
period as often as possible. This adversary sends cheap garbage
invitations to varying fractions of the peer population for varying periods of
time separated by a fixed recuperation period of 30 days. The adversary
sends invitations using poller addresses unknown to the
victims. These, when eventually admitted, cause those victims to enter
their refractory periods and drop all subsequent invitations from
unknown and indebted peers.
Figure 7 shows that these attacks have
little effect. The
access failure probability is raised to
 when
the duration of the attack reaches the entire duration of our
simulations (2 years) for full population coverage and a 600-AU collection. At that attack
intensity, loyal peers no longer admit poll invitations from unknown or
indebted loyal peers, unless supported by an introduction. This causes
discovery to operate more slowly; loyal peers waste their
resources on introductory effort proofs that are summarily rejected by
peers in their refractory period. This wasted effort, when sustained
over years, raises
the coefficient of friction by 33%, (much less than the
friction caused by pipe stoppage), and raises average machine load from
9% to 11%. The delay ratio is largely
unaffected by this adversary.
Consequently, the first effect of this adversary, increasing load in
loyal peers, is tolerable given
a practical level of over-provisioning. when
the duration of the attack reaches the entire duration of our
simulations (2 years) for full population coverage and a 600-AU collection. At that attack
intensity, loyal peers no longer admit poll invitations from unknown or
indebted loyal peers, unless supported by an introduction. This causes
discovery to operate more slowly; loyal peers waste their
resources on introductory effort proofs that are summarily rejected by
peers in their refractory period. This wasted effort, when sustained
over years, raises
the coefficient of friction by 33%, (much less than the
friction caused by pipe stoppage), and raises average machine load from
9% to 11%. The delay ratio is largely
unaffected by this adversary.
Consequently, the first effect of this adversary, increasing load in
loyal peers, is tolerable given
a practical level of over-provisioning.
We switch our attention to the other effect of this adversary, namely, the
suppression of invitations from unknown or indebted peers, which
introductions are intended to mitigate. We have repeated
the experiments with 600 AUs, in which the adversary attacks 100% of
the peer population, with introductions disabled. Without
introductions, the shorter attacks cause a higher coefficient of
friction, much closer to pipe stoppage attacks, whereas longer attacks
are largely unaffected. For comparison, suppressing introductions for
attack durations of 10 days raises the coefficient of friction from 1.03
to 1.16, vs. 1.51 for pipe stoppage; in contrast, suppressed
introductions for attack durations of six months raises the coefficient
of friction from 1.34 to 1.36, vs. 6700 for pipe stoppage. The absence
of introductions does not make this attack markedly worse in terms of
load increase.
The major consequence of unknown and indebted invitation
suppression without introductions is that victims call polls almost exclusively
composed of voters from their friends list, who are more likely to
accept a poll invitation from a fellow friend. This reliance increases
as the attack lasts longer.
It is undesirable because it allows an adversary to predict
closely the membership of a poll (mostly the poller's friends), promoting
focused poll disruptions.
The main function of introductions is thus to
ensure the unpredictability of poll memberships.
Note that techniques such as blacklisting,
commonly used to defeat denial-of-service attacks in the context of
email spam, or server selection [17] by which pollers
only invite voters they believe will accept, could significantly reduce
the friction caused by the admission control attack. However,
we have yet to explore whether
these defenses are compatible with our goal of protecting against
subversion attacks that operate by biasing the opinion poll sample toward
corrupted peers [30].
7.4 Targeting the Effort Filters
To attack filters downstream of the reciprocity filter, the
adversary must get through as fast as possible. We consider
an attack by a ``brute force'' adversary
who continuously sends enough
poll invitations with valid introductory efforts to
get past the random drops; such invitations cannot arrive from credit or
even identities at the steady attack state, because they are more frequent
than what is considered
legitimate. Since unknown peers suffer more
random drops than peers in debt,
the adversary
launches attacks from indebted addresses. We conservatively
initialize all adversary addresses with a debt grade
at all loyal peers. We also give
the adversary an oracle that allows him to inspect all the loyal
peers' schedules.
This avoids his wasting introductory efforts
due to scheduling conflicts at loyal peers.
Once through the reciprocity filter, the adversary can defect at
any stage of the protocol exchange: after providing
the introductory effort in the Poll message (INTRO) by never
following up with a PollProof, after providing the remaining
effort in the PollProof message (REMAINING) by never following up
with an EvaluationReceipt, or not defecting at all (NONE).
Table 1:
The effect of the brute force adversary
defecting at various points in the protocol on the coefficient of
friction, the cost ratio, the delay ratio, and the access failure
probability. For each point, the upper numbers correspond to the 50-AU
collection and the lower numbers correspond to the 600-AU collection.
| Defection |
Coeff. |
Cost |
Delay |
Access |
| |
friction |
ratio |
ratio |
failure |
| INTRO |
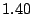 |
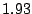 |
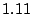 |
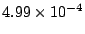 |
| |
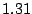 |
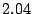 |
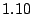 |
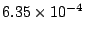 |
| REMAIN- |
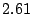 |
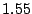 |
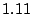 |
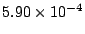 |
| ING |
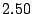 |
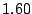 |
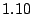 |
 |
| NONE |
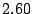 |
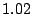 |
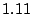 |
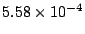 |
| |
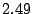 |
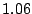 |
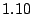 |
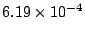 |
|
Table 1 shows that the brute
force adversary's most cost-effective strategy (i.e., with the lowest cost ratio
metric) is to participate fully
in the protocol; doing so he can raise loyal peers'
preservation cost (i.e., their coefficient of friction) to a factor of 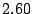 (
(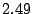 for the large collection, which equates to an average machine
load of 21%).
To defend against this increase in cost, LOCKSS peers must over-provision
their resources by a reasonable amount.
The baseline probability of access failure rises to for the large collection, which equates to an average machine
load of 21%).
To defend against this increase in cost, LOCKSS peers must over-provision
their resources by a reasonable amount.
The baseline probability of access failure rises to
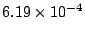 at a cost almost identical to that incurred by the
defenders (a cost ratio of at a cost almost identical to that incurred by the
defenders (a cost ratio of 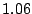 ). Fortunately, this continuous attack
even from a brute force adversary unconcerned by his own effort
expenditure is unable to increase the access failure probability of the
victims greatly; the rate limits prevent him from bringing his advantage
in resources to bear. Similar behavior in earlier
work [30] prevents a different
unconstrained adversary from stealthily modifying content. ). Fortunately, this continuous attack
even from a brute force adversary unconcerned by his own effort
expenditure is unable to increase the access failure probability of the
victims greatly; the rate limits prevent him from bringing his advantage
in resources to bear. Similar behavior in earlier
work [30] prevents a different
unconstrained adversary from stealthily modifying content.
Figure 8:
Coefficient of friction during brute force attacks against 50
AUs. The refractory period varies from 1 to 96 hours.
|
We measured the effectiveness of the refractory period in rate limiting
poll flood attacks
against the brute force adversary that does not defect, since this
strategy has the best cost/benefit ratio among the brute force strategies.
Figure 8 shows the
coefficient of friction during a brute force attack on 50 AUs where the
refractory period varies from 1 to 96 hours.
With a shorter refractory period, poll invitations from the attacker are
accepted by the victims at a greater rate, driving up the coefficient of
friction. With the refractory period at one hour, the average
machine load at the victim peers is 21%. If only 50 AUs
consume 21% of a peer's processing time, an average peer cannot support
600 AUs while under attack. With the refractory period of
24 hours, the peers' average load supporting 50 AUs is
only 2%.
On the other hand, the graph shows that lengthening the refractory
period beyond 24 hours would not greatly reduce the coefficient of friction.
Furthermore,
increasing the refractory period decreases the probability of a peer
accepting legitimate poll invitations from unknown or indebted peers,
since voters accept fewer of these invitations per unit time. A very
long refractory period stifles the discovery process of pollers
finding new voters and causes increased reliance on a poller's friends
list. Similar behavior occurs when introductions are removed from the
protocol (see Section 7.3).
Thus a shorter refractory period increases the probability of voters
accepting invitations from legitimate, unknown pollers, but it also
increases damage during a poll flood attack. Our choice of 24 hours
limits the harm an attacker can do while accepting enough legitimate
poll invitations from unknown or indebted peers for the discovery process
to function.
In the analysis above, we conservatively assume that the brute force
adversary uses
attacking identities in the debt grade of their
victims.
Space constraints lead us to omit experiments with an adversary
whose minions may be in either even or credit grade.
This adversary polls a victim only after he has supplied that
victim with a vote,
then defects in any of the ways described above.
He then recovers
his grade at the victim by supplying an appropriate number of valid
votes in succession.
Each vote he supplies is used to introduce new minions that thereby
bypass the victim's admission control before defecting.
This attack requires the victim to invite minions into polls
and is sufficiently rate-limited to be less effective than brute
force. It is further limited by the decay of first-hand reputation
toward the debt grade.
We leave
the details for an extended version of this paper.
8 Related Work
In this section we first describe the most significant ways
in which the new LOCKSS protocol differs
from our previous efforts. We then list work that
describes the nature and types of denial of service attacks,
as well as related work
that applies defenses similar to ours.
The protocol described here is derived from earlier
work [30] in which we covered
the background of the LOCKSS system.
That protocol used redundancy, rate limitation, effort balancing, bimodal
behavior (polls must be won or lost by a landslide) and friend bias (soliciting
some percentage of votes from peers on the friends list)
to prevent powerful adversaries from
modifying the content without detection, or discrediting the
system with false alarms.
In this work, we target the protocol's
vulnerability to attrition attacks by reinforcing
our previous defenses with admission control, desynchronization,
and redundancy.
Another major difference between
our prior work and the protocol described in this paper is our treatment
of repair. In the previous protocol voting and repair were
separated into two phases. When pollers determined repair
was necessary, they requested a complete copy of the document from
the publisher, if still available, or from a peer for whom they
had previously supplied votes. This had at least three problems. First,
pollers requested repairs only when needed, signaling the
vulnerability of those pollers' content to an adversary.
Second, the repair
mechanism was only exercised when content recovery was needed. Mechanisms
exercised only during emergencies are unlikely to work [35]. Finally,
this left the system more vulnerable to free-riding, since a peer could
supply votes but later defect when the poller requested a costly repair.
We address all three problems through restructuring the repair mechanism
(as described in Section 4.3)
to integrate block repairs,
including ``frivolous'' repairs, into the actual evaluation of votes.
A third significant difference in the protocol
supports our desynchronization defense. In the previous protocol, loyal
pollers needed to find a quorum of voters who could simultaneously
vote on an AU. Instead, the poller now
solicits and obtains votes one at a time, across the duration of a
poll, and only evaluates the outcome
of a poll once it has accumulated all requisite votes.
Our attrition adversary draws on a wide range of work in
detecting [23],
measuring [33],
and combating [2,27,41,42]
network-level DDoS attacks capable of
stopping traffic to and from our peers.
This work observes that current
attacks are not simultaneously of high intensity, long duration,
and high coverage (many peers) [33].
Redundancy is a key to survival during some DoS attacks,
because pipe stoppage appears
to other peers as a failed peer. Many systems use redundancy to mask
storage failure [25].
Byzantine Fault Tolerance [7]
is related to the LOCKSS opinion polling mechanism in its goal
of managing replicas in the face of attack. It provides stronger
guarantees but requires that no more than one third of the replicas
are faulty or misbehaving. In a distributed system, such as the LOCKSS system, that is spread
across the Internet, we cannot assume an upper bound on the number of
misbehaving peers. We
therefore aim for system performance to degrade gracefully
with increasing numbers of misbehaving peers, rather than fail suddenly
when a critical threshold is reached.
Routing along multiple redundant paths in Distributed Hash Tables (DHTs)
has been suggested as a way of increasing the probability that
a message arrives at its intended recipient despite nodes dropping
messages due to malice [6] or pipe
stoppage [24].
Rate limits are effective in slowing the
spread of viruses [43,48].
They have also been suggested for limiting the rate at which peers can
join a DHT [6,47] as a
defense against attempts to control part of the hash space.
Our work suggests that DHTs will need to rate limit not only joins
but also stores to defend against attrition attacks.
Another
study [40] suggests that the increased
latency this causes will not affect users' behavior.
Effort balancing is used as a defense against spam, which
may be considered an application-level DoS attack and has received
the bulk of the attention in this area. Our effort balancing defense draws
on pricing via processing concepts [15]. We measure cost by
memory cycles [1,14]; others use CPU
cycles [4,15]
or even Turing tests [44].
Crosby et al. [10] show that
worst-case behavior of application algorithms can be exploited in
application-level DoS attacks; our use of nonces and the bounded verification
time of MBF avoid this risk. In the LOCKSS system we avoid strong peer
identities and infrastructure changes, and therefore rule out many
techniques for
excluding malign peers such as Secure Overlay
Services [24].
Related to first-hand reputation is the use of game-theoretic analysis
of peer behavior by
Feldman et al. [17]
to show that a reciprocative strategy
in admission control policy can motivate
cooperation among selfish peers.
Admission control has been used to improve the usability of overloaded
services. For example,
Cherkasova et al. [8]
propose admission control strategies that help protect long-running
Web service sessions (i.e., related sequences of requests)
from abrupt termination. Preserving the responsiveness of
Web services in the face of demand spikes is critical,
whereas LOCKSS peers need only manage their resources to make progress
at
the necessary rate in the long term. They can treat demand spikes
as hostile behavior.
In a P2P context, Daswani et al. [11]
use admission control (with rate limiting) to mitigate the effects
of a query flood attack against superpeers in unstructured
file-sharing peer-to-peer networks.
Golle and Mironov [21] provide compliance enforcement in
the context of distributed computation using a receipt technique similar
to ours. Random auditing using challenges and hashing has been
proposed [9,47] as a means of enforcing trading
requirements in some distributed storage systems.
In DHTs waves of synchronized routing updates caused
by joins or departures result in instability during periods of high
churn. Bamboo's [36] desynchronization defense
using lazy updates is effective.
9 Future Work
We have three immediate goals for future work.
First, we observe that although the protocol is symmetric, the
attrition adversary's use of it is asymmetric. It may be that
adaptive behavior of the loyal peers can exploit this asymmetry. For
example, loyal peers could modulate the probability of acceptance of a
poll request according to their recent busyness. The effect would be
to raise the marginal effort required to increase the loyal peer's
busyness as the attack effort increases. Second, we need to
understand how our defenses against attrition work in a more dynamic
environment, where new loyal peers continually join the system over
time. Third, we need to consider combined adversary strategies;
an adversary could weaken the system with an attrition attack
in preparation for some other type of attack.
10 Conclusion
The defenses of this paper equip the LOCKSS system to resist attrition
well. First, application-level attrition attacks, even from adversaries with no
resource constraints and sustained for two years, can be defeated with
reasonable over-provisioning. Such over-provisioning is natural
in our application, but further work may significantly reduce the required
amount.
Second, the strategy that provides an unconstrained adversary with the greatest
impact on the system is to behave as a large number of new loyal peers.
Third, network-level attacks do not affect the system significantly
unless they are (a) intense enough to stop all communication between
peers, (b) widespread enough to target all of the peers,
and (c) sustained over months.
Digital preservation is an unusual application, in that the goal is to
prevent things from happening. The LOCKSS system resists failures and attacks from powerful
adversaries without normal defenses such as long-term secrets and
central administration. The techniques that we have developed
may be primarily applicable to preservation, but
we hope that our conservative design will assist others in building systems that
better meet society's need for more reliable and defensible systems.
Both the LOCKSS project and the Narses simulator are hosted at
SourceForge, and both carry BSD-style Open Source licenses.
Implementation of this protocol in the production LOCKSS system is in
progress.
11 Acknowledgments
We are grateful to Kevin Lai, Joe Hellerstein, Yanto Muliadi,
Prashanth Bungale, Geoff Goodell, Ed Swierk, Lucy Cherkasova, and Sorav
Bansal for their help. We owe many thanks to our shepherd,
Carla Ellis, and the anonymous reviewers for their
help in improving this paper. Finally,
we are especially thankful to Vicky Reich, the director of the LOCKSS
program.
This work is supported by the National Science Foundation (Grant No. 9907296) and by the Andrew W. Mellon Foundation.
Any opinions, findings, and conclusions or
recommendations expressed here are those of the authors and do not
necessarily reflect the views of these funding agencies.
- 1
-
ABADI, M., BURROWS, M., MANASSE, M., AND WOBBER, T.
Moderately Hard, Memory-bound Functions.
In NDSS (2003).
- 2
-
ARGYRAKI, K., AND CHERITON, D.
Active Internet Traffic Filtering: Real-time Response to Denial of
Service Attacks.
In USENIX (Apr. 2005).
- 3
-
ARL - ASSOCIATION OF RESEARCH LIBRARIES.
ARL Statistics 2000-01.
https://www.arl.org/stats/arlstat/01pub/intro.html, 2001.
- 4
-
BACK, A.
Hashcash - a denial of service counter measure, 2002.
https://www.hashcash.org/hashcash.pdf.
- 5
-
CANTARA, L.
Archiving Electronic Journals.
https://www.diglib.org/preserve/ejp.htm, 2003.
- 6
-
CASTRO, M., DRUSCHEL, P., GANESH, A., ROWSTRON, A., AND WALLACH, D. S.
Secure Routing for Structured Peer-to-Peer Overlay Networks.
In OSDI (2002).
- 7
-
CASTRO, M., AND LISKOV, B.
Practical Byzantine Fault Tolerance.
In OSDI (1999).
- 8
-
CHERKASOVA, L., AND PHAAL, P.
Session-Based Admission Control: A Mechanism for Peak Load
Management of Commercial Web Sites.
IEEE Trans. on Computers 51, 6 (2002).
- 9
-
COX, L. P., AND NOBLE, B. D.
Samsara: Honor Among Thieves in Peer-to-Peer Storage.
In SOSP (2003).
- 10
-
CROSBY, S., AND WALLACH, D. S.
Denial of Service via Algorithmic Complexity Attacks.
In USENIX Security Symp. (2003).
- 11
-
DASWANI, N., AND GARCIA-MOLINA, H.
Query-Flood DoS Attacks in Gnutella.
In ACM Conf. on Computer and Communications Security
(2002).
- 12
-
DEAN, D., AND STUBBLEFIELD, A.
Using Client Puzzles to Protect TLS.
In USENIX Security Symp. (2001).
- 13
-
DOUCEUR, J.
The Sybil Attack.
In 1st Intl. Workshop on Peer-to-Peer Systems (2002).
- 14
-
DWORK, C., GOLDBERG, A., AND NAOR, M.
On Memory-Bound Functions for Fighting Spam.
In CRYPTO (2003).
- 15
-
DWORK, C., AND NAOR, M.
Pricing via Processing.
In CRYPTO (1992).
- 16
-
ELECTRONIC FRONTIER FOUNDATION.
DMCA Archive.
https://www.eff.org/IP/DMCA/.
- 17
-
FELDMAN, M., LAI, K., STOICA, I., AND CHUANG, J.
Robust Incentive Techniques for Peer-to-Peer Networks.
In ACM Electronic Commerce (2004).
- 18
-
FLOYD, S., AND JACOBSON, V.
The Synchronization of Periodic Routing Messages.
ACM Trans. on Networking 2, 2 (1994).
- 19
-
GEER, D.
Malicious Bots Threaten Network Security.
IEEE Computer 38, 1 (Jan. 2005), 18-20.
- 20
-
GIULI, T., AND BAKER, M.
Narses: A Scalable, Flow-Based Network Simulator.
Technical Report arXiv:cs.PF/0211024, CS Department, Stanford
University, Nov. 2002.
- 21
-
GOLLE, P., AND MIRONOV, I.
Uncheatable Distributed Computations.
Lecture Notes in Computer Science 2020 (2001).
- 22
-
HORLINGS, J.
Cd-r's binnen twee jaar onleesbaar.
https://www.pc-active.nl/toonArtikel.asp?artikelID=508, 2003.
https://www.cdfreaks.com/news/7751.
- 23
-
HUSSAIN, A., HEIDEMANN, J., AND PAPADOPOULOS, C.
A Framework for Classifying Denial of Service Attacks.
In SIGCOMM (2003).
- 24
-
KEROMYTIS, A., MISRA, V., AND RUBENSTEIN, D.
SOS: Secure Overlay Services.
In SIGCOMM (2002).
- 25
-
KUBIATOWICZ, J., BINDEL, D., CHEN, Y., CZERWINSKI, S., EATON, P., GEELS,
D., GUMMADI, R., RHEA, S., WEATHERSPOON, H., WEIMER, W., WELLS, C., AND ZHAO,
B.
OceanStore: An Architecture for Global-Scale Persistent Storage.
In ASPLOS (2000).
- 26
-
KUZMANOVIC, A., AND KNIGHTLY, E. W.
Low-Rate TCP-Targeted Denial of Service Attacks (The Shrew vs. the
Mice and Elephants).
In SIGCOMM (2003).
- 27
-
MAHAJAN, R., BELLOVIN, S., FLOYD, S., IOANNIDIS, J., PAXSON, V., AND
SHENKER, S.
Controlling high bandwidth aggregates in the network.
Comp. Comm. Review 32, 3 (2002).
- 28
-
MALKHI, D., AND REITER, M.
Byzantine Quorum Systems.
J. Distributed Computing 11, 4 (1998), 203-213.
- 29
-
MANIATIS, P., GIULI, T., ROUSSOPOULOS, M., ROSENTHAL, D., AND BAKER, M.
Impeding Attrition Attacks on P2P Systems.
In SIGOPS European Workshop (2004).
- 30
-
MANIATIS, P., ROUSSOPOULOS, M., GIULI, T., ROSENTHAL, D. S. H., BAKER, M.,
AND MULIADI, Y.
Preserving Peer Replicas By Rate-Limited Sampled Voting.
In SOSP (2003).
- 31
-
MCKUSICK, M. K., JOY, W. N., LEFFLER, S. J., AND FABRY, R. S.
A Fast File System for UNIX.
ACM Trans. on Computer Systems 2, 3 (1984), 181-197.
- 32
-
MILLS, D. L.
Internet Time Synchronization: The Network Time Protocol.
IEEE Trans. on Communications 39, 10 (Oct. 1991), 1482-1493.
- 33
-
MOORE, D., VOELKER, G. M., AND SAVAGE, S.
Inferring Internet Denial-of-Service Activity.
In USENIX Security Symp. (2001).
- 34
-
NEEDHAM, R.
Denial of Service.
In ACM Conf. on Computer and Communications Security
(1993).
- 35
-
REASON, J.
Human Error.
Cambridge University Press, 1990.
- 36
-
RHEA, S., GEELS, D., ROSCOE, T., AND KUBIATOWICZ, J.
Handling churn in a DHT.
In USENIX (2004).
- 37
-
RODRIGUES, R., AND LISKOV, B.
Byzantine Fault Tolerance in Long-Lived Systems.
In FuDiCo (2004).
- 38
-
ROSENTHAL, D. S., ROUSSOPOULOS, M., GIULI, T., MANIATIS, P., AND BAKER,
M.
Using Hard Disks For Digital Preservation.
In Imaging Sci. and Tech. Archiving Conference (2004).
- 39
-
ROSENTHAL, D. S. H., AND REICH, V.
Permanent Web Publishing.
In USENIX, Freenix Track (2000).
- 40
-
SAROIU, S., GUMMADI, K., DUNN, R., GRIBBLE, S., AND LEVY, H.
An Analysis of Internet Content Delivery Systems.
In OSDI (2002).
- 41
-
SAVAGE, S., WETHERALL, D., KARLIN, A., AND ANDERSON, T.
Practical Network Support for IP Traceback.
In SIGCOMM (2000).
- 42
-
SNOEREN, A., PARTRIDGE, C., SANCHEX, L., JONES, C. E., TCHAKOUNTIO, F.,
KENT, S. T., AND STRAYER, T., W.
Hash-based IP Traceback.
In SIGCOMM (2001).
- 43
-
SOMAYAJI, A., AND FORREST, S.
Automated Response Using System-Call Delays.
In Usenix Security Symp. (2000).
- 44
-
SPAM ARREST, LLC.
Take Control of your Inbox.
https://spamarrest.com.
- 45
-
TALAGALA, N.
Characterizing Large Storage Systems: Error Behavior and
Performance Benchmarks.
PhD thesis, CS Div., Univ. of California at Berkeley, Berkeley, CA,
USA, Oct. 1999.
- 46
-
TENOPIR, C.
Online Scholarly Journals: How Many?
The Library Journal, 2 (2004).
https://www.libraryjournal.com/index.asp?layout=articlePrint&articleID=CA374956.
- 47
-
WALLACH, D.
A Survey of Peer-to-Peer Security Issues.
In Intl. Symp. on Software Security (2002).
- 48
-
WILLIAMSON, M.
Throttling Viruses: Restricting Propagation to Defeat Malicious
Mobile Code.
In Annual Computer Security Applications Conf. (2002).
Attrition Defenses for a Peer-to-Peer Digital
Preservation System
This document was generated using the
LaTeX2HTML translator Version 2002-2-1 (1.70)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 -show_section_numbers -local_icons hotel.tex
The translation was initiated by TJ Giuli on 2005-02-17



TJ Giuli
2005-02-17
|

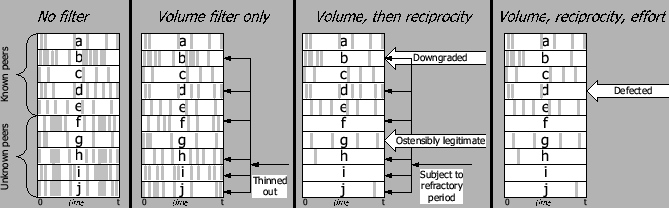
![]() through
through ![]() ),
), ![]() and
and ![]() maintain a steady balance of requested votes
throughout the time interval
maintain a steady balance of requested votes
throughout the time interval ![]() to
to ![]() .
Note that
.
Note that ![]() asks for two votes in
close succession; this is an instance of a peer expending its ``credit.''
In contrast,
asks for two votes in
close succession; this is an instance of a peer expending its ``credit.''
In contrast,
![]() requests many more votes in close succession than justified by its
grade and is downgraded to the debt
grade by the reciprocity filter,
eventually becoming subject to the refractory period.
requests many more votes in close succession than justified by its
grade and is downgraded to the debt
grade by the reciprocity filter,
eventually becoming subject to the refractory period. ![]() behaves with ostensible legitimacy with regards to the rate of
invitations it sends, but misbehaves by deserting (e.g., by not
supplying correct effort proofs) and, as a result, is
downgraded to the debt grade by the effort filter.
behaves with ostensible legitimacy with regards to the rate of
invitations it sends, but misbehaves by deserting (e.g., by not
supplying correct effort proofs) and, as a result, is
downgraded to the debt grade by the effort filter.
![]() 's subsequent invitations are subject to the refractory period.
's subsequent invitations are subject to the refractory period.
![]() is initially unknown and therefore
subject to the refractory period, but behaves ostensibly legitimately
and is upgraded to even or credit grade, freeing itself
from the refractory period. Peers
is initially unknown and therefore
subject to the refractory period, but behaves ostensibly legitimately
and is upgraded to even or credit grade, freeing itself
from the refractory period. Peers ![]() ,
, ![]() ,
, ![]() , and
, and ![]() request many
more votes than reasonable and occasionally send simultaneous
traffic
spikes which exceed link capacity; they are thinned out
by the volume
filter along with other peers' traffic. These peers,
as well as misbehaving peers
request many
more votes than reasonable and occasionally send simultaneous
traffic
spikes which exceed link capacity; they are thinned out
by the volume
filter along with other peers' traffic. These peers,
as well as misbehaving peers ![]() and
and ![]() , share
the same refractory period and therefore only one invitation from them
can be accepted per refractory period.
, share
the same refractory period and therefore only one invitation from them
can be accepted per refractory period.
![]() admission
probability), we set the introductory effort to be 20% of the total
effort required of a poller; by the time the adversary has gotten his
poll invitation admitted, even if he defects for the rest of the poll,
he has already expended on average 100% of the effort he would have, had he
behaved well in the first place.
admission
probability), we set the introductory effort to be 20% of the total
effort required of a poller; by the time the adversary has gotten his
poll invitation admitted, even if he defects for the rest of the poll,
he has already expended on average 100% of the effort he would have, had he
behaved well in the first place.
![]() is a simulation of 50 AUs on peers already
running a realistic workload of
is a simulation of 50 AUs on peers already
running a realistic workload of ![]() AUs.
The effect is to over-estimate the peer's busyness for AUs in higher
layers and under-estimate it for AUs in lower layers;
AUs in a layer compete for the resources left over by lower layers,
but AUs in lower layers are unaffected by the resources used in
higher layers.
We have validated this technique against unlayered simulations in
smaller collections, as well as against simulations in which inflated per-AU preservation
costs cause similar levels of peer load; we found negligible differences.
AUs.
The effect is to over-estimate the peer's busyness for AUs in higher
layers and under-estimate it for AUs in lower layers;
AUs in a layer compete for the resources left over by lower layers,
but AUs in lower layers are unaffected by the resources used in
higher layers.
We have validated this technique against unlayered simulations in
smaller collections, as well as against simulations in which inflated per-AU preservation
costs cause similar levels of peer load; we found negligible differences.
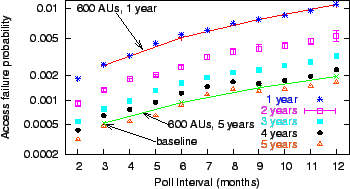
![]() for a 50-AU collection
and of
for a 50-AU collection
and of
![]() for a 600-AU collection correspond to our
interpoll interval of 3 months and a storage damage rate of one block
per 5 disk years. With these parameters, a machine preserving 600 AUs
has an average load of 9%, and a machine preserving 50 AUs
has a 0.7% average load.
for a 600-AU collection correspond to our
interpoll interval of 3 months and a storage damage rate of one block
per 5 disk years. With these parameters, a machine preserving 600 AUs
has an average load of 9%, and a machine preserving 50 AUs
has a 0.7% average load.
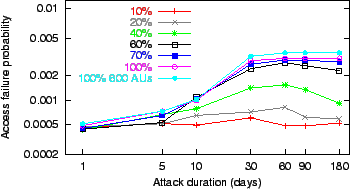
![]() ; this is within tolerable limits for services open to the
Internet.
; this is within tolerable limits for services open to the
Internet.
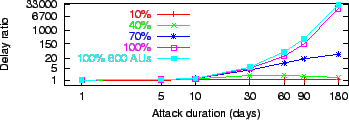
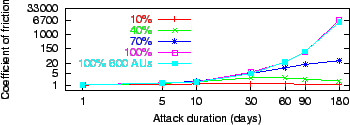
![]() the number absent attack.
However, the average machine load during
recuperation remains within 2 to 3 times the baseline load -- a result
of designing the protocol to limit increases in resource consumption
while under attack. Fewer successful polls and nearly constant
resource consumption for increasing attack durations drives up the
average cost of a successful poll, and with it the coefficient of
friction.
the number absent attack.
However, the average machine load during
recuperation remains within 2 to 3 times the baseline load -- a result
of designing the protocol to limit increases in resource consumption
while under attack. Fewer successful polls and nearly constant
resource consumption for increasing attack durations drives up the
average cost of a successful poll, and with it the coefficient of
friction.
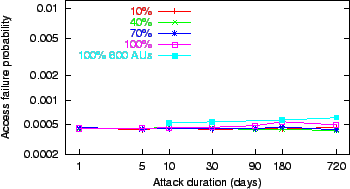
![]() when
the duration of the attack reaches the entire duration of our
simulations (2 years) for full population coverage and a 600-AU collection. At that attack
intensity, loyal peers no longer admit poll invitations from unknown or
indebted loyal peers, unless supported by an introduction. This causes
discovery to operate more slowly; loyal peers waste their
resources on introductory effort proofs that are summarily rejected by
peers in their refractory period. This wasted effort, when sustained
over years, raises
the coefficient of friction by 33%, (much less than the
friction caused by pipe stoppage), and raises average machine load from
9% to 11%. The delay ratio is largely
unaffected by this adversary.
Consequently, the first effect of this adversary, increasing load in
loyal peers, is tolerable given
a practical level of over-provisioning.
when
the duration of the attack reaches the entire duration of our
simulations (2 years) for full population coverage and a 600-AU collection. At that attack
intensity, loyal peers no longer admit poll invitations from unknown or
indebted loyal peers, unless supported by an introduction. This causes
discovery to operate more slowly; loyal peers waste their
resources on introductory effort proofs that are summarily rejected by
peers in their refractory period. This wasted effort, when sustained
over years, raises
the coefficient of friction by 33%, (much less than the
friction caused by pipe stoppage), and raises average machine load from
9% to 11%. The delay ratio is largely
unaffected by this adversary.
Consequently, the first effect of this adversary, increasing load in
loyal peers, is tolerable given
a practical level of over-provisioning.
![]() (
(![]() for the large collection, which equates to an average machine
load of 21%).
To defend against this increase in cost, LOCKSS peers must over-provision
their resources by a reasonable amount.
The baseline probability of access failure rises to
for the large collection, which equates to an average machine
load of 21%).
To defend against this increase in cost, LOCKSS peers must over-provision
their resources by a reasonable amount.
The baseline probability of access failure rises to
![]() at a cost almost identical to that incurred by the
defenders (a cost ratio of
at a cost almost identical to that incurred by the
defenders (a cost ratio of ![]() ). Fortunately, this continuous attack
even from a brute force adversary unconcerned by his own effort
expenditure is unable to increase the access failure probability of the
victims greatly; the rate limits prevent him from bringing his advantage
in resources to bear. Similar behavior in earlier
work [30] prevents a different
unconstrained adversary from stealthily modifying content.
). Fortunately, this continuous attack
even from a brute force adversary unconcerned by his own effort
expenditure is unable to increase the access failure probability of the
victims greatly; the rate limits prevent him from bringing his advantage
in resources to bear. Similar behavior in earlier
work [30] prevents a different
unconstrained adversary from stealthily modifying content.
