
16th USENIX Security Symposium Pp.
183–198 of the Proceedings


Integrity Checking in Cryptographic File Systems
with Constant Trusted Storage
Alina Oprea1 -
Michael K. Reiter2
Abstract:
In this paper we propose two new constructions for
protecting the integrity of files in cryptographic file systems. Our
constructions are designed to exploit two characteristics of many
file-system workloads, namely low entropy of file contents and high
sequentiality of file block writes. At the same time, our
approaches maintain the best features of the most commonly used
algorithm today (Merkle trees), including defense against replay of
stale (previously overwritten) blocks and a small, constant amount
of trusted storage per file. Via implementations in the EncFS
cryptographic file system, we evaluate the performance and storage
requirements of our new constructions compared to those of Merkle
trees. We conclude with guidelines for choosing the best integrity
algorithm depending on typical application workload.
1 Introduction
The growth of outsourced storage in the form of storage service
providers
underlines the importance of developing efficient security mechanisms
to protect files stored remotely. Cryptographic file systems
(e.g., [10,6,25,13,17,23,20])
provide means to protect file secrecy (i.e., prevent leakage of file
contents) and integrity (i.e., detect the unauthorized modification of
file contents) against the compromise of the file store and attacks on
the network while blocks are in transit to/from the file store.
Several engineering goals have emerged to guide the design of
efficient cryptographic file systems. First, cryptographic
protections should be applied at the granularity of individual blocks
as opposed to entire files, since the latter requires the entire file
to be retrieved to verify its integrity, for example. Second, the
application of cryptographic protections to a block should not
increase the block size, so as to be transparent to the underlying
block store. (Cryptographic protections might increase the number of
blocks, however.) Third, the trusted storage required by
clients (e.g., for encryption keys and integrity verification
information) should be kept to a minimum.
In this paper we propose and evaluate two new algorithms for
protecting file integrity in cryptographic file systems. Our
algorithms meet these design goals, and in particular implement
integrity using only a small constant amount of trusted storage per
file. (Of course, as with any integrity-protection scheme, this
trusted information for many files could itself be written to a file
in the cryptographic file system, thereby reducing the trusted
storage costs for many files to that of only one. The need for
trusted information cannot be entirely eliminated, however.) In
addition, our algorithms exploit two properties of many file-system
workloads to achieve efficiencies over prior proposals. First,
typical file contents in many file-system workloads have low
empirical entropy; such is the case with text files, for example.
Our first algorithm builds on our prior proposal that exploits this
property [26] and uses tweakable ciphers [21,15]
for encrypting file block contents; this prior proposal, however,
did not achieve constant trusted storage per file. Our second
algorithm reduces the amount of additional storage needed for
integrity by using the fact that low-entropy block contents can be
compressed enough to embed a message-authentication code inside the
block. The second property that we exploit in our algorithms to
reduce the additional storage needed for integrity is that blocks of
the same file are often written sequentially, a characteristic that,
to our knowledge, has not been previously utilized.
By designing integrity mechanisms that exploit these properties, we
demonstrate more efficient integrity protections in cryptographic
file systems than have previously been possible for many workloads.
The measures of efficiency that we consider include the amount of
untrusted storage required by the integrity mechanism (over and
above that required for file blocks); the integrity bandwidth,
i.e., the amount of this information that must be accessed (updated
or read) when accessing a single file block, averaged over all
blocks in a file, all blocks in all files, or all accesses in a
trace (depending on context); and the file write and read
performance costs.
The standard against which we compare our algorithms is the Merkle
tree [24], which to date is the overwhelmingly most popular
method of integrity protection for a file. Merkle trees can be
implemented in cryptographic file systems so as to meet the
requirements outlined above, in particular requiring trusted storage
per file of only one output of a cryptographic hash function (e.g., 20
bytes for SHA-1 [30]). They additionally offer an
integrity bandwidth per file that is logarithmic in the number of file
blocks. However, Merkle trees are oblivious to file block contents
and access characteristics, and we show that by exploiting these, we
can generate far more efficient integrity mechanisms for some
workloads.
We have implemented our integrity constructions and Merkle trees in
EncFS [14], an open-source user-level file system that
transparently provides file block encryption on top of
FUSE [12]. We provide an evaluation of the three approaches
with respect to our measures of interest, demonstrating how file
contents, as well as file access patterns, have a great influence on
the performance of the new integrity algorithms. Our experiments
demonstrate that there is not a clear winner among the three
constructions for all workloads, in that different integrity
constructions are best suited to particular workloads. We thus
conclude that a cryptographic file system should implement all three
schemes and give higher-level applications an option to choose the
appropriate integrity mechanism.
2 Random Access Integrity Model
We consider the model of a cryptographic file system that provides
random access to files. Encrypted data is stored on untrusted
storage servers and there is a mechanism for distributing the
cryptographic keys to authorized parties. A small (on the order of
several hundred bytes), fixed-size per file, trusted storage
is available for authentication data.
We assume that the storage servers are actively controlled by an
adversary. The adversary can adaptively alter the data stored on the
storage servers or perform any other attack on the stored data, but
it cannot modify or observe the trusted storage. A particularly
interesting attack that the adversary can mount is a replay
attack, in which stale data is returned to read requests of
clients. Using the trusted storage to keep some constant-size
information per file, and keeping more information per file on
untrusted storage, our goal is to design and evaluate integrity
algorithms that allow the update and verification of individual
blocks in files and that detect data modification and replay
attacks.
In our framework, a file  is divided into n
fixed-size blocks is divided into n
fixed-size blocks
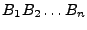 (the last block (the last block 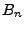 might be shorter
than the first n-1 blocks), each encrypted individually with the
encryption key of the file and stored on the untrusted storage
servers (n differs per file). The constant-size, trusted storage
for file might be shorter
than the first n-1 blocks), each encrypted individually with the
encryption key of the file and stored on the untrusted storage
servers (n differs per file). The constant-size, trusted storage
for file  is denoted TSF. Additional storage for file is denoted TSF. Additional storage for file  ,
which can reside in untrusted storage, is denoted USF; of course,
USF can be written to the untrusted storage server. ,
which can reside in untrusted storage, is denoted USF; of course,
USF can be written to the untrusted storage server.
The storage interface provides two basic operations to the clients:
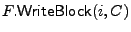 stores content C at block index i in file
stores content C at block index i in file
 and
and
 reads (encrypted) content from block index i in file reads (encrypted) content from block index i in file
 .
An integrity algorithm for an encrypted file system consists of five operations.
In the initialization algorithm Init for file .
An integrity algorithm for an encrypted file system consists of five operations.
In the initialization algorithm Init for file
 ,
the encryption key for the file is generated.
In an update operation ,
the encryption key for the file is generated.
In an update operation
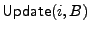 for file for file
 ,
an authorized client updates the
i-th block in the file with the encryption of block content B and updates the integrity information for the i-th block stored in TSF and USF.
In the check operation ,
an authorized client updates the
i-th block in the file with the encryption of block content B and updates the integrity information for the i-th block stored in TSF and USF.
In the check operation
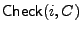 for file for file
 ,
an authorized client first decrypts C and then checks
that the decrypted block content is authentic, using the additional
storage TSF and USF for file ,
an authorized client first decrypts C and then checks
that the decrypted block content is authentic, using the additional
storage TSF and USF for file
 .
The check operation returns the decrypted block if it concludes that the block content is
authentic and .
The check operation returns the decrypted block if it concludes that the block content is
authentic and 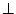 otherwise. A client can additionally perform an
append operation otherwise. A client can additionally perform an
append operation
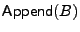 for file for file
 ,
in which a new block that contains the encryption of B is appended to the encrypted
file, and a ,
in which a new block that contains the encryption of B is appended to the encrypted
file, and a 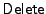 operation that deletes the last block in a
file and updates the integrity information for the file. operation that deletes the last block in a
file and updates the integrity information for the file.
Using the algorithms we have defined for an integrity scheme for an
encrypted file, a client can read or write at any byte offset in the
file. For example, to write to a byte offset that is not at a block
boundary, the client first reads the block to which the byte offset
belongs, decrypts it and checks its integrity using algorithm Check.
Then, the client constructs the new data block by replacing
the appropriate bytes in the decrypted block, and calls Update to
encrypt the new block and compute its integrity information.
In designing an integrity algorithm for a cryptographic file system,
we consider the following metrics. First is the size of the
untrusted storage USF; we will always enforce that the trusted
storage TSF is of constant size, independent of the number of
blocks. Second is the integrity bandwidth for updating and checking
individual file blocks, defined as the number of bytes from USF (updated or read) when accessing a block of file  ,
averaged over either: all blocks in ,
averaged over either: all blocks in  when we speak of a
per-file integrity bandwidth; all blocks in all files when we speak
of the integrity bandwidth of the file system; or all blocks
accessed in a particular trace when we speak of one trace. Third is
the performance cost of writing and reading files. when we speak of a
per-file integrity bandwidth; all blocks in all files when we speak
of the integrity bandwidth of the file system; or all blocks
accessed in a particular trace when we speak of one trace. Third is
the performance cost of writing and reading files.
Merkle trees [24] are used to authenticate n data items with
constant-size trusted storage. A Merkle tree for data items
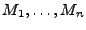 , denoted , denoted
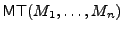 , is a binary tree that has , is a binary tree that has
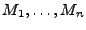 as leaves. An interior node of the tree with
children as leaves. An interior node of the tree with
children 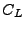 and and 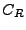 is the hash of the concatenation of its
children (i.e., is the hash of the concatenation of its
children (i.e.,
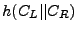 , for , for
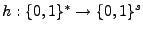 a second preimage resistant hash function [29]
that outputs strings of length s bits). If the root of the tree is
stored in trusted storage, then all the leaves of the tree can be
authenticated by reading from the tree a number of hashes
logarithmic in n. a second preimage resistant hash function [29]
that outputs strings of length s bits). If the root of the tree is
stored in trusted storage, then all the leaves of the tree can be
authenticated by reading from the tree a number of hashes
logarithmic in n.
We define the Merkle tree for a file
 with n blocks
with n blocks
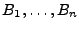 to be the binary tree to be the binary tree
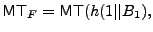
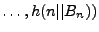 . A Merkle tree with a given set of leaves can
be constructed in multiple ways. We choose to append a new block in
the tree as a right-most child, so that the tree has the property
that all the left subtrees are complete. We define several
algorithms for a Merkle tree , for which we omit the
implementation details, due to space limitations. . A Merkle tree with a given set of leaves can
be constructed in multiple ways. We choose to append a new block in
the tree as a right-most child, so that the tree has the property
that all the left subtrees are complete. We define several
algorithms for a Merkle tree , for which we omit the
implementation details, due to space limitations.
- In the
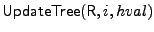 algorithm for tree T,
the hash stored at the i-th leaf of T counting from left to
right) is updated to algorithm for tree T,
the hash stored at the i-th leaf of T counting from left to
right) is updated to 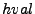 . This triggers an update of all the
hashes stored on the path from the i-th leaf to the root of the
tree. It is necessary to first check that all the siblings of the
nodes on the path from the updated leaf to the root of the tree are
authentic. Finally, the updated root of the tree is output in R. . This triggers an update of all the
hashes stored on the path from the i-th leaf to the root of the
tree. It is necessary to first check that all the siblings of the
nodes on the path from the updated leaf to the root of the tree are
authentic. Finally, the updated root of the tree is output in R.
- The
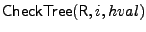 algorithm for tree T checks that the hash stored at the
i-th leaf matches algorithm for tree T checks that the hash stored at the
i-th leaf matches 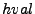 . All
the hashes stored at the nodes on the path from the i-th leaf to
the root are computed and the root of T is checked finally to
match the value stored in R. . All
the hashes stored at the nodes on the path from the i-th leaf to
the root are computed and the root of T is checked finally to
match the value stored in R.
- Algorithm
 for tree T a
new leaf u that stores the hash value for tree T a
new leaf u that stores the hash value 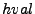 to the tree, updates
the path from this new leaf to the root of the tree and outputs the
new root of the tree in R. to the tree, updates
the path from this new leaf to the root of the tree and outputs the
new root of the tree in R.
- The
 algorithm for tree T
the last leaf from the tree, updates the remaining path to the root
of the tree and outputs the new root of the tree in R. algorithm for tree T
the last leaf from the tree, updates the remaining path to the root
of the tree and outputs the new root of the tree in R.
An encryption scheme consists of a key generation algorithm Gen thatoutputs an encryption key, an encryption algorithm 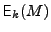 that outputs the encryption of a message
that outputs the encryption of a message 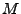 with secret key with secret key 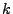 and
a decryption algorithm and
a decryption algorithm
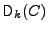 that outputs the decryption
of a ciphertext C with secret key that outputs the decryption
of a ciphertext C with secret key 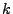 . A widely used secure
encryption scheme is AES [2] in CBC mode [8]. . A widely used secure
encryption scheme is AES [2] in CBC mode [8].
A tweakable cipher [21,15] is, informally, a
length-preserving encryption method that uses a tweak in both
the encryption and decryption algorithms for variability. A
tweakable encryption of a message 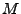 with tweak t and secret key with tweak t and secret key
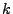 is denoted is denoted
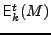 and, similarly, the decryption of
ciphertext C with tweak t and secret key and, similarly, the decryption of
ciphertext C with tweak t and secret key 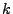 is denoted is denoted
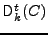 . The tweak is a public parameter, and the security
of the tweakable cipher is based only on the secrecy of the
encryption key. Tweakable ciphers can be used to encrypt fixed-size
blocks written to disk in a file system. Suitable values of the
tweak for this case are, for example, block addresses or block
indices in the file. There is a distinction between
narrow-block tweakable ciphers that operate on block lengths
of 128 bits (as regular block ciphers) and wide-block
tweakable ciphers that operate on arbitrarily large blocks (e.g.,
512 bytes or 4KB). In this paper we use the term tweakable ciphers
to refer to wide-block tweakable ciphers as defined by Halevi and
Rogaway [15]. . The tweak is a public parameter, and the security
of the tweakable cipher is based only on the secrecy of the
encryption key. Tweakable ciphers can be used to encrypt fixed-size
blocks written to disk in a file system. Suitable values of the
tweak for this case are, for example, block addresses or block
indices in the file. There is a distinction between
narrow-block tweakable ciphers that operate on block lengths
of 128 bits (as regular block ciphers) and wide-block
tweakable ciphers that operate on arbitrarily large blocks (e.g.,
512 bytes or 4KB). In this paper we use the term tweakable ciphers
to refer to wide-block tweakable ciphers as defined by Halevi and
Rogaway [15].
The security of tweakable ciphers implies an interesting property,
called non-malleability [15], that guarantees that if
only a single bit is changed in a valid ciphertext, then its
decryption is indistinguishable from a random plaintext. Tweakable
cipher constructions include CMC [15] and EME [16].
Oprea et al. [26] provide an efficient integrity
construction in a block-level storage system. This integrity
construction is based on the experimental observation that contents
of blocks written to disk usually are efficiently distinguishable
from random blocks, i.e., blocks uniformly chosen at random
from the set of all blocks of a fixed length. Assuming that data
blocks are encrypted with a tweakable cipher, the integrity of the
blocks that are efficiently distinguishable from random blocks can
be checked by performing a randomness test on the block contents.
The non-malleability property of tweakable ciphers implies that if
block contents after decryption are distinguishable from random,
then it is very likely that the contents are authentic. This idea
permits a reduction in the trusted storage needed for checking block
integrity: a hash is stored only for those (usually few) blocks that
are indistinguishable from random blocks (or, in short,
random-looking blocks).
An example of a statistical test IsRand [26] that can be
used to distinguish block contents from random blocks evaluates the
entropy of a block and considers random those blocks that have an
entropy higher than a threshold chosen experimentally. For a block
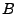 , , 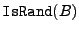 returns 1 with high probability if returns 1 with high probability if 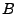 is a
uniformly random block in the block space and 0, otherwise. Oprea et
al. [26] provide an upper bound on the false negative rate
of the randomness test that is used in the security analysis of the
scheme. is a
uniformly random block in the block space and 0, otherwise. Oprea et
al. [26] provide an upper bound on the false negative rate
of the randomness test that is used in the security analysis of the
scheme.
We use the ideas from Oprea et al. [26] as a starting point
for our first algorithm for implementing file integrity in
cryptographic file systems. The main challenge to construct
integrity algorithms in our model is to efficiently reduce the
amount of trusted storage per file to a constant value. Our second
algorithm also exploits the redundancy in file contents to reduce
the additional space for integrity, but in a different way, by
embedding a message authentication code (MAC) in file blocks that
can be compressed enough. Both of these schemes build from a novel
technique that is described in Section 4.1 for
efficiently tracking the number of writes to file blocks.
All the integrity constructions for encrypted storage described in
the next section use write counters for the blocks in a file. A
write counter for a block denotes the total number of writes done to
that block index. Counters are used to reduce the additional storage
space taken by encrypting with a block cipher in CBC mode, as
described in Section 4.2. Counters are also a means of
distinguishing different writes performed to the same block address
and as such, can be used to prevent against replay attacks.
We define several operations for the write counters of the blocks in
a file  .
The .
The
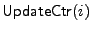 algorithm either initializes the
value of the counter for the i-th block in file algorithm either initializes the
value of the counter for the i-th block in file
 with 1, or it increments the counter for the i-th block if it has already
been initialized. The algorithm also updates the information for the
counters stored in USF. Function
with 1, or it increments the counter for the i-th block if it has already
been initialized. The algorithm also updates the information for the
counters stored in USF. Function
 returns the value of
the counter for the i-th block in file returns the value of
the counter for the i-th block in file
 .
When counters are used to protect against replay attacks, they need to be
authenticated with a small amount of trusted storage. For
authenticating block write counters, we define an algorithm AuthCtr
that modifies the trusted storage space TSF
of file .
When counters are used to protect against replay attacks, they need to be
authenticated with a small amount of trusted storage. For
authenticating block write counters, we define an algorithm AuthCtr
that modifies the trusted storage space TSF
of file
 to contain the trusted authentication information for the
write counters of
to contain the trusted authentication information for the
write counters of
 ,
and a function CheckCtr that checks the
authenticity of the counters stored in the trusted
storage TSF for file ,
and a function CheckCtr that checks the
authenticity of the counters stored in the trusted
storage TSF for file
 and returns true if the counters are authentic and false, otherwise. Both operations for
authenticating counters are invoked by an authorized client.
and returns true if the counters are authentic and false, otherwise. Both operations for
authenticating counters are invoked by an authorized client.
4.1 Storage and Authentication of Block Write Counters
A problem that needs to be addressed in the design of the various
integrity algorithms described below is the storage and
authentication of the block write counters. If a counter per file
block were used, this would result in significant additional storage
for counters. Here we propose a more efficient method of storing the
block write counters, based on analyzing the file access patterns in
NFS traces collected at Harvard University [9].
We performed experiments on the NFS Harvard
traces [9] in order to analyze the file access patterns.
We considered three different traces (LAIR, DEASNA and HOME02) for a
period of one week. The LAIR trace consists of research workload
traces from Harvard's computer science department. The DEASNA trace
is a mix of research and email workloads from the division of
engineering and applied sciences at Harvard. HOME02 is mostly the
email workload from the campus general purpose servers.
Ellard et al. [9] make the observation that a large number
of file accesses are sequential. This leads to the idea that the
values of the write counters for adjacent blocks in a file might be
correlated. To test this hypothesis, we represent counters for
blocks in a file using counter intervals. A counter interval
is defined as a sequence of consecutive blocks in a file that all
share the same value of the write counter. For a counter interval,
we need to store only the beginning and end of the interval, and the
value of the write counter.
Table 1 shows the average storage per file used
by the two counter representation methods for the three traces. We
represent a counter using 2 bytes (as the maximum observed value of
a counter was 9905) and we represent file block indices with 4
bytes. The counter interval method reduces the average storage
needed for counters by a factor of 30 for the LAIR trace, 26.5 for
the DEASNA trace and 7.66 for the HOME02 trace compared to the
method that stores a counter per file block. This justifies our
design choice to use counter intervals for representing counter
values in the integrity algorithms presented in the next section.
Table 1:
Average storage per file for two counter representation
methods.
|
LAIR |
DEASNA |
HOME02 |
|
Counter per block |
547.8 bytes |
1.46 KB |
3.16 KB |
| Counter intervals |
18.35 bytes |
55.04 bytes |
413.44 bytes |
|
The counter intervals for file
 are represented by two arrays: IntStartF keeps
the block indices where new counter intervals start
and CtrValF keeps the values of the write counter for each
interval. The trusted storage TSF for file
are represented by two arrays: IntStartF keeps
the block indices where new counter intervals start
and CtrValF keeps the values of the write counter for each
interval. The trusted storage TSF for file
 includes either the arrays IntStartF and CtrValF
if they fit into TSF, or, for
each array, a hash of all its elements (concatenated), otherwise. In
the limit, to reduce the bandwidth for integrity, we could build a
Merkle tree to authenticate each of these arrays and store the root
of these trees in TSF, but we have not seen in the Harvard traces
files that would warrant this. We omit here the implementation
details for the UpdateCtr, GetCtr, AuthCtr and CheckCtr algorithms on counters, due to space limitations.
includes either the arrays IntStartF and CtrValF
if they fit into TSF, or, for
each array, a hash of all its elements (concatenated), otherwise. In
the limit, to reduce the bandwidth for integrity, we could build a
Merkle tree to authenticate each of these arrays and store the root
of these trees in TSF, but we have not seen in the Harvard traces
files that would warrant this. We omit here the implementation
details for the UpdateCtr, GetCtr, AuthCtr and CheckCtr algorithms on counters, due to space limitations.
If the counter intervals for a file get too dispersed, then the size
of the arrays IntStartF and CtrValF might increase significantly.
To keep the untrusted storage for integrity low, we could
periodically change the encryption key for the file, re-encrypt all
blocks in the file, and reset the block write counters to 0.
4.2 Length-Preserving Stateful Encryption with Counters
Secure encryption schemes are usually not length-preserving.
However, one of our design goals stated in the introduction is to
add security (and, in particular, encryption) to file systems in a
manner transparent to the storage servers. For this purpose, we
introduce here the notion of a length-preserving stateful
encryption scheme for a file
 ,
an encryption scheme that encrypts blocks in a way that preserves the length of the original
blocks, and stores any additional information in the untrusted
storage space for the file. We define a length-preserving stateful
encryption scheme for a file ,
an encryption scheme that encrypts blocks in a way that preserves the length of the original
blocks, and stores any additional information in the untrusted
storage space for the file. We define a length-preserving stateful
encryption scheme for a file
 to consist of a key generation
algorithm Glen that generates an encryption key for the file, an
encryption algorithm Elen that encrypts block content B for
block index i with key
to consist of a key generation
algorithm Glen that generates an encryption key for the file, an
encryption algorithm Elen that encrypts block content B for
block index i with key 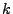 and outputs ciphertext C, and a
decryption algorithm Dlen that decrypts the encrypted content
C of block i with key and outputs ciphertext C, and a
decryption algorithm Dlen that decrypts the encrypted content
C of block i with key 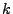 and outputs the plaintext B. Both
the Elen and Dlen algorithms also modify the untrusted
storage space for the file. and outputs the plaintext B. Both
the Elen and Dlen algorithms also modify the untrusted
storage space for the file.
Tweakable ciphers are by definition length-preserving stateful
encryption schemes. A different construction on which we elaborate
below uses write counters for file blocks. Let
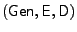 be
an encryption scheme constructed from a block cipher in CBC mode. To
encrypt an n-block message in the CBC encryption mode, a random
initialization vector is chosen. The ciphertext consists of n+1
blocks, with the first being the initialization vector. We denote by be
an encryption scheme constructed from a block cipher in CBC mode. To
encrypt an n-block message in the CBC encryption mode, a random
initialization vector is chosen. The ciphertext consists of n+1
blocks, with the first being the initialization vector. We denote by
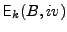 the output of the encryption of excluding the
initialization vector) using key the output of the encryption of excluding the
initialization vector) using key 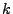 and initialization vector iv,
and similarly by and initialization vector iv,
and similarly by
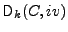 the decryption of
key the decryption of
key 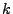 and initialization vector iv. and initialization vector iv.
We replace the random initialization vectors for encrypting a file
block with a pseudorandom function application of the block index
concatenated with the write counter for the block. This is
intuitively secure because different initialization vectors are used
for different encryptions of the same block, and moreover, the
properties of pseudorandom functions imply that the initialization
vectors are indistinguishable from random. It is thus enough to
store the write counters for the blocks of a file, and the
initialization vectors for the file blocks can be easily inferred.
The Glen, Elen and Dlen algorithms for a file
 are described in Figure 1. Here
are described in Figure 1. Here
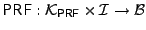 denotes a pseudorandom
function family with input space the set of all block indices concatenated with block counter
values and output space the block space
of E. denotes a pseudorandom
function family with input space the set of all block indices concatenated with block counter
values and output space the block space
of E.
Figure 1:
Implementing a length-preserving stateful encryption scheme
with write counters.
 |
5 Integrity Constructions for Encrypted Storage
In this section, we first present a Merkle tree integrity
construction for encrypted storage, used in file systems such as
Cepheus [10], FARSITE [1], and Plutus [17].
Second, we introduce a new integrity construction based on tweakable
ciphers that uses some ideas from Oprea et al. [26]. Third,
we give a new construction based on compression levels of block
contents. We evaluate the performance of the integrity algorithms
described here in Section 7.
In this construction, file blocks can be encrypted with any
length-preserving stateful encryption scheme and they are
authenticated with a Merkle tree. More precisely, if 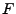 is a file
comprised of blocks is a file
comprised of blocks
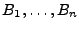 , then the untrusted storage for
integrity for file , then the untrusted storage for
integrity for file
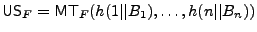 (for (for 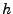 a second-preimage resistant hash function), and the
trusted storage TSF is the root of this tree. a second-preimage resistant hash function), and the
trusted storage TSF is the root of this tree.
The algorithm Init runs the key generation algorithm Glen of
the length-preserving stateful encryption scheme for file
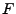 .
The algorithms Update, Check, Append and Delete of the MT-EINT
construction are given in Figure 2. We denote
here by .
The algorithms Update, Check, Append and Delete of the MT-EINT
construction are given in Figure 2. We denote
here by
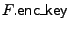 the encryption key for file generated in the Init algorithm) and the encryption key for file generated in the Init algorithm) and
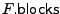 the number
of blocks in file the number
of blocks in file
 . .
- In the
 algorithm for file algorithm for file
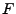 ,
the i-th leaf
in MTF is updated with the hash of the new block content using
the algorithm UpdateTree and the encryption of B is stored in
the i-th block of ,
the i-th leaf
in MTF is updated with the hash of the new block content using
the algorithm UpdateTree and the encryption of B is stored in
the i-th block of
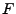 . .
- To append a new block B to file
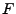 with algorithm
with algorithm
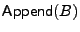 , a new leaf is appended to MTF with the
algorithm AppendTree, and then an encryption of B is stored in
the n+1-th block of , a new leaf is appended to MTF with the
algorithm AppendTree, and then an encryption of B is stored in
the n+1-th block of
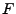 (for n the number of blocks of
(for n the number of blocks of
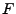 ). ).
- In the
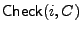 algorithm for file algorithm for file
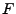 ,
block C is decrypted, and its integrity is checked using the CheckTree algorithm. ,
block C is decrypted, and its integrity is checked using the CheckTree algorithm.
- To delete the last block from a file
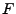 with algorithm
with algorithm
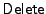 , the last leaf in MTF is deleted with the algorithm DeleteTree . , the last leaf in MTF is deleted with the algorithm DeleteTree .
The MT-EINT construction detects data modification and block
swapping attacks, as file block contents are authenticated by the
root of the Merkle tree for each file. The MT-EINT is
also secure against replay attacks, as the tree contains the hashes
of the latest version of the data blocks and the root of the Merkle
tree is authenticated in trusted storage.
Figure 2:
The Update, Check, Append and Delete algorithms for
the MT-EINT construction.
 |
Whereas in the Merkle tree construction any length-preserving
stateful encryption algorithm can be used to individually encrypt
blocks in a file, the randomness test construction uses the
observation from Oprea et al. [26] that the integrity of
the blocks that
are efficiently distinguishable from random blocks can be checked
with a randomness test if a tweakable cipher is used to encrypt
them. As such, integrity information is stored only for
random-looking blocks.
In this construction, a Merkle tree per file that authenticates the
contents of the random-looking blocks is built. The untrusted
storage for integrity USF for file
 comprised of blocks
comprised of blocks
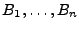 includes this tree includes this tree
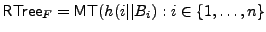 and and 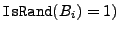 , and, in addition,
the set of block numbers that are random-looking , and, in addition,
the set of block numbers that are random-looking
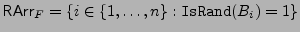 , ordered the same as the leaves in
the previous tree RTreeF. The root of the tree RTreeF is
kept in the trusted storage USF for file , ordered the same as the leaves in
the previous tree RTreeF. The root of the tree RTreeF is
kept in the trusted storage USF for file
 . .
To prevent against replay attacks, clients need to distinguish
different writes of the same block in a file. A simple
idea [26] is to use a counter per file block that denotes
the number of writes of that block, and make the counter part of the
encryption tweak. The block write counters need to be authenticated
in the trusted storage space for the file
 to prevent clients
from accepting valid older versions of a block that are considered
not random by the randomness test. To ensure that file blocks are
encrypted with different tweaks, we define the tweak for a file
block to be a function of the file, the block index and the block
write counter. We denote by
to prevent clients
from accepting valid older versions of a block that are considered
not random by the randomness test. To ensure that file blocks are
encrypted with different tweaks, we define the tweak for a file
block to be a function of the file, the block index and the block
write counter. We denote by
 the tweak-generating
function for file takes as input a block index and a
block counter and outputs the tweak for that file block. The
properties of tweakable ciphers imply that if a block is decrypted
with a different counter (and so a different tweak), then it will
look random with high probability. the tweak-generating
function for file takes as input a block index and a
block counter and outputs the tweak for that file block. The
properties of tweakable ciphers imply that if a block is decrypted
with a different counter (and so a different tweak), then it will
look random with high probability.
The algorithm Init selects a key at random from the key space of
the tweakable encryption scheme E. The Update, Check, Append and Delete
algorithms of RAND-EINT are detailed in
Figure 3. For the array RArrF,
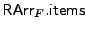 denotes the number of items in the array,
denotes the number of items in the array,
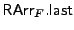 denotes
the last element in the array, and the function denotes
the last element in the array, and the function
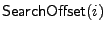 for
the array RArrF gives the position in the array where index
i is stored (if it exists in the array). for
the array RArrF gives the position in the array where index
i is stored (if it exists in the array).
- In the
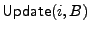 algorithm for file algorithm for file
 ,
the write counter for block i is incremented and the counter authentication
information from TSF is updated with the algorithm AuthCtr.
Then, the randomness test IsRand applied to block content B.
If B is not random looking, then the leaf corresponding to block i (
if it exists) has to be removed from RTreeF. This is done with the
algorithm ,
the write counter for block i is incremented and the counter authentication
information from TSF is updated with the algorithm AuthCtr.
Then, the randomness test IsRand applied to block content B.
If B is not random looking, then the leaf corresponding to block i (
if it exists) has to be removed from RTreeF. This is done with the
algorithm
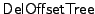 , described in Figure 4. On
the other hand, if B is random-looking, then the leaf
corresponding to block i has to be either updated with the new
hash (if it exists in the tree) or appended in RTreeF. Finally,
the tweakable encryption of B is stored in the i-th block of , described in Figure 4. On
the other hand, if B is random-looking, then the leaf
corresponding to block i has to be either updated with the new
hash (if it exists in the tree) or appended in RTreeF. Finally,
the tweakable encryption of B is stored in the i-th block of
 . .
- To append a new block B to file
 with n blocks using
the
with n blocks using
the
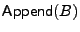 algorithm, the counter for block n+1 is updated
first with algorithm UpdateCtr. The counter authentication
information from trusted storage is also updated with algorithm
AuthCtr. Furthermore, the hash of the block index concatenated with
the block content is added to RTreeF only if the block is
random-looking. In addition, index n+1 is added to RArrF in
this case. Finally, the tweakable encryption of B is stored in
the n+1-th block of algorithm, the counter for block n+1 is updated
first with algorithm UpdateCtr. The counter authentication
information from trusted storage is also updated with algorithm
AuthCtr. Furthermore, the hash of the block index concatenated with
the block content is added to RTreeF only if the block is
random-looking. In addition, index n+1 is added to RArrF in
this case. Finally, the tweakable encryption of B is stored in
the n+1-th block of
 . .
- In the
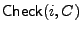 algorithm for file algorithm for file
 ,
the authentication information for the block counters is checked first.
Then block C is decrypted, and checked for integrity. If the
content of the i-th block is not random-looking, then by the
properties of tweakable ciphers we can infer that the block is valid
with high probability. Otherwise, the integrity of the B-th block
is checked using the tree RTreeF. If B is not a block index in
the tree, then the integrity of block B is unconfirmed and the
block is rejected. ,
the authentication information for the block counters is checked first.
Then block C is decrypted, and checked for integrity. If the
content of the i-th block is not random-looking, then by the
properties of tweakable ciphers we can infer that the block is valid
with high probability. Otherwise, the integrity of the B-th block
is checked using the tree RTreeF. If B is not a block index in
the tree, then the integrity of block B is unconfirmed and the
block is rejected.
- In the Delete algorithm for file
 ,
the hash of the last
block has to be removed from the tree by calling the algorithm DelOffsetTree
(described in Figure 4), in the case
in which the last block is authenticated through RTreeF. ,
the hash of the last
block has to be removed from the tree by calling the algorithm DelOffsetTree
(described in Figure 4), in the case
in which the last block is authenticated through RTreeF.
It is not necessary to authenticate in trusted storage the array
RArrF of indices of the random-looking blocks in a file. The
reason is that the root of RTreeF is authenticated in trusted
storage and this implies that an adversary cannot modify the order
of the leaves in RTreeF without being detected in the
AppendTree, UpdateTree or CheckTree algorithms.
The construction RAND-EINT protects against unauthorized
modification of data written to disk and block swapping attacks by
authenticating the root of RTreeF in the trusted storage space
for each file. By using write counters in the encryption of block
contents and authenticating the values of the counters in trusted
storage, this construction provides defense against replay attacks
and provides all the security properties of the MT-EINT construction.
Figure 3:
The Update, Check, Append and Delete algorithms for
the RAND-EINT construction.
 |
Figure 4:
The DelOffsetTree algorithm for a tree T deletes the
hash of block i from T and moves the last leaf to its
position, if necessary.
 |
This construction is again based on the intuition that many
workloads feature redundancy in file contents. In this construction,
the block is compressed before encryption. If the compression level
of the block content is high enough, then a message authentication
code (i.e., MAC) of the block can be stored in the block itself,
reducing the amount of storage necessary for integrity. The
authentication information for blocks that can be compressed is
stored on untrusted storage, and consequently a MAC is required.
Like in the previous construction, a Merkle tree RTreeF is built
over the hashes of the blocks in file  that cannot be
compressed enough, and the root of the tree is kept in trusted
storage. In order to prevent replay attacks, it is necessary that
block write counters are included either in the computation of the
block MAC (in the case in which the block can be compressed) or in
hashing the block (in the case in which the block cannot be
compressed enough). Similarly to scheme RAND-EINT, the write
counters for a file that cannot be
compressed enough, and the root of the tree is kept in trusted
storage. In order to prevent replay attacks, it is necessary that
block write counters are included either in the computation of the
block MAC (in the case in which the block can be compressed) or in
hashing the block (in the case in which the block cannot be
compressed enough). Similarly to scheme RAND-EINT, the write
counters for a file  need to be authenticated in the trusted
storage space TSF. need to be authenticated in the trusted
storage space TSF.
In this construction, file blocks can be encrypted with any
length-preserving encryption scheme, as defined in
Section 4.2. In describing the scheme, we need
compression and decompression algorithms such that
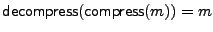 , for any message m. We can also
pad messages up to a certain fixed length by using the with an output of , for any message m. We can also
pad messages up to a certain fixed length by using the with an output of 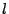 bytes, and unpad a padded message
with the such that bytes, and unpad a padded message
with the such that
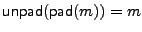 , for all
messages m of length less than , for all
messages m of length less than 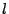 bytes. We can use standard
padding methods for implementing these algorithms [4]. To
authenticate blocks that can be compressed, we use a message
authentication code bytes. We can use standard
padding methods for implementing these algorithms [4]. To
authenticate blocks that can be compressed, we use a message
authentication code
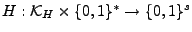 that outputs strings of length s bits. that outputs strings of length s bits.
The algorithm Init runs the key generation algorithm Glen of
the length-preserving stateful encryption scheme for file
 to generate key
to generate key 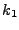 and selects at random a key and selects at random a key 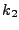 from the key
space KH of H. It outputs the tuple from the key
space KH of H. It outputs the tuple
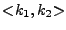 . The Update, Check, Append and Delete algorithms of
the COMP-EINT construction are detailed in Figure 5.
Here Lc is the byte length of the largest plaintext size for
which the ciphertext is of length at most the file block length less
the size of a MAC function output. For example, if the block size is
4096 bytes, HMAC [3] with SHA-1 is used for computing
MACs (whose output is 20 bytes) and 16-byte AES is used for
encryption, then Lc is the largest multiple of the AES block
size (i.e., 16 bytes) less than 4096-20=4076 bytes. The value of
Lc in this case is 4064 bytes. . The Update, Check, Append and Delete algorithms of
the COMP-EINT construction are detailed in Figure 5.
Here Lc is the byte length of the largest plaintext size for
which the ciphertext is of length at most the file block length less
the size of a MAC function output. For example, if the block size is
4096 bytes, HMAC [3] with SHA-1 is used for computing
MACs (whose output is 20 bytes) and 16-byte AES is used for
encryption, then Lc is the largest multiple of the AES block
size (i.e., 16 bytes) less than 4096-20=4076 bytes. The value of
Lc in this case is 4064 bytes.
- In the
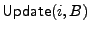 algorithm for file algorithm for file
 ,
the write counter for block i is incremented and the counter authentication
information from TSF is updated with the algorithm AuthCtr. Then
block content B is compressed to ,
the write counter for block i is incremented and the counter authentication
information from TSF is updated with the algorithm AuthCtr. Then
block content B is compressed to 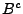 . If the length of . If the length of
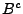 (denoted (denoted 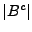 ) is at most Lc, then there is room
to store the MAC of the block content inside the block. In this
case, the hash of the previous block content stored at the same
address is deleted from the Merkle tree RTreeF, if necessary. The
compressed block is padded and encrypted, and then stored with its
MAC in the i-th block of ) is at most Lc, then there is room
to store the MAC of the block content inside the block. In this
case, the hash of the previous block content stored at the same
address is deleted from the Merkle tree RTreeF, if necessary. The
compressed block is padded and encrypted, and then stored with its
MAC in the i-th block of
 .
Otherwise, if the block cannot be
compressed enough, then its hash has to be inserted into the Merkle
tree RTreeF. The block content B is then encrypted with a
length-preserving stateful encryption scheme using the key for the
file and is stored in the i-th block of .
Otherwise, if the block cannot be
compressed enough, then its hash has to be inserted into the Merkle
tree RTreeF. The block content B is then encrypted with a
length-preserving stateful encryption scheme using the key for the
file and is stored in the i-th block of
 . .
- To append a new block B to file
 with n blocks using
the
with n blocks using
the
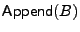 algorithm, the counter for block n+1 is updated
first with algorithm UpdateCtr. The counter authentication
information from trusted storage is also updated with algorithm
AuthCtr. Block B is then compressed. If it has an adequate
compression level, then the compressed block is padded and
encrypted, and a MAC is concatenated at the end of the new block.
Otherwise, a new hash is appended to the Merkle tree RTreeF and
an encryption of B is stored in the n+1-th block of algorithm, the counter for block n+1 is updated
first with algorithm UpdateCtr. The counter authentication
information from trusted storage is also updated with algorithm
AuthCtr. Block B is then compressed. If it has an adequate
compression level, then the compressed block is padded and
encrypted, and a MAC is concatenated at the end of the new block.
Otherwise, a new hash is appended to the Merkle tree RTreeF and
an encryption of B is stored in the n+1-th block of
 . .
- In the
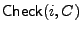 algorithm for file algorithm for file
 ,
the authentication information from TSF for the block counters is
checked first. There are two cases to consider. First, if the i-th
block of ,
the authentication information from TSF for the block counters is
checked first. There are two cases to consider. First, if the i-th
block of
 is authenticated through the Merkle tree RTreeF,
as indicated by RArrF, then the block is decrypted and algorithm
CheckTree is called. Otherwise, the MAC of the block content is
stored at the end of the block and we can thus parse the i-th
block of
is authenticated through the Merkle tree RTreeF,
as indicated by RArrF, then the block is decrypted and algorithm
CheckTree is called. Otherwise, the MAC of the block content is
stored at the end of the block and we can thus parse the i-th
block of
 as
as
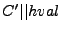 . . 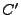 has to be decrypted,
unpadded and decompressed, in order to obtain the original block
content has to be decrypted,
unpadded and decompressed, in order to obtain the original block
content 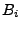 . The value . The value 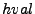 stored in the block is checked to
match the MAC of the block index i concatenated with the write
counter for block i and block content stored in the block is checked to
match the MAC of the block index i concatenated with the write
counter for block i and block content 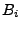 . .
- In the Delete algorithm for file
 ,
the hash of the last
block has to be removed from the tree by calling the algorithm DelOffsetTree
described in Figure 4), in the case
in which the last block is authenticated through RTreeF. ,
the hash of the last
block has to be removed from the tree by calling the algorithm DelOffsetTree
described in Figure 4), in the case
in which the last block is authenticated through RTreeF.
The construction against replay attacks by using
write counters for either computing a MAC over the contents of
blocks that can be compressed enough, or a hash over the contents of
blocks that cannot be compressed enough, and authenticating the
write counters in trusted storage. It meets all the security
properties of and RAND-EINT.
Figure 5:
The Update, Check, Append and Delete algorithms for
the COMP-EINT construction.
 |
6 Implementation
Our integrity algorithms are very general and they can be integrated
into any cryptographic file system in either the kernel or user
space. For the purpose of evaluating and comparing their
performance, we implemented them in EncFS [14], an
open-source user-level file system that transparently encrypts file
blocks. EncFS uses the FUSE [12] library to provide the file
system interface. FUSE provides a simple library API for
implementing file systems and it has been integrated into recent
versions of the Linux kernel.
In EncFS, files are divided into fixed-size blocks and each block is
encrypted individually. Several ciphers such as AES and Blowfish in
CBC mode are available for block encryption. We implemented in EncFS
the three constructions that provide integrity: , RAND-EINT and COMP-EINT.
While any length-preserving encryption scheme can be used in the and COMP-EINT constructions,
RAND-EINT is constrained to use a tweakable cipher for encrypting file blocks. We
choose to encrypt file blocks in MT-EINT and COMP-EINT with the
length-preserving stateful encryption derived from the AES cipher in
CBC mode (as shown in Section 4.2), and use the CMC
tweakable cipher [15] as the encryption method in RAND-EINT .
In our integrity algorithms, we use the SHA-1 hash function and the
message-authentication code HMAC instantiated also with the SHA-1
hash function. For compressing and decompressing blocks in use the zlib library.
Our prototype architecture is depicted in Figure 6. We
modified the user space of EncFS to include the CMC cipher for block
encryption and the new integrity algorithms. The server uses the
underlying file system (i.e., reiserfs) for the storage of the
encrypted files. The Merkle trees for integrity RTreeF and the
index arrays of the random-looking blocks RArrF are stored with
the encrypted files in the untrusted storage space on the server.
For faster integrity checking (in particular to improve the running
time of the SearchOffset algorithm used in the Update and Check algorithms of the
RAND-EINT and COMP-EINT constructions), we also
keep the array RArrF for each file, ordered by indices. The roots
of the trees RTreeF, and the arrays IntStartF and CtrValF
or their hashes (if they are too large) are stored in a trusted storage
space. In our current implementation, we use two extended attributes
for each file  , one for the root of RTreeF and the second for
the arrays IntStartF and CtrValF or their hashes. , one for the root of RTreeF and the second for
the arrays IntStartF and CtrValF or their hashes.
By default, EncFS caches the last block content written to or read
from the disk. In our implementation, we cached the last arrays
RArrF, IntStartF and CtrValF in a block update or check
operation. Since these arrays are typically small (a few hundred
bytes), they easily fit into memory. We also evaluate the effect of
caching of Merkle trees in our system in Section 7.1.
Figure 6:
Prototype architecture.
 |
7 Performance Evaluation
In this section, we evaluate the performance of the new randomness
test and compression integrity constructions for encrypted storage
compared to that of Merkle trees. We ran our experiments on a 2.8
GHz Intel D processor machine with 1GB of RAM, running SuSE Linux
9.3 with kernel version 2.6.11. The hard disk used was an 80GB SATA
7200 RPM Maxtor.
The main challenge we faced in evaluating the proposed constructions
was to come up with representative file system workloads. While the
performance of the Merkle tree construction is predictable
independently of the workload, the performance of the new integrity
algorithms is highly dependent on the file contents accessed, in
particular on the randomness of block contents. To our knowledge,
there are no public traces that contain file access patterns, as
well as the contents of the file blocks read and written. Due to the
privacy implications of releasing actual users' data, we expect it
to be nearly impossible to get such traces from a widely used
system. However, we have access to three public NFS Harvard
traces [9] that contain NFS traffic from several of
Harvard's campus servers. The traces were collected at the level of
individual NFS operations and for each read and write operation they
contain information about the file identifier, the accessed offset
in the file and the size of the request (but not the actual file
contents).
To evaluate the integrity algorithms proposed in this paper, we
perform two sets of experiments. In the first one, we strive to
demonstrate how the performance of the new constructions varies for
different file contents. For that, we use representative files from
a Linux distribution installed on one of our desktop machines,
together with other files from the user's home directory, divided
into several file types. We identify five file types of interest:
text, object, executables, images, and compressed files, and build a
set of files for each class of interest. All files of a particular
type are first encrypted and the integrity information for them is
built; then they are decrypted and checked for integrity. We report
the performance results for the files with the majority of blocks
not random-looking (i.e., text, executable and object) and for those
with mostly random-looking blocks (i.e., image and compressed). In
this experiment, all files are written and read sequentially, and as
such the access pattern is not a realistic one.
In the second set of experiments, we evaluate the effect of more
realistic access patterns on the performance of the integrity
schemes, using the NFS Harvard traces. As the Harvard traces do not
contain information about actual file block contents written to the
disks, we generate synthetic block contents for each block write
request. We define two types of block contents: low-entropy and
high-entropy, and perform experiments assuming that either all
blocks are low-entropy or all are high-entropy. These extreme
workloads represent the ``best'' and ``worst''-case for the new
algorithms, respectively. We also consider a ``middle''-case, in
which a block is random-looking with a 50% probability, and plot
the performance results of the new schemes relative to the Merkle
tree integrity algorithm for the best, middle and worst cases.
7.1 The Impact of File Block Contents on Integrity Performance
We consider a snapshot of the file system from one of our desktop
machines. We gathered files that belong to five classes of interest:
(1) text files are files with extensions .txt, .tex, .c, .h,
.cpp, .java, .ps, .pdf; (2) object files are system library
files from the directory /usr/local/lib; (3) executable files
are system executable files from directory /usr/local/bin; (4)
image files are JPEG files and (5) compressed files
are gzipped tar archives. Several characteristics of each set,
including the total size, the number of files in each set, the
minimum, average and maximum file sizes and the fraction of file
blocks that are considered random-looking by the entropy test are
given in Table 2.
Table 2:
File set characteristics.
| |
Total size |
No. files |
Min. file size |
Max. file
size |
Avg. file size |
Fraction of random-looking blocks |
|
|
Text |
245 MB |
808 |
27 bytes |
34.94 MB |
307.11 KB |
0.0351 |
|
| Objects |
217 MB |
28 |
15 bytes |
92.66 MB |
7.71 MB |
0.0001 |
|
| Executables |
341 MB |
3029 |
24 bytes |
13.21 MB |
112.84 KB |
0.0009 |
|
| Image |
189 MB |
641 |
17 bytes |
2.24 MB |
198.4 KB |
0.502 |
|
| Compressed |
249 MB |
2 |
80.44 MB |
167.65 MB |
124.05 MB |
0.7812 |
|
|
We consider three cryptographic file systems: (1)
MT-EINT with CBC-AES for encrypting file blocks; (2)RAND-EINT with CMC
encryption; (3)COMP-EINT with CBC-AES encryption. For each
cryptographic file system, we first write the files from each set;
this has the effect of automatically encrypting the files, and
running the Update algorithm of the integrity method for each file
block. Second, we read all files from each set; this has the effect
of automatically decrypting the files, and running the Check algorithm
of the integrity method for each file block. We use file blocks of size 4KB in the experiments.
We first present a micro-benchmark evaluation for the text and compressed
file sets in Figure 7. We plot the total time to
write and read the set of text and compressed files, respectively.
The write time for a set of files includes the time to encrypt all
the files in the set, create new files, write the encrypted contents
in the new files and build the integrity information for each file
block with algorithms Update and Append. The read time for a set
of files includes the time to retrieve the encrypted files from
disk, decrypt each file from the set and check the integrity of each
file block with algorithm Check. We separate the total time
incurred by the write and read experiments into the following
components: encryption/decryption time (either AES or CMC); hashing
time that includes the computation of both SHA-1 and HMAC;
randomness check time (either the entropy test for RAND-EINT or
compression/decompression time for COMP-EINT); Merkle tree operations
(e.g., given a leaf index, find its index in inorder traversal or
given an inorder index of a node in the tree, find the inorder index
of its sibling and parent); the time to update and check the root of
the tree (the root of the Merkle tree is stored as an extended
attribute for the file) and disk waiting time.
Figure 7:
Micro-benchmarks for text and compressed files.
 |
The results show that the cost of CMC encryption and decryption is
about 2.5 times higher than that of AES encryption and decryption in
CBC mode. Decompression is between 4 and 6 times faster than
compression and this accounts for the good read performance of
COMP-EINT.
A substantial amount of the MT-EINT overhead is due to disk
waiting time (for instance, 39% at read for text files) and the
time to update and check the root of the Merkle tree (for instance,
30% at write for compressed files). In contrast, due to smaller
sizes of the Merkle trees in the RAND-EINT and COMP-EINT file
systems, the disk waiting time and the time to update and check the
root of the tree for text files are smaller. The results suggests
that caching of the hash values stored in Merkle trees in the file
system might reduce the disk waiting time and the time to update the
root of the tree and improve the performance of all three integrity
constructions, and specifically that of the MT-EINT algorithm.
We present our results on caching next.
We implemented a global cache that
stores the latest hashes read from Merkle trees used to either
update or check the integrity of file blocks. As an optimization,
when we verify the integrity of a file block, we compute all the
hashes on the path from the node up to the root of the tree until we
reach a node that is already in the cache and whose integrity has
been validated. We store in the cache only nodes that have been
verified and that are authentic. When a node in the cache is
written, all its ancestors on the path from the node to the root,
including the node itself, are evicted from the cache.
We plot the total file write and read time in seconds for the three
cryptographic file systems as a function of different cache sizes.
We also plot the average integrity bandwidth per block in a log-log
scale. Finally, we plot the cumulative size of the untrusted storage for
all files from each set. We show the combined graphs for
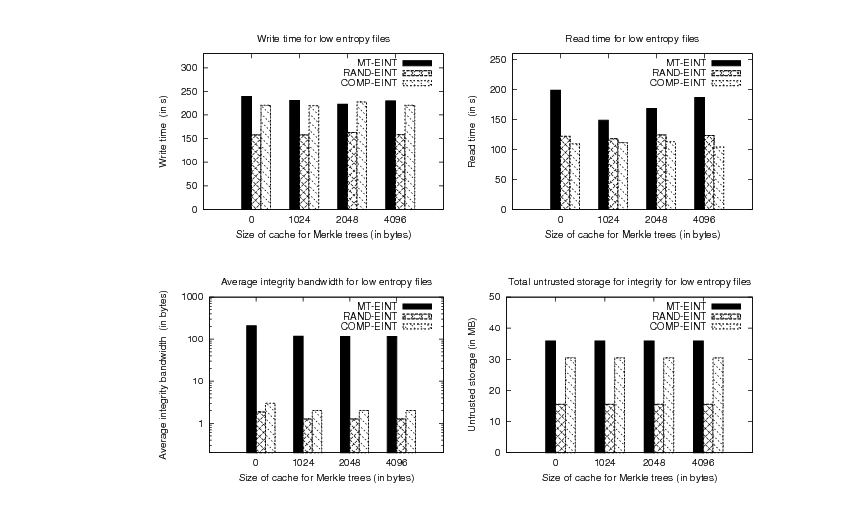
low-entropy files (text, object and executable files) in
Figure 8 and for high-entropy files (compressed and
image files) in Figure 9.
The results show that MT-EINT benefits mostly on reads by
implementing a cache of size 1KB, while the write time is not
affected greatly by using a cache. The improvements for MT-EINT using a cache of
1KB are as much as 25.22% for low-entropy files and 20.34% for high-entropy files in the read experiment. In the
following, we compare the performance of the three constructions for
the case in which a 1KB cache is used.
For sets of files with a low percent of random-looking blocks (text,
object and executable files), RAND-EINT outperforms MT-EINT with
respect to all the metrics considered. The performance of RAND-EINT compared to that of
MT-EINT is improved by 31.77% for writes
and 20.63% for reads. The performance of the COMP-EINT file system
is very different in the write and read experiments due to the cost
difference of compression and decompression. The write time of COMP-EINT
is within 4% of the write time of MT-EINT and in the
read experiment COMP-EINT outperforms MT-EINT by 25.27%. The
integrity bandwidth of RAND-EINT and COMP-EINT is 92.93 and 58.25
times, respectively, lower than that of MT-EINT . The untrusted
storage for integrity for RAND-EINT and COMP-EINT is reduced 2.3 and
1.17 times, respectively, compared to MT-EINT.
Figure 8:
Evaluation for low-entropy files (text, object and executable files).
 |
For sets of files with a high percent of random-looking blocks
(image and compressed files), RAND-EINT adds a maximum performance
overhead of 4.43% for writes and 18.15% for reads compared to MT-EINT for
a 1KB cache. COMP-EINT adds a write performance
overhead of 38.39% compared to MT-EINT, and performs within 1%
of MT-EINT in the read experiment. The average integrity
bandwidth needed by RAND-EINT and COMP-EINT is lower by 30.15% and
10.22%, respectively, than that used by MT-EINT. The untrusted
storage for integrity used by RAND-EINT is improved by 9.52%
compared to MT-EINT and that of COMP-EINT is within 1% of the
storage used by MT-EINT. The reason that the average integrity
bandwidth and untrusted storage for integrity are still reduced in
RAND-EINT compared to MT-EINT is that in the set of high-entropy
files considered only about 70% of the blocks have high entropy. We
would expect that for files with 100% high-entropy blocks, these
two metrics will exhibit a small overhead with both RAND-EINT and COMP-EINT
compared to MT-EINT (this is actually confirmed in the
experiments from the next section). However, such workloads with
100% high entropy files are very unlikely to occur in practice.
Figure 9:
Evaluation for high-entropy files (image and compressed files).
 |
7.2 The Impact of File Access Patterns on Integrity Performance
We considered a subset of the three NFS Harvard traces [9]
(LAIR, DEASNA and HOME02), each collected during one day. We show
several characteristics of each trace, including the number of files
and the total number of block write and read operations, in
Table 3. The block size in these traces is 4096
bytes and we have implemented a 1KB cache for Merkle trees.
Table 3:
NFS Harvard trace characteristics.
| |
Number of files |
Number of writes |
Number of reads |
|
|
|
LAIR |
7017 |
66331 |
23281 |
|
|
| DEASNA |
890 |
64091 |
521 |
|
|
| HOME02 |
183 |
89425 |
11815 |
|
|
|
We replayed each of the three traces with
three types of block contents: all low-entropy, all high-entropy and
50% high-entropy. For each experiment, we measured the total
running time, the average integrity bandwidth and the total
untrusted storage for integrity for RAND-EINT and COMP-EINT relative
to MT-EINT and plot the results in Figure 10. We
represent the performance of MT-EINT as the horizontal axis in
these graphs and the performance of RAND-EINT and COMP-EINT
relative to MT-EINT. The points above the horizontal axis are overheads
compared to MT-EINT, and the points below the horizontal axis
represent improvements relative to MT-EINT. The labels on the
graphs denote the percent of random-looking blocks synthetically
generated.
Figure 10:
Running time, average integrity bandwidth and storage for
integrity of RAND-EINT and COMP-EINT relative to MT-EINT. Labels
on the graphs represent percentage of random-looking blocks.
 |
 |
The performance improvements of RAND-EINT and COMP-EINT
compared to MT-EINT are as high as 56.21% and 56.85%, respectively, for
the HOME02 trace for low-entropy blocks. On the other hand, the
performance overhead for high-entropy blocks are at most 54.14% for
RAND-EINT (in the LAIR trace) and 61.48% for COMP-EINT (in the
DEASNA trace). RAND-EINT performs better than COMP-EINT when the
ratio of read to write operations is small, as is the case for the
DEASNA and HOME02 trace. As this ratio increases, COMP-EINT outperforms RAND-EINT.
For low-entropy files, both the average integrity bandwidth and the
untrusted storage for integrity for both RAND-EINT and COMP-EINT
are greatly reduced compared to MT-EINT. For instance, in the DEASNA
trace, MT-EINT needs 215 bytes on average to update or check the
integrity of a block, whereas RAND-EINT and COMP-EINT only require on
average 0.4 bytes. The amount of additional untrusted storage for
integrity in the DEASNA trace is 2.56 MB for MT-EINT and only 7
KB for RAND-EINT and COMP-EINT. The maximum overhead added by both
RAND-EINT and COMP-EINT compared to MT-EINT for high-entropy
blocks is 30.76% for the average integrity bandwidth (in the HOME02
trace) and 19.14% for the amount of untrusted storage for integrity
(in the DEASNA trace).
7.3 Discussion
From the evaluation of the three constructions, it follows that none
of the schemes is a clear winner over the others with respect to all
the four metrics considered. Since the performance of both RAND-EINT
and COMP-EINT is greatly affected by file block contents, it would
be beneficial to know the percentage of high-entropy blocks in
practical filesystem workloads. To determine statistics on file
contents, we have performed a user study on several machines from
our department running Linux. For each user machine, we have
measured the percent of high-entropy blocks and the percent of
blocks that cannot be compressed enough from users' home
directories. The results show that on average, 28% percent of file
blocks have high entropy and 32% percent of file blocks cannot be
compressed enough to fit a MAC inside.
The implications of our study are that, for cryptographic file
systems that store files similar to those in users' home
directories, the new integrity algorithms improve upon Merkle trees
with respect to all four metrics of interest. In particular,
COMP-EINT is the best option for primarily read-only workloads when
minimizing read latency is a priority, and RAND-EINT is the best
choice for most other workloads. On the other hand, for an
application in which the large majority of files have high-entropy
(e.g., a file sharing application in which users transfer mostly
audio and video files), the standard MT-EINT still remains the
best option for integrity. We recommend that all three constructions
be implemented in a cryptographic file system. An application can
choose the best scheme based on its typical workload.
The new algorithms that we propose can be applied in other settings
in which authentication of data stored on untrusted storage is
desired. One example is checking the integrity of arbitrarily-large
memory in a secure processor using only a constant amount of trusted
storage [5,7]. In this setting, a trusted checker
maintains a constant amount of trusted storage and, possibly, a
cache of data blocks most recently read from the main memory. The
goal is for the checker to verify the integrity of the untrusted
memory using a small bandwidth overhead.
The algorithms described in this paper can be used only in
applications where the data that needs to be authenticated is
encrypted. However, the COMP-EINT algorithm can be easily
modified to fit into a setting in which data is only authenticated
and not encrypted, and can thus replace Merkle trees in such
applications. On the other hand, the RAND-EINT integrity algorithm
is only suitable in a setting in which data is encrypted with a
tweakable cipher, as the integrity guarantees of this algorithm are
based on the security properties of such ciphers.
8 Related Work
Cryptographic file systems extend traditional file systems with
support for security in untrusted storage environments. Most
cryptographic file systems provide to their clients mechanisms for
encrypting data and checking data integrity. The cryptographic
operations are performed on the client side, as both the storage
devices and the network are untrusted.
We have focused on Merkle trees as our point of comparison, though
there are other integrity protections used on various cryptographic
file systems that we have elided due to their greater expense in
various measures. For example, a common integrity method used in
cryptographic file systems such as TCFS [6] and
SNAD [25] is to store a hash or message authentication code
for each file block for authenticity. However, these approaches
employ trusted storage linear in the number of blocks in the file
(either the hashes or a counter per block). In systems such as
SFS [22], SFSRO [11], Cepheus [10],
FARSITE [1], Plutus [17], SUNDR [20] and
IBM StorageTank [23,27], a Merkle tree per file is built
and the root of the tree is authenticated (by either digitally
signing it or storing it in a trusted meta-data server). In
SiRiUS [13], each file is digitally signed for
authenticity, and so in addition the integrity bandwidth to update
or check a block in a file is linear in the file size.
Tripwire [19] is a user-level tool that computes a hash per
file and stores it in trusted storage. While this approach achieves
constant trusted storage for integrity per file, the integrity
bandwidth is linear in the number of blocks in the file. For
journaling file systems, an elegant solution for integrity called
hash logging is provided by PFS [32]. The hashes of
file blocks together with the file system metadata are stored in the
file system log, a protected memory area. However, in this solution
the amount of trusted storage for integrity for a file is linear in
the number of blocks in the file.
Pletka and Cachin [27] describes a security
architecture for the distributed IBM StorageTank file system (also
denoted the SAN.FS file system) [23]. SAN.FS achieves its
scalability to many clients by separating the meta-data operations
from the data path. As such, the meta-data is stored on trusted
meta-data servers, while the data is stored on the storage devices
from a SAN. SAN.FS uses AES in CBC mode for confidentiality and
Merkle trees (with degree 16) for integrity protection of files. The
roots of the Merkle trees are stored together with the file system
meta-data on the meta-data servers. We believe that our techniques
could be used to good effect in this system, as well.
Riedel et al. [28] provides a framework for extensively
evaluating the security of storage systems. Wright et
al. [33] evaluates the performance of five cryptographic
file systems, focusing on the overhead of encryption. Two other
recent surveys about securing storage systems are by Sivathanu et
al. [31] and Kher and Kimand [18].
Another area related to our work is that of checking the
integrity of arbitrarily large untrusted memory using only a small,
constant-size trusted memory. A first solution to this
problem [5] is to check the integrity of each memory
operation using a Merkle tree. This results in a logarithmic
bandwidth overhead in the total number of memory blocks. Recent
solutions try to reduce the logarithmic bandwidth to almost a
constant value. The main idea by Clarke et al. [7] is to
verify the integrity of the memory only when a critical
operation is encountered. The integrity of sequences of operations
between critical operations is checked by aggregating these
operations in a log using incremental hash functions [].
In contrast, in our model we need to be able to check the integrity
of each file block read from the storage servers.
We have proposed two new integrity constructions, RAND-EINT and
COMP-EINT, that authenticate file blocks in a cryptographic file
system using only a constant amount of trusted storage per file. Our
constructions exploit the typical low entropy of block contents and
sequentiality of file block writes to reduce the additional costs of
integrity protection. We have evaluated the performance of the new
constructions relative to the widely used Merkle tree algorithm,
using files from a standard Linux distribution and NFS traces
collected at Harvard university. Our experimental evaluation
demonstrates that the performance of the new algorithms is greatly
affected by file block contents and file access patterns. For
workloads with majority low-entropy file blocks, the new algorithms
improve upon Merkle trees with respect to all the four metrics
considered.
-
- 1
-
A. Adya, W. J. Bolosky, M. Castro, G. Cermak, R. Chaiken, J. R. Douceur,
J. Howell, J. R. Lorch, M. Theimer, and R. P. Wattenhofer.
FARSITE: Federated, available, and reliable storage for an
incompletely trusted environment.
In Proc.th Symposium on Operating System Design and
Implementation (OSDI). Usenix, 2002.
- 2
-
Advanced encryption standard.
Federal Information Processing Standards Publication 197, U.S.
Department of Commerce/National Institute of Standards and Technology,
National Technical Information Service, Springfield, Virginia, Nov. 2001.
- 3
-
M. Bellare, R. Canetti, and H. Krawczyk.
Keying hash functions for message authentication.
In Proc. Crypto 1996, volume 1109 of Lecture Notes in
Computer Science, pages 1-15. Springer-Verlag, 1996.
- 4
-
J. Black and H. Urtubia.
Side-channel attacks on symmetric encryption schemes: The case for
authenticated encryption.
In Proc.1th USENIX Security Symposium, pages 327-338, 2002.
- 5
-
M. Blum, W. S. Evans, P. Gemmell, S. Kannan, and M. Naor.
Checking the correctness of memories.
Algorithmica, 12:225-244, 1994.
- 6
-
G. Cattaneo, L. Catuogno, A. D. Sorbo, and P. Persiano.
The design and implementation of a transparent cryptographic file
system for Unix.
In Proc. USENIX Annual Technical Conference 2001, Freenix
Track, pages 199-212, 2001.
- 7
-
D. E. Clarke, G. E. Suh, B. Gassend, A. Sudan, M. van Dijk, and S. Devadas.
Towards constant bandwidth overhead integrity checking of untrusted
data.
In Proc.6th IEEE Symposium on Security and Privacy, pages
139-153, 2005.
- 8
-
DES modes of operation.
Federal Information Processing Standards Publication 81, U.S.
Department of Commerce/National Bureau of Standards, National Technical
Information Service, Springfield, Virginia, 1980.
- 9
-
D. Ellard, J. Ledlie, P. Malkani, and M. Seltzer.
Passive NFS tracing of email and research workloads.
In Proc. Second USENIX Conference on File and Storage
Technologies (FAST), pages 203-216, 2003.
- 10
-
K. Fu.
Group sharing and random access in cryptographic storage file
systems.
Master's thesis, Massachusetts Institute of Technology, 1999.
- 11
-
K. Fu, F. Kaashoek, and D. Mazieres.
Fast and secure distributed read-only file system.
ACM Transactions on Computer Systems, 20:1-24, 2002.
- 12
-
FUSE: filesystem in userspace.
https://fuse.sourceforge.net.
- 13
-
E. Goh, H. Shacham, N. Modadugu, and D. Boneh.
SiRiUS: Securing remote untrusted storage.
In Proc. Network and Distributed Systems Security (NDSS)
Symposium 2003, pages 131-145. ISOC, 2003.
- 14
-
V. Gough.
EncFS encrypted filesystem.
https://arg0.net/wiki/encfs, 2003.
- 15
-
S. Halevi and P. Rogaway.
A tweakable enciphering mode.
In Proc. Crypto 2003, volume 2729 of Lecture Notes in
Computer Science, pages 482-499. Springer-Verlag, 2003.
- 16
-
S. Halevi and P. Rogaway.
A parallelizable enciphering mode.
In Proc. The RSA conference - Cryptographer's track
(RSA-CT), volume 2964 of Lecture Notes in Computer Science, pages
292-304. Springer-Verlag, 2004.
- 17
-
M. Kallahalla, E. Riedel, R. Swaminathan, Q. Wang, and K. Fu.
Plutus: Scalable secure file sharing on untrusted storage.
In Proc. Second USENIX Conference on File and Storage
Technologies (FAST), 2003.
- 18
-
V. Kher and Y. Kim.
Securing distributed storage: Challenges, techniques, and systems.
In Proc. First ACM International Workshop on Storage Security
and Survivability (StorageSS 2005), 2005.
- 19
-
G. H. Kim and E. H. Spafford.
The design and implementation of Tripwire: A filesystem integrity
checker.
In Proc. Second ACM Conference on Computer and Communication
Security (CCS), pages 18-29, 1994.
- 20
-
J. Li, M. Krohn, D. Mazieres, and D. Shasha.
Secure untrusted data repository.
In Proc.th Symposium on Operating System Design and
Implementation (OSDI), pages 121-136. Usenix, 2004.
- 21
-
M. Liskov, R. Rivest, and D. Wagner.
Tweakable block ciphers.
In Proc. Crypto 2002, volume 2442 of Lecture Notes in
Computer Science, pages 31-46. Springer-Verlag, 2002.
- 22
-
D. Mazieres, M. Kaminsky, M. Kaashoek, and E. Witchel.
Separating key management from file system security.
In Proc.7th ACM Symposium on Operating Systems Principles
(SOSP), pages 124-139. ACM Press, 1999.
- 23
-
J. Menon, D. Pease, R. Rees, L. Duyanovich, and B. Hillsberg.
IBM Storage Tank - a heterogeneous scalable SAN file system.
IBM Systems Journal, 42(2), 2003.
- 24
-
R. Merkle.
A certified digital signature.
In Proc. Crypto 1989, volume 435 of Lecture Notes in
Computer Science, pages 218-238. Springer-Verlag, 1989.
- 25
-
E. Miller, D. Long, W. Freeman, and B. Reed.
Strong security for distributed file systems.
In Proc. the First USENIX Conference on File and Storage
Technologies (FAST), 2002.
- 26
-
A. Oprea, M. K. Reiter, and K. Yang.
Space-efficient block storage integrity.
In Proc. Network and Distributed System Security Symposium
(NDSS). ISOC, 2005.
- 27
-
R. Pletka and C. Cachin.
Cryptographic security for a high-performance distributed file
system.
Technical Report RZ 3661, IBM Research, Sept. 2006.
- 28
-
E. Riedel, M. Kallahalla, and R. Swaminathan.
A framework for evaluating storage system security.
In Proc. First USENIX Conference on File and Storage
Technologies (FAST), pages 15-30, 2002.
- 29
-
P. Rogaway and T. Shrimpton.
Cryptographic hash-function basics: Definitions, implications, and
separations for preimage resistance, second-preimage resistance, and
collision resistance.
In Proc.1th International Workshop on Fast Software
Encryption (FSE 2004), volume 3017 of Lecture Notes in Computer
Science, pages 371-388. Springer-Verlag, 2004.
- 30
-
Secure hash standard.
Federal Information Processing Standards Publication 180-1, U.S.
Department of Commerce/National Institute of Standards and Technology,
National Technical Information Service, Springfield, Virginia, Apr. 1995.
- 31
-
G. Sivathanu, C. Wright, and E. Zadok.
Ensuring data integrity in storage: Techniques and applications.
In Proc. ACM Workshop on Storage Security and Survivability,
2005.
- 32
-
C. A. Stein, J. Howard, and M. I. Seltzer.
Unifying file system protection.
In Proc. USENIX Annual Technical Conference, pages 79-90,
2001.
- 33
-
C. P. Wright, J. Dave, and E. Zadok.
Cryptographic file systems performance: What you don't know can hurt
you.
In Proc. Second Intl. IEEE Security in Storage Workhsop
(SISW), 2003.
Integrity Checking in Cryptographic File Systems
with Constant Trusted Storage
This document was generated using the
LaTeX2HTML translator Version 2002-2-1 (1.70)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 -show_section_numbers -local_icons inteval_final.tex
The translation was initiated by Florin Oprea on 2007-05-14
Footnotes
- ... Oprea1
- Computer Science Department, Carnegie Mellon
University, Pittsburgh, PA, USA; alina@cs.cmu.edu
- ... Reiter2
- Electrical & Computer Engineering
Department and Computer Science Department, Carnegie Mellon
University, Pittsburgh, PA, USA; reiter@cmu.edu



Florin Oprea
2007-05-14
|
