|
Security '04 Paper
[Security '04 Technical Program]


Fairplay -- A Secure Two-Party Computation System
Dahlia Malkhi , Noam Nisan , Noam Nisan , Benny Pinkas , Benny Pinkas , and Yaron Sella , and Yaron Sella
 The School of Computer Science and Engineering The School of Computer Science and Engineering
The Hebrew University of Jerusalem
E-mail: {noam,dalia,ysella}@cs.huji.ac.il
 HP Labs HP Labs
E-mail: benny.pinkas@hp.com
Abstract:
Advances in modern cryptography coupled with rapid growth in processing and
communication speeds make secure two-party computation a realistic paradigm.
Yet, thus far, interest in this paradigm has remained mostly theoretical.
This paper introduces Fairplay [28], a full-fledged system that implements
generic secure
function evaluation (SFE). Fairplay comprises a high level procedural
definition language called SFDL tailored to the SFE paradigm; a compiler of
SFDL into a one-pass Boolean circuit presented in a language called SHDL;
and Bob/Alice programs that evaluate the SHDL
circuit in the manner suggested by Yao in [39].
This system enables us to present the first evaluation of an overall SFE in
real settings, as well as examining its components and identifying potential
bottlenecks. It provides a test-bed of ideas and enhancements concerning SFE,
whether by replacing parts of it, or by integrating with it. We exemplify its
utility by examining several alternative implementations of oblivious
transfer within the system, and reporting on their effect on overall
performance.
1 Introduction
Modern cryptography is usually considered to have its beginning in the
landmark papers of Diffie and Hellman [16], who introduced the concept
of public key encryption, and of Rivest, Shamir and Adelman [35]
who suggested a concrete public key system. The fundamental theoretical studies
along these lines originate in the late 1970's, and the results - the well-known
cryptographic primitives of public key encryption, authentication and digital
signature - have been widely applied in practice during the 1990's.
However, theoretical cryptography provided additional,
powerful (and perhaps less intuitive) tools. One of the most
attractive paradigms
in this category is a secure function evaluation (SFE).
It allows two participants to implement a joint computation that, in real life,
may be implemented using a trusted party, but does this digitally without
any trusted party. A classic simple example of such a computation is
the Millionaires' problem [39]: Two millionaires want to know who is
richer, without any of them revealing to the other his net worth.
More generally, informally, the two-party SFE problem is the following.
Alice has an input
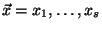 and Bob has an input and Bob has an input
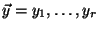 .
They both wish to learn .
They both wish to learn
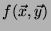 for some publicly known function for some publicly known function 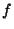 ,
without revealing any information on their inputs that cannot be inferred from ,
without revealing any information on their inputs that cannot be inferred from
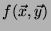 . (We refer the reader to, e.g. [20],
for a formal introduction to SFE.)
SFE is a universal building block, and many interesting cryptographic
protocols can be formulated as instances thereof, e.g., zero knowledge
proofs, private database mining, electronic auction and negotiation,
and voting protocols. . (We refer the reader to, e.g. [20],
for a formal introduction to SFE.)
SFE is a universal building block, and many interesting cryptographic
protocols can be formulated as instances thereof, e.g., zero knowledge
proofs, private database mining, electronic auction and negotiation,
and voting protocols.
Thus far,
SFE techniques are rarely applied in practice, and are
typically considered to have mostly theoretic significance.
In this paper, we suggest that it is prime time to start translating
these theoretical results into practical applications. We see three
main forces converging to make this transition possible:
1. New applications:
new applications are driven by advances in the communication infrastructure
(such as the ubiquity of the Internet or the emergence of web services),
coupled with increased demand for information based relationships (e.g.
for business or homeland security purposes). These applications often involve
sensitive information related to issues such as pricing, business processes,
or personal information, and their security often relies on trusting a
designated trusted party (such as eBay in the case of auctions).
Not all users feel completely confident giving this trust, especially when
high stakes are involved. SFE offers a solution for unmediated e-commerce
applications such as auctions and web services [32,17].
2. New cryptographic techniques: we have lately seen a growing
theoretical effort to overcome the main efficiency bottlenecks of
previous theoretical solutions. Such efforts include more efficient
cryptographic solutions for specific tasks such as auctions and certain
database access tasks (e.g. [31,13]), as well as
general theoretical results improving
on various efficiency parameters (e.g. [29,30,24]).
3. Improved CPU and communication speeds: while sending
megabytes of communication, or spending GigaFlops of processing power
would have seemed unreasonably expensive only a few years ago, such
effort is certainly acceptable now. It is not unreasonable to spend such
an effort even for tasks whose monetary value is a few dollars. Even
Gigabytes of communication, and TeraFlops of processing power are
reasonable for important tasks.
The goal of this work is to provide the first full fledged secure
two-party computation tool that is readily deployed by the community.
Fairplay provides the first solid answers to questions regarding the efficiency of the
overall computation, and its breakdown into parts. Thus, using this tool, we are
able to tell for the first time the overall price of solving a problem like
the above mentioned Millionaires' problem in real network settings
(the answer is 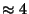 seconds over a wide area network,
see Section 6).
We further discern the cost of different components of the SFE,
and assess their relative effect on overall elapsed time.
Thus, for example, in Section 6 we analyze the relative
contribution of the public key operations performed as part of
the SFE protocol, and conclude that while 27%-77% of the time is
due to public key operations over a fast LAN, only 9%-42% is
accountable to public key operations over a wide area link. seconds over a wide area network,
see Section 6).
We further discern the cost of different components of the SFE,
and assess their relative effect on overall elapsed time.
Thus, for example, in Section 6 we analyze the relative
contribution of the public key operations performed as part of
the SFE protocol, and conclude that while 27%-77% of the time is
due to public key operations over a fast LAN, only 9%-42% is
accountable to public key operations over a wide area link.
Fairplay also serves as a test-bed of new ideas and algorithmic variations.
For demonstration, we already considered several flavors of oblivious
transfer (OT) algorithms within our tool. Specifically, we have implemented the
original scheme by Bellare and Micali from [6,7], the enhancements
suggested by
Naor and Pinkas in [30], and straight-forward communication batching.
Our experiments show a remarkable matching of the predicted 30% speedup of
the enhancement in [30] over [6]. The effect of communication
batching is observed to be up to nearly nine-fold speedup (see Section
6). Thus, our platform provides valuable guidance in trading
different parameters.
The first issue we tackle is the compilation paradigm.
The correct paradigm for addressing
the computation is to adopt the trusted party model for the definition of tasks,
and to compile these definitions into protocols that do not use any
trusted party.
In this way, the user specification is completely
oblivious to the actual protocol that implements it.
This is the common definition of secure computation used in
cryptography1(we refer the reader to cryptographic literature,
e.g. to [10,12,20], for an exact definition). Specifically, a definition
of a task using a trusted party involves the following elements:
- Exact specification of the interaction of the trusted party with
the participants. This includes specification of what the participants
tell and what they learn from the trusted party.
- Exact specification of the internal computations of the trusted
party.
In support of the user's high level view of the computation,
we provide our own high-level definition language called Secure Function
Definition Language (SFDL). SFDL is a procedural language that resembles
a subset of Pascal or C, and is tailored to our purpose. For convenience,
a syntax-driven GUI is provided that guides the program developer.
Once such a specification is given, a compiler
generates an intermediate level specification of the computation in the form of
a one-pass Boolean circuit. Whereas classical theory on SFE was
satisfied with the fact that it is provably possible to reduce any function to
a canonical Boolean representation,
we tackle for the first time actually automating the
transformation, while keeping efficiency in mind.
The language used for describing the Boolean circuit is named
Secure Hardware Definition Language (SHDL).
Developing an SFDL-to-SHDL compiler is a novel endeavor in itself,
because unlike common hardware compilers, our compiler may use no registers,
no loops or goto's, and moreover, may use every gate only once.
Its complete obliviousness makes compiling even the most primitive operations
like array indexing (e.g., ``a[i]'') a daunting task: it must create
essentially a multiplexer, such that all possible values of ``i'' are
hardwired into it. Thus, the SFDL-to-SHDL compiler includes many novel tricks
for reducing the number of resulting gates in the circuit,
and for optimizing the use of wires.
The final component of Fairplay is a Bob/Alice pair of programs,
whose input is an SHDL circuit, which together carry a secure
computation
protocol of the circuit in the manner suggested by Yao.
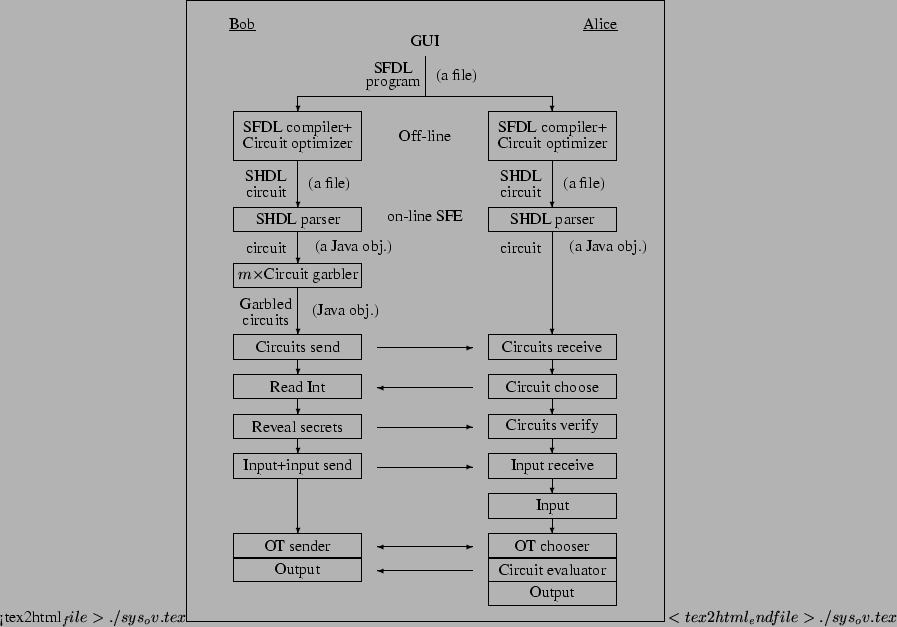
The entire computation structure of Fairplay is depicted in Figure
1.
The main security property guaranteed by the system is
the equivalence to the specified trusted party. I.e., each user is
guaranteed that whatever the other participant does, including using
completely different software for communicating with him, his security
is assured to the same level that the trusted party would have assured
it. In particular, the function is correctly computed on the reported
values and no information about the input of one party is leaked to the
other (beyond what is implied by the specified output).
Note, however, that, in principle, there is no way to ``force'' any
party what to tell the trusted party (e.g. force it to report its
``true'' input), and that in two-party secure
computation it is also impossible to prevent one party from terminating the
protocol
prematurely, before the other party learns its output - this is
detected, but cannot be recovered from.
The Fairplay system provides the guarantee above
based on common and widely accepted cryptographic assumptions. We
describe the security properties of Fairplay in more detail in
Section 5. The level of
security provided is asymmetric: Alice can only cheat with negligible
probability, but Bob can potentially cheat with probability 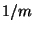 , where , where
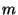 is a parameter that can be chosen at will and there is an overhead
that is proportional to is a parameter that can be chosen at will and there is an overhead
that is proportional to 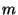 .2 .2
We contribute a generic two-party computation engine that we make
available for use by the security community. The tool is available
at Fairplay's web-site [28].
It includes a specially tailored high level description language (SFDL)
that describes a secure computation in the trusted third-party model.
It tackles the challenge of efficient compilation of SFDL into a one-pass Boolean circuit.
And it provides a Bob/Alice implementation that securely evaluates the circuit.
Fairplay enables experimenting with mechanisms related
to secure function evaluation, whether by replacing a component of it,
building on top of it, or interacting with it. Our preliminary investigation
introduces results concerning the overall cost of the SFE paradigm in
today's Internet settings; it presents a breakdown of costs into components
and bottlenecks; and it examines various enhancements that were introduced
in the literature.
2 System Overview
We start by a general overview of the computation being performed,
which also allows us to present the main entities and components of
our system.
Fairplay comprises two applications that are activated by the two players,
who want to engage in two-party secure function evaluation (SFE).
By convention we call these players/applications Bob and Alice.
Prior to executing the SFE protocol, the two players must define and coordinate
the function-to-be-evaluated. In order to do that, they use the Secure
Function Definition Language (SFDL), a language which was designed especially
for this purpose. The SFDL is a high-level programming language, which allows
humans to specify the function-to-be-evaluated in the form of a computer program.
Another language that the system uses is the Secure Hardware Definition
Language (SHDL). The SHDL is a low-level language designed for specifying
Boolean circuits. The SFE computation is done in several stages as shown
in Figure 1.
- An SFDL program file is written by the users using an SFDL editor.
- The SFDL program is translated by an SFDL compiler to an SHDL circuit file.
The circuit is optimized before it is passed on to the next stage.
- The SHDL circuit is parsed. The resulting circuit is in the form
of a Java object.
- Bob constructs
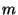 garbled/encrypted circuits and sends them to Alice.
Alice randomly chooses one of the circuits that will be evaluated. garbled/encrypted circuits and sends them to Alice.
Alice randomly chooses one of the circuits that will be evaluated.
- Bob exposes the secrets of the other
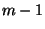 garbled/encrypted circuits,
and Alice verifies them against her reference circuit. garbled/encrypted circuits,
and Alice verifies them against her reference circuit.
- Bob specifies his inputs, and sends them to Alice in garbled form.
Alice inserts Bob's inputs in the garbled/encrypted circuit that she chose
to evaluate.
- Alice specifies her inputs, and then Bob and Alice engage in Oblivious
Transfers (OTs) in order for Alice to receive her inputs (in garbled form) from Bob,
while Bob learns nothing about Alice's inputs.
- Alice evaluates the chosen circuit, finds the garbled
outputs of both her and Bob, and sends the relevant garbled outputs to Bob.
- Each party interprets his/her garbled outputs and prints the results.
Figure 1:
Computation overview
 |
3 The SFDL, SHDL and their Compiler
The secure function evaluation protocol requires that the function to be
evaluated be given as a Boolean circuit. Designers, however, will desire the
function to be given in a more convenient high-level form. In the context
of secure protocols, this is even more important than the strong usual reasons
for writing in high-level programming languages. The starting point of any attempt
of security is a clear, formal, and easily-understandable definition of the requirements.
Such clarity of definition is almost impossible, for humans, using low-level
formalisms such as Boolean circuits. Clear high-level languages are needed.
The compiler will thus accept a function written in a high-level programming language
and compile it into a Boolean circuit that evaluates the same function.
In our case the compiler compiles an SFDL program into an SHDL circuit.
In addition to bridging the semantic gap between high and low level languages,
as done by every compiler, a compiler into hardware has to bridge another semantic gap:
that of obliviousness. Boolean circuits are oblivious - they perform the same sequence
of operations independently of the input (i.e. compute the values of
the gates one after the other).
Normal high-level languages change their flow of control according to the input: they
execute statements conditionally, loop for a variable number of steps, etc.
This semantic gap is not a technicality, but rather the central issue in hardware compilers.
On one hand this is one of the key reasons why it is humanly difficult to design efficient
Boolean circuits. On the other hand, the key reason why Boolean circuits were used as the
computation model for secure function evaluation protocols (rather than, e.g.,
a Turing machine)
is their obliviousness. Non-oblivious computations would seem to leak information from the
very identity of the operation being simulated (existing solutions
for running RAM based computations obliviously are quite complex [22]).
There do exist ``hardware compilers'' that compile a high-level language into low level
Boolean circuits. These hardware compilers are used for actual hardware construction, and serve
to ease the development effort. Most commonly used are the high level hardware description languages
VHDL [14] and Verilog [37] that do not ``look'' like ``normal''
programming languages. There are also many compilers that do aim to use languages that ``look''
like usual programming languages, e.g. the C programming language
(see e.g. [9,18,33,38,19]). There are some similarities and some
differences between the goals of such languages and our goals. The similarities are concerned
with issues like making conditional execution oblivious and the ``single assignment''
issue - each hardware bit can only be assigned a value once, but software allows
re-assigning values, e.g. in statement like x=x+1.
The main difference comes from the required output.
In our case the output should be a ``theoretician's Boolean circuit'': purely
combinatorial, with no sequential logic. Compilers into real hardware are actually mostly
concerned with the use (and re-use) of registers. Thus, for example,
consider a command like
for i = 1 to 16 do sum = sum + a[i].
Our compiler should produce a circuit that has
16 copies of the addition circuit. Real hardware compilers would produce a circuit with a
single register (sum) and a single addition circuit, where in each of the 16 clock cycles,
one value a[i] is added to the register's contents.
Additionally, our optimization metric is very simple:
the number of gates (weighed by the the gate size). We are not bound at all by technological
restrictions such as FPGA structure, delay considerations, or wiring issues.
Let us begin with the simple example of the Millionaires' problem:
program Millionaires {
type int = Int<4>; // 4-bit integer
type AliceInput = int;
type BobInput = int;
type AliceOutput = Boolean;
type BobOutput = Boolean;
type Output = struct {
AliceOutput alice, BobOutput bob};
type Input = struct {
AliceInput alice, BobInput bob};
function Output out(Input inp) {
out.alice = inp.alice > inp.bob;
out.bob = inp.bob > inp.alice;
}
}
First, note that the syntax is quite conventional, borrowing heavily from
the C and Pascal programming languages. Now, let us look at some of the main
ingredients of this program as well as the language in general. A full
description of the language may be found in Appendix A.
Type system.
The SFDL supports a full type system. The primitive types are Boolean, integer,
and enumerated. For maximum efficiency and since there is no pre-wired hardware word size,
integers may be declared to be of any bit-length and are always signed 2's-complement.
Similarly, enumerated types are allocated the minimal number of required bits.
Structures and arrays create more complex types from simpler ones.
Structure entries are accessed using dot-notation, s.f,
and array entries using the standard array notation a[i].
Access to arrays has a potential for non-obliviousness if the index is not a constant expression.
This is handled by the compiler, but users should be aware of the high price of such access.
Pointers do not exist - this is in order to maintain obliviousness.
Beyond their usual role as defining variable types, the type system is used to formalize the
input and output of the function to be evaluated. The special types AliceInput, AliceOutput,
BobInput, BobOutput, must be defined in every program, specifying the respective input and
output types of the two players. The types Input and Output are always defined to be
structures encapsulating the inputs (resp. outputs) of both players.
Program Structure and Functions.
An SFDL program consists of a sequence of functions (as in C, no nesting is allowed)
preceded by declarations of global constants and types.
Functions receive parameters and return values using the Pascal-like syntax of
assignment to a variable whose name is identical to the function name. As in Pascal,
a function must precede any function that calls it. Unlike Pascal,
no ``forward'' clause exists, and no recursion is allowed. The lack of recursion
is critical in order to maintain obliviousness. Functions may define and use local variables;
in the current implementation we forbid global variables.
The last function in the program is the one computing the desired output from the inputs.
By convention it is named output. It accepts a single parameter of type Input
and produces the result of type Output.
Assignments and expressions.
Expressions use the standard notations: they combine constants, variables (including,
recursively, array entries and
structure items), and function calls using operators and, optionally,
parenthesis. The allowed operators include arithmetic addition
and subtraction, Boolean logical operators (bitwise, for integers), and the standard
comparison operators. Due to their cost, multiplication and division are not provided
as primitive operators, but rather should be implemented as functions.
Data types of different widths may be combined, and sign-extension
is used.
Loops and Conditional Execution.
The SFDL has the standard if-then and if-then-else statements. It should be noted
that conditional execution is not oblivious, and thus the compiler generates hardware
that always computes both sides of the branch.
General loops are not oblivious and are not possible in the language. The language does provide
a for-loop where the number of iterations is known in advance (a compile-time constant).
The compiler reads the input program written in SFDL, and performs a sequence of
transformations on it. In the end of the sequence of transformations, a data structure
that corresponds to the hardware is obtained, and is then output in SHDL format.
The following example shows part of the SHDL output produced for the Millionaires'
problem above. Each line in the SHDL output file specifies a ``wire'' in the generated
circuit that is either an input bit or a Boolean gate with given truth-table and
input wires. This format is in a verbose form, in particular containing comments
(automatically generated, but ignored by the secure evaluation protocols).
0 input //output$input.bob$0
1 input //output$input.bob$1
2 input //output$input.bob$2
3 input //output$input.bob$3
4 input //output$input.alice$0
5 input //output$input.alice$1
6 input //output$input.alice$2
7 input //output$input.alice$3
8 gate arity 2 table [1 0 0 0]
inputs [4 5]
9 gate arity 2 table [0 1 1 0]
inputs [4 5]
10 gate arity 2 table [0 1 0 0]
inputs [8 6]
11 gate arity 2 table [1 0 0 1]
inputs [8 6]
12 gate arity 2 table [1 0 0 1]
inputs [10 7]
13 gate arity 2 table [0 0 0 1]
inputs [4 0]
14 gate arity 3 table [0 0 0 1 0 1 1 1]
inputs [13 9 1]
15 gate arity 3 table [0 0 0 1 0 1 1 1]
inputs [14 11 2]
16 gate arity 2 table [0 1 1 0]
inputs [12 3]
17 gate arity 2 table [0 1 1 0]
inputs [15 16]
18 output gate arity 1 table [0 1]
inputs [17] //output$output.alice$0
...
Additionally, the compiler outputs another file that gives
formatting instructions enabling the secure function evaluation protocol to input and output
values in a convenient user-friendly format. E.g. in the SHDL circuit produced above the
first 4 wires (numbered 0-3) while treated as just 4 arbitrary bits inside
the circuit, should be read from the user as an integer.
The following example is produced for the Millionaires' problem above:
Bob input integer "input.bob"
[0 1 2 3]
Alice input integer "input.alice"
[4 5 6 7]
Alice output integer "output.alice" [18]
Bob output integer "output.bob" [29]
Here is a short description of the sequence of steps performed by the compiler:
1. Parsing. Simple syntactic analysis and parsing, resulting in a
memory-resident data structure. Due to the simplicity of the language we have not
used any compiler-compiler tools.
2. Function inlining and loop unfolding. all function calls are treated as macros and
simply inlined where they are called. All for-loops are simply unfolded (note that the number
of iterations is a compile-time constant). These two transformations may seem quite inefficient
at first sight
but that is not the case: they are absolutely required in order to maintain obliviousness.
3. Transformation into single-bit operations. Every command that deals with multi-bit
values is transformed into a sequence of single-bit operations. In the simplest case, an
assignment of the form a=b where 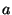 and and 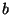 are 4-bit integers is converted into
the four single-bit assignments are 4-bit integers is converted into
the four single-bit assignments
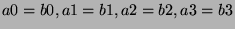 . In the case of expressions,
first a complex expression is transformed into a sequence of operations, e.g. . In the case of expressions,
first a complex expression is transformed into a sequence of operations, e.g. 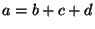 is converted into
is converted into
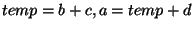 . Then, each multi-bit operator is converted into
its hardware implementation. E.g. an operation . Then, each multi-bit operator is converted into
its hardware implementation. E.g. an operation 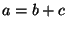 , where , where 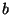 and and 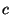 are 4-bit integers
is converted into a sequence of 4 "full-adders", implemented using 8 ternary gates. are 4-bit integers
is converted into a sequence of 4 "full-adders", implemented using 8 ternary gates.
4. Array access handling. Handling array indices that are compile-time constants
is simple: each array entry is treated as a separate variable, and the array access
logic is thus completely compile-time and incurs no hardware cost. Handling array indices
that are expressions must incur a significant hardware cost due to the semantic gap that
must be bridged. In particular, every access to a single array entry results in 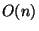 produced hardware gates, where
produced hardware gates, where 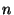 is the total array size. An access to the value of
an array entry, as in is the total array size. An access to the value of
an array entry, as in ![$a=b[i]$](img21.png) is obtained by constructing a multiplexor whose is obtained by constructing a multiplexor whose 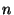 inputs are the entries of
inputs are the entries of 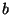 , and whose selection input bits are the bits of , and whose selection input bits are the bits of 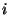 . Assigning
a value to an array entry, as in . Assigning
a value to an array entry, as in ![$a[i]=b$](img23.png) , is obtained essentially by using a demultiplexer.
More precisely by using, in effect, the sequence of , is obtained essentially by using a demultiplexer.
More precisely by using, in effect, the sequence of 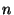 if-commands that contain only constant
array access indices:
if if-commands that contain only constant
array access indices:
if 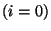 then then ![$a[0]=b$](img25.png) ; if ; if 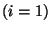 then then ![$a[1]=b$](img27.png) ; ... ; ...
5. Single variable assignment.
Normal code commonly assigns values to variables multiple times, as in
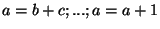 .
Hardware, does not allow this: each "variable", actually, wire, is assigned a single
value computed as an obliviously known operation on other wires. One of the main
challenges of every hardware compiler is to eliminate multiple assignments of values
to variables, and to transform them into single assignments. This issue has received much
attention in the literature (see e.g. work on SSA form [15]).
It seems that our algorithm for this
problem is new and superior to previous approaches. In particular, it runs in linear time
as long as the nesting depth of if statements in the program is bound by a constant. .
Hardware, does not allow this: each "variable", actually, wire, is assigned a single
value computed as an obliviously known operation on other wires. One of the main
challenges of every hardware compiler is to eliminate multiple assignments of values
to variables, and to transform them into single assignments. This issue has received much
attention in the literature (see e.g. work on SSA form [15]).
It seems that our algorithm for this
problem is new and superior to previous approaches. In particular, it runs in linear time
as long as the nesting depth of if statements in the program is bound by a constant.
Let us first look at the simple case shown above
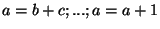 .
The single assignment transformation defines a new copy
of the variable for each assignment: .
The single assignment transformation defines a new copy
of the variable for each assignment:
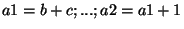 . Things get more
complicated, when the different assignments are interleaved with conditional execution, e.g. . Things get more
complicated, when the different assignments are interleaved with conditional execution, e.g.
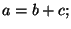 if if 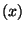 then then 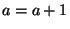 else else 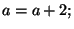 In this case, we must create new copies of In this case, we must create new copies of 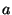 for each branch, and an additional copy combining them together after the loop ends:
for each branch, and an additional copy combining them together after the loop ends:
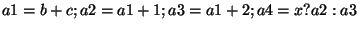 , where the last assignment uses the C-language "?:"
operator notation, which in hardware is a simple multiplexor. Note also that this transformation
has eliminated the "if" statement, yielding an oblivious circuit. The algorithm for the general case
is of independent interest and is described in the next subsection. , where the last assignment uses the C-language "?:"
operator notation, which in hardware is a simple multiplexor. Note also that this transformation
has eliminated the "if" statement, yielding an oblivious circuit. The algorithm for the general case
is of independent interest and is described in the next subsection.
6. Optimization. At this point we have obtained an in-memory image of a Boolean circuit.
This circuit is now optimized, i.e., its size is reduced. The optimization
step is crucial, often reducing the size of the circuit by an order of magnitude.
The optimization is done in linear time, and has three components:
- Peekhole optimization: local simplifications of code, e.g. (x and true
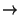 x),
(x or not x x),
(x or not x 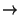 true), etc. true), etc.
- Duplicate code removal: a hash table of all values computed in the circuit is kept.
If some value is computed twice, then one of the duplicates is removed and replaced with direct access
to the other wire.
- Dead code elimination.
Peekhole optimization and duplicate removal are done in a single pass in topological order
over the circuit. Dead code elimination is then done in an additional single pass in
reverse topological order.
The input to this algorithm is code that contains assignment statements, where
each variable may be assigned a value multiple times and
(possibly nested) if statements. The output is straight line code where each
variables is assigned a value only once.
Data structure.
Our basic data structure is a stack of hash tables. It maintains a running
version number for each identifier. It supports the following operations:
- new(id): increases the version number of this identifier (and returns
the new version number). The first time an id is declared, its version number is
assigned to 1.
- get(id): returns the current version number of the identifier.
- push-scope(): starts a new version scope for all identifiers. The version
numbers of all identifiers are initialized to the current version numbers,
but all further
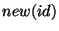 commands will only affect the new scope. commands will only affect the new scope.
- pop-scope(): ends the current version scope. All version numbers of all
identifiers are reset to their value in the previous scope.
- enum-scope(): enumerate all the variables in the current scope.
The implementation uses a new hash table for each version scope. A 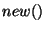 command updates
the version number in the current scope. A command updates
the version number in the current scope. A 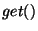 command traverses the stack of hash tables
(from the most recent backwards)
until it finds an instance of the desired identifier. Its running time is proportional to
the stack depth. command traverses the stack of hash tables
(from the most recent backwards)
until it finds an instance of the desired identifier. Its running time is proportional to
the stack depth.
Algorithm.
Assume that the input is a sequence of statements 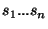 . For ease of exposition,
let us assume that all assignment commands involve two variables on the RHS, and that all
if-statements contain no else clauses. (An "if . For ease of exposition,
let us assume that all assignment commands involve two variables on the RHS, and that all
if-statements contain no else clauses. (An "if 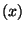 then then 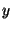 else else 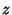 " command is
equivalent to "if " command is
equivalent to "if 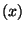 then then 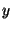 ; if ; if 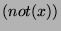 then then 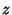 ".) The algorithm is now given by: ".) The algorithm is now given by:
For 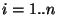 do do 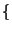
if 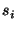 is a statement of the form is a statement of the form
" 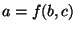 " then " then 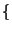
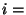 get get 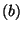
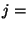 get get 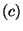
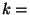 new new 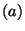
output: "
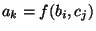 " "
if 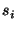 is a statement of the form is a statement of the form
" 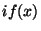 then then
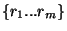 " then " then 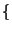
push-scope()
recursively process
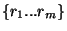
Let 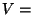 enum-scope() enum-scope()
For each 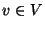 do do
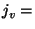 get get 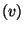
pop-scope()
For each 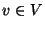 do do 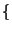
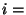 get get 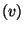
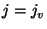
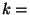 new new 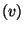
output: "
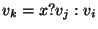 " "
4 Bob-Alice Two-Party SFE
This section describes the specific two-party SFE protocol that was implemented
in Fairplay, based on the protocol suggested by Yao in his seminal
work that introduced the notion of secure function evaluation [39].
We start with a general overview and then describe in detail how
Bob constructs garbled circuits and how Alice evaluates one. Finally we discuss
the oblivious transfer (OT) variants that were implemented thus far.
We do not prove here the security of the protocol, since it was mostly
borrowed from existing theoretical constructions
(however, Section 5 states the security guarantees of
the protocol,
describes the reasoning for the choice of the specific cryptographic
operations that we use, and suggests some variants of the current protocol).
4.1 General overview
Our SFE computation is given as input a Boolean circuit  made of gates and wires, described using SHDL.
Then Alice and Bob interact in order to evaluate
made of gates and wires, described using SHDL.
Then Alice and Bob interact in order to evaluate  securely.
The version of Yao's protocol that we implemented requires a single OT
per each
input wire of securely.
The version of Yao's protocol that we implemented requires a single OT
per each
input wire of 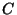 . In this version Bob constructs the circuit . In this version Bob constructs the circuit 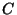 ,
and converts it into a garbled circuit. The garbled circuit is transferred
to Alice. Then Bob and Alice execute an OT once per each input wire.
After this step Alice evaluates the circuit independently without further
interaction with Bob. ,
and converts it into a garbled circuit. The garbled circuit is transferred
to Alice. Then Bob and Alice execute an OT once per each input wire.
After this step Alice evaluates the circuit independently without further
interaction with Bob.
Thwarting malicious behavior by Alice is guaranteed by Yao's protocol
and is based on the security of the symmetric function used for
encoding the secret (SHA-1, which is modeled, for this purpose, as a
pseudo-random function) and
on the security of the OT protocol
against malicious behavior. The same properties also prevent malicious
behavior of Bob, if we can guarantee the correctness of the circuit
encoding that he constructs. This last property was implemented using
a cut-and-choose
technique. Specifically, Bob sends 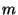 garbled circuits to Alice, and Alice
randomly chooses one circuit that will be evaluated. Bob must then reveal the
secrets associated with the circuits that were not
chosen by Alice for evaluation.
Alice verifies that these garbled circuits to Alice, and Alice
randomly chooses one circuit that will be evaluated. Bob must then reveal the
secrets associated with the circuits that were not
chosen by Alice for evaluation.
Alice verifies that these 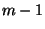 circuits indeed represent the
function circuits indeed represent the
function 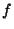 ,
by comparing them to a reference circuit that she constructed herself.
The two parties then evaluate the circuit Alice has chosen.
This method allows to catch a cheating Bob with probability ,
by comparing them to a reference circuit that she constructed herself.
The two parties then evaluate the circuit Alice has chosen.
This method allows to catch a cheating Bob with probability
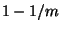 .
In real-world scenarios, where cheating leads to bad reputation, this may be
enough. We leave implementation of more complex cut-and-choose techniques
for future enhancements.3 .
In real-world scenarios, where cheating leads to bad reputation, this may be
enough. We leave implementation of more complex cut-and-choose techniques
for future enhancements.3
4.2 Circuit preparation and evaluation
This section describes how Bob converts the Boolean circuit 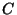 into a
garbled circuit, and how Alice evaluates that garbled circuit. into a
garbled circuit, and how Alice evaluates that garbled circuit.
We use the
notation
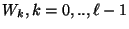 to denote all the wires that compose the circuit to denote all the wires that compose the circuit 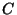 .
All the gates in SHDL circuits have a single Boolean output. The number of inputs
into a gate can be either 1, 2 or 3 (SHDL itself allows more inputs, but the
compiler produces only unary, binary or ternary gates). For simplicity
of exposition, in the description below, we focus only on binary gates.
The conversion of .
All the gates in SHDL circuits have a single Boolean output. The number of inputs
into a gate can be either 1, 2 or 3 (SHDL itself allows more inputs, but the
compiler produces only unary, binary or ternary gates). For simplicity
of exposition, in the description below, we focus only on binary gates.
The conversion of 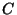 into a garbled circuit works as follows. into a garbled circuit works as follows.
- Bob assigns to each wire
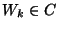 two random two random 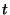 -bit strings -bit strings
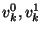 ( (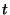 is a security parameter that was set to is a security parameter that was set to 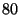 ).
The string ).
The string 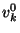 represents the bit represents the bit 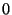 for for 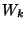 .
The string .
The string 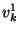 represents the bit represents the bit 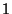 for for 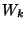 .
Bob also assigns to each wire .
Bob also assigns to each wire 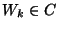 a random binary permutation
(i.e., a bit) a random binary permutation
(i.e., a bit) 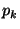 , and appends it to the pair , and appends it to the pair 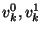 as follows: as follows:
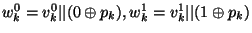 .
We let .
We let 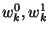 denote the final result. denote the final result.
- For each gate
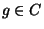 whose output wire is whose output wire is 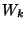 and whose input
wires are and whose input
wires are 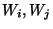 (see Figure 2) (see Figure 2)
Figure 2:
A gate in a circuit
 |
- The original truth table of
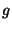 consists of four 0/1 entries.
Bob constructs the Garbled-Truth-Table ( consists of four 0/1 entries.
Bob constructs the Garbled-Truth-Table (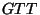 ) of ) of 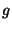 by replacing
every by replacing
every 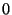 or or 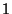 in the truth-table with in the truth-table with 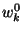 or or 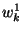 , respectively. , respectively.
- Bob constructs the Encrypted-Garbled-Truth-Table (
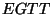 ) of ) of 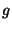 in the following way.
For entry
in the following way.
For entry 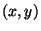 in in 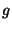 's 's 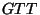 , define , define
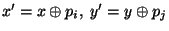 . The
entry is encrypted using . The
entry is encrypted using 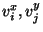 as
encryption-keys and as
encryption-keys and 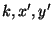 as an IV: as an IV:
![$EGTT[x,y] = Encrypt_{v_i^x, v_j^y, k, x', y'} (GTT[x,y])$](img90.png) . The encryption is done
by hashing . The encryption is done
by hashing
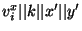 and and
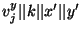 using
SHA-1, and XORing the
two results to the plaintext (see Section 5 for explanations). using
SHA-1, and XORing the
two results to the plaintext (see Section 5 for explanations).
- Bob constructs the Permuted-Encrypted-Garbled-Truth-Table (
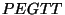 ) of ) of 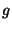 by swapping the entries in
by swapping the entries in 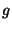 's 's 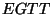 based on the permutation bits assigned
to based on the permutation bits assigned
to 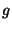 's input wires, namely 's input wires, namely 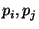 (the role of these permutations is to
make the position of a certain string in a (the role of these permutations is to
make the position of a certain string in a 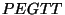 meaningless). I.e.,
if meaningless). I.e.,
if 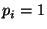 then the first two entries of the table are swapped with the
last two entries. If then the first two entries of the table are swapped with the
last two entries. If 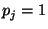 then the first and third entries are swapped
with the second and fourth entries. then the first and third entries are swapped
with the second and fourth entries.
- For each wire which carries a bit of Alice's output, Bob sends
an appropriate translation-table that allows Alice to interpret the circuit's
output from the garbled value of the wire. Namely, for every output
wire
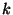 Bob sends a table of the form Bob sends a table of the form
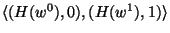 , where , where 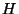 is a collision resistant hash function,
which we implemented as SHA-1. is a collision resistant hash function,
which we implemented as SHA-1.
Initially, Bob sends to Alice 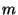 garbled circuits as well as
commitments to his garbled inputs to each circuit. Out of these,
Alice chooses at random garbled circuits as well as
commitments to his garbled inputs to each circuit. Out of these,
Alice chooses at random 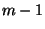 circuits which are opened by Bob to
prove that the circuits were prepared properly.4Bob then opens the commitments to the garbled strings that
represent his input bits of the remaining unopened circuit. Note that
Alice cannot interpret these strings
back to Bob's input bits, because the circuit is garbled.
Alice then uses oblivious transfer (OT) in order to obtain from Bob the
garbled strings that match
her input wires. The OT protocol that was implemented is discussed in the next
subsection. For now assume that for each input bit Alice obtains the
corresponding
garbled string. circuits which are opened by Bob to
prove that the circuits were prepared properly.4Bob then opens the commitments to the garbled strings that
represent his input bits of the remaining unopened circuit. Note that
Alice cannot interpret these strings
back to Bob's input bits, because the circuit is garbled.
Alice then uses oblivious transfer (OT) in order to obtain from Bob the
garbled strings that match
her input wires. The OT protocol that was implemented is discussed in the next
subsection. For now assume that for each input bit Alice obtains the
corresponding
garbled string.
Alice proceeds to evaluate the garbled circuit gate by gate.
Let 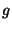 be a specific garbled gate whose output wire is be a specific garbled gate whose output wire is 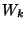 and whose input
strings are and whose input
strings are 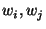 . Let the least significant bits of . Let the least significant bits of 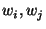 be be 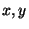 and the rest of the bits be
and the rest of the bits be 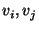 respectively. For each such gate: respectively. For each such gate:
- Alice uses
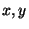 as indices into an entry to be decrypted in as indices into an entry to be decrypted in 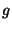 's 's 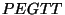 . .
- Alice uses
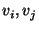 as decryption-keys, and as decryption-keys, and 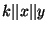 as an IV.
Namely, Alice sets as an IV.
Namely, Alice sets
![$w_k = Decrypt_{v_i, v_j, k, x, y} (PEGTT[x,y])$](img104.png) .
The decryption is done by hashing .
The decryption is done by hashing
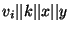 and and
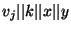 using SHA-1,
and XORing the two results to the ciphertext. using SHA-1,
and XORing the two results to the ciphertext.
Throughout the evaluation all that Alice obtains are garbled strings.
These do not leak information on the values of the bits flowing
through the circuit.
When Alice finds the garbled values of the output gates she uses the
translation tables to interpret the circuit's true output.
As for Bob's output, Alice sends him the garbled values of his output
wires. Bob associates them with the corresponding 0 or 1
values. (Note that in the case of a wire that carries an output bit
which should be revealed to Bob alone, Alice cannot decipher the value,
or change it without being detected by Bob. In the case of a wire that
carries an output bit which is revealed to both Bob and Alice, Alice
can, of course, decrypt the value but she cannot change it without
finding a collision in the hash function.)
If the parties are assumed
to be semi-honest (i.e. follow the protocol) then there is no need for
using cut-and-choose methods for verifying the circuits constructed by
Bob, and we can set 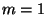 . The OT protocol, too, can be simplified,
since the current
implementation is secure against malicious parties.5 . The OT protocol, too, can be simplified,
since the current
implementation is secure against malicious parties.5
4.3 Oblivious Transfer
Two OT variants were implemented thus far (the system can be easily extended
to employ more variants). Both variants are based on the Diffie-Hellman
problem (and are implemented over a group 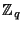 , which is a
sub-group of prime order , which is a
sub-group of prime order 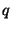 of
of
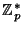 , where , where 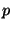 is prime and is prime and 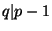 ).
The first one is the 1-out-of-2 oblivious transfer ( ).
The first one is the 1-out-of-2 oblivious transfer (
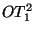 ) protocol due to
Bellare and Micali [6], which was adapted to using random
oracles [7].
The second protocol, which was proposed by Naor and Pinkas
in [30], is an
optimization of the first one, that uses the same ) protocol due to
Bellare and Micali [6], which was adapted to using random
oracles [7].
The second protocol, which was proposed by Naor and Pinkas
in [30], is an
optimization of the first one, that uses the same 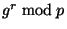 value for
multiple OT executions ( value for
multiple OT executions (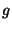 is a generator of the group is a generator of the group 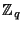 , , 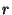 is a random
exponent). A detailed description of both protocols can be found in
[30].
Both these OT protocols are secure in the random oracle model
and were implemented using the SHA-1 hash function.
(There
are constant-round OT protocols secure in the standard
model [2,30]. The SFE application requires multiple
concurrent invocations
of these protocols, but on the other hand it is only required that the
SFE implementation, and not necessarily each OT invocation, provide
both privacy and correctness.) is a random
exponent). A detailed description of both protocols can be found in
[30].
Both these OT protocols are secure in the random oracle model
and were implemented using the SHA-1 hash function.
(There
are constant-round OT protocols secure in the standard
model [2,30]. The SFE application requires multiple
concurrent invocations
of these protocols, but on the other hand it is only required that the
SFE implementation, and not necessarily each OT invocation, provide
both privacy and correctness.)
5 Cryptographic Background
This section describes the rationale behind the choice of specific
cryptographic operations for Fairplay and suggests
several additional variants. We do not provide here proofs of the
correctness and security of the implementation, as it is mostly based on
existing constructions.
The protocol we implemented provides security guarantees which depend on the
following three assumptions:
- SHA-1 is modeled as a random oracle.
- The oblivious transfer protocol is secure (the security of
the OT protocol can be based on the computational Diffie-Hellman
assumption [2,30], but we use random-oracle
based protocols which are more efficient).
- Alice does not terminate the protocol before sending Bob's output to him.
We get the following guarantees:
- Bob is guaranteed that an
interaction with a malicious Alice is not different than an
interaction with the trusted third party, except for a negligible error
probability.
- Alice has the same guarantee with relation to
Bob, with error probability of
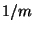 . .
Note that these guarantees means
that (1) a malicious party cannot learn more information about the other
party's input than it can learn in the trusted party model, and (2) a
malicious party cannot change the computed function. Also, if we are
assured that Bob does not change the circuit he provides to Alice
then his cheating probability is also negligible.
The basic symmetric cryptographic function that we use is SHA-1. We
preferred it to using a block cipher (such as AES) since it supports
a variable input length.
The encoding of the circuit (garbling) can be implemented using a
pseudo-random function (as is described in detail, for example,
in [31]), where the output of the function is used as a pad that
masks the values in the table representing a gate in the circuit.
We use the masking values SHA-1
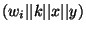 , SHA-1 , SHA-1
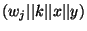 for entry for entry
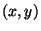 of the table of gate number of the table of gate number 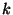 , whose input wires are , whose input wires are 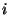 and and 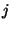 .
(Note that wires .
(Note that wires 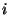 and and 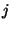 could be input into multiple gates.)
The underlying security assumption is that SHA-1 is pseudo-random function
keyed by could be input into multiple gates.)
The underlying security assumption is that SHA-1 is pseudo-random function
keyed by 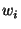 or or 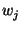 and applied to other parameters. and applied to other parameters.
The OT protocols are based on the random oracle model and
the computational Diffie-Hellman assumption.
Alternative two-round OT protocols that are secure in the standard
model and use only 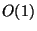 exponentiations were described
in [30,2]. We preferred not to use them in order to
reduce the number of exponentiations. exponentiations were described
in [30,2]. We preferred not to use them in order to
reduce the number of exponentiations.
Bob commits to his garbled inputs before
the cut-and-choose step. This is done in order to prevent him from
choosing his input based on Alice's choices in this step. We leave
it for future work to let Alice choose more than one circuit for
evaluation. This will reduce the cheating probability of Bob to be
exponentially small in the number of circuits that are evaluated, but
implementing this variant requires Bob to prove that he provides the same input
to all circuits, and this step incurs additional overhead. (An
alternative method for verifying the garbled circuit constructed by Bob is to
require him to prove, in zero-knowledge, that the tables are
correct. To the best of our knowledge, this approach requires an even
higher overhead.)
The protocol provides Alice
with the garbled values of Bob's output wires. If the value of an
output wire should become known only to Bob (and not to Alice) then she
receives no information about the relationship between actual and garbled
values of this wire. If the output is used by both Bob and Alice, she
receives hash values of the garbled values corresponding to 0 and
to 1. However, she is not able to provide Bob with a garbled value that
corresponds to a different output than the one she computed, since
this would mean that she can invert the hash function.
6 Experimental results
The first, immediate contribution of a system such as Fairplay is
that it can provide answers to very basic, concrete questions like:
- How much time does it take to execute the two-party SFE protocol for
the quintessential Millionaires' problem?
- What would be the time-penalty if the two tycoons in question were
actually Billionaires and not just Millionaires?
The experiments that we conducted using our system gave a very definite answer,
that even the tougher Billionaires' problem (i.e., using 32 bit inputs)
can be solved in very reasonable time.
It took our system only 1.25 seconds to solve the Billionaires' problem
using fast communication, and 4.01 seconds when communication was slow.
More generally, in this paper we report results for four functions,
which produced circuits ranging in size from tens of gates to thousands
of gates. A summary of the various size parameters of these four functions
is shown in Table 1 (their SFDL source code can be found in
Fairplay's web-site [28]).
The details of the four functions are as follows:
- AND - performs bit-wise AND on two registers.
The input size for both Alice and Bob is 8 bits. Total circuit size is
32 gates, out of which 16 are inputs and 16 are outputs.
- Billionaires - compares two integers.
The input size for both Alice and Bob is 32 bits. Total circuit size is
254 gates, out of which 64 are inputs and 2 are outputs.
- Keyed Database Search (KDS) - Bob has a database of 16 items,
each item is keyed by a 6-bit key and comprises of 24 data bits.
Alice privately retrieves the data of one item by specifying its key.
The input size for Bob is 480 bits and for Alice 6 bits. Total circuit size
is 1229 gates, out of which 486 are inputs and 24 are outputs.
- Median - finds the median of two sorted arrays.
The input for both Alice and Bob are ten 16-bit numbers. Total circuit
size is 4383 gates, out of which 320 are inputs and 32 are outputs.
The AND function was chosen as an example of the simplest possible
circuit, whose size is of the same order as the number of its inputs. The
KDS function demonstrates a circuit in which the size of Alice's input
(which defines the number of OTs) is much smaller than either the number of
Bob's inputs or the number of gates. The median function demonstrates
a circuit whose size is much greater than the number of inputs.
Another important contribution
of a working system is that it enables a systematic, realistic investigation
of the relative cost of its various ingredients. This can be done by utilizing
profiling tools, and by performing supervised experiments, in which the cost
of the different sub-components is measured in isolation. One specific question
that we found interesting in this area is the following: what is the relative
cost of the public key operations required by the two-party SFE protocol?
Since this relative cost is affected by the cost of communication,
and since communication delays vary dramatically in different environments,
we conducted our experiments in two extreme settings - LAN and WAN.
The LAN's latency is 0.4 ms, and its effective throughput is 617.8 MBPS
(Mega bit per second). The WAN's latency is 237.0 ms, and its effective
throughput is 1.06 MBPS. By activating our system on the four functions
described above, and profiling it under the LAN/WAN environments,
we discovered that the public key operations were responsible for
27%-77% of the total delay in the LAN setting, while in the WAN setting
the relative cost of the public key operations was only 9%-42%.
These results suggest that, at least for some interesting functions,
the relative cost of the communication is rather significant,
especially in a WAN environment where communication is slow.
In light of this, we also calculated the slowdown factor caused by moving
from LAN to WAN, which was found to be at least 2.34 and at most 6.89.
Communication batching
means that instead of sending 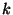 big integers (associated with different OTs)
in big integers (associated with different OTs)
in 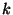 separate messages, we aggregate them together and send them in one
big message. It is useful because of the relatively large constant overhead
associated with any message being sent regardless of its size, and also due to
internal implementation details of TCP/IP.
By implementing and measuring the performance of two variants of the SFE protocol,
with and without communication batching, we were able to assess its contribution.
The observed speedup factors due to communication batching in a LAN setting were
between 1.89-2.72, while in a WAN setting they were between 2.11-8.75. separate messages, we aggregate them together and send them in one
big message. It is useful because of the relatively large constant overhead
associated with any message being sent regardless of its size, and also due to
internal implementation details of TCP/IP.
By implementing and measuring the performance of two variants of the SFE protocol,
with and without communication batching, we were able to assess its contribution.
The observed speedup factors due to communication batching in a LAN setting were
between 1.89-2.72, while in a WAN setting they were between 2.11-8.75.
We have also implemented an optimization technique for OT that was
proposed by Naor and Pinkas in [30], in which the sender uses
the same value of 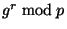 for multiple OTs, improving both
computation and communication. The maximum speedup factor of this optimization
method that was observed in our system was 1.32. for multiple OTs, improving both
computation and communication. The maximum speedup factor of this optimization
method that was observed in our system was 1.32.
There are many additional optimization techniques that may be considered,
implemented and tested (e.g., turning multiple 1-out-of-2 OTs to a single
1-out-of-n OT [30], or using computation batching of multiple
modular inverses). This is an area for future research
(see Section 8).
We conclude this section by presenting Table 2. This table shows the
elapsed execution times required for the aforementioned functions in both LAN
and WAN settings, and their breakdown into four main sub-tasks.
These sub-tasks are: IPCG - initializations, parsing and circuit garbling,
CC - circuits communication, OTs - Oblivious Transfers, EV - circuit evaluation.
(Note that the cost of the OTs includes contributions from both calculating
public key operations, and communicating their results back and forth.)
The results shown in Table 2 were obtained using the most optimized
method currently available in our system (namely, communication batching
and Naor-Pinkas 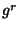 optimization with no communication/computation tradeoff).
The EET columns present the elapsed execution time (in seconds), which was
required for Alice to execute the entire two-party SFE protocol excluding
SFDL-to-SHDL compilation.6The number of garbled circuits for the cut-and-choose algorithm was set to optimization with no communication/computation tradeoff).
The EET columns present the elapsed execution time (in seconds), which was
required for Alice to execute the entire two-party SFE protocol excluding
SFDL-to-SHDL compilation.6The number of garbled circuits for the cut-and-choose algorithm was set to 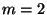 ,
and the size of the DL parameters ,
and the size of the DL parameters 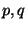 was 1024 and 160 bits, respectively.
Both Alice and Bob used Intel 2.4 GHz Linux machines.
The system was implemented in Java, and it used the TCP/IP protocol for
communication via Java sockets. The measurements were taken as the average of was 1024 and 160 bits, respectively.
Both Alice and Bob used Intel 2.4 GHz Linux machines.
The system was implemented in Java, and it used the TCP/IP protocol for
communication via Java sockets. The measurements were taken as the average of
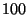 repetitions ( repetitions (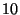 for the Median function) of the protocol. All iterations
used a single TCP/IP connection, which was established in the beginning. for the Median function) of the protocol. All iterations
used a single TCP/IP connection, which was established in the beginning.
Part of the future work includes a more fine grained analysis of the
performance. Namely, expressing the expected execution time
as a function of the number of OTs (Alice's input
bits), the number of gates, and the security parameter 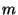 . .
7 Related work
There are very few previous actual implementations of secure
computation, and
even fewer automated compilers that generate an
implementation of a secure protocol from a program description in a
higher level language.
Kühne implemented a translator that takes a trusted-party
specification of a multi-party protocol and generates a specification
for running the protocol using the BGW paradigm [25]. (This
implementation is based on the specific
construction of Hirt and Maurer [23].) However, that
project does not have an ``evaluator'' part, which performs a
distributed implementation of the resulting BGW protocol.
MacKenzie et al. [27] implemented a compiler that automatically
generates protocols for secure two-party computation that use
arithmetic functions over groups and
fields of special form. The compiler receives a specification of a
protocol that uses a secret key, e.g., for signature generation or for
decryption, and implements a threshold crypto protocol
where the key is shared between two parties and only the two of them
together can perform the protocol. The key is generated by a TTP and
is given to the parties.
Compared to Fairplay, this is a compiler for a restricted but important
class of functions, which is particularly suitable for applications
where the secret key has to be closely guarded using threshold
cryptography.
In principle this type of functions can be
implemented by a Boolean circuit, but the result would be
an overwhelmingly large circuit.
An example of an automated security toolkit in a different domain is
AGVI, a toolkit for Automatic Generation, Verification, and Implementation
of Security Protocols [36]. AGVI receives as input a
system specification and security
requirements, and automatically finds
protocols for the specific application, proves their correctness
(using efficient search of a space representing the protocol execution), and
implements them in Java.
TEP [3] is a secure multi-party computation system that employs a
trusted third party. The trusted platform co-joins participants in a
joint computation, passing authenticated information among
participants over guarded communication channels. TEP users need to
annotate their program with information flow labels in order to
automatically verify that no information on any private data is leaked
through the TEP channels to other participants. In comparison, our system does
not employ a TTP, and does not require information flow labels by the user.
The secure program partitioning technique of
[40] takes a user program written in a
security-typed language, and automatically provides a distributed
partitioning of the program. The user annotated program contains
static information flow labels that specify which program components
may use what data and how. An automated compiler splits the program
to run on heterogeneously trusted hosts.
Compared with their approach, the secure program partitioning is
beneficial only for programs that naturally break into
communicating components, in a manner dictated by the user's annotation.
8 Future Work
The current implementation of the secure two-party computation system
can be extended in many ways.
The elapsed execution time is a function of the communication
delay and bandwidth, and of the processing time. Ideally the network
and the processor should run in parallel, and none of them should be
idle waiting for the other one to finish its job. The current implementation
does not perform this optimization.
The main computational overhead is incurred by running invocations of the
oblivious transfer protocol. It would be interesting to explore deployment
of further recent enhancements of OT, such as extending a small number of
OTs into a large number of OTs using symmetric cryptographic operations alone
[24], or using OT variants which are based on the hardness of breaking RSA,
rather than the DDH assumption.
The basic SFE protocol of Section 4 provides a weak security against
malicious parties. Namely, the cut-and-choose method guarantees with
probability 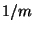 that the circuit that Bob prepares is correct.
Some additional care must be taken if we want to reduce Bob's
cheating probability to be exponentially small in
that the circuit that Bob prepares is correct.
Some additional care must be taken if we want to reduce Bob's
cheating probability to be exponentially small in 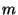 (see, e.g., [34]). (see, e.g., [34]).
No implementation can prevent a
malicious party from aborting the protocol
prematurely (e.g after learning its output and before the other party
learns its output).7Although there is no perfect solution for this issue and existing
solutions are quite complex, some solutions can be
implemented (e.g. [34]). We are currently extending our system with fair
termination mechanisms borrowing from [34].
Reactive secure computation
is an SFE which consists of
several steps,
where each step operates based on inputs from the parties and a state
information that it receives from the previous step.
For example, in each step the parties could compare two numbers and
receive the result of the
comparison, which they use to decide which inputs
to provide to the following step. In addition, secret state
information is communicated from round to round, and the inputs to all
rounds are used by the protocol for computing the output of the final
round (but should otherwise remain hidden from the parties).
This scenario,
as well as appropriate security definitions and constructions, was
described in [10,12]. (A protocol that uses reactive
computation for securely computing the median, in the presence of
malicious parties, was presented in [1].)
In order to implement secure reactive computation each step should
transfer a secret and authenticated state-information string to the
following step. In the two-party case this property can be enforced using a
modified implementation of Yao's protocol, see [1].
While the generic
construction of Yao can be used to implement any functionality, more
efficient constructions can be designed for specific tasks (e.g. for
bignum operations,
computing comparisons or intersections, evaluating
polynomials, or querying a database). A secure protocol for a more
complex task can use a
circuit whose inputs are the results of specialized constructions
(for example, the protocol in [11] runs a circuit that
computes statistics based on the results of secure database queries,
and the protocol in [26] runs a
circuit that uses uses the results of oblivious
polynomial evaluation).
The system we built
implements secure computation between two parties. There is
also a
large body of research on secure multi-party computation, for either
combinatorial or algebraic circuits, and using different trust
assumptions (see e.g. [21,8,5]). A natural next step
is to implement the compilation paradigm in the multi-party scenario.
An additional open challenge is to devise fair termination techniques
for multiple participants.
We are grateful for the proactive and valuable participation of
several research students in the project. Specifically,
Ziv Balshai and Amir Levy implemented the SFDL-to-SHDL compiler [4];
Dudi Einey wrote the program development GUI; and
Ori Peleg implemented fair termination.
- 1
-
G. Aggarwal, N. Mishra, and B. Pinkas.
Secure computation of the 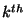 -ranked element. -ranked element.
In Avdances in Cryptology - Proc. of Eurocyrpt '04, 2004.
- 2
-
B. Aiello, Y. Ishai, and O. Reingold.
Priced oblivious transfer: How to sell digital goods.
In Proceedings of Eurocrypt '01, LNCS, volume 2045, 2001.
- 3
-
S. Ajmani, R. Morris, and B. Liskov.
A trusted third-party computation service.
Technical Report MIT-LCS-TR-847, MIT, May 2001.
- 4
-
Z. Balshai, A. Levy, and N. Nisan.
A secure funcation definition language (SFDL) compiler.
in preparation.
- 5
-
D. Beaver, S. Micali, and P. Rogaway.
The round complexity of secure protocols.
In Proceedings of the 22nd ACM Symposium on Theory of Computing
(STOC), pages 503-513, 1990.
- 6
-
M. Bellare and S. Micali.
Non-interactive oblivious transfer and applications.
In Proceedings of Crypto 89, pages 547-557, 1990.
- 7
-
M. Bellare and P. Rogaway.
Random oracles are practical: A paradigm for designing efficient
protocols.
In Proceedings of the 1st Annual Conference on Computer and
Communications Security, pages 62-73, 1993.
- 8
-
M. Ben-Or, S. Goldwasser, and A. Wigderson.
Completeness theorems for non cryptographic fault tolerant
distributed computation.
In Proceedings of the 20th Annual Symposium on the Theory of
Computing (STOC), pages 1-9, 1988.
- 9
-
R. Bergamaschi, R. Damiano, A. Drumm, and L. Trevillyan.
Synthesis for the '90s: Highlevel and logic synthesis techniques.
In ICCAD93 Tutorial Notes, 1993.
- 10
-
R. Canetti.
Universally composable security: A new paradigm for cryptographic
protocols.
In Proceedings of FOCS, 2001.
- 11
-
R. Canetti, Y. Ishai, R. Kumar, M. Reiter, R. Rubinfeld, and R. Wright.
Selective private function evaluation with applications to private
statistics.
In Proceedings of Twentieth ACM Symposium on Principles of
Distributed Computing (PODC), 2001.
- 12
-
R. Canetti, Y. Lindell, R. Ostrovsky, and A. Sahai.
Universally composable two party computation.
In Proceedings of the 34th ACM Symposium on the Theory of
Computing (STOC), 2002.
- 13
-
B. Chor, O. Goldreich, E. Kushilevitz, and M. Sudan.
Private information retrieval.
In Proceedings of the 36th FOCS, pages 41-50, 1995.
- 14
-
D. R. Coelho.
The VHDL Handbook.
Kluwer Academic Publisher, Norwell, MA, 1989.
- 15
-
R. Cytron, J. Ferrante, B. K. Rosen, M.N. Wegman, and F. K. Zadeck.
Efficiently computing static single assignment form and the control
dependence graph.
ACM Transactions on Programming Languages and Systems,
13(4):451-490, 1991.
- 16
-
W. Diffie and M. Hellman.
New directions in cryptography.
IEEE Transactions on Information Theory, 22(6):644-654, 1976.
- 17
-
J. Feigenbaum and S. Shenker.
Distributed algorithmic mechanism design: Recent results and future
directions.
In Proc. of the 6th International Workshop on Discrete
Algorithms and Methods for Mobile Computing and Communications, pages 1-13,
2002.
- 18
-
D. Galloway.
The transmogrifier c hardware description language and compiler for
fpgas.
In D. A. Buell and K. L. Pocek, editors, Proceedings of IEEE
Workshop on FPGAs for Custom Computing Machines, pages 136-144, April 1995.
- 19
-
M. Gokhale and E. Gomersall.
High level compilation for fine grained fpgas.
In J. Arnold and K. L. Pocek, editors, Proceedings of IEEE
Workshop on FPGAs for Custom Computing Machines, pages 165-173, April 1997.
- 20
-
O. Goldreich.
The Foundations of Cryptography - Volume 2, Ch. 7.
2004.
- 21
-
O. Goldreich, S. Micali, and A. Wigderson.
How to play any mental game.
In Proceedings of the 19th ACM Symposium on Theory of Computing
(STOC), pages 218-229, 1987.
- 22
-
O. Goldreich and R. Ostrovsky.
Software protection and simulation on oblivious RAMs.
Journal of the ACM, 43(3):431-473, 1996.
- 23
-
M. Hirt and U. Maurer.
Player simulation and general adversary structures in perfect
multiparty computation.
Journal of Cryptology: the journal of the International
Association for Cryptologic Research, 13(1):31-60, 2000.
- 24
-
Y. Ishai, J. Kilian, K. Nissim, and E. Petrank.
Extending oblivious transfers efficiently.
In Proceedings of Crypto '03, LNCS 2729, pages 145-161.
Springer-Verlag, 2003.
- 25
-
T. Kühne.
Evaluation, design and implementierung von multi-party-berechnungen.
Master's thesis, ETH Zürich, September 1997.
- 26
-
Y. Lindell and B. Pinkas.
Privacy preserving data mining.
Journal of Cryptology, 15(3):177-206, 2003.
- 27
-
P. MacKenzie, A. Oprea, and M. K. Reiter.
Automatic generation of two-party computations.
In Proceedings of the 10th ACM Conference on Computer and
Communications Security, October 2003.
- 28
-
D. Malkhi, N. Nisan, B. Pinkas, and Y. Sella.
The Fairplay project.
http://www.cs.huji.ac.il/labs/danss/Fairplay.
- 29
-
M. Naor and B. Pinkas.
Oblivious transfer and polynomial evaluation.
In Proceedings of the 31st Symposium on Theory of Computer
Science (STOC), pages 245-254, 1999.
- 30
-
M. Naor and B. Pinkas.
Efficient oblivious transfer protocols.
In Proceedings of SODA 01, 2001.
- 31
-
M. Naor, B. Pinkas, and R. Sumner.
Privacy preserving auctions and mechanism design.
In Proc. of the 1st ACM conf. on Electronic Commerce, 1999.
- 32
-
N. Nisan.
Algorithms for selfish agents - mechanism design for distributed
computation.
In STACS, 1999.
- 33
-
J. B. Peterson, R. B. O'Connor, and P. M. Athanas.
Scheduling and partitioning ansi-c programs onto multi-fpga ccm
architectures.
In J. Arnold and K. L. Pocek, editors, Proceedings of IEEE
Workshop on FPGAs for Custom Computing Machines, pages 178-187, April 1996.
- 34
-
B. Pinkas.
Fair secure two-party computation.
In Proceedings of Eurocrypt '03, LNCS 2656, pages 87-105.
Springer-Verlag, 2003.
- 35
-
R. L. Rivest, A. Shamir, and L. Adleman.
A method for obtaining digital signatures and public key
cryptosystems.
Communication of the ACM, (21):120-126, 1978.
- 36
-
D. Song, A. Perrig, and D. Phan.
AGVI -- automatic generation, verification, and
implementation of security protocols.
In 13th Conference on Computer Aided Verification (CAV), 2001.
- 37
-
D. E. Thomas and P. R. Moorby.
The Verilog hardware description language.
Kluwer Academic Publishing, Boston, MA, 1991.
- 38
-
T. Yamauchi, S. Nakaya, and N. Kajihara.
Sop: A reconfigurable massively parallel system and its controldata-
flow based compiling method.
In J. Arnold and K. L. Pocek, editors, Proceedings of IEEE
Workshop on FPGAs for Custom Computing Machines, pages 148-156, April 1996.
- 39
-
A. C. Yao.
How to generate and exchange secrets.
In Proceedings of the 27th IEEE Symposium on Foundations of
Computer Science, pages 162-167, 1986.
- 40
-
S. Zdancewic, L. Zheng, N. Nystrom, and A. C. Myers.
Untrusted hosts and confidentiality: Secure program partitioning.
ACM Transactions on Computer Systems, 20(3):283-328, 2002.
A. SFDL Overview
Programs in SFDL instruct a virtual "trusted party" what to do.
The SFDL compiler compiles it into a "Boolean circuit" low level format that
instructs a true client/server pair what to do. When the client/server pair
run the compiled form of the program, they implement correctly and securely the
fictional trusted party.
program <program-name> {
<type declarations>
<function declarations>
}
In the first part of a program, the type declarations, the programmer defines the
data types that he will use. The data types supported are Booleans, integers,
structs (records), and arrays. Of particular importance are the following data
types that must be defined in every program:
- 1. AliceInput
- - the data type of Alice's input
- 2. BobInput
- - ditto for Bob
- 3. AliceOutput
- - the data type of Alice's output
- 4. BobOutput
- - ditto for Bob
The data types Input and Output are automatically defined for each program
to be the structures of both inputs and both outputs, respectively:
1. type Input = struct {
AliceInput alice, BobInput bob};
2. type Output = struct {
AliceOutput alice, BobOutput bob};
In the second part of the program, the function definitions, the programmer defines
a sequence of functions. Each function may call the previous ones (but not later ones
nor itself). The main functionality of the program is the evaluation of the last
function defined. This function must be called output and must receive a single
parameter of type Input and return a value of type Output.
Constant definitions may appear in the  type declarations type declarations segment.
The syntax is standard, e.g.: segment.
The syntax is standard, e.g.:
const numberOfBits = 16;
Data types can be defined using the type command.
Here are the supported data types:
- Boolean: false/true
- Integer types: e.g. Int<30> - a 30-bit
integer (signed). Any number of bits is allowed.
- Enumerated types: e.g. enum {red, blue,
green}. Enumerated types are assigned the smallest
possible number of bits (in this case 2).
- Structures: e.g. struct { Boolean ranked, Int<7> level }
- Arrays: e.g. Boolean[7] - has entries indexed 0 .. 6
New data types can be defined using the type statement:
- type Short = Int<16>;
- type Byte = Boolean[8];
- type Void = struct {};
- type Color = enum {red, blue, green};
- type Pixel = struct {Color color,
Int<10>[2] coordinates};
The function header defines the number of parameters to the function,
their types, and the return data type. Function must always return a value.
After the header come local variable declarations, and finally the statements themselves.
function <return data type>
<function name>
( <arg1 type> <arg1 name>, ... )
{
<var declarations>
<function body>
}
Function values are returned Pascal-style, by assigning a value to a variable
with the function's name. E.g.:
function Int<9> double(Int<8> x) {
double = x + x;
}
var <type> <var name>, <var name>,
..., <var name>;
For example:
- var Int<10> xCoord, yCoord;
- var Color[8] palette;
All variables are initialized to 0.
Expressions are used for computing values. They are used in assignment statements,
to denote conditions, to send arguments to functions, etc.
Expressions are built from atomic values using operations.
The following are the atomic values allowed:
- A Boolean constant: false, true.
- An integer constant: e.g. 34, -56, 0, 123456789123456789.
- A variable name: e.g. i, price.
- A field in a struct using x.y notation.
(Here x is a struct, and y is a name of a field defined in that struct.)
- An array entry using x[i] notation.
(Here x is an array and i is an integer expression.)
The following operators are defined:
- +,- : addition and subtraction (in 2's complement).
Accepts k-bit long integers and return a (k+1)-bit long result.
-
 and, or, not, xor bitwise Boolean operations.
Accept k-bit long arguments and return k-bit long arguments. and, or, not, xor bitwise Boolean operations.
Accept k-bit long arguments and return k-bit long arguments.
-
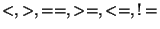 : 2's complement comparison operators.
Accept k-bit long arguments and return a 1-bit result. : 2's complement comparison operators.
Accept k-bit long arguments and return a 1-bit result.
- function call: e.g. f(x, y), where f is a previously defined function
and x, y, .. are arbitrary expressions that are passed as parameters by value.
Narrow and wide operands may be combined in an operation, and the narrower value is
always widened using sign-extension.
- Assignment:
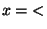 expression expression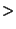 ; - any expression may appear on the RHS,
and any "lvalue" may appear on the LHS. An lvalue is a variable, a field of a struct,
or an array entry. ; - any expression may appear on the RHS,
and any "lvalue" may appear on the LHS. An lvalue is a variable, a field of a struct,
or an array entry.
- If: if
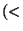 Boolean expression Boolean expression  statement statement
- If-else: if
 Boolean expression Boolean expression  statement statement else else  statement statement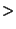
- For: for
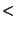 index index low val low val high val high val statement statement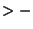 the range of the for loop must be a compile-time constant.
the range of the for loop must be a compile-time constant.
- block { statement,
 , statement } , statement }
Fairplay -- A Secure Two-Party Computation System
This document was generated using the
LaTeX2HTML translator Version 2K.1beta (1.48)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 -show_section_numbers -local_icons sys_USNX04_PVR.tex
The translation was initiated by Yaron Sella on 2004-05-19
Footnotes
- 1 An alternative definition uses simulation.
The two definitions are identical if the parties are assumed to be semi-honest,
but the trusted party definition is preferable for the case of malicious parties
and for defining secure composition of protocols.
-
- 2 While in principle logarithmic overhead
should suffice, it seems that this is still not practical using current techniques.
-
- 3 Bob's cheating probability can be reduced
to be exponentially small in m if the protocol lets Alice check a constant fraction
(e.g. m/2) of the circuits that Bob constructed, evaluate the remaining (m/2) circuits
and output the majority result. In that case, however, the protocol must have
additional, measures for ensuring that Bob provides the same input to all the circuits
evaluated by Alice (see, e.g., [34]).
-
- 4 Care must be taken to ensure that
a circuit can only be opened in a single way. In our implementation this
depends on the assumption that it is infeasible to find a,a',b,b'
such that H(a) XOR H(a') = H(b) XOR H(b'), where H is SHA-1.
-
- 5 An OT protocol for semi-honest parties
is very simple: Alice sends to Bob two strings, one of them random and the
other being the public key corresponding to a private key of her choice.
Bob encrypts each of the input items using the corresponding string,
and Alice is able to decrypt only one of them.
-
- 6 Compilation can and should be done
by the two parties off-line.
-
- 7 On the other hand,
a premature termination of the protocol by one party is detected
by the other party, which in many scenarios can then take measures
against the corrupt party. This is different than other types of
malicious activity which are not easily detected.
-



Yaron Sella
2004-05-19
|

![]() optimization with no communication/computation tradeoff).
The EET columns present the elapsed execution time (in seconds), which was
required for Alice to execute the entire two-party SFE protocol excluding
SFDL-to-SHDL compilation.6The number of garbled circuits for the cut-and-choose algorithm was set to
optimization with no communication/computation tradeoff).
The EET columns present the elapsed execution time (in seconds), which was
required for Alice to execute the entire two-party SFE protocol excluding
SFDL-to-SHDL compilation.6The number of garbled circuits for the cut-and-choose algorithm was set to ![]() ,
and the size of the DL parameters
,
and the size of the DL parameters ![]() was 1024 and 160 bits, respectively.
Both Alice and Bob used Intel 2.4 GHz Linux machines.
The system was implemented in Java, and it used the TCP/IP protocol for
communication via Java sockets. The measurements were taken as the average of
was 1024 and 160 bits, respectively.
Both Alice and Bob used Intel 2.4 GHz Linux machines.
The system was implemented in Java, and it used the TCP/IP protocol for
communication via Java sockets. The measurements were taken as the average of
![]() repetitions (
repetitions (![]() for the Median function) of the protocol. All iterations
used a single TCP/IP connection, which was established in the beginning.
for the Median function) of the protocol. All iterations
used a single TCP/IP connection, which was established in the beginning.
![]() .
.
![]() type declarations
type declarations![]() segment.
The syntax is standard, e.g.:
segment.
The syntax is standard, e.g.: